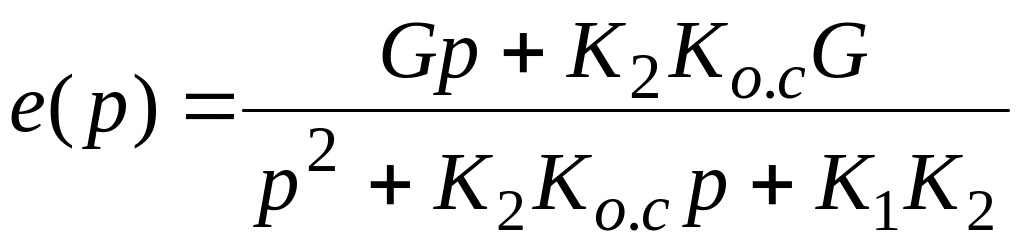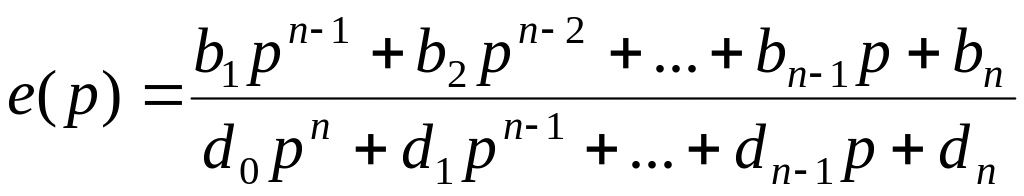Основные правила написания математических формул
1
Излагая математические выводы, не
рекомендуется использовать выражения:
«мы получили», «мы нашли», «определили»,
«получится», «выразится в виде», «будем
иметь» и т.п. Следует употреблять слова:
«получаем», «определяем», «находим»,
«преобразуем к виду» и т.д.
Связывающие формулы
слова «следовательно», «откуда»,
«поскольку», «так как», «или» и другие
располагают в тексте пояснительной
записки в начале строк, а знаки препинания
ставят на продолжении основной строки
формулы непосредственно за формулой.
Например:
Характеристическое
уравнение преобразуем к виду
.
Подставляя
,
получим
,
откуда находим
,
.
Следовательно,
;
.
Если в математических
выводах формулам предшествуют причастные
или деепричастные обороты, а также фразы
с обобщающим словом, то после них
необходимо ставить двоеточие. Например:
– Подставляя выражение (3.6) в уравнение
(3.2), получим:
.
– Из равенства (2.12) находим следующее
соотношение:
.
2
Математические формулы должны быть
вписаны отчетливо с точным размещением
знаков, цифр и букв. Каждую букву в
формулах и обозначениях необходимо
записывать в точном соответствии с
алфавитом, которому она принадлежит, и
с правилами написания строчных и
прописных букв. Образцы букв приведены
в приложении
Г. На
протяжении всей пояснительной записки
необходимо соблюдать в формулах следующие
размеры: 3-4 мм для строчных и 6-8 мм для
прописных цифр и букв. Все индексы и
показатели степени должны быть в 1,5-2
раза меньше по размерам буквенных
обозначений, к которым они относятся.
Знаки сложения,
вычитания, корня, равенства и т.д.
необходимо вписывать так, чтобы их
середина была расположена строго против
горизонтальной черты дроби.
3
Формулы, как правило, располагают на
отдельных строках симметрично тексту
пояснительной записки. Формулы должны
быть отделены от текста пробельными
строками. На рисунке 2.2 приведены примеры
расположения формул с указанием
расстояний между строками текста.
Рекомендуются
следующие межтекстовые промежутки для
вписывания формул:
– 24 мм
или 6 интервалов при машинописном способе
для простейших однострочных формул, в
которых отсутствуют знаки Σ, Π, ∫ и
т.п.;
– 32 мм или 8
интервалов для однострочных формул,
содержащих знаки Σ, Π, ∫ и т.п.;
– для формул,
содержащих две строки и более, а также
для сложных формульных выражений
межтекстовые промежутки необходимо
вычислять, используя рекомендации
пункты 2.4.2 и 2.4.3.
4
Короткие однотипные формулы разрешается
располагать на одной строке. В этом
случае их разделяют точкой с запятой.
Например:
Координаты x1
и x2
определяем по известным величинам X
и Y:
;
.
Пробельная
строка
24 мм (6 интервалов)
Пробельная
строка
Пробельная
строка
Пробельная
строка
32 мм (8 интервалов)
Пробельная
строка
Пробельная
строка
32 мм (8 интервалов)
Пробельная
строка
Пробельная
строка
48 мм (12 интервалов)
Рисунок 1 – Размеры
формул и их расположение между строками
текста пояснительной записки (к
пункту 3)
Несложные и короткие
формулы промежуточных и вспомогательных
выражений можно располагать непосредственно
в строке текста. Причем разрешается
увеличивать расстояние между строками
текста. Например:
Так как добротность системы
,
то на критической частоте
коэффициент усиления разомкнутой
системы
.
Следовательно, запас устойчивости по
усилению
.
5
При написании математических выражений
допускается перенос на следующую строку
самостоятельных членов формул. Причем
знак операции, на котором сделан перенос,
пишут два раза – в конце первой и в
начале второй строки. При переносе
формулы на знаке умножения применяют
знак «×».
Не допускаются
переносы на знаке деления, а также
выражений, относящихся к знакам корня,
интеграла, логарифма, тригонометрических
функций и т.п.
6
Все формулы, расположенные в отдельных
строках, нумеруют. Одним номером отмечают
также группу однотипных формул,
размещенных на одной строке.
Формулы рекомендуется
нумеровать в пределах раздела, которому
они подчинены. Цифровой индекс номера
формулы должен состоять из порядкового
номера раздела и отделенного от него
точкой порядкового номера формулы в
разделе, например: формула (2.7). Если в
разделе одна формула, ее также нумеруют,
например: формула (1.1).
Если в пояснительной
записке формул не очень много и в одних
разделах нет ссылок на формулы в других
разделах, то разрешается применять
сквозную нумерацию формул.
Формулы, помещаемые
в приложения, должны иметь отдельную
нумерацию в пределах каждого приложения.
Вначале указывают обозначение приложения,
затем ставят точку и приводят порядковый
номер формулы в данном приложении,
например (Б.2).
7
Порядковый номер формулы записывают
арабскими цифрами в круглых скобках у
правого края страницы. Причем номер
однострочной формулы располагают на
продолжении строки, занимаемой формулой.
При переносе
формулы с одной строки на другую номер
располагают на продолжении последней
строки.
Номер сложной
формулы (в виде дроби) записывают так,
чтобы середина номера располагалась
на уровне черты дроби.
Ссылки в тексте
пояснительной записки на порядковый
номер формулы следует приводить в
круглых скобках с обязательным указанием
слова «формула», «уравнение», «выражение»,
«равенство», «передаточная функция» и
т.д. Например:
Подставляя выражение
(3.6) в уравнение (3.2), получаем:
После формулы
следует помещать перечень тех примененных
в формуле символов и числовых коэффициентов,
которые не были ранее пояснены в тексте,
и расшифровать их значения. Причем
символы и числовые коэффициенты
необходимо отделять от их расшифровок
знаком тире, по которому выравнивают
перечень.
Каждую расшифровку
отделяют от последующего символа или
числового коэффициента в перечне точкой
с запятой. Размерность символа или
коэффициента указывают в конце расшифровки
и отделяют от текстовой части расшифровки
запятой.
Перечень начинают
со слова «где», которое для формул,
выделенных в отдельные строки, необходимо
записывать с новой строки без абзацного
отступа и в этой же строке после слова
«где» приводить первый поясняющий
символ. После слова «где» двоеточие не
ставят. Например:
При разгоне механизма до скорости
быстрого хода двигатель должен развивать
динамический момент Mдин,
Hм, который определяем по
формуле
,
(2.7)
где 1,2 – коэффициент, учитывающий
приведенный момент инерции редуктора;
– момент инерции двигателя, кг·м2;
– приведенный к валу двигателя момент
инерции механизма, кг·м2;
– ускорение вала двигателя, с–2.
Расшифровку
символов и числовых коэффициентов можно
начинать со слова «здесь». В этом случае
после формулы следует ставить точку, а
слово «здесь» писать с прописной буквы.
Например:
.
Здесь 1,2 – коэффициент, и т.д., как в
предыдущем примере.
Разрешается
расшифровку начинать с обобщающей
фразы, после которой следует ставить
двоеточие, а каждый поясняемый символ
и числовой коэффициент начинать с
красной строки. Например:
В формуле (2.7) обозначено:
1,2 – коэффициент, учитывающий, и т.д.
КАЛЕНДАРНЫЙ ПЛАН
МЕРОПРИЯТИЙ ПО ОРГАНИЗАЦИИ
И ПРОВЕДЕНИЮ
КУРСОВОГО ПРОЕКТИРОВАНИЯ В БГУИР
|
Наименование мероприятия |
Срок исполнения |
Ответственные за |
|
1 |
2 |
3 |
|
1. Разработка тематики курсовых |
До начала учебного семестра, в котором |
Заведующие кафедрами |
|
2. Выдача студентам заданий по курсовому |
Дневная и вечерняя формы обучения Осенний Весенний 1–3 4–5 Заочная Выдача Представление Осенний Весенний семестр – |
Руководители курсовых проектов (работ) |
|
3. Представление информации в деканаты 1-я контрольная точка |
Для всех форм обучения Осенний Весенний |
Руководители курсовых проектов (работ) |
|
4. 2-я контрольная точка |
Для всех форм обучения Осенний Весенний |
Руководители курсовых проектов (работ) |
|
5. 3-я контрольная точка |
Для всех форм обучения Осенний Весенний |
Руководители курсовых проектов (работ) |
|
6. Представление студентами готовых |
Дневная и вечерняя формы обучения Осенний 1–3 4–5 Весенний 1–3 4 Заочная Не Дистанционная Не |
Студенты первой ступени высшего |
|
1 |
2 |
3 |
|
7. Представление информации в деканаты |
Дневная и вечерняя формы обучения Осенний 1–3 4–5 Весенний 1–3 4 Заочная За три дня до начала |
Руководители курсовых проектов (работ) |
|
8. Защита студентами |
Дневная и вечерняя формы обучения Осенний 1–3 4–5 Весенний 1–3 4 Заочная В Дистанционная В |
Заведующие кафедрами, руководители |
|
9. Представление информации в деканаты |
Дневная и вечерняя формы обучения Осенний 1–3 4–5 Весенний 1–3 4 Заочная За один день до |
Заведующие кафедрами, руководители курсовых |
Приложение
А
Пример
оформления задания по курсовому проекту
(работе)
(к
пункту 2.7)
Учреждение
образования
«Белорусский
государственный университет информатики
и радиоэлектроники»
Факультет
информационных технологий и управления
УТВЕРЖДАЮ
Заведующий кафедрой
––––––––––––––––––––––––
(подпись)
–––––––––––––––––––––––––201
г.
ЗАДАНИЕ
по курсовому
проектированию
Студенту
Успенскому
Эдуарду Алексеевичу–––––––––––––––––––
1. Тема
проекта Комплекс
устройств телемеханики для
территориально-распределённых
объектов––––––––––––––––––––––– –– ––––
2. Срок
сдачи студентом законченного проекта–––––XX
***** 20XХ
г.–––––
3. Исходные
данные к проекту
Число
КП – 99; число сообщений ТС с КП – 120;
число сообщений ТИН с ПУ – 120; тип объекта
управления – двухпозиционный; число
кодовых команд задания установок
регуляторам – 48; расположение объектов
– территориально-распределённое; вся
информация, поступающая на ПУ, должна
вводиться в ЭВМ; защита сообщений ТС,
ТИИ, ТУ и КК – кодом с двухкратным
повторением и дополнительной защитой
каждого байта кодом с защитой по паритету;
защита сообщений ТИТ и ПСИ – кодом с
защитой по паритету; все адреса,
передаваемые с ПУ на КП, защищаются
информационной обратной связью;
сигнализация неисправности оборудования
и линии связи – после трёхкратного
сбоя; удельная мощность шума Po = 10–2
Вт/Гц; регистрирующие устройства –
аналоговые и
цифровые––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– —–––
4.
Содержание
расчетно-пояснительной записки (перечень
вопросов, которые подлежат разработке)
Введение.
1. Выбор структуры системы, линии связи
и структуры сигналов._______
2.
Алгоритм функционирования системы.
3. Разработка структурной схемы
системы. 4. Расчёт частотных и временных
параметров. 5. Выбор и энергетический
расчёт линии связи. 6. Выбор элементной
базы системы. 7. Проектирование
принципиальной электрической схемы
системы. 8. Системные расчёты: скорости
передачи сообщений, пропускной способности
канала связи
спектра сигнала в линии связи, расчёт
помехоустойчивости, расчёт надёжности.
9. Разработка программного обеспечения.
Заключение
5.
Перечень графического материала (с
точным
обозначением
обязательных
чертежей
и
графиков)
1. Схема алгоритма
работы системы
––––––––––––––––––––––––––––––
2. Схема
электрическая
структурная––––––––––––––––––––––––––––––––––
3. Схема
электрическая
принципиальная––––––––––––––––––––––––––––––––
––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
6.
Консультант по проекту (с
обозначением
разделов
проекта) Крупский
А.
М.–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– –
7.
Дата выдачи задания –––––XX
хххххххх 20ХX
г.––––––––––––––––––––––– –
8.
Календарный график работы над проектом
на весь период проектирования (с
обозначением
сроков
выполнения
и
трудоемкости
отдельных
этапов):
разделы 1,2 к xx
xx
– 15 %;–––––––––––––––––––––––––––––––––––––––
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
11.05.2015180.21 Кб57рупорная.xmcd
- #
- #
- #
Содержание:
- § 1 Правило нахождения пути по скорости и времени (формула пути)
- § 2 Формула нахождения периметра прямоугольника
- § 3 Формула периметра квадрата
§ 1 Правило нахождения пути по скорости и времени (формула пути)
В этом уроке Вы познакомитесь с таким понятием как формула. Научитесь составлять формулы и решать по ним различные задания.
Давайте рассмотрим задачу № 1:
Велосипедист-любитель, двигаясь по дороге на своем велосипеде со скоростью 14 километров в час, заметил, что находился в пути ровно 3 часа. Какой путь преодолел велосипедист?
Решение:
Чтобы узнать, сколько километров преодолел велосипедист, надо умножить его скорость на время пути, т.е. найти произведение:
Ответ: Велосипедист преодолел 42 км.
Запишем правило нахождения пути по скорости и времени движения в буквенном виде.
Для этого обозначим путь латинской буквой S, скорость буквой V, и время буквой t.
Получим равенство: S = Vt
Оно читается так: расстояние равно время умножить на скорость.
Это равенство называют формулой пути.
Таким образом, получили определение:
Запись какого–либо правила с помощью букв называют формулой.
Давайте рассмотрим еще несколько видов задач, которые можно решить с помощью формулы пути.
Задача № 2:
Скорость автобуса, осуществляющего междугородний рейс равна 80 км/ч.
За какое время он преодолеет путь в 640 километров?
Решение:
Заменим в формуле пути (S = Vt) буквы S и V их значениями, т.е. 640 и 80, тем самым получим уравнение: 640 = 80 t.
Значит, чтобы проехать 640 км автобус должен двигаться 8 часов.
Ответ: за 8 часов.
Задача № 3:
Группа туристов должна преодолеть участок пути протяженностью 30 километров до конца дня, т.е. за 5 часов.
С какой скоростью им следует двигаться?
Решение:
Заменим в формуле пути (S = Vt) буквы S и t их значениями 30 и 5.
Решив уравнение, получим V = 6.
Значит, туристы должны двигаться со скоростью 6 километров в час.
Ответ: 6 км в час.
§ 2 Формула нахождения периметра прямоугольника
А теперь, рассмотрим формулу для нахождения периметра прямоугольника.
Для ее записи обозначим длину прямоугольника латинской буквой а, ширину – буквой b. Сам периметр принято обозначать буквой Р.
Так как периметр прямоугольника – это сумма длин всех его сторон, то
Решим задачу:
Найдите периметр прямоугольника со сторонами 7 и 5 сантиметров.
Решение:
Периметр P = 2(а + в).
Подставим вместо а и b значения 7 и 5, получим P = 2(7 + 5), т.е. P = 2 умножить на 12, равно 24.
Ответ: Периметр прямоугольника – 24 см.
§ 3 Формула периметра квадрата
Рассмотрим еще одну формулу – формулу периметр квадрата.
Для ее записи обозначим длину стороны квадрата латинской буквой а, сам периметр снова обозначим буквой Р.
Так как периметр квадрата – это сумма длин всех его сторон, то Р = а + а + а + а = 4а.
Задача:
Найдите периметр квадрата со стороной 7 см.
Решение:
Подставляем в формулу Р =4а значение а=7, т.е. 4 умножить на 7 будет 28.
Ответ: периметр квадрата – 28 сантиметров.
Таким образом, в этом уроке Вы познакомились с таким понятием как формула. Научились составлять формулы и решать по ним различные задачи.
Список использованной литературы:
- Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. — М: 2013.
- Дидактические материалы по математике 5 класс. Автор — Попов М.А. – 2013.
- Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор — Минаева С.С. – 2014.
- Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. – 2010.
- Контрольные и самостоятельные работы по математике 5 класс. Авторы — Попов М.А. — 2012.
- Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009.
Правила обозначения действий для математической формулы
Символическая запись логического суждения (законченного) — это и есть не что иное, как математическая формула, применяемая также и в прикладных науках для осуществления расчетов, приведения в соответствие различных величин.
Составлять подобные выражения часто требуется в процессе обучения, написания важных научных работ, а некоторым даже в рамках профессиональной деятельности.
И если с буквенными и числовыми обозначениями все понятно, то вот с «маркировкой» действий иногда возникают проблемы. Каждый из символов имеет право на существование. Но, вместе с этим, использование различных знаков для одного и того же действия в рамках одной работы (контрольной, дипломной, курсовой и т. д.) недопустимо.
Поэтому разграничим области для каждого такого «значка».
Вычитание и сложение
Здесь все относительно просто. Для обозначения действий используются знаки «+» и «-«, которые в большинстве случаев связывают 2 слагаемых (так называют аргументы не только для операции сложения, но и вычитания).
Однако, иногда существует необходимость приписывания унарного (одиночного) знака «-» перед первой переменной (или численным значением) в формуле. Таким образом, с него может начинаться запись математической формулы.
Знак умножения при составлении формулы по математике
- Отсутствие символа. Если данный способ обозначения операции умножения двух буквенных обозначений (или выражений, стоящих в скобках) не даст двусмысленности, то он допустим.
- «•» — точка, центрированная вверху. Общепринятое обозначение.
- «*» — звездочка. Не всегда разрешается к использованию в формулах, лучше вместо нее использовать точку.
- Знак «$times$» ориентирован на школьную программу по математике, обозначение специальных операций в высшей математике (например, векторное умножение), а также некоторые технические описания. Применяется «крестик» и в случае переноса формул по математике на другую строку.
Деление в математических формулах
- Знак «:» используется при составлении учебников и методической литературы для школьной программы по арифметике.
- Черта — «/» (знак дроби) чаще используется в специализированной математической литературе, а также при проведении расчетов в технических областях.
Возведение в степень
- ху — первое обозначение, которое и сегодня является наиболее популярным. Его можно использовать как при составлении выражений на бумаге, так и в современных компьютерных редакторах.
- «^» — знак, пришедший из языка программирования Basic. Он используется для маркировки степени числа в компьютерных программах, которые не поддерживают первый формат. Например, х^у — выражения для MS Excel.
- Прочие метки вроде «^^» и «**» не прижились и используются крайне редко.
К правильному обозначению формул по математике стоит привыкать с самого начала. Нужно знать все способы обозначения действий, а также сферу их использования. И тогда при изучении любой профильной литературы, а также самостоятельном написании формул не возникнет никаких проблем.
Нужно решение задач? Обязательно поможем
Формула

4.6
Средняя оценка: 4.6
Всего получено оценок: 87.
4.6
Средняя оценка: 4.6
Всего получено оценок: 87.
Формула – это одно из важнейших понятий в математике. Основные формулы облегчают расчет и экономят время при решении уравнений. Поговорим о том, что такое формула, откуда они берутся и выделим основные формулы математики.
Что это такое?
Формула – это всегда равенства. С левой стороны находится выражение, которое можно преобразовать, а с правой результат преобразования. Правильно использованная формула позволяет пропустить ряд действий, сохранив при этом правильный результат.
Формулу можно использовать в обе стороны. В геометрии это называют обратным действием, но чаще говорят просто: свернуть. Если выражение из левой части формулы превращается в правую, про него говорят, что свернули по формуле. Если наоборот: раскрыли скобки.
Посмотрим на примере. Воспользуемся формулой квадрата суммы: $(a+b)^2=a^2+2*ab+b^2$.
Имеется следующее выражение: $(2a+7b)^2=(2a)^2+2*(2a)*(7b)+(7b)^2=4a^2+28ab+49b^2$ – вот мы и раскрыли скобки по формуле квадрата суммы. Если нам потребуется конечное выражение превратить в начальное, то это будет уже обратное действие формулы.
Основные формулы математики
Основными формулами математики считаются формулы быстрого умножения. Их не так много, поэтому лучше все заучить наизусть. Всего формул семь, каждая из них была выведена, для облегчения счета. Заучивают формулы в 4 этапа.
- Первыми идут формулы суммы и разности квадратов. Формулу суммы мы уже знаем.
$$(a+b)^2=a^2+2ab+b^2$$
Квадрат разности не сильно отличается.
$$(a-b)^2=a^2-2ab+b^2$$
Знак минуса вполне логичен, и его достаточно просто запомнить.
- Следующими запоминают куб суммы и куб разности. Они учатся быстрее, просто запоминаясь по аналогии.
$$(a+b)^3=a^3+3a^2*b+3a*b^2+b^3$$
$$(a-b)^3=a^3-3a^2*b+3a*b^2-b^3$$
- Дальше идут формулы суммы и разности кубов, а так же разность квадратов. Разность квадратов записывается достаточно легко.
$a^2+b^2=(a+b)(a-b)$ – а вот формулы суммы квадратов нет. В начале курса 5 класса по математике ученики очень часто путаются формулы квадрата разности и разности квадратов. Попробуем научиться их различать.
Что такое разность квадратов? Это два числа в квадрате, из одного вычитается другое. А что такое квадрат разности? Из одного числа вычли другое, а результат возвели в квадрат. Достаточно один раз запомнить, а лучше понять, это объяснение и проблем с этими двумя формулами не будет никогда.
- Следующими и последними идут формулы суммы и разности кубов. Они немного сложнее и для облегчения их запоминания придумали понятие неполного квадрата суммы и неполного квадрата разности.
Вспомним формулу квадрата суммы.
$$(a+b)^2=a^2+2ab+b^2$$
Обратим внимание на вторую часть.
$$a^2+2ab+b^2$$ – это и называется полным квадратом суммы. А неполным называется выражение:
$$a^2+ab+b^2$$. Это легко запомнить. По аналогии неполный квадрат разности: $a^2-ab+b^2$.
Теперь приведем формулы суммы и разности кубов.
$$a^3+b^3=(a+b)( a^2-ab+b^2)$$ – сумма кубов это произведение суммы чисел на неполный квадрат разности этих чисел.
$$a^3+b^3=(a-b)( a^2+ab+b^2)$$ – разность кубов это произведение разности чисел на квадрат суммы этих чисел.
Как показывает практика, последние две формулы проще запомнить в словесной форме. К тому же эти формулы часто встречаются при решении простых уравнений. Поэтому, дабы не бежать каждый раз в интернет – проще их запомнить.
Что мы узнали?
Мы дали определение понятию формулы, привели основные формулы математики и обозначили, что формулой можно пользоваться в обе стороны от знака равенства.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 87.
А какая ваша оценка?
Как написать математическую формулу
Наиболее распространенное сегодня компьютерное средство создания и редактирования текстовых документов — текстовый процессор Microsoft Word из офисного пакета программ от производителя ОС Windows. Начиная с версии 2007, это приложение в базовой конфигурации имеет набор инструментов для помещения в текст математических формул. В более ранних версиях соответствующую надстройку было нужно устанавливать дополнительно.

Инструкция
Запустите текстовый процессор, загрузите в него документ, в который требуется поместить математическую формулу, и установите курсор ввода в нужную позицию текста.
Начиная с версии 2007, стандартный интерфейс текстового процессора имеет два меню. Одно из них открывается щелчком по большой круглой кнопке, которую Microsoft назвал Office, а другое помещается над страницей открытого документа и в русском переводе документации названо производителем «лентой». Перейдите в раздел «Вставка» этой самой ленты и в секции «Символы» кликните по пиктограмме «Формула». Если вы попадете по помещенной у ее правого края метке, то раскроете список с набором наиболее употребительных, по мнению Microsoft, формул и сможете выбрать одну из них. Если же щелкните пиктограмму ближе к центру, то запустите редактор формул.
Выберите в наибольшей степени соответствующий вашей формуле вариант изо всех размещенных в секции «Структуры» раздела «Конструктор» на ленте Word. Этот раздел по умолчанию отсутствует и появляется лишь при редактировании формул. Если на предыдущем шаге вы выбрали один из вариантов в списке по умолчанию, то формула в тексте уже будет заполнена соответствующими обозначениями и выбирать структуру будет не нужно. Этим списком по умолчанию можно воспользоваться и сейчас — кнопка продублирована в секции «Сервис» раздела «Конструктор».
Выделите любой знак в формуле, если его требуется изменить. После этого вы можете выбрать вариант замены в секции «Символы» раздела «Конструктор». Щелчок по правой нижней кнопке на полосе прокрутки в этой секции открывает выпадающий список, верхняя строка которого в свою очередь содержит выпадающий перечень групп символов (греческие буквы, операторы, математические символы и т.д.).
Щелкните созданную формулу, чтобы вновь включить конструктор формул, если впоследствии возникнет необходимость внести в нее изменения.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.