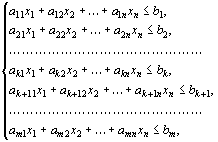Двойственная задача линейного программирования
Время на прочтение
9 мин
Количество просмотров 27K

Обычно с задачей линейного программирования (ЗЛП) связана другая линейная задача, называемая двойственной. Обе эти задачи можно считать двойственными одну по отношению к другой, считать равносильными. Первая задача называется обычно исходной, или прямой, другая — обратной. Переменные, используемые в двойственной задаче называются двойственными или множителями Лагранжа. На них не накладывается ограничений по знаку. Рассматриваются двойственные критерии оптимальности. Специальные случаи называют симметричными двойственными задачами линейного программирования. Связь между оптимальными решениями двойственных задач устанавливается теоремой двойственности.
Теорема двойственности
Важнейшие свойства пары двойственных задач математического программирования сформулированы в трех основных теоремах.
Теорема двойственности
Допустимый вектор решения прямой задачи программирования оптимален тогда и только тогда, когда существует такой допустимый вектор решения двойственной задачи, что целевые функции прямой и двойственной задачи равны. Допустимый вектор двойственной задачи оптимален тогда и только тогда, когда существует допустимый вектор прямой задачи и целевые функции обеих задач равны.
Теорема существования решения
Если существуют допустимые векторы решений прямой и двойственной задач, то обе задачи имеют оптимальные векторы. Если одна из двух задач не имеет допустимого вектора, то ни одна из них не имеет оптимального вектора решения.
Теорема (принцип) дополняющей нежесткости
-
Если (xQ , xL) – оптимальное решение прямой задачи, а (yQ, yL) – решение двойственной задачи, то (xQ , xL, yQ , yL) – решение задачи Лагранжа. В частности, в этом случае удовлетворяются соотношения между переменными прямой и двойственной задач и условия дополняющей нежесткости.
-
Оптимальное решение прямой задачи программирования получается только при одном значении xQ. Это справедливо и для переменной yQ в двойственной задаче.
Теоремы двойственности
Основное неравенство двойственности. Для любых допустимых решений Х<n> и Y<n>пары двойственных ЗЛП имеет место неравенство
Экономически это означает, что для любого допустимого плана производства и любого дополнительного вектора оценок ресурсов (на складе) стоимость изготовленного продукта не превосходит оценки ресурсов.
Теорема существования (малая тероема двойственности)
Чтобы прямая и двойственная задачи имели opt решения, необходимо и достаточно, чтобы существовали допустимые решения для каждой из них.
Теорема 1 двойственности.
Если одна из пары двойственных задач имеет opt решение, то и другая его имеет. Причем экспериментальные решения их целевых ф. равны; если же ЦФ одной из задач не ограничена, то система ограничений другой противоречива. Интерпретация: оптимальное использование ресурсов – opt план. Суммарная оценка ресурсов = оценке продукта полученного при opt плане. Любой другой план не рентабелен. Cj – стоимость единицы продукции (внешняя оценка) yi – стоимость единицы ресурса (внутренняя оценка). Эти двойственные оценки выступают как инструменты балансирования затрат и результатов. Имеет место xj <-> ym +j ; xn+i <-> yi.
Теорема 2 двойственности (о дополняющей нежесткости)
Для того, чтобы допустимые решения X и Y пары двойственных задач были оптимальными, необходимо и достаточно выполнить условия:
То есть, если какое-либо ограничение одной ЗЛП обращается ее opt планом в строгое равенство, то соответствующая переменная двойственной задачи в ее opt плане равна нулю; если же какая-либо переменная opt-го решения одной ЗЛП положительна, то соответствующее ограничение в двойственной ЗЛП ее opt планом обращается в точное равенство.
Теорема Кёнига хорошо иллюстрирует использование принципа двойственности ЗЛП.
Формулирование теоремы. Максимальное число попарно неколлинеарных единиц любой булевой матрицы равно минимальному числу линий, покрывающих все единицы матрицы.
Доказательство. Для нахождения максимального числа попарно неколлинеарных единиц булевой матрицы достаточно сформулировать и решить линейную задачу:
Минимальное число линий, покрывающих все единицы матрицы [Cij], найдем, решив линейную задачу:
Оптимальному решению (u*i, v*j) последней задачи отвечает минимальное покрытие, состоящее из множества строк I, для которых u*i = 1 и столбцов J, для которых u*j =1.
Матрицы А и АТ коэффициентов (*), (**), (***) являются абсолютно унимодулярными, как матрицы двудольного графа. Поэтому условия целочисленности переменных заменяем на условие их неотрицательности, и тогда получаем пару двойственных задач линейного программирования и согласно теореме двойственности имеем:
Линией матрицы называется ее строка или столбец. Два элемента матрицы называются неколлинеарными, если они не лежат на одной линии.
Матрица называется абсолютно унимодулярной, если все ее ненулевые миноры равны 1, либо -1.
Следствие. Матрица инциденций неориентированного графа G абсолютно унимодулярна тогда и только тогда, когда G – двудольный граф. В двудольном графе все простые циклы имеют четкую длину
Принцип двойственности в задачах линейного программирования.
Предположим, что руководство предприятия из анализа конъюнктуры рынка продукции приняли решение: производство сократить, а от запасов сырья избавиться, (продать на рынке) и при этом не нанести себе убытков.
С этой целью руководство должно назначить стоимости yi за единицу сырья вида Si, стремясь при этом минимизировать общую стоимость сырья (чтобы быстрее продать сырье): Ф = Σ4i=1 biyi
Выручка предприятия от продажи сырья, расходуемого на единицу продукции Пi, составит: Σ4i=1 aij yi
И по условию она не должна быть меньше Сj (в противном случае предприятию выгоднее не продавать сырье, а использовать его для нужд производства, выпуска продукции).
Сформулируем исходную и двойственную задачи:
Обе задачи по отношению друг к другу называются двойственными или сопряженными. Анализ таблицы позволяет сделать выводы:
-
Если первая задача сформулирована на поиск максимума, то вторая формулируется на поиск минимума линейной функции.
-
Коэффициенты ЦФ первой задачи являются свободными членами системы ограничений второй.
-
Свободные члены системы ограничений первой задачи являются коэффициентами линейной системы во второй задаче.
-
Матрица коэффициентов второй задачи является транспонированной к матрице коэффициентов ограничений первой задачи.
-
Знаки неравенств в ограничениях второй задачи противоположны знакам неравенств в ограничениях первой задачи.
Оптимальный план Xopt<n> одной из задач тесно связан с оптимальным планом Yopt<n> другой. Если одна из задач имеет решение, то другая также разрешена, причем для оптимальных клонов Xopt<n> =<x1, x2,…xn> и Yopt<m> =<y1, y2,…ym> справедливо равенство Q( Xopt ) =Q’( Yopt ). Если линейная форма одной из задач неограниченна, то условия другой задачи несовместны. Если A-1 обратная матрица к матрице В, состоящей из векторов базиса оптимального плана исходной задачи, то оптимальный план двойственной задачи равен Yopt<m> =СВ -1, здесь С – вектор базисных переменных. Решение двойственной задачи получается в последней симплексной таблице исходной задачи, в (m+1) строке, в столбцах, соответствующих дополнительным параметрам.
Для того чтобы векторы Xopt<n> =<x1, x2,…xn> и Yopt<m> =<y1, y2,…ym> были решениями пары задач, необходимо и достаточно, чтобы их компоненты удовлетворяли следующим условиям:
Эти условия называют принципом дополняющей нежесткости. Если исходная (прямая) задача задана в канонической форме, то двойственная к ней называется несимметричной. Для несимметричной двойственной задачи соблюдается условие yi ≥ 0.
Теория ЗЛП доказывает, что компоненты оптимальных планов взаимно двойственных задач, приведенных к каноническому виду, соответствуют одни другим. То есть базисные переменные основной задачи соответствуют свободным переменным двойственной задачи и наоборот, j = 1(1)n, x*j y*m +j ; x*n+i y*i ; i = 1(1)m.
Размерности в табличке m и n берутся в задаче для y-ков записанной в канонической форме.
Пример. Двойственный симплекс метод.
Исходная задача. Имеется три вида продуктов Пj, причем единица веса каждого из видов продуктов содержит aij единиц (питательных веществ). Для нормальной жизнедеятельности человек должен потреблять не менее bi единиц вещества Bi в сутки. Стоимость единицы продукта Пj равняется Cj. Требуется составить оптимальный суточный рацион питания, т.е. найти количество xj продукта, которое должен потреблять человек, чтобы стоимость питания была бы минимальной, если известно, что
такие значения его компонентов xj, j = 1(1)3, которые минимизируют целевую функцию (Ц) Q = 3x1 + 2x2 + x3 и удовлетворяют ограничениям неравенствам
0,3x1 + 0,2x2 + 0, 4x3 ≥ 0,2;
0,4x1 + 0,3x2 + 0,45x3 ≥ 0,5;
0,2x1 + 0,3x2 + 0, 1 x3 ≥ 0,6;
0,1x1 + 0,2x2 + 0,05x3 ≥ 0,1;
xj ≥ 0; j = 1(1)3 = n
Для приведения задачи к каноническому виду введем дополнительные переменные x4, x5, x6, x7, переменных стало больше чем уравнений n – m = 7 – 4 = 3, следовательно, части из них (трем любым,) для получения решения можно задать произвольные значения (задают, как правило, нулевые значения), возникает число сочетаний из n по m вариантов. Система ограничений примет вид равенств
0,3x1 + 0,2x2 + 0,4x3 – x4 = 0,2;
0,4x1 + 0,3x2 + 0,45x3 – x5 = 0,5;
0,2x1 + 0,3x2 + 0,1x3 – x6 = 0, 6;
0,1x1 + 0,2x2 + 0,05x3 – x7 = 0, 1;
xj ≥ 0; j = 1(1)3 = n, i = 1(1)4 = m.
Назначаем опорный план. Выбор в качестве базисных переменных x4, x5, x6, x7 приводит к недопустимому опорному плану. Так как знаки левой и правой частей различны. (Свободные переменные x1 = x2 = x3 = 0) Метод искусственного базиса приводит к увеличению числа неизвестных задач, что нежелательно. Анализ задачи показывает, что число уравнений в системе ограничений больше числа переменных. Поэтому попытаемся применить принцип двойственности, т.е. вначале решим двойственную ЗЛП, а затем найдем решение исходной.
Двойственная задача. Коэффициентами линейной формы в двойственной задаче выступают правые части bi , i = 1(1)4 = m, исходной основной задачи. Переменные получают другие имена y1, y2, y3, y4, и формулируется двойственная задача иначе. Найти максимум линейной формы Q’:
Q’=0,2y1 + 0,5y2 + 0,6y3 + 0,1y4;
при ограничениях
0,3y1 + 0, 4y2 + 0,2y3 + 0,1y4 ≤ 3;
0,2y1 + 0, 3y2 + 0,3y3 + 0,2y4 ≤ 2;
0,4y1 + 0,45y2 + 0,1y3 + 0,05y4 ≤ 1;
yi ≥ 0; i = 1(1)4.
Приведем задачу к каноническому виду, вводим дополнительные неотрицательные переменные y5 , y6 , y7 :
Найти минимум ЦФ (знаки у коэффициентов ЦФ поменяли на противоположные): Q’= — 0,2y1 — 0,5y2 — 0, 6y3 — 0,1y4;
при ограничениях (в ограничения добавили новые переменные):
0,3y1 + 0, 4y2 + 0,2y3 + 0, 1y4 + y5 = 3;
0,2y1 + 0, 3y2 + 0,3y3 + 0, 2y4 + y6 = 2;
0,4y1 + 0,45y2 + 0,1y3 + 0,05y4 + y7 = 1,
yi ≥ 0; i = 1(1)7.
Задача решается симплекс методом. Исходный опорный план в качестве переменных может иметь y5, y6, y7 и свободные переменные y1 = y2 = y3 = y4 = 0, т.е. Y<7> = [0, 0, 0, 0, 3, 2, 1] .
Базисные переменные y5, y6, y7 и ЦФ выражаем через свободные переменные, т.е. из свободных членов (правых частей, обозначенных γi ) вычитаем левые части ограничений
y5 = 3 – (0,3y1 + 0,4y2 + 0,2y3 + 0,1y4);
y6 = 2 – (0,2y1 + 0,3y2 + 0,3y3 + 0,2y4);
y7 = 1 – (0,4y1 + 0,45y2 + 0,1y3 + 0,05y6);
Q’1=γ0 — Σ4i=1 γi yi = 0 -(0,2y1 + 0,5y2 + 0, 6y3 + 0,1y4);
γ0 =0, так как ЦФ не содержит свободного члена.
и строим симплекс таблицу с двумя полуклетками. Направляющий столбец y3, направляющая строка y6.
Анализ таблицы показывает, что все коэффициенты ЦФ при свободных переменных положительны. Следовательно, план Y<7> не является оптимальным, ЦФ можно уменьшить, увеличивая значения соответствующих свободных переменных.
Находим γ = max{γi} =max {0,2; 0,5; 0,6; 0,1} = 0,6. Переменную y3 надо ввести в базис. После этого устанавливаем, существует ли оптимальный план. В направляющем столбце все коэффициенты положительны, следовательно, оптимальный план существует. В базисе есть переменные, которые можно уменьшать до нуля увеличивая значения y3, тем самым минимизируя ЦФ. Раньше других в нуль обратиться переменная y6 и ее исключаем из базиса.
После замены переменных в базисе переходим к новой симплексной таблице.
Анализ этой таблицы показывает, что все коэффициенты в выражении ЦФ свободных переменных отрицательны. Следовательно, опорный план Y<7>= [0, 0, 20/3, 0, 5/3, 0, 1/3] является оптимальным. ЦФ при этом Q’1 = — 4 достигла наименьшего значения. Возвращаемся к двойственной задаче. Используя соответствие между оптимальными планами двойственных задач ЛП, определяем: базисными переменными в оптимальном плане будут x2 x4 x5 x7; их значения с противоположным знаком записаны в последней строке таблицы. Таким образом, Xopt<n> =<0; 2; 0; 0; 2; 0; 1; 0; 1/30>, т.е. оптимальный рацион из двух единиц продукта П2. Стоимость такого рациона минимальна и составляет 4 единицы. Это значение с противоположным знаком записано в той же таблице.
Литература
-
Ваулин А. Е. Методы цифровой обработки данных.– СПб.: ВИККИ им. А. Ф. Можайского, 1993.– 106 с.
-
Гэри М., Джонсон Д. Вычислительные машины и трудно решаемые задачи. М.: Мир, 1982.
-
Квейд Э. Методы системного анализа // Новое в теории и практике управления производством в США.–М.: Прогресс, 1971.– с.78-99. .
-
Корбут А.А., Финкельштейн Ю. Ю. Дискретное программирование М. Наука. Гл. ред. физ.-мат. лит. 1969.
-
Макаров И. М. и др. Теория выбора и принятия решений.– М.: Наука, 1982.– 328 с.
-
Пфанцагль И. Теория измерений. – М.: Наука, 1988.–384 с.
-
Таха Х. А. Введение в исследование операций. 7-е изд. М.: Изд. дом «Вильямс», 2005.
-
Фишберн П. С. Теория полезности для принятия решений. – М.: Наука,1978. –352 с.
Прямая
и двойственная задача линейного
программирования
Определение
двойственной задачи
Каждой
задаче линейного программирования
можно определенным образом сопоставить
некоторую другую задачу (линейного
программирования), называемую двойственной или
сопряженной по отношению к исходной
или прямой задаче. Дадим определение
двойственной задачи по отношению к общей
задаче линейного программирования,
состоящей, как мы уже знаем, в нахождении
максимального значения функции
(32)
при
условиях
(33)
(34)
Определение
1. Задача,
состоящая в нахождении минимального
значения функции
(35)
при
условиях
(36)
(37)
называется двойственной
по отношению
к задаче (32) – (34). Задачи (32) – (34) и (35) –
(37) образуют пару задач, называемую в
линейном программировании двойственной
парой. Сравнивая
две сформулированные задачи, видим, что
двойственная задача составляется
согласно следующим правилам:
1.
Целевая функция исходной задачи (32) –
(34) задается на максимум, а целевая
функция двойственной (35) – (37) – на
минимум.
2.
Матрица
(38)
составленная
из коэффициентов при неизвестных в
системе ограничений (33) исходной задачи
(32) – (34), и аналогичная матрица
(39)
в
двойственной задаче (35) – (37) получаются
друг из друга транспонированием (т. е.
заменой строк столбцами, а столбцов –
строками).
3.
Число переменных в двойственной задаче
(35) – (37) равно числу ограничений в системе
(33) исходной задачи (32) – (34), а число
ограничений в системе (36) двойственной
задачи – числу переменных в исходной
задаче.
4.
Коэффициентами при неизвестных в целевой
функции (35) двойственной задачи (35) –
(37) являются свободные члены в системе
(33) исходной задачи (32) – (34), а правыми
частями в соотношениях системы (36)
двойственной задачи – коэффициенты
при неизвестных в целевой функции (32)
исходной задачи.
5.
Если переменная xj исходной
задачи (32) – (34) может принимать только
лишь положительные значения, то j–е
условие в системе (36) двойственной задачи
(35) – (37) является неравенством вида
“? ”.
Если же переменная xj может
принимать как положительные, так и
отрицательные значения, то1
– соотношение
в системе (54) представляет собой уравнение.
Аналогичные связи имеют место между
ограничениями (33) исходной задачи (32) –
(34) и переменными двойственной задачи
(35) – (37). Если i –
соотношение в системе (33) исходной задачи
является неравенством, то i–я
переменная двойственной задачи
. В
противном случае переменная уj может
принимать как положительные, так и
отрицательные значения.
Двойственные
пары задач обычно подразделяют на симметричные
и несимметричные. В симметричной паре
двойственных задач ограничения (33)
прямой задачи и соотношения (36) двойственной
задачи являются неравенствами вида
“
”.
Таким образом, переменные обеих задач
могут принимать только лишь неотрицательные
значения.
Пример
1. Составить
двойственную задачу по отношению к
задаче, состоящей в максимизации функции
(40)
при
условиях
(41)
(42)
Решение. Для
данной задачи
и 
Число
переменных в двойственной задаче равно
числу уравнений в системе (41), т. е. равно
трем. Коэффициентами в целевой функции
двойственной задачи являются свободные
члены системы уравнений (41), т.е. числа
12, 24, 18.
Целевая
функция исходной задачи (40) – (42)
исследуется на максимум, а система
условий (41) содержит только уравнения.
Поэтому в двойственной задаче целевая
функция исследуется на минимум, а ее
переменные могут принимать любые
значения (в том числе и отрицательные).
Так как все три переменные исходной
задачи (40) – (42) принимают только лишь
неотрицательные значения, то в системе
условий двойственной задачи должны
быть три неравенства вида “? ”.
Следовательно, для задачи (40) – (42)
двойственная задача такова: найти
минимум функции
при
условиях

Пример
2. Для
задачи, состоящей в максимизации функции
при
условиях

сформулировать
двойственную задачу.
Решение. Для
данной задачи
, 
В
соответствии с общими правилами задача,
двойственная по отношению к данной,
формулируется следующим образом: найти
минимум функции
при
условиях

Связь между решениями прямой и двойственной задач
Рассмотрим
пару двойственных задач, образованную
основной задачей линейного программирования
и двойственной к ней. Исходная задача:
найти максимум функции
(43)
при
условиях
(44)
(45)
Двойственная
задача: найти минимум функции
(46)
при
условиях
(47)
Каждая
из задач двойственной пары (43) – (45) и
(46), (47) фактически является самостоятельной
задачей линейного программирования и
может быть решена независимо одна от
другой. Однако при определении симплексным
методом оптимального плана одной из
задач тем самым находится решение и
другой задачи.
Существующие
зависимости между решениями прямой и
двойственной задач характеризуются
сформулированными ниже леммами и
теоремами двойственности.
Лемма
1. Если
Х – некоторый план исходной задачи (43)
– (45), a Y –
произвольный план двойственной задачи
(46), (47), то значение целевой функции
исходной задачи при плане Х всегда не
превосходит значения целевой функции
двойственной задачи при плане Y, т. е.
Лемма
2. Если
для
некоторых планов X* и
Y* задач
(43) – (45) и (46), (47), то X* –
оптимальный план исходной задачи, а
Y* –
оптимальный план двойственной задачи.
Теорема
8 (первая
теорема двойственности). Если одна из
задач двойственной пары (43) – (45) или
(46), (47) имеет оптимальный план, то и другая
имеет оптимальный план и значения
целевых функций задач при их оптимальных
планах равны между собой, т. е.
Если
же целевая функция одной задачи из
двойственной пары неограничена (для
исходной (43) – (45) – сверху, для двойственной
(46), (47) – снизу), то другая задача вообще
не имеет планов.
Теорема
9 (вторая
теорема двойственности). План
задачи
(43) – (45) и план
задачи
(46), (47) являются оптимальными планами
этих задач тогда и только тогда, когда
для любого
выполняется
равенство
Геометрическая интерпретация двойственных задач
Если
число переменных в прямой и
двойственной задачах, образующих данную
пару, равно двум, то, используя
геометрическую интерпретацию задачи
линейного программирования, можно легко
найти решение данной пары задач. При
этом имеет место один из следующих трех
взаимно исключающих друг друга случаев:
1) обе задачи имеют планы; 2) планы имеет
только одна задача; 3) для каждой задачи
двойственной пары множество планов
пусто.
Пример
3. Для
задачи, состоящей в определении
максимального значения функции
при
условиях

составить
двойственную задачу и найти решение
обеих задач.
Решение. Двойственной
задачей по отношению к исходной является
задача, состоящая в определении
минимального значения функции
при
условиях

Как
в исходной, так и в двойственной задаче
число неизвестных равно двум. Следовательно,
их решение можно найти, используя
геометрическую интерпретацию задачи
линейного программирования (рис. 7 и 8).
Как
видно из рис. 8, максимальное значение
целевая функция исходной задачи принимает
в точкеВ. Следовательно, Х*=(2,
6) является оптимальным планом, при
котором
.
Минимальное значение целевая функция
двойственной задачи принимает в
точке Е (рис.
8). Значит, Y*=(1;
4) является оптимальным планом двойственной
задачи, при котором
Таким
образом, значения целевых функций
исходной и двойственной задач при их
оптимальных планах равны между собой.

Из рис.
7 видно, что при всяком плане исходной
задачи значение целевой функции не
больше 46. Одновременно, как видно из рис.
8, значение целевой функции двойственной
задачи при любом ее плане не меньше 46.
Таким образом, при любом плане исходной
задачи значение целевой функции не
превосходит значения целевой функции
двойственной задачи при ее произвольном
плане.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
08.06.20152.48 Mб83Процессы и аппараты нефтегазо- переработки.docx
- #
- #
- #
- #
- #
- #
- #
Двойственные задачи линейного программирования
Двойственность является важным понятием в линейном программировании, имеющим экономическое (практическое) применение. Например, для задачи оптимального распределения ресурсов для производства некоторых видов товаров пара прямой и двойственной задачи принимает следующий экономический смысл:
Прямая задача: Сколько и какой продукции xj необходимо производить, чтобы при заданных доходах Cj и объемах ресурсов bi максимизировать доход от продажи продукции?
Двойственная задача: Какова должна быть «теневая» цена каждого ресурса yi, чтобы при заданных количествах bi и доходах Cj минимизировать затраты?
Для составления двойственных задач используют специальные правила, при решении же выбирают один из наиболее подходящих методов решения ЗЛП: симплекс-метод, графический метод. Более того, так как между парой двойственных задач существует связь, иногда достаточно решить только одну из задач, чтобы получить решение второй.
Примеры составления и решения двойственных задач линейного программирования приведены в этом разделе — изучайте, ищите похожие, решайте. Если вам нужна помощь в выполнении подобных заданий — Решение контрольных по линейному программированию.
Лучшее спасибо — порекомендовать эту страницу
Примеры составления и решения двойственных задач онлайн
Задача 1. Записать математическую модель двойственной ЗЛП по заданной прямой:
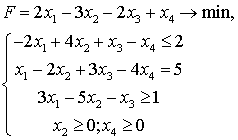
Задача 2. Составить задачу, двойственную исходной задаче:
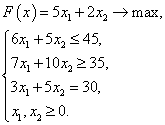
Задача 3. Решить задачу линейного программирования; составить задачу, двойственную данной, и также найти ее решение:
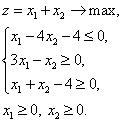
Качественно решаем задачи линейного программирования