Рабочая тетрадь по Информатике 7 класс Босова
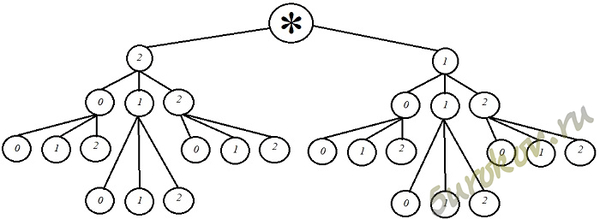
Задание 14. . Какие трёхзначные числа можно составить из цифр 0, 1, 2? Решите задачу, достроив дерево возможных вариантов.
Из цифр 0, 1 и 2 можно составить 18 трёхзначных чисел: 100, 101, 102, 110, 111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212, 220, 221 и 222.
Ответ: 100, 101, 102, 110, 111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212, 220, 221 и 222
<- Предыдущее заданиеСледующее задание ->
Нашли ошибку?
Войдите:
Методы решения комбинаторных задач
Перебор возможных вариантов
Простые задачи решают обыкновенным полным перебором возможных вариантов без составления различных таблиц и схем.
Задача 1.
Какие двузначные числа можно составить из цифр 1, 2, 3, 4, 5?
Ответ: 11, 12, 13, 14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43, 44, 45, 51, 52, 53, 54, 55.
Задача 2.
В финальном забеге на 100 м участвуют Иванов, Громов и Орлов. Назовите возможные варианты распределения призовых мест.
Ответ:
Вариант 1: 1) Иванов, 2) Громов, 3) Орлов.
Вариант 2: 1) Иванов, 2) Орлов, 3) Громов.
Вариант 3: 1) Орлов, 2) Иванов, 3) Громов.
Вариант 4: 1) Орлов, 2) Громов, 3) Иванов.
Вариант 5: 1) Громов, 2) Орлов, 3) Иванов.
Вариант 6: 1) Громов, 2) Иванов, 3) Орлов.
Задача 3.
В кружок бального танца записались Петя, Коля, Витя, Олег, Таня, Оля, Наташа, Света. Какие танцевальные пары девочки и мальчика могут образоваться?
Ответ:
1) Таня — Петя, 2) Таня — Коля, 3) Таня — Витя, 4) Таня — Олег, 5) Оля — Петя, 6) Оля — Коля, 7) Оля — Витя, 
Дерево возможных вариантов
Самые разные комбинаторные задачи решаются с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда и название метода — дерево возможных вариантов.
Задача 4.
Какие трехзначные числа можно составить из цифр 0, 2, 4?
Решение. Построим дерево возможных вариантов, учитывая, что 0 не может быть первой цифрой в числе.
Ответ: 200, 202, 204, 220, 222, 224, 240, 242, 244, 400, 402, 404, 420, 422, 424, 440, 442, 444.
Задача 5.
Школьные туристы решили совершить путешествие к горному озеру. Первый этап пути можно преодолеть на поезде или автобусе. Второй этап — на байдарках, велосипедах или пешком. И третий этап пути — пешком или с помощью канатной дороги. Какие возможные варианты путешествия есть у школьных туристов?
Решение. Построим дерево возможных вариантов, обозначив путешествие на поезде П, на автобусе — А, на байдарках — Б, велосипедах — В, пешком — Х, на канатной дороге — К.
Ответ: На рисунке перечислены все 12 возможных вариантов путешествия школьных туристов.
Задача 6.
Запишите все возможные варианты расписания пяти уроков на день из предметов: математика, русский язык, история, английский язык, физкультура, причем математика должна быть вторым уроком.
Решение. Построим дерево возможных вариантов, обозначив М — математика, Р — русский язык, И — история, А — английский язык, Ф — физкультура.
Ответ: Всего 24 возможных варианта:
|
Р |
Р |
Р |
Р |
Р |
Р |
И |
И |
И |
И |
И |
И |
А |
А |
А |
А |
А |
А |
Ф |
Ф |
Ф |
Ф |
Ф |
Ф |
Задача 7.
Саша ходит в школу в брюках или джинсах, к ним одевает рубашки серого, голубого, зеленого цвета или в клетку, а в качестве сменной обуви берет туфли или кроссовки.
а) Сколько дней Саша сможет выглядеть по-новому?
б) Сколько дней при этом он будет ходить в кроссовках?
в) Сколько дней он будет ходить в рубашке в клетку и джинсах?
Решение. Построим дерево возможных вариантов, обозначив Б — брюки, Д — джинсы, С — серая рубашка, Г — голубая рубашка, З — зеленая рубашка, Р — рубашка в клетку, Т — туфли, К — кроссовки.
Ответ: а) 16 дней; б) 8 дней; в) 2 дня.
Составление таблиц
Решить комбинаторные задачи можно с помощью таблиц. Они, как и дерево возможных вариантов, наглядно представляют решение таких задач.
Задача 8.
Сколько нечетных двузначных чисел можно составить из цифр 1, 3, 4, 6, 7, 8, 9?
Решение. Составим таблицу: слева первый столбец — первые цифры искомых чисел, вверху первая строка — вторые цифры.
Ответ: 28.
Задача 9.
Маша, Оля, Вера, Ира, Андрей, Миша и Игорь готовились стать ведущими на Новогоднем празднике. Назовите возможные варианты, если ведущими могут быть только одна девочка и один мальчик.
Решение. Составим таблицу: слева первый столбец — имена девочек, вверху первая строка — имена мальчиков.
Ответ: Все возможные варианты перечисляются в строках и столбцах таблицы.
Правило умножения
Этот метод решения комбинаторных задач применяется, когда не требуется перечислять все возможные варианты, а нужно ответить на вопрос — сколько их существует.
Задача 10.
В футбольном турнире участвуют несколько команд. Оказалось, что все они для трусов и футболок использовали белый, красный, синий и зеленый цвета, причем были представлены все возможные варианты. Сколько команд участвовали в турнире?
Решение.
Трусы могут быть белого, красного, синего или зеленого цвета, т.е. существует 4 варианта. Каждый из этих вариантов имеет 4 варианта цвета майки.
4 х 4 = 16.
Ответ: 16 команд.
Задача 11.
6 учеников сдают зачет по математике. Сколькими способами их можно расположить в списке?
Решение.
Первым в списке может оказаться любой из 6 учеников,
вторым в списке может быть любой из оставшихся 5 учеников,
третьим — любой из оставшихся 4 учеников,
четвертым — любой из оставшихся 3 учеников,
пятым — любой из оставшихся 2 учеников,
шестым — последний 1 ученик.
6 х 5 х 4 х 3 х 2 х 1 = 720.
Ответ: 720 способами.
Задача 12.
Сколько четных двузначных чисел можно составить из цифр 0, 2, 3, 4, 6, 7?
Решение.
Первой в двузначном числе может быть 5 цифр (цифра 0 не может быть первой в числе), второй в двузначном числе может быть 4 цифры (0, 2, 4, 6, т.к. число должно быть четным).
5 х 4 = 20.
Ответ: 20 чисел.
Скачать материал

Скачать материал


- Сейчас обучается 26 человек из 17 регионов




- Сейчас обучается 24 человека из 18 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Комбинаторные задачи:
дерево возможных вариантов -
2 слайд
Имя урока: Комбинаторика
Девиз урока: «Услышал – забыл,
Увидел – запомнил,
Сделал – понял»
Китайская поговорка -
3 слайд
В странных русских сказаниях повествуется, как богатырь или другой добрый молодец, доехав до распутья, читает на камне:
Вперёд поедешь – голову сложишь.
Налево поедешь – меча лишишься.
А дальше говорится, как он выходит из того положения, в которое попал в результате выбора.
Направо поедешь – коня потеряешь.Но выбирать разные пути или варианты приходится и современному человеку. Эти пути и варианты складываются в самые разнообразные комбинации.
-
4 слайд
Что такое КОМБИНАТОРИКА?
Задачи, в которых требуется осуществить перебор всех возможных вариантов, или, как обычно говорят в таких случаях, всех возможных комбинаций, называют комбинаторными.
Область математики, изучающая комбинаторные задачи, называется комбинаторикой.
Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить. -
5 слайд
Задача №1
Запишите все трёхзначные числа, для записи которых употребляются только цифры 1 и 2.
1 2
1
1
2
2
1
1
1
1
2
2
2
2
Ответ: 111, 112, 121, 122, 211, 212, 221, 222 – восемь чисел.
Такой метод решения комбинаторных задач называется деревом выбора(дерево возможных вариантов) -
6 слайд
Задача №2
Запишите все трёхзначные числа, для записи которых употребляются только цифры 0,7. -
7 слайд
Задача 3
В 5 «А» классе в среду 4 урока: математика, информатика, русский язык, английский язык. Сколько можно составить вариантов расписания на среду?
Решение: построим картину-схему.
Для удобства закодируем названия предметов:
математика – м,
информатика – и,
русский язык – р,
английский язык – а. -
8 слайд
Решение задачи 3
Расписание1 урок м и р а
2 урок и р а м р а м и а м и р
3 урок р а и а и р р а м а м р и а м а м и и р м р м и
4 урок а р а и р и а р а м р м а и а м и м р и р м и м
Ответ: 24 варианта: мира, миар, мриа, мраи, маир, мари, имра, имар, ирма, ирам, иамр, иарм, рмиа, рмаи, рима, риам, рами, раим, амир, амри, аимр, аирм, арми, арим.
-
9 слайд
Построенная схема напоминает перевернутое дерево: от ствола («расписание») отходят ветки, сначала четыре (м, и, р, а), от каждой из четырех веток – еще по три, затем еще по две и еще по одной. Видимо поэтому такую схему называют деревом возможных вариантов.
Дерево возможных вариантов можно считать геометрической моделью рассматриваемой ситуации. -
10 слайд
Задача №4
В правление фирмы входят 5 человек. Из своего состава правления должно выбрать президента и вице-президента. Сколькими способами это можно сделать?
Президент
1Вице – президент
2 3 4 5
2
1 3 4 5
3
1 2 4 54
1 2 3 4
5
1 2 3 5
Такой метод решения комбинаторных задач называется правилом умножения.
Выбрать президента можно пятью способами, а для каждого выбранного президента четырьмя способами можно выбрать вице-президента . Следовательно, общее число способов выбрать президента и вице-президента фирмы равно: 5*4=20. -
11 слайд
Можно решить Задачу 3 короче, если применить правило умножения. Существует 4 варианта выбора первого урока. Для выбора второго урока есть только три варианта, так как один из четырех уроков мы уже выбрали. Тогда для третьего урока существует два варианта, а для четвертого только один. Применив правило умножения, получим
4 ∙ 3 ∙ 2 ∙1= 24
Ответ: 24 варианта. -
12 слайд
Задача №5
В классе 15 мальчиков и 10 девочек. Сколькими способами можно выбрать двух дежурных(одну девочку и одного мальчика)? -
13 слайд
Задача 2.
В 6 классе в четверг 5 уроков: математика, информатика, русский язык, английский язык, физкультура.
а) Сколько имеется вариантов расписания при условии, что физкультура – последний урок?
б) Сколько имеется вариантов расписания при условии, что физкультура – последний урок, а математика – первый?
-
14 слайд
Задача 2 (продолжение).
В 6 классе в четверг 5 уроков: математика, информатика, русский язык, английский язык, физкультура.в) Сколько всего можно составить вариантов расписания на четверг?
г) Сколько времени потратит завуч на запись всех вариантов, если известно, что на запись одного варианта у него уходит 30 секунд?
-
-
-
17 слайд
Задача №1
Запишите все трёхзначные числа, для записи которых употребляются только цифры 0,7.
Задача №2
Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7? Нарисуйте дерево выбора на альбомном листе.
Задача №3
Составьте комбинаторную задачу, которая решается с помощью правила умножения. Сделайте к ней рисунок.
Задача № 4
Тренер попросил Филю составить трехзначное число из цифр 1, 2, 3, 4, причем цифры в числе
могут повторяться. Сколько чисел может составить Филя?
Задача № 5
Тренер попросил Филю составить трехзначное число из цифр 1, 2, 3, 4 так, чтобы цифры в числе
не повторялись. Сколько чисел может составить Филя?
Домашнее задание
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 264 901 материал в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 24.04.2017
- 1094
- 0
- 24.04.2017
- 626
- 0
- 24.04.2017
- 1131
- 0
Рейтинг:
4 из 5
- 24.04.2017
- 32734
- 272
- 24.04.2017
- 2577
- 2
- 24.04.2017
- 7019
- 11
- 24.04.2017
- 847
- 3
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
-
Главная
-
ГДЗ
- 5 класс
- Математика
-
Виленкин учебник
- 12
Новая редакция 2018-2023 г.
Смотрите также:
-
Задание 12 в старой редакции (2011 — 2017 г.)
- Учебник старой редакции (2011 — 2017 г.)
Вернуться к содержанию учебника
Страница 11
7
8
9
10
11
12
13
14
15
16
17
Вопрос
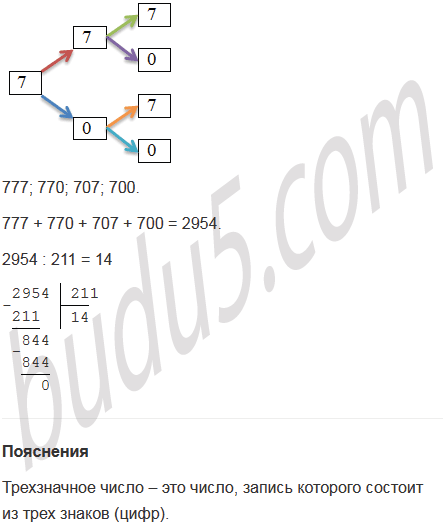
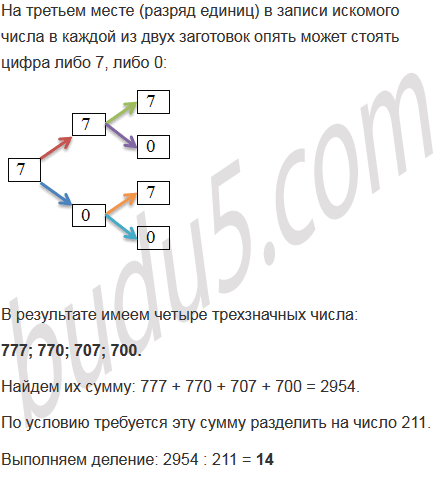
Составьте дерево возможных вариантов и запишите все трехзначные числа, для записи которых употребляются только цифры 0 и 7. Найдите сумму этих чисел и разделите ее на 211.
Подсказка
Вспомните:
- Какие числа называют трехзначными.
- Сложение натуральных чисел.
- Деление натуральных чисел.
Ответ
7
8
9
10
11
12
13
14
15
16
17
7
8
9
10
11
12
13
14
15
16
17
Вернуться к содержанию учебника
Смотрите также:
-
Задание 12 в старой редакции (2011 — 2017 г.)
- Учебник старой редакции (2011 — 2017 г.)
Слайд 1
Дерево возможных вариантов
Выполнили ученики
10 «а» класса
Фионин Роман

Короткевич Алина
Слайд 2
Самые разные комбинаторные задачи решаются с помощью

составления специальных схем. Внешне такая схема напоминает дерево, отсюда
и название метода — дерево возможных вариантов.
Слайд 3
Задача 1
Какие трехзначные числа можно составить из цифр

0, 2, 4?
Слайд 4
Решение. Построим дерево возможных вариантов, учитывая, что 0

не может быть первой цифрой в числе.
Ответ: 200, 202,
204, 220, 222, 224, 240, 242, 244, 400, 402, 404, 420, 422, 424, 440, 442, 444.
Слайд 5
Задача 2
Запишите все возможные варианты расписания пяти уроков

на день из предметов: математика, русский язык, история, английский
язык, физкультура, причем математика должна быть вторым уроком.
Слайд 6
Решение. Построим дерево возможных вариантов, обозначив М —
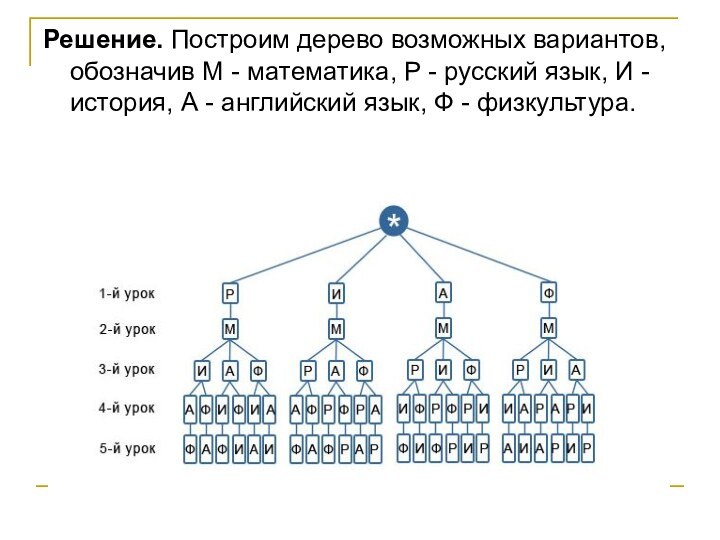
математика, Р — русский язык, И — история, А
— английский язык, Ф — физкультура.
Слайд 7
Ответ: Всего 24 возможных варианта: