Как составить бытовой алгоритм

МИНИСТЕРСТВО
ОБРАЗОВАНИЯ, НАУКИ И МОЛОДЕЖИ

РЕСПУБЛИКИ
КРЫМ

Государственное
бюджетное образовательное учреждение дополнительного образования Республики
Крым «Малая академия наук «Искатель»

Республиканский
конкурс исследовательских работ и проектов учащихся младшего школьного возраста
«Я – исследователь» в 2019 году

Направление:
техника и технологии

Алгоритмы в быту

Работу выполнила:

Носова
Дарья Игоревна, 

обучающаяся
3 класса

Муниципального бюджетного

общеобразовательного учреждения

«Ялтинская средняя школа № 12

с углубленным изучением

иностранных языков»

муниципального образования

городской округ Ялта

Республики Крым

Научный
руководитель:

Юнчик Анна
Ивановна,

учитель
начальных классов

Муниципального бюджетного

общеобразовательного учреждения

«Ялтинская средняя школа № 12

с углубленным изучением

иностранных языков»

муниципального образования

городской округ Ялта

Республики Крым

г.
Ялта – 2019

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

В повседневной жизни мы не замечаем,
как используем те или иные алгоритмы. Приготовить еду, собраться на работу,
перейти дорогу − все эти действия выполняются в определенной
последовательности. Человек ежедневно пользуется различными алгоритмами.
Например, правила умножения, деления, сложения, вычитания чисел; грамматические
правила правописания слов и предложений, а также разнообразные инструкции,
рецепты и указания – всё это алгоритмы. Мы все живем в огромном потоке
информации. Информация – постоянный спутник человека. Всегда люди стремились к
тому, чтобы облегчить свой труд с помощью каких-нибудь машин и механизмов. И
таким механизмом для работы с информацией стал компьютер. Интересно то, что нас
в нашей жизни почти везде окружают алгоритмы, любой человек выполняет какие-то
действия по порядку, раздумывая, поступает ли он правильно.

Актуальность: умение выделять
алгоритмическую суть явления и строить алгоритмы очень важно для человека любой
профессии. Алгоритмическое мышление – искусство размышлять, умение планировать
свои действия, способность предусматривать различные обстоятельства и поступать
соответственно с ними. Понятие алгоритма ценно не только практическим
использованием, оно имеет важное общеобразовательное и мировоззренческое
значение. Навыки алгоритмического мышления способствуют формированию особого
стиля культуры человека, составляющими которого являются:

·       
целеустремленность и сосредоточенность;

·       
объективность и точность;

·       
логичность и последовательность в
планировании и выполнении своих действий;

·       
умение четко и последовательно выражать
свои мысли; правильно ставить задачу и находить окончательные пути ее решения;

·       
быстро ориентироваться в стремительном
потоке информации.

Гипотеза моей работы:
алгоритмы систематизируют и упрощают жизнь человека.

Цель: изучить алгоритмы и
их роль в жизни людей.

Для достижения цели поставлены
следующие задачи:

1. Изучить историю возникновения понятия «алгоритм».

2. Выяснить, какие существуют алгоритмы.

3. Проанализировать, где встречаются алгоритмы в повседневной
жизни.

Объект исследования – алгоритмы.

ГЛАВА
1.

1.1. История возникновения понятия
«алгоритм». Понятие алгоритма

Слово «алгоритм» произошло от имени
выдающегося математика средневекового Востока Мухаммеда аль — Хорезми. Он жил и
творил в IX веке. Арабский оригинал его арифметических трудов потерян, но существует
перевод XII века на латинском языке, по нему западная Европа ознакомилась с
десятичной системой счисления и правилами выполнения в ней арифметических
действий.

Аль – Хорезми стремился к тому, чтоб
правила, сформулированные им, были понятны для всех грамотных людей. Достичь
такого в веке, когда только была разработана математическая символика (знаки
операций, скобки, буквенные обозначения и т. п.) было очень трудно. Но ему
удалось выстроить в своих трудах чёткий и строгий стиль словесного предписания,
который не позволял читателю отклониться от предписанного или пропустить
некоторые действия.

В латинском переводе книги Мухаммеда
аль — Хорезми правила начинались со слов «Алгоризми сказал». Со временем люди
позабыли, что «Алгоризми» − это автор правил, и стали правила называть
алгоритмами. Постепенно «Алгоризми сказал» преобразовалось в «алгоритм гласит».

На
протяжении нескольких веков понятие «алгоритм» было связано с числами и
простыми действиями над ними. В основном алгоритмы составлялись в виде
математических формул. Порядок шагов такого алгоритма задавался расстановкой
скобок, а сами шаги заключались в выполнении арифметических операций и операций
отношений. Часто эти вычисления были объёмными, а вычисления вручную –
трудоемкими, но суть такого вычислительного процесса оставалась очевидной.

Существуют проблемы, алгоритм для
которых вообще не может существовать. Мысль о существовании алгоритмически
неразрешимых задач оказалась верной, но для того, чтоб обосновать её, было
необходимо дать точное определение алгоритма. Попытки получить такое
определение привели к возникновению теории алгоритмов, в которую вошли труды некоторых
известных математиков.

Слово «алгоритм» стало вновь
употребляться, когда появились электронные вычислительные машины для
обозначения группы действий, составляющих определённый процесс. Здесь имеется в
виду не только процесс решения какой-нибудь математической задачи, но также
инструкции по использованию утюга или стиральной машины, и технология
приготовления какого-нибудь блюда, и многие правила, которые не имеют отношения
к математике, – все эти правила тоже являются алгоритмами. Понятие «алгоритм» в
наши дни хорошо известно каждому, это слово настолько уверенно шагнуло в
разговорную речь, что сейчас нередко в выступлениях политиков, на страницах
газет можно встретить выражения «алгоритм поведения», «алгоритм успеха» и т.д.

Каждый человек сталкивается в своей
жизни с необходимостью решения задач разнообразной сложности. Некоторые из этих
задач требуют долгих размышлений для поиска решений (но иногда его найти не
удается), другие же, столь просты и привычны, что решаются автоматически. При
этом выполнение даже очень простой задачи происходит в несколько
последовательных этапов (шагов).

Таким образом, как научный термин
«алгоритм» первоначально обозначал только правила выполнения действий в
десятичной системе счисления. Со временем этот термин приобрел более широкий
смысл и стал обозначать любые точные правила действий.

Алгоритм – это понятное и точное
предписание исполнителю выполнить конечную последовательность команд,
направленных на достижение поставленной цели.

1.2.
Свойства и виды алгоритмов

Исполнитель алгоритма – это объект,
который способен выполнить действия, предписываемые алгоритмом.

Характеристика
исполнителя:

·       
среда (место обитания исполнителя);

·       
элементарные действия;

·       
система команд исполнителя;

·       
отказы.

Каждый
исполнитель имеет свой перечень команд, которые он может выполнить. Этот
перечень называется системой команд исполнителя.

После
каждого вызова команды исполнитель совершает определённое элементарное
действие. Отказы исполнителя возникают, когда команда вызывается при
недопустимом для нее состоянии среды.

Любой алгоритм обладает следующими
свойствами.

1. Последовательность.
Процесс решения задачи должен быть разбит на последовательность отдельно
выполняемых команд, которые следуют в определенном порядке.

2. Понятность.
Каждая определённая команда должна быть понятна тому, кто исполняет алгоритм
(исполнителю).

3. Определенность.
Команды, которые образуют алгоритм должны быть очень чёткими и однозначными.

4. Конечность
(результативность). Результат выполнения алгоритма обязательно должен быть
получен. Выполнение алгоритма должно завершиться за конечное число команд.

5. Массовость.
Это возможность применения алгоритма для решения целого класса конкретных
задач.

Разработать алгоритм – это разбить
задачу на последовательно выполняемые шаги.

При
всем многообразии алгоритмов в них можно выделить три основных вида:

·       
линейный;

·       
разветвляющийся;

·       
циклический.

Линейным называется такой
алгоритм, в котором все действия выполняются однократно в заданном порядке.

Примеры
линейного алгоритма.

1) Соберись
в школу.

Встань
с кровати. Сделай зарядку. Умойся. Оденься. Позавтракай. Сложи учебные
принадлежности в сумку.

2) Найди
периметр прямоугольника.

Начало.

Даны
стороны прямоугольника a = 4 см и b = 5 см.

Периметр
прямоугольника найти по формуле P = (a + b) * 2

P
= (4 + 5) * 2 = 18 см

Конец.

Алгоритмы, в которых существует выбор
действий в зависимости от некоторого условия, называются разветвляющимися
алгоритмами.

Примеры
разветвляющегося алгоритма.

1) Пойти
на прогулку.

Начало.

Одеться.

Посмотреть
в окошко.

Если
на улице хорошая погода, то пойти гулять, иначе сидеть дома.

Конец.

Графические примеры описания разветвляющихся алгоритмов «Собери
грибы» с полным и неполным ветвлением представлены в Приложении 1 (полное
ветвление) и Приложении 2 (неполное ветвление).

Циклический алгоритм – описание
действий, которые должны повторяться указанное число раз или пока не выполнится
заданное условие. Циклом называется набор действий, которые несколько раз
повторяются.

По
количеству выполнения циклы делятся на циклы с неопределенным числом повторений
и циклы с заранее заданным числом повторений. Количество повторений зависит от
соблюдения условия, которое задаёт необходимость выполнения цикла. При этом
условие может проверяться в начале цикла — это цикл с предусловием, или в конце
— это цикл с постусловием.

Пример
циклического алгоритма.

1) Приготовить
яичницу.

Начало.
Разогреть сковороду. Положить кусочек масла на сковородку. Аккуратно разбить
яйцо в чашку. Вылить его на сковородку. Проверить, есть ли ещё яйцо? Если есть,
то перейти к пункту 4. Если нет, то перейти к пункту 9. Посолить. Немножко
подождать. Яичница готова. Конец.

Графические примеры циклических алгоритмов представлены в
приложении 3 и 4:

Цикл с предусловием (тело
цикла расположено после проверки условия; цикл может ни разу не выполниться) −
пример описания циклического алгоритма «Собери ягоды» (Приложение 3).

Цикл с постусловием (тело
цикла расположено до проверки условия; цикл выполняется хотя бы один раз) –
описание циклического алгоритма «Налови рыбы» (Приложение 4).

1.3.
Способы записи алгоритмов

Алгоритм должен быть формализован по
некоторым правилам посредством конкретных изобразительных средств. К ним
относятся следующие способы записи алгоритмов: словесный, графический,
псевдокоды, программный.

Выбор способов записи алгоритма
зависит от назначения самого алгоритма, а также от того, кто или что будет его
исполнителем.

Словесное
описание представляет структуру алгоритма на естественном языке. 

Пример словесного описания линейного
алгоритма:

«Даны
две стороны прямоугольника a, b. Найти площадь прямоугольника»

Начало.

Ввод
a и b.

S
= a * b.

Вывести
значение S.

Конец.

Пример словесного описания
циклического алгоритма:

«Налови
рыбы»

Начало.

Насади
наживку.

Забрось
крючок.

Вытащи
рыбу.

Сними
рыбу с крючка.

Положи
в ведро.

Если
надоело ловить рыбу или ведро уже полное, то перейти к пункту 9.

Если
не надоело ловить рыбу или ведро неполное, то перейти к пункту 2.

Иди
домой.

Конец.

Пример словесного описания
разветвляющегося алгоритма:

Алгоритм
«Вычисление»

Начало.

Задать
число Х

К
заданному числу прибавить 2.

Если
результат больше 7, то перейти к пункту 5.

Вычесть
3 и перейти к пункту 8.

Если
результат меньше 7, то перейти к пункту 7.

Умножить
на 2 и перейти к пункту 8.

Записать
результат.

Конец.

Псевдокод − описание структуры
алгоритма на естественном, частично формализованном языке, которое позволяет
выявить главные этапы решения задачи, перед точной его записью на языке
программирования. В псевдокоде используется математическая символика и
некоторые формальные конструкции. Для записи псевдокода не существует строгих
синтаксических правил. Что облегчает запись некоторого алгоритма и позволяет
описать его, используя любой набор команд. Но в псевдокоде обычно используются
некоторые конструкции, принадлежащие формальным языкам, что облегчает переход
от псевдокода к записи алгоритма на языке программирования. Формального или
единого определения псевдокода не существует, поэтому возможны разные псевдокоды,
которые отличаются набором используемых слов и конструкций.

Примеры
записи алгоритма с использованием псевдокода:

Если
<условие>

то
серия 1

иначе
серия 2

Конец

1.
Начало.

2.
Задать число Х

3.
К заданному числу прибавить 5.

4.
Если результат больше 20,

то
вычесть 10,

иначе
умножить на 3.

5.
Записать результат.

6.
Конец.

Благодаря своей наглядности
наибольшее распространение получил графический способ записи алгоритмов.
Блок-схемой называется графическое изображение логической структуры алгоритма,
в котором каждые его действия изображаются в виде геометрических фигур
(блоков), а связи между действиями указываются при помощи стрелок, которые
соединяют эти фигуры.

ГЛАВА
2.

2.1.
Алгоритмы в повседневной жизни

В нашей жизни мы постоянно
сталкиваемся с алгоритмами в различных сферах человеческой деятельности,
рассмотрим некоторые из них:

1)
Алгоритмы в кулинарных рецептах.

Любой
кулинарный рецепт – это алгоритм. Имя алгоритма – это название производимого
продукта.

Алгоритм
«Приготовление бутерброда»

начало

взять
доску

взять
нож

отрезать
кусок хлеба

отрезать
кусок масла

намазать
масло на хлеб

отрезать
кусок сыра

положить
кусок сыра на хлеб

конец

У
каждой хозяйки много кулинарных рецептов и все они являются алгоритмами.

2)
Алгоритмы из окружающего мира

Режим
дня

Помощь
родителям по хозяйству (как убирать квартиру, сходить в магазин и т.д.)

Как
отремонтировать велосипед

3)
Алгоритмы из школьной жизни

Расписание
уроков

Расписание
подачи звонков

Расписание
кружков и секций

4)
Учебные алгоритмы

Как
писать изложение, диктант

Как
решать задачи по математике

Как
выучить стихотворение и т.д.

Использование алгоритмов в игровых задачах

Игры привлекают к себе участников и
наблюдателей (болельщиков) из-за неопределенности исхода, заранее неизвестно,
кто выигрывает, а кто проигрывает. Во многих играх случайные события специально
предусмотрены правилами игры: подбрасывается монета, кидается с нанесенными на
грани точками, вращается колесо рулетки и т.д. В таких играх нельзя дать алгоритм
выигрышного поведения игрока, так как исход игры не зависит от его действий.

Но существует игры, в которых выигрыш
зависит не от случайного стечения обстоятельств, а от смекалки игрока и
предварительного расчета. Проанализировав различные варианты своего поведения
и, сравнив эти варианты, можно выбрать тот, который ведает к наилучшему
результату. Игры этого типа называются комбинаторными. В качестве примеров
комбинаторных игр можно назвать шашки и шахматы. Неопределенность исхода игр
связана лишь с тем, что количество возможных вариантов (комбинаций) в игре
слишком велико, так что игрок практически не может перебрать и проанализировать
все эти варианты. Именно поэтому и шашки и шахматы относятся к играм, требующим
большого мастерства и смекалки.

Пример 1: Игра в «Одиннадцать
предметов» (игра Баше).

На
столе 11 предметов, например камешков, орехов или спичек. Количество предметов
необязательно должно быть 11, оно может 15, 19 и т.д. Соперники ходят по
очереди, и за каждый ход любой из игроков может взять 1,2 или 3 предмета.
Проигрывает тот, кто вынужден брать последний предмет.

Алгоритм выигрыша для первого игрока
имеет следующий вид:

Первый
ход. Взять два предмета.

Второй
и все последующие ходы. Брать столько предметов, чтобы количество предметов,
взятых вместе с соперником за очередной ход, в сумме составляло 4.

Человек, пользующийся данным
алгоритмом, всегда будет выигрывать. Для успешной игры от него требуется только
строго следовать алгоритму.

Пример
2: Алгоритм победителя.

Из
кучки, содержащей любое определенное количество каких-либо предметов, двое
играющих берут по очереди каждый раз по одному или по два предмета. Выигрывает
тот, кто своим очередным ходом сможет забрать все оставшиеся предметы.

Алгоритм выигрыша будет иметь вид:

Если
число предметов в кучке кратно 3, то уступить ход противнику, иначе (т.е. исходное
число не кратное 3 – начать игру

При
каждом ходе оставить число предметов кратным 3 т.е., своим очередным ходом 
каждый раз дополнять число взятых предметов до 3.

Алгоритмы
в пословицах (Приложение 5)

1)
Пословица «Куй железо, пока горячо»
2) Пословица «Любишь кататься – люби и саночки возить»

Алгоритмы в песнях

Песня
«Кабы не было зимы»

Кабы
не было зимы

В
городах и селах,

Никогда
б не знали мы

Этих
дней веселых.

Если
б не было зимы в городах и сёлах

то
никогда б не знали мы этих дней весёлых.

Песня
«Если с другом вышел в путь»

Если
с другом вышел в путь

то
веселей дорога.

Алгоритмы
в сказках (Приложение 6).

2.2.Теория
решения изобретательских задач

Представьте, перед вами встала
проблема, как улучшить какую-то вещь, или как что-то заставить работать. Как
придумать что-то новое? Для этого и была придумана Теория решения
изобретательских задач.

ТРИЗ  − это наука, изучающая объективные закономерности развития
технических систем. Она разрабатывает практические методы и приемы решения изобретательских
задач (технических проблем) с целью повышения качества систем и дает правила
организации творческого мышления.
Автор ТРИЗ — Генрих Саулович Альтшуллер.

                  Основные функции и области применения ТРИЗ:

1.    
Решение творческих и
изобретательских задач любой сложности во
всех сферах деятельности человека без перебора вариантов.

2.    
Прогнозирование развития
искусственных и технических
систем и получение
перспективных решений (в том числе и принципиально новых).

3.    
Пробуждение, тренировка
и грамотное использование природных способностей человека в
изобретательской деятельности (прежде всего образного воображения и системного
мышления).

4.    
Развитие качеств творческой
личности.​

Сегодня
ТРИЗ в результате своего развития вышла за рамки решения изобретательских
задач в технической области и используется во всех областях деятельности
человека.

Как работает ТРИЗ:

Во-первых, ТРИЗ позволяет
перейти от неясной и расплывчатой проблемы к конкретным задачам и способам их
решения.

Во-вторых, решить эти задачи с
помощью инструментов ТРИЗ.

В-третьих, получить сразу
несколько идей (решений), из которых осознанно выбрать наиболее подходящие в
данный момент времени.

В-четвертых, спрогнозировать и
предупредить будущие проблемы.

Что дает ТРИЗ:

• Инженер, владеющий
  ТРИЗ, эффективно решает проблемы и задачи предприятия и совершенствует
  постоянно устаревающие технические системы;
• Директор, владеющий
  методологией, может принимать сильные решения во всех направлениях деятельности
  компании (персонал, маркетинг, реклама, производство, сбыт).
• У педагога,
  использующего ТРИЗ, дети рассматривают проблемную задачу как систему и
  видят все факторы, влияющие на ее решение. Видят в любой проблеме
  увлекательную и интеллектуальную задачу.
• Бизнесмены обходят
  конкурентов и повышают свои доходы, максимально эффективно используя
  внутренние ресурсы, рассматривают кризисные ситуации как шанс обойти
  конкурентов.
• Политики выигрывают
  выборы и принимают сильные политические решения.

                              ТРИЗ сегодня:

Знание ТРИЗ
(применение и результаты) в крупнейших корпорациях мира (Ford, Caterpillar, Procter & Gamble, IВМ, Motorola,
Renault, SAAB, Peugeot-Citroen, Siemens, Philips, Bourjois-Chanel) сегодня обязательно
для любого специалиста, имеющего отношение к созданию инновационных идей и
решений. Владея ТРИЗ, человек владеет универсальным инструментом решения
проблем.

Жизненная ситуация: в хорошую погоду
окна в квартире должны быть открыты, но если на улице пойдет дождь, то появится
необходимость их закрыть. У нас нет желания следить за этим и закрывать их
самостоятельно. Какое решение приходит в голову?

Интересный факт: нам всегда приходят
на ум вещи, которые мы когда-то уже видели, или просто какие-то готовые
решения.

           
Рассмотрим обычную чашку. Если в нее налить кипяток, то она сама станет
горячей, и её будет нелегко удержать в руках. Но ведь мы хотим ей воспользоваться!
              Сформулируем  противоречие: нам нужно, чтобы в чашку можно было
налить что-то горячее, и не ошпариться при этом, взяв в руки.

Один из способов сохранить
температуру налитой жидкости, не допуская нагрева чашки, — это сделать ее из
более толстого материала. Это не приведет к существенным изменениям в
производстве кроме дополнительных затрат на материал. Аналогичным решением
будет считаться изменение материала, из которого делают чашку.
А если ли другие варианты? Можно сделать так, чтобы у чашки было не
нагревающееся место. Эта мысль и привела к созданию ручки у чашек.
Чашка осталась чашкой и почти не приобрела в весе. Дополнительные затраты
минимальны, так как ручка состоит из того же материала.

Чем
проще решение, тем проще его применить.
Технический объект идеален, если его нет, а функция выполняется
Другими словами, решение наилучшее, если оно не требует ничего, кроме того, что
у нас есть в условии.

Находясь
в условиях полной темноты, требуется ориентироваться в пространстве. Если мы не
можем видеть, то кто может? (про себя сразу формируем противоречие: человек не
может видеть в темноте, но нужно, чтобы он мог в ней ориентироваться).
           Тут можно вспомнить животных, которые хорошо ощущают себя в темноте.
На эту роль больше всего претендуют кошки и летучие мыши. В первом варианте
нужен хотя бы слабый источник света (прямого или отраженного). А в случае с
летучей мышью свет и вовсе не нужен, они перемещаются при помощи отраженного
звука.
              На примере летучих мышей были сделаны эхолокаторы, а вот в основу
очков ночного видения легла способность кошек ориентироваться при малом свете.

Другой
пример.

             
И ещё пример из мира животных: как избавиться от шнуровки в одежде? Одно из
хороших решений — повязывать одежду дополнительным лоскутом этой самой одежды,
что и легло в основу большинства халатов.
Второе достаточно распространенное решение состоит в том, чтобы вместо
креплений использовать закрепки, вариантом которых являются липучки (их
прототипом в свое время служили плоды репейника).

И
еще несколько примеров:

         Жил
был простой деревенский парень Том. Как-то раз в солнечный день

прогуливался
он по полю, на котором росли одни ромашки. Вдруг увидел

крошечного
старичка. “Это эльф, – догадался Том. – Вот так удача – ведь у

всех
эльфов где-то в земле припрятан кувшин с золотом!” Том быстро

схватил
малютку-эльфа и грозно спросил:

—
Где твое золото? Показывай!

Эльф
хотел вырваться и убежать, но где там! Пришлось ему согласиться…

–
Копай здесь и найдешь большой кувшин, полный золотых монет, – сказал

он,
указав на одну из ромашек.

Но
вот досада! Том не мог выкопать кувшин! Нужно было бежать домой за

лопатой.
А чтобы не ошибиться, где копать, он достал из кармана красную

ленточку
и завязал ее на ромашку. Но тут же засомневался и сказал эльфу:

–
Поклянись, что ты не снимешь эту ленточку с ромашки!

Старичок
поклялся верой и правдой, что пальцем не тронет ее, очень вежливо

попрощался
с Томом и исчез среди густых ромашек.

         Обычно
эльфы помогают людям, но Том вел себя грубо, поэтому

маленькому
человечку совсем не хотелось отдавать ему сокровище. Но что

можно
сделать – ведь он поклялся Тому не трогать ромашку…

Вот
краткий алгоритм решения творческих задач:

Точно
понять задачу.

Сформулировать
противоречие.

Сформулировать
ИКР.

Применить
приёмы разрешения противоречий.

Сформулировать
несколько решений.

Выбрать
самое сильное решение.

ПРОТИВОРЕЧИЕ:
ленточка указывает на место клада, но нельзя трогать ленточку на ромашке.

ИКР
(идеальный конечный результат): сделать ромашку с ленточкой

неузнаваемой.

ПРИЁМ
РАЗРЕШЕНИЯ ПРОТИВОРЕЧИЯ: обратим вред в пользу. Нам

мешает
красная ленточка. Сделать так, чтобы она не мешала.

РЕШЕНИЕ:
обвязать красными ленточками все ромашки.

ДОПОЛНЕНИЕ.
Если по-другому сформулировать противоречие, то можно найти другое решение (из
тех, что упоминаются).

Подсказка.
Эльфы всегда говорят правду, значит, под этой ромашкой на самом деле

был
закопан кувшин. И ромашка обвязана ленточкой. Как сделать так, чтобы

ромашку
невозможно было узнать?

Ответ.
Том быстро сбегал домой и вернулся с лопатой. И что же он увидел?

Эльф
свое слово сдержал: красную ленточку Тома не тронул… Но зато

обвязал
точно такой же красной ленточкой стебель каждой ромашки, что

росла
в поле.

Могут
быть и другие решения этой задачи. Например, не трогать ленточку, но

перенести
ромашку с ленточкой в другое место. Или перенести в другое

место
кувшин, пока Том бегал за лопатой.

         Жила-была
в лесу Атаманша со своими лесными разбойниками.

Однажды
сидела она в своей пещере со своим помощником и пила чай. Вдруг

в
дверь постучали, и вошел злой королевский советник.

—
Есть у меня к тебе дело секретное и неотложное, — сказал советник.

Только
нужно, чтобы никто о нем не знал, кроме нас двоих.

Выгнала
Атаманша помощника из пещеры и под страхом смерти запретила

ему
подслушивать.

         Что
же делать помощнику, когда страсть как хочется узнать о секретном

деле,
а подслушать боязно — у Атаманши разговор с ослушниками короткий?

ПРОТИВОРЕЧИЕ:
подслушивать самому нельзя, но хочется узнать о

секретном
разговоре.

ИКР
(идеальный конечный результат): знать содержание разговора без

подслушивания.

ПРИЁМ
РАЗРЕШЕНИЯ ПРОТИВОРЕЧИЯ: используем приём «посредник».

РЕШЕНИЕ:
помощник подговорил своих товарищей подслушать секретный

разговор.
Им ведь никто не запрещал!

Краткую
схему применения ТРИЗ в общем виде можно представить:
1. Определить задачу и сформулировать ее (проблема как дана и проблема как
понятна).
2. Найти противоречие и то, что мешает решить задачу (в чем проблема ситуации).
3. Выделить ресурсы, которыми обладаем.
4. Применить уже имеющиеся приемы решений (в пространстве, временной экран,
решение из других областей и так далее).
5. Проанализировать решение и понять, можно ли его улучшить.

ЗАКЛЮЧЕНИЕ

В своей работе я дала определение
алгоритму, выделила классификацию алгоритмов, решила игровые задачи с помощью
алгоритмов, проанализировала, где встречаются алгоритмы в повседневной жизни,
рассмотрела алгоритмы в теории решения изобретательских задач.

         Это
не все алгоритмы, которые я смогла увидеть и разделить на группы, но моя
гипотеза о том, что алгоритмы систематизируют и упрощают жизнь людей
подтвердилась. В будущем я хочу продолжить это исследование, обогатив свои
знания на уроках и используя информацию из повседневной жизни.

СПИСОК
ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1.    
Алексеев А.Г., Евсеев Г.А. Специальная
информатика. – М.: АСТ Пресс, 2014, – 450 с.

2.    
Гейн А.Г., Сенокосов А.И. Информатика. –
М.: Дрофа, 2012. – 237 с.

3.    
Симонович С.В., Евсеев Г.А. Практическая
информатика. – М.: АСТ Пресс, 2015. – 480 с.

4.    
Симонович С.В. Компьютер в вашей школе. –
М.: АСТ Пресс, 2011.
– 335 с.

5.    
Шауцукова
Л.З. Информатика 10-11. Книга 1. Теория (с задачами и решениями). – М.: Просвещение, 2008. – 420 с.

6.    
Алгоритм [Электронный ресурс] – режим доступа: 
http://ru.wikipedia.org/wiki/Алгоритм

7.    
Теория решения изобретательских задач на
пальцах [Электронный ресурс] − режим доступа: https://habr.com/post/314336/

8.    
Художественные произведения, пословицы.

ПРИЛОЖЕНИЯ

Приложение
1. Разветвляющийся алгоритм «Собери грибы» с полным ветвлением

Приложение 2. Разветвляющийся
алгоритм «Собери грибы» с неполным ветвлением

Приложение 3. Циклический
алгоритм «Собери ягоды» (цикл с предусловием)

Приложение 4. Циклический
алгоритм «Налови рыбы» (цикл с постусловием)

Приложение 5. Алгоритмы в пословицах

Приложение 6. Алгоритмы в сказках
(«Репка»)

Роль алгоритмов в жизни человека велика. Это и распорядок дня, и рецепты, и план работы, и инструкция по использованию, т.е. любую деятельность человека можно описать с помощью алгоритмов. Каждый школьник ежедневно использует сотни различных алгоритмов. Например, правила сложения, вычитания, деления, умножения чисел; грамматические правила правописания слов и предложений.

Алгоритмы полезно научиться составлять. Алгоритмическое мышление поможет человеку научиться размышлять, анализировать, планировать свои действия, отчетливо увидеть шаги, ведущие к цели.

Необходимо разработать систему мыслительных приёмов направленных на решение задач. Чем легче мы умеем понимать чужие алгоритмы и строить свои, тем лучше. Другими словами, полезно знать и понимать, как и что устроено.

В программе начального образования одним из планируемых результатов является «…создать условия для овладения основами логического и алгоритмического мышления, пространственного воображения и математической речи, приобретения навыков измерения, пересчета, прикидки и оценки, наглядного представления о записи и выполнении алгоритмов..», «…научить выполнять устно и письменно арифметические действия с числами и числовыми выражениями. Решать текстовые задачи, действовать в соответствии с алгоритмом и строить простейшие алгоритмы…».

Составление алгоритмов — сложная задача, поэтому важно уже на начальной ступени образования в школе, ставить целью ее решение, способствуя тем самым развитию логического мышления школьников.

Для этого, необходимо, прежде всего, учить детей «видеть» алгоритмы и осознавать алгоритмическую сущность тех действий, которые они выполняют. Начинать эту работу следует с простейших алгоритмов, доступных и понятных им. Можно составить алгоритм перехода улицы, алгоритмы пользования различными бытовыми приборами, приготовления какого-либо блюда и т.д. Такие задания можно выполнять на проектной деятельности

Алгоритм в системе обучения — это прежде всего точное и легко понимаемое описание того, что шаг за шагом выполняет ученик, которое после последовательного выполнения всегда приводит к правильному решению поставленных задач. Таким образом, алгоритмирование определяет строгую логическую последовательность, непрерывность мыслительной деятельности, постепенно подводящей ученика к самостоятельному «открытию» истины и позволяющей избежать логических провалов.

Действуя с конкретными объектами и обобщениями в виде правил, дети овладевают умением выделять элементарные шаги своих действий и определять их последовательность. А для этого необходимо научить детей:

• находить общий способ действия;
• выделять основные, элементарные действия, из которых состоит данное;
• планировать последовательность выделенных действий;
• правильно записывать данную последовательность действий.

Для решения учебных задач на уроках в начальных классах часто используются алгоритмы. Алгоритм относят к особой группе УУД — знаково-символическим действиям. Алгоритмы, по утверждению психолога Л.А.Венгера, помогают наиболее эффективно трансформировать наглядно-образное мышление в наглядно-схематическое, которое во многих случаях способно выступать в качестве логического мышления. Алгоритмы помогают планировать свою деятельность.

Овладение алгоритмом выполнения какой — либо операции включает три этапа: подготовительный, основной и этап сокращения операций.

Рассмотрим на примере темы «Алгоритм сложения столбиком» (учебник «Математика» 3 класс часть 1 А.Л.Чекин)

1. Подготовительный этап

Подготовка базы для работы с новым материалом, актуализация знаний, необходимых для введения и обоснования алгоритма.

— У вас на карточке — таблица разрядов

— Запишите в неё числа под диктовку:

— Запишите число, в котором 4 дес. тысяч 5 сот. 2 дес. и 8 ед.;

— Запишите число, в котором 7 дес. тысяч 6 ед. тысяч 3 сотни 6 дес. и 1 ед.

— Сложите числа поразрядно.

Учащиеся, после выполнения данного задания, будут подготовлены к выполнению всех элементарных операций алгоритма

2. Основной этап

Дети работают в группах по предложенному плану.

— Откройте учебник на с. 64. Задание №215 (Математика 3 класс А.Л.Чекин) выполните в группе

— Обсудите в группе ответы на вопросы,

— Кратко составьте последовательность действий (алгоритм), напишите его на листах.

— Представьте свой вариант алгоритма.

— Помните, что алгоритм должен быть:

• правильным
• последовательным
• с использованием грамотной математической речи

№215 с. 64. Сформулируй алгоритм сложения столбиком, ответив на следующие вопросы:

• Как нужно записывать слагаемые
• С какого разряда нужно начинать сложение и к какому переходить далее?
• Что нужно записывать в данный разряд значения суммы, когда при сложении в этом разряде получается однозначное число, и что — когда двузначное?
• Что нужно сделать с результатом сложения в данном разряде, если при сложении в предыдущем разряде получилось двузначное число?
• Как нужно действовать, если в данном разряде представлено только одно слагаемое?
• Когда нужно завершить сложение?

Сравните свой алгоритм с предложенным. (Дети сравнивают свой алгоритм с образцом)

Алгоритм сложения многозначных чисел

1. Пишу…(единицы под единицами, десятки под десятками, сотни под сотнями и т.д.)
2. Складываю единицы.( если получаю однозначное число, то пишу его в значение суммы под единицами, если двузначное, единицы пишу под единицами, а один дес. запоминаю, прибавлю его к следующему разряду)
3. Складываю десятки… и увеличиваю количество десятков на один( если при сложении единиц получилось двузначное число)Результат пишу под десятками.
4. Складываю сотни… Пишу под сотнями
5. Выполняю сложение всех разрядов
6. Читаю ответ

3. Этап сокращения операций

Переведем данный алгоритм в знаково-символическую модель.

— Запишите символически четырехзначное число (каждую цифру обозначаем прямоугольником)

— Под ним запишите еще одно четырехзначное число, разряд под разрядом

— Слева поставь знак сложения (+)

— Поставьте черту равенства

— Результаты сложения записывайте под тем разрядом, который складывали.

— Есть ли в вашей модели переход через разряд? Если нет, то попробуйте изменить модель. Добавьте условное обозначение, которое покажет, что десяток перешёл в десятки.

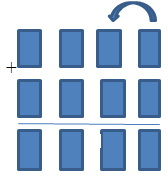
Своевременному свертыванию алгоритма способствуют сокращенные комментарии и образцы.

Алгоритм можно задать несколькими способами: словесным, графическим, и табличным.

Существует три основных типа алгоритмов: линейный, разветвленный, циклический.

Линейный алгоритм — это алгоритм, действия (команды) которого выполняются последовательно друг за другом.

Н-р: Алгоритм разбора слов по составу:

Алгоритм с ветвлением — это алгоритм, в котором в зависимости от условия выполняется либо одна, либо другая последовательность действий. В словесном описании разветвленного алгоритма используются слова «если», «то», «иначе».

Н-р: Алгоритм правописания приставок на «з» и «с».

1.Выдели корень слова.

2.

А) Если корень начинается со звонкого согласного, в приставке пиши «з», перейди к пункту 3.

Б) Если корень начинается с глухого согласного, в приставке пиши «с», перейди к пункту 3.

3. Запиши слово.

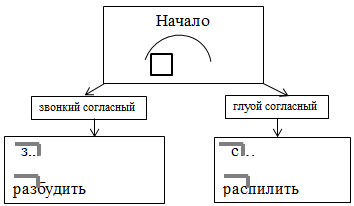
Учебное задание:

От данных глаголов образуйте слова, выбирая подходящую приставку раз-/рас-, из-/ис-.

Бросать, глядеть, гадать, бить, следовать, пугать, бежать, царапать.

Н-р: Алгоритм правописание имен существительных мужского и женского рода с шипящим на конце.

1. Произнеси слово.

2. Прислушайся: есть ли шипящий согласный звук на конце слова? Если есть, то определи часть речи.

3. Если это имя существительное, то определи род.

4.

а) Если это имя существительное женского рода, то после шипящего мягкий знак пишется, перейди к пункту 5.

б) Если это имя существительное мужского рода, то после шипящего мягкий знак не пишется, перейди к пункту 5.

5. Запиши слово.

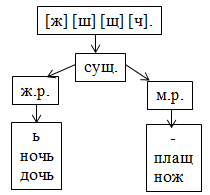
Учебное задание:

Напиши данные имена существительные в единственном числе:

Ландыши, калачи, кровати, мыши, ножи, вещи, кони, кирпичи.

Циклический алгоритм — это алгоритм, в котором действия повторяются конечное число раз.

Н-р: Алгоритм деления уголком трёхзначного числа на однозначное вида: 248 : 2

Учебник по математики 2 часть, 3 класс, авторы: И.И.Аргинская, Е.И.Ивановская, С.Н.Кормишина. С. 20 , № 296

• 396 : 3
• 448 : 4
• 842 : 2
• 639 : 3
• 248 : 2

Алгоритм

1. Определить количество цифр в значении частного
2. Разделить сотни
3. Разделить десятки
4. Разделить единицы
5. Записать результат

Рассуждения по алгоритму

Циклический алгоритм деления

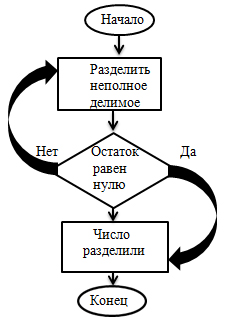
Алгоритмический метод в сочетании с другими методами обучения (метод целесообразных задач, проблемное обучение и др.) повышает осмысленность усвоения, облегчает и ускоряет изучение программного материала.

Наряду с уже готовыми алгоритмами, предлагаемыми авторами учебников при изучении многих тем, опираясь на наблюдения и в результате диалога, можно самостоятельно с учащимися создавать другие алгоритмы деятельности.

Правила разработки любого алгоритма:

• определить цель достижения, по которой будет создан алгоритм;
• наметить план действий для достижения поставленной цели;
• выбрать среду и объекты, посредством которых алгоритм будет реализован;
• детализировать алгоритм с учетом особенностей выбранной среды.

Использование алгоритмов упорядочивает процесс обучения, упрощает его, дает возможность быстро изложить новый материал, тем самым, освободив время для закрепления.

Это умение формируется на протяжении всего периода обучения в школе. Задания, выраженные в виде алгоритма (алгоритмического предписания), очень разнообразны. Успешность их выполнения зависит от умения учащихся чётко исполнять заданный алгоритм.

Из вышеизложенного вытекает следующий вывод: алгоритмирование играет важнейшую роль в формировании ключевых и предметных компетентностей и универсальных учебных действий:

Общеучебные универсальные действия:

• поиск и выделение необходимой информации;
• умение осознанно и произвольно строить речевое высказывание в устной
• форме;
• самостоятельное выделение и формулирование познавательной цели;
• знаково-символическое моделирование — преобразование объекта из чувственной формы в модель, где выделены существенные хар-ки объекта и преобразование модели с целью выявления общих законов, определяющих данную предметную область;

Регулятивные УУД:

• способность принимать, сохранять цели и следовать им в учебной деятельности;
• умение контролировать процесс и результаты своей деятельности.

Универсальные логические действия

• анализ объектов с целью выделения признаков;
• синтез как составление целого из частей;
• установление причинно-следственных связей;
• построение логической цепи рассуждений;
• доказательство.

Коммуникативные УУД:

• готовность слушать собеседника и вести диалог;
• готовность признавать возможность существования различных точек зрения и право каждого иметь свою;
• умение договариваться, находить общее решение практической задачи.

С применением алгоритмизации на уроках, учебный процесс направлен на развитие логического и критического мышления, воображения, самостоятельности. Дети заинтересованы, приобщены к творческому поиску; активизирована мыслительная деятельность каждого. Процесс становится не скучным, однообразным, а творческим.

Повседневные алгоритмы в жизни современного школьника

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение.

У большинства людей понятие алгоритм неразрывно связано с программированием. Многие думают, что это что-то очень сложное в понимании и применении, и под силу только людям определенных профессий. А между тем, многие из нас даже не догадываются, что буквально на каждом шагу изо дня в день мы с вами постоянно сталкиваемся с алгоритмами. И более того, без них мы даже шагу не можем ступить. Простые алгоритмы мы применяем в различных жизненных ситуациях, где сталкиваемся с проблемой выбора и оптимизацией процесса.

Алгоритмы помогают нам понятными и доступными для нас способами, принимать верные решения и достигать поставленных целей. Как это сделать с максимально возможной гарантией успеха, попробуем разобраться вместе.

Цель исследования: изучить понятие, что такое алгоритм, его виды и способы представления. Выяснить с какими алгоритмами встречается в своей повседневной жизни школьник, почему алгоритмы так необходимы и как их применять с пользой для себя. Какую помощь они оказывают для достижения успешной учебы. Составить свой алгоритм «Расписание занятий». Записать его в виде блок схемы и программы.

Объект исследования: современный школьник, ученица 4 класса.

Методы исследования: наблюдение, моделирование и программирование.

Гипотеза исследования: предположим, что алгоритм, это не только инструмент программиста, а очень необходимая вещь в жизни обыкновенного школьника.

Теоретическая часть

1.1. Что такое алгоритм

В повседневной жизни, во время учебы, школьник решает большое количество задач разной сложности. Некоторые из этих задач настолько просты, что он даже не задумывается над процессом их реализации, а делает это автоматически. А между тем решение даже самой простой задачи, выполняется за несколько простых шагов. Такая последовательность называется алгоритмом.

Алгоритм-это определенная последовательность действий, строгое выполнение которых приводит исполнителя к решению поставленной перед ним задачи. Алгоритм содержит несколько шагов. Шаг-это отдельное, законченное действие. Исполнителем алгоритма может быть как человек, так и любой механизм, электронный прибор, робот или вычислительная машина. Но разрабатывать алгоритмы может только человек.

Само название алгоритм произошло от имени среднеазиатского математика Аль-Хорезми жившего в 783-850гг. В своей книге он изложил правила записи натуральных чисел с помощью арабских цифр и правила действия над ними «столбиком» известные теперь каждому школьнику.

1.2. Свойства алгоритмов

Выделяют следующие свойства алгоритмов.

1. Понятность. Каждый шаг алгоритма должен быть понятен исполнителю. Не допускается какой-либо неопределенности, неоднозначности или двусмысленности в толковании действий. Все должно быть четко и ясно.

2. Дискретность. Путь решения задачи разделен на отдельные шаги, действия.

3. Конечность. Любой выполняемый алгоритм должен приводить к результату за конечное число шагов.

4. Результативность. Каждый алгоритм должен быть направлен на достижение результата за конечное число шагов.

5. Массовость. Качественный алгоритм способен решать не одну задачу, а целый ряд однотипных задач.

1.3. Представление алгоритмов

Алгоритмы можно записывать разными способами. Выбор средств, для записи алгоритмов зависит от его назначения и от того, кто будет его исполнять.

1.3.1. Словесная форма. Данный способ описания алгоритма представляет словесный перечень действий на естественном языке. Никаких правил составления данного описания не существует. Любая инструкция по применению чего-либо — это алгоритм, записанный в словесной форме.

Например, в учебнике русского языка есть памятка «Как составить план текста». Для этого необходимо:

1.Разделить текст на законченные по смыслу части.

2.Определить основную мысль каждой части.

3. Озаглавить каждую часть текста.

Данный алгоритм записан в виде текста. Его последовательное выполнение приведет ученика к необходимому результату. Все правила в учебнике «Русского языка» записаны в виде словесного алгоритма: как разобрать слово по составу, синтаксический разбор предложений, правило правописания гласных в корне слова и другие.

1.3.2. Графический способ. Для изображения алгоритма графически используют блок-схемы. Они представляют собой геометрические фигуры (блоки), соединенные между собой стрелками. Стрелки показывают связь между этапами и порядок их выполнения. Каждый блок имеет свое значение и сопровождается надписью.

Этот способ имеет ряд приемуществ. Благодаря наглядности он обеспечивает понятность алгоритма и явно отображает порядок выполнения определенных команд.

Словесная и графическая формы представления алгоритмов предназначены для человека.

1.3.3. Программы. Алгоритм, записанные на языке программирования называется программой. Такие алгоритмы пишутся для компьютеров, вычислительной техники, электронных приборов и т.д. Выполнение даже очень простых расчетов могут поставить человеа в тупик, если их надо будет произвести тысячу раз. А если операцию надо произвести миллион раз, это просто может свести с ума. Компьютер же справится с этой задачей всего за несколько секунд. Для этого и пишутся программы-алгоритмы.

1.4. Виды алгоритмов

Различают несколько видов алгоритмов.

1.4.1. Линейные алгоритмы. Это алгоритмы, в которых команды выполняются однократно, последовательно одна за другой. Они являются самыми распространенными в нашей жизни. Например, утром я встаю и собираясь на тренировку, выполняю действия по линейному алгоритму: встать, умыться, заправить кровать, одеться, позавтракать и я уже готова. Или написание исследователькой работы тоже происходит по линейному алгоритму. Запишем данный алгоритм графически.

Придерживаясь данного алгоритмы действий, можно эффективно распределить силы и время. План работы позволит упростить сбор и анализ информации, поможет сэкономить время в написании работы.

1.4.2. Разветвляющиеся алгоримты. В этих алгоритмах помимо действий содержится хотябы одно условие, проверка которого обеспечивает переход на один из возможных вариантов решения. Каждый возможный путь называется ветвью алгоритма. Ветвящийся процесс, имеющий две ветви называется простым, если в алгоритме более двух ветвей, такой алгоритм называется сложным. Напрвление ветвления выбирается логической проверкой условия, в результате которой возможны толко два ответа: «да»- условие выполнено или «нет»- условие не выполнено.

Разветвляющиеся алгоритмы также встречаются в повседневной жизни школьника. Например, измерение температуры при входе в школу.

Условие: «температура выше нормы?» Если «да», то идешь домой и вызываешь врача. Если «нет», то проходишь в школу на занятия. Запишем данный алгоритм графически.

Это простой ветвящийся алгоритм с двумя ветвями.

1.4.3. Циклические алгоритмы. Такие алгоритмы предусматривают многократное повторение некоторой последовательности действий. Количество повторений зависит от условий задачи. Например, я в школу добираюсь на трамвае. Я знаю, что мне нужно выйти на остановке «ЦУМ». Каждый раз, когда трамвай останавливается я проверяю условие «Это остановка ЦУМ?». Если «да», то я выхожу, если «нет», то еду до следующей остановки и снова проверяю свое условие. Эта последовательность будет повторятся до тех пор, пока условие не будет выполнено. Это и есть цикличность. Запишем этот алгоритм графичесим спомобом.

2. Практическая часть

Для того, чтобы максимально рационально использовать свое время я составлю для себя алгоритм «Расписание занятий». Запишу его ввиде блок-схемы. Также напишу программу на языке программирования Python.

С понедельника по пятницу кроме учебы в школе, я три раза в неделю занимаюсь в секции каратэ «Киокушинкай» и дополнительно два раза в неделю английским языком. Уроки в школе в зависимости от дня недели, начинаются и заканчиваются в разное время. Чтобы ничего не забыть, не перепутать и не опаздывать на занятия надо обработать имеющуюся информацию и составить расписание занятий на неделю.

2.1. Построение блок-схемы

Построение начинается с блока «Начало». Затем следует блок ввода исходной информации. В моем случае это дни недели: понедельник, вторник, среда, четверг, пятница. Для упрощения ввода присвоим каждому дню недели определённую преременную a, b, c, d, e соответственно. Теперь проверяем первое условие: «Какой день недели?» Если понедельник, среда или пятница, то в блоке вывода информации записываем «8:30-10:30 каратэ», если нет, то «10:00-11:00 английский язык». Затем аналогично проверяем еще несколько условий «День недели понедельник?», «День недели среда?», «День недели вторник?» После проверки этих условий в зависимости от ответв «да» или «нет» выводится информация о начале и окончании занятий в школе, а так же предметов на этот день. В результате построения блок-схемы у нас получился сложный разветвляющийся алгоритм.

Для наглядности полученное расписание занятий я занесла в таблицу.

2.2. Исходный код

Так же свое расписание я записала в виде программы. Программа задаёт вопрос: «Какой завтра день недели?» Вводя любой день недели, я получаю в ответ расписание занятий на этот день. Это поможет мне накануне подготовиться к необходимым предметам , собрать портфель и распланировать оптимально свое время, начиная с подъема.

Для записи разветвляющегося алгоритма на языке Python используют условный оператор IF—ELSE (если-иначе). Для вывода текста на печать пишем PRINT. Знаки для записи условий обозначаются следующим образом: ==равно, <= больше, >=меньше, != не равно. Исходную переменную обозначаем dn— день недели. В результате записи нашего алгоритма на языке Python получили исходный код.

Заключение

В результате проведенного мною исследования, я изучила понятие алгоритма, пронаблюдала и выяснила: где, как и когда в своей жизни я использую алгоритмы. Составила свой алгоритм «Расписание занятий», записала его в виде блок-схемы, результаты занесла в таблицу. Написала для данного алгоритма программу на языке Python и разместила на своем ноутбуке, на рабочем столе, для удобства её использования. На основании проделанной работы я пришла к выводу, что даже если бы я не знала язык программирования и не умела писать программы, я все равно использую алгоритмы в моей повседневной жизни. По дороге в школу и домой, в учебном процессе, в режиме дня они сопровождают меня повсюду. Значит гипотеза, выдвинутая мною в начале исследования, что область использования алгоритмов не сводится только к программированию — полностью подтвердилась.

В большинстве случаев результат моей деятельности напрямую зависит от того, насколько четко я понимаю алгоритмическую сущность своих действий: что делать в каждый момент, в какой последовательности и каким должен быть итог этих действий. Умение составлять и использовать различные алгоритмы формируют особый вид мышления — алгоритмический. Данный вид мышления позволяет экономить мое время и решать поставленные передо мной задачи с максимальной эффективностью.

Список литературы

Панос Луридас. Алгоритмы. Самый краткий и понятный курс. — Москва: «Бомбора», 2022.-192с.

Бхаргава Адитья. Грокаем алгоритмы. Иллюстрированное пособие для программистов и любопытствующих. — Санкт-Петербург: «Питер», 2022.-208с.

Овчинникова Г.Н. Информатика-4. Основы алгоритмизации. – Пермь: «Издательство Пермского университета», 1999.-56с.

Чан Джейми. Python: быстрый старт. — Санкт-Петербург: «Прогресс книга», 2022.-224с.

Тони Геддис. Начинаем программировать на Python.- Санкт-Петербург: «БХВ», 2019.- 768с.

Алгоритмы и способы их написания. [Электронный ресурс]: Информатика. учебное пособие. http://psk68.ru/files/metod/uchebnik_Informatika/glav.html

Алгоритм и его свойства. [Электронный ресурс]. Фоксфорд. https://foxford.ru/wiki/informatika/algoritm—i—ego—svoystva

Просмотров работы: 182

Составте алгоритм выполнения домашнего задания

! Способы записи алгоритмов:

1. словесная (текстовая) форма записи;

2. графическая форма записи — схемы
   алгоритмов;

3. программная — запись алгоритма
   на алгоритмическом языке;

4. псевдокоды.

1. Словесная запись
алгоритма содержит тщательно отобранный
набор фраз, без повторений и неоднозначностей
Команды алгоритма нумеруются, чтобы
иметь возможность на них ссылаться. В
командах помимо слов могут использоваться
символы и формулы. Форма записи команд
не формализованная. Команды такого
алгоритма выполняются в естественной
последовательности, если не оговорено
противное. Словесная запись алгоритма
ориентирована на исполнителя – человека.

Важно
лишь, чтобы каждая команда была понятна
исполнителю, точно определяла все его
действия и могла быть им выполнена.

Приведем
в качестве примера словесной формы
записи алгоритма алгоритм «бытовой
сферы».

Пример:

Алгоритм «Посади дерево»

1. Возьми лопату и
   саженец.

2. Выкопай ямку.

3. Возьми саженец.

4. Посади саженец в
   ямку.

5. Засыпь ямку землей.

6. Возьми лейку с водой
   и полей саженец.

7. Поставь лопату и
   лейку на место.

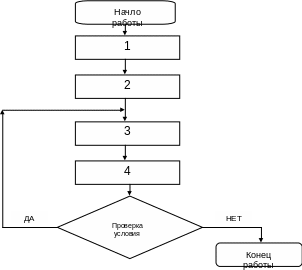
2. Схемы алгоритмов
– это графическое представление
метода решения задачи.

Схемы представляют
алгоритм в наглядной форме. Команды
алгоритма помещаются внутрь блоков,
соединенных стрелками, показывающими
очередность выполнения команд алгоритма.
Приняты определенные стандарты
графических изображений:

Рис. 1

Для
записи внутри блоков используется
естественный язык с элементами
математической символики. В блоке
«Проверка условия» в результате проверки
условия возникают два возможных пути
продолжения алгоритма. Эти пути отражаются
стрелками с соответствующими надписями
“Да” и “Нет”.

Рассмотрим
алгоритм “бытовой сферы”, записанный
двумя способами: словесной записью и с
помощью схемы алгоритма.

Пример:

Алгоритм «Заточи сломанные карандаши»

1. Собери все сломанные
   карандаши.

2. Возьми точилку.

3. Возьми один сломанный
   карандаш.

4. Заточи его.

5. Если есть еще
   сломанные карандаши, перейди к пункту
   3.

Блок-схема алгоритма

Рис. 2

Схемы
алгоритмов обладают большей наглядностью,
чем словесная запись алгоритма. Однако,
эта наглядность быстро теряется при
изображении очень большого алгоритма,
т. к. в этом случае схема получается
плохо обозрима.

1. Псевдокод
   – это
   язык записи структурированных алгоритмов,
   состоит из смеси языка высокого уровня
   и фраз родного языка исполнителя.
   Стандартов на псевдокод нет, существует
   он как средство разработки программ.
   По сравнению со словесным алгоритмом
   псевдокод ближе программным конструкциям.
   Основное достоинство псевдокода – он
   позволяет пользователю легко разобраться
   в самом длинном и сложном алгоритме,
   поэтому чаще всего псевдокод используется
   для документирования программ.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #

  19.04.2015730.62 Кб7376.doc

• #
• #
• #