Нередко при алгоритмическом решении задачи возникает необходимость создания цикла, содержащего в своем теле другой цикл. Такие вложенные друг в друга циклы относятся к структурам вложенных циклов. Порядок вложенности циклов, когда в теле внутреннего цикла содержатся другие циклы, может быть достаточно большим. Этот порядок определяется методом, с помощью которого достигается решение поставленной задачи. Так, при обработке одномерных массивов, как правило, удается построить алгоритмическую схему без вложения циклов. Однако в ряде случаев при решении таких задач без вложенных циклов не обойтись.
Отметим, что все вложенные друг в друга циклы, включая наружный, должны иметь счетчики с различными именами. Вне этих циклов счетчики могут быть использованы как обычные переменные или как счетчики других циклов.
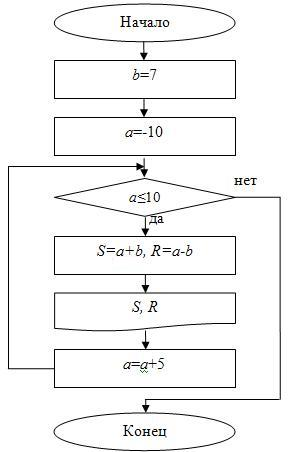
Пример 1. Рассмотрим задачу сортировки одномерного массива Z длины N. Отсортировать массив – значит расположить его элементы в порядке роста или убывания.
Опишем метод сортировки массива в порядке роста. Сначала выполняется проход по массиву с целью определения в нем наименьшего элемента. Затем производится перестановка этого элемента с первым. Далее совершается второй проход по массиву, начиная со второго элемента. Найденный наименьший элемент переставляется со вторым и т. д. После (N-1)-го прохода с выполнением названных операций массив окажется отсортированным.
Блок-схема этого алгоритма сортировки показана на рисунок 1. Она включает 12 блоков. После начала работы в блоке 2 переменная N и массив Z заполняются константами. Затем в блоке 3 проверяется условие о том, нужно ли сортировать массив.
Это сводится к установлению факта наличия в массиве нескольких элементов, т. к. массив из одного элемента всегда отсортирован. Если этот факт установлен, то алгоритм приступает к сортировке. Процедура сортировки выполняется в цикле, объединяющем блоки 4-10. В теле этого цикла содержится другой цикл, который образован блоками 6-8. Его назначение станет ясно из дальнейшего разбора алгоритма.
После входа в наружный цикл его счетчик i примет значение 1, что в рамках нашего метода подразумевает первый проход по массиву.
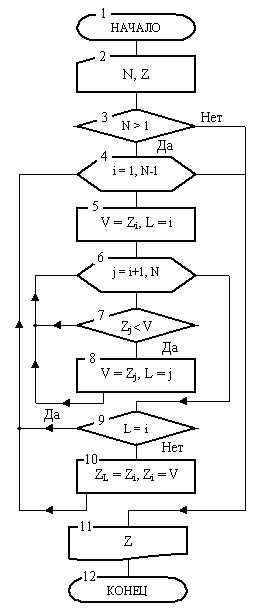
Далее будут выполнены блоки 5-10, составляющие тело наружного цикла. В блоке 5 размещены две вспомогательные переменные V и L. Первая из них предназначена для фиксирования наименьшего элемента, а вторая – для запоминания его индекса. Так как i = 1, то при первом проходе в блоке 5 V примет значение первого элемента, а L значение 1. Затем во внутреннем цикле, образованном блоками 6-8, где его счетчик j будет изменяться от 2 до N, последовательно проводится сравнение соответствующих элементов массива Z со значением переменной V. При этом всякий раз, как будет найден меньший чем v элемент, значение V будет заменено на значение этого элемента, а в переменной L будет зафиксирован его индекс. Понятно, что после выполнения внутреннего цикла в переменной V будет содержаться значение, равное наименьшему элементу, а в L – индекс этого элемента. В блоке 9 далее проверяется, не является ли наименьший элемент первым элементом массива. Если это не так, то в блоке 10 на место наименьшего элемента (его номер L) запишется первый (т. к. при первом проходе L =1 ), а на место первого элемента – наименьший (он равен V). После этого произойдет возврат управления к заголовку наружного цикла блоку 4. В нем значение счетчика станет равным i = 2.
Затем вновь выполняется его тело, но уже для нового значения счетчика i. Теперь с помощью блоков 5-10 отыскивается наименьший элемент массива начиная с номера 2. Затем в блоках 9-10 он займет второе место в массиве и т. д. Когда тело наружного цикла выполнится (N-1), раз массив будет отсортирован.
В блоке 12 отсортированный массив будет выведен и в блоке 13 алгоритм окончит работу.
Алгоритмы со структурами вложенных циклов часто используют при решении задач обработки двумерных массивов. В таких алгоритмах счетчики циклов используются для манипуляции с индексами массивов.
Пример 2. Дан двумерный квадратный массив Z, состоящий из N строк и N столбцов. Необходимо найти среднее арифметическое S его отрицательных элементов и заменить положительные элементы побочной диагонали массива средним арифметическим S.
Блок-схема алгоритма показана на рисунок 2. Она состоит из 13 блоков. В блоке 2 переменная N и весь массив Z заполняются константами. В блоке 3 рабочие переменные S и К получает значение нуль. Переменная S сначала будет играть роль сумматора отрицательных элементов массива, затем после накопления суммы она примет значение среднего арифметического. Переменная К нужна для подсчета количества отрицательных элементов массива.
В блоках 4-7 выполняется накопление суммы отрицательных элементов массива.
Эти блоки образует два вложенных цикла, причем внутренний цикл со счетчиком j является телом наружного цикла со счетчиком i. Проанализируем работу этой структуры.
После входа в наружный цикл в блоке 4 переменная i примет значение i = 1. Далее будет выполнено его тело ( блоки 5-7 ), которое, в свою очередь, также является циклом. После входа во внутренний цикл в блоке 5 переменная j примет значение j = 1. Затем в блоке 6 проверяется на отрицательность элемент массива Z, расположенный в первой строке и первом столбце, т. к. i = 1 и j = 1.
Если он окажется отрицательным, то в блоке 7 переменная К увеличится на 1, а к S добавляется значение этого элемента. После этого выполняется возврат к блоку 5, т. е. к заголовку внутреннего цикла. Здесь j увеличится на 1, станет равной j = 2 и управление перейдет к блоку 6. В нем проверяется элемент, стоящий все в той же первой строке, но во втором столбце (i = 1, j = 2). Если он окажется отрицательным, то К снова увеличится на 1, а к накопленному к этому времени S добавляется значение этого элемента и т.д. Когда полностью выполнится внутренний цикл, т. е. переменная j «пробежит» от 1 до N, в переменную S накопится сумма всех отрицательных элементов первой строки массива, а в К – их количество. Теперь управление передается к блоку 4 заголовка наружного цикла, где i станет равной i = 2. Снова будет отработано его тело, т. е. цикл 5-7. При этом будет найдена уже сумма отрицательных элементов первых двух строк массива, а в К сохранится количество этих элементов. Когда выполнится весь наружный цикл, в S будет константа, равная сумме отрицательных элементов всего массива, а в К – их количество. Теперь управление перейдет к блоку 8. Если окажется, что в массиве есть отрицательные элементы (К>0), то в блоке 9 вычисляется среднее арифметическое как отношение суммы элементов к их количеству. Результат помещается а ту же переменную S. Отметим, что если бы блок 8 проверки отсутствовал, то при К = 0 (в массиве нет ни одного отрицательного элемента) в блоке 9 из-за деления на нуль возникла бы ошибка. Эта ошибка повлекла бы аварийное завершение вычислений до окончания работы алгоритма.
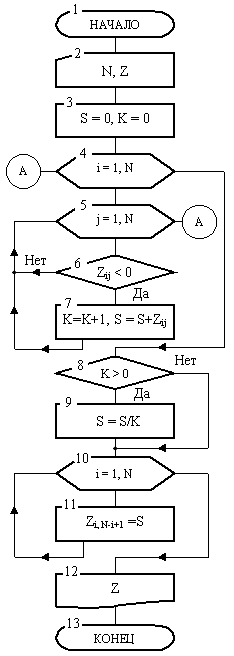
Далее выполняется блоки 10-11, которые также образует цикл. В нем производится замена элементов побочной диагонали на среднее арифметическое S (побочной диагональю является прямолинейная цепочка ячеек в диапазоне от нижнего левого угла до верхнего правого угла массива). Обратите внимание, на то что переменная i, которая использовалась ранее, в целях экономии памяти применяется вновь.
Проследим работу этого цикла. После входа в блок 10 счетчик примет значение i = 1. Затем в блоке 11 при этом значении будет вычислен индекс столбца элемента N – 1 + i = N. Таким образом, элемент с индексами (1, N) станет равным S. На втором круге цикла i увеличится на 1 и станет i = 2. Нетрудно видеть, что теперь элемент (2, N-1) станет равным S и т. д. На последнем круге цикла элемент (N, 1) получит значение S, что завершит изменение значений всех элементов побочной диагонали на среднее арифметическое S.
Наконец, в блоке 12 измененный массив будет выведен и в блоке 13 алгоритм закончит работу.
Занятие 4. Графическая реализация циклического алгоритма
В рассмотрении циклического алгоритма следует выделить несколько понятий.
Тело цикла – это набор инструкций, предназначенный для многократного выполнения.
Итерация – это единичное выполнение тела цикла.
Переменная цикла – это величина, изменяющаяся на каждой итерации цикла.
Каждый цикл должен содержать следующие необходимые элементы:
- первоначальное задание переменной цикла,
- проверку условия,
- выполнение тела цикла,
- изменение переменной цикла.
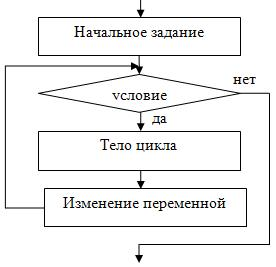
Циклы бывают двух видов – с предусловием и с постусловием. В цикле с предусловием сначала проверяется условие входа в цикл, а затем выполняется тело цикла, если условие верно. Цикл с предусловием представлен на рис. 2.9. Цикл с предусловием также может быть задан с помощью счетчика. Это удобно в тех случаях, когда точно известно количество итераций. В общем виде блок-схема, реализующая цикл с предусловием, представлена ниже. Сначала задается начальное значение переменной цикла, затем условие входа в цикл, тело цикла и изменение переменной цикла. Выход из цикла осуществляется в момент проверки условия входа в цикл, когда оно не выполняется, т.е. условие ложно. Цикл с предусловием может ни разу не выполниться, если при первой проверке условия входа в цикл оно оказывается ложным.
Рис.
2.9.
Циклический алгоритм с предусловием в общем виде
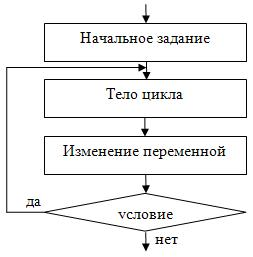
В цикле с постусловием сначала выполняется тело цикла, а потом проверяется условие. Циклический алгоритм с постусловием представлен на рис. 2.10.
Рис.
2.10.
Циклический алгоритм с постусловием в общем виде
Если условие верно, то итерация повторяется, если же неверно, то осуществляется выход из цикла. В отличие от цикла с предусловием, любой цикл с постусловием всегда выполнится хоть раз.
Примечание. Как видно из представленных блок-схем для циклов с предусловием и постусловием, условие записывается внутри блока условия (формы ромба), как и в разветвляющемся алгоритме. Принципиальная разница между разветвляющимся и циклическим алгоритмами при графической реализации состоит в том, что в циклическом алгоритме в обязательном порядке присутствует стрелка, идущая наверх. Именно эта стрелка обеспечивает многократный повтор тела цикла.
Приведем простейшие примеры, соответствующие циклическому алгоритму.
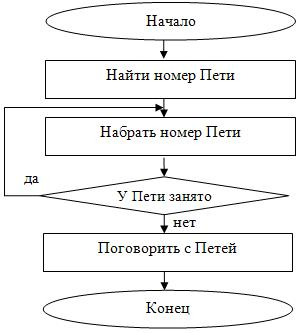
Пример 7. Вася звонит Пете, но у Пети может быть занята линия. Составить блок-схему действий Васи в этом случае.
Решение. Когда телефонная линия занята, то необходимо снова и снова набирать номер, пока Петя не закончит предыдущий разговор, и телефонная линия не окажется вновь свободной. Блок-схема представлена на рис. 2.11.
Рис.
2.11.
Блок-схема для примера 7
Здесь тело цикла состоит из одного действия «Набрать номер Пети», т.к. именно это действие следует повторять, пока линия будет занята. Под итерацией цикла понимается очередная попытка дозвониться до Пети. Как таковой переменной цикла здесь нет, т.к. ситуация взята из жизни. Выход из цикла происходит в тот момент, когда условие «У Пети занято» стало неверным, т.е. телефонная линия свободна – действительно, нет необходимости больше набирать номер Пети. В данном примере применен цикл с постусловием, т.к. сначала необходимо набрать номер Пети, ведь иначе мы не можем ответить на вопрос – занята ли линия у Пети.
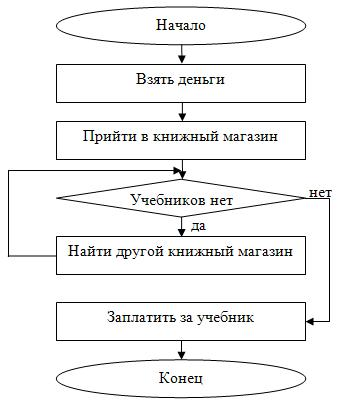
Пример 8. Ученику требуется купить учебник. Составить блок-схему, описывающую действия ученика в случае, если учебника нет в ряде магазинов.
Решение. Действия ученика в данном примере очевидны: когда он приходит в первый и любой последующий магазины, то возможны два варианта – учебник имеется в наличии или учебника нет в продаже. Если учебника нет в продаже, то ученику следует пойти в другой книжный магазин и спросить данный учебник, и т.д. пока учебник не будет куплен, т.к. перед учеником стоит конечная цель – купить учебник. Мы будем использовать цикл с предусловием, т.к. сначала требуется найти магазин, имеющий в наличии данный учебник. Цикл будет выполняться, пока условие «В данном магазине нет учебника» будет верным, а выход из цикла осуществится, когда условие станет ложным, т.е. когда ученик придет в магазин, в котором есть данный учебник. Действительно, в этом случае ученик купит нужный ему учебник и не будет больше искать книжные магазины. Результат блок-схемы представлен на рис. 2.12.
Рис.
2.12.
Блок-схема для примера 8
Здесь тело цикла состоит из одного действия «Найти другой книжный магазин». Переменной цикла в явном виде нет, но можно подразумевать номер магазина, в который пришел ученик в очередной раз. Как любой другой цикл с предусловием, данный цикл может ни разу не выполниться (не иметь итераций), если в первом же магазине окажется нужный учебник.
Примечание. Если в данную задачу добавить условие выбора учебника в жесткой или мягкой обложке, как в примере 5, то оно появится после выхода из цикла. На реализацию циклического алгоритма данное условие не повлияет.
Пример 9. Даны числа 







Решение. В отличие от примеров 3 и 6 здесь число 






Рис.
2.13.
Блок-схема для примера 9 (с предусловием)
Тело цикла состоит из нескольких действий: вычисление суммы, вычисление разности и вывод полученных данных на экран. Таким образом, у нас получится несколько значений сумм и разностей, т.к. 

Данная задача может быть сделана и с циклом с предусловием, и с постусловием. В этом случае тело цикла, условие и изменение переменной цикла будут такими же, как и в цикле с предусловием, но сначала необходимо выполнить тело цикла, а потом проверить условие для выполнения следующей итерации.
Приведем блок-схему, использующую цикл с постусловием, на рис. 2.14.
Рис.
2.14.
Блок-схема для примера 9 (с постусловием)
В данной задаче также могут быть соединены циклический и разветвляющийся алгоритмы, если по условию задачи требуется сравнить полученные значения суммы и разности, как в примере 6. В этом случае цикл можно реализовать как с предусловием, так и с постусловием, а сравнение суммы и разности добавится внутрь тела цикла, т.к. следует сравнить между собой все полученные суммы и разности. Организация самого цикла останется прежней. Приведем на рис. 2.15а блок-схему с предусловием, а на рис. 2.15б блок-схему с постусловием.
Рис.
2.15.
Блок-схема с ветвлением для примера 9: а) с предусловием, б) с постусловием
Схема — это абстракция какого-либо процесса или системы, наглядно отображающая наиболее значимые части. Схемы широко применяются с древних времен до настоящего времени — чертежи древних пирамид, карты земель, принципиальные электрические схемы. Очевидно, древние мореплаватели хотели обмениваться картами и поэтому выработали единую систему обозначений и правил их выполнения. Аналогичные соглашения выработаны для изображения схем-алгоритмов и закреплены ГОСТ и международными стандартами.
На территории Российской Федерации действует единая система программной документации (ЕСПД), частью которой является Государственный стандарт — ГОСТ 19.701-90 «Схемы алгоритмов программ, данных и систем» [1]. Не смотря на то, что описанные в стандарте обозначения могут использоваться для изображения схем ресурсов системы, схем взаимодействия программ и т.п., в настоящей статье описана лишь разработка схем алгоритмов программ.
Рассматриваемый ГОСТ практически полностью соответствует международному стандарту ISO 5807:1985.
Содержание:
- Элементы блок-схем алгоритмов
- Примеры блок-схем
- Нужны ли блок-схемы? Альтернативы
Элементы блок-схем алгоритмов
Блок-схема представляет собой совокупность символов, соответствующих этапам работы алгоритма и соединяющих их линий. Пунктирная линия используется для соединения символа с комментарием. Сплошная линия отражает зависимости по управлению между символами и может снабжаться стрелкой. Стрелку можно не указывать при направлении дуги слева направо и сверху вниз. Согласно п. 4.2.4, линии должны подходить к символу слева, либо сверху, а исходить снизу, либо справа.
Есть и другие типы линий, используемые, например, для изображения блок-схем параллельных алгоритмов, но в текущей статье они, как и ряд специфических символов, не рассматриваются. Рассмотрены лишь основные символы, которых всегда достаточно студентам.
 |
Терминатором начинается и заканчивается любая функция. Тип возвращаемого значения и аргументов функции обычно указывается в комментариях к блоку терминатора. |
 |
В ГОСТ определено множество символов ввода/вывода, например вывод на магнитные ленты, дисплеи и т.п. Если источник данных не принципиален, обычно используется символ параллелограмма. Подробности ввода/вывода могут быть указаны в комментариях. |
 |
В блоке операций обычно размещают одно или несколько (ГОСТ не запрещает) операций присваивания, не требующих вызова внешних функций. |
 |
Блок в виде ромба имеет один вход и несколько подписанных выходов. В случае, если блок имеет 2 выхода (соответствует оператору ветвления), на них подписывается результат сравнения — «да/нет». Если из блока выходит большее число линий (оператор выбора), внутри него записывается имя переменной, а на выходящих дугах — значения этой переменной. |
 |
Вызов внешних процедур и функций помещается в прямоугольник с дополнительными вертикальными линиями. |
 |
Символы начала и конца цикла содержат имя и условие. Условие может отсутствовать в одном из символов пары. Расположение условия, определяет тип оператора, соответствующего символам на языке высокого уровня — оператор с предусловием (while) или постусловием (do … while). |
 |
Символ «подготовка данных» в произвольной форме (в ГОСТ нет ни пояснений, ни примеров), задает входные значения. Используется обычно для задания циклов со счетчиком. |
 |
В случае, если блок-схема не умещается на лист, используется символ соединителя, отражающий переход потока управления между листами. Символ может использоваться и на одном листе, если по каким-либо причинам тянуть линию не удобно. |
 |
Комментарий может быть соединен как с одним блоком, так и группой. Группа блоков выделяется на схеме пунктирной линией. |
Примеры блок-схем
В качестве примеров, построены блок-схемы очень простых алгоритмов сортировки, при этом акцент сделан на различные реализации циклов, т.к. у студенты делают наибольшее число ошибок именно в этой части.
Сортировка вставками
Массив в алгоритме сортировки вставками разделяется на отсортированную и еще не обработанную части. Изначально отсортированная часть состоит из одного элемента, и постепенно увеличивается.
На каждом шаге алгоритма выбирается первый элемент необработанной части массива и вставляется в отсортированную так, чтобы в ней сохранялся требуемый порядок следования элементов. Вставка может выполняться как в конец массива, так и в середину. При вставке в середину необходимо сдвинуть все элементы, расположенные «правее» позиции вставки на один элемент вправо. В алгоритме используется два цикла — в первом выбираются элементы необработанной части, а во втором осуществляется вставка.
В приведенной блок-схеме для организации цикла используется символ ветвления. В главном цикле (i < n) перебираются элементы необработанной части массива. Если все элементы обработаны — алгоритм завершает работу, в противном случае выполняется поиск позиции для вставки i-того элемента. Искомая позиция будет сохранена в переменной j в результате выполнения внутреннего цикла, осуществляющем сдвиг элементов до тех пор, пока не будет найден элемент, значение которого меньше i-того.
На блок-схеме показано каким образом может использоваться символ перехода — его можно использовать не только для соединения частей схем, размещенных на разных листах, но и для сокращения количества линий. В ряде случаев это позволяет избежать пересечения линий и упрощает восприятие алгоритма.
Сортировка пузырьком
Сортировка пузырьком, как и сортировка вставками, использует два цикла. Во вложенном цикле выполняется попарное сравнение элементов и, в случае нарушения порядка их следования, перестановка. В результате выполнения одной итерации внутреннего цикла, максимальный элемент гарантированно будет смещен в конец массива. Внешний цикл выполняется до тех пор, пока весь массив не будет отсортирован.
На блок-схеме показано использование символов начала и конца цикла. Условие внешнего цикла (А) проверяется в конце (с постусловием), он работает до тех пор, пока переменная hasSwapped имеет значение true. Внутренний цикл использует предусловие для перебора пар сравниваемых элементов. В случае, если элементы расположены в неправильном порядке, выполняется их перестановка посредством вызова внешней процедуры (swap). Для того, чтобы было понятно назначение внешней процедуры и порядок следования ее аргументов, необходимо писать комментарии. В случае, если функция возвращает значение, комментарий может быть написан к символу терминатору конца.
Сортировка выбором
В сортировке выбором массив разделяется на отсортированную и необработанную части. Изначально отсортированная часть пустая, но постепенно она увеличивается. Алгоритм производит поиск минимального элемента необработанной части и меняет его местами с первым элементом той же части, после чего считается, что первый элемент обработан (отсортированная часть увеличивается).
На блок-схеме приведен пример использования блока «подготовка», а также показано, что в ряде случаев можно описывать алгоритм более «укрупнённо» (не вдаваясь в детали). К сортировке выбором не имеют отношения детали реализации поиска индекса минимального элемента массива, поэтому они могут быть описаны символом вызова внешней процедуры. Если блок-схема алгоритма внешней процедуры отсутствует, не помешает написать к символу вызова комментарий, исключением могут быть функции с говорящими названиями типа swap, sort, … .
На блоге можно найти другие примеры блок-схем:
- блок-схема проверки правильности расстановки скобок арифметического выражения [2];
- блок-схемы алгоритмов быстрой сортировки и сортировки слиянием [3].
Часть студентов традиционно пытается рисовать блок-схемы в Microsoft Word, но это оказывается сложно и не удобно. Например, в MS Word нет стандартного блока для терминатора начала и конца алгоритма (прямоугольник со скругленными краями, а не овал). Наиболее удобными, на мой взгляд, являются утилиты MS Visio и yEd [5], обе они позволяют гораздо больше, чем строить блок-схемы (например рисовать диаграммы UML), но первая является платной и работает только под Windows, вторая бесплатная и кроссплатфомренная. Все блок-схемы в этой статье выполнены с использованием yEd.
Частные конторы никакие блок-схемы не используют, в книжках по алгоритмам [6] вместо них применяют словесное описание (псевдокод) как более краткую форму. Возможно блок-схемы применяют на государственных предприятиях, которые должны оформлять документацию согласно требованиям ЕСПД, но есть сомнения — даже для регистрации программы в Государственном реестре программ для ЭВМ никаких блок-схем не требуется.
Тем не менее, рисовать блок-схемы заставляют школьников (примеры из учебников ГОСТ не соответствуют) — выносят вопросы на государственные экзамены (ГИА и ЕГЭ), студентов — перед защитой диплом сдается на нормоконтроль, где проверяется соответствие схем стандартам.
Разработка блок-схем выполняется на этапах проектирования и документирования, согласно каскадной модели разработки ПО, которая сейчас почти не применяется, т.к. сопровождается большими рисками, связанными с ошибками на этапах проектирования.
Появляются подозрения, что система образования прогнила и отстала лет на 20, однако аналогичная проблема наблюдается и за рубежом. Международный стандарт ISO 5807:1985 мало чем отличается от ГОСТ 19.701-90, более нового стандарта за рубежом нет. Там же производится множество программ для выполнения этих самых схем — Dia, MS Visio, yEd, …, а значит списывать их не собираются. Вместо блок-схем иногда применяют диаграммы деятельности UML [6], однако удобнее они оказываются, разве что при изображении параллельных алгоритмов.
Периодически поднимается вопрос о том, что ни блок-схемы, ни UML не нужны, да и документация тоже не нужна. Об этом твердят программисты, придерживающиеся методологии экстремального программирования (XP) [7], ходя даже в их кругу нет единого мнения.
В ряде случаев, программирование невозможно без рисования блок-схем, т.к. это один процесс — существуют визуальные языки программирования, такие как ДРАКОН [8], кроме того, блок-схемы используются для верификации алгоритмов (формального доказательства их корректности) методом индуктивных утверждений Флойда [9].
В общем, единого мнения нет. Очевидно, есть области, в которых без чего-то типа блок-схем обойтись нельзя, но более гибкой альтернативы нет. Для формальной верификации необходимо рисовать подробные блок-схемы, но для проектирования и документирования такие схемы не нужны — я считаю разумным утверждение экстремальных программистов о том, что нужно рисовать лишь те схемы, которые помогают в работе и не требуют больших усилий для поддержания в актуальном состоянии [10].
Список использованных источников:
- ГОСТ 19.701–90 (ИСО 5807–85) «Единая система программной документации».
- Алгоритм. Свойства алгоритма https://pro-prof.com/archives/578
- Алгоритмы сортировки слиянием и быстрой сортировки https://pro-prof.com/archives/813
- yEd Graph Editor https://www.yworks.com/products/yed
- Книги: алгоритмы https://pro-prof.com/books-algorithms
- Рамбо Дж., Якобсон А., Буч Г. UML: специальный справочник. -СПб.: Питер, 2002. -656 с.
- Кент Бек Экстремальное программирование: разработка через тестирование – СПб.: Питер – 2003
- Визуальный язык ДРАКОН https://drakon.su/
- Шилов Н.В. Верификация шаблонов алгоритмов для метода отката и метода ветвей и границ. Моделирование и анализ информационных систем, ISSN 1818 – 1015, т.18, №4, 2011
- Брукс Ф., Мифический человеко — месяц или как создаются программные системы. СПб. Символ Плюс, 1999 — 304 с. ил.
Циклы с параметрами
Цель: дать понятие о циклах с параметром, блок-схемах, изображающих такие циклы. Учить на частных примерах составлять блок-схемы и программы с циклами; дать понятие о различиях между циклами с предусловием, постусловием и циклом с параметром; учить в одной программе использовать разные циклы, если программа содержит несколько циклов; вводить и выполнять программы, используя компиляторы BPW или Turbo Pascal.
1. Оператор цикла for … to … do …
Иногда заранее известно, сколько раз должен выполняться цикл. Для задач такого типа в языке Паскаль имеются операторы циклов с параметрами.
Формат записи таких операторов следующий:
for <пар.цикла> := <нач.знач> to <кон.знач.> do <оператор>.
Здесь for, to, do — зарезервированные слова (для, до, выполнить);
<пар. цикла> — параметр цикла — переменная типа integer (точнее, любого порядкового типа);
<нач. знач.> — начальное значение — число или выражение того же типа;
<кон. знач.> — конечное значение — число или выражение того же типа;
<оператор> — произвольный оператор Паскаля.
Если операторов несколько, тогда, как и в операторе while … do …, используются операторные скобки: begin … end.
Например, возможны такие записи оператора цикла:
for i := a to b do s1;
for j := a to b do begin s1; s2; …, sn end; или
for k := p to m do
begin
s1;
s2;
…
sn
end;
Здесь s1, s2, s3, … sn — операторы цикла.
При выполнении оператора for вначале вычисляется выражение <нач .знач.> и осуществляется присваивание его значения переменной цикла
<пар .цикла> := <нач. знач.>.
После этого циклически повторяются:
1) проверка условия <пар .цикла> <кон. знач.>; если условие не выполнено, оператор for завершает работу;
2) выполнение оператора <оператор> или операторов s1; s2; s3; … sn;
3) переменная цикла <пар. цикла> увеличивается на единицу.
Надо сразу заметить, что задать шаг цикла, отличный от 1 в этом операторе, нельзя.
Графическое изображение циклов for будет таким (см. рис. 33):
Рис. 33
Здесь: i — переменная цикла; n — ее начальное значение; k — ее конечное значение. Тело цикла составляет оператор или несколько операторов: s1; s2; … sn;, которые нарисованы в прямоугольнике.
Для иллюстрации работы оператора for рассмотрим пример уже ставший традиционным при изучении работы этого оператора.
Пример 1. Составить программу вычисления факториала числа n, т. е. n!.
Вспомним из математики, что факториал числа n равен произведению чисел от 1 до n.
Например:
Замечание. В математике принято: 0! = 1.
Блок-схема
Рис. 34
Программа
Program Problem1; { Вычисление факториала числа n! }
uses WinCrt;
var
n, f, i : longint;
begin
write(«Введите натуральное число «); readln(n);
f := 1;
if n <> 0 then for i := 1 to n do f := f*i;
writeln(«Факториал числа «, n, » равен «, f)
end.
Переменная n — для вводимого пользователем числа, факториал которого надо найти; f — переменная, в которой будет «накапливаться» значение факториала числа n; i — переменная цикла.
Устанавливается первоначальное значение переменной f := 1.
Далее начинается цикл. Переменной i присваивается начальное значение 1; оно сравнивается с конечным — n (1 <= n), если условие истинно, тогда выполняется оператор (в этой программе он один): f := f*i, 1*1=1; значение переменной цикла увеличивается на 1, т. е. станет равным: i := i + 1, 1 + 1 = 2 и цикл повторяется.
Когда значение i станет равным n, тогда цикл выполнится последний раз, потому что следующее значение i будет n + 1, что больше конечного значения n, условие i <= n — ложно, цикл не выполняется.
2. Оператор цикла for…downto…do…
Существует другая форма оператора цикла for:
for <пар .цик.> := <нач. зн.> downto <кон. зн.> do <оператор>.
Замена зарезервированного слова to на downto означает, что шаг параметра цикла равен (-1).
Изменение значения параметра идет от большего значения к меньшему, т. е.
<нач. знач.> <кон. знач.>.
Программу вычисления факториала числа можно составить, используя этот оператор цикла.
Программа
Program Problem1a;
uses WinCrt;
var
n, i, f : longint;
begin
write(«Введите натуральное число «); readln(n);
f := 1;
if n <> 0 then for i := n downto 1 do f := f*i;
writeln(«Факториал числа «, n, » равен «, f)
end.
Задание 1
1. Выполните программу примера 1 на компьютерах.
2. Измените и дополните ее так, чтобы она вычисляла следующую сумму:
Разберем другие, на мой взгляд, более интересные примеры с использованием циклов for … to … do …, а также вложенных друг в друга циклов (циклов в циклах), совмещение циклов с параметром с другими циклами.
Пример 2. Квадрат любого натурального числа n равен сумме n первых нечетных чисел:
12 = 1
22 = 1 + 3
32 = 1 + 3 + 5
42 = 1 + 3 + 5 + 7
52 = 1 + 3 + 5 + 7 + 9
. . . . . . . . . . . . . . . . . . .
Основываясь на этом свойстве, составить программу, позволяющую напечатать квадраты натуральных чисел от 1 до n.
Ясно, что цикл в программе надо организовать от 1 до n, в котором выполнять всего три оператора: находить сумму нечетных чисел (а их как раз столько, сколько раз будет выполняться цикл); выдавать полученную сумму на экран; «получать» следующее нечетное число.
Блок-схема
Рис. 35
Программа
Program Problem2;
uses WinCrt;
var
i, n, s, k: integer;
begin
writeln(«Введите натуральное число, до которого надо»);
write(«выводить квадраты чисел «); readln(n);
writeln(«Квадраты чисел следующие:»);
s := 0; k := 1;
for i := 1 to n do
begin
s := s + k;
writeln(«Квадрат числа «, i, » равен «, s);
k := k + 2
end
end.
Задание 2
1. Измените программу так, чтобы она выдавала на экран не таблицу квадратов чисел от 1 до n, а квадрат только одного числа n, введенного пользователем.
2. Измените и дополните программу так, чтобы она выдавала значение квадрата числа и те нечетные числа, сумме которых он равен.
3. Продолжая тему возведения натуральных чисел в степень, без операций умножения, рассмотрим еще два интересных примера. В первом из них нам придется совмещать, «вкладывать» друг в друга два цикла for, а во втором, циклы for и repeat.
Пример 3. Куб любого натурального числа n равен сумме n нечетных чисел, следующих по порядку за числами, сумма которых составляла куб предыдущего числа n — 1:
13 = 1
23 = 3 + 5
33 = 7 + 9 + 11
43 = 13 + 15 + 17 + 19
. . . . . . . . . . . . . . . . . . . . . .
Основываясь на этом свойстве, создайте программу, позволяющую напечатать таблицу кубов натуральных чисел.
Вот здесь уже нужны два цикла. Один — внешний, по количеству нечетных чисел, которое равно возводимому в куб числу, например, для 43 этот цикл должен выполняться 4 раза. В этом же цикле надо будет после подсчета суммы выводить ее значение на экран вместе с числом, которое возводится в куб.
Второй — внутренний, который будет суммировать нечетные числа и «вырабатывать» нужные нечетные числа для суммирования.
Блок-схема
Рис. 36
Программа
Program Problem3; { Кубы натуральных чисел от 1 до n }
uses WinCrt;
var
i, j, n, s, k : longint;
begin
writeln(«Введите натуральное число, до которого надо»);
write(«выводить кубы чисел «); readln(n);
writeln(«Кубы чисел следующие:»);
k := 1;
for i := 1 to n do
begin
s := 0;
for j := 1 to i do
begin
s := s + k;
k := k + 2
end;
writeln(«Куб числа «, i, » равен «, s)
end
end.
Разберем работу этой программы
Переменные i и j нужны в качестве переменных первого — внешнего и второго — внутреннего циклов. Переменная k для нечетных чисел, а s для суммы чисел. Тип этих переменных установлен целый, но longint, так как могут быть достаточно большие целые числа, большие 32767.
Программа начинается с запроса для пользователя с помощью операторов writeln и write о вводе натурального числа, до которого надо выдавать таблицу кубов чисел. Затем с помощью оператора readln это значение вводится в память компьютера и присваивается переменной n.
Выводится надпись «Кубы чисел следующие«. Она дана перед началом циклов по понятным причинам. В циклах ее дать нельзя, — она будет повторяться несколько раз. По окончании циклов тоже, тогда она будет написана внизу, после вывода самих чисел. Переменной k присваивается первое нечетное значение 1.
Начинается внешний цикл по количеству чисел, от 1 до n. В цикле несколько операторов, поэтому «открываются» операторные скобки: — begin …
Перед началом внутреннего цикла обнуляется переменная s — сумма. Причем такое обнуление будет происходить каждый раз, когда повторяется внешний цикл, перед началом выполнения внутреннего цикла.
Внутренний цикл выполняется от 1 до i. Почему? В цикле вычисляется сумма и увеличивается нечетное k на 2, т. е. «вырабатывается» следующее нечетное число.
Заметьте! Переменной k не присваивается перед началом каждого внутреннего цикла 1. Почему?
Следующим оператором writeln внутри внешнего цикла выдается информация на экран. Почему он размещен во внешнем цикле?
Пример 4. Из математики известно, что всякая натуральная степень числа n есть сумма n последовательных нечетных натуральных чисел. Составьте программу, которая для любой степени натурального числа n находила бы последовательность нечетных чисел, сумме которых равна эта степень.
Например, для 53 она выдавала бы последовательность чисел: 21, 23, 25, 27, 29.
План составления программы
1. Определим цель составления программы: надо показать, что действительно любую натуральную степень натурального числа можно представить в виде суммы последовательных нечетных чисел.
А если это так, тогда нам совершенно необходимо знать значение степени числа n с показателем k.
Это можно сделать с помощью простого цикла:
s := 1;
for i := 1 to k do s := s*n;
Значение степени будут накапливаться в переменной s, для этого ей устанавливается первоначальное значение 1.
В цикле, значение переменной s последовательно, k раз умножается на основание степени n. После выполнения цикла переменная s получит значение степени числа n с показателем k.
2. Вся острота вопроса состоит в том, что неизвестно первое нечетное число, от которого надо начинать суммирование последовательных нечетных чисел.
Для этого надо пробовать складывать нечетные числа вначале от 1 и далее (известно их количество — n);
1 + 3 + 5 + 7 + 9 …,
а затем проверять полученный результат, сравнивая со значением степени s. Если равенство выполняется, тогда закончить цикл и вывести на экран полученные нечетные числа, если равенство не выполняется, тогда надо начинать суммирование со следующего нечетного числа — 3: 3 + 5 + 7 + 9 … и т.д.
Этот процесс легче организовать с помощью цикла repeat. Переменной j, которая будет задавать начальные нечетные числа надо установить перед началом цикла первоначальное значение 1.
Общий вид такого цикла:
j := 1;
repeat
. . . . . .
j := j + 2
until …= s;
3. Осталось продумать, как подсчитывать суммы последовательных нечетных чисел. Мы уже сталкивались с этим вопросом и знаем, что для этого надо создать цикл от 1 до n, в котором в одну из переменных, скажем m, накапливать эту сумму, а вторая переменная должна «вырабатывать» следующее нечетное число.
Этот цикл можно записать так:
p := j; m := 0;
for i := 1 to n do
begin
m := m + p;
p := p + 2
end;
Обратите внимание! Переменная p, каждый цикл repeat, (внешний по отношению к данному), будет получать новое начальное значение нечетного числа, а переменная m — для суммы должна обнуляться перед каждым новым суммированием для другой последовательности нечетных чисел.
4. Наконец, когда последовательность нечетных чисел найдена, ее надо вывести на экран. Для этого надо устроить еще один цикл от 1 до n, в котором выдавать значения этих нечетных чисел. За первое нечетное число из последовательности надо взять значение j, но так как оно уже увеличилось на 2, то из j следует вычесть 2. Этот цикл будет:
j := j — 2;
for i := 1 to n do
begin
write(j, » «);
j := j + 2
end
Блок-схема
Рис. 37
Программа
Program Problem4;
uses WinCrt;
var
n, i, k, j, m, s, p : longint;
begin
write(«Введите натуральное число — основание степени «); readln(n);
write(«Введите натуральное число — показатель степени «); readln(k);
s := 1; j := 1;
for i := 1 to k do s := s*n;
repeat
p := j;
m := 0;
for i := 1 to n do
begin
m := m + p;
p := p + 2
end;
j := j + 2
until m=s;
write(«Степень с основанием «, n);
writeln(» и показателем «, k, » т. е. «, s);
writeln(«равна сумме следующих нечетных чисел»);
j := j — 2;
for i:=1 to n do
begin
write(j, » «);
j := j + 2
end
end.
Чтобы лучше понять ее работу, возьмите степень 25 и проверьте как будут последовательно выполняться операторы программы.
Задание 3
1. Выполните эту программу на компьютерах.
2. Составьте блок-схему и программу, которая выясняет, может ли произведение
а) трех; б) четырех последовательных натуральных чисел равняться некоторой степени некоторого натурального числа (квадрату, кубу, и т. д.)?
4. Разные задачи
Пример 5. Напечатать все четырехзначные числа, в десятичной записи которых нет двух одинаковых цифр.
Замечание. Перед началом составление блок-схемы этой задачи следует знать, как изображаются циклы в циклах, для циклов с параметрами. Общая конструкция двух вложенных циклов с параметрами будет такой:
Рис. 38
Сразу возникает мысль составить программу по следующей схеме:
организовать цикл по числу тысяч, t от 1 до 9, а затем внутренние циклы: по числу сотен, s от 0 до 9; по числу десятков, d от 0 до 9; по числу единиц, e от 0 до 9; проверка условия: если цифры различны, тогда составленное из них четырехзначное число выдавать на экран.
Блок-схема
Рис. 39
Программа
Program Problem5; { 1 — й способ }
uses WinCrt;
var
t, s, d, e : integer;
begin
writeln(«Все четырехзначные числа из разных цифр»);
for t := 1 to 9 do
for s := 0 to 9 do
for d := 0 to 9 do
for e := 0 to 9 do
if (t <> s) and (t <> d) and (t <> e) and (s <> d) and
(s <> e) and (d <> e)
then write(t*1000 + s*100 + d*10 + e, » «)
end.
Понятно, что эта программа выполнена нерационально. В ней все циклы выполняются полностью.
Программу можно усовершенствовать таким путем. Когда выполняется цикл сотен, тогда следующий цикл десятков надо начинать выполнять, если цифра сотен s не равна цифре тысяч t, в противном случае, иначе, цикл сотен надо продолжить, т. е. взять следующую цифру сотен.
Для цифры десятков, также установить условие, что следующий цикл единиц будет выполняться, если цифра десятков d не равна цифре сотен и тысяч, в противном случае, иначе, надо переходить к следующей цифре десятков.
И тогда, «внутри» цикла единиц достаточно записать условие, если цифры единиц e не равны цифре десятков d, сотен s и тысяч t, тогда четырехзначное число является искомым и оно выводится на экран.
Блок-схема
Рис. 40
Программа
Program Problem5a; { 2 — й способ }
uses WinCrt;
var
t, s, d, e : integer;
begin
writeln(«Все четырехзначные числа из разных цифр»);
for t := 1 to 9 do
for s := 0 to 9 do if s <> t then
for d := 0 to 9 do if (d <> s) and (d <> t) then
for e := 0 to 9 do
if (e <> d) and (e <> s) and (e <> t)
then write((((t*10 + s)*10 + d)*10) + e, » «)
end.
Задание 4
1. Дополните и измените эту программу так, чтобы она выдавала на экран не только различные четырехзначные числа, но и их количество.
2. При умножении четырехзначного числа, состоящего из разных цифр, на 9 получилось в произведении число, которое отличалось от множимого только тем, что между цифрами тысяч и сотен оказался нуль. Найти множимое. Составить блок-схему и программу.
Пример 6. Тройки натуральных чисел a, b, c, удовлетворяющих равенству: — называются Пифагоровыми числами.
Например, 3, 4 и 5 являются Пифагоровыми числами, поскольку
Составить программу для нахождения и печати всех Пифагоровых чисел, не превышающих 20.
Математика этого вопроса проста. Для чисел a, b и c возможные значения — это натуральные числа от 1 до 20.
Первоначальное значение a — единица, a = 1. Будем просматривать всевозможные значения b от 1 до 20, а также значения c от 1 до 20 и проверять выполнение равенства a a + b b = c c. Как только равенство будет выполняться, тогда выводить на экран значения a, b и c.
Далее надо брать значение a = 2 и проверять значения b уже от 2 до 20. Почему не от 1, а от 2? Да потому, что набор двух чисел из 1 и 2 уже был рассмотрен при значениях a = 1 и b = 2, чтобы не повторять значения a и b, т.е. избежать появления двух одинаковых пар чисел, значения b следует начинать просматривать или до значения a или от a до 20.
В связи с этим, возможны несколько способов организации циклов для переменных a и b.
1-й способ:
for a := 1 to 20 do
for b := a to 20 do
2-й способ:
for a := 20 downto 1 do
for b := 1 to a do
3-й способ:
for a := 1 to 20 do
for b := 1 to a do
Нетрудно видеть, что при каждом из этих способов не будут повторяться пары чисел. Проверьте это самостоятельно.
Для значений c мы обязаны проверять все натуральные числа от 1 до 20 для каждой пары чисел a и b. Поэтому цикл для c должен быть таким: for c := 1 to 20 do
Блок-схема
Рис. 41
Программа
Program Problem6;
uses WinCrt;
var
a, b, c : integer;
begin
writeln(«Тройки Пифагоровых чисел из промежутка [1; 20]»);
for a := 1 to 20 do
for b := 1 to a do
for c := 1 to 20 do
if a*a + b*b = c*c then writeln(a, » «, b, » «, c)
end.
Задание 5
1. Составьте блок-схему и программу, которая находит все решения уравнения где n — заданное число, из промежутка [2; 100].
2. Найти все натуральные x из промежутка [1; 1000], для которых выражение является квадратом натурального числа.
Пример 7. Сколькими способами заданное натуральное число n можно представить в виде суммы двух кубов натуральных чисел:
Перестановка слагаемых нового способа не дает. Операцией возведения в степень 1/3 пользоваться нельзя.
Сразу возникает следующая простая идея составления программы.
Организовать два цикла, один — внешний цикл с переменной i от 1 до n, а второй — внутренний цикл по j, также от 1 до n.
Сущность работы программы будет заключаться в следующем:
первое значение i равно 1, оно умножается трижды само на себя (этим заменяется возведение в 3-ю степень);
затем «перебираются» все значения j от 1 до n, каждое из которых также умножается трижды на себя и складывается со значением i i i, т. е. i в кубе;
далее, эта сумма проверяется, равна ли она значению n, если равенство выполняется, тогда счетчик, заведомо определенный в программе увеличивается на 1, а значения i и j можно вывести на экран;
цикл по i продолжается, i принимает второе значение — 2 и снова начинает выполняться внутренний цикл по j от 1 до n и так далее.
Если мы составим программу по этому плану, то она будет иметь два существенных недостатка:
1) проделывается много бесполезной работы — оба цикла организованы от 1 до n и среди них много лишних (достаточно брать значения от 1 до корня кубического из n);
2) программа будет выдавать значения, которые получаются при перестановки слагаемых, например: 2 2 2 + 3 3 3 = 35 и 3 3 3 + 2 2 2 = 35, что является недопустимым по условию задачи. Как устранить эти недостатки?
Первый недостаток устраним, если предварительно выясним, сколько значений для каждого из чисел надо рассматривать, чтобы выполнялось неравенство
Для этого можно организовать цикл с предусловием, цикл «пока«, в который включить счетчик — k, который бы подсчитывал, сколько раз такой цикл будет выполняться.
Это можно сделать так:
k := 0; i := 1;
while i*i*i + 1 <= n do
begin
k := k + 1;
i := i + 1
end;
Теперь можно значительно уменьшить число циклов для «испытуемых» чисел и организовать их от 1 до k, ибо при значениях i больше k, даже при самом маленьком значении j (j := 2) неравенство i i i + 1 <=n не выполняется.
Чтобы устранить второй недостаток, т. е., чтобы не выдавать варианты с перестановкой слагаемых можно поступить так:
внешний цикл по i первого числа устроить от k до 1, а внутренний цикл для второго числа по j делать от 1 до i. Получится такая часть программы:
p := 0;
for i := k downto 1 do
for j := 1 to i do
if i*i*i + j*j*j = n
then
begin
p := p + 1;
writeln(i, «*», i, «*», i, «+», j, «*», j, «*», j, «=», n)
end;
Внимательно разберитесь с этой частью программы и подумайте, почему в этом случае мы избегаем повторения вариантов и исключаем случаи перестановки слагаемых?
Осталось красиво закончить программу. Ведь очень часто будут встречаться случаи, когда число вообще нельзя представить в виде суммы кубов двух чисел. Надо учесть и это обстоятельство.
Для этого, после выполнения всех циклов введем условный оператор, в котором, в зависимости от значений счетчика p будут выдаться соответствующие сообщения.
Если p = 0, тогда выдать сообщение, что число нельзя представить в виде суммы кубов двух чисел, а иначе, выдать сообщение о количестве способов.
Эта часть программы может быть выполнена так:
if p = 0
then
begin
write(«Число «, n, » нельзя представить в виде «);
writeln(«суммы кубов двух чисел»)
end
else writeln(«Число способов равно «, p)
Блок-схема
Рис. 42
Программа
Program Problem7;
uses WinCrt;
var
i, j, n, k, p : longint;
begin
write(«Введите натуральное число «); readln(n);
k := 0; i := 1;
while i*i*i + 1 <= n do
begin
k := k + 1; i := i + 1
end;
p := 0;
for i := k downto 1 do
for j := 1 to i do
if i*i*i + j*j*j=n
then
begin
p := p + 1;
writeln(i, «*», i, «*», i, «+», j, «*», j, «*», j, «=», n)
end;
if p = 0
then
begin
write(«Число «, n, » нельзя представить в виде «);
writeln(«суммы кубов двух чисел»)
end
else writeln(«Число способов равно «, p)
end.
Еще одно решение этой задачи
Program Problem7b;
uses WinCrt;
label 1, 2;
var
i, j, m, k, n : longint;
begin
write(«Введите натуральное число «); readln(n);
m := 0; i := 1; j := 1;
while j*j*j + 1 < n do j := j + 1;
repeat
k := i*i*i + j*j*j;
if k = n then m := m + 1;
if k <= n then i := i + 1;
if k >= n then j := j — 1;
until i > j;
if m = 0 then goto 1;
write(«Число «,n,» можно представить в виде суммы»);
writeln(» кубов двух чисел «,m,» способами»); goto 2;
1: write(«Это число не представимо в виде»);
writeln(» суммы кубов двух чисел»);
2: end.
Задание 6
Дано натуральное n. Можно ли n представить в виде суммы трех квадратов натуральных чисел? Если можно, то указать все тройки x, y, z таких натуральных чисел, что Перестановка слагаемых нового способа не дает. Составить блок-схему и программу.
5. Преобразование типов
Пример 8. Двузначное десятичное число в сумме с числом, записанным теми же цифрами, но в обратном порядке, дает полный квадрат. Найти все такие числа.
Пусть искомое двузначное число = a 10 + b, тогда число, записанное теми же цифрами, но в обратном порядке будет = b 10 + a, например, 12 и 21, 13 и 31 и т. п.
Сумма этих чисел должна давать полный квадрат, т.е. точный квадрат целых чисел. Как это проверить?
Проверку можно было бы выполнить так: извлечь квадратный корень из полученной суммы; затем округлить результат до целого числа, а потом умножить полученный результат на себя, если снова получится сумма этих чисел, то значит она является точным или полным квадратом.
Например, 12 + 21=33, извлекаем квадратный корень из 33, он равен 5.74…; округляем, будет 6; умножаем 6 само на себя и получаем 36.
Мы не получили исходного результата, значит сумма 33 не является точным квадратом.
Еще один пример, чтобы вам была понятна идея решения. Пусть двузначное число 29, тогда число, записанное теми же цифрами, но в обратном порядке — 92, в сумме они дают 121. Извлекаем квадратный корень из 121 и получаем 11. Умножив 11 само на себя, снова получим 121. Делаем вывод, что получен точный квадрат, а значит двузначное число 29 является искомым.
Чтобы составить программу по этому принципу, придется извлекать квадратный корень из суммы, что можно сделать с помощью стандартной функции sqrt(x). Результат функции sqrt(x) является вещественным числом, его надо округлить или отбросить дробную часть, а нам неизвестно, как это сделать.
Но, даже более существенным, является то, что если квадратный корень в множестве целых чисел извлекается нацело, как для 121 (он равен 11), то на множестве вещественных чисел мы не получим строго число 11, а результат будет очень близок к 11 и после умножения на себя всё равно не получится 121, т.е. возникает необходимость преобразовать вещественное значение в целое.
Итак перед нами две задачи: 1) выяснить как округлять числа и; 2) установить, как преобразовывать вещественный тип в целый.
Для этого в Паскале есть стандартные функции round(x) и trunc(x)
Стандартные функции round и trunc предназначены для замены значений вещественного типа значениями целого типа.
Функция round(x) округляет вещественное число x до целого — ее значение есть ближайшее целое число:
round(4.2) = 4, round(4.7) = 5, round(4.5)=5,
round(-4.2) = -4, round(-4.7) = -5, round(-4.5) = -5.
Функция trunc(x) отбрасывает (без округления) дробную часть вещественного числа x:
trunc(1.2) = 1, trunc(5.8) = 5, trunc(-1.2) = -1,
trunc(-5.8) = -5, trunc(-6.7) = -6, trunc(8,9) = 8
Функции округления связаны так:
trunc(x + 0.5) = round(x), если x 0,
trunc(x — 0.5) = round(x), если x < 0.
Итак, в программе можно воспользоваться одной из этих функций. Какой? Подумайте сами и попробуйте применить в программе вначале функцию trunc, а потом замените ее на round и сравните полученные результаты.
Блок-схема
Рис. 43
Программа
Program Problem8;
uses WinCrt;
var
d, e, k : integer;
begin
writeln(«Искомые двузначные числа»);
for d := 1 to 9 do
for e := 1 to 9 do
begin
k := round(sqrt(d*10 + e + e*10 + d));
if k*k = d*10 + e + e*10 + d
then write(d*10 + e, » «)
end
end.
Задание 7
Найти целые числа из заданного промежутка [m; n], которые являются точными квадратами и остаются таковыми после приписывания к ним справа единицы (в десятичной системе записи). Составить блок-схему и программу.
Упражнения
- Составьте программу, которая находит 4 последовательных натуральных числа, произведение которых равно 1680.
- Показать, что четырехзначное число, у которого цифры тысяч и десятков одинаковы и цифры сотен и единиц тоже одинаковы, не может быть точным квадратом.
- Произведение шести последовательных натуральных чисел может быть равно произведению трех последовательных натуральных чисел. Например, 1 2 3 4 5 6 = 8 9 10 = 720. Есть ли еще такие числа?
- Доказать, что произведение четырех последовательных целых чисел в сумме с единицей дает полный квадрат.
- Найдите 11 последовательных натуральных чисел, сумма квадратов которых есть квадрат целого числа.
- Существуют ли такие целые числа, которые уменьшаются в 57 раз при зачеркивании их первой (слева) цифры?
- Найти четырехзначное число, зная, что оно является квадратом натурального числа и что цифры его распадаются на две пары, состоящие из одинаковых цифр.
- Найдите все семизначные числа, которые делятся на 15 и записываются только цифрами 0 и 1.
- Шестизначное число начинается с цифры 1. Если эту цифру переставить в конец числа, то новое число будет в три раза больше первоначального. Найдите число.
- Сколько точных квадратов можно составить из цифр 3, 4, 5, 6?
- Даны 20 различных натуральных чисел, не больших 50. Найдите два из них, разность которых равна 4, 5 или 9.
- Во сколько раз увеличится двузначное число, если справа к нему приписать такое же двузначное число?
- Определить наибольшее значение отношения трехзначного числа к числу, равному сумме цифр этого числа.
- Найти трёхзначное число, кратное 45, если разность между этим числом и числом, записанным теми же цифрами, но в обратном порядке равна 297.
- Найти четырёхзначное число , кратное 11, при условии: b + c = a и есть полный квадрат.
- Найти трёхзначное число, равное сумме цифры десятков, квадрата цифры сотен и куба цифры единиц.
- Найти два числа, произведение которых есть трёхзначное число, являющееся кубом некоторого числа, а частное является квадратом этого числа.
- Разность между числом и произведением его цифр равна сумме цифр этого числа. Найти это число.
- Найти все значения числа m, для которых сумма 1! + 2! + ,,, + m! является полным квадратом.
- Найти положительное четырёхзначное число, кратное 7 и представляющее собою сумму куба и квадрата некоторого числа.
- Некоторое число при делении на 7 дает в остатке 3; его квадрат при делении на 72 дает остаток 44; его куб при делении на 73 даёт остаток 111. Найти это число.
- При каком натуральном значении a число a2 + a + 1589 будет точным квадратом?
- Найти совершенное число вида 16p.
- Найти два числа, если сумма их квадратов равна 468, а сумма их общего наибольшего делителя и наименьшего кратного равна 42.
Автор: Тишин Владимир Иванович
|
Первое тысячелетие путь к познанию
Средние века, с начала IV и до XV вв. включительно, были периодом значительного упадка в развитии естественнонаучных знаний на европейском континенте. Причинами тому были гибель к началу этого периода вместе с разрушением государства Византии первого в Европе греко-римского центра культуры и науки. Завоеватели — северные «варвары» с одной стороны, и арабские племена с Аравийского … |
Откуда прилетают и как падают на Землю метеориты
Орбиты метеоритов. Все как-то привыкли к тому, что астероиды кружатся вокруг Солнца на огромных расстояниях. Они в 2—3 раза дальше от Солнца, чем наша Земля. Лишь немногие астероиды приближаются к Земле, но происходит это не из-за малых размеров орбит, а из-за большого их эксцентриситета. Афелии орбит таких астероидов всегда остаются за орбитой Марса. Метеориты, … |
|
Расчет массы вещества в растворе по его массовой доле
Задание: Сколько граммов сахара и воды необходимо взять для получения 200 г 5 % раствора? № п/п 1. 2. 3. … |
To have has got
В разговорной речи для выражения значения ‘иметь, обладать’ в настоящем времени употребляется оборот ‘to have/ has got’: HAVE (хэв), HAS (хэз), GOT (гот). I/ you/ we/ they/ you HAVE(got). Можно делать сокращения : |
Блок-схемы используются для визуального представления алгоритмов.
Определение:
Алгоритм — это последовательность шагов, ведущая к решению задачи
Определение:
Блок-схема — это схематическое изображение, иллюстрирующее последовательность операторов, которые необходимо выполнить для достижения результата
Инструкции изображаются, используя специальные символы. Символы связываются между собой стрелками, для указания порядка выполнения.
Блок-схемы широко используются при написании программ, так как они:
- Гораздо проще для понимания, чем запись в виде команд.
- Упрощают процесс отладки.
- Позволяют составить эффективную программную документацию.
- Облегчают процесс демонстрации и обсуждения программы.
Блоки, из которых составляются блок-схемы, представлены на Рисунке 1.
Рис. 1
Рассмотрим работу с блок-схемами на примере. Для этого нарисуем блок-схему программы нахождения суммы двух чисел:
Блок-схема, показанная на Рисунке 2, иллюстрирует линейную логику. Здесь нет повторений и ветвления.
Рис. 2
ВЕТВЛЕНИЕ
Способность сравнивать значения и исполнять, в зависимости от полученного результата, различные участки программы превращает компьютер из большого калькулятора в мощное средство решения различных практических задач. Операторы выбора применяются для:
- Сравнения данных
- Выбора одного из альтернативных путей решения задачи.
Например, при снятии денег с банковского счета производится сравнение снимаемой суммы с суммой на счете. Если снимаемая сумма меньше, то заказ выполняется. В противном случае происходит отказ от обслуживания.
Определение:
Ветвление — это процесс выбора из двух, или более альтернативных путей вычисления. Рассмотрим ветвление на следующих примерах:
Пример 1. Посмотрим на то, как будет выглядеть блок-схема алгоритма проверки чисел на четность:
Рис. 3
- Ветвление используется в том случае, когда необходимо разделить поток вычислений на два и более альтернативных варианта. Основанием для выбора маршрута является результат проверки истинности условия ветвления.
Пример 2. Рассмотрим блок-схему алгоритма, определяющего максимальное из 3-х чисел (см. рис. 4):
Рис. 4
Как мы видим, ветвление производится, когда нам необходимо выбрать дальнейший маршрут в зависимости от истинности некоего условия, называемого также условием ветвления.
Основные типы блок-схем, использующих ветвление, представлены на Рисунке 5:
Рис. 5
На Рисунке 5(а) представлена неполная конструкция условного ветвления. Здесь, в зависимости от выбранного маршрута движения, выполняется один или несколько вычислительных шагов, или происходит дальнейшее движение без вычислений, до момента слияния маршрутов.
На Рисунке 5(b) представлен полный вариант условного ветвления. Здесь, в зависимости от выбранного маршрута движения, выполняется одна или другая последовательность вычислений, после чего маршруты вновь сливаются.
ЦИКЛЫ
Определение:
Цикл — это многократно выполняемый участок алгоритма.
Тело цикла-это последовательность выполняемых в цикле операторов.
Итерация — однократное выполнение тела цикла.
Циклы бывают двух типов:
- С фиксированным числом итераций
- С переменным числом итераций
Рассмотрим различия между этими двумя типами на следующих примерах:
Пример 3. Пусть есть данные о расходах за каждый месяц года. Блок-схема алгоритма подсчитывающего расходы за год будет иметь вид:
Рис. 6
Рисунок 6 иллюстрирует цикл с фиксированным числом итераций — число месяцев в году известно и последовательность вычислений не может быть повторена более 12 раз.
Мы читаем расходы за один месяц и добавляем их к общему результату. После этого номер месяца сравнивается с 12.
Если номер месяца равен 12, то цикл завершается, и выводятся данные о расходах за год. В противном случае цикл повторяется для следующего месяца.
Пример 4. Пусть есть информация о каждом жителе города (имя, возраст, пол и т.д.). Необходимо составить список жителей старше 50 лет. Блок-схема соответствующего алгоритма будет иметь вид:
Рис. 7
Рисунок 7 иллюстрирует цикл с переменным числом итераций — нам заранее неизвестно число жителей города старше 50 лет. Этот цикл выполняется до тех пор, пока есть еще неучтенные люди. Цикл представляется в виде следующей элементарной блок-схемы:
Рис. 8
- В цикле с фиксированным числом итераций количество итераций известно заранее. Вычисления, производящиеся внутри цикла, не оказывают никакого влияния на число итераций.
- Цикл с переменным числом итераций выполняется до тех пор, пока не будет выполнено некоторое условие. Количество итераций в таком цикле может варьироваться.
- Циклы обычно выполняются до тех пор, пока какое-либо условие не примет значение true или false.
РАЗДЕЛЕНИЕ БЛОК-СХЕМ НА ЧАСТИ
При работе с блок-схемами мы часто сталкиваемся со следующими проблемами:
- Блок-схема может не поместиться на одной странице.
- Может оказаться сложным связать все элементы блок-схемы друг с другом непосредственно.
Для решения этих проблем блок-схемы обычно разбивают на отдельные части, для состыковки которых используются элементы- соединители.
Соединительный элемент имеет свой собственный, уникальный номер и состоит из двух частей. Эти части изображаются в местах разрыва соединительных линий. Для определения принадлежности частей соединительному элементу, номер элемента записывается на каждой из частей.
Например, разбив на 2 части блок-схему, изображенную на Рисунке 2 мы получим:
Рис. 9
- Соединители вставляются в местах разрыва блок-схемы. Расположение каждого объединения указывается с помощью уникального номера.
- В блок-схеме может быть только одна вершина Начало и только одна вершина Конец.
- Используйте машинно-независимые элементы.
- Не обязательно представлять в блок-схеме каждый шаг программы. Можно ограничиться наиболее важными блоками.
- Желательно использовать наглядные названия переменных и блоков.
- Помните, программа должна быть написана так, чтобы любой другой программист смог бы легко понять ее.
МЕТОД ПРОГОНКИ
Метод прогонки используется для проверки правильности работы программы без использования компьютера. Для этого составляется специальная таблица, в которую записываются значения переменных по шагам. Этот метод позволяет эффективно находить и устранять логические ошибки. Проиллюстрируем этот метод следующим примером:
Пример 5
Step 1. Start
Step 2. Х=10
Step 3. Y=5
Step 4. М=0
Step 5. M=X+Y+(X*Y)
Step 6. Y=Y+4
Step 7. M=M+Y
Step 8. Display X,Y,M
Step 9. End
ТАБЛИЦА ПОШАГОВОГО ПРОГОНА
| X | Y | М | |||
| Начальные значения | 10 | 5 | 0 | ||
| после шага 5 | 10 | 5 | 65 | ||
| после шага 6 | 10 | 9 | 65 | ||
| после шага 7 | 10 | 9 | 74 | ||
Таким образом, на 8-м шаге на экран будет выведено: 10, 9 и 74.
Задания для самопроверки