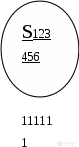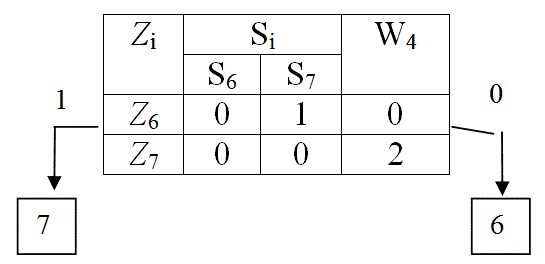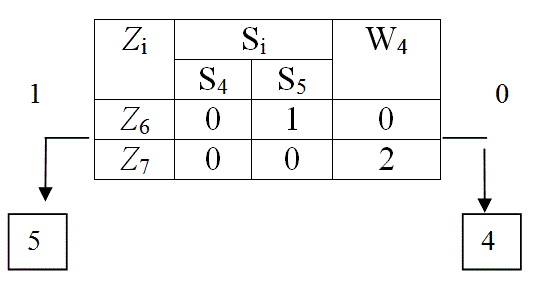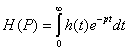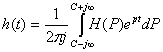Как составить алгоритм поиска неисправностей

Сразу хочу сказать, что здесь никакой воды про составление алгоритма отыскания неисправностей, и только нужная информация. Для того чтобы лучше понимать что такое
составление алгоритма отыскания неисправностей , настоятельно рекомендую прочитать все из категории Диагностика, обслуживание и ремонт электронной и радиоаппаратуры.

Цель: научиться составлять программы диагностики и отыскания неисправностей анализируемой схемы
Радиоэлектронная аппаратура, если ее параметры удовлетворяют всем техническим требованиям, предъявляемым на этапе хранения или эксплуатации, находится в исправном состоянии, в противном случае — в неисправном.
Цель методики обнаружения неисправности РЭА и состоит в выявлении причин несоответствия параметров аппаратуры техническим требованиям. В основу методики положен принцип оптимального разбиения РЭА на функционально законченные блоки. Критерием оптимальности методики поиска неисправности может служить время их поиска. Реализация методики возможна в
следующей последовательности:

• 1) устанавливается неработоспособность аппаратуры;
• 2) определяется отказавший блок с точностью до сборочной единицы;
• 3) в отказавшем блоке находится неисправный элемент;
• 4) восстанавливается отказавший блок (элемент);
• 5) проверяется работоспособность аппаратуры;
• 6) производится настройка аппаратуры.

Следует подчеркнуть, что выявление места неисправности требует, как правило, более высокой квалификации радиомеханика (чем контроль работоспособности аппаратуры).
Для определения технического состояния РЭА (исправное, неисправное) используются два способа:
1) воздействие тестовыми сигналами на входные и промежуточные точки аппаратуры и анализ отклика на них;
2) анализ с помощью контрольно-измерительной аппаратуры (КИА) выходных и промежуточных сигналов в реальных условиях работы аппаратуры. Оба способа можно представить в виде
алгоритма диагностики состояния РЭА (рис. 3.1). Основные шаги алгоритма следующие:

• 1) контроль технического состояния аппаратуры;
• 2) проверка параметров для выявления соответствия номинальным значениям;
• 3) устранение неисправного состояния;
• 4) послеремонтный контроль.

Алгоритм диагностики состояния РЭА отличается высокой экономичностью и поэтому находит широкое применение. Число шагов и структура алгоритма зависят от конфигурации путей прохождения сигналов в блоке обработки сигнала. Различают последовательное, последовательнопараллельное и параллельное прохождение сигналов.
В процессе эксплуатации на основании методик и разрабатываемых алгоритмов, приводимых в паспортной документации, эксплуатирующий персонал производит оценку работоспособно-
сти или отыскание неисправностей. Главная цель таких алгоритмов – минимальные затраты по времени и аппаратуре. Применять такие алгоритмы возможно и на производстве – в отделах технического контроля в процессе диагностики изготовленной аппаратуры. Данная методика входит в состав испытаний и служит для отбраковки или приемки изделий. На этапе эксплуатации – для оценки работоспособности аппаратуры.

Рис.3.1 Алгоритм диагностики БРЭА по состоянию
1 Диагностика – процесс контроля некоторых выходных параметров аппаратуры и сравне-
ние их с номинальными значениями параметров и их допусками (производственными или эксплуа-
тационными). Обязательным условием диагностики является подача на вход (имитация) всех вход-
ных воздействий, режимов и сигналов в соответствии с паспортной документацией. В процессе раз-
работки алгоритма (последовательности) диагностики первыми в списке должны оказываться те
выходные параметры, информация о величине и соответствии номинальным у которых потребует:
А) минимум аппаратурных затрат
Б) минимум времени на их исследование
В) даст заключение о работоспособности максимального числа внутренних блоков и о том, что сигналы между ними – номинальные.

Цель диагностики – установление факта наличия неисправности перед отправкой в ремонт или годности изделия после ремонта.
Методика проведения диагностики может быть представлена в различных вариантах: табличном или алгоритмическом.

2. Поиск неисправностей – последовательность действий для отыскания отказавшего элемента.
Главная цель – наикратчайшим путем отыскать неисправный элемент. Как и в случае с диагностикой используют табличный (текстовый) или алгоритмический способы представления алгоритма по ремонту

Рис 3.6 Алгоритм поиска неисправности блока питания телевизора
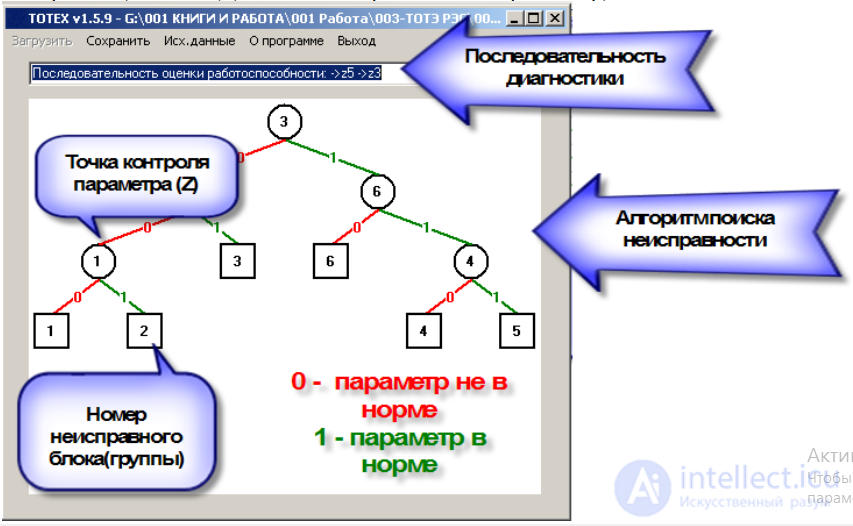
Для расчета последовательности диагностики и отыскания неисправности используется программа TOTEX v1.5.9.exe

Рис 3.9 Данные о программе
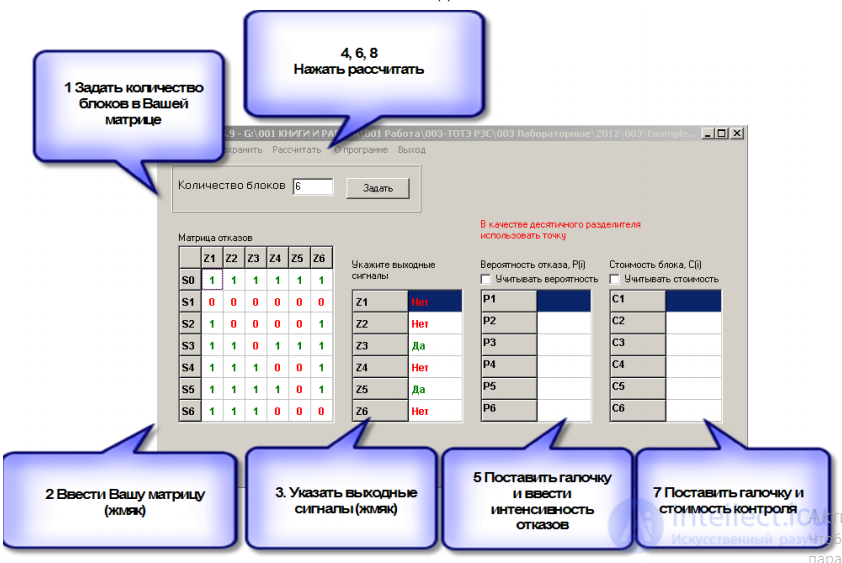
Для ее использования следует выполнить следующие шаги (Рис 3.10 )

Рис 3.10 Порядок использования программы

ОБРАТИТЕ ВНИМАНИЕ! Расчет повторяется трижды. По их окончании их следует сравнить и сохранить (Рис 3.11) (в закладке сохранить – экспорт в *bmp).

Рис 3.11 Полученные данные
Преобразовать (адаптировать) выведенный алгоритм в форму на примере, приведенном ниже

на рисунке . Об этом говорит сайт https://intellect.icu . Рис 3.12
Правила оформления алгоритмов можно найти в литературе Электротехнические чертежи и
схемы(Александров 1990) стр 237

Задание 1. Для заданной функциональной модели составить таблицу состояний

Рис.1

Таблица 1

Предположим, что система находится в состоянии S2 (010000), которое соответствует неисправности второго элемента X2. Тогда реакция Z2 этого элемента недопустима. Второй элемент предшествует третьему X3 и четвертому X4, а четвертый — пятому X5 и шестому X6 элементам. Следовательно, реакции элементов Z3, Z4, Z5, Z6 также недопустимы. Исходы проверок П2, П3, П4, П5, П6 отрицательны, так как на них влияет состояние элемента X2. Исход проверки П1 положителен, так как на него не влияет состояние элемента X2.

Таким образом, в строке S2 таблицы состояний (табл.1) будет записан код 100000. Аналогичным образом проводится анализ функциональной модели для других состояний.

Тождественность строк S4 и S6 таблицы означает, что отказ элемента X4 проявляется так же, как и отказ элемента X6. Поэтому с помощью всех возможных проверок нельзя определить, какой из этих двух элементов отказал. Такие состояния называются неразличимыми. Неразличимость состояний объясняется тем, что элементы X4 и X6 взаимоохвачены обратной связью, то есть соединены в кольцо.

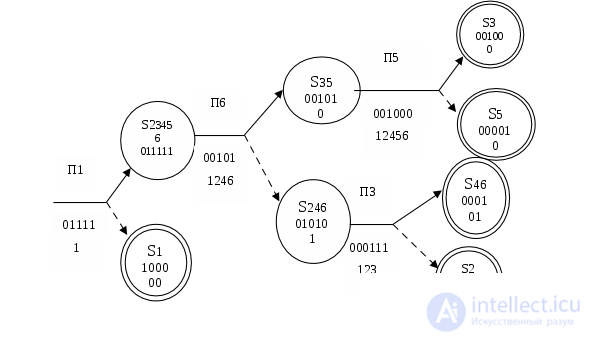
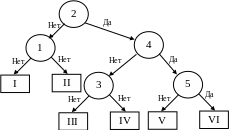
Задание 2. Составить все возможные алгоритмы последовательного поиска неисправностей

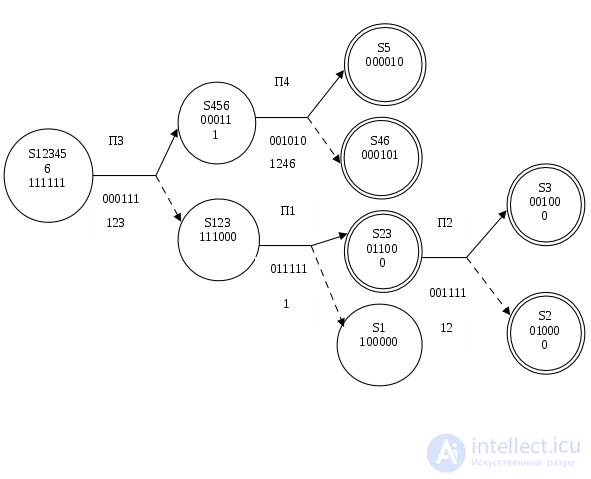
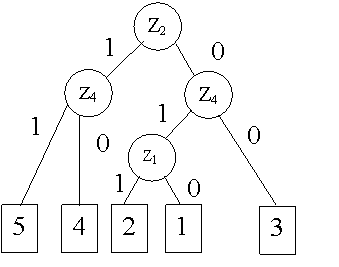
Приведем пример составления последовательного алгоритма (рис.2) для функциональной модели рис.1. Первая проверка выбирается произвольно, например П3. До начала проверок неисправным может быть любой узел объекта.

При положительном исходе проверки неисправными могут быть только узлы, ею не охваченные. Тогда возможны только состояния S4, S5, S6 системы. Для дальнейшей локализации неисправностей выбираем проверку П4. Положительному исходу проверки соответствует состояние S5, а отрицательному — S46. Мы получили конечные результаты. Аналогично составляется другая ветвь данного алгоритма.

Рис.2

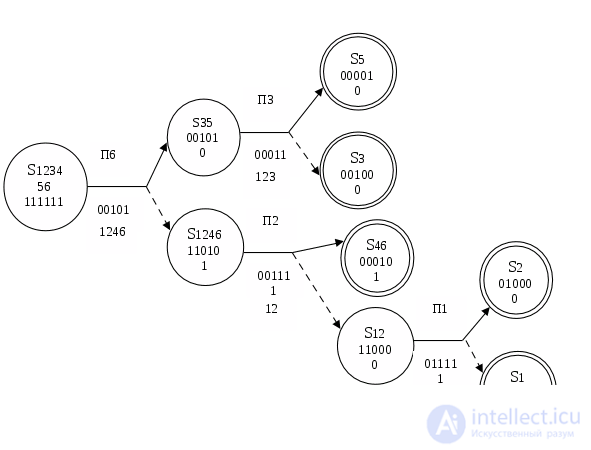
Рассмотрим еще один алгоритм поиска неисправностей (рис.3).

Рис.3

Задание 3.

Таблица 2

Условная вероятность

Таблица 3

Условная трудоемкость

Для заданных значений qi и ti выбрать квазиоптимальный по информационному критерию алгоритм и рассчитать для него среднее и максимальное время локализации неисправностей.

Функциональная модель 2

Рис.4

Составим по модели (рис.4) таблицу состояний, включив в нее только обязательные проверки и исключив проверки на разветвляющихся выходах.

Оценим эффективность всех проверок:

Вычислим вероятности положительных исходов проверок по формуле:

Р (Пi+) =∑qi (1)

i Є Mн

Вероятность положительного исхода проверки Р (Пi+) определяется суммой условных вероятностей отказов элементов подмножества Мн, не охваченных данной проверкой.

Р (П1+) =q2+q3+q4+q5+q6=0,05+0,1+ 0,2+0,3+0,2=0,85

Р (П3+) =q4+q5+q6=0,2+0,3+0,2=0,7

Р (П5+) =q3 =0,1

Р (П6+) =q3+q5=0,1+0,3=0,4

Информативность проверок определим по графику: I (П1) =0,6;

I (П3) =0,88; I (П5) =0,5; I (П6) =0,97

Вычислим эффективность каждой из проверок по формуле:

Fi=I (Пi) /ti (2)

Эффективность проверки определяется как отношение получаемого в результате проверки количества информации к затратам времени на проверку:

F1=0,6/0,05=12 F3=0,88/ 0,3=2,93; F5=0,5/0,2=2,5;

F6=0,97/0,1=9,7

В качестве первой выбираем проверку П1, обладающую максимальной эффективностью.

2. Определим информационное состояние, соответствующее положительному результату П1, перемножая код исходного состояния S0 на код проверки П1: 111111*011111=011111. Информационное состояние, соответствующее положительному результату — S23456.

Находим информационное состояние, соответствующее отрицательному результату проверки, перемножая код исходного состояния S0 на инверсный код проверки П1: 111111*100000=100000. Искомое состояние S1 — конечный результат.

3. Проведем для состояния S23456 оценку эффективности всех возможных проверок П3, П5, П6 т.е. проверок, не имеющих всех нулей или всех единиц в строках возможных неисправностей:

3.1 Расчет проводится по формуле: n

Р (Пi+) =Pi/∑Pi; (3)

i=1

Р (П3+) =q4+q5+q6/q2+q3+q4+q5+q6=0,2+0,3+0,2/0,05+0,1+0,2+0,3+0,2=0,7/0,85=0,82

Р (П5+) =q3/q2+q3+q4+q5+q6=0,1/0,85=0,12;

P (П6+) =q3+q5/q2+q3+q4+q5+q6=0,1+0,3/0,85=0,47

3.2 Определим информативность этих проверок:

I (П3) =0,68; I (П5) =0,54; I (П6) =0,99

3.3 Вычислим эффективности проверок:

F3=0,68/0,3=2,266; F5=0,54/0,2=2,7; F6=0,99/0,1=9,9

Выбираем проверку П6, обладающую наибольшей эффективностью. Она должна проводиться в состоянии S23456.

4. Найдем информативные состояния, соответствующие положительному результату проведения проверки П6 в состоянии S23456: 011111*001010=001010 — S35; отрицательному результату соответствуют состояния: 011111*110101=010101- S246.

5.1 В состоянии S35 возможны проверки П3 и П5. Оценим эффективность проверок:

Р (П3+) =q5/q3+q5=0,3/0,1+0,3=0,75;

Р (П5+) =q3/q3+q5=0,1/0,4=0,25

5.2 Информативность определяем по графику: I (П3) =0,8; I (П5) =0,82

5.3 F3=0,8/0,3=2,66; F5=0,82/0,2=4,1

Выбираем проверку П5.

6. В состоянии S246 возможна единственная проверка П3: при положительном исходе 010101*000111=000101 — S46; при отрицательном исходе 010101*111000=010000 — S2. Состояния S46 и S2 являются конечными.

Таким образом, выбраны все проверки и составлен оптимальный алгоритм поиска неисправностей.

Рис.5

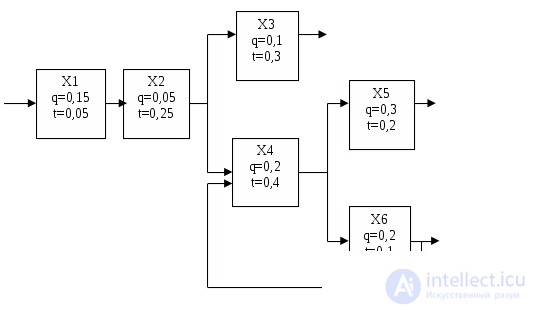
Среднее время локализации неисправностей для найденного алгоритма:

tср=q1*t1+ (q3+q5) * (t1+t6+t5) + (q4+q6+q2) * (t1+t6+t3) =0,15*0,05+ (0,1+0,3) * (0,05+0,1++0,2) + (0,2+0,2+0,05) * (0,01+0,1+0,3) =0,0075+0,14+0,1845=0,332 (4)

Максимальное время локализации неисправностей:

tmax=t1+t6+t5 +t3=0,05+0,1+0,2+0,3=0,65 (5)

*

Литература

1. Цыпин Б.В. Оптимизация поиска неисправностей при технической диагностике оборудования: Учеб. пособие/ Б.В. Цыпин, Ю.М. Крысин, А.Г. Схиртладзе, В.А. Скрябин. — Пенза: Изд-во Пенз. гос. ун-та, 2002. — 112с

См. также

• неисправности оперативной памяти , неисправности ram ,
• ремонт портов ввода-вывод , ремонт com ,
• производительности материнской платы , производительность процессора ,
• структурная схема узи , функциональная схема узи ,
• диагностика активных элементов , диагностика пассивных элементов ,
• диагностика неисправностей видеокарты , ремонт видеокарты ,
• неисправность ata-диска , ata-диск ,
• неисправности материнской платы , оборудование для диагностики материнки ,
• ремонт тв , диагностика монитора ,
• неисправности аппаратной части hdd нжмд их характер проявления алгоритм их устранения ,
• поиск неисправностей , методы поиска неисправностей ,
• неисправность блока питания , алгоритмы нахождения неисправностей блока питания пк ,
• алгоритм диагностики неисправности , поиск неисправностей ,
• неисправности сетевого оборудования , блок-схема диагностики сети ,

Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про составление алгоритма отыскания неисправностей Надеюсь, что теперь ты понял что такое составление алгоритма отыскания неисправностей
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Диагностика, обслуживание и ремонт электронной и радиоаппаратуры

Вводное слово.

Несколько лет назад я написал заметку: «Методы поиска и устранения неисправностей, а также причин неработоспособности в РЭА.». Недавно дошли руки привести ее в относительный порядок. Тогда же была задумана и эта статья. Дело в том, что,обладая даже самым совершенным инструментом, можно не уметь его использовать. Соответственно, эта заметка о правильном, на мой взгляд, использовании инструментов при поиске неисправности. Естественно, я не претендую на построение исчерпывающей, безупречной схемы, по которой можно было бы найти любую неисправность и решить любую проблему. Этот текст лишь попытка обобщить мой опыт.

Основная часть.

Порядок действий.

Порядок действий всегда хочется свести к простой и понятной схеме. У меня сначала была мысль выразить все это в универсальной блок-схеме, но процесс поиска всегда слишком многовариантен и требует внимания к мелочам.

Не пренебрегать мелочами.

На решение проблемы может натолкнуть даже минимальная, случайно полученная крупица информации. По этому необходимо собрать информацио об обстоятельствах появления и развития отказа. В медицине это называется «анамнез».  Небходимо понимать, что  начальная информация всегда низкого качества, и выбор фактора, на основании которого следует начать действовать, во многом носит интуитивный характер. Естественно, это не значит, что ремонт тождественен гаданию на кофейной гуще, или случайному перебору, но фактор случайности всегда присутствует. Конечно, при тщательном и последовательном подходе к анализу мы получим положительный результат.

Понимать цели и верно подбирать средства.

Прежде всего нужно запомнить, что всякое действие должно быть направлено на локализации неисправности. И, хотя на первых этапах локализация может быть не точной, но все равно нужно понимать, к чему вы стремитесь и что ожидаете от того или иного измерения. Сначала всегда следует применять быстрые методы, такие, как » внешний осмотр» и «выяснение истории возникновения неисправности». Не стоит пренебрегать этими вещами. Они очень эффективны.

Понимать и учитывать обстоятельства.

Действия при ремонте изделия, бывшего в эксплуатации и при запуске нового изделия несколько отличаются. Когда мы имеем изделие из эксплуатации,мы можем предположить, что оно работало, иначе говоря, нет ошибок в объемном монтаже, нет ошибок в монтаже на печатные платы, все элементы правильного номинала и типа.

В то же время, в новом изделии перед его включением мы должны проверить печатный монтаж, проверить правильность объемного монтажа. И только затем попытаться включить изделие (в более или менее сложных и массовых изделиях).

Примерная блок схема действий.

Составить универсальный порядок действий, конечно, невозможно, но нарисовать схему в общих чертах можно.

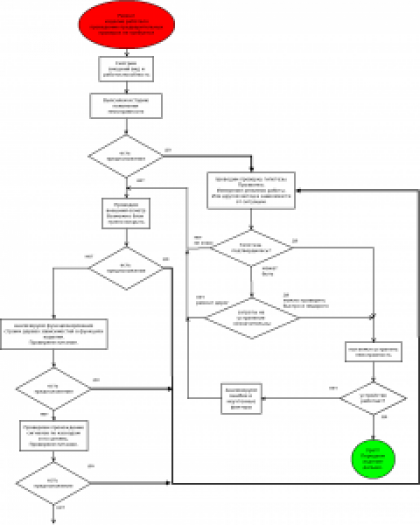
На рисунке в общих чертах предоставлена схема действий:

Пояснения к рисунку: Под проведением предварительных проверок подразумеваются проверки на соответствие документации, такие как: правильность монтажа, отсутствие замыканий, отсутствие загрязнений и прочее в зависимости от условий производства.

Как видно, поиск неисправности носит циклический характер, кроме самого простого случая. При отрицательном результате на очередном цикле следует применять более глубокое исследование изделия. При этом проверка работоспособности может осуществляться в зависимости от ситуации наиболее удобным методом. После странения заявленной проблемы изделие следует протестировать в полном объеме.

Применение методов.

Когда применяем тот или иной метод мы, преследуем несколько целей: сбор информации , проверка гипотезы о неисправности, локализация неисправности. И на каждом шаге наших действий мы и получаем новую информацию, и проверяем гипотезу, и локализуем неисправность. Следует понимать , что — первично на текущем шаге, а что — вторично. В то же время не следует пренебрегать вторичными эффектами. Например, когда основная цель действия — проверка гипотезы, то и информация, полученная, во время этой проверки может послужить к уточнению выдвинутой гипотезы или позволит выдвинуть новое предположение.

Для более быстрой локализации неисправности применяйте принцип: «Разделяй и властвуй» . Для этого нужно сначала получить контроль над ключевыми точками схемы. Знание основного, главного  избавит вас от необходимости вдаваться в излишние подробности.

Я попробую описать общую схему действий на примере. Имеется большая система, которая работает неправильно. Сначала вычленяем отдельный блок в системе. Блок включаем вне системы и в блоке вычленяем отдельный модуль. Затем включаем модуль и выходим на элемент.

В этой стройной системе есть одна проблемка. Например, модуль сам по себе работает правильно, а в блоке начинаются ошибки. Это проблема несоответствия условий работы модуля (блока, элемента — не важно ) в системе и на стенде проверки. Такие различия есть всегда! Не следует себя обманывать.

В первую очередь, конечно, думают о различиях в электрических сигналах, разнице в температуре, охлаждении. На практике эти различия не всегда очевидны. Например, в моей практике был интересный случай, когда существенным фактором оказалась вибрация. Причем, на плате не было элементов чувствительных к вибрации, плата была достаточно прочной и т.д. Но замененные симисторы выгорали раз за разом. Причина оказалась в графитовой пыли, которая забилась под разъемы в силовых цепях и в условиях вибрации создавала короткое замыкание, в то время как на стенде все работало замечательно.

Вычленение ключевых точек бывает достаточно сложным и требует хорошего знания принципов работы устройства и его структуры. В простейших случаях устройство следует разбить на структуры типа «звезда» и последовательные структуры. В структурах типа «звезда» сначала исследуют (если есть возможность ) центральный узел и на основе его работы делают вывод о работе его и прочих узлов. Если исследование центрального узла затруднительно, то «сначала обрубаем ветви, если сразу не можем срубить ствол». То есть сначала исследуем периферию, что более трудоемко, но позволит получить информацию, необходимую для исследования центрального узла. В последовательных структурах следует удостовериться, что на вход поступают правильные сигналы , на выходе сигналы — неправильные. Значит, структура где-то не работает. Для максимально быстрого устранения неисправности следует разбить последовательность каскадов пополам и проверить сигналы в среднем каскаде. Таким образом мы узнаем где находится неисправность в начале или в конце. Затем разделяем предполагаемую область опять пополам и т.д. Но бывает, что подобная стратегия действий неудобна по технологическим соображениям, или нам для каждого каскада приходится анализировать сигналы на основе сигналов в предыдущем каскаде. В этом случае приходится проверять каскады последовательно от начала к концу или от конца к началу, в зависимости от условий и структуры устройства.

Хорошее питание.

Всегда в первую очередь (или как можно раньше) следует проверять цепи питания и качество питающих напряжений.

Держать в голове цель и к месту ее менять.

Проблема в том, что нельзя составить четкой схемы действий. Мы всегда вынуждены держать в голове все принципы, методы поиска и постоянно искать, что использовать в данный момент.

Итоги:

Необходимо понимать, на что направлено то или иное действие. На сбор обшей информации, на проверку гипотезы , на проверку того или иного блока. В тоже время необходимо вовремя оценить результат действия и вовремя переходить к следующему этапу. Когда вы собираете информацию, нужно вовремя оценить, что необходимая информация уже собрана и необходимо переходить к анализу. Не нужно зацикливаться на каком либо этапе. Это бывает не всегда просто и не всегда очевидно.

Сформулируем основные стратегические принципы:

• Сначала использовать быстрые и неточные методы, затем уточняем;
• Цикличность при отрицательном результате, со все более углубленным исследованием на каждом цикле;
• Оценка целесообразности;
• «Разделяй и властвуй»;
• Контроль ключевых точек;
• «Не можешь срубить ствол, сруби ветви»;
• Не навреди

3.1. Метод последовательного функционального анализа

3.2. Метод половинного разбиения

3.3. Метод «время-вероятность»

3.4. Метод на основе информационного критерия

3.5. Инженерный метод

3.6. Метод на основе иерархического принципа

3.7. Метод ветвей и границ

3.8. Метод диагностики на основе «белого шума»

3.9. Метод диагностики на основе ортогонального анализа отклика системы по базису гармонических функций

Выбор того или иного метода использования информации о техническом состоянии диагностируемой аппаратуры обусловлен структурой ОД и требуемой глубиной поиска неисправностей. Он накладывает определенные требования на принципы построения и структуру системы контроля и диагностики.

Вид алгоритма (программы) поиска неисправностей существенно влияет на эффективность процесса контроля и диагностики. При разработке алгоритма поиска обычно решают две задачи:

а) определяют наилучший набор контролируемых параметров;

б) получают наилучшую последовательность измерения контролируемых параметров;

Рассмотрим наиболее распространенные методы построения алгоритмов поиска неисправностей в РЭА.

3.1. Метод последовательного функционального анализа

Построение алгоритма поиска неисправностей методом последовательного функционального анализа, заключается в последовательном измерении параметров схемы, начиная «с конца», то есть с выхода устройства, где либо вовсе отсутствует сигнал, либо он находится вне допуска, до тех пор, пока не появится на каком – либо блоке (узле, элементе) сигнал, находящийся в поле допуска. Такой поиск можно проводить и «с начала», с входа устройства. Основные функции, характеризующие исправность ОД, например:

а) электрического питания;

б) приема и преобразования сигналов заданной частоты;

в) управления;

г) генерирования колебаний.

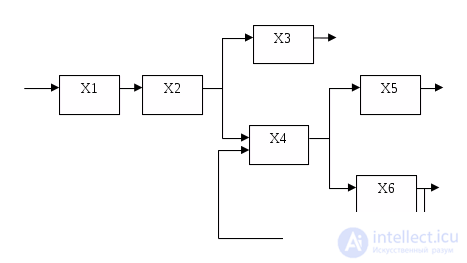
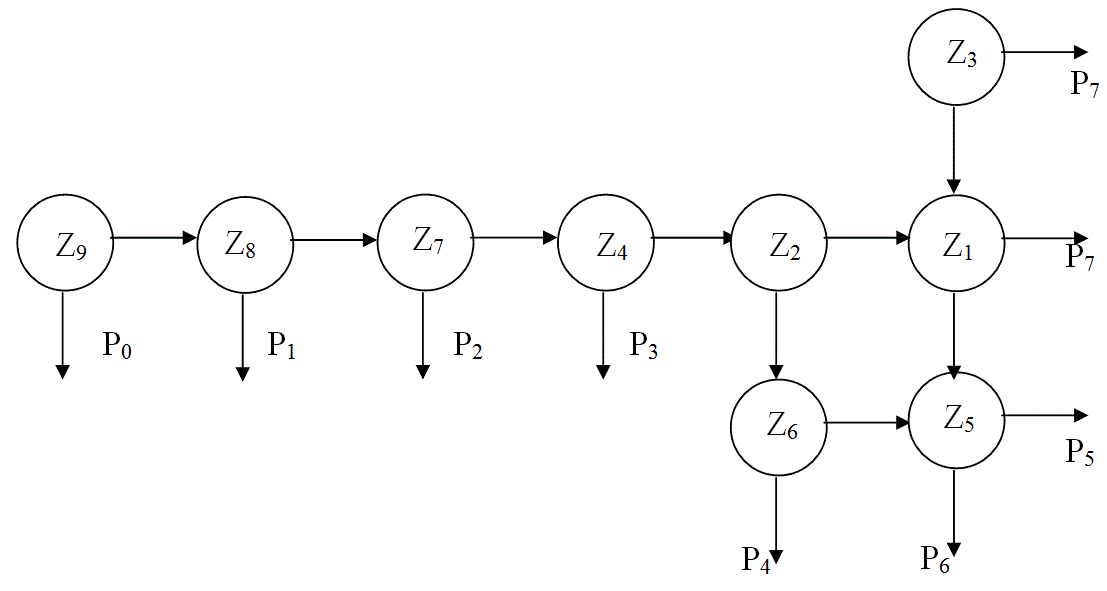
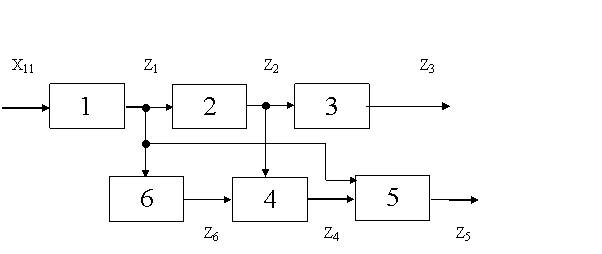
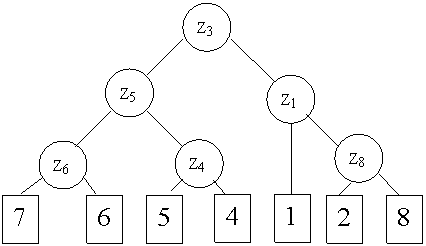
Рассмотрим составление алгоритма поиска неисправностей на примере канала звукового сопровождения телевизора типа УПИМЦТ (Рис. 4). Основной функцией этого канала является усиление и преобразование сигналов звукового сопровождения. Эта функция выполняется, если при входном сигнале с фиксированными параметрами на выходе будет наблюдаться вполне определенный сигнал. В процессе контроля принимается решение об исправности или неисправности канала. Последовательно контролируя сигналы на выходе каждого каскада, можно определить неисправный каскад. Получающуюся при этом схему поиска называют деревом функций (Рис. 5), а решения представляют обычно в виде матрицы:

Табл. 3

Рис. 5 Схема поиска неисправностей

Данный метод прост, нагляден, требует минимум информации от ОД, однако он не оптимален ни по времени, ни по средним затратам.

3.2. Метод половинного разбиения

Этот метод часто используется в разработке алгоритмов поиска неисправностей в РЭА с последовательно соединенными элементами. Первым для контроля выбирается параметр, делящий всю схему пополам. При положительном результате контроля (сигнал на выходе элемента находится в допуске) следующим для контроля выбирается элемент, делящий неисправную часть схемы пополам и так далее до определения неисправного элемента (блока, узла). Такой алгоритм возможен в том случае, когда вероятности состояний P(S_i) одинаковы для всех элементов, стоимости контроля выходных параметров Z_i также одинаковы.

В том случае, когда вероятности состояний P(S_i) для функциональных элементов неодинаковы, тогда вероятности необходимо первым контролировать такой параметр Z_k , который делит ОД на части, вероятности состояния которых близки к 0,5.

Неопределенность состояния ОД до контроля оценивается величиной энтропии

_N

H₀ = — ∑ P(S_i)*log₂ P(S_i) = log₂ N (13)

ⁱ⁼¹

Неопределенность состояния ОД при контроле параметра Z_k будет:

H(Z_k) = — (P_k *log₂ P_k + (1- P_k) *log₂ (1- P_k)) , (14)

_N

где P_k = ∑ P(S_i) , i = 1, 2, 3, …

ⁱ⁼¹

Величина H(Z_k) будет максимальна, если разность (P_k – 0,5) минимальна.

После контроля параметра (Z_k) ОД будет разделен на две части: первая содержит K, а вторая (N — K) элементов. При выборе очередного параметра для контроля необходимо вероятности состояний в каждой из этих частей пронормировать, пересчитать по формулам:

_k

P'(S_i) = P(S_i)/ ∑ P(S_i) , i = 1, 2, 3, … k (15)

^{i = 1}

_N

P» (S_i) = P(S_i)/ ∑ P(S_i) , i = k + 1, k + 2, … , N (16)

^i=k+1

При этом

_{k N}

∑ P’ (S_i) = 1 и ∑ P» (S_i) = 1. (17)

^{i = 1 i=k+1}

Тогда вторым параметром выбирается Z_ll , который делит одну из частей на две, вероятности которых

_l

∑P» (S_i) = 0,5 (18)

ⁱ⁼¹

Такое деление продолжается до тех пор, пока состояние ОД не будет определено с заданной глубиной.

Метод половинного разбиения применим и для случая, когда в ОД неисправно несколько элементов.

3.3. Метод «время-вероятность»

Этот способ находит применение для РЭА, в которой функциональные элементы соединены произвольно и имеют разные вероятности P(S_i) состояний и различные стоимости проведения контроля параметров С(Z_i). Эффективность метода оценивается средним временем поиска неисправного элемента или средним временем контроля одного параметра. Последовательность контроля параметров устанавливается в порядке уменьшения величины:

P(S₁)/ t₁> P(S₂)/ t₂> …> P(S_N)/ t_N (19)

Располагая в порядке уменьшения величины P(S_i)/t_i , получим следующую последовательность для контроля параметров:

Z_N → … → Z_K → … → Z_M → … → Z_C

3.4. Метод на основе информационного критерия

Метод построения алгоритма поиска неисправностей на основе информационного критерия позволяет выбрать минимальное количество контролируемых параметров и определить последовательность их контроля.

Исходными данными являются функциональная модель и таблица неисправностей.

Предварительно ОД разделяются на N функциональных элементов, вероятности состояний, которых принимаем одинаковыми

P(S_i) = P(S₁) = P(S₂) = …= P(S_N) =1/N (20)

Неопределенность состояний ОД до контроля определяется оценивается величиной энтропии

H₀ = log₂ N (21)

Результат контроля к — го параметра ОД дает некоторое количество информации о его контроле:

I_K = H₀ — H_K (22)

где H_K — средняя условная энтропия ОД при условии контроля к — го параметра.

H_K = P(Z’_K) Н_Z‘K + P(Z⁰_K) Н_Z0K (23)

P(Z’_K) = 1/N ; P(Z⁰_K) = (N – m)/N, (24)

где m – количество единиц в к — ой строке.

H_K = log₂ m + log₂ (N – m) (25)

Контроль к – го параметра дает следующее количество информации:

(26)

Последовательно вычисляем значения I_K (где к = 1, N) и по убыванию I_K определяем значимость параметра Z_K . Первым контролируется параметр Z_K , дающий максимальное количество информации.

После контроля первого параметра определяют количество информации, получаемое при контроле каждого n оставшегося параметра относительно состояния, характеризующегося энтропией Н_ZK . Условная энтропия

H(z_n/z_K) = P(z’_n/z’_K)*Hz’_n/z’_K + P(z⁰_n/z⁰_K)*Hz⁰_n/z⁰_K +

+P(z⁰_n/z’_K)*Hz⁰_n/z’_K + P(z’_n/z⁰_K)*Hz’_n/z⁰_K (27)

где P(z’_n/z’_K) = m₁/N – вероятность положительного решения при контроле параметра Z_n в случае положительного решения при контроле параметра Z_K; m₁ – количество единиц в n-ой строке таблицы состояний относительно m единиц в к-ой строке; m₂ – количество единиц в n-ой строке относительно (N – m) нулей к-ой строки.

(28)

(29)

(30)

Hz’_n/z’_K = log₂ m₁ ; (31)

Hz⁰_n/z’_K = log₂ (m — m₁ ) ; (32)

Hz’_n/z⁰_K = log₂ m₂ ; (33)

Hz⁰_n/z⁰_K = log₂ (N — m — m₂ ) ; (34)

I (z_n / z_K) = H_K – H(z_n / z_K) . (35)

Выражение для вычисления количества условной информации имеет вид:

(36)

По максимуму условной информации выбирается второй контролируемый параметр. По такой же схеме выбираются все остальные параметры.

После всех расчетов строим схему поиска неисправностей.

Пример 3.4.1

Рис. 6 Функциональная модель ОД

Табл. 4

Из анализа табл. 4 находим, что контроль параметра Z₅ для поиска неисправностей не дает никакой информации, поэтому его можно из дальнейшего рассмотрения исключить. Тогда энтропия (21) до контроля будет

H₀ = log₂ 5 = 2,32

Количество информации (22) при контроле каждого параметра следующее:

I₁ =

I₂ =

I₃ =

I₄ =

Для контроля берем Z₂ . После его контроля могут быть приняты два решения: значение параметра Z₂ в допуске – функциональные элементы 1,2,3 исправны, а неисправность в элементе 4 или 5; (см. Рис. 6); значение параметра Z₂ не в допуске — функциональные элементы 4 и 5 исправны, а не исправность в элементах 1, 2, 3 .

В соответствии с этим решением перестраиваем матрицу состояний (табл. 5)

Табл. 5

Теперь вычислим количество информации (36), которое дает контроль параметров Z₁ , Z₃ , Z₄ при условии, что Z₂ проконтролирован:

Следовательно, вторым для контроля выбираем Z₄ . Исключим из табл. 5 строку Z₂ (табл. 6)

Табл. 6

В результате построения алгоритма поиска неисправностей в заданном ОД получаем, что для поиска неисправностей достаточно контролировать последовательность из трех параметров (Z₂ , Z₄ , Z₁) по определенной схеме (Рис. 7). Контроль параметра Z₄ при условии, что Z₂ = 1 дает два решения: если Z₄=0, то неисправен элемент 4, если Z₄=1, то неисправен элемент 5.

Если Z₂ = 0 и Z₄ = 0, то неисправен элемент 3 . Если Z₂ = 0 и Z₄ = 1, то надо контролировать параметр Z₁ . Если Z₁ = 0, то неисправен элемент 1, если Z₁ = 1, то неисправен элемент 2 (Табл. 7).

Табл. 7

Рис.7 Схема поиска неисправностей

3.5. Инженерный метод

Этот метод построения алгоритмов диагностирования основан на вычислении функции предпочтения. При этом исходными данными являются функциональная модель ОД и таблица неисправностей.

Функция предпочтения выбирается в соответствии с решаемой задачей диагностики и исходными данными. При этом рассматриваются три случая определения перечня параметров:

а) для оценки работоспособности;

б) для поиска неисправностей;

в) для оценки работоспособности и поиска неисправностей.

Функция предпочтения при оценке работоспособности

N

W₁= max Wi (Z_i) = ∑ S₀ (i j) , (37)

^{i N j=1}

где S₀ (i j) = 1, если состояние i j–го матричного элемента описывается нулем, и S₀ (i j) = 0, если состояние i j–го матричного элемента описывается единицей.

Первым для контроля берут параметр Z_i, у которого функция W₁ (Z_i) имеет максимальное значение. В результате контроля данного параметра матрица состояний делится на две части. В одну часть входят состояния, для которых результаты контроля выбранного параметра имеют положительные, а в другую отрицательные решения. В дальнейшем надо контролировать только первую часть, так как нужно фиксировать только факт исправности или отказа. Для нее аналогичным образом нужно вычислить значения Wi (_Zi) и выбрать для контроля параметр по максимуму W_i (Z_i).

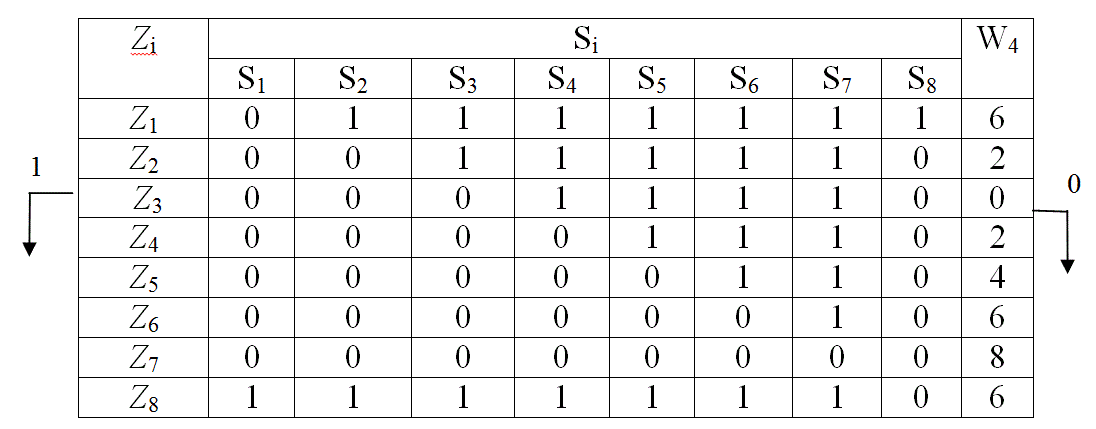
Пример 3.5.2

Рис. 8 Функциональная модель ОД

Табл. 8

Первым для контроля выбираем Z₅ по максимуму W₁ (Z₅). В результате контроля в строке Z₅ положительное решение имеет только Z₃ , следовательно следующим для контроля следует выбрать Z₃ .

Если для ОД известны вероятности состояний Р(S_i), то функция предпочтения

W₂ = max W₂ (Z_i) , (38)

^{i N}

_N

W₂ (Z_i) = ∑ P (S_i)S₀ (i j) , (39)

^{i =1}

Если для ОД известны и стоимости контроля параметров С(Z_i), то функция предпочтения

(40)

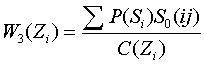
Рассмотрим составление алгоритма поиска неисправностей. Максимальное количество информации дает контроль параметра, который делит все возможные состояния на две равные части. Тогда функция предпочтения

_{N N}

W₄ (Z_i) = min | ∑ S₀ (i j) — ∑ S₁ (i j)| (41)

^{j =1 j =1}

где S₁(i j) = 1, если состояние матричного элемента описывается единицей, и S₁ (i j) = 0, если состояние матричного элемента описывается нулем, S₀ (i j) = 1, если состояние матричного элемента описывается нулем, S₀ (i j) = 0, если состояние матричного элемента описывается единицей.

Первым для контроля выбирается параметр, для контроля которого функция предпочтения W₄ минимальна. Результаты контроля Z_i разделяют матрицу состояний на две части. В первую часть входят состояния, для которых результат контроля отрицателен (на пересечении Z_i – S_J стоит нуль), во вторую часть входят состояния, для которых результат контроля положителен. Для полученных частей вновь вычисляют функции предпочтения. По их минимальным значениям выбирают второй контролируемый параметр (при положительном исходе контроля первого выбранного параметра) или третий контролируемый параметр (при отрицательном результате контроля первого выбранного параметра). Совокупность параметров и последовательность их контроля выбирается до тех пор, пока множество N возможных состояний ОД не будет разделено на отдельные различимые состояния с требуемой глубиной поиска.

В случае, когда заданы вероятности состояний P(S_i) диагностируемой аппаратуры и стоимости контроля параметров С(Z_i) функциональных элементов, функции предпочтения примут вид

_{N N}

W₅ (Z_i) = min | ∑ P(S_i)S₀ (i j) — ∑ P(S_i)S₁ (i j)| (42)

^{j =1 j =1}

_{N N}

W₆ (Z_i) = min С(Z_i) | ∑ P(S_i)S₀ (i j) — ∑ P(S_i)S₁ (i j)| (43)

^{j =1 j =1}

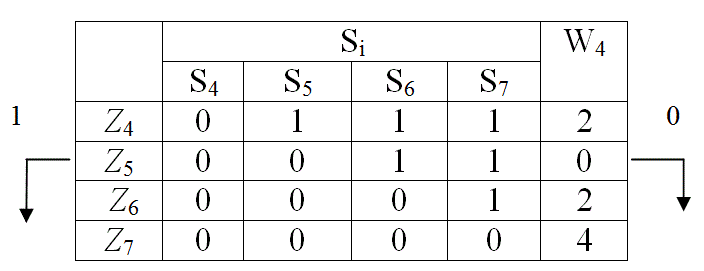
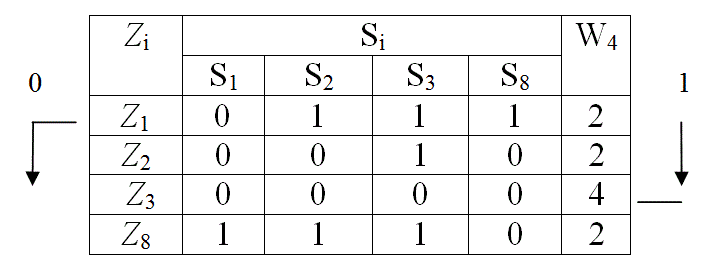
Пример 3.5.3

Рис. 9 Функциональная модель ОД

Табл. 9

Для каждого параметра Z_i табл. 9 по формуле (41) определяется значение W₄ . Полученные значения записывают в табл. 10 и по минимальному значению выбирают для контроля параметр Z₃ .

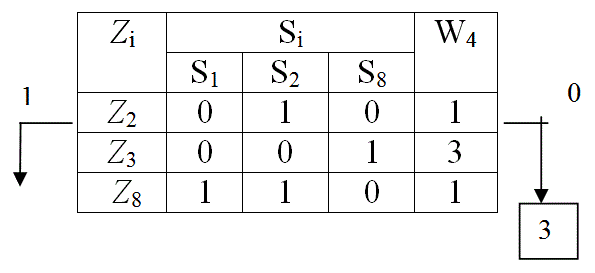
Табл. 10

В результате контроля параметра Z₃ табл. 10 делится на две части: в первую часть входят функциональные элементы 4, 5, 6 и 7, для которых результат контроля Z₃ положителен, в другую часть входят функциональные элементы 1, 2, 3 и 8, для которых результат контроля отрицателен, что означает неисправность одного из этих элементов. При поиске неисправностей контролю подлежат обе части матрицы, поэтому каждую часть из них представляем в виде табл. 11, а другую табл. 12. Для каждой из полученных таблиц определяем значения функций предпочтения W₄. По минимуму W₄ в табл. 11 выбираем для контроля параметр Z₁ , в табл. 12 выбираем для контроля параметр Z₅ . Аналогичные деления показаны в табл. 13 – 15. Схема поиска неисправностей показана на рис. 10.

Табл. 11

Табл. 12

Табл. 13

Табл. 14

Табл. 15

Рис. 10 Схема поиска неисправностей в диагностируемом устройстве

3.6. Метод на основе иерархического принципа

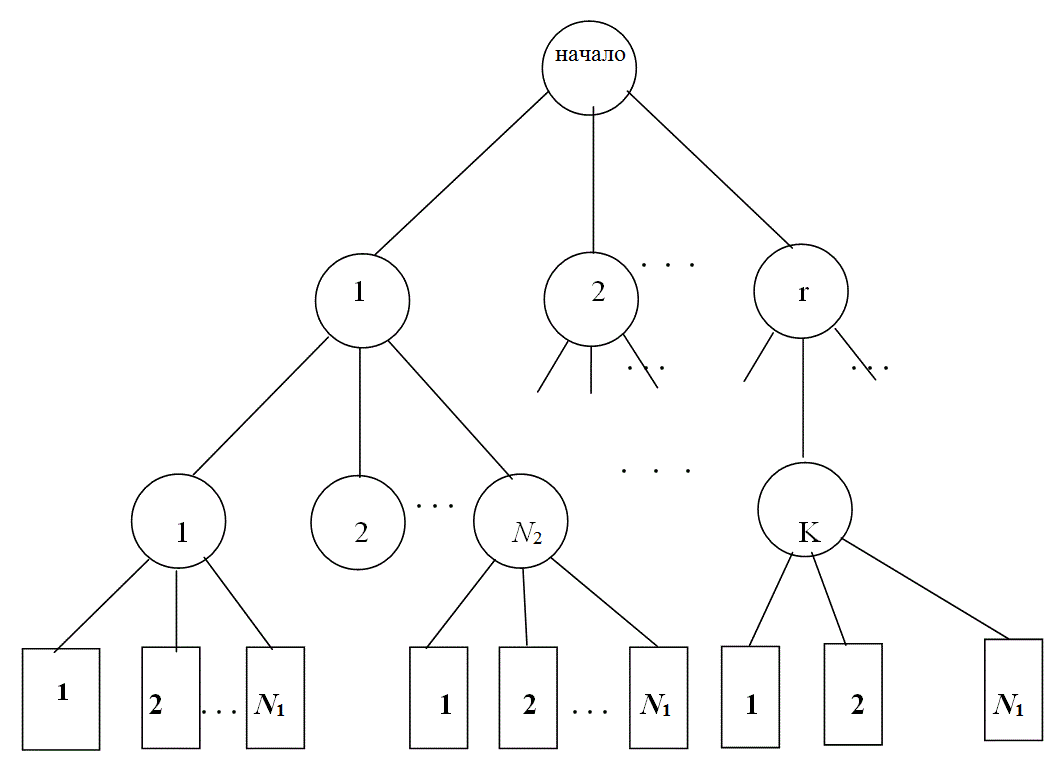
Построение алгоритмов диагностирования по иерархическому принципу целесообразно использовать для РЭА со встроенными устройствами контроля. При данном методе N первичных функциональных элементов ОД разбиваются к групп по N₁ элементов в каждой группе. Выходные параметры первичных функциональных элементов объединяются в одной точке с измерительным устройством и индикатором неисправности. Таких индикаторов будет к штук. Последние еще разбиваются на r групп по N₂ штук в каждой группе и т. д. В результате придем к одному индикатору неисправности.

В такой системе при выходе из строя функционального элемента последний индикатор покажет неисправность ОД. Для обнаружения неисправного функционального элемента просматриваются показания индикаторов первой ступени и при обнаружении индикатора, указывающего на неисправность, просматриваются индикаторы следующей ступени, соединенные только с этим индикатором. Проверки проверяются в указанной последовательности до тех пор, пока не будет обнаружен неисправный первичный элемент (рис. 11).

Поиск неисправного первичного функционального элемента по приведенной схеме позволяет значительно сократить время поиска по сравнению с поиском среди N элементов. Минимальное среднее время поиска неисправностей:

(44)

где

P(N) – вероятность пропуска неисправного элемента.

При и достигает максимума при z=4. Тогда количество ступеней иерархии

e = lnN /lnz (45)

Рис. 11 Схема поиска неисправности по иерархическому принципу

3.7. Метод ветвей и границ

Способ построения алгоритма поиска неисправностей методом ветвей и границ используется для синтеза алгоритмов поиска неисправностей в РЭА, функциональная модель, которой представляет собой произвольную структуру. Он позволяет определить наилучшую последовательность поиска среди возможных. Исходными данными являются функциональная модель ОД, таблица неисправностей с вероятностями различных состояний и стоимости контроля выходных параметров функциональных элементов. Целью данного метода является определить такую последовательность контроля параметров, которая будет обладать минимальной средней стоимостью при поиске любого неисправного элемента.

Средняя стоимость произвольной программы поиска неисправностей

или , (46)

где C_i – стоимость контроля i – параметра;

— сумма вероятностей состояний, которые рассматриваются при контроле i – параметра.

Расчет поиска начинается с любого i – параметра, который разбивает всё множество возможных состояний S на два подмножества: S₀ (z_i) и S₁ (z_i), соответствующие отрицательному и положительному результатам контроля параметра z_i соответственно.

Последовательность контроля остальных параметров из приведенных подмножеств неизвестна, и определить значение средней стоимости алгоритма поиска невозможно. Поэтому значения средней стоимости заменяются их нижними границами С_н(S₀) и С_н(S₁) при контроле соответствующих параметров в подмножествах S₀(z_i) и S₁(z_i). Тогда нижняя граница средней стоимости всей программы поиска, которая начинается с контроля первого параметра, определяется как

(47)

Вычислив нижние границы стоимостей С_н(S₀) и С_н(S₁) для всех возможных алгоритмов поиска, выбирают первым такой параметр, контроль которого дает минимальную среднюю стоимость нижней границы алгоритма поиска.

Затем для подмножеств S₀(z_i) и S₁(z_i) вычисляют нижние границы стоимостей для всех возможных пар контролируемых параметров между первым и оставшимися для каждого подмножества.

Пусть для подмножества S₀(z_i) контролируется параметр z_к , а для подмножества S₁(z_i) – параметр z_j . Тогда нижняя граница средней стоимости программы поиска, начинающейся с контроля i – параметра, будет:

(48)

В общем виде записывается:

(49)

где (50)

(51)

где и — суммы вероятностей в подмножествах и соответственно.

Значения рассчитываются по формулам (46-48) для подмножеств

— подмножество состояний ОД, образующееся при отрицательном результате контроля параметров Z_iи Z_к;

— подмножество состояний ОД, образующееся при отрицательном результате контроля параметра Z_iи положительном результате контроля параметра Z_к;

— подмножество состояний ОД, образующееся при положительном результате контроля параметра Z_к и отрицательном результате контроля параметра Z_i;

— подмножество состояний ОД, образующееся при положительном результате контроля параметром Z_к и Z_i;

Вторым выбирается такой параметр, при контроле которого обеспечивается минимальная средняя стоимость нижней границы из всех возможностей алгоритмов поиска.

Аналогичным образом выбирают третий параметр и последующие параметры, пока получаемые пи контроле подмножества будут содержать более двух состояний ОД.

Рис. 12 Функциональная модель ОД

Матрица неисправностей и вероятности состояний

Таб.16

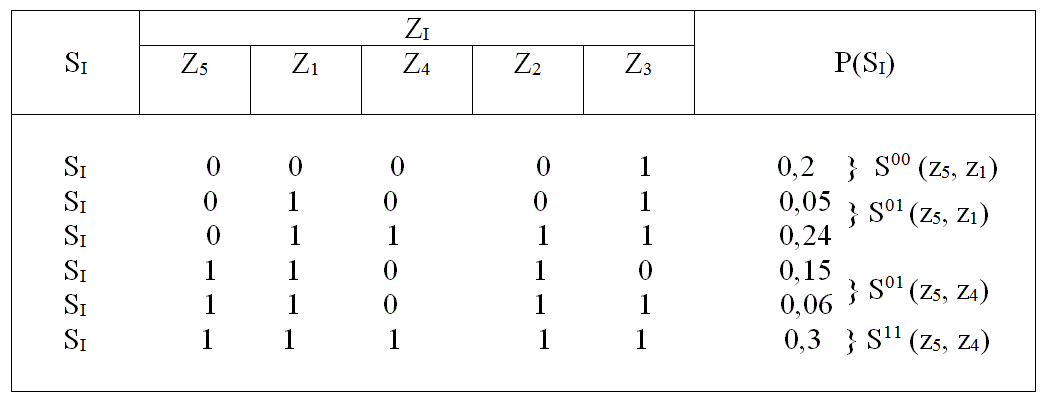
Пусть первым контролируется параметр Z₁. Тогда множество возможных состояний разбивается на два подмножества S₀(Z₁) и S₁(Z₁).Для подмножества S₀(Z₁) последовательность состояний вероятностей будет состоять из одного состояния Р(S₁) =0,2 , а подмножества S₁(Z₁) составим первую последовательность: Р(S₂) = 0,05; Р(S₅) =0,06; Р(S₄) =0,15; Р(S₃) =0,24; Р(S₆) =0,3. Затем определим сумму двух наименьших вероятностей: Р*₁ = 0,05 + 0,06 = 0,1.

Составим вторую последовательность: Р*₁ = 0,1; Р(S₄) = 0,15; Р(S₃) =0,24; Р(S₆) =0,03. Затем определим Р*₂ = 0,11 + 0,15 = 0,26.

Составим третью последовательность: Р(S₃) = 0,24; Р*₂ = 0,26; Р(S₆) =0,3. Затем определим Р*₃ = 0,24 + 0,26 = 0,5.

И наконец, составим четвертую последовательность: Р(S₆) =0,3; Р*₃ = 0,5 и определим Р*₄ = 0,3 + 0,5 = 0,8.

При этом нижняя граница средней стоимости

_{N 0 6-1-1}

С_н(Z₁) = С [ ∑ Р(S_i) + ∑ Р_λ + ∑ Р*_ν] = C (1 +0 +1,67) = 2,67 C

^{i=1 λ=1 ν=1}

Следует указать, что если подмножество S₀(Z_i) содержит одно состояние, то нижняя граница стоимости С_н(S₁) = 0.

Разделение множества возможных состояний на два подмножества S₀(Z₁) и S₁(Z₁) при контроле параметра Z₁ как показано в табл. 16.

При контроле параметра Z₂ множество возможных состояний разбивается на два подмножества: S₀(Z₂) и S₁(Z₂) (табл. 17).

Таб.17

Si	Zi	Pi
Z1	Z2	Z3	Z4	Z5	Z6
S1	0	0	1	0	0	0	S0 (Z2)
S2	1	0	1	0	0	0
S3	1	1	0	0	1	0	S0 (Z2)
S4	1	1	1	0	1	0
S5	1	1	1	1	0	0
S6	1	1	1	1	1	0

Для подмножества S₀(Z₂) последовательность двух значений вероятностей будет из двух значений: Р(S₂) = 0,05 и Р(S₁) = 0,2 , и тогда Р*₁ = 0,05 + 0,2 = 0,25.

Для подмножества S₁(Z₂) первая последовательность будет иметь вид Р(S₅) =0,06; Р(S₄) =0,15; Р(S₃) =0,24; Р(S₆) = 0,3 , и тогда Р*₁ = 0,21; Р*₂ = 0,45; Р*₃ = 0,75.

Следовательно, нижняя граница средней стоимости при контроле параметра

_{N 0 6-1-1}

С_н(Z₂) = С [ ∑ Р(S_i) + ∑ Р_λ + ∑ Р*_ν] = C (1 +0,25 +1,41) = 2,66 C.

^{i=1 λ=1 ν=1}

Поступая аналогичным образом при контроле параметров z₃ , z₄ и z₅ , получим нижние границы стоимости при контроле соответствующих параметров: С_Н ( z₃ ) = 2,59C; С_Н (z₄) = 2,60С; С_Н (z₅) = 2,50С.

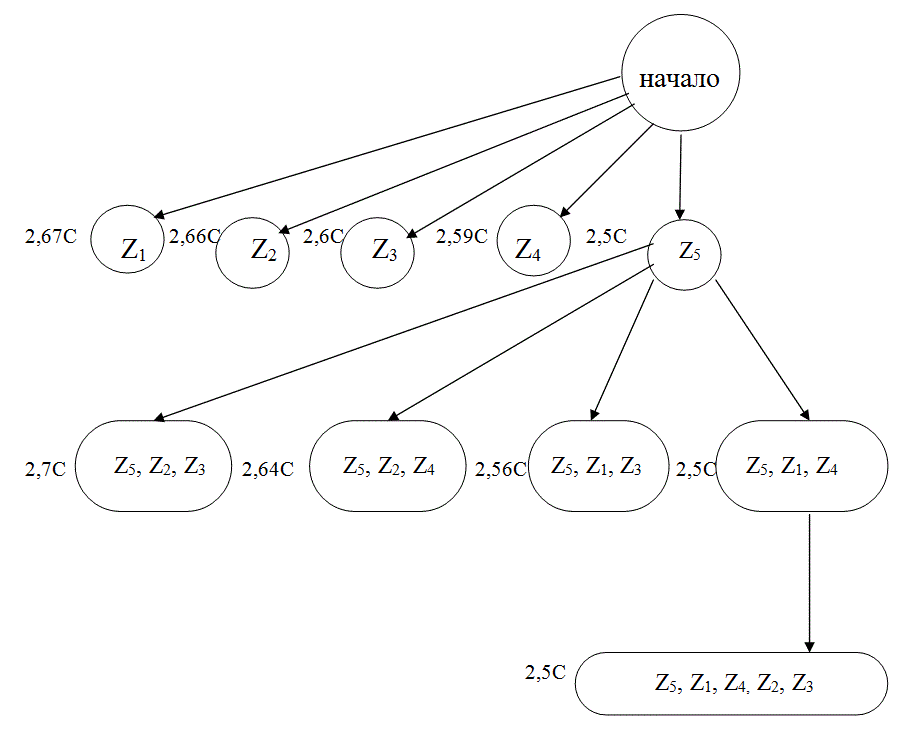
Из результатов вычислений нижних границ средней стоимости следует, что минимальной стоимостью будет обладать алгоритм поиска, начинающийся с контроля параметра z₅.

Посмотрим матрицу (табл. 18) состояний подмножества:

S₀ (z₅) и S₁ (z₅).

Анализируя табл. 18 , видим, что в случае отрицательного исхода при контроле параметра z₅ следующими можно контролировать параметры z₁ , z₂ , z₅. Параметр z₃ контролировать не имеет смысла, так как подмножество S₀(z₅) не разбивает при его контроле на более мелкие подмножества. При положительном исходе можно контролировать параметры z₃ , z₄.

Таким образом, необходимо вычислить значения стоимостей нижних границ алгоритма поиска при контроле таких наборов параметров z₅ , z₁ , z₃ , z₅ , z₁ , z₅ , z₂ , z₃ , z_{5 ,} z₂ , z₄. Для этого воспользуемся формулой:

,

где

;

Таблица 18

,

где ∑ Р(S_K) и ∑ Р(S_J) суммы вероятностей Р(S) диагностируемого объекта, которые различаются контролем параметров z_K и z_J в подмножествах и соответственно.

Вычислим значения стоимостей нижних границ при контроле параметров z₅ , z₁ , z₃ . Контроль параметров z₁ позволяет различать состояния S₁ , S₂ , S₅ , следовательно,

∑ P(S_K) = Р(S₁) + Р(S₂) + Р(S₂) = 0,2 + 0,05 + 0,06 = 0,31

Также при контроле параметра z_I выделяется из подмножества S₀(z_К) только одно состояние S⁰⁰₁ , тогда C_Н (S⁰⁰₁) = 0 , а значения C_Н (S₁⁰¹) вычисляется аналогичным способом , как и C_Н (S⁰₁) :

_К

C_Н (S₁⁰¹) = С ∑Р*_V = С [Р (S₂) + Р (S₅)] = C (0,05 + 0,06) = 0,11C

При контроле параметра z₃ различаются состояния S₃ , S₄ , S₆ , следовательно:

∑ P(S_J) = Р(S₃) + Р(S₄) + Р(S₆) = 0,24 + 0,15 + 0,3 = 0,69

Кроме того, при отрицательном исходе из множеств S₁(z₅) выделяется только одно состояние, а при положительном – два , следовательно:

C_Н (S¹⁰_J) = C_Н (S¹⁰₃) = 0

_К

C_Н (S¹¹_J) = С ∑ Р*_V = С [Р (S₄) + Р (S₆)] = C (0,15 + 0,3) = 0,45C

^V

Тогда значение стоимости нижней границы при контроле параметров z₅ , z₁ , z₃ будет равно

C_Н (z₅ , z₁ , z₃,) = С(1 + 0,31 + 0,11 + 0,69 + 0,45) = 2,56С

При контроле других последовательностей параметров вычисления осуществляются аналогично. Приведем результаты этих вычислений:

C_Н (z₅ , z₁ , z₄,) = 2,5С

C_Н (z₅ , z₂ , z₄,) = 2,64С

C_Н (z₅ , z₂ , z₃,) = 2,7С

Анализ результатов вычислений стоимостей нижних границ показывает, что минимальной стоимостью будет обладать последовательность параметров z₅ , z₁ , z_4.

Таблица19

Преобразуем таблицу неисправностей в соответствии с результатами контроля последовательности параметров z₅ , z₁ , z₄ (табл. 19) .

Из таблицы видно, что при отрицательном исходе контроля параметров z₅ и z₁ выделяется состояние S₁ , а при отрицательном исходе контроля z₅ и положительном z₁ необходимо следующим контролировать параметр z₂ (контроль параметра z₃ не позволяет разделить подмножество S⁰¹ на более мелкие).

При положительном исходе контроля параметров z₅ и z₄ выделяется состояние S₆ , а при отрицательном исходе контроля параметров z₅ и отрицательном z₄ необходимо контролировать параметр z₃. Поскольку других вариантов нет, на этом заканчивается построение алгоритма поиска неисправностей, обладающего минимальной средней стоимостью (Рис. 13).

Таким образом, последовательность контролируемых параметров z₅ , z₁, z₄, z₂ , z₃ дает среднюю стоимость С_СР = 2,5С.

Рис. 13 Схема алгоритма поиска неисправностей, построенного методом ветвей и границ

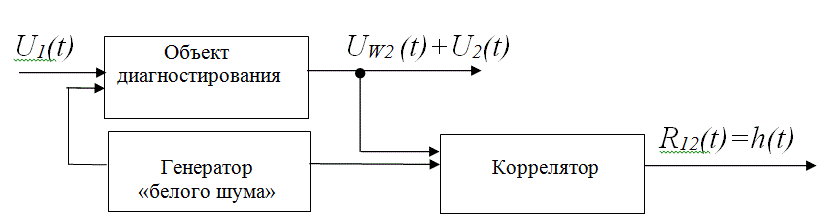
3.8. Метод диагностики на основе «белого шума»

Интегральный метод диагностики на основе «белого шума» позволяет определить отклик диагностируемой системы во время ее нормальной работы, то есть без отключения. Известно, что для «белого шума» автокорреляционная функция равна нулю при всех значениях τ, кроме точки τ = 0, где случайная функция умножается сама на себя:

(51)

где U_ш1 (t) – напряжение белого шума на входе ОД.

Связь между напряжениями входа и выхода диагностируемой системы через отклик h(t) определяется уравнением

(52)

Известно, что взаимная корреляционная функция входа и выхода системы выражается через автокорреляционную функцию

(53)

После перемены аргументов τ и t получим

(54)

Если на вход системы подать стимулирующее напряжение

δ(t) = U₁(t) (55)

то уравнение (52) упрощается и напряжение на выходе системы становится равным отклику диагностируемой аппаратуры:

U₂ (t) = h (t) (56)

Из сравнения выражений (52), (53) и (56) следует, что при подаче на вход ОД сигнала в виде «белого шума», корреляционная функция которого является дельта-функцией R₁₁(t) = δ(t), взаимно корреляционная функция входа и выхода будет равна отклику системы:

R₁₂(t) = h (t) (57)

Рис. 14 Схема для определения отклика диагностируемой системы.

Равенство (7) позволяет синтезировать схему (рис.1), которая с помощью коррелятора может определить отклик системы по напряжению «белого шума» на ее входе.

Если на вход подать напряжение U_с1 (t), то на ее выходе получим суммарный сигнал

U₂ (t) = U_ш2 (t) + U_с2 (t) (58)

где U_с2 (t) – напряжение, которое появляется на выходе контролируемой аппаратуры после прохождения через нее сигнала U_с1 (t), U_ш2 (t) – напряжение на выходе аппаратуры.

3.9. Метод диагностики на основе ортогонального анализа отклика системы по базису гармонических функций

Известно, что динамические свойства любой радиотехнической системы можно описать её откликом h(t). Если отклик системы разложить в ряд Фурье и установить аналитическую связь между коэффициентами ряда Фурье для отклика и параметрами диагностируемой системы, то на этой основе можно проводить диагностирование. Отклик любой системы

< (59)

где М и С₀ – постоянные положительные действительные числа:

h(t) = 0 при t < 0 и h(t) 0 при t > 0.

Для отклика системы, удовлетворяющего условию (59) можно применить преобразование Лапласа:

(60)

где функция h(t) является оригиналом, а функция Н(р) является изображением функции по Лапласу.

Учитывая условие (59) в формулах (60) можно положить С = 0 и р = jω.

Тогда получим преобразование Фурье:

(61)

Разложение функции h(t) в ряде Фурье в комплексной форме имеет вид:

(62)

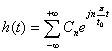
где t₀ – для отклика h(t);

С_n – комплексные коэффициенты.

(63)

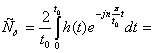
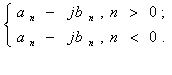
Из сравнения (60) и (63) получаем формулы для определения коэффициентов Фурье:

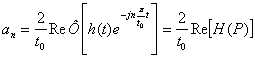
, при (64)

, при (65)

Используя преобразование Лапласа, можно получить изображение выходного сигнала и передаточной функции.

S₂ (P) = S₁ (P)*K(p) (66)

Зная параметры элементов системы, можно вычислить её передаточную функцию К(р). Если параметры входного сигнала S₁(P) будут неизменными, то любые отклонения параметров системы за допустимые пределы будут отражаться в спектре выходного сигнала.

Связь между параметрами системы и коэффициентами ряда Фурье разложения передаточной функции можно продемонстрировать на примере.

Пример 3.9.5 Передаточная функция видеосигнала.

(67)

где {х} = К, Т₁, Т₂ – диагностируемые параметры (вторичные).

Решение. Определить вещественную и мнимую часть передаточной функции:

;

;

;

ω = n*ω₀ , где n – номер гармоники;

ω₀ – частота основной гармоники.

Для определения текущих значений диагностируемых параметров, составим систему уравнений, используя действительную часть передаточной функции:

;

(68)

.

Используя мнимую часть передаточной функции, получим другую систему уравнений:

;

(69)

.

В дальнейшем для упрощения вычислений используем относительные коэффициенты разложения:

В₁ = b₁/a₁ ; B₂ = b₂/a₂ ; …; B_n = b_n/a₂ . (70)

Используя текущие значения в относительных коэффициентов, составим систему уравнений:

(71)

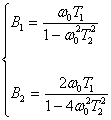
Систему уравнений приведем к виду:

(72)

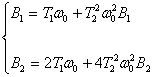
Решая систему уравнений (71) и (72) относительно Т₁ и Т₂ , получим выражения для параметров диагностируемой системы:

(73)

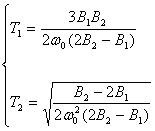
Для определения коэффициента усиления К видеоусилителя воспользуемся уравнением:

. (74)

Отсюда:

. (75)

Полученные значения параметров сравниваются с их номинальными значениями. Параметр, вышедший из допуска, и определяет место неисправности.

Методы поиска неисправностей

Негласно среди ремонтников в любой отрасли существуют два метода:

1. Обезьяний метод. Это  метод, при котором проверяется каждый узел сломанного устройства визуально или «методом тыка». «А что будет, если я сделаю так и эдак?». То есть ставим опыты и смотрим на реакцию сломанного устройства. Чаще всего такой метод очень сильно экономит время и нервы.
   
2. Метод умного специалиста. Надеваем очки и делаем умный вид). Берем книжки с инструкциями и описаниями, измерительные приборы, схемы, карты Таро и тд))). Сначала внимательно изучаем схемы, читаем книги, все анализируем в голове и только уже потом начинаем ковырять устройство. Этот метод очень длительный и муторный, но со временем дает хороший результат. Он в основном применяется интеллектуалами. Его также используют и простые ремонтники, после того, как не сработал первый метод)
   

Алгоритм поиска неисправности

Анализируем ситуацию

Анализ ситуации предполагает обзор и исследование  возникшей проблемы. Будьте Шерлоками Холмсами! Ответьте себе на все вопросы: где, куда, откуда, как, почему, когда, зачем??? Нужно внимательно осмотреть пациента, перед тем как его вскрывать. Может кто смотрел сериал Доктор Хаус? Всю серию они анализируют ситуацию, и только уже потом лечат. Если вы все-таки не знаете с чего начать, вот вам небольшой план:

• обсудите неисправность с владельцем данного электронного устройства
• может вы раньше ремонтировали что то подобное, вспомните что-нибудь похожее из своей практики, бывает так, что узлы радиоэлектронных устройств строятся по одинаковому принципу.
• а если все-таки неисправности нет, просто у владельца нет толка общения с данным устройством. Помню как то у мужичка громкость не добавлялась на мобиле, так он оказывается ее не теми кнопками пытался добавить))).
• определите различия между поломанным устройством и с тем какое оно должно быть при правильной работе.
• оцените ситуацию и сделайте правильные выводы из всего выше сказанного

Определяем причину

Самый большой  по времени и серьезный шаг. Начните с подготовки соответствующих схем. Не старайтесь сократить этот этап, бросаясь сразу работать и тратя много времени на исправление устройства, в то время как простое чтение руководства по техническому обслуживанию может способствовать скорейшему решению проблемы. Когда вы подготовились, выполните следующие операции:

• опишите проблему про себя
• сравните ситуацию с условиями работы устройства до возникновения неисправности
• вспомните различные симптомы которые были замечены при возникновении дефекта. Это может быть какой-то шум, запах, искры, дым и тд.
• сравните компоненты. Какие компоненты в порядке, а какие нет. Например, большой резистор во включенной аппаратуре должен быть чуть нагретый.
• сделайте тестирование оборудования с помощью мультика и других приборов.

Принимаем решение

На этом этапе рассматриваем различные варианты решения проблем. Ремонтировать его или выкинуть? Что дешевле и проще? Покупать микросхему или выпаять ее из другого устройства? Смотрим, что будет экономнее по времени и по деньгам. Решать вам.

Помните о необходимости всегда выполнять эти три фазы. Для того, чтобы стать первоклассным специалистом, нужно строго им следовать.

Поиск неисправности лабораторного блока питания

Анализ ситуации

Поиск неисправностей  начинаем с анализа ситуации.

Итак, у нас в ремонте лабораторный блок питания. Ну что, ситуацию я проанализировал. Перегрузка по питанию, в результате чего он  стал выдавать 24 Вольта, вместо положенных 0-15 Вольт. Напряжение не регулируется. Значит, помер какой-то радиоэлемент. Для того, чтобы определить причину возникновения неисправности, мы должны найти на него схему и вскрыть наш блок питания. Как говорится, «вскрытие покажет».

Вскрываем наш блок питания

Находим причину возникновения неисправности

На этом этапе мы должны определить причину возникновения поломки, а также параллельно анализировать ситуацию. Как обычно, начинаем осмотр с источника питания. Трансформатор у нас в норме, как и по схеме, он выдает нам переменное напряжение 20 Вольт. После диодного моста на конденсаторе напряжение 35 Вольт. Идем таким путем, проверяя все элементы на своем пути. Для того, чтобы научиться проверять радиоэлементы, нужно прочитать статьи:

Как измерить:

• ток мультиметром
• как проверить и измерить напряжение
• сопротивление мультиметром

Как проверить:

• биполярный транзистор мультиметром
• диод мультиметром
• конденсатор мультиметром
• предохранитель мультиметром

а лучше вообще прочитать все статьи сайта)

Ваши органы чувств — ваши помощники

Для того, чтобы определить неисправность, очень часто помогают наши пять чувств, но будем пользоваться четырьмя:

1. Зрение (глаза)
2. Осязание (кожа) 
3. Обоняние (запах)
4. Слух (уши)

Используйте их как можно чаще. Визуальный осмотр может дать Вам 80% нахождения неисправности. Это может быть сгоревший элемент, или печатная дорожка, а также обрыв или наоборот короткое замыкание. Не поленитесь, осмотрите хорошенько со всех сторон сломанную вещь.

Осязание может также сильно помочь вам в поиске неисправности. Если прибор включить в сеть и потрогать большие резисторы ( их мощность рассеивания, как правило, большая), то  они должны быть теплые или даже чуток горячие. Если холодные, значит или в резисторах обрыв, либо напряжение до них не доходит. Микросхемы  должны быть холодноватые или чуточку теплые. Процессоры или мощные микросхемы горяченькие.  Если уж слишком горячие — то следовательно микросхеме или процессору хана. Холодными должны быть конденсаторы и катушки индуктивности.

Все это приходит с опытом. Используйте осязание как можно чаще, но будьте очень осторожны. Если коснетесь выводов элементов, то вас хорошенько может «дернуть» током, ну смотря, конечно, в какой цепи какой ток.

Читай интересную статью про мощность электрического тока.

Настоящий электронщик должен знать запах горелого кремния, проводов, запах горелого трансформатора, горелой платы и тд наизусть. Напрягите свой нюх и попробуйте уловить «аромат» неисправности. Если аппаратура сгорела при вас, то сразу принюхивайтесь и визуально осмотрите ее.

Прислушайтесь к работе неисправной аппаратуры. Может слышится какое-то потрескивание, писк, гудение или еще что-то. Например, гудение асинхронного двигателя говорит о том, что может быть оборвана одна из фаз или не крутятся подшипники. Если гудит трансформатор, то это может значить короткое замыкание в обмотках.

Определяем дефектный узел

Вскрыв блок питания, я обнаружил, что у меня микросхема греется очень сильно при включении блока питания в сеть  и нажатия кнопки POWER на самом блоке. Скорее всего в ней возникло короткое замыкание. Находим в интернете даташит  на эту микросхему. В моем случае — это LM723. Она является регулятором напряжения.

Но беда не приходит одна. Сгорел еще и транзистор —  BD140.

Принимаем решение

Пошел в магазин за новыми запчастями. Итого, микросхема 20 рублей, транзистор — 10 рублей. Вместе 30 рублей.

Ну что же, надо отпаять микросхему, для этого используем наш оловоотсос.  На фото вид платы снизу микросхемы.

Получаем

Выдергиваем микросхему с помощью нехитрого инструмента экстрактора

Подготавливаем новую микросхему, и лудим ее выводы флюсом ЛТИ-120

Вставляем ее в наши отверстия, где находилась микросхема. Вставляйте точно также, как стояла дохлая микросхема! Кто не помнит, как она стояла, производители аппаратуры часто рисуют ее образ на плате. Получается, что выемка микросхемы должна быть справа.

Вставляем ее как надо

Смазываем площадки гелевым флюсом

И запаиваем по очереди каждую контактную площадку капелькой припоя на кончике паяльника.

Все те же самые операции проводим и с транзистором.

Блок питания у меня заработал как надо. Можно, конечно, его доработать, но на это требуется время и соответствующие знания. Но меня пока что вполне устраивает.

Заключение

Поиск неисправностей приходит с опытом и с годами. Следуйте этим простым этапам определять работоспособность компонентов, и вы никогда не будете носить аппаратуру мастеру-электронику, который сдерет с вас ого-го! Во-первых, вы сэкономите деньги, во-вторых, свою репутацию, ну и в-третьих, получите реальные знания на опыте.

И буду благодарен, если ты прочитаешь что такое протон.

Если
время, затраченное на ремонт изделия,
принять за 100%, то поиск неисправного
элемента занимает 64%. Поскольку количество
элементов в объектах средств автоматизации
и особенно в автоматических системах
очень велико, то прямой перебор элементов
для оценки их состояния невозможен.
Поэтому разработка мер по правильному
выбору последовательности операций
поиска позволяет обеспечить наиболее
быстрое определение неисправностей,
уменьшить физическую и умственную
нагрузку обслуживающего персонала.

При
выполнении работ по поиску, устранению
неисправностей необходимо придерживаться
определенных правил. Технология поиска
может быть разбита на основные операции
указанные на рисунке 3.2.

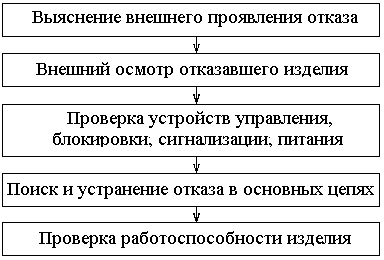
Рисунок
3.2 – Технология поиска отказов
(неисправностей)

Процесс
поиска неисправностей сводится к
проведению различных проверок и принятию
решения о дальнейшем развитии поиска
на основе результатов проверки.

Независимо
от применяемых средств процесс поиска
неисправностей имеет две стадии: выбор
последовательности проверки элементов;
выбор методики (способа) проведения
отдельных операций проверки.

Поиск
может проводиться по заранее определенной
последовательности проверок или ход
каждой последующей проверки определяется
результатом предыдущей. В зависимости
от этого различают следующие методы
проверок: последовательных поэлементных,
последовательных групповых и
комбинационных.

Выбор
той или иной последовательности проверок
зависти от конструкции изделий в целом
или их части, в которой появилась
неисправность, и может изменяться в
процессе накопления информации по
надежности и трудоемкости проверки
элементов.

Метод
последовательных поэлементных проверок
заключается в том, что элементы изделий
при поиске неисправности проверяются
поодиночке в определенной, заранее
установленной последовательности. Если
очередной проверяемый элемент оказался
исправным, то переходят к проверке
следующего элемента. При обнаружении
неисправного элемента поиск прекращается,
и элемент заменяется (ремонтируется).
Затем объект проверяется на
работоспособность. Если при этом объект
(система) не функционирует нормально,
то приступают к дальнейшей проверке.
Причем проверка начинается с той позиции,
на которой был обнаружен неисправный
элемент. При обнаружении второго
неисправного элемента он также заменяется
или ремонтируется (восстанавливается),
и объект вновь проверяется на
работоспособность. Если объект работает
ненормально, то поиск вновь возобновляется,
и так до тех пор, пока объект или система
не будут функционировать нормально.

Рисунок
3.3 – Структурная схема системы
автоматического регулирования типа
“Кристалл”

Простейшим
примером использования такого метода
может служить поиск неисправности в
системе автоматического регулирования
одного из параметров технологического
процесса. Сначала проверяется регулирующий
орган, затем исполнительный механизм,
затем усилитель и т.д. Таким образом,
устанавливается объект, неисправность
которого послужила причиной нарушения
нормального функционирования САР
(рисунок 3.3).

При
обнаружении, например, неисправности
в исполнительном механизме, рассматривается
поэлементная структура этого устройства
(объекта). Предположим, что в качестве
исполнительного устройства используется
электромеханический привод, представляющий
электродвигатель постоянного тока,
соединительную муфту (например,
фрикционную) и редуктор (рисунок 3.4).

Рисунок
3.4

Здесь
можно установить следующую последовательность
проверки элементов: 1-2-3-4-5-6-7-8. наиболее
уязвимыми из них могут оказаться элементы
1,2,4,7 и 8. Поэтому при использовании
поэлементного метода проверки возможны
два способа очередности контроля
элементов. Если в изделии (системе)
используются элементы, длительность
проверки которых примерно одинакова,
то проверку надо начинать с элементов,
обладающих наименьшей надежностью. Для
нашего случая это элементы 1,2,4. Если
надежность элементов данного изделия
примерно одинакова, то целесообразно
начинать проверку с элемента, для
проверки которого требуется наименьшее
время. Например, с защитного устройства
1; затем 2; затем 4. Для успешного
использования этих правил необходимо
знать не только функциональные и
принципиальные схемы объектов и систем,
но иметь четкое представление о надежности
их элементов.

Недостаток
метода – сравнительно большое
количество проверок. Объясняется это
тем, что в этом методе при поиске не
используются функциональные связи
элементов, хотя это делает метод
универсальным, т.к. он не зависит от
функциональной схемы системы.

Метод
последовательных групповых проверок
состоит в том, что все элементы объекта
с учетом их функциональных связей
разбиваются на отдельные группы и
контролируется исправность каждой
группы в целом. Последовательность
проведения проверок определяется
результатом предыдущей проверки. По
мере проведения проверок численность
подлежащих проверке элементов уменьшается.
На последнем этапе контроля в группе
должен быть один элемент.

Пример
проведения поиска неисправности по
такому методу приведен в функциональной
схеме системы на рисунке 3.5 одной из
видов САУ.

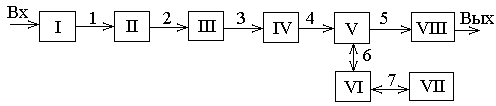
Рисунок
3.5 – Пример структурной схемы САУ

Схема
разбивается на группы I-VIII.
Затем структура разбивается на две
подгруппы и т.д. При этом последовательность
проверок будет следующая:

а)
Контролируется сигнал в точке 4. Если
он нормальный, то переходят к точке 6,
т.к. при этом предполагается, что
неисправный элемент находится в группе
V, VI, VII,
VIII. Если сигнал в точке 4
не соответствует норме, то проверяется
сигнал в точке 2, т.к. неисправен один из
элементов I, II,
III, IV. Если
сигнал в точке 2 в норме, то элементы I,
II исправны, и следует
проверять точку 3. При этом выявляется,
какой из элементов III или
IV неисправен.

б) Если
при контроле точек 4 и 6 сигнал соответствует
требуемым параметрам, то контролируется
точка 5, в результате чего определяется
неисправный элемент V или
VIII.

При
таком методе поиска неисправностей
необходимо знать параметры сигналов в
контрольных точках, а также типы
измерительных приборов и правила их
эксплуатации.

Если
в объекте (системе) будет несколько
неисправностей, то схема поиска
неисправностей не изменится. Двигаясь
по одной из ветвей структуры, неизбежно
приходят к одному из неисправных
элементов. После устранения этой
неисправности (восстановления элемента)
проверяется работоспособность объекта,
которая покажет, существует или нет еще
неисправность.

При
наличии неисправности процесс поиска
продолжается (повторяется), что должно
привести ко второму неисправному
элементу и т.д.

Такой
метод еще называется методом средней
точки. Однако, в общем случае число, на
которое разбивается структурная схема
объекта (системы), может быть и не равна
двум. Разбивать систему нужно, учитывая
функциональные связи отдельных элементов
и надежность их работы.

При
групповом методе проверок различают
проверки “с исключением” и “без
исключения”. Проверка “с исключением”
состоит в том, что заключение о
работоспособности одной из групп
элементов делается на основании проверки
других групп. Например, имеем три группы
элементов. По результатам проверки
установили исправность групп 1 и 2. Не
делая проверок, заключаем, что неисправный
элемент находится в 3-й группе.

При
проверках “без исключения” контролируется
работоспособность всех групп. На конечном
этапе всегда проводится проверка “без
исключения”, что устраняет возможность
ошибки.

Достоинство
этой последовательности проверок –
значительное сокращение времени поиска
неисправности. Однако этот метод
требует знания функциональных связей
отдельных элементов и их надежности.

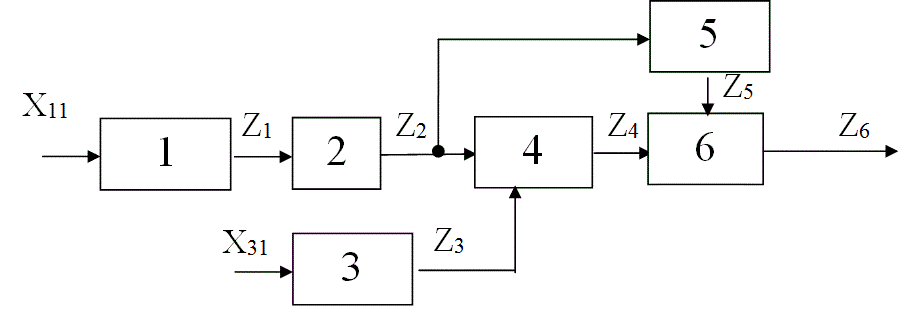
Сущность
комбинационного метода проверок
заключается в одновременном измерении
нескольких параметров (например параметра
А, В, С, Д на рисунке 3.6). По результатам
измерений всех параметров делается
заключение о неисправном элементе.

Для
удобства пользования таким методом
составляют таблицы состояния контролируемых
параметров. В качестве элементов в этом
случае следует выбирать блок, узел,
последовательную неразветвленную
группу каскадов.

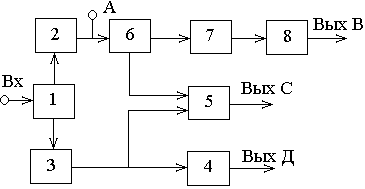
Рисунок
3.6 – К использованию комбинационного
метода проверок.

Таблица
3.2 – График состояний

Элементы	Параметры
А	В	С	Д
1	0	0	0	0
2	0	0	0	1
3	1	1	0	0
4	1	1	1	0
5	1	1	0	1
6	1	0	0	1
7	1	0	1	1
8	1	0	1	1

В первом
вертикальном столбце таблицы 3.2 указаны
элементы структурной схемы, а в первой
строке – их параметры. Таблицу заполняют
по стрелкам в соответствии со следующими
правилами.

Поочередно
предполагается неисправность только
в данном элементе. Данная неисправность
приводит к выводу соответствующих
параметров за пределы допусков. Против
этих параметров в таблице ставится «0».
Если же заданная неисправность не влияет
на какой-то параметр, то против этого
параметра ставится «1».

Полагаем,
что элемент 1 (рисунке 3.6) неисправен.
Тогда, очевидно, что все параметры А, В,
С и Д выйдут за пределы допусков. Против
этих параметров в таблице ставится
«0», т.е. первая строка таблицы 2 будет
состоять из одних нулей. Затем предполагаем,
что неисправен элемент 2 , при этом
параметры А, В и С будут не соответствовать
нормам, а параметр Д будет в норме. Во
второю строку следует записать «0001».
Таким образом перебирают все элементы
и анализируют состояние параметров.
Одинаковые стоки (7 и 8 таблицы 3.2) говорят
о не различении данной системой (объектом)
параметров неисправностей элементов
7 и 8. В этом случае элементы объединяются
в один или вводят дополнительный параметр
для их различения.

Для
обнаружения неисправного элемента с
помощью такой таблицы, поступают
следующим образом. Оператор записывает
значения параметров в виде числа,
состоящего из нулей и единиц, по указанному
правилу. Для определения неисправного
элемента сравнивают полученное число
с числами в строках таблицы. С какой
строкой таблицы совпадают результаты
измерения параметров, тот элемент и
неисправен. Если результат измерения
параметров (числа) не совпадает ни с
одной строкой таблицы, неисправны
несколько элементов.

Достоинство
этого метода – относительно малое время
поиска неисправности, однако реализация
его трудна.

Последовательность
процесса поиска неисправностей носит
название программы поиска. Определенная
последовательность проверок, обеспечивающая
минимальное значение математического
ожидания времени проверок, просчитывается
с помощью создания математической
модели процесса поиска отказавшего
элемента.

Объект,
в котором появилась неисправность,
состоит из n элементов.
Отказы элементов независимы. При отказе
любого из элементов отказывает объект.
Для контроля исправности элемента
имеется возможность подать на вход
контрольный сигнал и проверить на выходе
реакцию на этот сигнал. Известны
интенсивности отказов элементов q
и потребное время τ на проверку их
исправности. Определяют последовательность
проверок элементов, обеспечивающих
наименьшее время поиска неисправности.

Оптимальная
последовательность должна обладать
следующим свойством:

,
(3.8)

где τ
– среднее время проверки исправного
элемента; q – условная
вероятность отказа элемента.

Если
время контроля исправности всех элементов
равны, то оптимальная последовательность
принимает вид:

q₁>q₂>…>q_n-1,
(3.9)

Т.е.
контроль исправности элемента следует
производить в порядке убывания условной
вероятности отказов элементов.

Последовательность
(3.9) можно записать более удобном виде:

λ₁>
λ ₂>…>
λ _n-1,
(3.10)

Среднее
время поиска неисправностей по программе
вычисляют по формуле:

,
(3.11)

где
τ_ИЗ.i – врем,
расходуемое на измерения при отказе
i-го элемента.

В свою
очередь:

,
(3.12)

где τ_R
– время, расходуемое на измерения в
точке К схемы; r_i
– число измерений по программе для
выявления отказа i-го
элемента.

С учетом
(3.12):

,
(3.13)

Порядок
построения программ можно рассмотреть
на примерах.

Пример 3.1.

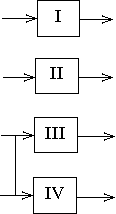
Рисунок 3.7 –
Структурная схема изделия А.

Имеется
схема, представленная на рисунке 3.7.
Интенсивности отказов элементов: λ₁=0,1
1/ч; λ₂=0,2
1/ч; λ₃=0,2
1/ч; λ₄=0,5
1/ч. Время измерения в точках схемы: τ₁=5
мин.; τ₂=8
мин.; τ₃=12
мин.; τ₄=18
мин. Требуется составить оптимальную
схему программы поиска неисправности
при условии, что один их элементов
изделия А отказал.

Определяются
условные вероятности отказов. Для метода
последовательных поэлементных проверок
условные вероятности отказов q
по значению соответствуют λ. Тогда
q₁=0,1;
q₂=0,2;
q₃=0,2;
q₄=0,5.
Определяют частные: τ₁/
q₁=50;
τ₂/
q₂=40;
τ₃/
q₃=60;
τ₄/
q₄=36;

Согласно
(3.8) первое измерение необходимо
производить на выходе четвертого (IV)
элемента. Если сигнал нужного вида на
выходе элемента IV,
то следует продолжать поиск и очередные
измерения производить на выходе второго
(II)
элемента и т.д.

Для аналитического
представления процесса поиска
неисправности, как правило, применяют
его графическое изображение в виде
программы поиска неисправностей.
Условное обозначение элемента производят
в виде прямоугольника, а измерение в
виде круга внутри с номерами элемента,
за которым производится измерение.
Тогда программа поиска неисправности
будет представлена ветвящейся схемой,
состоящей из кружочков с двумя выходами,
обозначающих результат измерения (есть
нужный сигнал или нет – “да” или ”нет”)
и оканчивающейся прямоугольниками,
обозначающими неисправный элемент.

Программа поиска
для примера 3.1 приведена на рисунке 3.8.

Рисунок
3.8 – Программа поиска неисправностей
в изделии А

Среднее время
поиска неисправностей по программе
вычисляется по формуле (3.13). Тогда:

Т_ПН=q₁(τ₄+τ₂+τ₁)+q₂(τ₄+τ₂)+q₃(τ₄+τ₂+τ₁)+q₄τ₄=0.1(18+8+5)+0.2(18+6)+0.2(18+8+5)+0.5*18=23.5
мин.

Пример 3.2.

Имеется
схема, представленная на рисунке 3.9.
Интенсивности отказов элементов:
λ₁=0,56*10^-4
1/ч; λ₂=0,48*10^-4
1/ч; λ₃=0,26*10^-4
1/ч; λ₄=0,2*10^-4
1/ч; λ₅=0,32*10^-4
1/ч; λ₆=0,18*10^-4
1/ч. Время измерения во всех точках
одинаково и составляет 2 мин. Требуется
составить оптимальную программу поиска
неисправности при условии, что один из
элементов отказал.

Рисунок 3.9 –
Структурная схема изделия Б

Рисунок 3.10 –
Программа поиска неисправностей в
изделии Б.

Для сокращения
времени поиска неисправности используется
метод последовательной погрупповой
проверки, т.е. измерение реакции на
контрольный сигнал производится в точке
схемы, которая делит предполагаемую
неисправную схему по вероятности
(интенсивности) пополам.

Отсюда
условная вероятность отказов соответствует
значению интенсивности с коэффициентом
0,5 (половинной величине).

Тогда
условные вероятности отказов: q₁=0,28;
q₂=0,24; q₃=0,13;
q₄=0,10; q₅=0,16;
q₆=0,09.

Схема
состоит из последовательно соединенных
элементов. Можно использовать один
контрольный сигнал, подаваемый на вход
первого элемента. В этом случае первое
измерение необходимо производить после
второго элемента, ибо q₁+;q₂=0,52,
ближе всего к делению схемы по вероятности
пополам. Если нужного сигнала нет после
второго элемента, то делается вывод о
неисправности первого или второго
элемента и измерение производится после
первого элемента. Если после второго
элемента ест нужный сигнал, то делается
вывод о неисправности правой части
схемы, которая по вероятности лучше
всего делится пополам в точке измерения
после четвертого элемента и т.д.

Программа
поиска неисправности в этой схеме
приведена на рисунке 3.10. Среднее время
поиска неисправности по программе:

Т_П.Н.=0,28(2+2)+0,24(2+2)+0,13(2+2+2)+0,20(2+2+2)+0,16(2+2+2)+0,9(2+2+2)=5,56
мин.

При
поиске неисправностей, кроме выбора
метода и программы поиска неисправности
объекта (системы), необходимо выбрать
методику (способы) проверки исправности
отдельных элементов. Наиболее
распространенные способы проверок
исправности элементов:

• внешний осмотр;

• контрольные
  переключения и регулировки;

• промежуточные
  измерения;

• замена;

• сравнение;

• характерные
  неисправности;

• изоляция блока или
  каскада, узла;

• тест – сигналы.

Внешний
осмотр обычно подразумевает
использование зрения и слуха. Они
позволяют контролировать состояние
монтажа СА, кабелей, отдельных элементов,
печатных плат и т.п., а также проверять
работу ряда агрегатов, реже на слух.

Преимущество
этого вида проверок в простоте. Однако
возможности определения неисправного
элемента ограничены. Неисправность
может быть определена только при явно
выраженных внешних признаках: изменение
цвета элемента под воздействием
температуры, искрения, появление дыма
и запаха от горения изоляции проводов
и т.д. Такие признаки возникают сравнительно
редко. Кроме того, на практике часто
встречаются взаимозависимые отказы,
поэтому даже если внешним осмотром
обнаружен неисправный элемент, необходимо
провести дополнительные проверки для
выявления истинных причин отказа
(например, при выходе из строя
предохранителя, перегоревшую нить
которого видно “на глаз”).

Способ
контрольных переключений и регулировок
требует оценки внешних признаков
неисправностей путем анализа схем и
использованием органов переключения,
регулировок, текущего контроля (сигнальные
лампочки, встроенные приборы, автоматы
защиты и т.п.). При этом определяется
неисправный узел, блок или тракт схемы
объекта (системы), т.е. совокупность
элементов, выполняющих определенную
функцию объекта (преобразовательный,
индикаторный блоки, блок защиты или
коммутации, передающий тракт и т.д.).

Достоинство
способа в быстроте и простоте проверки
предположения о состоянии участков
схемы объекта.

Недостаток
– ограниченность, т.к. позволяет
определить участки, а не конкретное
место повреждения.

Способ
промежуточных измерений является
наиболее распространенным и основным
для электрических и электронных
устройств. Параметры системы, блока,
узла или элемента определяются с помощью
ручной портативной или автоматизированной
встроенной контрольно – измерительной
аппаратуры (КИА) или придаваемых к
средствам автоматизации специальных
измерительных устройств, систем
автоматического контроля.

При
этом измеряются режимы питания, параметры
линий связи, проводятся измерения в
контрольных точках. Быстроту отыскания
неисправности в немалой мере обеспечивает
умение обслуживающего персонала грамотно
проводить измерения. Полученные значения
параметров сравнивают с их значениями
из технической документации, с таблицами
режимов данного изделия, например.

Способ
замены заключается в тои, что вместо
подозреваемого в неисправности элемента
(узла, блока и т.п.) устанавливают
аналогичный заведомо исправный элемент.
После замены проверяют объект (систему)
на функционирование. Если при этом
параметры системы лежат в пределах
нормы, то делается вывод о том, что
замененный элемент неисправен.
Преимущество данного способа – простота.
Но на практике этот способ имеет
ограничения, во-первых, из-за отсутствия
запасных элементов, во-вторых, из-за
необходимости проведения регулировок
вследствие недостаточной взаимозаменяемости.

Зависимые
отказы могут привести к выходу их строя
вновь установленного элемента, поэтому
этот вид проверки используют, когда
подозреваемый элемент легко съемный и
недорогой.

Способ
сравнения – режим неисправного
участка (узла, блока) объекта или системы
сравнивается с режимом однотипного
участка исправного объекта. Достоинство
способа в отсутствии необходимости
знаний абсолютных значений, измеряемых
величин и параметров. В то же время этот
способ позволяет определять довольно
сложные неисправности. Недостаток
способа – необходимость запасного
(стендового) комплекта оборудования и,
как следствие, возможность применения
этого способа только в условиях
лаборатории.

При
способе характерных неисправностей
отказ отыскивается на основании известных
характерных признаков. Такие неисправности
и их признаки представляются в виде
таблиц в инструкции по эксплуатации
СА.

Таблицы
характерных неисправностей обладают
рядом недостатков, из которых наиболее
существенны следующие:

• таблицы не обеспечивают
  однозначной связи между признаками
  отказа и возможными неисправностями:
  к одному признаку привязываются
  несколько различных неисправностей и
  обычно без каких –либо указаний на
  особенности их появления;

• в таблицах часто
  отсутствует указания о проведении
  испытаний, направленных на уточнение
  причины отказов. Отдельный внешний
  признак не может указать на конкретную
  причину отказа, а для ее отыскания
  необходимо логическое сопоставление
  целого ряда внешних признаков, включая
  показания устройств контроля и результаты
  испытаний;

• действия по поиску
  отказа, рекомендуемые таблицами, не
  содержат причинно-следственных связей
  и не распределяются в порядке их
  следования, в то время как реальный
  поиск представляет собой четкую
  последовательность различных проверок
  (испытаний).

Тест-сигналы
широко применяются в различных
вычислительных машинах, в счетно-решающих
устройствах. При этой проверке на вход
контролируемого устройства подается
сигнал с определенными характеристиками.
Анализ выходного сигнала позволяет
определять место неисправного элемента.

Изоляция
блока (узла, участка, каскада) обоснована
тем, что в ряде случаев блок или каскад
связан большим числом функциональных
связей с другими частями объекта. При
отказе такого блока трудно определить,
где возникла неисправность – в самом
блоке или в функционально связанных с
ним частях изделия. Отсоединение
некоторых функциональных связей
позволяет иногда локализовать
местонахождение неисправного элемента.

Каждый
из рассмотренных частных способов
поиска неисправностей имеет существенные
ограничения, поэтому в практике ремонта
КИП и СА обычно применяют совместно
несколько частных способов. Такое
совмещение способов позволяет сократить
общее время поиска и тем самым способствует
его успеху.