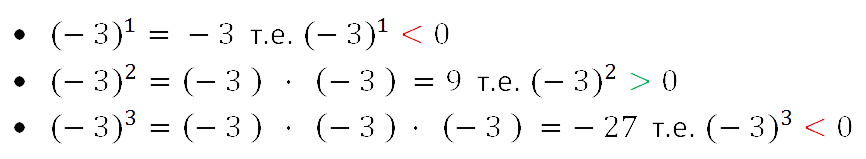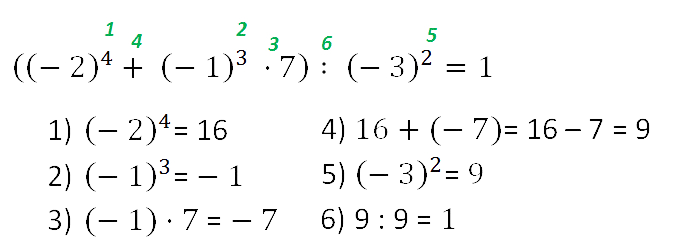Корни и степени
-
Степень с натуральным показателем
-
Степень с целым показателем
-
Кубический корень
-
Корень -ной степени
-
Сравнение арифметических корней
-
Как избавиться от иррациональности в знаменателе
-
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения
Степенью называется выражение вида .
Здесь — основание степени,
— показатель степени.
к оглавлению ▴
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
По определению, .
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
.
Возвести число в куб — значит умножить его само на себя три раза.
.
Возвести число в натуральную степень — значит умножить его само на себя
раз:
к оглавлению ▴
Степень с целым показателем
Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.
По определению,
.
Это верно для . Выражение 00 не определено.
Определим также, что такое степень с целым отрицательным показателем.
Конечно, все это верно для , поскольку на ноль делить нельзя.
Например,
Заметим, что при возведении в минус первую степень дробь переворачивается.
Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где
— целое,
— натуральное.
Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.
Определение.
Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен
.
Согласно определению,
В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение для нас сейчас имеет смысл только при
.
Выражение всегда неотрицательно, т.е.
. Например,
.
Свойства арифметического квадратного корня:
Запомним важное правило:
По определению, 
к оглавлению ▴
Кубический корень
Аналогично, кубический корень из — это такое число, которое при возведении в третью степень дает число
.
Например, , так как
;
, так как
;
, так как
.
Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.
Теперь мы можем дать определение корня -ной степени для любого целого
.
к оглавлению ▴
Корень  -ной степени
-ной степени
Корень -ной степени из числа
— это такое число, при возведении которого в
-ную степень получается число
.
Например,
Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.
Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.
Итак, — такое число, что
. Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.
По определению,
в общем случае .
Сразу договоримся, что основание степени больше 0.
Например,
Выражение по определению равно
.
При этом также выполняется условие, что больше 0.
Например,
Запомним правила действий со степенями:
— при перемножении степеней показатели складываются;
— при делении степени на степень показатели вычитаются;
— при возведении степени в степень показатели перемножаются;
Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:
1.
Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.
2.
3.
Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.
4. Найдите значение выражения при
Решение:
При получим
Ответ: -0,5.
5. Найдите значение выражения при
Решение:
При a = 12 получим
Мы воспользовались свойствами степеней.
Ответ: 144.
6. Найдите значение выражения при b = — 5.
Решение:
При b = — 5 получим:
Ответ: -125.
7. Расположите в порядке возрастания:
Решение:
Запишем выражения как степени с положительным показателем и сравним.
Так как
то
Так как
то
Сравним и
для этого оценим их разность:
значит
Получим : поэтому
Ответ:
8. Представьте выражение в виде степени:
Решение:
Вынесем за скобку степень с меньшим показателем:
Ответ:
9. Упростите выражение:
Решение:
Приведем основания 6 и 12 к основаниям 2 и 3:
(выполним деление степеней с одинаковыми основаниями)
Ответ: 0,25.
10. Чему равно значение выражения при
?
Решение:
При получим
Ответ: 9.
к оглавлению ▴
Сравнение арифметических корней
11. Какое из чисел больше: или
?
Решение:
Возведем в квадрат оба числа (числа положительные):
Найдем разность полученных результатов:
так как
Значит, первое число больше второго.
Ответ:
к оглавлению ▴
Как избавиться от иррациональности в знаменателе
Если дана дробь вида то нужно умножить числитель и знаменатель дроби на
:
Тогда знаменатель станет рациональным.
Если дана дробь вида или
то нужно умножить числитель и знаменатель дроби на сопряженное выражение, чтобы получить в знаменателе разность квадратов.
Сопряженные выражения — это выражения, отличающиеся только знаками. Например,
и
и
— сопряженные выражения.
Пример:
12. Вот несколько примеров — как избавиться от иррациональности в знаменателе:
Пример 1.
Пример 2.
Пример 3.
Пример 4.
Совет. Если в знаменателе дана сумма двух корней, то в разности первым числом пишите то, которое больше, и тогда разность квадратов корней будет положительным числом.
Пример 5.
13. Сравните и
1)
2) Сравним и 14.
то и
а значит,
Ответ: меньше.
к оглавлению ▴
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения
Покажем несколько примеров.
14. Упростите: выражения:
Пример 5.
т.к.
Пример 6.
Пример 7.
так как
Следующие несколько задач решаются с помощью формулы:
Решение:
Получим уравнение
Ответ:
19. Вычислите значение выражения:
Решение:
Ответ: 1.
20. Вычислите значение выражения:
Решение:
Ответ: 1.
21. Вычислите значение выражения: если
Решение.
Если то
следовательно
Ответ: — 1.
22. Вычислите:
Решение:
Ответ: 1.
Рассмотрим уравнение вида где
Это равенство выполняется, только если
Подробно об таких уравнениях — в статье «Показательные уравнения».
При решении уравнений такого вида мы пользуемся монотонностью показательной функции.
23. Решите уравнение:
а)
б)
в)
Решение.
23. Решите уравнение:
Решение:
тогда
Ответ: -1.
24. Решите уравнение:
Решение:
Ответ: 4.
25. Решите уравнение:
Решение:
Значит,
Ответ: -0,2.
Если вы хотите разобрать большее количество примеров — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Корни и степени» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Загрузить PDF
Загрузить PDF
Степень используется для упрощения записи операции умножения числа само на себя. Например, вместо записи 


Примечание: если вам необходимо решить показательное уравнение (в таком уравнении неизвестное находится в показателе степени), прочитайте эту статью.
-
1
Терминология. Например, дана степень
. Здесь 2 — это основание степени, а 3 — это показатель степени. Число
озвучивается так: два в третьей степени или два в кубе.
- Если в показателе степени присутствует цифра 2, например,
, то такой показатель называется квадратом, то есть наш пример озвучивается так: пять в квадрате.
- Если в показателе степени присутствует цифра 3, например,
, то такой показатель называется кубом, то есть наш пример озвучивается так: десять в кубе.
- Если число не имеет показателя степени, то это означает, что показатель степени равен 1. Например,
.
- Любое число (дробь, выражение), возведенное в нулевую степень, равно 1, то есть
или
Более подробную информацию вы найдете в разделе «Советы».
- Если в показателе степени присутствует цифра 2, например,
-
2
Умножьте основание степени само на себя числом раз, равным показателю степени. Если вам нужно решить задачу со степенями вручную, перепишите степень в виде операции умножения, где основание степени умножается само на себя. Например, дана степень
. В этом случае основание степени 3 нужно умножить само на себя 4 раза:
. Вот другие примеры:
-
3
Для начала перемножьте первые два числа. Например,
=
. Не волнуйтесь — процесс вычисления не такой сложный, каким кажется на первый взгляд. Сначала перемножьте первые две четверки, а затем замените их полученным результатом. Вот так:
-
4
Умножьте полученный результат (в нашем примере 16) на следующее число. Каждый последующий результат будет пропорционально увеличиваться. В нашем примере умножьте 16 на 4. Вот так:
-
5
Решите следующие задачи. Ответ проверьте при помощи калькулятора.
-
6
На калькуляторе найдите клавишу, обозначенную как «exp», или «
», или «^». При помощи этой клавиши вы будете возводить число в степень. Вычислить степень с большим показателем вручную практически невозможно (например, степень
), но калькулятор с легкостью справится с этой задачей. В Windows 7 стандартный калькулятор можно переключить в инженерный режим; для этого нажмите «Вид» –> «Инженерный». Для переключения в обычный режим нажмите «Вид» –> «Обычный».
- Проверьте полученный ответ при помощи Google. Воспользовавшись клавишей «^» на клавиатуре компьютера, введите выражение в поисковик, который моментально отобразит правильный ответ (и, возможно, предложит аналогичные выражения для изучения).
Реклама
-
1
Складывать и вычитать степени можно только в том случае, если у них одинаковые основания. Если нужно сложить степени с одинаковыми основаниями и показателями, то вы можете заменить операцию сложения операцией умножения. Например, дано выражение
. Помните, что степень
можно представить в виде
; таким образом,
(где 1 +1 =2). То есть посчитайте число подобных степеней, а затем перемножьте такую степень и это число. В нашем примере возведите 4 в пятую степень, а затем полученный результат умножьте на 2. Помните, что операцию сложения можно заменить операцией умножения, например,
. Вот другие примеры:[2]
-
2
При перемножении степеней с одинаковым основанием их показатели складываются (основание не меняется). Например, дано выражение
. В этом случае нужно просто сложить показатели, оставив основание без изменений. Таким образом,
. Вот наглядное объяснение этого правила:
-
3
-
4
Степень с отрицательным показателем следует преобразовать в дробь (в обратную степень). Не беда, если вы не знаете, что такое обратная степень. Если вам дана степень с отрицательным показателем, например,
, запишите эту степень в знаменатель дроби (в числителе поставьте 1), а показатель сделайте положительным. В нашем примере:
. Вот другие примеры:
-
5
При делении степеней с одинаковым основанием их показатели вычитаются (основание при этом не меняется). Операция деления противоположна операции умножения. Например, дано выражение
. Вычтите показатель степени, стоящей в знаменателе, из показателя степени, стоящей в числителе (основание не меняйте). Таким образом,
= 16.
-
6
Ниже приведены некоторые выражения, которые помогут вам научиться решать задачи со степенями. Приведенные выражения охватывают материал, изложенный в этом разделе. Для того, чтобы увидеть ответ, просто выделите пустое пространство после знака равенства.
Реклама
-
1
-
2
-
3
Складывайте, вычитание и перемножайте дробные показатели по общим правилам. Проще складывать и вычитать дробные показатели еще до того, как вы преобразуете степени в корни или в числа. Если даны степени с одинаковыми основаниями и показателями, то они складываются и вычитаются по общим правилам. Если даны степени только с одинаковыми основаниями, то их можно умножать и делить (только если вы помните правила сложения и вычитания дробей). Например:
Реклама
Советы
- Упрощение выражения — это приведение его к такой форме (при помощи выполнения математических операций), которую легче решить.
- На некоторых калькуляторах есть кнопка для вычисления степеней (сначала нужно ввести основание, затем нажать кнопку, а затем ввести показатель). Она обозначается как ^ или x^y.
- Помните, что любое число в первой степени равно самому себе, например,
Более того, любое число, умноженное или разделенное на единицу, равно самому себе, например,
и
.
- Знайте, что степени 00 не существует (такая степень не имеет решения). При попытке решить такую степень на калькуляторе или на компьютере вы получите ошибку. Но помните, что любое число в нулевой степени равно 1, например,
- В высшей математике, которая оперирует мнимыми числами:
, где
; е — константа, примерно равная 2,7; а — произвольная постоянная. Доказательство этого равенства можно найти в любом учебнике по высшей математике.
Реклама
Предупреждения
- При увеличении показателя степени ее значение сильно возрастает. Поэтому если ответ кажется вам неправильным, на самом деле он может оказаться верным. Вы можете проверить это, построив график любой показательной функции, например, 2x.
Реклама
Об этой статье
Эту страницу просматривали 115 942 раза.
Была ли эта статья полезной?
Возведение в степень – это такая же математическая операция, как сложение, вычитание, умножение или деление.
Сейчас объясню все человеческим языком на очень простых примерах. Будь внимателен. Примеры элементарные, но объясняющий важные вещи. Начнем со сложения.
Сложение
( 2+2+2+2+2+2+2+2=16 )
Объяснять тут нечего. Ты и так все знаешь: нас восемь человек. У каждого по две бутылки колы. Сколько всего колы? Правильно – 16 бутылок. Теперь умножение.
Умножение
Тот же самый пример с колой можно записать по-другому: (displaystyle 2cdot 8=16).
Математики — люди хитрые и ленивые. Они сначала замечают какие-то закономерности, а потом придумывают способ как быстрее их «считать».
В нашем случае они заметили, что у каждого из восьми человек одинаковое количество бутылок колы и придумали прием, который называется умножением.
Согласись, (displaystyle 2cdot 8=16) считается легче и быстрее, чем (displaystyle 2+2+2+2+2+2+2+2=16).
И еще одна важная деталь. Ошибок при таком счете делается гораздо меньше. Математики из Стэнфорда, кстати, считают, что человек, знающий приемы счета, делает это в два раза легче и быстрее и совершает в два раза меньше ошибок. Работы меньше, а результат лучше.
Круто, да?
Итак, чтобы считать быстрее, легче и без ошибок, нужно всего лишь запомнить таблицу умножения. Ты, конечно, можешь делать все медленнее, труднее и с ошибками, но лучше ее запомнить! Вот таблица умножения. Выучи ее наизусть.
И другая таблица, красивее:
А какие еще хитрые приемы счета придумали ленивые математики? Правильно – возведение числа в степень.
Далее, почему говорят «степень числа с натуральным показателем»?
Ты уже наверное, догадался: потому что показатель степени – это натуральное число. Да, но что такое натуральное число? Элементарно! Натуральные это те числа, которые используются в счете при перечислении предметов: один, два, три… Мы же когда считаем предметы не говорим: «минус пять», «минус шесть», «минус семь». Мы так же не говорим: «одна третья», или «ноль целых, пять десятых». Это не натуральные числа. А какие это числа как ты думаешь?
Числа типа «минус пять», «минус шесть», «минус семь» относятся к целым числам.
Вообще, к целым числам относятся все натуральные числа, числа противоположные натуральным (то есть взятые со знаком минус), и число ( displaystyle 0) . Ноль понять легко – это когда ничего нет.
А что означают отрицательные («минусовые») числа? А вот их придумали в первую очередь для обозначения долгов: если у тебя баланс на телефоне ( displaystyle -100) рублей, это значит, что ты должен оператору ( displaystyle 100) рублей.
Всякие дроби — это рациональные числа. Как они возникли, как думаешь? Очень просто. Несколько тысяч лет назад наши предки обнаружили, что им не хватает натуральных чисел для измерения длинны, веса, площади и т.п. И они придумали рациональные числа… Интересно, правда ведь?
Есть еще иррациональные числа. Что это за числа? Если коротко, то бесконечная десятичная дробь. Например, если длину окружности разделить на ее диаметр, то в получится иррациональное число ( displaystyle 3,141592…).
Итак…
Откуда взялись, например, первые два свойства? Сейчас покажу.
1. ( displaystyle {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}})
Посмотрим: что такое ( displaystyle {{a}^{n}}) и ( displaystyle {{a}^{m}}) ?
По определению:
( displaystyle left. begin{array}{l}{{a}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}\{{a}^{m}}=underbrace{acdot acdot …cdot a}_{mtext{ множителей}}text{ }end{array} right|Rightarrow text{ }{{a}^{n}}cdot {{a}^{m}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}cdot underbrace{acdot acdot …cdot a}_{mtext{ множителей}}text{ }leftarrow )
Сколько здесь множителей всего?
Очень просто: к ( displaystyle n) множителям мы дописали ( displaystyle m) множителей, итого получилось ( displaystyle n+m) множителей.
Итак, в правой части этого выражения получается такое произведение:
( displaystyle {{a}^{n}}cdot {{a}^{m}}=underbrace{acdot acdot …cdot a}_{n+mtext{ множителей}})
Но по определению это степень числа ( displaystyle a) с показателем ( displaystyle n+m) , то есть: ( displaystyle {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}}) , что и требовалось доказать.
Пример: Упростите выражение ( displaystyle {{5}^{4}}cdot {{5}^{7}}cdot {{5}^{9}}) .
Решение: ( displaystyle {{5}^{4}}cdot {{5}^{7}}cdot {{5}^{9}}={{5}^{4+7+9}}={{5}^{20}})
Пример: Упростите выражение ( displaystyle {{3}^{5}}cdot {{3}^{8}}cdot {{5}^{7}}) .
Решение:
Важно заметить, что в нашем правиле обязательно должны быть одинаковые основания!
Поэтому степени с основанием ( displaystyle 3) мы объединяем, а ( displaystyle {{5}^{7}}) остается отдельным множителем:
( displaystyle {{3}^{5}}cdot {{3}^{8}}cdot {{5}^{7}}={{3}^{5+8}}cdot {{5}^{7}}={{3}^{13}}cdot {{5}^{7}})
Еще одно важное замечание: это правило – только для произведения степеней!
Ни в коем случае нельзя написать, что ( displaystyle {{2}^{4}}+{{2}^{6}}={{2}^{10}}).
Начнем с показателя, равного ( displaystyle 0) .
Любое число в нулевой степени равно единице:
( displaystyle {{a}^{0}}=1, ane 0)
Как всегда, зададимся вопросом: почему это так?
Рассмотрим какую-нибудь степень с основанием ( displaystyle 3). Возьмем, например ( displaystyle {{3}^{5}}), и домножим на ( displaystyle {{3}^{0}}):
( displaystyle {{3}^{5}}cdot {{3}^{0}}underset{text{по правилу умножения}}{mathop{=}},{{3}^{5+0}}={{3}^{5}})
Итак, мы умножили число ( displaystyle {{3}^{5}}) на ( displaystyle {{3}^{0}}) и получили то же, что и было – ( displaystyle {{3}^{5}}). А на какое число надо умножить, чтобы ничего не изменилось? Правильно, на ( displaystyle 1) . Значит ( displaystyle {{3}^{0}}=1) .
Можем проделать то же самое уже с произвольным числом ( displaystyle a):
( displaystyle {{a}^{n}}cdot {{a}^{0}}underset{по правилу умножения}{mathop{=}},{{a}^{n+0}}={{a}^{n}}={{a}^{n}}cdot 1text{ }Rightarrow text{ }{{a}^{0}}=1)
Повторим правило:
Любое число в нулевой степени равно единице.
Но из многих правил есть исключения. И здесь оно тоже есть – это число ( displaystyle 0) (в качестве основания).
С одной стороны, ( displaystyle 0) в любой степени должен равняться ( displaystyle 0) – сколько ноль сам на себя ни умножай, все-равно получишь ноль, это ясно. Но с другой стороны, ( displaystyle {{0}^{0}}) , как и любое число в нулевой степени, должен равняться ( displaystyle 1) . Так что из этого правда? Математики решили не связываться и отказались возводить ноль в нулевую степень.
То есть теперь нам нельзя не только делить на ноль, но и возводить его в нулевую степень.
Поехали дальше. Кроме натуральных чисел и числа ( displaystyle 0) к целым относятся отрицательные числа.
Чтобы понять, что такое отрицательная степень, поступим как в прошлый раз: домножим какое-нибудь нормальное число на такое же в отрицательной степени:
( displaystyle {{3}^{5}}cdot {{3}^{-5}}underset{text{по правилу умножения}}{mathop{=}},{{3}^{5+left( -5 right)}}={{3}^{5-5}}={{3}^{0}}=1)
Отсюда уже несложно выразить искомое ( displaystyle {{3}^{-5}}) :
( displaystyle {{3}^{5}}cdot {{3}^{-5}}=1text{ }Rightarrow text{ }{{3}^{-5}}=frac{1}{{{3}^{5}}})
Теперь распространим полученное правило на произвольную степень:
( displaystyle {{a}^{n}}cdot {{a}^{-n}}={{a}^{n+left( -n right)}}={{a}^{0}}=1text{ }Rightarrow text{ }{{a}^{-n}}=frac{1}{{{a}^{n}}})
Итак, сформулируем правило:
Число в отрицательной степени обратно такому же числу в положительной степени. Но при этом основание не может быть нулевым: ( displaystyle ane 0) (т.к. на ( displaystyle 0) делить нельзя).
( displaystyle {{a}^{-n}}=frac{1}{{{a}^{n}}}, ane 0)
( displaystyle {{a}^{-n}}=frac{1}{{{a}^{n}}}, ane 0)
( displaystyle {{a}^{-n}}=frac{1}{{{a}^{n}}}, ane 0)
Подведем итоги:
I. Выражение ( {{0}^{k}}) не определено в случае ( kle 0) . Если ( k>0) , то ( {{0}^{k}}=0) .
II. Любое число в нулевой степени равно единице: ( displaystyle {{a}^{0}}=1, ane 0) .
III. Число, не равное нулю, в отрицательной степени обратно такому же числу в положительной степени: ( displaystyle {{a}^{-n}}=frac{1}{{{a}^{n}}}, ane 0).
( displaystyle {{6}^{-1}}=frac{1}{6})
( displaystyle {{left( frac{3}{2} right)}^{-2}}=frac{4}{9})
Чтобы понять, что такое «дробная степень», рассмотрим дробь ( displaystyle frac{1}{n}) :
пусть ( displaystyle {{3}^{frac{1}{n}}}=x) .
Возведем обе части уравнения в степень ( displaystyle n) :
( displaystyle {{left( {{3}^{frac{1}{n}}} right)}^{n}}={{x}^{n}})
Теперь вспомним правило про «степень в степени»:
( displaystyle {{x}^{n}}={{left( {{3}^{frac{1}{n}}} right)}^{n}}={{3}^{frac{1}{n}cdot n}}={{3}^{1}}=3)
Какое число надо возвести в степень ( displaystyle n) , чтобы получить ( displaystyle 3) ?
Эта формулировка – определение корня ( displaystyle n) -ой степени.
Напомню: корнем ( displaystyle n) -ой степени числа ( displaystyle a) (( displaystyle sqrt[n]{a}) ) называется число, которое при возведении в степень ( displaystyle n) равно ( displaystyle a) .
То есть, корень ( displaystyle n) -ой степени – это операция, обратная возведению в ( displaystyle n) степень: ( displaystyle sqrt[n]{a}=btext{ }Leftrightarrow text{ }a={{b}^{n}}) .
Получается, что ( displaystyle x={{3}^{frac{1}{n}}}=sqrt[n]{3}) . Очевидно, этот частный случай можно расширить: ( displaystyle {{a}^{frac{1}{n}}}=sqrt[n]{a}) .
Теперь добавляем числитель: что такое ( displaystyle {{a}^{frac{m}{n}}}) ? Ответ легко получить с помощью правила «степень в степени»:
( displaystyle {{a}^{frac{m}{n}}}={{a}^{frac{1}{n}cdot m}}={{left( {{a}^{frac{1}{n}}} right)}^{m}}={{left( sqrt[n]{a} right)}^{m}}) или ( displaystyle sqrt[n]{{{a}^{m}}}) .
Но может ли основание ( displaystyle a) быть любым числом? Ведь корень можно извлекать не из всех чисел.
Например, можно ли посчитать число ( displaystyle sqrt[4]{-16}) ? То есть, какое число нужно возвести в ( displaystyle 4) степень, чтобы получить ( displaystyle -16) ?
Никакое!
Вспоминаем правило: любое число, возведенное в четную степень – число положительное. То есть, извлекать корни четной степени из отрицательных чисел нельзя!
А это значит, что нельзя такие числа возводить в дробную степень с четным знаменателем, то есть выражение ( displaystyle {{left( -1 right)}^{frac{1}{2}}}) не имеет смысла.
А что насчет выражения ( displaystyle {{left( -1 right)}^{frac{1}{3}}}) ?
Его уже вроде бы можно посчитать: это ( displaystyle sqrt[3]{-1}=-1) .
Но тут возникает проблема.
Число ( displaystyle frac{1}{3}) можно представить в виде дргих, сократимых дробей, например, ( displaystyle frac{2}{6}) или ( displaystyle frac{4}{12}) .
И получается, что ( displaystyle {{left( -1 right)}^{frac{1}{3}}}) существует, но ( displaystyle {{left( -1 right)}^{frac{2}{6}}}) не существует, а ведь это просто две разные записи одного и того же числа.
Или другой пример: раз ( displaystyle sqrt[3]{-8}=-2) , то можно записать ( displaystyle {{left( -8 right)}^{frac{1}{3}}}=-2) . Но стоит нам по-другому записать показатель, и снова получим неприятность: ( displaystyle {{left( -8 right)}^{frac{1}{3}}}={{left( -8 right)}^{frac{2}{6}}}=sqrt[6]{{{left( -8 right)}^{2}}}=sqrt[6]{64}=2) (то есть, получили совсем другой результат!).
Чтобы избежать подобных парадоксов, рассматриваем только положительное основание степени с дробным показателем.
Итак, если:
- ( a>0);
- ( m) – натуральное число;
- ( n) – целое число;
Тогда:
( {{a}^{frac{n}{m}}}=sqrt[m]{a^n})
Примеры:
( {{a}^{frac{1}{2}}}=sqrt{a})
( {{a}^{frac{1}{5}}}=sqrt[5]{a})
( {{a}^{-frac{3}{4}}}=frac{1}{sqrt[4]{a^3}})
( displaystyle frac{{{5}^{-frac{1}{2}}}cdot {{left( {{5}^{frac{5}{6}}} right)}^{frac{3}{10}}}cdot {{3}^{-frac{5}{4}}}}{{{3}^{-frac{3}{2}}}}={{5}^{-frac{1}{2}}}cdot {{5}^{frac{5}{6}cdot frac{3}{10}}}cdot {{3}^{left( -frac{5}{4}+frac{3}{2} right)}}=)
( displaystyle={{5}^{left( -frac{1}{2}+frac{1}{4} right)}}cdot {{3}^{frac{1}{4}}}={{5}^{-frac{1}{4}}}cdot {{3}^{frac{1}{4}}}={{left( frac{3}{5} right)}^{frac{1}{4}}}=sqrt[4]{frac{3}{5}})
Степени с рациональным показателем очень полезны для преобразования выражений с корнями, например:
( displaystyle frac{sqrt[9]{6}cdot sqrt[18]{6}}{sqrt[6]{6}}=frac{{{6}^{frac{1}{9}}}cdot {{6}^{frac{1}{18}}}}{{{6}^{frac{1}{6}}}}={{6}^{frac{1}{9}+frac{1}{18}-frac{1}{6}}}={{6}^{frac{2+1-3}{18}}}={{6}^{0}}=1)
При изучении степеней с натуральным, целым и рациональным показателем, мы каждый раз составляли некий «образ», «аналогию», или описание в более привычных терминах.
Например, степень с натуральным показателем – это число, несколько раз умноженное само на себя; число в нулевой степени – это как-бы число, умноженное само на себя ( 0) раз, то есть его еще не начали умножать, значит, само число еще даже не появилось – поэтому результатом является только некая «заготовка числа», а именно число ( 1) ; степень с целым отрицательным показателем – это как будто произошел некий «обратный процесс», то есть число не умножали само на себя, а делили.
Вообразить степень с иррациональным показателем крайне сложно (так же, как сложно представить 4-мерное пространство). Это, скорее, чисто математический объект, который математики создали, чтобы расширить понятие степени на все пространство чисел.
Между прочим, в науке часто используется степень с комплексным показателем, то есть показатель – это даже не действительное число. Но в школе мы о таких сложностях не думаем, постичь эти новые понятия тебе представится возможность в институте.
Итак, что мы делаем, если видим иррациональный показатель степени? Всеми силами пытаемся от него избавиться!:)
Например: ( {{3}^{sqrt{2}}}cdot {{3}^{1-sqrt{2}}}={{3}^{sqrt{2}+1-sqrt{2}}}=3)
Или: ( frac{{{2}^{3sqrt{3}}}}{{{8}^{sqrt{3}-1}}}=frac{{{2}^{3sqrt{3}}}}{{{2}^{3left( sqrt{3}-1 right)}}}={{2}^{3sqrt{3}-3sqrt{3}+3}}=8)
И еще: ( {{left( {{5}^{sqrt[3]{4}}} right)}^{sqrt[3]{2}}}={{5}^{sqrt[3]{8}}}={{5}^{2}}=25).
Определение степени
Степенью называется выражение вида: ( {{a}^{b}}), где ( a) – основание степени и ( b) – показатель степени.
Степень с натуральным показателем {n = 1, 2, 3,…}
- ( {{a}^{1}}=a)
- ( {{a}^{2}}=acdot a)
- ( {{a}^{3}}=acdot acdot a)
Возвести число в натуральную степень n — значит умножить число само на себя ( n) раз:
- ( {{a}^{n}}=underbrace{acdot acdot acdot …a}_{n})
Степень с целым показателем {0, ±1, ±2,…}
Если показателем степени является целое положительное число:
( {{a}^{n}}={{a}^{n}}, n>0)
Возведение в нулевую степень:
( {{a}^{0}}=1, ane 0) . ( {{0}^{0}}) – выражение неопределенное, т.к., с одной стороны, ( 0) в любой степени – это ( 0) , а с другой – любое число в ( 0) -ой степени – это ( 1) .
Если показателем степени является целое отрицательное число:
( {{a}^{-n}}=frac{1}{{{a}^{n}}}, ane 0) (т.к. на ( 0) делить нельзя).
Еще раз о нулях: выражение ( {{0}^{k}}) не определено в случае ( kle 0). Если ( k>0) , то ( {{0}^{k}}=0) .
Примеры:
( {{6}^{-1}}=frac{1}{6})
( {{left( frac{3}{2} right)}^{-2}}=frac{4}{9})
Степень с рациональным показателем
Если,
- ( a>0);
- ( m) – натуральное число;
- ( n) – целое число;
Тогда:
- ( {{a}^{frac{n}{m}}}=sqrt[m]{{{a}^{n}}})
Примеры:
( {{a}^{frac{1}{2}}}=sqrt{a})
( {{a}^{frac{1}{5}}}=sqrt[5]{a})
( {{a}^{-frac{3}{4}}}=frac{1}{sqrt[4]{{{a}^{3}}}})
Свойства степеней
| Произведение степеней | ( {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}}) ( {{a}^{n}}cdot {{b}^{n}}={{left( acdot b right)}^{n}}) |
| Деление степеней | ( frac{{{a}^{n}}}{{{a}^{m}}}={{a}^{n-m}}) ( frac{{{a}^{n}}}{{{b}^{n}}}={{left( frac{a}{b} right)}^{n}}) |
| Возведение степени в степень | ( {{left( {{a}^{m}} right)}^{n}}={{a}^{mcdot n}}) |
Чтобы проще было решать задачи, попробуем понять: откуда эти свойства взялись? Докажем их.
Доказательства свойств степени
1. ( displaystyle {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}})
Посмотрим: что такое ( displaystyle {{a}^{n}}) и ( displaystyle {{a}^{m}}) ?
По определению:
( displaystyle left. begin{array}{l}{{a}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}\{{a}^{m}}=underbrace{acdot acdot …cdot a}_{mtext{ множителей}}text{ }end{array} right|Rightarrow text{ }{{a}^{n}}cdot {{a}^{m}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}cdot underbrace{acdot acdot …cdot a}_{mtext{ множителей}})
Сколько здесь множителей всего? Очень просто: к ( displaystyle n) множителям мы дописали ( displaystyle m) множителей, итого получилось ( displaystyle n+m) множителей.
Итак, в правой части этого выражения получается такое произведение:
( displaystyle {{a}^{n}}cdot {{a}^{m}}=underbrace{acdot acdot …cdot a}_{n+mtext{ множителей}})
Но по определению это степень числа ( displaystyle mathbf{a}) с показателем ( displaystyle mathbf{n}+mathbf{m}), то есть:
( displaystyle {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}}) , что и требовалось доказать.
Пример: Упростите выражение ( displaystyle {{5}^{4}}cdot {{5}^{7}}cdot {{5}^{9}}) .
Решение: ( displaystyle {{5}^{4}}cdot {{5}^{7}}cdot {{5}^{9}}={{5}^{4+7+9}}={{5}^{20}}) .
Пример: Упростите выражение ( displaystyle {{3}^{5}}cdot {{3}^{8}}cdot {{5}^{7}}) .
Решение: Важно заметить, что в нашем правиле обязательно должны быть одинаковые основания. Поэтому степени с основанием ( displaystyle 3) мы объединяем, а ( displaystyle {{5}^{7}}) остается отдельным множителем:
( displaystyle {{3}^{5}}cdot {{3}^{8}}cdot {{5}^{7}}={{3}^{5+8}}cdot {{5}^{7}}={{3}^{13}}cdot {{5}^{7}}) .
Еще одно важное замечание: это правило – только для произведения степеней!
Ни в коем случае нелья написать, что ( displaystyle {{2}^{4}}+{{2}^{6}}={{2}^{10}}) .
2. ( displaystyle {{a}^{n}}cdot {{b}^{n}}={{left( acdot b right)}^{n}})
Так же, как и с предыдущим свойством, обратимся к определению степени:
( displaystyle left. begin{array}{l}{{a}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}\{{b}^{n}}=underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}end{array} right|Rightarrow text{ }{{a}^{n}}cdot {{b}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}cdot underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}) .
Перегруппируем это произведение так:
( displaystyle {{a}^{n}}cdot {{b}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}cdot underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}=underbrace{left( acdot b right)cdot left( acdot b right)cdot …cdot left( acdot b right)}_{ntext{ множителей}}).
Получается, что выражение ( displaystyle acdot b) умножается само на себя ( displaystyle n) раз, то есть, согласно определению, это и есть ( displaystyle n) -я степень числа ( displaystyle acdot b) :
( displaystyle {{a}^{n}}cdot {{b}^{n}}={{left( acdot b right)}^{n}}), ч.т.д.
По сути это можно назвать «вынесением показателя за скобки». Но никогда нельзя этого делать в сумме: ( displaystyle {{2}^{4}}+{{3}^{4}}ne {{left( 2+3 right)}^{4}}) !
Вспомним формулы сокращенного умножения: сколько раз нам хотелось написать ( displaystyle {{left( a+b right)}^{2}}={{a}^{2}}+{{b}^{2}}) ? Но это неверно, ведь ( displaystyle {{left( a+b right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}) .
3. ( displaystyle frac{{{a}^{n}}}{{{a}^{m}}}={{a}^{n-m}})
И снова используем определение степени:
( displaystyle left. begin{array}{l}{{a}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}\{{a}^{m}}=underbrace{acdot acdot …cdot a}_{mtext{ множителей}}text{ }end{array} right|Rightarrow text{ }frac{{{a}^{n}}}{{{a}^{m}}}=frac{underbrace{acdot acdot …cdot a}_{ntext{ множителей}}}{underbrace{acdot acdot …cdot a}_{mtext{ множителей}}})
Здесь, очевидно, можем сократить. Но с одной оговоркой: чтобы степень получилась натуральная, нам придется предположить, что ( displaystyle n>m) (то есть, в числителе множителей должно быть больше, чем в знаменателе). Тогда ( displaystyle m) множителей числителя сокращаются со всеми ( displaystyle m) множителями знаменателя. Таким образом множители остаются только в числителе, причем в количестве ( displaystyle n-m) штук:
( displaystyle frac{{{a}^{n}}}{{{a}^{m}}}=frac{underbrace{acdot acdot …cdot a}_{ntext{ множителей}}}{underbrace{acdot acdot …cdot a}_{mtext{ множителей}}}=frac{underbrace{acdot acdot …cdot a}_{n-mtext{ множителей}}}{1}={{a}^{n-m}}) , ч.т.д.
4. ( displaystyle frac{{{a}^{n}}}{{{b}^{n}}}={{left( frac{a}{b} right)}^{n}})
Все как обычно – записываем определение степеней ( displaystyle {{a}^{n}}) и ( displaystyle {{b}^{n}}) , делим их друг на друга, разбиваем на пары ( displaystyle frac{a}{b}) и получаем:
( displaystyle left. begin{array}{l}{{a}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}\{{b}^{n}}=underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}end{array} right|Rightarrow text{ }frac{{{a}^{n}}}{{{b}^{n}}}=frac{underbrace{acdot acdot …cdot a}_{ntext{ множителей}}}{underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}}=underbrace{frac{a}{b}cdot frac{a}{b}cdot …cdot frac{a}{b}}_{ntext{ множителей}}={{left( frac{a}{b} right)}^{n}}) , ч.т.д.
Прежде чем разобрать последнее правило, решим несколько примеров.
Возведение числа в степень является важнейшей математической операцией, часто используемой для различных вычислений. В зависимости от вида основания и показателя значение степени рассчитывается по-разному. Ниже будут подробно рассмотрены основные правила нахождения значений степеней.
Возведение числа в степень с натуральным показателем
Прежде чем приступить к изучению операции возведения в степень необходимо рассмотреть базовое понятие натуральной степени числа.
Определение
Натуральной степенью n числа а называют произведение, состоящее из n множителей, каждый из которых равен a.
[a^{n}=underbrace{a times a times ldots times a}_{text {п множсителей }}]
Таким образом, для натурального показателя степень представляет собой укороченную запись умножения одинаковых множителей. В данном случае чтобы найти значение степени, следует перемножить число, которое является основанием, само на себя указанное количество раз.
Пример 1
Рассмотрим возведение числа 3 в степень 5. Согласно приведенному выше базовому определению:
35 = 3 × 3 × 3 × 3 × 3 = 243
Для операций возведения во вторую и третью степень имеются устоявшиеся названия: возведение в квадрат и куб, соответственно. Таким образом, выражение «32» может быть прочитано как «три во второй степени» или «три в квадрате», оба варианта будут верными.
Значение степенных выражений с дробным основанием и натуральным показателем находится по той же схеме. В то же время, в соответствии с правилом умножения дробей, операция возведения дроби в степень может быть разбита на два действия, когда числитель и знаменатель возводятся в соответствующую показателю степень по отдельности.
Пример 2
Найдем, чему будут равны [ frac{2}{5} ] в степени 3:
[left(frac{2}{5}right)^{3}=frac{2}{5} times frac{2}{5} times frac{2}{5}=frac{2^{3}}{5^{3}}=frac{8}{125}]
Операция возведения в натуральную степень имеет определенные особенности при работе с отрицательными числами. Рассмотрим следующий пример:
Пример 3
Найдем значения степенных выражений (-5)3 и (-5)4. Для этого, согласно базовому определению, необходимо умножить основание само на себя 3 и 4 раза соответственно:
(-5)3 = (-5) × (-5) × (-5) = -125
(-5)4 =(-5) × (-5) × (-5) × (-5) = 625
Из приведенного примера можно видеть, что в первом случае полученный результат является отрицательным числом, а во втором – положительным. Это связано с правилом перемножения отрицательных чисел. Следствием из него является то, что если показатель степени отрицательного числа представляет собой четное число, результат будет положительным, если нечетное – отрицательным. Таким образом, степень с отрицательным основанием и четным показателем будет равна степени с таким же показателем и основанием, равным по модулю, но противоположным по знаку.
(-a)2n = a2n
Если требуется возвести в натуральную степень иррациональное число, то его необходимо предварительно округлить до той значащей цифры, которая позволит получить ответ с требуемой точностью. Рассмотрим данный случай на примере числа π.
Пример 4
Выполним возведение в степень 3 числа π.
π – это бесконечное иррациональное число. С точностью до 10 знаков после запятой оно записывается следующим образом:
π = 3,1415926536
Допустим, нам необходим результат с точностью два знака после запятой. Тогда число π может быть округлено до 3,14.
(3,14)3 = 3,14 × 3,14 × 3,14 ≈ 30,96
Отдельно следует отметить, чему будет равно число в степени 1. В соответствии с базовым определением
[a^{n}=underbrace{a times a times ldots times a}_{text {п множсителей }}]
вне зависимости от значения основания, число в степени 1 равно самому себе.
На практике возможны и более сложные случаи, когда требуется найти значение степенного выражения, в котором показатель не является натуральным числом. Ниже будут рассмотрены ситуации, когда показатель степени представляет собой целое, дробное, рациональное или иррациональное число.
Вычисление степеней с целым показателем
Все операции по возведению в целую степень можно разделить на три группы: когда показатель является целым положительным (натуральным) числом, когда он равен нулю, и когда он является отрицательным числом.
Случай с натуральным показателем был рассмотрен ранее, поэтому мы не будем к нему возвращаться.
В случае, когда показатель равен нулю, для любого не равного нулю основания значение степени будет равно единице. Если же и основание, и показатель степени равны нулю значение выражения будет не определено.
Пример 5
Рассмотрим возведение в нулевую степень натурального, дробного, иррационального чисел, а также нуля:
100 = 1
0,50 = 1
π0 = 1
00 – не определено.
Осталось рассмотреть нахождение значения степенного выражения с целым отрицательным показателем. Число а в степени -n представляет собой дробь, числитель которой равен единице, а знаменатель – числу а в степени n.
[a^{-n}=frac{1}{a^{n}}]
Можно видеть, что знаменатель дроби является натуральной степенью, вычисление которой было рассмотрено ранее. Таким образом, две степени, у которых основания одинаковы, а показатели противоположны по знаку, но равны по модулю, будут являться обратными числами. Рассмотрим возведение в отрицательную степень целого и дробного чисел:
Пример 6
Вычислим, чему равно 7 в степень -3:
[7^{-3}=frac{1}{7^{3}}=frac{1}{7 times 7 times 7}=frac{1}{343}]
Пример 7
Найдем значение степенного выражения [left(frac{2}{9}right)^{-2}]
При возведении дробного числа в отрицательную степень на определенном этапе осуществляется «переворот» дроби. Он может быть выполнен как в конце вычислений:
[left(frac{2}{9}right)^{-2}=frac{1}{left(frac{2}{9}right)^{2}}=frac{1}{frac{2}{9} times frac{2}{9}}=frac{1}{frac{4}{81}}=frac{81}{4}=20 frac{1}{4}]
так и в начале:
[left(frac{2}{9}right)^{-2}=left(frac{9}{2}right)^{2}=frac{81}{4}=20 frac{1}{4}]
Из-за указанного в примере «переворота», при возведении десятичной дроби в отрицательную степень рекомендуется предварительно преобразовать основание к форме обыкновенной дроби. Рассмотрим данную ситуацию на примере:
Пример 8
Найдем значение степенного выражения 0,5-2:
[0,5^{-2}=left(frac{5}{10}right)^{-2}=left(frac{10}{5}right)^{2}=frac{10^{2}}{5^{2}}=frac{100}{25}=4]
Отдельно следует упомянуть о выражениях с целым отрицательным показателем, основание которых равно нулю. Подобное выражение будет не определено, поскольку его преобразование будет приводить к дроби, знаменатель которой равен нулю.
[0^{-n}=frac{1}{0^{n}}] ‒ выражение не определено.
Возведение числа в дробную степень
Прежде чем приступить к вычислению, следует рассмотреть базовое определение степени с дробным показателем. В виде формулы оно может быть записано следующим образом:
[a^{m / n}=sqrt[n]{a^{m}}, text { где }]
a – положительное число;
m – целое число;
n – натуральное число.
Из указанного определения следует, что операция нахождения алгебраического корня любой степени также может быть представлена в форме возведения в дробную степень, когда числитель показателя равен единице, а знаменатель – основанию корня.
[sqrt[n]{a}=a^{1 / n}]
При этом не следует воспринимать данное свойство как способ преобразования иррационального числа в рациональное. Изменяется только форма записи. Например, если число √2 является иррациональным, то при записи его в форме [2^{1 / 2}] оно также останется иррациональным.
При нахождении значения степени с дробным показателем следует последовательно выполнить два математических действия: возведение основания в степень с целым показателем m и извлечение корня n-ной степени. При этом согласно свойству корней, указанные действия можно выполнить и в обратной последовательности, то есть можно сначала извлечь из основания корень n-й степени, а затем возвести полученный результат в степень m.
[sqrt[n]{a^{m}}=(sqrt[n]{a})^{m}]
Рассмотрим оба способа вычисления степеней с дробным показателем на конкретном примере.
Пример 9
Найдем значение степенного выражения [128^{5 / 7}].
Способ 1. Возведение в степень подкоренного выражения с последующим извлечением корня
[128^{5 / 7}=sqrt[7]{128^{5}}=sqrt[7]{34359738368}=32]
В данном случае из-за большого значения числа под корнем найти значение выражения, не прибегая к помощи калькулятора, невозможно.
Способ 2. Извлечение корня из основания с последующим возведением в степень.
[128^{5 / 7}=(sqrt[7]{128})^{5}=2^{5}=32]
Указанный способ нахождения значения степени существенно легче. При этом результат вычислений не отличается, то есть можно выбирать тот способ, который будет удобнее в конкретном случае.
Если показатель степени представлен в форме десятичной дроби, то удобнее будет записать его в виде обычной.
Пример 10
Вычислим значение степени [243^{0,4}]:
[243^{0,4}=243^{4 / 10}=243^{2 / 5}=(sqrt[5]{243})^{2}=3^{2}=9]
В случае, когда показатель представляет собой смешанное число, для удобства вычислений он может быть записан в виде неправильной дроби.
Пример 11
Вычислим значение выражения:
[left(12 frac{1}{4}right)^{1 frac{1}{2}}=left(frac{49}{4}right)^{3 / 2}=left(sqrt{frac{49}{4}}right)^{3}=left(frac{7}{2}right)^{3}=frac{343}{8}=42 frac{7}{8}]
Следует обратить внимание на математическую операцию возведения в отрицательную дробную степень. В этом случае вычисления производятся в три этапа: нахождение числа, обратного исходному, извлечение корня, степень которого соответствует значению знаменателя показателя, и возведение в степень, соответствующую числителю дробного показателя. Как и в случае с положительным дробным показателем, указанные действия могут выполняться в любой последовательности.
Пример 12
Найдем значение выражения [49^{-1 / 2}].
Выполним преобразование числа в обратное ему:
[49^{-1 / 2}=frac{1}{49^{1 / 2}}]
Найдем значение степени в знаменателе полученной дроби:
[frac{1}{49^{1 / 2}}=frac{1}{sqrt{49}}=frac{1}{7}]
Также необходимо рассмотреть случай, когда основанием степени является ноль, а показателем – дробное число. Как и в случае с целыми показателями, подобные выражения имеют смысл лишь в том случае, когда показатель больше нуля. В противном случае выражение будет не определено.
Нет времени решать самому?
Наши эксперты помогут!
Нахождение степеней с иррациональным показателем
Иногда возникает необходимость нахождения значения степени, показатель которой представляет собой иррациональное число. Проблема заключается в том, что найти точное значение подобного выражения невозможно. Однако для решения любой практической задачи, как правило, достаточно нахождения значения степенного выражения с определенной степенью точности. В этом случае иррациональный показатель округляется до требуемого десятичного знака, после чего вычисление осуществляется согласно правилам, принятым для дробного показателя.
Рассмотрим решение подобной задачи на конкретном примере:
Пример 13
Предположим, что нам необходимо найти значение выражения 2 в степени √2. Показатель степени является иррациональным числом. В виде бесконечной десятичной дроби оно может быть записано следующим образом:
√2 = 1,41421356…
Найдем значение выражения с различной степенью приближения.
Вариант 1.
Округлим значение иррационального числа до двух цифр после запятой и найдем приближенное значение степени:
[√2≈1,41]
[2^{sqrt{2}} approx 2^{1,41} approx 2,65737]
Вариант 2.
Округлим значение иррационального числа до четырех цифр после запятой и найдем приближенное значение степени:
[√2≈1,4142]
[2^{sqrt{2}} approx 2^{1,4142} approx 2,66512]
Можно видеть, что полученные значения различаются во втором знаке после запятой, при этом второе значение является более точным.
В большинстве случаев вычисление степеней с иррациональными показателями является сложной задачей, для решения которой используется вычислительная техника.
Обращаем ваше внимание, что в данном разделе разбирается
понятие степени только с натуральным показателем и нулём.
Понятие и свойства степеней с рациональными показателями
(с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.
Итак, разберёмся, что такое степень числа.
Для записи произведения числа самого на себя несколько раз
применяют сокращённое обозначение.
Вместо
произведения шести одинаковых множителей
4 · 4 · 4 · 4 · 4 · 4 пишут
46 и произносят «четыре в шестой степени».
4 · 4 · 4 · 4 · 4 · 4 = 46
Выражение 46 называют степенью числа, где:
- 4 — основание степени;
- 6 — показатель степени.
В общем виде степень с основанием «a» и
показателем «n» записывается с помощью выражения:
Запомните!
Степенью числа «a» с натуральным показателем «n»,
бóльшим 1, называется произведение «n»
одинаковых множителей, каждый из которых равен числу
«a».
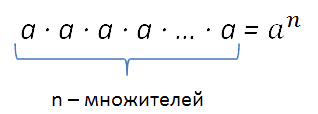
Запись «an» читается так:
«а в степени
n» или «n-ая степень числа
a».
Исключение составляют записи:
- a2 — её можно произносить как «а в квадрате»;
- a3 — её можно произносить как «а в кубе».
Конечно, выражения выше можно читать и по определению степени:
- a2 — «а во второй степени»;
- a3 — «а в третьей степени».
Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0).
Запомните!
Степенью числа «а» с показателем n = 1 является само это число:
a1 = a
Любое число в нулевой степени равно единице.
a0 = 1
Ноль в любой натуральной степени равен нулю.
0n = 0
Единица в любой степени равна 1.
1n = 1
Выражение 00 (ноль в нулевой степени) считают лишённым смысла.
- (−32)0 = 1
- 0253 = 0
- 14 = 1
При решении примеров нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в
степень.
Пример. Возвести в степень.
- 53 = 5 · 5 · 5 = 125
- 2,52 = 2,5 · 2,5 = 6,25
- ()4
=
··
·
=
3 · 3 · 3 · 3 4 · 4 · 4 · 4 =
Возведение в степень отрицательного числа
Основание степени (число, которое возводят в степень) может быть любым
числом — положительным, отрицательным или нулём.
Запомните!
При возведении в степень положительного числа
получается положительное число.
При возведении нуля в натуральную степень получается ноль.
При возведении в степень отрицательного числа в результате может получиться
как положительное число, так и отрицательное число. Это зависит от того чётным или
нечётным числом был показатель степени.
Рассмотрим примеры возведения в степень отрицательных чисел.
Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень,
то получается отрицательное число. Так как произведение
нечётного количество отрицательных сомножителей отрицательно.
Если же отрицательное число возводится в чётную степень, то получается положительное число.
Так как произведение чётного количество отрицательных сомножителей положительно.
Запомните!
Отрицательное число, возведённое в
чётную степень, есть число
положительное.
Отрицательное число, возведённое в
нечётную степень, — число
отрицательное.
Квадрат любого числа есть положительное число или нуль, то есть:
a2 ≥ 0 при любом a.
- 2 · (−3)2 = 2 · (−3) · (−3) = 2 · 9 = 18
- −5 · (−2)3 = −5 · (−8) = 40
Обратите внимание!
При решении примеров на возведение в степень часто делают ошибки, забывая, что записи
(−5)4 и
−54 это разные выражения. Результаты возведения
в степень данных выражений будут разные.
Вычислить (−5)4 означает найти значение четвёртой степени отрицательного числа.
(−5)4 = (−5) · (−5) · (−5) · (−5) = 625
В то время как найти «−54» означает, что пример нужно решать в 2 действия:
- Возвести в четвёртую степень положительное число 5.
54 = 5 · 5 · 5 · 5 = 625 - Поставить перед полученным результатом знак «минус» (то есть выполнить
действие вычитание).
−54 = −625
Пример. Вычислить: −62 − (−1)4
−62 − (−1)4 = −37
- 62 = 6 · 6 = 36
- −62 = −36
- (−1)4 = (−1) · (−1) · (−1) · (−1) = 1
- −(−1)4 = −1
- −36 − 1 = −37
Порядок действий в примерах со степенями
Вычисление значения называется действием возведения в степень. Это действие третьей ступени.
Запомните!
В выражениях со степенями, не содержащими скобки, сначала выполняют
вовзведение в степень, затем умножение и деление, а в
конце сложение и вычитание.
Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках,
а потом оставшиеся действия в том же порядке слева направо.
Пример. Вычислить:
Для облегчения решения примеров полезно знать и пользоваться
таблицей степеней, которую вы можете бесплатно скачать на нашем сайте.
Для проверки своих результатов вы можете воспользоваться на нашем сайте калькулятором
«Возведение в степень онлайн».
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
14 апреля 2020 в 14:01
Bmw Touring
Профиль
Благодарили: 0
Сообщений: 1
Bmw Touring
Профиль
Благодарили: 0
Сообщений: 1
Скажите пожалуйста почему или как получился такой ответ?
Как именно получилось 104 ?
0,4 · 105 = 4 · 104
спасибо за внимание!
0
Спасибо
Ответить
3 мая 2020 в 20:38
Ответ для Bmw Touring
Денис Волков
Профиль
Благодарили: 0
Сообщений: 3
Денис Волков
Профиль
Благодарили: 0
Сообщений: 3
0.4 · 105 = 0.4 · 10 · 104=(0.4 · 10 ) · 104=4 · 104
0
Спасибо
Ответить
5 марта 2017 в 17:00
Виктория Горловская
Профиль
Благодарили: 0
Сообщений: 2
Виктория Горловская
Профиль
Благодарили: 0
Сообщений: 2
помогите пожалуйста
нужно правило что такое степень с натуральным показателем
0
Спасибо
Ответить
5 марта 2017 в 18:22
Ответ для Виктория Горловская
Виктория Горловская
Профиль
Благодарили: 0
Сообщений: 2
Виктория Горловская
Профиль
Благодарили: 0
Сообщений: 2
0
Спасибо
Ответить
7 марта 2017 в 20:29
Ответ для Виктория Горловская
Валерий Шакиров
Профиль
Благодарили: 0
Сообщений: 1
Валерий Шакиров
Профиль
Благодарили: 0
Сообщений: 1
Степенью числа a с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен a. Степенью числа a споказателем 1 называется само число a (a1 = a).. Степенью ненулевого числа a с показателем 0 равна единице (a0 = 1).
0
Спасибо
Ответить
7 декабря 2016 в 8:58
Мирослава Заруцкая
Профиль
Благодарили: 0
Сообщений: 3
Мирослава Заруцкая
Профиль
Благодарили: 0
Сообщений: 3
мне не понятны степени как их упрощать 23· 24 можно с объяснением
0
Спасибо
Ответить
7 декабря 2016 в 9:01
Ответ для Мирослава Заруцкая
Мирослава Заруцкая
Профиль
Благодарили: 0
Сообщений: 3
Мирослава Заруцкая
Профиль
Благодарили: 0
Сообщений: 3
СРОЧНО ОТВЕТЬТЕ ПОЖАЛУЙТА
0
Спасибо
Ответить
7 декабря 2016 в 9:03
Ответ для Мирослава Заруцкая
Мирослава Заруцкая
Профиль
Благодарили: 0
Сообщений: 3
Мирослава Заруцкая
Профиль
Благодарили: 0
Сообщений: 3
ПОЖАЛУЙСТАААА
0
Спасибо
Ответить
7 декабря 2016 в 12:12
Ответ для Мирослава Заруцкая
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
А учебник открыть лень?
0
Спасибо
Ответить
20 ноября 2016 в 22:14
Злата Крамаренко
Профиль
Благодарили: 0
Сообщений: 3
Злата Крамаренко
Профиль
Благодарили: 0
Сообщений: 3
2x2 + 2y2 — 2xy + 1 — 2y = 1/3
0
Спасибо
Ответить
21 ноября 2016 в 4:21
Ответ для Злата Крамаренко
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
x = 1/3; y = 2/3.
0
Спасибо
Ответить
21 ноября 2016 в 22:31
Ответ для Злата Крамаренко
Злата Крамаренко
Профиль
Благодарили: 0
Сообщений: 3
Злата Крамаренко
Профиль
Благодарили: 0
Сообщений: 3
Спасибо. А как разложить данное уравнение? Можно узнать, пожалуйста?
0
Спасибо
Ответить
22 ноября 2016 в 1:12
Ответ для Злата Крамаренко
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Сверни квадраты
+ = 0.
0
Спасибо
Ответить
1 марта 2016 в 10:42
Екатерина Гулиева
Профиль
Благодарили: 0
Сообщений: 1
Екатерина Гулиева
Профиль
Благодарили: 0
Сообщений: 1
какое число больше 7
в 3 раза, какое число меньше 7
в 3 раза
0
Спасибо
Ответить
1 марта 2016 в 14:12
Ответ для Екатерина Гулиева
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Если число больше в 3 раза, это значит, что текущее число, надо умножить на 3, а если меньше в 3 раза-разделить.
1) 7 ·3= ·3==21
Ответ : 21 в 3 раза больше, чем 7
2)7 : 3 = : 3 = = =2 =2
Ответ: 2 в 3 раза меньше, чем 7
0
Спасибо
Ответить
27 декабря 2015 в 19:36
Надежда Егина
Профиль
Благодарили: 0
Сообщений: 2
Надежда Егина
Профиль
Благодарили: 0
Сообщений: 2
56 · 125 : 254
0
Спасибо
Ответить
10 января 2016 в 1:43
Ответ для Надежда Егина
Татьяна Почтарёва
Профиль
Благодарили: 0
Сообщений: 2
Татьяна Почтарёва
Профиль
Благодарили: 0
Сообщений: 2
56·53:58=51=5
0
Спасибо
Ответить
25 октября 2015 в 10:21
Валерия Соколова
Профиль
Благодарили: 0
Сообщений: 1
Валерия Соколова
Профиль
Благодарили: 0
Сообщений: 1
((?2)?2)?2
0
Спасибо
Ответить
12 июня 2016 в 2:47
Ответ для Валерия Соколова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
2.
0
Спасибо
Ответить
16 октября 2015 в 18:02
Влада Данилова
Профиль
Благодарили: 0
Сообщений: 1
Влада Данилова
Профиль
Благодарили: 0
Сообщений: 1
Представьте в виде степени с основание 4 число 16
0
Спасибо
Ответить
17 октября 2015 в 0:14
Ответ для Влада Данилова
Людмила Кундина
Профиль
Благодарили: 0
Сообщений: 1
Людмила Кундина
Профиль
Благодарили: 0
Сообщений: 1
42
0
Спасибо
Ответить
7 октября 2015 в 18:02
Елена Облупина
Профиль
Благодарили: 0
Сообщений: 1
Елена Облупина
Профиль
Благодарили: 0
Сообщений: 1
Число 9 возвели в степень 5, полученный результат возвели в степень2. В какую степень за два раза возвели число 9????
0
Спасибо
Ответить
12 сентября 2016 в 16:02
Ответ для Елена Облупина
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
(95)2=910При возведении степени в степень, степени перемножаются. Свойство №3
0
Спасибо
Ответить
16 сентября 2015 в 15:45
Евгений Куринной
Профиль
Благодарили: 0
Сообщений: 4
Евгений Куринной
Профиль
Благодарили: 0
Сообщений: 4
Помогите пожалуйста решить: корень 4 степени из дроби: в числителе 81, в знаменателе 16
0
Спасибо
Ответить
16 сентября 2015 в 15:54
Ответ для Евгений Куринной
Евгений Куринной
Профиль
Благодарили: 0
Сообщений: 4
Евгений Куринной
Профиль
Благодарили: 0
Сообщений: 4
Это я уже решил, помогите решить этот: корень 8 степени из 16 в -4 степени
0
Спасибо
Ответить
16 сентября 2015 в 16:00
Ответ для Евгений Куринной
Евгений Куринной
Профиль
Благодарили: 0
Сообщений: 4
Евгений Куринной
Профиль
Благодарили: 0
Сообщений: 4
Уже решил
0
Спасибо
Ответить
5 сентября 2016 в 14:24
Ответ для Евгений Куринной
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Отличная ветка математического форума ) Так держать! =) Если будет необходимо, подробнее о действиях со степенями можно прочесть здесь: http://math-prosto.ru/index.php?page=pages/stepeni/stepeni2.php
0
Спасибо
Ответить