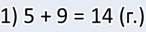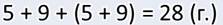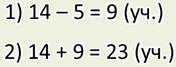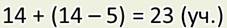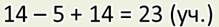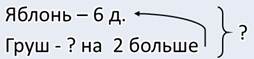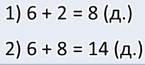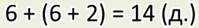Чтобы составить задачу, которая приведёт к этим выражениям, например, с двумя неизвестными, нужно сначала поиграться с числами.
Берём две машины. Одна движется со скоростью 60 км/час, а вторая на 20 быстрее 80 км/час. У этих скоростей оптимальный общий множитель 48. Увеличиваем его в 10 раз получится 480 км.
Первой машине потребуется 8 часов, для преодоления этого расстояния, а второй 6 на 2 часа меньше. 480 км — это известное расстояние. Неизвестные величины — это скорость и время.
Напускаем туману. Определяемся, что скорость 1-й машины на 20 км/час меньше второй машины. Но вторая выехала на 2 часа позже и догнала первую на расстоянии 480 км. Задача готова. Нужно хитро задать вопрос. Например: Через какое время 2-я машина будет на расстоянии в 100 км от первой после из встречи.
Чтобы решить такую задачу потребуется составлять выражение. Принимать за «х» скорость первой или второй машины до встречи. За «у» время первой или второй машины также до встречи. Или обходиться одним «х», а можно и просто обойтись числами. Но это не для составителя. Составитель оперирует известными ему числами, а «решала» составляет выражения.
Конечно это интересно. Составить хитрую математическую задачку, и чтобы её не быстро решили. А выдёргивать с интернета любой может. Я составляю сама. Бывает до взрыва мозга, а не такую легкотню, как написала выше. Например вот эта: про курагу, чернослив и инжир.
Содержание
- Числовые и буквенные выражения
- Числовые выражения: что это
- Буквенные выражения
- Выражения с переменными
- Запись решения задачи выражением
- Урок 15. Математика 2 класс ФГОС
- В данный момент вы не можете посмотреть или раздать видеоурок ученикам
- Получите невероятные возможности
- Конспект урока «Запись решения задачи выражением»
Числовые и буквенные выражения
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
- 23 + 5 = 28
- 5 — 2 = 3
- 52 * 3 = 156
- 28 : 7 = 4
Это простые числовые выражения.
Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:
- (5 * 3) — (5 * 2) = 5
- 6 : (7 — 4) = 2
- (45 + 45) : 9 = 10
- 11 * (5 * 5) = 275
Это сложные числовые выражения.
Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
- Сначала выполняется действие, записанное в скобках.
- Затем выполняется деление/умножение.
- В последнюю очередь выполняется сложение/вычитание.
Пример 1. Найдите значение числового выражения: 3 * (2 + 
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
(6 + 7) * (13 + 2) = 195
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
- Сначала находим значение первого выражения:
6 + 8 = 14
Затем находим значение второго выражения:
2 * 2 = 4
Сравниваем получившиеся результаты:
14 больше 4
14 > 4
6 + 8 > 2 * 2
Пример 2. Сравните следующие числовые выражения:
5 * (12 — 2) — 7 и (115 + 9) — (7 — 3)
- Находим значение первого выражения, соблюдая порядок выполнения арифметических действий:
12 — 2 = 10
5 * 10 = 50
50 — 7 = 43
5 * (12 — 2) — 7 = 43
Затем находим значение:
115 + 9 = 124
7 — 3 = 4
124 — 4 = 120
Сравниваем полученные результаты:
43 меньше 120
43
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
- Сначала следует прочитать его полностью.
- Затем оно записывается.
- Третьим шагом идет подстановка значения неизвестного в выражение.
- А затем производится вычисление, согласно очередности выполнения арифметических действий.
Пример 1. Найдите значение выражения: 5 + x.
- Читаем: найдите сумму числа 5 и x.
- Подставляем вместо неизвестного x число 4.
- Вычисляем: 5 + 4 = 9.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x).
- Читаем: найдите произведение суммы числа 4 и а и суммы числа 2 и x.
- Подставляем вместо неизвестного a число 2.
- Вычисляем 4 + 2 = 6.
- Подставляем вместо неизвестного x число 5.
- Вычисляем 2 + 5 = 10.
- Находим произведение 6 * 10 = 60.
- Записываем результат: (4 + 2) * (2 + 5) = 60.
Выражения с переменными
Переменная — это значение буквы в буквенном выражении.
- Например, в выражении x + a — 8
x — переменная
a — переменная
Если вместо переменных подставить числа, то буквенное выражение x + a — 8 станет числовым выражением. Вот так:
- подставляем вместо переменной x число 5, а вместо переменной a — число 10, получаем 5 + 10 — 8.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
После подстановки значения переменных находим значение x + a — 8 = 5 + 10 — 8 = 7.
Часто можно встретить буквенные выражения, записанные следующим образом:
5x — 4a
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
- Сумма 6 и a.
- Разность 8 и x.
- Сумма x — 2 и 6
- Разность 15 и x — y
- Сумма 45 + 5 и 12 — 6
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: (b — 345) + (180 + x).
Задание три.
Составьте буквенное выражение:
Разность разности 30 и y и разности a и b.
Ответ: (30 — y) — (a — b).
Задание четыре.
Составьте выражение для решения задачи и найдите его значение.
Ролл «Калифорния» стоит 480 рублей — это на 40 рублей меньше, чем ролл «Филадельфия». Сколько будут стоить оба ролла?
Как решаем:
Калифорния — 480 рублей.
Филадельфия — 480 + 40.
Калифорния + Филадельфия = ?
480 + (480 + 40).
Мы помним, что выполнение арифметических действий в числовом выражении имеет строгую последовательность. Сначала — действие в скобках:
480 + 520 = 1 000.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
Маша — 150 видео.
Лена — 150 + 13 видео.
Маша + Лена = ? видео.
150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.
Задание шесть.
Вычислите:
(500 + 300) : a — 15,
при условии, что a = 10.
Подставляем число 10 (значение переменной) вместо переменной
(500 + 300) : 10 — 15
Затем выполняем сначала арифметическое действие в скобках: 500 + 300 = 800.
Затем выполняем деление 800 : 10 = 80.
Выполняем вычитание 80 — 15 = 65.
Ответ: (500 + 300) : 10 — 15 = 65.
Задание семь.
Вычислите:
(270 — 120) * (x — 10),
при условии, что x = 45.
Как решаем: подставляем число 45 (значение переменной) вместо переменной x
(270 — 120) * (45 — 10).
Затем выполняем сначала арифметическое действие в скобках: 270 — 120 = 150.
Выполняем арифметическое действие во вторых скобках: 45 — 10 = 35.
Затем выполняем умножение 150 * 35 = 5 250
Ответ: (270 — 120) * (45 — 10) = 5 250.
Задание восемь.
Вычислите:
(50 * x) — (3 * y)
при условии, что x = 2; y = 10
Подставляем число 2 вместо переменной x
(50 * 2) — (3 * y).
Подставляем число 10 вместо переменной y
(50 * 2) — (3 * 10).
Затем выполняем сначала арифметическое действие в скобках: 50 * 2 = 100.
Выполняем арифметическое действие во вторых скобках: 3 * 10 = 30.
Затем выполняем вычитание 100 — 30 = 70
Источник
Запись решения задачи выражением
Урок 15. Математика 2 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Запись решения задачи выражением»
— Плюс. Плююююс! Ты где?
Привет, Плюс! Чего так долго? Включай скорее компьютер. Сейчас у нас будет в скайпе разговор с царицей Математикой.
— Здравствуй, Минус. Как это я забыл! Включаю.
— Здравствуйте, Дорогие Плюс и Минус!
Сегодня я хочу проверить, как вы умеете решать задачи. Я дам несколько задач и предлагаю вам устроить соревнование — кто сможет их решить быстрее, но при этом, конечно, правильно.
— Да, царица, мы Вас внимательно слушаем.
— Мы очень внимательно слушаем.
— Ну что же, приступим. Итак, вот первая задача:
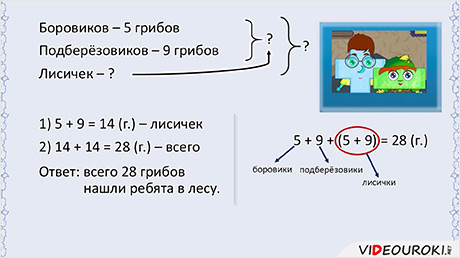
Ребята в лесу собирали грибы. Они нашли 5 боровиков, 9 подберёзовиков, а лисичек столько, сколько боровиков и подберёзовиков вместе. Сколько всего грибов нашли ребята в лесу?
Ну, Плюс и Минус, я жду вашего решения. Может быть и ребята, которые на вас смотрят, попробуют решить эту задачу.
— Всё, я готов! Могу даже объяснить, как я решал эту задачу.
Нам даны два числа: количество боровиков — их 5, и количество подберёзовиков — их 9. Но неизвестно количество лисичек. Про них сказано, что их столько, сколько боровиков и подберёзовиков вместе. А ещё неизвестно, сколько всего грибов.
В задаче два неизвестных, значит, задача составная, то есть в ней не одно действие, а два. В первом действии я узнаю, сколько лисичек.
А так как боровиков и подберёзовиков вместе столько же, сколько и лисичек, то общее количество грибов я нашёл вот так:
Ответ: всего 28 грибов нашли ребята в лесу.
— А я решал задачу другим способом. Вот посмотрите:
— Да, Минус, чувствуется, что сложение — это не твой конёк. Конечно, задачу ты решил правильно. Но при этом у тебя получилось не два, а три действия. При этом первое и второе действия повторяются. Для этой задачи такой способ записи не очень удобен. Хотя некоторые задачи действительно удобно записывать не по действиям, как это сделал я, а числовым выражением. А вот, кстати, царица Математика уже даёт нам новую задачу.
— Тихо, Плюс, слушаем!
— На уроке физкультуры присутствовало 14 мальчиков. А девочек — на 5 меньше. Сколько всего учащихся присутствовало на уроке физкультуры?
— Ну что же, начинаем решать. Ребята, и вы попробуйте с нами решать!
— Я уже решил. Вот посмотрите, в задаче известно количество мальчиков, Их 14. Но неизвестно количество девочек. Ведь сказано, что их на 5 меньше, чем мальчиков.
А в задаче надо узнать количество девочек, и только потом — сколько всего детей. Я так и узнавал:
Ответ: всего 23 учащихся присутствовало на уроке физкультуры.
— А вот я записал решение этой задачи по-другому:
И ещё можно вот так:
— Но ведь ты мне только что говорил, что такой способ решения неудобен! Зачем же ты решил задачу другим способом — записью выражения.
— В первой задаче он действительно был неудобен, а в этой — очень даже удобен. Во-первых, это не другой способ решения задачи. Посмотри, в моём решении есть те же действия, что и в твоём, и даже в той же последовательности.
Ты первым действием узнаёшь, сколько девочек, и я тоже. Ведь это действие я записал в скобках. А то, что записано в скобках, всегда выполняется первым.
Во втором действии к 14 прибавляем полученное в первом действии число 9. А в этой записи слагаемые меняются местами — к 9 прибавляется 14.
И получается, что это не другой способ решения задачи — ведь все действия одинаковы, а другой способ записи решения. Ты решал по действиям, а я — выражением. Способ решения одинаковый, а способ записи этого решения — разный. Но посмотри, моя запись получилась короче. В ней нет номеров действий и пояснений. Поэтому такая запись помогает экономить и время, и бумагу.
— Ты, Плюс, как всегда. Все тебе надо складывать да экономить. Хотя, наверное, ты прав. Эта запись действительно удобная. А хотелось бы и мне попробовать такую запись задачи выражением.
Ваше величество, госпожа королева. Не могли бы Вы задать нам ещё одну задачу?
— Ну что же, слушайте:
В моём саду растёт 6 яблонь. А груш на 2больше. Сколько всего яблонь и груш растёт в моём саду?
Я хочу видеть у вас оба способа записи решения — и по действиям, и выражением.
— Ну вот что у меня получилось. Прежде, чем узнать, сколько всего яблонь и груш, необходимо узнать, сколько груш. Ведь нам это неизвестно. Сказано, что их на 2 больше, чем яблонь.
Значит, в саду царицы растёт 14 яблонь и груш.
А вот как получилась запись выражением:
Сначала я нашёл, количество груш. Но, так как это действие стоит не в начале записи, я выделил его скобками. А потом нашёл сумму чисел. Ответ такой же, как и при записи по действиям — 14.
— Хорошо. Задача решена, верно. А теперь расскажите, чему вы научились.
— Можно я начну первый.
Записывать решение задачи можно по действиям и выражением.
— При записи по действиям мы пишем номер действия и пояснения к каждому действию, а при записи выражением только пояснение к значению записанного выражения.
— При записи выражения первое действие часто записываем в скобках, и конечно, не забываем записать ответ задачи.
— Ну что же, молодцы, Плюс и Минус. Вы справились с заданием. И сейчас вы можете пойти погулять в мой сад и полакомиться яблоками и грушами.
Источник
—
Плюс!….. Плююююс! Ты где?
Привет,
Плюс! Чего так долго? Включай скорее компьютер. Сейчас у нас будет в скайпе разговор
с царицей Математикой.
—
Здравствуй, Минус. Как это я забыл! Включаю.
—
Здравствуйте, Дорогие Плюс и Минус!
Сегодня
я хочу проверить, как вы умеете решать задачи. Я дам несколько задач и предлагаю
вам устроить соревнование — кто сможет их решить быстрее, но при этом, конечно,
правильно.
—
Да, царица, мы Вас внимательно слушаем.
—
Мы очень внимательно слушаем.
—
Ну что же, приступим. Итак, вот первая задача:
Ребята
в лесу собирали грибы. Они нашли 5 боровиков, 9 подберёзовиков, а лисичек
столько, сколько боровиков и подберёзовиков вместе. Сколько всего грибов нашли
ребята в лесу?
Ну,
Плюс и Минус, я жду вашего решения. Может быть и ребята, которые на вас
смотрят, попробуют решить эту задачу.
—
Всё, я готов! Могу даже объяснить, как я решал эту задачу.
Нам
даны два числа: количество боровиков — их 5, и количество подберёзовиков — их 9.
Но неизвестно количество лисичек. Про них сказано, что их столько, сколько
боровиков и подберёзовиков вместе. А ещё неизвестно, сколько всего грибов.
В
задаче два неизвестных, значит, задача составная, то есть в ней не одно
действие, а два. В первом действии я узнаю, сколько лисичек.
А
так как боровиков и подберёзовиков вместе столько же, сколько и лисичек, то
общее количество грибов я нашёл вот так:
Ответ:
всего 28 грибов нашли ребята в лесу.
—
А я решал задачу другим способом. Вот посмотрите:
—
Да, Минус, чувствуется, что сложение — это не твой конёк. Конечно, задачу ты
решил правильно. Но при этом у тебя получилось не два, а три действия. При этом
первое и второе действия повторяются. Для этой задачи такой способ записи не
очень удобен. Хотя некоторые задачи действительно удобно записывать не по
действиям, как это сделал я, а числовым выражением. А вот, кстати,
царица Математика уже даёт нам новую задачу.
—
Тихо, Плюс, слушаем!
—
На уроке физкультуры присутствовало 14 мальчиков. А девочек — на 5 меньше.
Сколько всего учащихся присутствовало на уроке физкультуры?
—
Ну что же, начинаем решать. Ребята, и вы попробуйте с нами решать!
—
Я уже решил. Вот посмотрите, в задаче известно количество мальчиков, Их 14. Но
неизвестно количество девочек. Ведь сказано, что их на 5 меньше, чем мальчиков.
А
в задаче надо узнать количество девочек, и только потом — сколько всего детей. Я
так и узнавал:
Ответ:
всего 23 учащихся присутствовало на уроке физкультуры.
—
А вот я записал решение этой задачи по-другому:
И
ещё можно вот так:
—
Но ведь ты мне только что говорил, что такой способ решения неудобен! Зачем же
ты решил задачу другим способом — записью выражения.
—
В первой задаче он действительно был неудобен, а в этой — очень даже удобен.
Во-первых, это не другой способ решения задачи. Посмотри, в моём решении есть
те же действия, что и в твоём, и даже в той же последовательности.
Ты
первым действием узнаёшь, сколько девочек, и я тоже. Ведь это действие я
записал в скобках. А то, что записано в скобках, всегда выполняется первым.
Во
втором действии к 14 прибавляем полученное в первом действии число 9. А в этой
записи слагаемые меняются местами — к 9 прибавляется 14.
И
получается, что это не другой способ решения задачи — ведь все действия
одинаковы, а другой способ записи решения. Ты решал по действиям, а я —
выражением. Способ решения одинаковый, а способ записи этого решения —
разный. Но посмотри, моя запись получилась короче. В ней нет номеров действий и
пояснений. Поэтому такая запись помогает экономить и время, и бумагу.
—
Ты, Плюс, как всегда. Все тебе надо складывать да экономить. Хотя, наверное, ты
прав. Эта запись действительно удобная. А хотелось бы и мне попробовать такую
запись задачи выражением.
Ваше
величество, госпожа королева. Не могли бы Вы задать нам ещё одну задачу?
—
Ну что же, слушайте:
В
моём саду растёт 6 яблонь. А груш на 2больше. Сколько всего яблонь и груш
растёт в моём саду?
Я
хочу видеть у вас оба способа записи решения — и по действиям, и выражением.
—
Хорошо.
—
Хорошо.
—
Ну вот что у меня получилось. Прежде, чем узнать, сколько всего яблонь и груш,
необходимо узнать, сколько груш. Ведь нам это неизвестно. Сказано, что их на 2
больше, чем яблонь.
Получаем:
Значит,
в саду царицы растёт 14 яблонь и груш.
А
вот как получилась запись выражением:
Сначала
я нашёл, количество груш. Но, так как это действие стоит не в начале записи, я
выделил его скобками. А потом нашёл сумму чисел. Ответ такой же, как и при
записи по действиям — 14.
—
Хорошо. Задача решена, верно. А теперь расскажите, чему вы научились.
—
Можно я начну первый.
Записывать
решение задачи можно по действиям и выражением.
—
При записи по действиям мы пишем номер действия и пояснения к каждому действию,
а при записи выражением только пояснение к значению записанного выражения.
—
При записи выражения первое действие часто записываем в скобках, и конечно, не
забываем записать ответ задачи.
—
Ну что же, молодцы, Плюс и Минус. Вы справились с заданием. И сейчас вы можете
пойти погулять в мой сад и полакомиться яблоками и грушами.
—
Ура!!!
Запись решения задачи выражением
—
Плюс!….. Плююююс! Ты где?
Привет,
Плюс! Чего так долго? Включай скорее компьютер. Сейчас у нас будет в скайпе разговор
с царицей Математикой.
—
Здравствуй, Минус. Как это я забыл! Включаю.
—
Здравствуйте, Дорогие Плюс и Минус!
Сегодня
я хочу проверить, как вы умеете решать задачи. Я дам несколько задач и предлагаю
вам устроить соревнование — кто сможет их решить быстрее, но при этом, конечно,
правильно.
—
Да, царица, мы Вас внимательно слушаем.
—
Мы очень внимательно слушаем.
—
Ну что же, приступим. Итак, вот первая задача:
Ребята
в лесу собирали грибы. Они нашли 5 боровиков, 9 подберёзовиков, а лисичек
столько, сколько боровиков и подберёзовиков вместе. Сколько всего грибов нашли
ребята в лесу?
Ну,
Плюс и Минус, я жду вашего решения. Может быть и ребята, которые на вас
смотрят, попробуют решить эту задачу.
—
Всё, я готов! Могу даже объяснить, как я решал эту задачу.
Нам
даны два числа: количество боровиков — их 5, и количество подберёзовиков — их 9.
Но неизвестно количество лисичек. Про них сказано, что их столько, сколько
боровиков и подберёзовиков вместе. А ещё неизвестно, сколько всего грибов.
В
задаче два неизвестных, значит, задача составная, то есть в ней не одно
действие, а два. В первом действии я узнаю, сколько лисичек.
А
так как боровиков и подберёзовиков вместе столько же, сколько и лисичек, то
общее количество грибов я нашёл вот так:
Ответ:
всего 28 грибов нашли ребята в лесу.
—
А я решал задачу другим способом. Вот посмотрите:
—
Да, Минус, чувствуется, что сложение — это не твой конёк. Конечно, задачу ты
решил правильно. Но при этом у тебя получилось не два, а три действия. При этом
первое и второе действия повторяются. Для этой задачи такой способ записи не
очень удобен.
Хотя некоторые задачи действительно удобно записывать не по
действиям, как это сделал я, а числовым выражением. А вот, кстати,
царица Математика уже даёт нам новую задачу.
—
Тихо, Плюс, слушаем!
—
На уроке физкультуры присутствовало 14 мальчиков. А девочек — на 5 меньше.
Сколько всего учащихся присутствовало на уроке физкультуры?
—
Ну что же, начинаем решать. Ребята, и вы попробуйте с нами решать!
—
Я уже решил. Вот посмотрите, в задаче известно количество мальчиков, Их 14. Но
неизвестно количество девочек. Ведь сказано, что их на 5 меньше, чем мальчиков.
А
в задаче надо узнать количество девочек, и только потом — сколько всего детей. Я
так и узнавал:
Ответ:
всего 23 учащихся присутствовало на уроке физкультуры.
—
А вот я записал решение этой задачи по-другому:
И
ещё можно вот так:
—
Но ведь ты мне только что говорил, что такой способ решения неудобен! Зачем же
ты решил задачу другим способом — записью выражения.
—
В первой задаче он действительно был неудобен, а в этой — очень даже удобен.
Во-первых, это не другой способ решения задачи. Посмотри, в моём решении есть
те же действия, что и в твоём, и даже в той же последовательности.
Ты
первым действием узнаёшь, сколько девочек, и я тоже. Ведь это действие я
записал в скобках. А то, что записано в скобках, всегда выполняется первым.
Во
втором действии к 14 прибавляем полученное в первом действии число 9. А в этой
записи слагаемые меняются местами — к 9 прибавляется 14.
И
получается, что это не другой способ решения задачи — ведь все действия
одинаковы, а другой способ
записи решения. Ты решал по действиям, а я —
выражением. Способ решения одинаковый, а способ записи этого решения —
разный. Но посмотри, моя запись получилась короче. В ней нет номеров действий и
пояснений. Поэтому такая запись помогает экономить и время, и бумагу.
—
Ты, Плюс, как всегда.
прав. Эта запись действительно удобная. А хотелось бы и мне попробовать такую
запись задачи выражением.
Ваше
величество, госпожа королева. Не могли бы Вы задать нам ещё одну задачу?
—
Ну что же, слушайте:
В
моём саду растёт 6 яблонь. А груш на 2больше. Сколько всего яблонь и груш
растёт в моём саду?
Я
хочу видеть у вас оба способа записи решения — и по действиям, и выражением.
—
Хорошо.
—
Хорошо.
—
Ну вот что у меня получилось. Прежде, чем узнать, сколько всего яблонь и груш,
необходимо узнать, сколько груш. Ведь нам это неизвестно. Сказано, что их на 2
больше, чем яблонь.
Получаем:
Значит,
в саду царицы растёт 14 яблонь и груш.
А
вот как получилась запись выражением:
Сначала
я нашёл, количество груш. Но, так как это действие стоит не в начале записи, я
выделил его скобками.
записи по действиям — 14.
—
Хорошо. Задача решена, верно. А теперь расскажите, чему вы научились.
—
Можно я начну первый.
Записывать
решение задачи можно по действиям и выражением.
—
При записи по действиям мы пишем номер действия и пояснения к каждому действию,
а при записи выражением только пояснение к значению записанного выражения.
—
При записи выражения первое действие часто записываем в скобках, и конечно, не
забываем записать ответ задачи.
—
Ну что же, молодцы, Плюс и Минус. Вы справились с заданием. И сейчас вы можете
пойти погулять в мой сад и полакомиться яблоками и грушами.
—
Ура!!!
Урок «Решение задач выражением»
Тема: РЕШЕНИЕ
ЗАДАЧ И ВЫРАЖЕНИЙ
Педагогические задачи:
продолжать работу над задачами и выражениями изученных видов; нормировать
умение группировать слагаемые, находить удобный способ решения выражений;
:отрабатывать умение находить периметр многоугольника; развивать логическое
мышление, внимание, наблюдательность.
Планируемые образовательные
результаты:
Личностные:
принимают и осваивают социальную роль обучающегося; стремятся развивать
внимание, память, логическое мышление, навыки сотрудничества со сверстниками и
со взрослыми; проявляют самостоятельность, личную ответственность.
Предметные:
знают: свойства сложения; устную и письменную нумерацию чисел в пределах 100;
отличительные особенности задачи; что такое периметр многоугольника; умеют:
применять свойства сложения для нахождения значения числового выражения; решать
задачи изученных видов; соотносить задачу с данными чертежом и выражениями;
составлять задачи, обратные данной; находить периметр треугольника.
Метапредметные
(критерии сформированности оценки компонентов УУД): регулятивные:
формулируют учебную задачу урока; контролируют в форме сличения способа
действия его результата с заданным эталоном, при необходимости вносят
корректировки; оценивают собственную деятельность и деятельность партнеров;
способны к мобилизации волевых усилий;
познавательные: формулируют
познавательную цель, создают алгоритм деятельности; анализируют объекты с целью
выделения существенных признаков, сравнивают их, строят логическую цепочку
рассуждений, устанавливают причинно-следственные связи;
коммуникативные:
правильно выражают свои мысли в речи; уважают в общении и сотрудничестве
партнера и самого .
спорных ситуаций не создают конфликтов.
Методы
и формы обучения: частично-поисковый; индивидуальная,
фронтальная, групповая.
Образовательные
ресурсы: http://www.fizkult-ura.ru/node/l
13,
электронное приложение к учебнику « Математика 2 класс М.И.Моро и др.»
Оборудование: интерактивная
доска, компьютер.
Наглядно-демонстрационный
материал: кораблики для устного счета, кораблики из
геометрических фигур, карта путешествий с паровозиком из Ромашково
Основные понятия и
термины: сложение, свойства сложения, сложить,
вычесть, слагаемое, сумма, значение суммы, уменьшаемое, вычитаемое, разность,
значение разности, задача, простая задача, составная задача, чертеж, выражение,
сравнить, периметр, многоугольник, треугольник.
Ход урока.
1.Каллиграфическая
минутка.
28 28
28 30 30 30
2.
Сядьте поудобнее, у нас разминка для ума.
«Проверяй
не зевай – очень быстро отвечай».
1. Какой
день недели предшествует субботе? (пятница)
2. Как
называется емкость, в которой находится зубная паста? (тюбик)
3. У
Иванушки –дурачка были три брата и три сестры. Сколько в семье мальчиков? (четыре)
4. Пассажир
такси ехал в село. По дороге он встретил 5 грузовиков и 3 автомашины. Сколько
всего машин шло в село? (одна машина – такси)
5. Бежали
по дорожке два гуся, кошка, собачка. Сколько лапок топало той дорожкой по
полю? (8 лапок)
6. В
лесу жил в избушке смешной толстячок
С
ним был неразлучен сосед – Пятачок.
Читал
он вопилки приятелю вслух.
Скажите,
кто он? (Винни-Пух)
Путешествовать по королевству математики мы отправимся с паровозиком из
Ромашково. Вы помните мультфильм про паровозик из Ромашково?
3.Устный
счёт…станция «Отвечай-ка»
1)Круговые
примеры.
Весёлые кораблики
Соедини кораблики
В игрушечном
порту Волшебною чертой
У каждого
кораблика Ответом предыдущего
Примеры на
борту Чтоб стал корабль
другой.
2) Какое число пропущено?
+ 7=13 84- = 80
— 6 = 8 90 + □ = 100
3) Который час?
На доске: несколько моделей часов, которые показывают разное
время.
Электронное приложение
( Числа от 1 до 100сложение и
вычитание
«Час .Минута.» задание2.)
III. Сообщение темы и
целей учебной деятельности.
— Сегодня на уроке
вы будете совершенствовать умения: решать выражения, используя известные вам
свойства сложения; решать задачи с опорой на схематический чертеж; решать
геометрические задачи.
Тема сегодняшнего урока:
«Решение задач и выражений».
IV. Решение
выражений. Станция « Сосчитай-ка».
А
примеры-то, примеры
Ждут давно уж нас они
Их решайте побыстрее
Все мы будем молодцы!
— Рассмотрите
выражения, записанные на доске:
5 7-7+1 20
— (2 + 
11-7
14-9 6 + 7
19+ (9-8) 5 + 8
— Разделите
выражения на группы так, чтобы в каждой группе оказались похожие выражения.
14-9 6 + 7
20-(2+ 
11-7 5 + 8
19 + (9-8) 7 6-6+1
— Найдите значения
этих выражений. Третий и четвертый столбики выполните с подробным
объяснением.
Станция «Поиграй-ка».
Задания на смекалку и логическое мышление.
Электронное
приложение « Воздушные шарики»
(Числа
от1до 100 сложение и вычитание .
«Числовое
выражение.» задание 2)
— Решите выражения
из задания 1 (с. 46).
Желательно, чтобы выражения были записаны на доске.
— Применяя правило,
с которым вы познакомились на прошлом уроке, найдите самый удобный способ
решения выражений.
(Задание выполняется с комментированием.)
Например:
50 + 6 + 30.
Удобно к пятидесяти
прибавить сначала 30, а затем к полученному результату прибавить 6. Сумма чисел
50 и 30 равна 80. К 80 прибавить 6 — будет 86. Значение суммы чисел 50, 6 и
30равно 86.
7 + 20 + 3 + 70.
Удобно к семи прибавить три,
а к семидесяти прибавить двадцать, после чего полученные результаты сложить.
Сумма чисел 7 и 3 равна 10. Сумма чисел 70 и 20 равна 90. К девяноста прибавить
10- получим 100. Значение суммы чисел 7, 20, 3 и 70 равно 100. И т. д.
Станция «
Отдыхай-ка.»
Физкультминутка
( Хлопки над головой в
ладоши.)
(Повороты туловища
влево-вправо.
Наклоны туловища
влево-вправо.)
(Хлопки над головой в
ладоши.
Машут руками как крыльями.)
(Садятся на корточки, руки
под щеку -засыпают.)
(Хлопки над головой в
ладоши.)
Вот под елочкой зеленой
Скачут весело вороны:
«Кар-кар-кар!» (Громко.)
Целый день они кричали,
Спать ребятам не давали:
«Кар-кар-кар!» (Громко.)
Только к ночи умолкают
И все вместе засыпают:
«Кар-кар-кар!» (Тихо.)
V. Работа над задачами. Станция «Знай-ка».
Прочитайте текст задачи 4
(с. 46) и соотнесите его со схемой-чертежом, приведенной ниже.
Что в задаче известно? Как
это показано на чертеже?
Что требуется узнать? Как
это показано на чертеже?
Запишите решение задачи.
Сформулируйте и запишите ответ задачи.
Прочитайте задачу 5 (с.
46) и сопоставьте ее со схемой-чертежом.
Чем похожи задачи? Чем
отличаются? (Первая задача простая, вторая — составная.)
Рассмотрите выражения,
записанные ниже.
Что узнаем, если к 30
прибавим 20? (Число каменных домов.)
Что узнаем, решив второе
выражение? (Сколько всего домов в дачном поселке.)
Какое из выражений является
решением задачи? (Второе.)
Запишите его и решите. Дайте
ответ на вопрос задачи.
VI. Работа с геометрическим материалом. Станция « Измеряй-ка».
Как называется фигура,
изображенная на полях учебника (с. 46) (Треугольник.)
Что вы можете сказать о
данном треугольнике?
(Все стороны треугольника
имеют разную длину.)
Проверьте, правы ли вы,
измерив стороны треугольника.
Найдите периметр данного
треугольника. Проверьте работу друг друга.
VII. Задание по
образцу.
Рассмотрите данный предмет
–Что это? (кораблик)
-назовите геометрические
фигуры, из которых состоит кораблик.
(3 треугольника и 1 квадрат)
А теперь сравните кораблик с
другими геометрическими фигурами .
-«Какой фигуры не хватает?».
VIII. Рефлексия
учебной деятельности.
Чему научил вас урок?
Какое задание было для вас
самым интересным?
А какое самым трудным?
Что помогло справиться с
трудностями?
Подведение
итогов урока-путешествия
Мы сегодня
на уроке
Провели опрос не строгий.
Повторили, что знакомо,
Что учили в классе , дома.
И учились мы считать, складывать и вычитать!
Дети
получают карточки с различными лицами (весёлое ,грустное, обычное).
-С каким
настроение вы уходите с урока ? Покажите.
Как писать текстовые задачи в виде уравнений — Криста Кинг Математика
Как слова и фразы переводятся в математику
Поначалу задачи со словами могут показаться сложными.
Некоторые фразы всегда означают одну и ту же операцию в математике.
Приведенная ниже таблица поможет вам выучить распространенные математические фразы и операции, которые они обозначают.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Перевод слов и фраз в выражения:
Примеры преобразования текстовых задач в математические выражения и уравнения
Пройти курс
Хотите узнать больше об Алгебре 1? У меня есть пошаговый курс для этого. 🙂
Узнать больше
Запись фразы в виде алгебраического выражения
Пример
Запишите фразу в виде алгебраического выражения.
«Четыре меньше, чем вдвое ???x???»
Фраза «дважды ???x???» означает «???2??? раз ???х???” что, как мы знаем, означает умножение, поэтому мы можем записать его как ???2x???.
«Четыре меньше, чем ???2x???»
Меньше означает вычитание, поэтому мы вычтем ???4??? от ???2x???.
???2x-4???
Может возникнуть соблазн написать ???4??? сначала и вычтите ???2x???. Давайте воспользуемся цифрами, чтобы визуализировать это. Когда мы говорим ???4??? менее ???10??? Вы знаете, что вам придется вычесть ???4??? от???10???, записывается как???10-4???. Так ???4??? менее ???2x??? будет ???2x-4???.
Фраза «дважды х» означает «в 2 раза х», что, как мы знаем, означает умножение, поэтому мы можем написать это как 2x.
Пример
Найдите значение выражения.
???frac{1}{4}??? из ???120???
В математике слово «из» (сразу после правильной или неправильной дроби) говорит нам умножать. Следовательно, математическое выражение фразы будет
???frac{1}{4} cdot 120???
Поскольку нас попросили найти значение выражения, мы выполним умножение, чтобы получить упрощенное значение.
???30???
Мы можем не только переводить фразы в выражения, но и составлять уравнения из некоторых фраз.
Например, предположим, что вы хотите использовать алгебру для решения следующей текстовой задачи:
Возраст Джона на четыре месяца меньше, чем удвоенный возраст Мэри. Если Мэри ???18???, сколько лет Джону?
Первым шагом в решении такой задачи со словами является определение переменных. Это означает, что нужно указать конкретное количество, которое обозначает каждая переменная.
В этой задаче у нас есть две величины: возраст Мэри и возраст Джона. Итак, мы определим переменные, сказав «Let ???x??? быть в возрасте Марии, и пусть ???y??? быть в возрасте Джона». (Мы могли бы использовать любые буквы алфавита для переменных, но люди часто используют ???x??? для одной из переменных, а если есть одна или две дополнительные переменные, они, как правило, используют ???y?? ? и ???z???, именно в таком порядке.)
Следующим шагом в решении задач со словами является «перевод» каждого слова или фразы в математические символы.
Как насчет слова «является» (в «Возраст Джона на четыре меньше, чем удвоенный возраст Марии»)? Ну, «есть» переводится как знак равенства. Чтобы убедиться в этом, полезно подумать о том, что слово «есть» имеет то же значение (в математике), что и «равно».
Объединяя все это, мы получаем уравнение
???y=2x-4???
Третий шаг в решении текстовой задачи — использовать данные и решить уравнение. Здесь нам дан возраст Мэри как ???18???, поэтому мы заменяем ???18??? для ???х??? а затем решить для ???y???.
???y=2(18)-4???
???y=36-4???
???y=32???
Последний шаг — ответить на заданный вопрос. Здесь нас спрашивают о возрасте Джона. Поскольку мы определили ???y??? как возраст Джона, ответ ???32???.
Предположим, вместо этого нам дали следующую текстовую задачу:
В настоящее время возраст Джона на четыре месяца меньше, чем удвоенный возраст Мэри. Если Мэри сейчас ???18???, сколько лет будет Джону через семь лет?
Для решения этой задачи было бы удобно определить ???x??? сколько сейчас лет Мэри, и ???y??? как возраст Джона сейчас, потому что нам дано соотношение между возрастом Марии (сейчас) и возрастом Джона (сейчас).
Получить доступ к полному курсу Алгебра 1
Начать
Изучайте математикуКриста Кинг 16 ноября 2020 г. математика, учитесь онлайн, онлайн-курс, онлайн-математика, алгебра, алгебра 1, алгебра i, текстовые задачи, написание текстовых задач в виде уравнений, перевод фраз в математику, перевод текстовых задач в математику
0 лайков
В чем разница между выражениями и уравнениями?
В чем разница между выражениями и уравнениями?
Jana Russick
23 июня 2021 г.
онлайн-репетитор школьный математический класс. Но знаете ли вы реальную разницу? Они оба могут иметь числа и переменные, но есть одно ключевое отличие.
В чем разница между выражениями и уравнениями?
Алгебраическое выражение включает числа, переменные или их комбинацию. Как видно из следующих выражений, здесь отсутствует один элемент из уравнений:
Знаков равенства нет! Это то, что отличает написание выражений от написания уравнений.
Как уравнения, так и выражения могут иметь переменные, коэффициенты, целые числа, десятичные дроби, показатели степени, сложение, вычитание, умножение и деление. Но в отличие от выражений, алгебраические уравнения всегда должны включать знак равенства:
Как видно из приведенных выше простых уравнений, есть две части уравнения: правая и левая. Итак, технически уравнение состоит из двух выражений. Знак равенства устанавливает две части уравнения как эквивалентные выражения.
Теперь, когда мы знаем разницу между выражениями и уравнениями, давайте научимся их упрощать.
Упрощение выражений и уравнений
Упрощение уравнения означает переписывание выражений, чтобы вы могли найти значение рассматриваемой переменной.
Ниже приведено многоступенчатое уравнение. Оно состоит из двух выражений, соединенных знаком равенства.
Решение подобных уравнений начинается с использования порядка операций. В этом случае мы умножим значения и переменные внутри круглых скобок на числа вне их:
Следующим шагом к упрощению этого математического выражения является объединение одинаковых членов. Для этого сначала переместим одинаковые члены по разные стороны от знака равенства.
Наш следующий шаг — объединить одинаковые члены путем вычитания значений, связанных с нашей переменной x. Мы также добавим числа, не связанные с переменной.
Теперь, когда мы упростили это уравнение, остался только один шаг. Чтобы получить х сам по себе, нам нужно найти частное от деления 52 на -2:
Понимание выражений и уравнений
Числовое выражение можно определить как группу чисел и переменных без знака равенства.