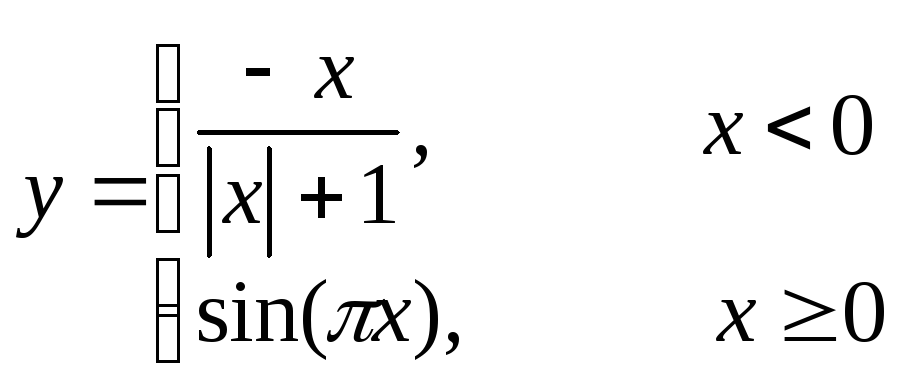Как правильно составить таблицу для графика функции

Пример
1. ( Функция
одной переменной для шагового аргумента).
Построить
таблицу значений функции

для аргумента x,
изменяющегося от 0 до 1,5 с шагом 0,1.
Построить график функции.

Решение.
Решение
разбивается на два основных этапа:
построение таблицы значений функции и
построение графика функции.

Построение
таблицы

Наберем заголовки
столбцов для x
и y
в ячейках A1,
B1.
Наберем первое
значение x,
равное 0, в ячейку A2.
Выполним команду
Правка|Заполнить|Прогрессия,
зададим в диалоге Расположение
в столбце,
Арифметическая
прогрессия, Шаг
0,1, Предельное
значение 2.
Заполнятся ячейки A4:A22.
В ячейку B2
введем формулу: =SIN(4*A2)^2/(A2+1)
и скопируем ее в ячейки B3:B22
Выполним
форматирование данных (чисел) и обрамление
таблицы. Фрагмент рабочего листа с
таблицей показан на рис.5.1.

П
остроение
графика функции. Для
построения графика выделим диапазон
данных (ячейки A1:B22)
и построим точечную диаграмму, вид
которой представлен на рис. 5.2.

Рис.
5.1. Таблица значений функции для примера
1

Рис. 5.2. График
(точечная диаграмма) примера 1

Пример
2. (Функция,
заданная различными аналитическими
выражениями (сложная функция)). Построить
таблицу значений и график функции

для аргумента x
, изменяющегося от -2 до 2 с шагом 0,2

Решение

Построение
таблицы.
Решение
выполним
в том же файле, что и предыдущий пример,
но
на новом листе Excel.
Последовательность заполнения ячеек
аналогична примеру 1.

В
ячейку B2
введем формулу:

=ЕСЛИ(A2<0;-A2/(ABS(A2)+1);SIN(ПИ()*A2))

и скопируем ее в
нижележащие ячейки для всех значений
x
.

Рис. 5.4. График
сложной функции

Рис.
5.3. Таблица значений сложной функции

остроение
графика функции также
полностью аналогично построению
предыдущего примера, если заданная
функция непрерывна.

Замечание.
Если функция терпит разрыв при переходе
от одного аналитического выражения к
другому, то нужно построить на одной
диаграмме два графика, каждый из которых
отвечает области непрерывности функции.
В случае разрывной функции можно строить
один график, если выбрать вид графика
из отдельных точек

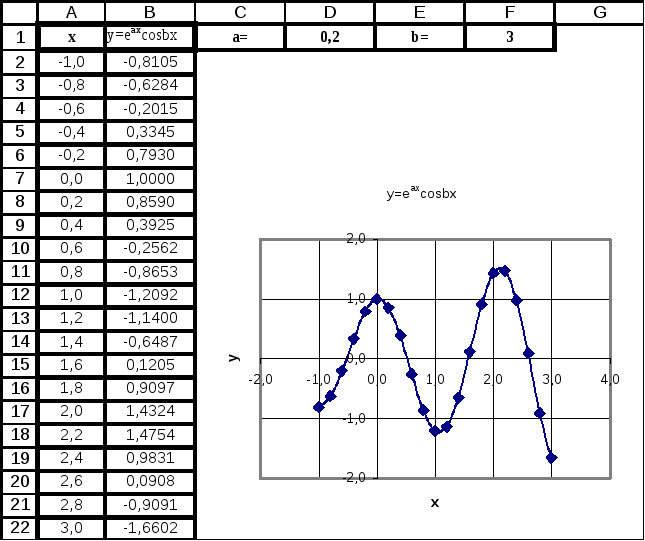
Пример
3. (Функция,
зависящая от параметра). Построить
таблицу значений и график функции

для аргумента x
, изменяющегося
от -1 до 3 с шагом 0,2 при заданных значениях
a
и b.

Решение

Введем заголовки
столбцов для x
и y
в ячейки A1,
B1
и значения a,
b
в отдельные ячейки D1,
F1.
Заполним столбец
A2:A22
значениями x.
Введем формулу
для y
в ячейку B2

=EXP($D$1*A2)*COS($F$1*A2)
и скопируем ее в ячейки B3:B22.

П

Рис. 5.5. Таблица и
график функции, зависящей от параметра

остроим
график аналогично примеру 1 (см. рис.5.5)

Замечание.
Меняя значения параметров, можно получить
совершенно другое поведение функции.
Рекомендуется проанализировать поведение
функции при a>0
и a<0,
а также
рассмотреть уменьшение и увеличение
b.

Пример
4. (Функция,
заданная параметрическими уравнениями).
Вычислить
таблицу значений функции, заданной
параметрическими уравнениями и построить
ее график. В качестве примера рассмотрим
построение окружности.

Параметрические
уравнения окружности рассмотрим для
значений параметра, пробегающих полный
оборот вокруг начала координат:

(1)

Построение
таблицы значений функции

Перейдем на новый
рабочий лист.
Зададим заголовки
столбцов t,
x,
y.
Заполним первый
столбец значениями t,
применив еще один способ задания
аргумента: каждое последующее значение
вычислим через предыдущее, добавляя
шаг. В ячейке D2
вычислим

по формуле =ПИ()/16. В ячейку A2
введем 0, в ячейку A3
введем формулу =A2+$D$2,
которую копируем вниз до значения 2.
Введем в ячейку
B2
формулу =COS(A2);
в ячейку C2
формулу =SIN(A2)
Выделим ячейки
B2,
C2
и копируем их для всех значений t
с помощью заполнения.
Форматируем
таблицу по образцу.

Построение
графика функции

Выделим диапазон
B1:C22
Вызовем Мастер
диаграмм и
построим точечную диаграмму. В процессе
построения зададим заголовки диаграммы
и осей, уберем легенду, назначим линии
сетки.
Затем отредактируем
диаграмму: по команде Формат
оси зададим
точность – один знак после запятой, по
команде Формат
области построения укажем
рамку Невидимая.
Выполним
растяжение-сжатие диаграммы, так чтобы
получилась окружность, а не эллипс.

Результат
построения показан на рис. 5.7.

Рис.
5.7. График функции, заданной параметрическими
уравнениями

Рис.
5.6. Таблица функции, заданной
параметрическими уравнениями

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

В этой статье разобран самый простой метод получения графика функции.

Суть метода: найти несколько точек принадлежащих графику, расставить их на координатной плоскости и соединить. Этот способ не лучший (лучший – построение графиков с помощью элементарных преобразований), но если вы все забыли или ничего не учили, то знайте, что у вас всегда есть план Б – возможность построить график по точкам.

Итак, алгоритм по шагам:

1. Представьте, как выглядит ваш график.

Строить гораздо легче, если вы понимаете, что примерно должны получить в итоге. Поэтому сначала посмотрите на функцию и представьте, как примерно должен выглядеть ее график. Все виды графиков элементарных функций вы можете найти здесь. Этот пункт желательный, но не обязательный.

Пример: Построить график функции (y=-)(frac{2}{x})

Данная функция — гипербола с ветвями расположенными во второй и четвертой четверти. Её график выглядит как-то так:

2. Составьте таблицу точек, принадлежащих графику:

Теперь подставим разные значения «иксов» в функцию, и для каждого икса посчитаем значение «игрека».

Пример: (y=-)(frac{2}{x})

при (x=-1)		(y=-)(frac{2}{-1})(=2)
при (x=0)		(y) — не существует (делить на ноль нельзя)
при (x=1)		(y=-)(frac{2}{1})(=-2)
при (x=2)		(y=-)(frac{2}{2})(=-1)
при (x=3)		(y=-)(frac{2}{3})
при (x=4)		(y=-)(frac{2}{4})(=-)(frac{1}{2})

Результат вычислений удобно представлять в виде таблицы, примерно такой:

(x)	(-1)	(0)	(1)	(2)	(3)	(4)
(y)	(2)	(-)	(-2)	(-1)	(-)(frac{2}{3})	(-)(frac{1}{2})

Как вы могли догадаться, полученные пары «икс» и «игрек» — это точки, лежащие на нашем графике.

4. Постройте координатную плоскость и отметьте на ней точки из таблицы.

Пример:

5. Если нужно, найдите еще несколько точек и нанесите их на координатную плоскость.

Пример: Чтобы построить график мне не хватает нескольких точек из отрицательной части, а также рядом с осью игрек, поэтому я добавлю столбцы с (x=-2), (x=-4), (x=)(frac{1}{2}) и (x=-)(frac{1}{2})

при (x=-2)		(y=-)(frac{2}{-2})(=1)
при (x=-4)		(y=-)(frac{2}{-4})(=)(frac{1}{2})
при (x=)(frac{1}{2})		(y=-)(frac{2}{frac{1}{2}})(=-2:)(frac{1}{2})(=-2 cdot 2=-4)
при (x=-)(frac{1}{2})		(y=-)(frac{2}{-frac{1}{2}})(=-2:(-)(frac{1}{2})())(=-2 cdot (-2)=4)

(x)	(-1)	(0)	(1)	(2)	(3)	(4)	(-2)	(-4)	(frac{1}{2})	(-)(frac{1}{2})
(y)	(2)	(-)	(-2)	(-1)	(-)(frac{2}{3})	(-)(frac{1}{2})	(1)	(frac{1}{2})	(-4)	(4)

6. Постройте график

Теперь аккуратно и плавно соединяем точки.

Готово!

Источник

Определить правило, по которому зависимая величина будет меняться, значит задать функцию. Вариантов задания функции несколько:

Словесно, например: «игрек равен двум х». Запись будет выглядеть так: $у = 2times x$
Аналитический способ, то есть сразу с помощью записи формулы, например: $f(x) = x-3$
Графический способ
Табличный способ

Графический способ

Графический способ подразумевает чертеж на прямоугольной координатной плоскости, например:

Линия, изображенная на рисунке, называется графиком функции.

Определение:

Графиком функции называется множество точек плоскости, абсциссы которых равны значениям аргумента $x$, а ординаты – соответствующим значениям функции $y$.

Линия может быть разной: прямой или кривой.

Функция (и ее график) может быть:

возрастающей (линия идет вверх, как на рисунке выше), если вторая зависимая величина увеличивается вместе с первой;
убывающей (линия идет вниз), если вторая величина уменьшается при увеличении первой, например:

Функция (и ее график) может быть убывающей или возрастающей как на всей области определения, так и на определенном промежутке:

Графический способ не дает возможности предельно точного определения численных значений $x$ и $у$, но он наглядно показывает поведение функции (убывает или возрастает, максимум, минимум, непрерывность и т. д.) и является важным способом ее исследования.

Подробный урок о том, как строить график линейной функции.

Табличный способ

Часто используется табличный (то есть в виде таблицы) способ задания функции. В таблице для каждого значения аргумента $x$ указывается соответствующее ему конкретное значение функции $y$, например:

$x$	$1$	$2$	$3$	$5$
$y$	$10$	$20$	$30$	$50$

Каждое значение аргумента и функции нумеруется. В данном случае в таблице значению $x_1$, равному $1$, соответствует единственное значение $у_1$, равное $10$. Значению $x_2$, равному $2$, соответствует $у_2$, равное $20$ и т. д.

Не трудно догадаться, что в таблице выше отражена зависимость

$y = 10x$.

Ее можно продолжить для любых значений $x$, так при

$x_{100} = 100$

$y_{100}$ будет равен $1000$.

Табличный способ позволяет быстро найти конкретные значения $x$ и $у$.

Заполним таблицу для функции

Попробуем заполнить таблицу функции $у=3x+2$, для значений $x$, равных $1$, $3$, $4$, $8$.

Подставим в формулу $у=3x+2$ значения $x_1$, $x_2$, $x_3$, $x_4$.

Получим:

$у_1 = 3times 1 + 2 = 5$

$у_2 = 3times 3 + 2 = 11$

$у_3 = 3times 4 + 2 = 14$

$у_4 = 3times 8 + 2 = 26$

Заполним таблицу:

$x$	$1$	$3$	$4$	$8$
$у$	$5$	$11$	$14$	$26$

Источник

Построение графиков функций

В данном пособии рассматриваются различные способы построения графиков функций. Приводятся примеры построения графиков различными методами, задания для самостоятельной работы.Пособие рекомендовано для учащихся старших классов и учителей школ, гимназий, лицеев для организации работы, как на уроке, так и на факультативах и дополнительных занятиях по данной теме, а также для подготовки к экзаменам.

При построении графика функции по точкам иногда указывают шаг, т.е. число, через которое выбирается последующее значение аргумента. Чем меньше шаг, тем точнее получается график.

Задание 1. Постойте по точкам график функции…

Пример 2. Постройте график функции у=х²—3, на интервале [ — 4; 4] с шагом 1.

Решение. Функция у=х²—3 определена на всем интервале. Составим таблицу значений. Первое значение аргумента — 4. Следующее с учетом шага — 4+1=-3 и т. д. пока не получим последнее значение 4.

Отметим точки на координатной плоскости и построим график:

Задание 2. Постройте график функции на заданном интервале с указанным шагом…

Смотрите также

Источник

Данная статья не содержит графических
иллюстраций. Поэтому знакомиться с ее
содержанием будет удобнее, имея под рукой лист
бумаги и карандаш.

1. Линейная функция

При изучении линейной функции на уроках алгебры в 7-м
классе учащиеся довольно успешно осваивают
способ построения прямой по двум точкам. При этом
составляется таблица, в которой задаются
значения х и вычисляются соответствующие
значения y. Однако при построении прямой
часто допускаются неточности: из-за того, что
выбранные точки очень близко расположены друг к
другу, построенная прямая “уходит в сторону”.
Построить график линейной функции можно гораздо
быстрее, если заметить определенные
закономерности. Рассмотрим примеры.

Пример 1. Построить график функции .

Решение Составим таблицу значений функции.

Порядковый №	1	2	3	4	5
x	0	1	2	3	4
y	-3	-1	1	3	5

Первая точка выбирается традиционно – точка
пересечения прямой с осью ординат. А дальше
обратим внимание, что разность значений функции , т.е. совпадает
со значением углового коэффициента заданной
функции. А значит, для построения точек на
координатной плоскости вся информация заложена
в коэффициентах заданной линейной функции.
Алгоритм построения точек следующий:

строим первую точку ;
переносим ее на 1 единицу вправо и две единицы
вверх (это вторая точка, принадлежащая прямой):
вторую точку снова перемещаем на 1 единицу
вправо и две единицы вверх и получаем третью
точку искомой прямой;
далее все повторяется любое число раз.

Пример 2. Построить график функции .

Решение Первая точка имеет координаты . Каждая
следующая получается из предыдущей смещением на
1 единицу вправо и на 3 единицы вниз.

Рассмотрим теперь случай, когда угловой
коэффициент линейной функции задается дробью.

Пример 3. Построить график функции .

Решение Составим таблицу значений функции.
Чтобы получить точки прямой с целочисленными
координатами, возьмем значения х, кратные
трем. Ну. а первая точка, по-прежнему, – точка
пересечения прямой с осью ординат.

x	0	3	6	9	12
y	-4	-2	0	2	4

Построим точки на координатной плоскости.
Видно, что каждая следующая точка получается из
предыдущей сдвигом на 3 единицы вправо и 2 единицы
вверх. Проводим прямую.

Пример 4. Построить график функции .

Решение Первая точка имеет координаты . Заметим, что
угловой коэффициент прямой . Значит, каждая следующая точка
прямой будет получена из предыдущей смещением на
5 единиц вправо и на 4 единицы вниз. Строим точки и
проводим прямую.

Обратите внимание, что в случае дробного
углового коэффициента линейной функции
знаменатель дроби указывает количество единиц
для перемещения точки вправо, а числитель –
количество единиц, на которые переместится точка
вверх (при )
или вниз (при k<0).

2. Квадратичная функция

2.1. С графиком квадратичной функции учащиеся
знакомятся еще в седьмом классе. При этом, для
построения параболы, как правило, записывается
таблица значений функции для , затем полученные точки строят
на координатной прямой и рисуют параболу. Более
продвинутые ученики записывают таблицу только
для , строят
полученные точки и проводят правую ветвь
параболы. Затем, воспользовавшись симметрией
графика относительно оси ординат, строят точки
параболы для
и рисуют вторую ветвь параболы.

Записи таблицы можно избежать, если заметить
одну закономерность в расположении указанных
точек. Посмотрим таблицу значений функции :

В третьей строке таблицы записана разность
двух последующих значений функции. Видно, что
полученные числа образуют последовательность
нечетных чисел (легко убедиться, что эта
закономерность выполняется и далее, например, ). Этот факт
легко запоминается. А с учетом этой
закономерности построить характеристические
точки параболы можно так:

первая точка – начало координат;
вторая точка получается из первой смещением на
одну единицу вправо и на одну единицу вверх;
третья получается смещением второй точки на
один вправо и три вверх;
четвертая точка получается переносом третьей
на один вправо и пять вверх;
затем строятся точки левой ветви параболы за
счет симметрии графика относительно оси ординат.

Остается провести плавную линию через
полученные точки, и парабола построена.

2.2. Перейдем теперь к квадратичной
функции вида ,
которая изучается уже в восьмом классе. Учащиеся
узнают, что коэффициент а определяет
направление ветвей параболы, а также растяжение
или сжатие графика вдоль оси ординат. А для
построения графика все равно просчитывают
координаты точек. Но без этого можно обойтись,
если знать указанную выше закономерность
построения точек параболы . И если для нее сдвиг точек вдоль
оси OY задавался последовательностью чисел , то для функции эта
последовательность чисел будет .

Пример 5. Построить график функции .

Решение Графиком функции служит парабола,
ветви которой направлены вниз, а вершина
находится в начале координат. Для построения
других точек параболы вспомним про нечетные
числа ,
умножим их на ,
получаем последовательность чисел Знак говорит о том , что смещение
точек будет сделано вниз. На словах алгоритм
построения звучит так: от начала координат одна
единица вправо и две вниз; от новой точки одна
единица вправо и шесть вниз; строим точки,
симметричные полученным относительно оси
ординат; проводим параболу.

Пример 6. Построить график функции .

Решение Графиком функции – парабола, ветви
которой направлены вверх. Вершина параболы
находится в начале координат. Для построения
других точек воспользуемся последовательностью При получаем
следующий порядок перемещений вдоль оси ординат . Строим точки
на координатной плоскости: от точки 1 клетка вправо и
полклетки вверх, от полученной точки снова одна
клетка вправо и полторы клетки вверх, потом от
новой точки опять одна клетка вправо и две с
половиной клетки вверх и т.д. (ясно, что в
указанном случае за единичный отрезок на осях
координат принимается одна клеточка в тетрадном
листе). Затем строим точки левой ветви параболы
за счет симметрии графика относительно оси OY и
рисуем параболу.

2.3. В 9-м классе учащиеся изучают
квадратичную функцию . Для построения ее графика с учетом
выше сказанного можно применять следующий
алгоритм:

найти координаты вершины параболы ;
построить в системе координат полученную точку
и провести оси вспомогательной системы
координат (прямые и );
по коэффициенту а определить направление
ветвей параболы;
построить во вспомогательной системе координат
характеристические точки функции , следуя алгоритму пункта
2.2.
провести плавную линию через указанные точки.
График готов.

Пример 7. Построить график функции .

Решение Графиком функции – парабола.

Вычисляем координаты вершины параболы: .
Строим точку
и проводим пунктиром вспомогательные оси
координат (прямые проходят через указанную точку
и параллельны осям ОХ и ОY).
Коэффициент при х² в данной функции
равен 1. Значит, для построения
характеристических точек параболы применим ряд
чисел 1,3,5,…. , т.е. строим стандартную параболу, но
во вспомогательной системе координат (пункт 2.1.).
Проводим плавную линию через полученные точки.
Парабола построена.