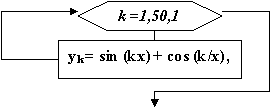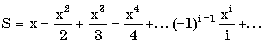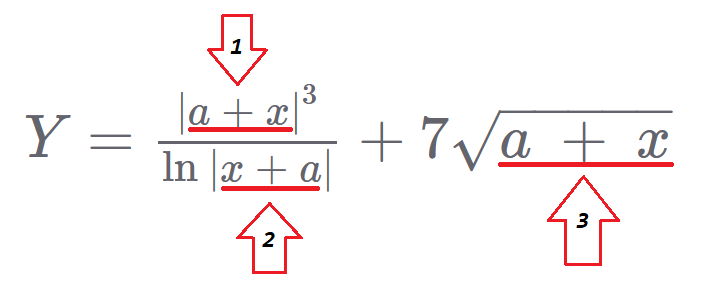2.1 Разработка алгоритма.
2.2 Блок-схема.
2.3 Структуры алгоритмов.
2.1 Разработка алгоритма.
Алгоритм — это
a. описание последовательности действий для решения задачи или достижения поставленной цели;
b. правила выполнения основных операций обработки данных;
c. описание вычислений по математическим формулам.
Перед началом разработки алгоритма необходимо четко уяснить задачу: что требуется получить в качестве результата, какие исходные данные необходимы и какие имеются в наличии, какие существуют ограничения на эти данные. Далее требуется записать, какие действия необходимо предпринять для получения из исходных данных требуемого результата.
На практике наиболее распространены следующие формы представления алгоритмов:




Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задается в произвольном изложении на естественном языке.
Пример. Записать алгоритм нахождения наибольшего общего делителя (НОД) двух натуральных чисел.
Алгоритм может быть следующим:
1. задать два числа;
2. если числа равны, то взять любое из них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма;
3. определить большее из чисел;
4. заменить большее из чисел разностью большего и меньшего из чисел;
5. повторить алгоритм с шага 2.
Описанный алгоритм применим к любым натуральным числам и должен приводить к решению поставленной задачи. Убедитесь в этом самостоятельно, определив с помощью этого алгоритма наибольший общий делитель чисел 125 и 75.
Словесный способ не имеет широкого распространения по следующим причинам:



Графический способ представления алгоритмов является более компактным и наглядным по сравнению со словесным.
При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.
Такое графическое представление называется схемой алгоритма или блок-схемой.
Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов.
Он занимает промежуточное место между естественным и формальным языками.
С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи.
В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя. Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда. Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций.
2.2 Блок-схема.
Блок-схемой называют графическое представление алгоритма, в котором он изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.
В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий.
Приведем наиболее часто употребляемые символы.
| Название символа | Обозначение и пример заполнения | Пояснение |
| Процесс | Вычислительное действие или последовательность действий | |
| Решение |  |
Проверка условий |
| Модификация | 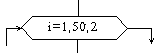 |
Начало цикла |
| Предопределенный процесс |  |
Вычисления по подпрограмме, стандартной подпрограмме |
| Ввод-вывод | 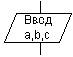 |
Ввод-вывод в общем виде |
| Пуск-останов |  |
Начало, конец алгоритма, вход и выход в подпрограмму |
| Документ |  |
Вывод результатов на печать |
Блок «процесс» применяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.
Блок «решение» используется для обозначения переходов управления по условию. В каждом блоке «решение» должны быть указаны вопрос, условие или сравнение, которые он определяет.
Блок «модификация» используется для организации циклических конструкций. (Слово модификация означает видоизменение, преобразование). Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.
Блок «предопределенный процесс» используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.
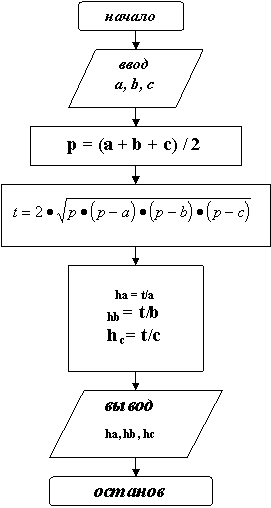
Пример. Составить блок-схему алгоритма определения высот ha, hb, hc треугольника со сторонами a, b, c, если
где p = (a + b + c) / 2.
Решение. Введем обозначение 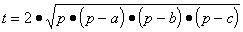
2.3 Структуры алгоритмов.
Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых (т.е. основных) элементов. Естественно, что при таком подходе к алгоритмам изучение основных принципов их конструирования должно начинаться с изучения этих базовых элементов
Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: следование, ветвление, цикл.
Характерной особенностью базовых структур является наличие в них одного входа и одного выхода.
1. Базовая структура следование. Образуется из последовательности действий, следующих одно за другим:
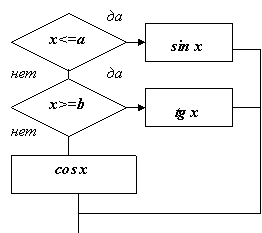
2. Базовая структура ветвление. Обеспечивает в зависимости от результата проверки условия (да или нет) выбор одного из альтернативных путей работы алгоритма. Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран.
Структура ветвление существует в четырех основных вариантах:




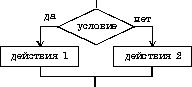
1) если-то если условие то действия конец если2) если-то-иначе если условие то действия 1 иначе действия 2 конец если
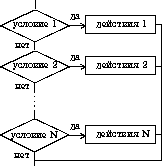
3) выбор выбор при условие 1: действия 1 при условие 2: действия 2 . . . . . . . . . . . . при условие N: действия N конец выбора
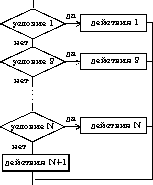
4) выбор-иначе выбор при условие 1: действия 1 при условие 2: действия 2 . . . . . . . . . . . . при условие N: действия N иначе действия N+1 конец выбора

Пример. Составить блок-схему алгоритма вычисления функции
Базовая структура цикл. Обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла.
Структура цикл существует в трех основных вариантах:
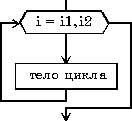
Цикл типа для.
Предписывает выполнять тело цикла для всех значений некоторой переменной (параметра цикла) в заданном диапазоне.
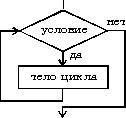
Цикл типа пока.
Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное после слова пока.
Цикл типа делать — пока.
Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное после слова пока. Условие проверяется после выполнения тела цикла.
Заметим, что циклы для и пока называют также циклами с предпроверкой условия а циклы делать — пока — циклами с постпроверкой условия. Иными словами, тела циклов для и пока могут не выполниться ни разу, если условие окончания цикла изначально не верно. Тело цикла делать — пока выполнится как минимум один раз, даже если условие окончания цикла изначально не верно.
цикл для i от i1 до i2 шаг i3 тело цикла (последовательность действий) конец циклацикл пока условие тело цикла (последовательность действий) конец цикла
цикл делать тело цикла (последовательность действий) пока условие конец цикла

Пример. Составить блок-схему алгоритма вычисления функции
yk = sin (kx) + cos (k/x), k = 1, 2, …, 50
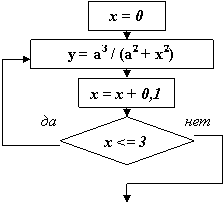
Пример. Составить блок-схему вычисления функции
y = a3 / (a2 + x2)
при x, изменяющимся от x = 0 до x = 3 с шагом Dx = 0,1
Итерационные циклы. Особенностью итерационного цикла является то, что число повторений операторов тела цикла заранее неизвестно. Для его организации используется цикл типа пока. Выход из итерационного цикла осуществляется в случае выполнения заданного условия.
На каждом шаге вычислений происходит последовательное приближение и проверка условия достижения искомого результата.
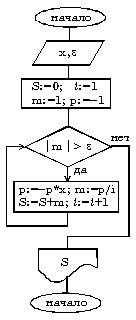
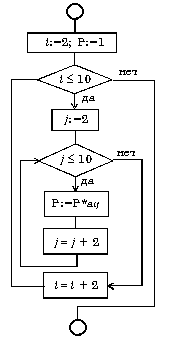
Пример. Составить алгоритм вычисления суммы ряда
с заданной точностью (для данного знакочередующегося степенного ряда требуемая точность будет достигнута, когда очередное слагаемое станет по абсолютной величине меньше).
Вычисление сумм — типичная циклическая задача. Особенностью же нашей конкретной задачи является то, что число слагаемых (а, следовательно, и число повторений тела цикла) заранее неизвестно. Поэтому выполнение цикла должно завершиться в момент достижения требуемой точности.
При составлении алгоритма нужно учесть, что знаки слагаемых чередуются и степень числа х в числителях слагаемых возрастает.
Решая эту задачу «в лоб» путем вычисления на каждом i-ом шаге частичной суммы
S:=S+(-1)**(i-1)*x**i/i ,
мы получим очень неэффективный алгоритм, требующий выполнения большого числа операций. Гораздо лучше организовать вычисления следующим образом: если обозначить числитель какого-либо слагаемого буквой р, то у следующего слагаемого числитель будет равен -р*х (знак минус обеспечивает чередование знаков слагаемых), а само слагаемое m
будет равно p/i, где i — номер слагаемого.
Алгоритм, в состав которого входит итерационный цикл, называется итерационным алгоритмом. Итерационные алгоритмы используются при реализации итерационных численных методов. В итерационных алгоритмах необходимо обеспечить обязательное достижение условия выхода из цикла (сходимость итерационного процесса). В противном случае произойдет зацикливание алгоритма, т.е. не будет выполняться основное свойство алгоритма — результативность.
Вложенные циклы.
Возможны случаи, когда внутри тела цикла необходимо повторять некоторую последовательность операторов, т. е. организовать внутренний цикл. Такая структура получила название цикла в цикле или вложенных циклов. Глубина вложения циклов (то есть количество вложенных друг в друга циклов) может быть различной.
При использовании такой структуры для экономии машинного времени необходимо выносить из внутреннего цикла во внешний все операторы, которые не зависят от параметра внутреннего цикла.
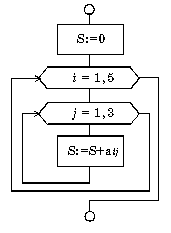
Пример вложенных циклов для. Вычислить сумму элементов заданной матрицы А(5,3).
Пример вложенных циклов пока. Вычислить произведение тех элементов заданной матрицы A(10,10), которые расположены на пересечении четных строк и четных столбцов.
Время выполнения4 часа Цель работыНаучиться использовать язык программирования Visual Basic for Applications (VBA) для разработки модулей в Excel на основе линейных алгоритмов. Задачи лабораторной работыПосле выполнения данной работы студент должен знать и уметь:
Перечень обеспечивающих средствДля обеспечения выполнения работы необходимо иметь компьютер со следующим математическим обеспечением: операционная система Windows XP, электронные таблицы Excel с приложением в виде языка Visual Basic for Applications. Общие теоретические сведенияVBA – это язык объектно-ориентированного программирования. Основными парадигмами являются объект, свойство, метод, событие, класс и семейство объектов. Объект – это инкапсуляция данных вместе с кодом, предназначенным для их обработки. Семейство – объект, содержащий несколько других объектов того же типа: Worksheets (“Лист 1”) – рабочий лист с имени Лист1, Worksheets (1) – первый лист рабочей книги. Классы – это проект, на основе которого будет создан объект, т.е. класс определяет имя объекта, его свойства и действия, над ним выполняемые. А каждый объект, свою очередь, является экземпляром класса. Методы – это действия, выполняемые над объектом. Объект.метод – синтаксис метода Пример. Application.Quit – закрыть объект Application. Worksheets (“Лист1”).Chartobjects.Delete – удалит все диаграммы с листа “Лист1”. Свойства – это атрибут объекта, определяющий его характеристики: размер, цвет, положение на экране или состояние (доступность, видимость). Для изменения характеристик меняют его свойства: Объект.Свойство=Значение свойства Пример. Worksheets.Visible = False Есть свойства, возвращающие объект: ActiveCell возвращает активную ячейку активного листа активной рабочей книги. ActiveWindow – активное окно. Свойства ActiveCell, ActiveWindow. ActiveCell и Application. ActiveWindow. ActiveCell возвращают одну и ту же активную ячейку. События – это действия, распознаваемые объектом. Суть программирования на VBA и заключается в том, чтобы на событие получить отклик. Пример 1. Написать программу, которая вычисляет периметр треугольника. Запись программы в виде блок-схемы (рис. 1) и визуальное представление формы для ввода данных (рис. 2) и результата (рис. 3): Рисунок 1. Блок-схема решения задачи Рисунок 2. Ввод исходных данных в процессе выполнения программы Рисунок 3. Вывод результата в процессе выполнения программы Программный код Option Explicit Sub ПериметрТреугольника() Dim ВтораяСторона, ТретьяСторона, Периметр As Single ВтораяСторона = 3.5 ТретьяСторона = InputBox(«Введите значение третьей стороны треугольника», «Третья сторона») Периметр = Cells(1, 4) + ВтораяСторона + ТретьяСторона MsgBox «Периметр треугольника = » & Периметр End Sub Пример 2. Вычислите значение квадратного корня из суммы трех переменных. Запись программы в виде блок-схемы (рис. 4) и визуальное представление формы для ввода данных (рис. 5) и результата (рис. 6): Рисунок 4. Блок-схема решения задачи а) б) в) Рисунок 5. Ввод исходных данных в процессе выполнения программы Рисунок 6. Вывод результата в процессе выполнения программы Программный код Option Explicit Sub КореньКвадратныйИзСуммыТрехПеременных() Dim ПерваяПеременная, ВтораяПеременная, ТретьяПеременная, Сумма As Single Dim Корень As Double ПерваяПеременная = InputBox(«Введите значение первой переменной», «Первая Переменная») ВтораяПеременная = InputBox(«Введите значение второй переменной», «Вторая Переменная») ТретьяПеременная = InputBox(«Введите значение третьей переменной», «Третья Переменная») Сумма = ТретьяПеременная + ВтораяПеременная + ПерваяПеременная Корень = Sqr(Сумма) MsgBox «Корень из суммы трех переменных = » & Корень End Sub Пример 3. Вычислить Y, задав значения переменным: Программный код Sub Main() Dim x, b, a, res As Single x = -3 b = 2 a = 0,5 res = (Sqr(5 * x ^ 4 + 2 * Sin(b) ^ 2)) / Cos(Abs(a ^ 3 — 3 * Tan(b))) MsgBox «res=» & CStr(res) End Sub Private Sub CommandButton1_Click() Dim x, b, a, res As Single x = Cells(3, 1) b = Cells(3, 2) a = Cells(3, 3) res = (Sqr(5 * x ^ 4 + 2 * Sin(b) ^ 2)) / Cos(Abs(a ^ 3 — 3 * Tan(b))) Cells(5, 2) = res End Sub Визуальное представление решения задачи представлено на рис. 7. Рисунок 7. Визуальное представление решения задачи Пример 4. Вычислить f, задав значения переменным: Программный код Sub Main() Dim x, y, t, res As Single x = -3 y = 2 t = 0.5 res = (x / (4.8 * x ^ 3 — y) ^ 3) + 1 / 4 * (t — 3 / x) MsgBox «res=» & CStr(res) End Sub Private Sub CommandButton2_Click() Dim x, y, t, res As Single x = Cells(3, 9) y = Cells(3, 10) t = Cells(3, 11) res = (x / (4.8 * x ^ 3 — y) ^ 3) + 1 / 4 * (t — 3 / x) Cells(5, 10) = res End Sub Визуальное представление решения задачи представлено на рис. 8. Рисунок 8. Визуальное представление решения задачи Видеоурок по выполнению заданий лабораторной работы Варианты заданийТехнология выполнения работы
Содержание отчета
Вопросы для защиты работы
|
Цель работы:
-
Закрепить
правила записи
арифметических выражений
на VBA. -
Применить
умения при составлении алгоритма
решения задачи в виде блок-схемы. -
Освоить
приемы программирования с использованием
диалоговых окон ввода и вывода. -
Получить навыки
составления программ линейной структуры.
Ход работы:
1) Способ представления алгоритма в виде блок-схемы.
Разработанный
алгоритм
(строгая последовательность действий,
приводящая от исходных данных к
результату) должен быть представлен в
виде удобном для последующего перевода
его в программу. Наиболее простой формой
записи алгоритмов является естественный
язык. Его словесная формулировка
присутствует в сознании разработчика,
пусть даже не нанесенная на бумагу. Чаще
всего используют графическую форму
записи алгоритмов.
Описание
алгоритма в виде графических элементов
и связей между ними называется блок-схемой.
От
чисто текстовой записи на естественном
языке блок-схема отличается следующим:
-
каждому
действию соответствует определенный
вид фигуры: овал, прямоугольник,
параллелограмм, ромб, шестиугольник
(Приложение 1); -
внутри
фигур записываются формулы или краткая
инструкция; -
фигуры
соединяются линиями со стрелками,
которые называются линиями
потока и
указывают направления перехода от
одной операции к другой; -
фигуры или блоки
в блок-схемах могут иметь номера,
проставляемые слева в разрыве верхней
линии; -
линии
потока не должны пересекаться, поэтому
при необходимости используются
соединители
– элементы с буквой или цифрой внутри.
2) Линейная структура программы в vba.
Программа
на VBA
представляет собой последовательность
строк. Выполнение линейной программы
осуществляется построчно. Основными
компонентами программы являются
операторы, из которых и состоят строки.
Одна строка программы может содержать
один или несколько операторов, операторы
в строке отделяются друг от друга
двоеточием.
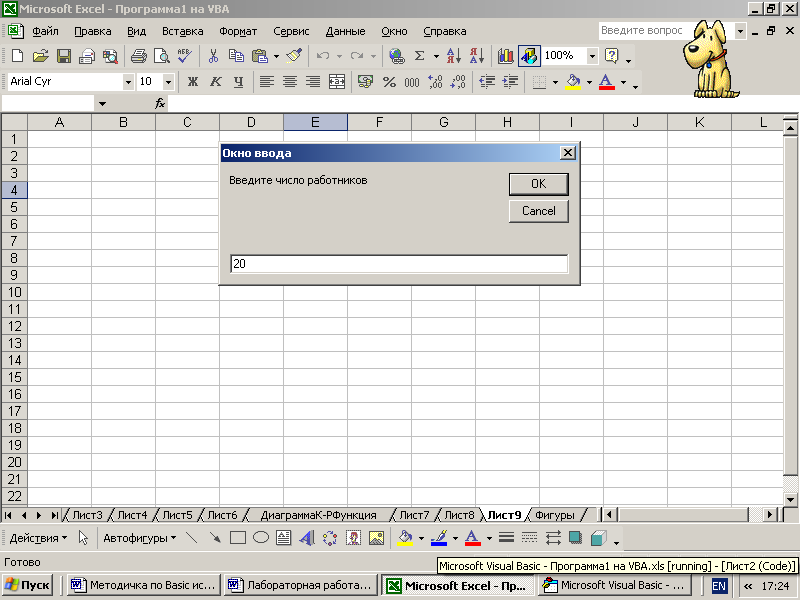
Пример
1. Составить
в виде блок-схемы и программы алгоритм
вычисления объёма розничного товарооборота
T
= R*N
с учётом того, что среднесписочное число
работников составляет R=20
и средний оборот на одного работника
N=80,50
руб.
Решение:
Прежде, чем проводить вычисления по
формуле необходимо ввести значения
переменных. Среднесписочное работников
R
имеет целочисленное значение (Integer),
средний оборот на одного работника N
имеет вещественное значение (Single),
результат — объём розничного товарооборота,
переменная Т так же имеет вещественное
значение (Single).
Блок-схема данного
алгоритма имеет вид:
Sub
Пример1( )
Dim
R As Integer
Dim N, T As Single
R = InputBox(«Введите
число работников», «Окно ввода»)
N = InputBox(«Введите
средний оборот», «Окно ввода»)
T = R * N
MsgBox «Объём
товарооборота = » & T
End Sub
Рис.
14. Блок-схема
алгоритма и текст программы Примера
1 на языке VBA
3)
Наберите в Окне редактирования кода
Листа программу
(рис. 14), в которой выполнено описание
переменных, их ввод в диалоговое окно
ввода, вычисление проведено при помощи
оператора присваивания и вывод
осуществляется в диалоговое окно вывода.
4
)
Запустите программу на счёт
кнопкой Run
Sub
;
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
| ВНИМАНИЕ | Для получения макроса, функции, блок-схемы своего варианта пишите на наш электронный адрес proglabs@mail.ru |
Цель работы
Изучить основы VBA: типы данных, правила именования переменных, правила объявления переменных, базовые операторы, реализующие линейный алгоритм. Приобретение навыков написания пользовательских функций и процедур.
Постановка задания
Задание для всех вариантов звучит так (или, возможно, немного изменено, так как могут быть разные издания учебного пособия):
Согласно варианту задания, составьте алгоритм, решите задачу с помощью макроса и функции.
Варианты заданий
| № | Функция |
| 1 | $Y = frac{|a + x|^3}{ln|x + a|} + 7 sqrt{a + x}$ |
| 2 | $Y = frac{a + b}{x^5 + x^3} — frac{sqrt{a + x}}{2a}$ |
| 3 | $Q = frac{b cdot x^2 — s}{e^{s cdot x} — 1} + e^{sqrt{|x|}}$ |
| 4 | $Y = e^{0.2} + sqrt[3]{|b — x|}$ |
| 5 | $Z = sqrt[4]{|e^x — sin(frac{Pi cdot x}{2})}$ |
| 6 | $F = ln(a +x^5) + sin^2{frac{a}{x}}$ |
| 7 | $X = frac{1}{b cdot x} + frac{a}{b^2} cdot ln|frac{x}{a cdot x + b}|$ |
| 8 | $X = (y + b)^3 + frac{sqrt{y + b}}{y cdot Pi} + e^y$ |
| 9 | $Z = 3^{-x} cdot sqrt{x + sqrt[4]{|x|}}$ |
| 10 |
$Z = frac{4.187 + Pi^2 + sin{frac{x cdot Pi}{7}}}{e^7(frac{3 cdot Pi}{4} + x cdot Pi)}$ |
Лабораторная работа №2 предполагает создание блок-схемы, а затем написание программ (функции и макроса) на языке VBA for Excel. При заказе работы своего варианта вы получите аккуратную ГОСТовую блок-схему и качественно написанные и хорошо прокомментированные программы: функцию и макрос.
Образец выполнения (вариант №1)
Условие задания
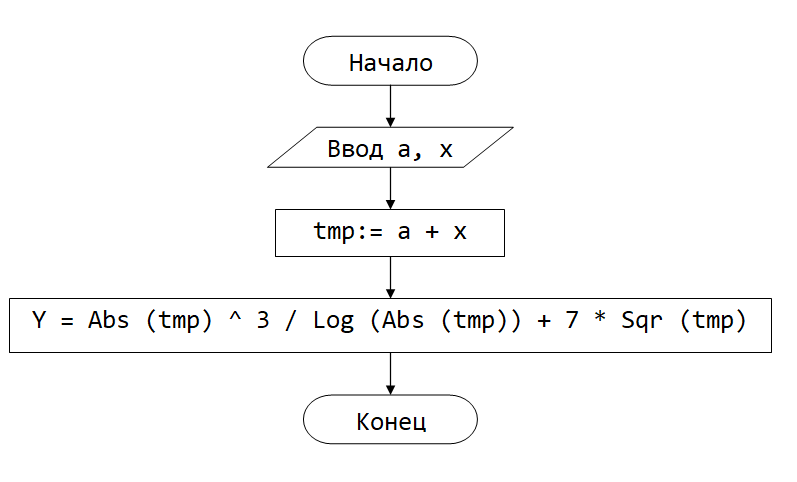
$Y = frac{|a + x|^3}{ln|x + a|} + 7 sqrt{a + x}$
Алгоритм решения задачи
Прежде чем переходить непосредственно к кодированию данной лабораторной работы, нужно провести ее алгоритмизацию. Данный этап является обязательным и ни один профессиональный программист не опускает его в своей работе.
Если внимательно посмотреть на заданную аналитически функцию $Y$, то нетрудно заметить, что есть фрагменты, которые встречаются в записи формулы чаще $1$-го раза.
Как известно из курса школьной математики:
От перемены мест слагаемых сумма не меняется.
Следовательно, суммы $a + x$ и $x + a$ равносильны. То есть сумма $a + x$ встречается целых $3$ раза. Чтобы упростить вычисление заданной функции, введем вспомогательную переменную, отвечающую за эту сумму.
Блок-схема алгоритма
Решение задачи с использованием макроса
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
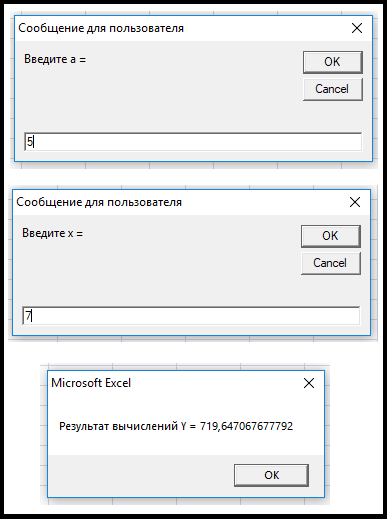
‘ процедура, вычисляющая значение функции Y, при заданных с клавиатуры аргументах (а и х) Sub Formula() ‘ блок объявления переменных Dim a As Double, x As Double ‘ входные значения Dim tmp As Double ‘ вспомогательная переменная для хранения промежуточных результатов Dim Y As Double ‘ результирующая переменная ‘ запрашиваем вводом с клавиатуры входные данные a = InputBox(«Введите a = «, «Сообщение для пользователя») x = InputBox(«Введите х = «, «Сообщение для пользователя») ‘ получаем вспомогательное значение, которое многократно будет использоваться в последующих вычислениях tmp = a + x ‘ вычисляем конечное значение функции Y (получаем результат) Y = Abs(tmp) ^ 3 / Log(Abs(tmp)) + 7 * Sqr(tmp) ‘ выводим результат на экран пользователю через диалоговое окно MsgBox («Результат вычислений Y = «) & Y End Sub |
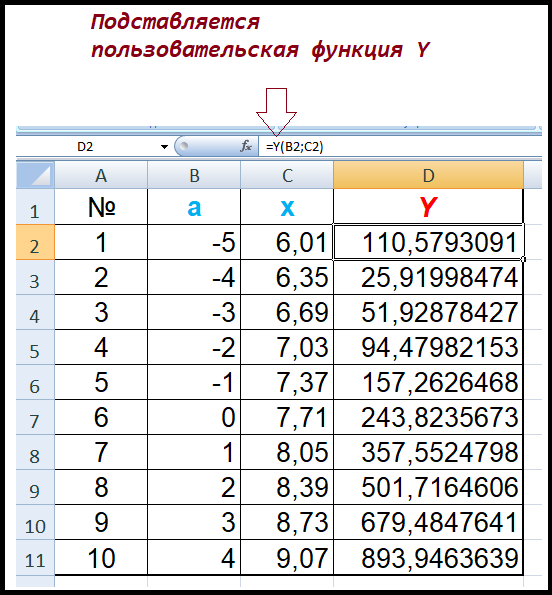
Решение задачи с использованием функции
|
‘ функция, принимающая на вход 2 параметра и вычисляющая на их основе значение заданной функции Y Function Y(a As Double, x As Double) As Double ‘ блок объявления переменных Dim tmp As Double ‘ вспомогательная переменная для хранения промежуточных результатов ‘ получаем вспомогательное значение, которое многократно будет использоваться в последующих вычислениях tmp = a + x ‘ вычисляем конечное значение функции Y (получаем результат) Y = Abs(tmp) ^ 3 / Log(Abs(tmp)) + 7 * Sqr(tmp) End Function |
Результаты работы программы
Результаты, полученные с помощью макроса
Результаты, полученные с помощью пользовательской функции
| ВНИМАНИЕ | Для получения макроса, функции, блок-схемы своего варианта пишите на наш электронный адрес proglabs@mail.ru |
Алгоритмическая структура «ветвление»
на языке Visual Basic
Основные
алгоритмические структуры:
Линейный алгоритм
Алгоритмическая структура
«Ветвление»
Алгоритмическая структура
«Выбор»
Алгоритмическая структура
«Цикл»
«Ветвление» —
алгоритм, в котором та или иная серия команд выполняется в зависимости от истинности условия.
Условие – логическое выражение
(простое или сложное).
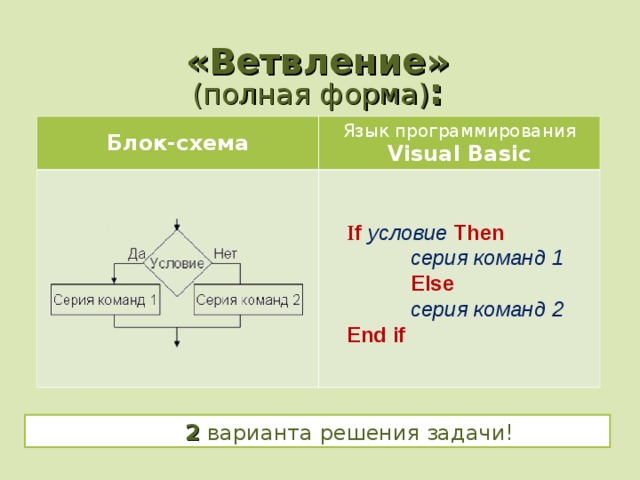
«Ветвление»
(полная форма) :
Блок-схема
Язык программирования
Visual Basic
I f условие Then
серия команд 1
Else
серия команд 2
End if
2 варианта решения задачи!

Задача 1:
Выяснить направление ветвей параболы.
Dim a As Integer
…
a = TextBox1.Text
I f a0 Then
TextBox2.Text = “ветви направлены вверх”
Else
TextBox2.Text = “ветви направлены вниз”
End if
Задача 2:
Компьютер должен перемножить 2 числа. Если полученное произведение превысит 1000, то он должен напечатать: ПРОИЗВЕДЕНИЕ БОЛЬШОЕ , иначе – ПРОИЗВЕДЕНИЕ МАЛЕНЬКОЕ . А после этого печатает само произведение.
«Ветвление»
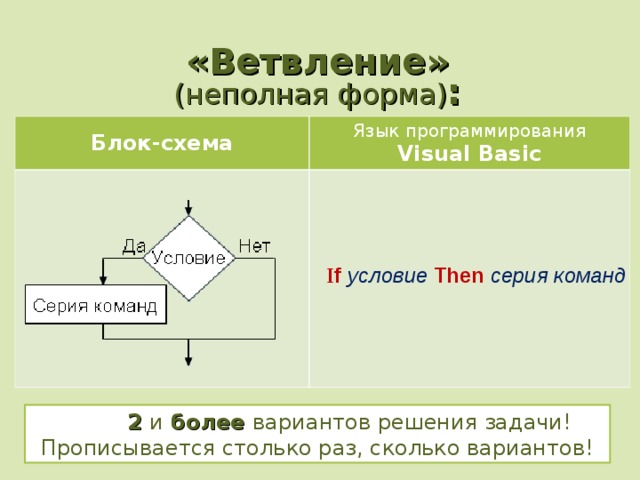
(неполная форма) :
Блок-схема
Язык программирования
Visual Basic
I f условие Then серия команд
2 и более вариантов решения задачи!
Прописывается столько раз, сколько вариантов!

Задача 3:
Выяснить количество корней квадратного уравнения.
Dim a, b, c, d As Integer
…
a = TextBox1.Text
b = TextBox2.Text
c = TextBox3.Text
d = b^2 – 4*a*c
I f d0 Then TextBox4.Text = “2 корня”
I f d=0 Then TextBox4.Text = “1 корень”
I f dThen TextBox4.Text = “нет действительных корней”

Задача 4:
Компьютер должен перемножить 2 числа. Если полученное произведение превысит 1000, то он должен напечатать это произведение.
Dim a, b, p As Integer
…
a = TextBox1.Text
b = TextBox2.Text
p = a * b
I f p 1000 Then TextBox4.Text = p

ФРАГМЕНТ ПРОГРАММЫ
a=10
If a2 Then TextBox1.text=»!!!» Else TextBox1.text=»!»
a=4
If a5 Then a=a+10 Else a=a-1
TextBox1.text=a
s=6
If s-80 Then s=2*s
TextBox1.text=s
s=6
If sThen s=2*s
s=s+1
TextBox1.text=s

Логические операции And, Or, Not
ФРАГМЕНТ
РЕЗУЛЬТАТ
a=8
b=6
If ab And b1 Then k=1 Else k=0
k=1
a=8
b=6
If ab And b7 Then k=1 Else k=0
k=0
If 82 And 35 Then k=1 Else k=0
k=0
If cd And cThen k=1 Else k=0
k=0

ФРАГМЕНТ
РЕЗУЛЬТАТ
a=8
b=6
If ab Or b7 Then k=1 Else k=0
k=1
a=8
b=6
If aOr b7 Then k=1 Else k=0
k=0
If 12 Or 5Then k=1 Else k=0
k=0
Домашнее задание:
- В компьютер вводятся длины трех отрезков. Компьютер должен ответить на вопрос, можно или нельзя из этих отрезков образовать треугольник.
- Найти значение функции:

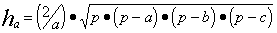
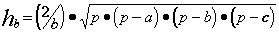
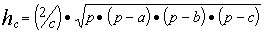

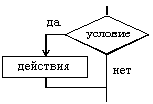 2) если-то-иначе
если условие
то действия 1
иначе действия 2
конец если
2) если-то-иначе
если условие
то действия 1
иначе действия 2
конец если
 3) выбор
выбор
при условие 1: действия 1
при условие 2: действия 2
. . . . . . . . . . . .
при условие N: действия N
конец выбора
3) выбор
выбор
при условие 1: действия 1
при условие 2: действия 2
. . . . . . . . . . . .
при условие N: действия N
конец выбора
 4) выбор-иначе
выбор
при условие 1: действия 1
при условие 2: действия 2
. . . . . . . . . . . .
при условие N: действия N
иначе действия N+1
конец выбора
4) выбор-иначе
выбор
при условие 1: действия 1
при условие 2: действия 2
. . . . . . . . . . . .
при условие N: действия N
иначе действия N+1
конец выбора

 цикл пока условие
тело цикла (последовательность действий)
конец цикла
цикл пока условие
тело цикла (последовательность действий)
конец цикла
 цикл делать
тело цикла (последовательность действий)
пока условие
конец цикла
цикл делать
тело цикла (последовательность действий)
пока условие
конец цикла