План урока:
Модуль числа
Решение уравнений с модулем
Уравнения с параметрами
Модуль числа
Напомним, что такое модуль числа. Так называют значение числа, взятое без учета его знака. То есть модуль чисел 9 и (– 9) одинаков и равен 9. Для обозначения модуля применяют специальные прямоугольные скобки:
|9| = |– 9| = 9
|674| = |– 674| = 674
|2,536| = |– 2,536| = 2,536
Грубо говоря, операция нахождения модуля сводится к отбрасыванию у числа знака «минус», если он у него есть. Вообще, если число х неотрицательно, то его модуль |х| = х. Если же число отрицательно, то его модуль имеет противоположное значение: |х| = х. Математически это можно записать так:
Именно такое определение обычно и применяется в математике.
Модуль играет важную роль в математике. Дело в том, с его помощью удобно записывать расстояние между двумя точками на координатной прямой. Пусть на ней отмечены точки a и b. Расстояние между ними равно |a – b|, причем неважно, какое из этих чисел больше, а какое меньше:
Также модуль возникает при извлечении квадратного корня из четной степени числа:
В частности, если n = 1, получим формулу:
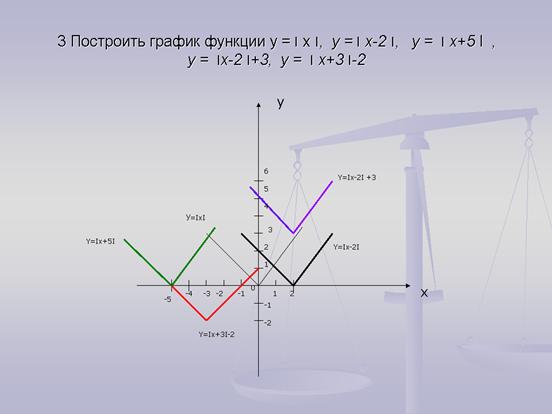
Для того чтобы получить график функции у = |x|, сначала надо построить график функции без учета знака модуля:
Далее следует выполнить преобразование. Те точки графика, которые располагаются выше оси Ох, остаются на своем месте. В данном случае это та часть графика, которая находится в I четверти. Те же точки, которые располагаются ниже оси Ох, должны быть симметрично (относительно этой самой оси Ох) отображены. В результате они окажутся выше оси Ох:
В результате получилась «галочка».
Пример. Постройте график ф-ции у = |х2 – 4х + 3|
Решение. Для построения графика функции, содержащей модуль, сначала надо построить график для «подмодульного» выражения. Поэтому построим график у = х2 – 4х + 3. Это квадратичная ф-ция, ее график – это парабола:
Часть графика, в промежутке от 1 до 3, находится ниже оси Ох. Чтобы построить ф-цию у = |х2 – 4х + 3|, надо перевернуть эту часть графика:
Решение уравнений с модулем
Изучим простейший случай уравнения, содержащего модуль, когда вся его слева записано выр-ние в модульных скобках, а справа находится число. То есть уравнение имеет вид
|у(х)| = b
где b – какое-то число, а у(х) – произвольная ф-ция.
Если b< 0, то ур-ние корней не имеет, ведь модуль не может быть отрицательным.
Пример. Найдите корни ур-ния
|125x10 + 97x4– 12,56х3 + 52х2 + 1001х – 1234| = – 15
Решение: Справа стоит отрицательное число. Однако модуль не может быть меньше нуля. Это значит, что у ур-ния отсутствуют корни.
Ответ: корни отсутствуют.
Если b = 0, то мы получим какое-то произвольное ур-ние у(х) = 0, у которого могут быть корни. Проще говоря, модульные скобки в таком случае можно просто убрать.
Пример. Решите ур-ние
|13х – 52| = 0
Решение.
Ясно, что подмодульное выр-ние равно нулю:
13х – 52 = 0
13х = 52
х = 4
Ответ: 4.
Наиболее интересен случай, когда b> 0, то есть в правой части стоит положительное число. Ясно, что тогда под модулем находится либо само это число b, либо противоположное ему число – b:
|b| = b
|– b| = b
То есть мы получаем два различных ур-ния: у(х) = bи у(х) = – b.
Пример. Решите ур-ние
|х| = 10
Решение. В правой части – положительное число, поэтому либо х = – 10, либо х = 10.
Ответ: 10; (– 10).
Пример. Решите ур-ние
|10х + 5| = 7
Решение. Исходное ур-ние разбивается на два других ур-ния:
10х + 5 = 7 или 10х + 5 = – 7
10х = 2 или 10х = – 12
х = 0,2 или х = – 1,2
Ответ: 0,2; (– 1,2).
Пример. Найдите корни ур-ния
|x2– 2х – 4| = 4
Решение. Снова заменим исходное равенство на два других:
x2– 2х – 4 = 4 или x2– 2х – 4 = – 4
Имеем два квадратных ур-ния. Решим каждое из них:
x2– 2х – 4 = 4
x2– 2х – 8 = 0
D = b2– 4ас = (– 2)2 – 4•1•(– 
х1 = (2 – 6)/2 = – 2
х2 = (2 + 6)/2 = 4
Нашли корни (– 2) и 4. Решаем второе ур-ние:
x2– 2х – 4 = – 4
x2– 2х = 0
х(х – 2) = 0
х = 0 или х – 2 = 0
х = 0 или х = 2
Получили ещё два корня: 0 и 2.
Ответ: – 2, 4, 0, 2
Встречаются случаи, когда в уравнении, содержащем знак модуля, под ним находятся обе части равенства:
|у(х)| = |g(x)|
Здесь возможны два варианта. Либо подмодульные выр-ния равны друг другу (у(х) = g(x)), либо у них противоположные значения (у(х) = – g(x)). То есть снова надо решить два ур-ния.
Пример. Решите ур-ние
|x2 + 2x– 1| = |х + 1|
Решение. Выр-ния справа и слева (без знака модуля) либо равны, либо противоположны. Можно составить два ур-ния:
x2 + 2x– 1 = х + 1 или x2 + 2x– 1 = – (х + 1)
х2 + х – 2 = 0 или х2 + 3х = 0
Решим 1-ое ур-ние:
х2 + х – 2 = 0
D = b2– 4ас = 12 – 4•1•(– 2) = 1 + 8 = 9
х1 = (1 – 3)/2 = – 1
х2 = (1 + 3)/2 = 2
Теперь переходим ко 2-омуур-нию:
х2 + 3х = 0
х(х + 3) = 0
х = 0 или х + 3 = 0
х = 0 или х = – 3
Всего удалось найти 4 корня: (– 1), (– 2), 2 и 0.
Ответ:(– 1), (– 2), 2, 0.
Возможен случай, когда в левой части равенства находится модуль выр-ния, а в правой – обычное выражение, без модуля. Такое ур-ние имеет вид |у(х)| = g(x). Здесь также возможны два варианта: у(х) = g(x) или у(х) = – g(x). Однако следует учитывать ещё один факт. Модуль не может быть отрицательным, а потому должно выполняться нер-во g(x)⩾ 0. Но это неравенство не надо решать. Достаточно просто подставить в него все полученные корни и проверить, справедливо ли нер-во.
Пример. Найдите решение уравнения, содержащего модуль:
|х2 + 3,5х – 20| = 4,5х
Решение. Рассмотрим два отдельных равенства:
х2 + 3,5х – 20 = 4,5х илих2 + 3,5х – 20 = – 4,5х
х2 – х – 20 = 0 или х2 + 8х – 20 = 0
Решим каждое из полученных квадратных ур-ний.
х2 – х – 20 = 0
D = b2– 4ас = 12 – 4•1•(– 20) = 1 + 80 = 81
х1 = (1 – 9)/2 = – 4
х2 = (1 + 9)/2 = 5
х2 + 8х – 20 = 0
D = b2– 4ас = 82 – 4•1•(– 20) = 64 + 80 = 144
х3 = (– 8 – 12)/2 = – 10
х4 = (– 8 + 12)/2 = 2
Итак, получили 4 корня: (– 4), 5, (– 10) и 2. Однако правая часть исходного ур-ния, 4,5x, не может быть отрицательной, ведь модуль числа – это всегда неотрицательная величина:
4,5х ≥ 0
Для х = – 4 и х = – 10 это условие не выполняется, поэтому эти корни должны быть исключены.
Ответ: 2 и 5
Мы рассмотрели три случая, когда ур-ние имеет вид:
- у(х) = b (b– это некоторая константа)
- |у(х)| = |g(x)|
- |у(х)| = g(x)
Однако порою ур-ние не удается свести ни к одному из этих видов. Тогда для решения уравнений и неравенств, содержащих модуль, следует рассматривать их на отдельных интервалах, где подмодульные выр-ния не изменяют свой знак.
Пример. Найдите корни ур-ния
|x + 1| + |x– 4| = 6
Решение. Выр-ния х + 1 и х – 4 меняют знак при переходе через точки (– 1) и 4:
Если отметить обе точки на прямой, то они образуют на ней 3 интервала:
Исследуем ур-ние на каждом из полученных промежутков.
Так как при х <– 1 оба подмодульные выр-ния отрицательны, то можно записать, что
|x + 1| = – (х + 1) = – х – 1
|x– 4| = – (х – 4) = – х + 4
Тогда ур-ние примет вид
|x + 1| + |x– 4| = 6
– х – 1 – х + 4 = 6
–2х = 3
х = – 1,5
Это значение удовлетворяет условию х <– 1, поэтому корень верный.
Далее изучим случай, когда х∊[– 1; 4). Здесь отрицательно только выражение x– 4, поэтому модули заменяются так:
|x + 1| = х + 1
|x– 4| = – (х – 4) = – х + 4
Ур-ние примет вид:
|x + 1| + |x– 4| = 6
x + 1 – x+ 4 = 6
5 = 6
Получили неверное тождество. Получается, что на промежутке [– 1; 4) корней нет.
При х ≥4 выр-ния х – 4 и х + 1 положительны, поэтому
|x + 1| = х + 1
|x– 4| = х – 4
Исходное ур-ние будет выглядеть так
|x + 1| + |x– 4| = 6
х + 1 + х – 4 = 6
2х = 9
х = 4,5
Найденный корень удовлетворяет условию х ≥4, поэтому он также должен быть включен в ответ.
Уравнения с параметрами
Изучим ур-ния:
5х = 10
5х = 15
5х = 20
Для решения каждого из них надо число справа поделить на 5 (множитель перед х). В итоге получаем значения х, равные 2, 3 и 4.
Теперь обозначим число в правой части буквой, например, как v. Тогда все эти ур-ния будут выглядеть одинаково:
5х = v
Решением таких ур-ний будет дробь v/5.
Надо понимать разный смысл, который мы вкладываем при этом в буквы х и v. Через х мы обозначили переменную, то есть ту величину, значение которой необходимо найти. Под буквой v подразумевалась заранее известная величина, то есть константа, которая известна заранее в каждом конкретном ур-нии. Такую величину называют параметром, а ур-ние 5х = v называют уравнением с параметром.
Изучая уравнение с параметром, мы рассматриваем не одно конкретное ур-ние, а сразу целую группу, или семейство ур-ний. Например, все ур-ния первой степени можно описать в виде
ах + b= 0
где х – это переменная величина, а числа а, b– это параметры. Для описания квадратного ур-ния в общем виде необходимы уже три параметра (а, b и с):
ах2 + bx + c = 0
Параметры встречаются не только при описании ур-ний, но и, например, при рассмотрении функций. Так, линейная функция задается формулой у = kx + b. Здесь числа k и b являются параметрами. Так как ур-ние у = kx + b задает на плоскости прямую линию, то величины k и b порою называют параметрами уравнения прямой.
Если при решении обычного ур-ния мы определяем значение его корней в виде конкретных чисел, то при решении ур-ний с параметром находят формулу, позволяющую при заданном значении параметра вычислить значение корня.
Пример. Решите ур-ние
х2 – 2ах = 0
и найдите его корни при значении параметра а, равном 3.
Решение. Вынесем множитель х за скобки:
х2 – 2ах = 0
х(х – 2а) = 0
х = 0 или х – 2а = 0
х = 0 или х = 2а
Получили, что при любом значении параметра а ур-ние имеет два корня. Один из них равен нулю при любом значении а, а второй вычисляется по формуле х = 2а:
при а = 3х = 2•3 = 6
Ответ: есть два корня – 0 и 2а. При а = 2 корни равны 0 и 6.
Пример. Решите ур-ние
р2х – 3рх = р2 – 9
Решение. Слева вынесем за скобки множитель рх, а выр-ние справа преобразуем, используя формулу разности квадратов:
рх(р – 3) = (р – 3)(р + 3)
Возникает желание поделить обе части рав-ва на р(р – 3), чтобы выразить х. Однако сразу так делать нельзя, ведь если величина р(р – 3) равна нулю, то получится деление на ноль.
Поэтому сначала изучим случаи, когда один из множителей слева равен нулю. Если р = 0, то мы получим рав-во
0•х•(0 – 3) = (0 – 3) (3 – 0)
0 = – 9
Это неверное тождество, а потому при р = 0 ур-ние корней не имеет.
Если р – 3 = 0, то есть р = 3, получится следующее
3•х•0 = 0•(3 + 3)
0 = 0
Это равенство верно при любом х. Значит, при р = 3 корнем ур-ния является любое число.
Если же р≠ 0 и р ≠ 3, то произведение р(р – 3) также не равно нулю, а потому обе части равенства можно поделить на р(р – 3). Тогда получим
В этом случае ур-ние имеет единственный корень.
Ответ: при р = 0 корней нет; при р = 3 корнем является любое число; при других рх = (р + 3)/р.
Часто в задаче требуется не выразить корень ур-ния через параметр, а лишь оценить количество корней ур-ния или диапазон их значений.
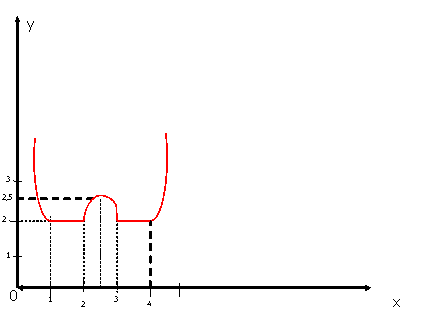
Пример. Сколько корней имеет ур-ние
|х2 – 6х + 5| = b
при различных значениях параметра b.
Решение. Будем решать ур-ние графическим методом. Для этого сначала построим график у = |х2 – 6х + 5|. В модульных скобках находится обычная квадратичная функция, чьи ветви смотрят вверх. Найдем нули функции:
х2 – 6х + 5 = 0
D = b2– 4ас = (– 6)2 – 4•1•5 = 36 + 20 = 16
х1 = (6 – 4)/2 = 1
х2 = (6 + 4)/2 = 5
Итак, нули ф-ции – это точки 1 и 5. Найдем координату х0 вершины параболы по формуле:
х0 = –b/2a = 6/2 = 3
Подставив х0 в квадратичную ф-цию найдем координату у0 вершины параболы:
32 – 6•3 + 5 = 9 – 18 + 5 = – 4
Теперь построим квадратичную ф-цию:
Для построения графика, содержащего модуль функции, надо отобразить точки с отрицательными ординатами (они находятся ниже оси Ох) симметрично относительно оси Ох:
Мы построили график левой части ур-ния. График правой части представляет собой горизонтальную прямую у = b. Можно выделить 5 различных случаев взаимного расположения этих графиков:
При b< 0 прямая пролегает ниже графика. Общих точек у графиков нет, а потому ур-ние корней не имеет.
При b = 0 прямая у = 0 касается графика в 2 точках: (1; 0) и (5; 0). Получаем 2 корня.
Если 0 <b< 4, то прямая пересекает график в 4 точках.
При b = 4 прямая у = 4 касается перевернутой вершины параболы, а также пересекает ветви ещё в 2 точках. Итого 3 корня.
Наконец, при b>4 есть горизонтальная прямая пересекает график лишь в 2 точках, то есть получаем 2 корня.
Ответ: нет корней при b< 0; 2 корня при b = 0 и b> 4; 3 корня при b = 4; 4 корня при 0 <b< 4.
Пример. При каком а ур-ние
х4 – (а + 2)х2 + 3а – 3 = 0
имеет ровно 4 корня?
Решение. Это ур-ние является биквадратным, то есть для его решения нужно произвести замену у = х2:
у2 – (а + 2)у + 3а – 3 = 0 (1)
Для того, чтобы исходное ур-ние имело 4 корня, необходимо, чтобы у квадратного уравнения с параметром(1) было два положительных корня: у1 и у2. Тогда, проводя обратную замену х2 = у1 и х2 = у2, мы получим два разных квадратных ур-ния, корни которых будут равны
Если же хоть один из двух корней, например, у1, окажется равным нулю, то величины
Совпадут (они обе будут равны нулю), и останется лишь 3 корня. Если же у1 будет отрицательным числом, то ур-ние
х2 = у1
вовсе не будет иметь решений, и тогда останется не более 2 корней.
Итак, решим ур-ние (1):
у2 – (а + 2)у + 3а – 3 = 0
D = b2– 4ас = (– (а + 2))2 – 4•1•(3а – 3) = (а + 2)2 – 12 а + 12 =
= а2 + 4а + 4 – 12а + 12 = а2 – 8а + 16 = а2 – 2•4•а + 42 = (а – 4)2
Чтобы у ур-ния (1) было два различных корня, дискриминант должен быть положительным. Величина (а – 4)2 положительна при всех значениях а, кроме а = 4, которое обращает дискриминант в ноль. Значит, а ≠ 4.
Извлечем корень из дискриминанта:
Корни ур-ния (1) можно вычислить по формулам:
И у1, и у2 должны быть положительными величинами, однако у1 меньше, чем у2 (ведь для его вычисления дискриминант брали со знаком «минус», а не «плюс»). Поэтому достаточно записать нер-во:
Получили неравенство, содержащее модуль. Для избавления от модульных скобок в нер-ве рассмотрим 2 случая. Если а – 4>0, то есть а > 4, выполняется равенство
|а – 4| = а – 4
Тогда имеем
а + 2 – (а – 4) > 0
6> 0
Это нер-во выполняется при любом допустимом значении а, поэтому при а >4 исходное ур-ние имеет 4 корня.
Если а < 4, то справедливо соотношение
|а – 4| = – (а – 4)
Тогда получится следующее:
а + 2 – |а – 4|> 0
а + 2 – (– (а – 4)) > 0
а + 2 + а – 4 > 0
2а > 2
а > 1
Итак, при условии, что а< 4, должно выполняться нер-во а > 1. Это значит, что а∊(1; 4). С учетом первого случая, при котором было получено решение
а > 4
можно записать окончательный ответ: а∊(1; 4)∪(4; + ∞).
Ответ: а∊(1; 4)∪(4; + ∞).
Пример. При каких параметрах а у ур-ния
х2 – 2(а + 1)х + а2 + 2а – 3 = 0
существует два корня, которые принадлежат интервалу (– 5; 5)?
Решение. Данное ур-ние является квадратным. Найдем его дискриминант:
D = b2– 4ас = (– 2(а + 1))2 – 4•1•( а2 + 2а – 3) = 4(а2 + 2а + 1) – 4(а2 + 2а – 3) =
= 4(а2 + 2а + 1 – а2– 2а + 3) = 4•4 = 16
Получаем, что при любом а дискриминант положителен, а потому уур-ния 2 корня. Вычислить их можно по формулам
Для того, чтобы оба решения уравнения с параметром принадлежали интервалу (– 5; 5), нужно, чтобы меньший из них (это х1) был больше – 5, больший (это х2) – меньше – 5:
Значит, должны выполняться два нер-ва
х1>– 5и х2<5
а – 1 >– 5 и а + 3 < 5
а >– 4 и а < 2
Эти два нер-ва выполняются, если а∊(– 4; 2)
Ответ: (– 4; 2)
Цель урока. Решение уравнений с
параметрами и модулями, применяя свойства
функций в неожиданных ситуациях и освоение
геометрических приемов решения задач.
Нестандарные уравнения.
Задачи:
- Образовательные: научить решать некоторые
виды уравнений уравнений модулями и
параметрами; - Развивающие: развивать культуру мысли,
культуру речи и умение работать с тетрадью и
доской. - Воспитательные: воспитывать
самостоятельность и умение преодолевать
трудности.
Оборудование: наглядный материал для
устного счёта и объяснения новой темы.
Интерактивная доска, мультимедийное
оборудование урока.
Структура урока:
- Повторение изученного материала (устный счёт).
- Изучение нового материала.
- Закрепление изученного материала.
- Итог урока.
- Домашнее задание.
ХОД УРОКА
1. Повторение важнейшего
теоретического материала по темам:
«Уравнения, содержащие модуль», «Решение
уравнений с параметрами»
1) «Уравнения, содержащие модуль»
Абсолютной величиной или модулем числа a
называется число a, если a > 0, число – a,
если a < 0, нуль, если a = 0. Или
| | a | ={ | a, если a > 0 |
| 0, если a = 0 | |
| – a, если a < 0 |
Из определения следует, что | a | > 0
и | a | > a для всех a € R .
Неравенство | x | < a, (если a
> 0) равносильно двойному неравенству – a <
х < a.
Неравенство | x | < a, (если a < 0)
не имеет смысла, так как | х | >0.
Неравенство | x | > a, (если a > 0)
равносильно двум неравенствам
Неравенство | x | > a, (если a < 0)
справедливо для любого х € R.
2) «Решение уравнений с параметрами»
Решить уравнение с параметрами – значит
указать, при каких значениях параметров
существуют решения и каковы они.
а) определить множество допустимых значений
неизвестного и параметров;
б) для каждой допустимой системы значений
параметров найти соответствующие множества
решений уравнения.
2. Устные упражнения
1. Решить уравнение | x – 2 | = 5; Ответ:
7; – 3
| x – 2 | = – 5; Ответ: решения нет
| x – 2 | = х + 5; Ответ: решения нет; 1,5
| x – 2 | = | x + 5 |; Ответ: решения
нет; – 1,5; решения нет; – 1,5;
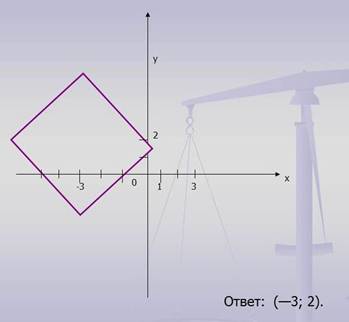
2. Решить уравнение: | x + 3 | + | y
– 2 | = 4;
Расcмотрим четыре случая
1.
| { | x + 3 > 0 | { | x > – 3 |
| y – 2 > 0 | y > 2 | ||
| x + 3 + y – 2 = 4 | y = – x + 3 |
2.
| { | x + 3 > 0 | { | x > – 3 |
| y – 2 < 0 | y < 2 | ||
| x + 3 – y + 2 = 4 | y = x + 1 |
3.
| { | x + 3 < 0 | { | x < – 3 |
| y + 2 > 0 | y > – 2 | ||
| – x – 3 – y – 2 = 4 | y = x + 9 |
4.
| { | x + 3 < 0 | { | x < – 3 |
| y + 2 < 0 | y < – 2 | ||
| – x – 3 – y – 2 = 4 | y = – x – 9 |
В результате мы получаем квадрат, центр
которого (–3; 2), а длина диагонали равна 8, причем
диагонали параллельны осям координат.
Из наглядных соображений можно сделать вывод:
что уравнение вида | х + a | + | у + b
| = с; задает на плоскости квадрат с
центром в точке (– а; – b), диагоналями
параллельными осям OX и ОУ, и длина каждой
диагонали равна 2с. Ответ: (– 3; 2).
2. Решить уравнение aх = 1
Ответ: если a = 0, то нет решения; если a =
0, то х = 1/ a
3. Решить уравнение (а2 – 1) х = а
+ 1.
Решение.
Нетрудно сообразить, что при решении этого
уравнения достаточно рассмотреть такие случаи:
1) а = 1; тогда уравнение принимает вид ОX = 2 и
не имеет решения
2) а = – 1; получаем ОX = О , и очевидно х –
любое.
1
3) если а = + 1, то х = –––
а
– 1
Ответ:
если а = – 1, то х – любое;
если а = 1, то нет решения;
1
если а = + 1 , то х = –––
а
– 1
3. Решения примеров (из вариантов С)
1. При каком значении параметра р уравнение | х2
– 5х + 6 | + | х2 – 5х + 4 | = р
имеет четыре корня.
Решение.
Рассмотрим функцию у = | х2 – 5х + 6
| + | х2 – 5х + 4 |
Так как х2 – 5х + 6 = (х – 2)(х
– 3) и х2 – 5х + 4 = (х – 1)(х
– 4), то y = | (х – 2)(х – 3) | + | (х –
1)(х – 4) |, корни квадратных трехчленов
отметим на числовой прямой
1
2 3
4
х
Числовая прямая при этом разбивает на 5
промежутков
1.
| { | x < 1 | { | x < 1 |
| y = x2 – 5x + 6 + x2 – 5x + 4 |
y = 2x2 – 10x + 10 |
2.
| { | 1 < x < 2 | { | 1 < x < 2 |
| y = x2 – 5x + 6 – x2 + 5x – 4 |
y = 2 |
3.
| { | 2 < x < 3 | { | 2 < x <3 |
| y = – 2x2 + 10x – 10 | y = – x2 + 5x – 6 – x2 + 5x – 4 |
4.
| { | 3 < x < 4 | { | 3 < x < 4 |
| y = 2 | y = x2 – 5x + 6 – x2 + 5x – 4 |
5.
| { | x > 4 | { | x > 4 |
| y = 2x2 – 10x + 10 | y= x2 – 5x + 6 + x2 –5x + 4 |
Для случая 3) х0 = – b | 2a = 2, y0
= 25 : 2 + 25 – 10 = 2,5
Итак, (2,5; 2,5) – координаты вершины параболы y
= – 2x2 + 10x – 10.
Построим график функции, заданной равенством
Как видно из рисунка, исходное уравнение имеет
четыре корня, если 2 < а < 2,5
Ответ: при 2 < а < 2,5
4. Самостоятельная работа по уровням
1 уровень
1. Решить уравнение х2 – | x | = 6
2. При каких целых значениях а имеет единственное
решение уравнение ах2 – (а + 1) + а2
+ а = 0?
2 уровень
1. Решить уравнение: | x – 5 | – | 2x + 3 | = 10
2. Найти все значениях параметра а, при
которых уравнение (а –12) х2 + 2 =
2(12 – а) имеет два различных корня?
3 уровень
1. Решить уравнение | x – 5 | – | 2x + 3| = 10
2. Найти все значениях параметра а, при
которых уравнение (а – 12) х2 + 2 = 2(12
– а) имеет два различных корня?
5. Итог урока
1. Определение модуля.
2. Что значит решить уравнение с параметром?
6. Задание на дом. C5 варианта №11 Ф.Ф.
Лысенко. Математика, 2012
Описание презентации по отдельным слайдам:
-
1 слайд
Решение параметрических уравнений и неравенств с модулями
(схема) -
2 слайд
Способы решения
По определению
Исходя из геометрического смысла
По общей схеме
Использование специальных соотношений и свойств модуля -
-
4 слайд
Исходя из геометрического смысла
– расстояние на числовой прямой от точки 0 до точки -
5 слайд
Использование геометрического смысла модуля (при )
1.
2.
3.
4. -
6 слайд
По общей схеме
Найти ОДЗ
Найти нули всех подмодульных функций
Отметить нули на ОДЗ и разбить ОДЗ на интервалы
Найти решение в каждом интервале ( и проверить, входит ли решение в этот интервал) -
7 слайд
Использование специальных соотношений и свойств модуля
2.
3.
4.
5.
1. -
8 слайд
6.
7.
8.
9.
1 свойство:2 свойство:
3 свойство
4 свойство:5 свойство:
-
9 слайд
6 свойство:
7 свойство:
8 свойство:
9 свойство: -
10 слайд
Графические приемы решения задач с параметрами
Применение параллельного переноса
Применение поворота
Применение гомотетии и сжатия к прямой
Параметр как равноправная переменная на плоскости -
11 слайд
Применение параллельного переноса
1. Сколько корней имеет уравнение, в зависимости от значений параметра
-
12 слайд
Построим в одной системе координат
графики функций
и . -
-
14 слайд
Ответ: при корней нет;
при или два корня;
при четыре корня;
при три корня.
-
15 слайд
2. Сколько корней имеет уравнение
, в зависимости от значений параметра ?
-
16 слайд
Построим в одной системе координат
графики функций и .
-
-
-
19 слайд
Ответ: при или корней нет;
при два корня;
при три корня;
при четыре корня.
-
20 слайд
3. При каких значениях параметра уравнение
имеет ровно три решения?
-
21 слайд
Ответ: при
или
. -
-
-
24 слайд
Ответ: при нет решений;
при ;
при .
-
25 слайд
5. При каких значениях параметра
неравенство имеет хотя бы одно
отрицательное решение?
-
-
27 слайд
6. При каких значениях параметра
уравнение
имеет единственное решение?
-
-
29 слайд
Применение поворота
1. При каких значениях параметра уравнение
имеет ровно три решения? -
-
-
-
-
34 слайд
3. Сколько корней имеет уравнение
в зависимости от значений параметра ?
-
-
36 слайд
Ответ: при один корень;
при два корня;
при три корня;
при четыре корня;
при два корня;
при корней нет;
при один корень.
-
37 слайд
Применение гомотетии и сжатия к прямой
Сколько решений имеет системауравнений ?
-
-
39 слайд
Ответ: при
решений нет; при
четыре решения; при
восемь решений; при
четыре решения; при
решений нет. -
40 слайд
2. Сколько решений имеет уравнение
-
41 слайд
Построим в одной системе координат графики
функций
и . Вторая функция задает на
плоскости семейство «уголков» с вершиной в точке (2;0).
-
-
43 слайд
Ответ: при
нет решений; при
один корень; при
два корня; при
три корня; при
четыре корня. -
44 слайд
Параметр как равноправная переменная на плоскости
При каких значениях параметра
уравнение
имеет ровно три решения? -
45 слайд
Данное уравнение равносильно совокупности уравнений
-
-
47 слайд
2. При каких значениях параметра
уравнение
имеет ровно два решения?
-
48 слайд
Данное уравнение равносильно совокупности
-
-
-
51 слайд
Ответ: при
нет решений; при; при
-
52 слайд
4. При каких значениях параметра
уравнение
имеет ровно три решения?
-
53 слайд
Выражая через получаем
-
-
55 слайд
5. При каких значениях параметра неравенство
имеет хотя бы одно отрицательное решение? -
56 слайд
Данное неравенство равносильно совокупности
-
-
58 слайд
5. При каких значениях параметра
уравнение
имеет единственное решение?
-
-
60 слайд
6. При каких значениях параметра
уравнение
имеет ровно три решения?
-
-
Автор материала — Анна Малкова
Какими были задачи с параметрами на ЕГЭ-2022? На этой странице — обзор всех типов задач №17, предложенных на ЕГЭ по математике в этом году, с полным решением и оформлением.
Напомним, что «параметры» — одна из дорогостоящих задач ЕГЭ. Она оценивается в 4 первичных балла.
Основной темой задач с параметрами на ЕГЭ этого года были модули.
Если вы не помните, что такое модуль числа, — вам сюда.
Способы решения — разные. В одних задачах удобнее графический способ, в других — аналитический.
Мы начнем с тех задач, которые решаются графическим способом. В первых трех, которые мы здесь разбираем, нам встретится уравнение окружности.
Почитать о нем подробно можно здесь.
1. При каких значениях параметра уравнение
имеет ровно 4 решения?
Решение:
Вспомним, как решать уравнения вида
Поэтому исходное уравнение равносильно системе:
Получим:
Изобразим решения системы в координатах
Уравнение задает окружность
с центром
и радиусом 5; уравнение
задает окружность
с центром
и радиусом
; при этом должно выполняться условие
Заметим, что обе окружности проходят через точки и
Найдем, при каких значениях параметра исходное уравнение имеет ровно 4 решения.
При прямая
проходит через точку
общую для двух окружностей; уравнение имеет ровно 3 решения.
Если прямая проходит через точку
(нижнюю точку окружности
), уравнение также имеет 3 решения.
При этом поскольку разность ординат точек Q и A равна
то есть радиусу окружности
При уравнение имеет 4 решения.
Если решений меньше 4.
Если уравнение имеет ровно 3 решения, т.к. точка O(0; 0) общая для обеих окружностей.
Если прямая проходит через B — верхнюю точку окружности
уравнение имеет ровно 3 решения.
В этом случае
При уравнение имеет ровно 4 решения.
Если решений меньше, чем 4.
Объединив случаи, получим ответ.
Ответ:
2. При каких значениях параметра уравнение
имеет ровно 2 решения?
Решение:
Раскроем модуль по определению.
Уравнение (1) задает окружность с центром в точке Р (4; 3) и радиусом 5,
уравнение (2) задает окружность с центром в точке Q(-3; 4) и радиусом 5.
Изобразим график совокупности двух систем в системе координат (x;a).
При получаем часть окружности (1), лежащую ниже прямой a = 7x;
при получаем часть окружности (2), лежащую выше прямой a = 7x.
Исходное уравнение имеет ровно два различных решения, если прямая пересекает график совокупности двух систем ровно два раза.
Прямая проходящая через точку С, пересекает график совокупности двух систем один раз.
Найдем координаты С — самой нижней точки и Е — самой верхней точки правой окружности.
Для этих точек x = 4. Найдем координату a:
или
Координаты точек С (4; и Е (4; 8).
Найдем координаты D — самой нижней точки и F — самой верхней точки левой окружности
Для этих точек x = — 3, найдем координату a.
или
Координаты точек: D (3;
1), F(
3; 9).
Точки А и В, в которых пересекаются две окружности, лежат на прямой
a = 7x (так как при a = 7x выражение под модулем равно нулю).
Подставив a = 7x в уравнение окружности (1) получим:
x = 0 или x = 1.
Получили точки В (0; 0) и А (1; 7).
Прямая пересекает график совокупности двух систем ровно два раза в следующих случаях:
1) если прямая проходит выше точки С, но ниже точки D:
2) если прямая проходит выше точки В, но ниже точки А:
3) если прямая проходит выше точки Е, но ниже точки F:
Если или
то решений нет.
Если или a = 9, уравнение имеет ровно одно решение.
Если или a = 8, ровно три решения.
Если или
ровно четыре решения. Эти случаи нам не подходят.
Ответ: a
3. При каких значениях параметра уравнение
имеет ровно 2 корня?
Решение:
Раскрыв модуль, получим:
Решим систему графически в координатах
Прямая — это биссектриса первого и третьего координатных углов.
Неравенство задает полуплоскость, расположенную ниже прямой
Уравнение задает окружность
1 с центром в точке
и радиусом
Уравнение задает окружность
2 с центром в точке
и радиусом
Заметим, что обе окружности проходят через точки О(0; 0) и М(1; 1). В этом легко убедиться, подставив координаты этих точек в уравнения окружностей.
Исходное уравнение имеет ровно 2 корня, если прямая пересекает совокупность двух окружностей ровно в двух точках, лежащих не выше прямой a = x.
Это происходит в следующих случаях:
1) Прямая проходит выше точки А и ниже точки В на рисунке, где А — нижняя точка окружности
2, В — нижняя точка окружности
1.
2) Прямая проходит выше точки С и ниже точки D на рисунке, где D — верхняя точка окружности
2, С — верхняя точка окружности
1.
3) Прямая проходит выше точки О(0; 0) и ниже точки М(1;1).
Найдем координаты точек А, В, С, D.
Получим, что
Ответ:
Заметим, что в каждом из уравнений присутствовало выражение — как в уравнении окружности. Именно поэтому становилось понятно, что их можно решить графически в координатах x; a.
Теперь — следующий тип задач. Здесь окружностей уже не будет. Зато будет разложение на множители.
4. При каких значениях параметра уравнение
имеет ровно 4 решения?
Решение:
Раскроем модуль. Уравнение равносильно совокупности двух систем:
Упростим по очереди каждую из них.
1) Случай
Найдем дискриминант и корни этого квадратного уравнения.
2) Случай
В этом случае также найдем дискриминант и корни квадратного уравнения.
Получим:
или
.
Решим совокупность двух систем графически в координатах
Если уравнение имеет меньше 4 решений.
Если также меньше 4 решений.
Если прямая проходит через точку A или точку B, уравнение имеет ровно 3 решения.
В точке A пересекаются прямые и
, значит, для этой точки
В точке B пересекаются прямые и
, то для точки B:
.
Уравнение имеет ровно 4 решения, если или
или
.
Ответ:
Следующие две задачи мы решим (для разнообразия) аналитическим способом.
5. При каких значениях параметра уравнение
имеет меньше 4 решений?
Решение:
Уравнение равносильно совокупности:
Рассмотрим каждый случай отдельно
1)
2)
Каждое из уравнений — квадратное и не может иметь больше 2 корней.
Если уравнение (1) имеет 2 неотрицательных корня, а уравнение (2) имеет 2 отрицательных корня, исходное уравнение имеет ровно 4 решения. Найдем, при каких значениях это происходит, а затем исключим эти значения. Получим случай, когда исходное уравнение имеет менее 4 корней.
Исходное уравнение имеет ровно 4 решения, если уравнение имеет два неотрицательных корня, а уравнение
имеет два отрицательных корня.
1 уравнение:
По теореме Виета,
для уравнения

При этом
Оценим и
Сравним т.к.
также
Получим:
2 уравнение:
При этом т.е.
— верно при всех a.
Получим:
Исходное уравнение имеет ровно 4 решения, если выполняется система условий:
При всех остальных значениях a — меньше четырёх решений. Значит, подходят значения
Ответ:
6. Найдите все положительные значения a, при каждом из которых уравнение
имеет ровно 4 корня.
Решение:
Раскроем модуль по определению.
Мы получили совокупность двух систем. Чтобы исходное уравнение имело ровно 4 корня, нужно, чтобы каждая система имела ровно два решения. Решим каждую из систем отдельно.
1) Первая система:
Чтобы квадратное уравнение имело два неотрицательных корня, необходимо и достаточно выполнения условий:
Другой способ: можно рассмотреть квадратичную функцию
и воспользоваться условиями:
Найдем дискриминант соответствующего квадратного уравнения.
при этом
Получим:
Корни уравнения
Отсюда
2) Вторая система:
Чтобы система имела ровно 2 решения, для квадратичной функции
необходимо и достаточно выполнения условий:
— верно для всех
Решение второй системы:
Исходное уравнение имеет ровно 4 различных решения, если
Ответ:
Как всему этому научиться? Если вы решили освоить тему «Параметры» — не нужно начинать со сложных задач. Вначале — подготовительная работа. Элементарные функции и их графики, базовые элементы для решения задач с параметрами. Кроме того, надо отлично знать методы алгебры: разложение выражений на множители, выделение полных квадратов, решение уравнений и неравенств всех типов и многое другое.
Изучить все это можно на Онлайн-курсе подготовки к ЕГЭ по математике. На нем мы решаем и такие задачи, и более сложные. Изучаем не менее 11 методов решения задач с параметрами. Выпускники Онлайн-курса отлично справились с «параметрами» на ЕГЭ-2022.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задачи с параметрами на ЕГЭ-2022: модули, окружности, квадратные уравнения» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Пора начать разбираться с один и самых сложных заданий на ЕГЭ – с параметрами. Этот номер может принести целых 4 балла.
Итак, параметр – это буква (обычно в заданиях используют букву а), вместо которой можно подставить число.
Решить задачу с параметром – значит найти такое значение параметра а, при котором будет выполняться условие задачи. Стоит отметить, что существует огромное количество различных вариантов формулировки задачи. Самым популярным является: «Найти все значения параметра а, при котором уравнение такое-то имеет столько-то корней».
Что нужно знать, чтобы научиться решать параметры?
Таким вопросом задаются многие школьники. Ответ прост: буквально всё. Параметры – самая обширная тема ЕГЭ, тут может быть и тригонометрия, и функции (здесь надо уметь исследовать функцию при помощи производной), и степени, и логарифмы, и дроби и всё-всё-всё остальное, а возможно и все темы сразу. Причём не только в уравнениях, но и в неравенствах.
Так что прежде чем браться за параметры, убедись, что ты отлично решаешь обычные уравнения, щёлкаешь неравенства, а первая часть занимает у тебя не более 15-ти минут.
Краткий алгоритм решения параметров, где дробь равна нулю:
1) необходимо перейти к системе, состоящей из двух условий: знаменатель не равен 0, а числитель равен 0.
2) далее нужно дать условие, чтобы уравнение (числитель) имело два корня, следовательно его дискриминант больше 0.
3) выписать дискриминант, обозначить, что он больше 0 и решить неравенство.
4) выразить из неравенства (которое вышло из знаменателя) а и подставить в уравнение (числитель).
5) дать условие, что при подстановке а в уравнение не должно получаться верное равенство.
6) выписать промежуток из пункта 3 и выколоть точки, которые получились в пункте 5. Это и будет ответ.
Параметры с модулем
Для начала стоит вспомнить, что же такое модуль и как его раскрыть.
Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:
|a| > 0
Модуль положительного числа равен самому числу.
|a| = a, если a > 0
Модуль отрицательного числа равен противоположному числу.
|−a| = a
Модуль нуля равен нулю.
|0| = 0, если a = 0
Противоположные числа имеют равные модули.
|−a| = |a| = a
Когда писать систему, а когда совокупность?
Многие ученики, решая параметры (и не только их) задаются вопросом: тут ставить систему или совокупность?
В двух словах это можно прокомментировать так:
Если надо пересечь решения, то будет система, а если объединить – совокупность. Или, сформулировав по-другому, скажем: система – это когда мы говорим «выполняется и одно условие, и другое», а совокупность – «и то, и другое».
Допустим, мы решаем квадратное уравнение, в котором дискриминант больше нуля. Следовательно оно будет иметь два корня. Но ведь х не может быть двумя числами одновременно, а значит мы говорим, что х – это такое-то число или другое число.
(по оформлению: такое-то число и другое число сделать более бледным, серым)
В этом случае мы используем совокупность.
Заметим, что когда мы решаем квадратное уравнение по теореме Виета (а кто-то вообще использует теорему Виета вместо дискриминанта?), то условие о сумме и произведении мы записываем в системе, ведь они должны выполняться одновременно:
x2+px+q=0
{ x1+x2=-p
x1*x2=q
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!