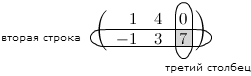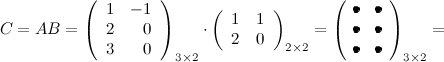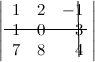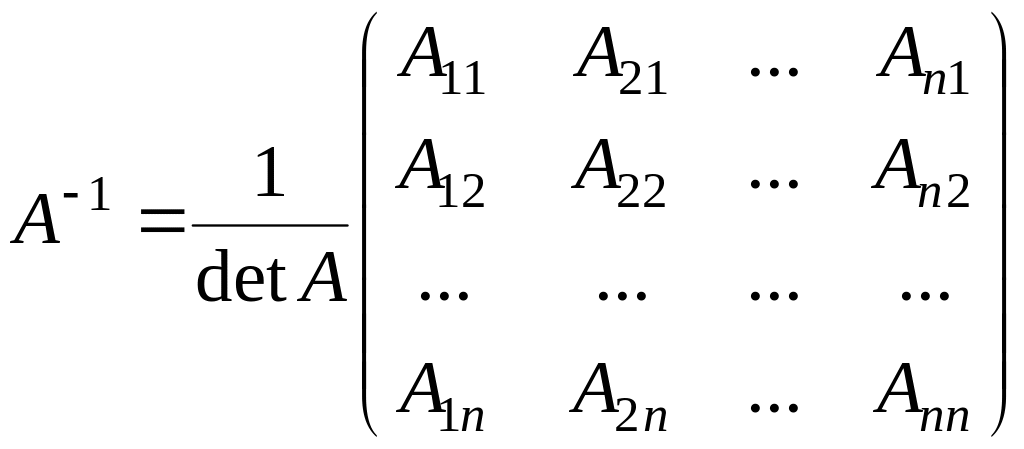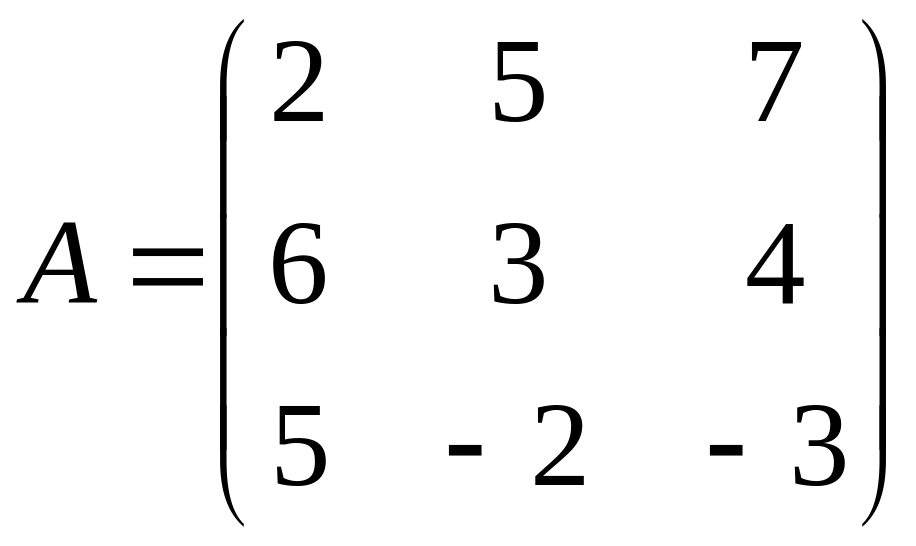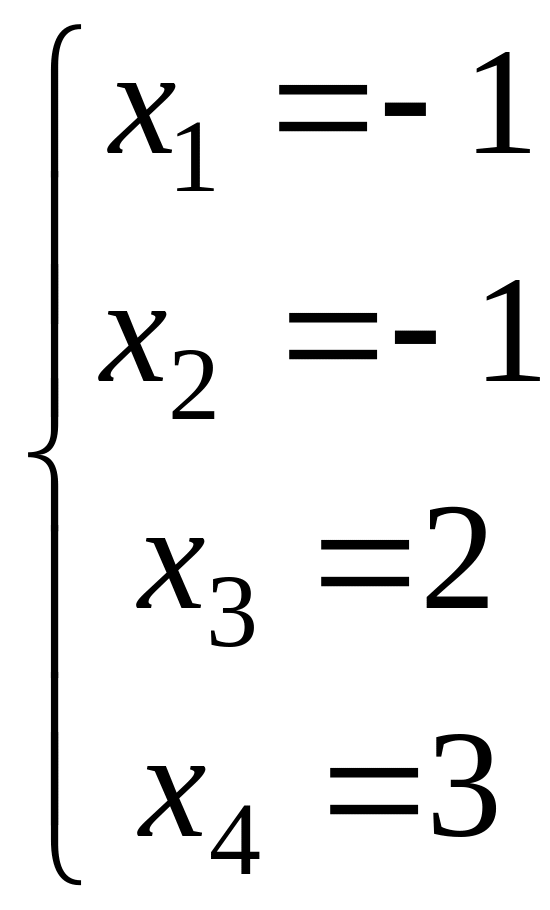Возведение матрицы в степень. Вычисление результатов выражений с матрицами.
Здесь мы продолжим начатую в первой части тему операций над матрицами и разберём пару примеров, в которых потребуется применять несколько операций сразу.
Возведение матрицы в степень.
Пусть k – целое неотрицательное число. Для любой квадратной матрицы $A_{ntimes n}$ имеем:
$$
A^k=underbrace{Acdot Acdot ldots cdot A}_{k ; раз}
$$
При этом полагаем, что $A^0=E$, где $E$ – единичная матрица соответствующего порядка.
Пример №4
Задана матрица $
A=left(begin{array} {cc} 1 & 2 \ -1 & -3 end{array} right)$. Найти матрицы $A^2$ и $A^6$.
Решение
Согласно определению $A^2=Acdot A$, т.е. для нахождения $A^2$ нам просто нужно умножить матрицу $A$ саму на себя. Операция умножения матриц рассматривалась в первой части темы, поэтому тут просто запишем процесс решения без подробных пояснений:
$$
A^2=Acdot A=left(begin{array} {cc} 1 & 2 \ -1 & -3 end{array} right)cdot
left(begin{array} {cc} 1 & 2 \ -1 & -3 end{array} right)=
left(begin{array} {cc} 1cdot 1+2cdot (-1) & 1cdot 2+2cdot (-3) \ -1cdot 1+(-3)cdot (-1) & -1cdot 2+(-3)cdot (-3) end{array} right)=
left(begin{array} {cc} -1 & -4 \ 2 & 7 end{array} right).
$$
Чтобы найти матрицу $A^6$ у нас есть два варианта. Вариант первый: банально продолжить домножать $A^2$ на матрицу $A$:
$$
A^6=A^2cdot Acdot Acdot Acdot A.
$$
Однако можно пойти несколько более простым путём, используя свойство ассоциативности умножения матриц. Расставим скобки в выражении для $A^6$:
$$
A^6=A^2cdot Acdot Acdot Acdot A=A^2cdot (Acdot A)cdot (Acdot A)=A^2cdot A^2cdot A^2.
$$
Если при решении первым способом потребовалось бы четыре операции умножения, то для второго способа – лишь две. Поэтому пойдём вторым путём:
$$
A^6=A^2cdot A^2cdot A^2=left(begin{array} {cc} -1 & -4 \ 2 & 7 end{array} right)cdot left(begin{array} {cc} -1 & -4 \ 2 & 7 end{array} right)cdot left(begin{array} {cc} -1 & -4 \ 2 & 7 end{array} right)=\=
left(begin{array} {cc} -1cdot (-1)+(-4)cdot 2 & -1cdot (-4)+(-4)cdot 7 \ 2cdot (-1)+7cdot 2 & 2cdot (-4)+7cdot 7 end{array} right)cdot
left(begin{array} {cc} -1 & -4 \ 2 & 7 end{array} right)=
left(begin{array} {cc} -7 & -24 \ 12 & 41 end{array} right)cdot
left(begin{array} {cc} -1 & -4 \ 2 & 7 end{array} right)=\=
left(begin{array} {cc} -7cdot(-1)+(-24)cdot 2 & -7cdot (-4)+(-24)cdot 7 \ 12cdot (-1)+41cdot 2 & 12cdot (-4)+41cdot 7 end{array} right)=
left(begin{array} {cc} -41 & -140 \ 70 & 239 end{array} right).
$$
Ответ: $A^2=left(begin{array} {cc} -1 & -4 \ 2 & 7 end{array} right)$, $A^6=left(begin{array} {cc} -41 & -140 \ 70 & 239 end{array} right)$.
Пример №5
Заданы матрицы $
A=left(begin{array} {cccc}
1 & 0 & -1 & 2 \
3 & -2 & 5 & 0 \
-1 & 4 & -3 & 6
end{array} right)$,
$
B=left(begin{array} {ccc}
-9 & 1 & 0 \
2 & -1 & 4 \
0 & -2 & 3 \
1 & 5 & 0
end{array} right)$,
$
C=left(begin{array} {ccc}
-5 & -20 & 13 \
10 & 12 & 9 \
3 & -15 & 8
end{array} right)$. Найти матрицу $D=2AB-3C^T+7E$.
Решение
Вычисление матрицы $D$ начнем с нахождения результата произведения $AB$. Матрицы $A$ и $B$ можно перемножать, так как количество столбцов матрицы $A$ равно количеству строк матрицы $B$. Обозначим $F=AB$. При этом матрица $F$ будет иметь три столбца и три строки, т.е. будет квадратной (если этот вывод кажется неочевидным, посмотрите описание умножения матриц в первой части этой темы). Найдем матрицу $F$, вычислив все её элементы:
$$
F=Acdot B=left(begin{array} {cccc}
1 & 0 & -1 & 2 \
3 & -2 & 5 & 0 \
-1 & 4 & -3 & 6
end{array} right)cdot left(begin{array} {ccc}
-9 & 1 & 0 \
2 & -1 & 4 \
0 & -2 & 3 \
1 & 5 & 0
end{array} right)\
begin{aligned}
& f_{11}=1cdot (-9)+0cdot 2+(-1)cdot 0+2cdot 1=-7; \
& f_{12}=1cdot 1+0cdot (-1)+(-1)cdot (-2)+2cdot 5=13; \
& f_{13}=1cdot 0+0cdot 4+(-1)cdot 3+2cdot 0=-3;\ \
& f_{21}=3cdot (-9)+(-2)cdot 2+5cdot 0+0cdot 1=-31;\
& f_{22}=3cdot 1+(-2)cdot (-1)+5cdot (-2)+0cdot 5=-5;\
& f_{23}=3cdot 0+(-2)cdot 4+5cdot 3+0cdot 0=7;\ \
& f_{31}=-1cdot (-9)+4cdot 2+(-3)cdot 0+6cdot 1=23; \
& f_{32}=-1cdot 1+4cdot (-1)+(-3)cdot (-2)+6cdot 5=31;\
& f_{33}=-1cdot 0+4cdot 4+(-3)cdot 3+6cdot 0=7.
end{aligned}
$$
Итак, $F=left(begin{array} {ccc}
-7 & 13 & -3 \
-31 & -5 & 7 \
23 & 31 & 7
end{array} right)$. Пойдём далее. Матрица $C^T$ – транспонированная матрица для матрицы $C$, т.е.
$
C^T=left(begin{array} {ccc}
-5 & 10 & 3 \
-20 & 12 & -15 \
13 & 9 & 8
end{array} right)
$. Что же касаемо матрицы $E$, то это есть единичная матрица. В данном случае порядок этой матрицы равен трём, т.е. $E=left(begin{array} {ccc}
1 & 0 & 0 \
0 & 1 & 0 \
0 & 0 & 1
end{array} right)$.
В принципе, мы и дальше можем идти пошагово, но оставшееся выражение лучше рассматривать целиком, не отвлекаясь на вспомогательные действия. По сути, нам остались лишь операции умножения матриц на число, а также операции сложения и вычитания.
$$
D=2AB-3C^T+7E=2cdot left(begin{array} {ccc}
-7 & 13 & -3 \
-31 & -5 & 7 \
23 & 31 & 7
end{array} right)-3cdot left(begin{array} {ccc}
-5 & 10 & 3 \
-20 & 12 & -15 \
13 & 9 & 8
end{array} right)+7cdot left(begin{array} {ccc}
1 & 0 & 0 \
0 & 1 & 0 \
0 & 0 & 1
end{array} right)
$$
Умножим матрицы в правой части равенства на соответствующие числа (т.е. на 2, 3 и 7):
$$
2cdot left(begin{array} {ccc}
-7 & 13 & -3 \
-31 & -5 & 7 \
23 & 31 & 7
end{array} right)-3cdot left(begin{array} {ccc}
-5 & 10 & 3 \
-20 & 12 & -15 \
13 & 9 & 8
end{array} right)+7cdot left(begin{array} {ccc}
1 & 0 & 0 \
0 & 1 & 0 \
0 & 0 & 1
end{array} right)=\=
left(begin{array} {ccc}
-14 & 26 & -6 \
-62 & -10 & 14 \
46 & 62 & 14
end{array} right)-left(begin{array} {ccc}
-15 & 30 & 9 \
-60 & 36 & -45 \
39 & 27 & 24
end{array} right)+left(begin{array} {ccc}
7 & 0 & 0 \
0 & 7 & 0 \
0 & 0 & 7
end{array} right)
$$
Выполним последние действия: вычитание и сложение:
$$
left(begin{array} {ccc}
-14 & 26 & -6 \
-62 & -10 & 14 \
46 & 62 & 14
end{array} right)-left(begin{array} {ccc}
-15 & 30 & 9 \
-60 & 36 & -45 \
39 & 27 & 24
end{array} right)+left(begin{array} {ccc}
7 & 0 & 0 \
0 & 7 & 0 \
0 & 0 & 7
end{array} right)=\
=left(begin{array} {ccc}
-14-(-15)+7 & 26-30+0 & -6-9+0 \
-62-(-60)+0 & -10-36+7 & 14-(-45)+0 \
46-39+0 & 62-27+0 & 14-24+7
end{array} right)=
left(begin{array} {ccc}
8 & -4 & -15 \
-2 & -39 & 59 \
7 & 35 & -3
end{array} right).
$$
Задача решена, $D=left(begin{array} {ccc}
8 & -4 & -15 \
-2 & -39 & 59 \
7 & 35 & -3
end{array} right)$.
Ответ: $D=left(begin{array} {ccc}
8 & -4 & -15 \
-2 & -39 & 59 \
7 & 35 & -3
end{array} right)$.
Пример №6
Пусть $f(x)=2x^2+3x-9$ и матрица $
A=left(begin{array} {cc}
-3 & 1 \
5 & 0
end{array} right)
$. Найти значение $f(A)$.
Решение
Если $f(x)=2x^2+3x-9$, то под $f(A)$ понимают матрицу:
$$
f(A)=2A^2+3A-9E.
$$
Именно так определяется многочлен от матрицы. Итак, нам нужно подставить матрицу $A$ в выражение для $f(A)$ и получить результат. Так как все действия были подробно разобраны ранее, то тут я просто приведу решение. Если процесс выполнения операции $A^2=Acdot A$ для вас неясен, то советую глянуть описание умножения матриц в первой части этой темы.
$$
f(A)=2A^2+3A-9E=2Acdot A+3A-9E=2 left(begin{array} {cc} -3 & 1 \ 5 & 0 end{array} right)cdot left(begin{array} {cc} -3 & 1 \ 5 & 0 end{array} right)+3 left(begin{array} {cc} -3 & 1 \ 5 & 0 end{array} right)-9left(begin{array} {cc} 1 & 0 \ 0 & 1 end{array} right)=\
=2 left(begin{array} {cc} (-3)cdot(-3)+1cdot 5 & (-3)cdot 1+1cdot 0 \ 5cdot(-3)+0cdot 5 & 5cdot 1+0cdot 0 end{array} right)+3 left(begin{array} {cc} -3 & 1 \ 5 & 0 end{array} right)-9left(begin{array} {cc} 1 & 0 \ 0 & 1 end{array} right)=\
=2 left(begin{array} {cc} 14 & -3 \ -15 & 5 end{array} right)+3 left(begin{array} {cc} -3 & 1 \ 5 & 0 end{array} right)-9left(begin{array} {cc} 1 & 0 \ 0 & 1 end{array} right)
=left(begin{array} {cc} 28 & -6 \ -30 & 10 end{array} right)+left(begin{array} {cc} -9 & 3 \ 15 & 0 end{array} right)-left(begin{array} {cc} 9 & 0 \ 0 & 9 end{array} right)=left(begin{array} {cc} 10 & -3 \ -15 & 1 end{array} right).
$$
Ответ: $f(A)=left(begin{array} {cc} 10 & -3 \ -15 & 1 end{array} right)$.
Функции от матриц
Пусть — числовая квадратная матрица и
— скалярная функция переменной
. В этом разделе понятие функции распространяется на матричные значения аргумента. Если
— многочлен, то задача нахождения многочлена
, получающегося при подстановке матрицы
вместо переменной
, была решена ранее. Требуется определить, что следует понимать под выражением
для достаточно произвольной функции
. Разумеется, что определение функции от матрицы, когда функция является многочленом, должно совпадать с определением многочлена от матрицы.
Функции, определенные на спектре матрицы
Напомним, что спектром квадратной матрицы называется совокупность всех ее собственных значений (корней характеристического многочлена). Все собственные значения являются также корнями минимального многочлена (см. свойство 3 минимального многочлена):
(7.54)
где — корень кратности
,
— корень кратности
и т.д. Степень
минимального многочлена не превосходит порядка
матрицы
.
Говорят, что скалярная функция переменной
определена на спектре матрицы
, если для функции
определены значения
(7.55)
т.е. функция определена в окрестности каждой точки
вместе со своими производными до указанного порядка. Совокупность (7.55) значений функции и ее производных будем обозначать
.
Две функции и
называются равными на спектре матрицы
, если
(7.56)
Эти равенства будем записывать в форме .
Теорема 7.10 (основное свойство многочленов от матриц). Если и
— многочлены, то
(7.57)
т.е. многочлены, равные на спектре матрицы, имеют равные матричные значения, и наоборот, если равны матричные значения многочленов, то равны их значения на спектре матрицы. Другими словами, значения многочлена на спектре матрицы полностью определяют его значение
от матрицы
.
В самом деле, пусть , тогда разность
является аннулирующим многочленом:
. Разделим его на минимальный многочлен
(свойство 1 в разд.7.2.4). Из (7.54) следует, что число
является корнем многочлена
, причем его кратность больше или равна
. Тогда:
что равносильно (7.56). Следовательно, . Достаточность доказана. Для доказательства необходимости нужно все рассуждения провести в обратном порядке, либо вернуться ко второму способу нахождения многочлена от матрицы: в системе (7.46), которая позволяет найти коэффициенты искомого многочлена, левые части уравнений являются значениями многочлена
на спектре матрицы
.
Определение и свойства функций от матриц
Основное свойство (7.57), справедливое для многочленов, переносится на произвольные функции и фактически берется за основу определения функции от матрицы.
Пусть — произвольная функция, определенная на спектре матрицы
. Значение
функции
от матрицы
определяется равенством
(7.58)
где — любой многочлен, принимающий на спектре матрицы
те же значения, что
.
Поскольку функции от матриц определяются через многочлены, то на них переносятся свойства многочленов от матриц.
1. Функции от подобных матриц подобны.
2. Функция от блочно-диагональной матрицы является блочно- диагональной матрицей, т.е. если матрица имеет вид
, где
некоторые квадратные матрицы, то
3. Функция от жордановой клетки
имеет вид
(7.59)
Это верхняя треугольная матрица r-го порядка, на главной диагонали которой стоят значения функции в точке
, над диагональю — значения первой производной в этой же точке и т.д., т.е. коэффициенты формулы Тейлора для функции
.
Способы нахождения функций от матриц
Из определения функции от матрицы следует, что первый и второй способы нахождения многочлена от матрицы, пригодны и для любой функции, определенной на спектре матрицы. Поэтому они могут считаться первым и вторым способами нахождения функции от матрицы. Далее излагается третий (интерполяционный) способ решения этой же задачи.
Пример 7.21. Найти функцию от матрицы
.
Решение. Первый способ. 1. Жорданова форма и преобразующая матрица
были найдены в примере 7.15:
2. Жорданова форма состоит из одной жордановой клетки
2-го порядка, соответствующей собственному значению
. Найдем значение функции
и ее производной
. Запишем функцию от жордановой формы (7.59):
3. Найдем функцию от матрицы
Второй способ. 1. Минимальный многочлен матрицы А найден в примере 7.18: . Степень v минимального многочлена равна 2. Значит, многочлен (7.44) линейный:
.
2. Для двойного корня составляем уравнения (7.46):
3. Решая систему, получаем и
.
4. Находим функцию от матрицы
Полученные разными способами результаты, разумеется, совпадают.
Интерполяционный способ нахождения функции от матрицы
Рассмотрим сначала частный случай, когда все корни минимального многочлена простые: . В этом случае значения функции на спектре матрицы
— это совокупность значений функции
в точках
. Обозначим через
интерполяционный многочлен Лагранжа:
(7.60)
для которого . Тогда
Таким образом, для нахождения функции от матрицы
в случае простых корней минимального многочлена, нужно выполнить следующие действия.
1. Найти минимальный многочлен одним из способов, рассмотренных ранее. Убедиться в том, что все корни
минимального многочлена простые.
2. Вычислить значения функции на спектре матрицы
и составить по формуле (7.60) интерполяционный многочлен Лагранжа
.
3. Найти значение функции от матрицы .
Пример 7.22. Найти функцию от матрицы
.
Решение. Интерполяционный способ (случай простых корней). 1. Минимальный многочлен найден в примере 7.12: . Все его корни
простые.
2. Находим значения функции на спектре матрицы . Составляем по формуле (7.60) интерполяционный многочлен Лагранжа:
3. Находим функцию от матрицы
Рассмотрим общий случай, когда минимальный многочлен (7.54)
имеет кратные корни: — корень кратности от
,
— корень кратности
и т.д. Степень
минимального многочлена не превосходит порядка
матрицы
.
Многочлен степени меньшей, чем
, удовлетворяющий условиям:
называется интерполяционным многочленом Лагранжа-Сильвестра для функции , определенной на спектре матрицы
.
Многочлен Лагранжа-Сильвестра однозначно определяется значениями функции на спектре матрицы и находится по формуле:
(7.61)
где — многочлен, равный отношению минимального многочлена и соответствующего элементарного делителя:
, а выражение в квадратных скобках равно сумме первых от, членов разложения функции
по формуле Тейлора, то есть
Замечания 7.10.
1. Если минимальный многочлен имеет один корень (кратности ):
то многочлен Лагранжа-Сильвестра совпадает с многочленом Тейлора. Действительно, в этом случае
, поэтому формула (7.61) принимает вид
что совпадает с первыми членами ряда Тейлора.
2. Если все корни минимального многочлена простые: , тогда
поэтому формула (7.61) принимает вид (7.60), т.е. многочлен Лагранжа-Сильвестра совпадает с многочленом Лагранжа.
Для нахождения функции от матрицы
при наличии кратных корней минимального многочлена нужно выполнить следующие действия.
1. Найти минимальный многочлен матрицы одним из способов, рассмотренных ранее:
2. Для каждого корня кратности
найти многочлен
и вычислить коэффициенты
разложения функции
в точке
по формуле Тейлора:
3. Составить по формуле (7.61) интерполяционный многочлен Лагранжа-Сильвестра.
4. Найти значение функции от матрицы .
Пример 7.23. Найти функцию от матрицы
.
Решение. Интерполяционный способ (случай кратных корней). 1. Минимальный многочлен найден в примере7.15: . Корень
— двойной, а
— простой, т.е. количество различных корней
, кратности корней
.
2. Для двойного корня находим многочлен
и соответствующие коэффициенты
Для простого корня находим многочлен
и коэффициент
.
3. Составляем по формуле (7.61) интерполяционный многочлен Лагранжа–Сильвестра:
4. Находим функцию от матрицы
Проверим полученный результат, используя первый способ нахождения функции от матрицы.
1. В примере 7.15 были найдены жорданова форма матрицы и преобразующая матрица
2. Жорданова форма состоит из двух жордановых клеток 2-го и 1-го порядков
, соответствующих собственным значениям
и
. Найдем значения функции на спектре матрицы:
и
. Запишем функцию от жордановой формы
Найдем функцию от матрицы
Результаты, полученные разными способами, совпадают.
Свойства функций от матриц
Многие свойства функций скалярного аргумента распространяются на функции от матриц. Рассмотрим некоторые из них.
1. Если функция разлагается в степенной ряд
(7.62)
сходящийся в круге , то для любой матрицы
, собственные значения которой лежат внутри круга сходимости, справедливо разложение
(7.63)
Здесь предел последовательности матриц (частичных сумм ряда) понимается поэлементно, как совокупность пределов элементов матрицы. Напомним, что .
В самом деле, степенной ряд можно почленно дифференцировать любое число раз внутри круга сходимости. Поэтому функция определена на спектре любой матрицы, собственные значения которой лежат внутри круга сходимости.
Из свойства 1 следуют, например, разложения в ряд (7.62) при
справедливые для любой квадратной матрицы .
2. Если функция разлагается в степенной ряд, а собственные значения функциональной матрицы
при всех
лежат внутри круга сходимости этого ряда, то определена сложная функция
, производная которой находится по формуле:
В самом деле, подставим в ряд (7.62) вместо матрицу
Найдем производную этой матричной функции. Учитывая, что многочлены от одной и той же матрицы перестановочны, по правилу 3 дифференцирования произведения матриц получаем
то есть . Поэтому
.
Сравнивая полученный ряд с производной ряда (7.62) при подстановке вместо
матрицы
, приходим к доказываемому равенству.
Пример 7.24. Используя разложение в степенной ряд, найти матричную функцию
где
Решение. Запишем степенной ряд (7.63)
Учитывая разложение , получаем
Результат совпадает с полученным в примере 7.23.
Применение функций от матриц для решения систем дифференциальных уравнений
Рассмотрим систему линейных дифференциальных уравнений с постоянными коэффициентами
(7.64)
где — коэффициенты системы,
— заданные, a
— неизвестные функции аргумента
. При описании непрерывных динамических систем аргумент
обозначает время.
Систему (7.64) можно записать в матричном виде:
(7.65)
где — квадратная матрица n-го порядка,
— столбец заданных функций, a
— столбец неизвестных.
Решением системы (7.65) называют столбец дифференцируемых функций, при подстановке которых в (7.65) получаются верные равенства, тождественно выполняющиеся при
.
Поставим задачу нахождения решения системы (7.65), удовлетворяющего начальным условиям
(7.66)
где — заданный столбец.
Как известно, решение системы (7.65) с начальными условиями (7.66) имеет вид:
(7.67)
В самом деле, найдем производную функции (7.67). Применяя правило Лейбница
и свойство 2 функций от матриц, получаем
т.е. является решением системы (7.65). При
формула (7.67) дает
, где
— нулевая, а
— единичная матрицы. Равенство
следует, например, из разложения в ряд функции
. Следовательно, решение (7.67) удовлетворяет и начальным условиям (7.66).
Поэтому для нахождения решения нужно выполнить следующие действия.
1. Найти выражение для функции одним из способов, рассмотренных ранее.
2. Записать искомое решение по формуле (7.67).
Замечания 7.11.
1. Нахождение функции от функциональной матрицы
облегчается, если учитывать, что собственные значения
матрицы
пропорциональны собственным значениям
матрицы
. Действительно, характеристический многочлен матрицы
имеет вид
Поэтому, если число — корень характеристического многочлена матрицы
, то число
— корень многочлена
, причем той же кратности. Такая же связь между корнями минимальных многочленов
и
: если
— корень минимального многочлена
, то
— корень минимального многочлена
.
2. Решение линейного дифференциального уравнения с постоянными коэффициентами сводится к решению системы вида (7.64), получающейся после замены
.
3. Для нахождения функции можно использовать следующий способ. Найти
линейно независимых решений
однородной системы
и составить из этих столбцов фундаментальную матрицу
системы (7.65). В силу линейной независимости столбцов
определитель фундаментальной матрицы (определитель Вронского) отличен от нуля:
для
. Поэтому определена обратная матрица
. Функция
(называемая матрицей Коши, или переходной матрицей) может быть найдена по формуле
Пример 7.25. Найти решение системы дифференциальных уравнений, удовлетворяющее начальным условиям
, матричным способом:
Решение. 1. Составим матрицу коэффициентов системы:
и функцию
. Найдем выражение для функции
от матрицы
(т.е. функции
), используя второй способ нахождения функции от матрицы. Минимальный многочлен
матрицы
был найден в примере 7.18. Согласно пункту 1 замечаний 7.11, минимальный многочлен матрицы
имеет вид
. Степень
минимального многочлена равна 2. Значит, многочлен (7.44) линейный:
. Для двойного корня
составляем уравнения (7.46) (см. пример 7.21):
Решая систему, получаем и
. Находим функцию
от матрицы
По формуле (7.67) записываем искомое решение
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Содержание:
- Матрицы: основные определения и понятия
- Умножение матрицы на число
- Сложение и вычитание матриц
- Умножение матриц
- Транспонирование матрицы
- Минор и алгебраическое дополнение
- Вычисление определителя
- Нахождение обратной матрицы
- Нахождение ранга матрицы
Матрицы широко применяются в математике для
компактной записи СЛАУ или систем дифференциальных уравнений. Тогда количество
строк матрицы соответствует количеству уравнений системы, а количество столбцов равно количеству неизвестных. Матричный
аппарат позволяет свести решение громоздких СЛАУ к компактным
операциям над матрицами.
На практике, они позволяют не делать лишних операций и сократить время выполнения задач.
Поэтому, будущим специалистам очень важно понять теорию матриц и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по матрицам, прочитать
все определения и свойства. Список тем находится в правом меню.
Примеры по темам:
- Матрицы: основные определения и понятия
- Умножение матрицы на число
- Сложение и вычитание матриц
- Умножение матриц
- Транспонирование матрицы
- Минор и алгебраическое дополнение
- Вычисление определителя
- Нахождение обратной матрицы
- Нахождение ранга матрицы
Матрицы: основные определения и понятия
Теоретический материал по теме — основные определения и понятия матриц.
Пример
Задание. Чему равен элемент $ a_{23} $
матрицы $ A=left( begin{array}{rrr}{1} & {4} & {0} \ {-1} & {3} & {7}end{array}right) $ ?
Решение. Находим элемент, который стоит на пересечении второй строки и третьего столбца:
Таким образом, $a_{23}=7$.
Ответ. $a_{23}=7$
Умножение матрицы на число
Теоретический материал по теме — умножение матрицы на число.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Пусть $A=left( begin{array}{r}{3} \ {-1}end{array}right)$ .
Найти матрицу 2$A$.
Решение. $2 A=2 cdot left( begin{array}{r}{3} \ {-1}end{array}right)=left( begin{array}{c}{2 cdot 3} \ {2 cdot(-1)}end{array}right)=left( begin{array}{r}{6} \ {-2}end{array}right)$
Ответ. $2 A=left( begin{array}{r}{6} \ {-2}end{array}right)$
Сложение и вычитание матриц
Теоретический материал по теме — сложение и вычитание матриц.
Пример
Задание. Найти $A+B$, если
$A=left( begin{array}{rrr}{1} & {-2} & {4} \ {2} & {0} & {-1}end{array}right)$,
$B=left( begin{array}{lll}{5} & {2} & {3} \ {4} & {6} & {2}end{array}right)$
Решение. $C=A+B=left( begin{array}{rrr}{1} & {-2} & {4} \ {2} & {0} & {-1}end{array}right)+left( begin{array}{lll}{5} & {2} & {3} \ {4} & {6} & {2}end{array}right)=$
$=left( begin{array}{rrr}{1+5} & {-2+2} & {4+3} \ {2+4} & {0+6} & {-1+2}end{array}right)=left( begin{array}{lll}{6} & {0} & {7} \ {6} & {6} & {1}end{array}right)$
Ответ. $C=left( begin{array}{lll}{6} & {0} & {7} \ {6} & {6} & {1}end{array}right)$
Пример
Задание. Найти матрицу $C=A-3 B$,
если $A=left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right), B=left( begin{array}{rr}{-1} & {1} \ {1} & {2} \ {0} & {0}end{array}right)$
Решение. $C=A-3 B=left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right)-3 cdot left( begin{array}{rr}{-1} & {1} \ {1} & {2} \ {0} & {0}end{array}right)=$
$left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right)-left( begin{array}{rr}{-3} & {3} \ {3} & {6} \ {0} & {0}end{array}right)=left( begin{array}{cc}{1-(-3)} & {2-3} \ {2-3} & {-1-6} \ {3-0} & {0-0}end{array}right)=left( begin{array}{rr}{4} & {-1} \ {-1} & {-7} \ {3} & {0}end{array}right)$
Ответ. $C=left( begin{array}{rr}{4} & {-1} \ {-1} & {-7} \ {3} & {0}end{array}right)$
Умножение матриц
Теоретический материал по теме — умножение матриц.
Пример
Задание. Вычислить $A B$ и $B A$,
если $A=left( begin{array}{rr}{1} & {-1} \ {2} & {0} \ {3} & {0}end{array}right), B=left( begin{array}{ll}{1} & {1} \ {2} & {0}end{array}right)$
Решение. Так как $A=A_{3 times 2}$ , а
$B=B_{2 times 2}$ , то произведение возможно и результатом операции умножения будет матрица
$C=C_{3 times 2}$ , а это матрица вида $C=left( begin{array}{cc}{c_{11}} & {c_{12}} \ {c_{21}} & {c_{22}} \ {c_{31}} & {c_{32}}end{array}right)$ .
Вычисли элементы матрицы $C$ :
$ c_{11}=a_{11} cdot b_{11}+a_{12} cdot b_{21}=1 cdot 1+(-1) cdot 2=-1 $
$ c_{12}=a_{11} cdot b_{12}+a_{12} cdot b_{22}=1 cdot 1+(-1) cdot 0=1 $
$ c_{21}=a_{21} cdot b_{11}+a_{22} cdot b_{21}=2 cdot 1+0 cdot 2=2 $
$ c_{22}=a_{21} cdot b_{12}+a_{22} cdot b_{22}=2 cdot 1+0 cdot 0=2 $
$ c_{31}=a_{31} cdot b_{11}+a_{32} cdot b_{21}=3 cdot 1+0 cdot 2=3 $
$ c_{31}=a_{31} cdot b_{12}+a_{32} cdot b_{22}=3 cdot 1+0 cdot 0=3 $
Итак, $C=A B=left( begin{array}{rl}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$ .
Выполним произведения в более компактном виде:
$=left( begin{array}{rrr}{1 cdot 1+(-1) cdot 2} & {1 cdot 1+(-1) cdot 0} \ {2 cdot 1+0 cdot 2} & {2 cdot 1+0 cdot 0} \ {3 cdot 1+0 cdot 2} & {3 cdot 1+0 cdot 0}end{array}right)=left( begin{array}{rr}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$
Найдем теперь произведение $D=B A=B_{2 times 2} cdot A_{3 times 2}$. Так как
количество столбцов матрицы $B$ (первый сомножитель) не совпадает с
количеством строк матрицы $A$ (второй сомножитель), то данное произведение
неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ. $A B=left( begin{array}{rr}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$ .
В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы
$B$ не совпадает с
количеством строк матрицы $A$ .
Транспонирование матрицы
Теоретический материал по теме — транспонирование матрицы.
Пример
Задание. Найти матрицу $A^{T}$, если
$A=left( begin{array}{rl}{1} & {0} \ {-2} & {3}end{array}right)$
Решение. $A^{T}=left( begin{array}{rr}{1} & {0} \ {-2} & {3}end{array}right)^{T}=left( begin{array}{rr}{1} & {-2} \ {0} & {3}end{array}right)$
Ответ. $A^{T}=left( begin{array}{rr}{1} & {-2} \ {0} & {3}end{array}right)$
Минор и алгебраическое дополнение
Теоретический материал по теме — минор и алгебраическое дополнение.
Пример
Задание. Найти минор
$M_{23}$ к элементу
$a_{23}$ определителя
$left| begin{array}{rrr}{1} & {2} & {-1} \ {1} & {0} & {3} \ {7} & {8} & {4}end{array}right|$ .
Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:
тогда $M_{23}=left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Ответ. $M_{23}=left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Пример
Задание. Найти алгебраическое дополнение
$A_{23}$ к элементу
$a_{23}$ определителя
$left| begin{array}{rrr}{1} & {2} & {-1} \ {1} & {0} & {3} \ {7} & {8} & {4}end{array}right|$ .
Решение. $A_{23}=(-1)^{2+3} cdot M_{23}=(-1)^{5} cdot left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|=-left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Ответ. $A_{23}=-left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Вычисление определителя
Теоретический материал по теме — методы вычисления определителей.
Пример
Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$
Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$
Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.
Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Пример
Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.
$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{cccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$
$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Пример
Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$
$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$
Ответ. $Delta=-80$
Нахождение обратной матрицы
Теоретический материал по теме — нахождение обратной матрицы.
Пример
Задание. Для матрицы $A=left( begin{array}{ll}{7} & {4} \ {5} & {3}end{array}right)$
найти обратную методом присоединенной матрицы.
Решение. Приписываем к заданной матрице
$A$ справа единичную матрицу второго порядка:
$Aleft|E=left( begin{array}{ll|ll}{7} & {4} & {1} & {0} \ {5} & {3} & {0} & {1}end{array}right)right.$
От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):
$Aleft|E sim left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {5} & {3} & {0} & {1}end{array}right)right.$
От второй строки отнимаем две первых:
$Aleft|E sim left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {1} & {1} & {-2} & {3}end{array}right)right.$
Первую и вторую строки меняем местами:
$Aleft|E sim left( begin{array}{rr|r|rr}{1} & {1} & {-2} & {3} \ {2} & {1} & {1} & {-1}end{array}right)right.$
От второй строки отнимаем две первых:
$Aleft|E sim left( begin{array}{rr|rr}{1} & {1} & {-2} & {3} \ {0} & {-1} & {5} & {-7}end{array}right)right.$
Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:
$Aleft|E sim left( begin{array}{rr|rr}{1} & {0} & {3} & {-4} \ {0} & {1} & {-5} & {7}end{array}right)right.$
Итак, слева получили единичную матрицу, а значит матрица, стоящая в
правой части (справа от вертикальной черты), является обратной к исходной.
Таким образом, получаем, что $A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right)$
Ответ. $A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right)$
Пример
Задание. Найти обратную матрицу для $A=left( begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right)$
Решение. Шаг 1. Находим определитель: $Delta=left| begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right|=2-1=1 neq 0$
Шаг 2. $A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$
Шаг 3. $A^{-1}=frac{1}{Delta} cdot A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$
Ответ. $A^{-1}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$
Пример
Задание. Найти обратную матрицу к матрице $A=left( begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right)$
Решение. Вычисляем определитель матрицы:
$Delta=left| begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right|=1 cdot(-1) cdot(-1)+2 cdot 3 cdot 2+0 cdot 1 cdot 1-$
$-1 cdot(-1) cdot 2-3 cdot 1 cdot 1-2 cdot 0 cdot(-1)=1+12+0+2-3+0=12 neq 0$
Так как определитель не равен нулю, то матрица имеет обратную.
Обратная матрица $A^{-1}$ к матрице
$A$ находится по формуле:
$A^{-1}=frac{1}{Delta} cdot widetilde{A}^{T}$
Найдем союзную матрицу $check{A}$ , для этого вычислим алгебраические
дополнения к элементам матрицы $A$ :
$A_{11}=(-1)^{1+1} left| begin{array}{rr}{-1} & {1} \ {3} & {-1}end{array}right|=(-1) cdot(-1)-3 cdot 1=1-3=-2$
$A_{12}=(-1)^{1+2} left| begin{array}{rr}{2} & {1} \ {1} & {-1}end{array}right|=-[2 cdot(-1)-1 cdot 1]=-(-2-1)=3$
$A_{13}=(-1)^{1+3} left| begin{array}{rr}{2} & {-1} \ {1} & {3}end{array}right|=2 cdot 3-1 cdot(-1)=6+1=7$
$A_{21}=(-1)^{2+1} left| begin{array}{rr}{0} & {2} \ {3} & {-1}end{array}right|=-[0 cdot(-1)-3 cdot 2]=-(0-6)=6$
$A_{22}=(-1)^{2+2} left| begin{array}{rr}{1} & {2} \ {1} & {-1}end{array}right|=1 cdot(-1)-1 cdot 2=-1-2=-3$
$A_{23}=(-1)^{2+3} left| begin{array}{cc}{1} & {0} \ {1} & {3}end{array}right|=-[1 cdot 3-1 cdot 0]=-(3-0)=-3$
$A_{31}=(-1)^{3+1} left| begin{array}{rr}{0} & {2} \ {-1} & {1}end{array}right|=0 cdot 1-(-1) cdot 2=0+2=2$
$A_{32}=(-1)^{3+2} left| begin{array}{cc}{1} & {2} \ {2} & {1}end{array}right|=-[1 cdot 1-2 cdot 2]=-(1-4)=3$
$A_{33}=(-1)^{3+3} left| begin{array}{rr}{1} & {0} \ {2} & {-1}end{array}right|=1 cdot(-1)-2 cdot 0=-1-0=-1$
Таким образом, $tilde{A}=left( begin{array}{rrr}{-2} & {3} & {7} \ {6} & {-3} & {-3} \ {2} & {3} & {-1}end{array}right)$
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):
$widetilde{A}^{T}=left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$
Итак, $A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$
Ответ. $A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$
Нахождение ранга матрицы
Теоретический материал по теме — нахождение ранга матрицы.
Пример
Задание. Найти ранг матрицы $A=left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {4} & {8} & {18} & {7} \ {10} & {18} & {40} & {17} \ {1} & {7} & {17} & {3}end{array}right)$
Решение. С помощью элементарных преобразований над ее строками приведем матрицу $A$ к
ступенчатому виду. Для этого вначале от третьей строки отнимем две вторых:
$A sim left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {4} & {8} & {18} & {7} \ {2} & {2} & {4} & {3} \ {1} & {7} & {17} & {3}end{array}right)$
От второй строки отнимаем четвертую строку, умноженную на 4; от третьей — две четвертых:
$A sim left( begin{array}{rrrr}{0} & {4} & {10} & {1} \ {0} & {-20} & {-50} & {-5} \ {0} & {-12} & {-30} & {-3} \ {1} & {7} & {17} & {3}end{array}right)$
Ко второй строке прибавим пять первых, к третьей — три третьих:
$A sim left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {0} & {0} & {0} & {0} \ {1} & {7} & {17} & {3}end{array}right)$
Меняем местами первую и вторую строчки:
$A sim left( begin{array}{cccc}{0} & {0} & {0} & {0} \ {0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {1} & {7} & {17} & {3}end{array}right)$
Далее четвертую и первую строки:
$A sim left( begin{array}{cccc}{1} & {7} & {17} & {3} \ {0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {0} & {0} & {0} & {0}end{array}right) Rightarrow r a n g A=2$
Ответ. $operatorname{rang} A=2$
Пример
Задание. Найти ранг матрицы $A=left( begin{array}{rrrr}{1} & {2} & {-1} & {-2} \ {2} & {4} & {3} & {0} \ {-1} & {-2} & {6} & {6}end{array}right)$ ,
используя метод окаймления миноров.
Решение. Минорами минимального порядка являются миноры первого порядка, которые равны элементам
матрицы $A$ . Рассмотрим, например, минор
$M_{1}=1 neq 0$ . расположенный в первой строке и первом
столбце. Окаймляем его с помощью второй строки и второго столбца, получаем минор
$M_{2}^{1}=left| begin{array}{ll}{1} & {2} \ {2} & {4}end{array}right|=0$ ; рассмотрим еще один минор второго
порядка, для этого минор $M_{1}$ окаймляем при
помощи второй строки и третьего столбца, тогда имеем минор $M_{2}^{2}=left| begin{array}{rr}{1} & {-1} \ {2} & {3}end{array}right|=5 neq 0$ ,
то есть ранг матрицы не меньше двух. Далее рассматриваем миноры третьего порядка, которые окаймляют минор
$M_{2}^{2}$ . Таких миноров два: комбинация
третьей строки со вторым столбцом или с четвертым столбцом. Вычисляем эти миноры:
$M_{3}^{1}=left| begin{array}{rrr}{1} & {2} & {-1} \ {2} & {4} & {3} \ {-1} & {-2} & {6}end{array}right|=0$
так как содержит два пропорциональных столбца (первый и второй); второй минор
$M_{3}^{2}=left| begin{array}{rrr}{1} & {-1} & {-2} \ {2} & {3} & {0} \ {-1} & {6} & {6}end{array}right|$
преобразуем следующим образом: к первой строке прибавим третью, а ко второй две третьих:
$M_{3}^{2}=left| begin{array}{rrr}{0} & {5} & {4} \ {0} & {15} & {12} \ {-1} & {6} & {6}end{array}right|=0$
И так как первая и вторая строки пропорциональны, то минор равен нулю.
Таким образом, все окаймляющие миноры третьего порядка равны нулю. А, значит, ранг матрицы $A$
равен двум: $operatorname{rang} A=2$
Ответ. $operatorname{rang} A=2$
Читать первую тему — основные определения и понятия матриц,
раздела матрицы.
Определение 14. Пусть дан многочлен
и пусть
– квадратная матрица, тогда значением
многочлена
от матрицы
называется матрица
,
где
– единичная матрица,
– матрица, получающаяся при умножении
матрицы
на себя
раз.
№ 827 (П).
Найти значение многочлена
от матрицы
.
Р е ш е н и е.
Найдем
.

;
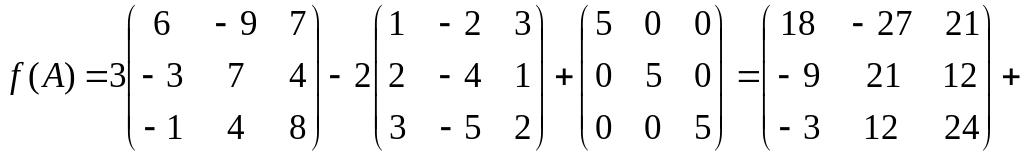
.
Ответ:
.
-
Обратная матрица
Определение 15. Матрица
называется обратной к квадратной
матрице
,
если
.
Определение 16. Квадратная матрица
называется невырожденной, если
она имеет единственную обратную матрицу
.
В противном случае
– вырожденная матрица.
Утверждение. Квадратная матрица
порядка
является невырож-денной в том и только
том случае, если определитель этой
матрицы отличен от нуля.
Для отыскания обратной матрицы
существуют два способа.
-
Припишем
к матрицесправа единичную матрицу и, применяя
метод Гаусса (см. §5), преобразуем
расширенную матрицу так, чтобы слева
стояла единичная матрица, тогда справа
будет находиться обратная матрица
:
.
.
Обоснование этого способа состоит в
следующем.
Пусть нам дана невырожденная квадратная
матрица. Задачу нахождения обратной
матрицы можно рассматривать как задачу
решения матричного уравнения
,
которое эквивалентно системе
уравнений с
неизвестными.
Эта система является объединением
систем уравнений, каждая из которых
содержит
неизвестных. Умножая поочередно строки
матрицы
на 1-й столбец матрицы
и приравнивая к 1-му столбцу матрицы
,
получим систему уравнений, матричная
форма записи которой имеет вид
(1.2.1)
С помощью элементарных операций над
строками матрицы систему уравнений
можно привести к виду
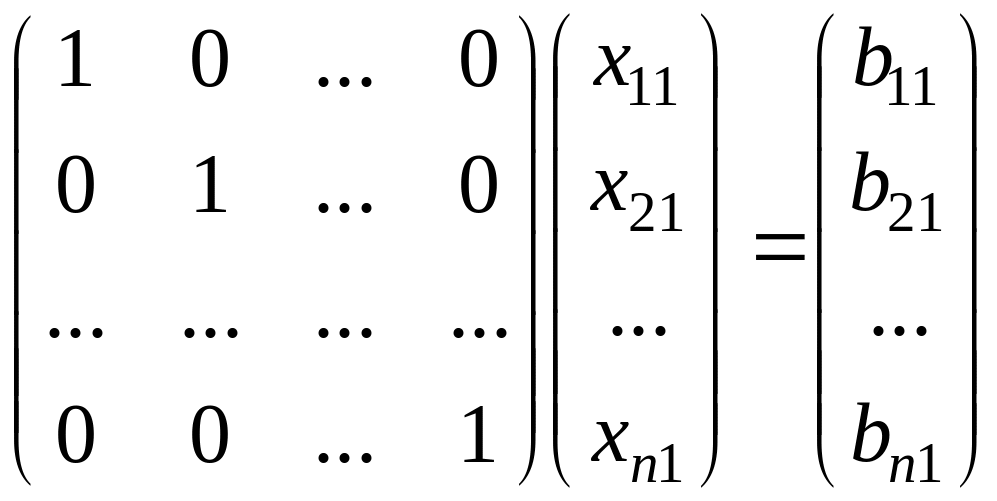
Умножая
поочередно строки матрицы
на второй столбец матрицы
и приравняв ко второму столбцу матрицы
,
получим систему уравнений
.
(1.2.2)
С помощью тех же элементарных операций,
что применялись для решения системы
(1.2.1), мы приведем систему (1.2.2) к виду
и т.д.
Поэтому
для нахождения обратной матрицы и был
предложен описанный выше способ.
-
,
где
– алгебраические дополнения к элементу
,
– определитель матрицы
(см. §2).
№ 840 (П).
Найти обратную матрицу для матрицы
.
Р е ш е н и е.
I
способ.


.
Ответ:
.
II
способ.

;
;
;
;
;
;
;
;
;
.
Таким образом,
.
Ответ:
.
№ 861 (П).
Решить матричное уравнение
.
Р е ш е н и е.
1 вариант.
Пусть
,
тогда
.
.
Ответ:
.
2 вариант.
Очевидно, что
.
Найдем матрицу, обратную к матрице
.
I
способ:
.
II
способ:
.
Таким образом,
.
Ответ:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #