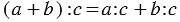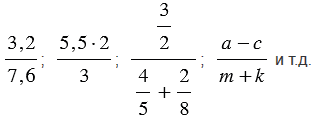Формулировка задачи: Найдите значение выражения (деление дробей).
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 1 (Действия с дробями).
Рассмотрим, как решаются подобные задачи на примерах.
Пример задачи 1:
Найдите значение выражения:
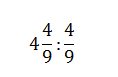
Решение:
Вычислим значение выражения. Для этого преобразуем смешанные числа в неправильные дроби, перевернем вторую дробь и изменим знак деления на умножение, сократим дроби и выполним умножение:
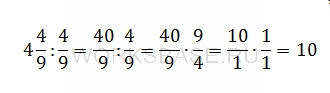
Ответ: 10
Пример задачи 2:
Найдите значение выражения 0,86: 43/20.
Решение:
Вычислим значение выражения. Для этого переведем обе дроби в обыкновенные или десятичные, перевернем вторую дробь и изменим знак деления на умножение, сократим дроби и выполним умножение. При необходимости переведем результат в десятичную дробь:
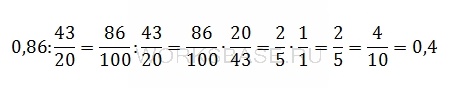
Ответ: 0,4
План урока:
Умножение обыкновенных дробей
Нахождение дроби от числа
Деление обыкновенных дробей
Нахождение числа по заданному значению его дроби
Дробные выражения
Умножение обыкновенных дробей
Разберем ситуацию.
На уроке технологии девочки занимались выпечкой. Они готовили печенье. По рецепту на изготовление одного килограмма печенья уходит 3/8 килограмма сахара. Сколько сахара необходимо принести детям, чтобы приготовить 1/2 килограмма печенья?
Чтобы ответить на главный вопрос задачи, нам необходимо узнать количество сахара нужное для изготовления 1/2 килограмма печенья. По условию, мы знаем, что для выпечки 1 кг лакомства требуется 3/8 кг сахара. Следовательно, чтобы вычислить требуемую массу сахарного песка необходимо найти произведение 3/8 и 1/2 . Известные множители представлены в виде обыкновенных дробей. Чтобы выполнить умножение обыкновенных дробей нужно использовать правило:
числитель умножаем на числитель, а знаменатель на знаменатель. Первый результат пишем над чертой дроби, второй под чертой:
Получается, чтобы испечь нужное количество печенья школьницы должны подготовить 3/16 килограмма сахарного песка.
Нахождение дроби от числа
Разберем следующую ситуацию и узнаем, как найти дробь от числа.
Вениамин очень любит уроки изобразительного искусства. В его альбоме для рисования 48 листов. Мальчик удивленно заметил, что своими рисунками уже заполнил 7/8 альбома. Сколько всего рисунков получилось у школьника?
Задачу можно решить двумя способами. Подробно рассмотрим каждый из них.
Способ 1.
Чтобы ответить на главный вопрос задачи нам нужно узнать, сколько листов соответствует записи 7/8. Для этого давайте вспомним, о чем нам говорят компоненты дробных выражений:
Теперь, можно сказать, что весь альбом разделили на 8 частей, а использовали только 7. Попробуем посчитать. Вначале, делим 48 на 8:
48 : 8 = 6.
6 листов приходится на 1/8 часть альбома. Зная, что таких частей было взято 7, найдем произведение 6 и 7 :
6 × 7 = 42.
Мы выяснили, что Вениамин нарисовал 42 рисунка.
Для решения задачи таким способом, нужно выполнить два действия, а это не всегда удобно. Так же, такой способ может вызывать трудности при вычислениях, если компоненты не делятся нацело.
В таких ситуациях, логичнее будет использование второго способа.
Способ 2.
По условию нам известно число и часть этого числа, выраженная обыкновенной дробью. Нужно найти числовое значение соответствующее данной дроби. Задания такого вида имеют собственное название «Нахождение дроби от числа» и правило, используя, которое можно с легкостью вычислить любое числовое значение соответствующее дробному выражению:
Применим изученное правило на практике. Чтобы найти 7/8 от 48 нам нужно, просто умножить 7/8 на 48:
Мальчик нарисовал 42 рисунка.
Запомните оба способа, и применяйте их для решения различных заданий.
Деление обыкновенных дробей
Разберем пример.
Строительная бригада выполняла ремонт городской дороги.На ремонт определенного участка дороги, рабочие потратили 7/9 тонны асфальта. Определите, сколько километров дороги отремонтировали рабочие, если на ремонт одного километра уходит 3/7 тонны строительного материала.
По условию нам известно, что всего было использовано 7/9 тонны материала, при этом мы знаем, что на один километр требуется 3/7 тонны. Чтобы ответить на главный вопрос задачи нужно количество использованного асфальтаразделить на количество строительного материала, необходимое для починки одного километра. В результате мы получим число отремонтированных километров. В данном случае, в качестве делимого и делителя выступают обыкновенные дроби. И перед нами возникает проблема «Как же выполнить деление обыкновенных дробейс разными знаменателями?».
В арифметике на этот случай имеется определенное правило, которое расскажет, как выполнить деление обыкновенных дробей.
Выполним деление имеющихся чисел с применением рассмотренного правила
Выполним деление, имеющихся дробных чисел с применением рассмотренного правила. Разделим 7/9 на 3/7. Делимое 7/9 оставляем без изменений, а делитель 3/7 переворачиваем, и получаем 7/3. Находим произведение данных выражений:
Все очень просто. Главное помните, что при выполнении деления дробей с разными знаменателями делитель переворачиваем и находим произведение перевернутого делителя и делимого!
Нахождение числа по заданному значению его дроби
В школе проходила неделя экологии. Учащиеся шестого класса были приглашены лесничеством на высадку деревьев. До обеда, ребята высадили 6/11 всех саженцев. Сколько растений осталось высадить школьникам, если до обеда дети высадили 54 дерева?
Чтобы ответить на главный вопрос задачи, нужно определить число по заданному значению его дроби. В арифметике существует правило, используя, которое возможно с легкостью найти любое число по значению его дроби:
Теперь мы знаем, что для вычисления общего количества саженцев, нужно известное значение дроби разделить на саму дробь. Зная, что число – 54, а дробь – 6/11, имеем:
В результате получили неправильную дробь. Выделим из полученного произведения целую часть.Для этого разделим числитель на знаменатель:
594 : 6 = 99.
Выходит, что за целый день школьникам нужно высадить 99 растений.
В математике часто встречаются задания, в которых требуется вычислить значение «многоэтажных» дробей. Как называются такие дробные выражения, каким способом их вычислять рассмотрим далее.
Дробные выражения
Когда ученик видит в учебнике задание в виде выражения:
то желание заниматься математикой сразу пропадает. Сегодня мы узнаем,как решать дробные выражения и докажем, что даже такие выражения совершенно не сложные, и выполнить вычисления сможет каждый желающий после изучения нашего урока!
Никого не пугает запись обыкновенной дроби – 3/7, 4/15, 8/14.
Каждый понимает, что дробная черта заменяет привычный знак деления – : .
Например:
10/21 = 10 : 21 или 7/18 = 7 : 18.
Выходит, что частное чисел или выражений, в случае замены знака деления чертой дроби, называют дробным выражением.
Вот так, проведя два простых вычисления, мы выполнили задание, вызывающее недоумение у школьников. Математика интересная и простая наука. Если приложите немного внимания и терпения, то результат не заставит себя ждать!
Знаешь ли ты?
1) Ученые – селекционеры вывелиновый вид яблонь. Удивительным является то, что корни растения уходит в землю более чем на 49/50километра (около 980 метров), а общая длина корневища достигает 4000 метров.
2) За всю жизнь человек выпивает примерно 75 тонн воды. Подсолнечнику, например, достаточно 1/4 тонны(250 литров), чтобы вырасти и принести семена.
3) Италия в который раз удивила весь мир. Около вулкана Этна растет каштан, диаметр ствола которого, составляет,3/50 километра (около 60 метров),это чуть ли не половина футбольного стадиона.
4) Пальма Рафия Тедигера встречается только в Бразилии. Она интересна тем, что её листья имеют гигантские размеры. Черенок листка достигает1/200 километра (5 метров), длина листика – более1/50 километра (более 20 метров), ширина – более 5 метров (1/200 километра).
5) По сообщениям ихтиологов(ученых, занимающихся изучением рыб), самую большую длину в мире,имеют ремень-рыбы. Во взрослом возрасте они достигают длины более 1/100километра(более 10 метров), а длина молодых особей находится в пределах 0,003 километра или 3 метров.
Математика
5 класс
Урок № 66
Решение задач с использованием деления дробей
Перечень рассматриваемых вопросов:
– деление дробей;
– вычисление значения выражения, содержащего несколько действий.
Тезаурус
Частное дробей – это дробь, которая при умножении на делитель даёт делимое.
Частное двух натуральных чисел равно дроби, числитель которой равен делимому, а знаменатель – делителю.
Обязательная литература
- Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
На прошлом уроке мы сформулировали понятие частного дробей, а также рассмотрели правило деления. Давайте вспомним его.
Чтобы одну дробь разделить на другую, отличную от нуля, можно делимое умножить на дробь, обратную делителю.
Частное любых двух натуральных чисел равно дроби, числитель которой равен делимому, а знаменатель – делителю.
Запишем равенство, которое можно получить на основании правила деления.
p и s – целые числа, при этом s не равно нолю.
Рассмотрим свойство деления дроби на натуральное число.
Чтобы разделить дробь на натуральное число, надо знаменатель дроби умножить на это число.
Запомните: делить на ноль нельзя.
Число 0, делённое на любую дробь, отличную от ноля, равно 0.
При вычислении значений числовых выражений, содержащих дроби, пользуются теми же правилами порядка действий, что и для натуральных чисел.
Найдём значение числового выражения:
Это решение можно записать короче.
Теперь решим задачи.
Значит, Аня потратит на выполнение всего домашнего задания 1 час 30 минут.
Ответ: 1 час 30 минут.
Задача 2. Детская песочница имеет вид квадрата с периметром 9 м. Найдите длину стороны квадрата.
Решение.
У квадрата четыре равные стороны. Периметр квадрата – это сумма всех его сторон. Значит, чтобы найти длину одной стороны, нужно 9 разделить на 4:
Решение. Будем решать по действиям.
Затем значение, полученное в числителе в третьем действии, разделим на знаменатель, полученный в шестом действии.
Тренировочные задания
№ 1. Разместите нужные подписи под изображениями.
Варианты ответов: делитель; частное; делимое.
Чтобы правильно подписать название дробей, вспомните определение делимого, делителя и частного.
Правильный ответ:
№ 2. Вставьте в текст нужные слова.
При вычислении значений числовых ___, содержащих дроби, пользуются теми же правилами ___ действий, что и для ___чисел.
Варианты слов для вставки: числителей; произведению; знаменатель; частному; выражений; порядка; натуральных.
Чтобы правильно вписать слова, вспомните, как вычисляются значения числового выражения.
Правильный ответ: при вычислении значений числовых выражений, содержащих дроби, пользуются теми же правилами порядка действий, что и для натуральных чисел.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Обыкновенные дроби
- Деление и дроби
Не всегда можно одно натуральное число разделить на другое, так, например, 2 нельзя разделить на 3, в таком случае деление можно заменить дробью 

Пример:
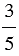
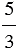
В результате деления двух натуральных чисел может получится натуральное число или дробное число.
Пример:
20 : 4 = 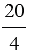
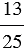
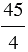
Пример:
а) 1 = 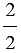
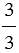
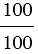
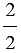
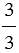
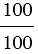
Получаем, что число 1 можно представить в виде дроби, у которой числитель и знаменатель равны.
б) 7 = 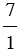
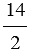
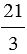
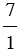
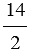
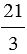
Свойство деления суммы на число
Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные частные.
Пример:
(64 + 72) : 8 = 64 : 8 + 72 : 8 = 8 + 9 = 17.
Дробные выражения
Частное от деления одного выражения на другое можно записать с помощью черты дроби. Например, выражение (3,5 — 1,1) : (7,3 + 2,7) можно записать в виде 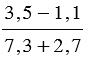
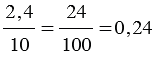
Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.
К дробным выражениям относятся:
Числитель дробного выражения — выражение, стоящее над чертой.
Знаменатель дробного выражения — выражение, стоящее под чертой.
Обратите внимание, в числителе и в знаменателе дробного выражения могут стоять любые числа (натуральные числа, обыкновенные дроби, десятичные дроби и т.д.), а также числовые или буквенные выражения (смотри примеры выше).
Если числитель и знаменатель дробного выражения разделить или умножить на одно и то же число отличное от нуля, то получим дробное выражение, равное данному. Данное свойство часто используют, когда преобразуют дробное выражение с десятичными дробями в обыкновенную дробь.
Пример:
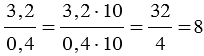
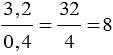
То есть, получается, что мы переносим запятую в числителе и знаменателе дробного выражения на одинаковое количество цифр вправо, при этом если в одном числе цифр после запятой больше, чем в другом, то переносим запятую на большее количество цифр, а там где цифр после запятой меньше дописываем нули.
Пример:
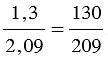
Советуем посмотреть:
Доли. Обыкновенные дроби
Сравнение дробей
Делители и кратные
Признаки делимости на 10, на 5 и на 2
Четные и нечетные числа
Признаки делимости на 9 и на 3
Простые и составные числа
Разложение на простые множители
Наибольший общий делитель
Наименьшее общее кратное
Сложение и вычитание дробей с одинаковыми знаменателями
Смешанное число
Сложение и вычитание смешанных чисел
Основное свойство дроби
Решето Эратосфена
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Умножение обыкновенных дробей
Деление обыкновенных дробей
Обыкновенные дроби
Правило встречается в следующих упражнениях:
5 класс
Задание 1058,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1154,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1223,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1564,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1582,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 2,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Номер 761,
Мерзляк, Полонский, Якир, Учебник
Номер 765,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 443,
Мерзляк, Полонский, Якир, Учебник
Номер 649,
Мерзляк, Полонский, Якир, Учебник
Номер 740,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Задание 696,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 700,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 848,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1151,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1280,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1509,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 48,
Мерзляк, Полонский, Якир, Учебник
Номер 53,
Мерзляк, Полонский, Якир, Учебник
Номер 407,
Мерзляк, Полонский, Якир, Учебник
Номер 526,
Мерзляк, Полонский, Якир, Учебник
Номер 573,
Мерзляк, Полонский, Якир, Учебник
Номер 743,
Мерзляк, Полонский, Якир, Учебник
Номер 859,
Мерзляк, Полонский, Якир, Учебник
Номер 1049,
Мерзляк, Полонский, Якир, Учебник
Номер 1070,
Мерзляк, Полонский, Якир, Учебник
Номер 1230,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 54,
Мерзляк, Полонский, Якир, Учебник
Номер 60,
Мерзляк, Полонский, Якир, Учебник
Номер 89,
Мерзляк, Полонский, Якир, Учебник
Номер 133,
Мерзляк, Полонский, Якир, Учебник
Номер 197,
Мерзляк, Полонский, Якир, Учебник
Номер 202,
Мерзляк, Полонский, Якир, Учебник
Номер 207,
Мерзляк, Полонский, Якир, Учебник
Номер 217,
Мерзляк, Полонский, Якир, Учебник
Номер 307,
Мерзляк, Полонский, Якир, Учебник
Деление дробей онлайн
Чтобы разделить дробь на дробь нужно умножить первую дробь на дробь обратную второй.
Правила деления дробей
Чтобы разделить дробь на дробь, нужно делимое умножить на дробь обратную делителю
Как делить обыкновенные дроби
Чтобы разделить обыкновенную дробь на обыкновенную дробь, нужно вторую дробь сделать обратной затем умножить на вторую дробь по правилам умножения дробей.
Разберём пример: разделим дробь 1/4 на 1/3. Для этого развернём вторую дробь 3/1. Получится выражение 1/4 × 3/1. Перемножим числители 1 × 3 = 3 и знаменатели 4 × 1 = 4 в итоге у нас получится дробь 3/4
Как разделить натуральное число на дробь
Чтобы разделить натуральное число на дробь, нужно сделать дробь обратной. Числитель обратной дроби умножить на натуральное число а знаменатель обратной дроби останется без изменения.
Как разделить смешанную дробь на целое число
Чтобы разделить смешанную дробь на целое число нужно смешанную дробь перевести в неправильную. Затем целое число представить в виде обратной дроби и умножить на неправильную дробь. После чего выполнить умножение обыкновенных дробей.
Разберём пример: разделим смешанную дробь 3 целые 3/4 на целое число 7.
Перед делением нужно смешанную дробь перевести в неправильную 3 целые 3/4 = 15/4. Представим целое число в виде обратной дроби7 это 1/7. Умножим дроби 15/4 и 1/7. Перемножим числители 15*1 = 15, перемножим знаменатели4*7 = 28
Как разделить смешанную дробь на смешанную дробь
Для деления смешанной дроби ра смешанную дробь нужно обе дроби представить в виде неправильных. Затем вторую дробь преобразовать в обратную. После чего перемножить обе дроби по правилам умножения обыкновенных дробей.
Разберём пример: разделим смешанную дробь 2 целые 3/5 на смешанную дробь 3 целые 1/2
Преобразуем обе дроби в неправильные
Развернём вторую дробь и изменим знак деления на умножение
Перемножим дроби по правилам умножения обыкновенных дробей
Похожие калькуляторы