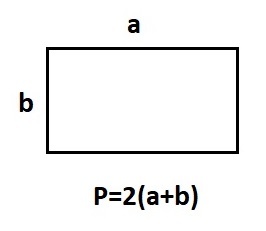
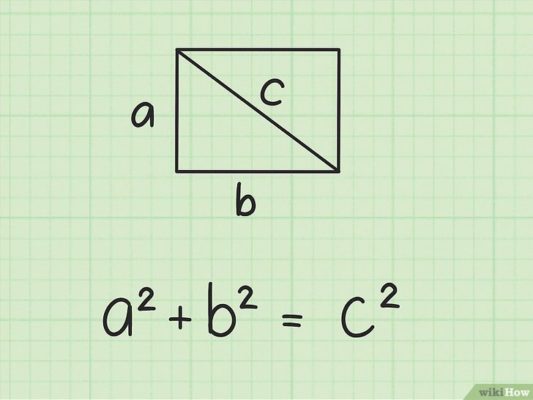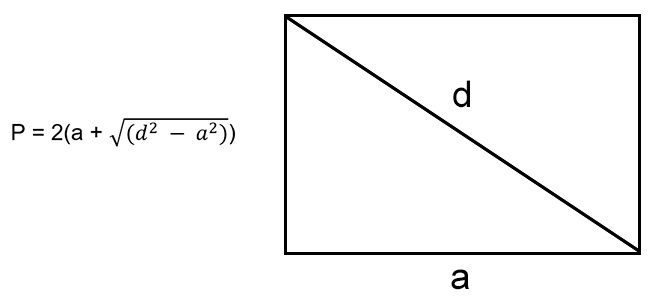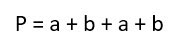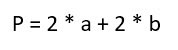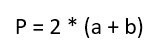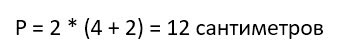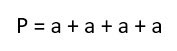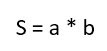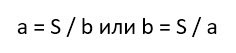Прямоугольник. Формулы и свойства прямоугольника
Определение.
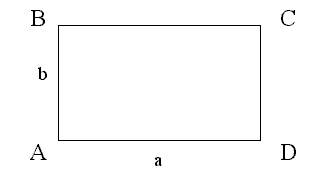
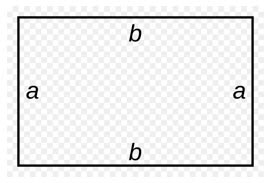
Прямоугольник — это четырехугольник у которого две противоположные стороны равны и все четыре угла одинаковы.
Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.
Длинную сторону прямоугольника называют длиной прямоугольника, а короткую — шириной прямоугольника.
Стороны прямоугольника одновременно является его высотами.
Основные свойства прямоугольника
Прямоугольником могут быть параллелограмм, квадрат или ромб.
1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:
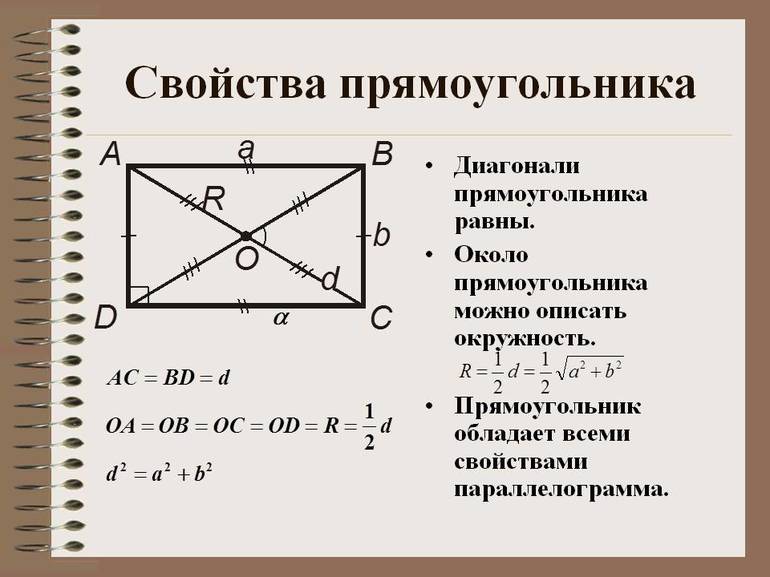
AB = CD, BC = AD
2. Противоположные стороны прямоугольника параллельны:
AB||CD, BC||AD
3. Прилегающие стороны прямоугольника всегда перпендикулярны:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
4. Все четыре угла прямоугольника прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
5. Сумма углов прямоугольника равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника имеют одинаковой длины:
AC = BD
7. Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
2d2 = 2a2 + 2b2
8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.
9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:
10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
11. Диагональ прямоугольника является диаметром описанной окружности
12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:
∠ABC + ∠CDA = 180° ∠BCD + ∠DAB = 180°
13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника — квадрат).
Стороны прямоугольника
Определение.
Длиной прямоугольника называют длину более длинной пары его сторон. Шириной прямоугольника называют длину более короткой пары его сторон.
Формулы определения длин сторон прямоугольника
1. Формула стороны прямоугольника (длины и ширины прямоугольника) через диагональ и другую сторону:
a = √d2 — b2
b = √d2 — a2
2. Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:
3. Формула стороны прямоугольника (длины и ширины прямоугольника) через периметр и другую сторону:
4. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол α:
a = d sinα
b = d cosα
5. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол β:
Диагональ прямоугольника
Определение.
Диагональю прямоугольника называется любой отрезок соединяющий две вершины противоположных углов прямоугольника.
Формулы определения длины диагонали прямоугольника
1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):
d = √a2 + b2
2. Формула диагонали прямоугольника через площадь и любую сторону:
| d = | √S2 + a4 | = | √S2 + b4 |
| a | b |
3. Формула диагонали прямоугольника через периметр и любую сторону:
| d = | √P2 — 4Pa + 8a2 | = | √P2 — 4Pb + 8b2 |
| 2 | 2 |
4. Формула диагонали прямоугольника через радиус описанной окружности:
d = 2R
5. Формула диагонали прямоугольника через диаметр описанной окружности:
d = Dо
6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
7. Формула диагонали прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника
d = √2S : sin β
Периметр прямоугольника
Определение.
Периметром прямоугольника называется сумма длин всех сторон прямоугольника.
Формулы определения длины периметру прямоугольника
1. Формула периметру прямоугольника через две стороны прямоугольника:
P = 2a + 2b
P = 2(a + b)
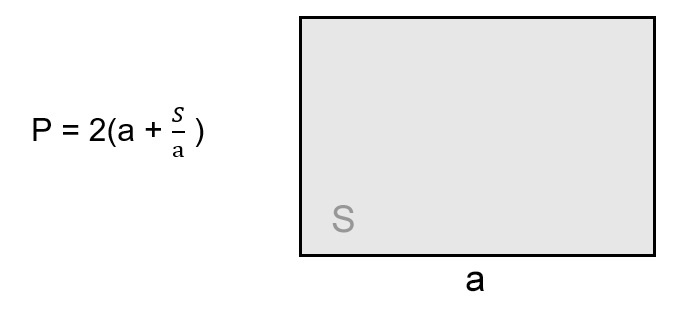
2. Формула периметру прямоугольника через площадь и любую сторону:
| P = | 2S + 2a2 | = | 2S + 2b2 |
| a | b |
3. Формула периметру прямоугольника через диагональ и любую сторону:
P = 2(a + √d2 — a2) = 2(b + √d2 — b2)
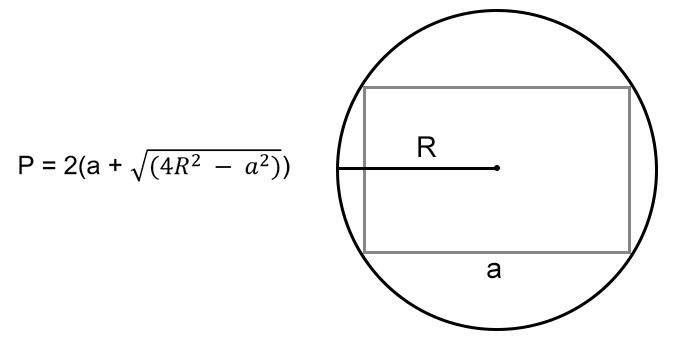
4. Формула периметру прямоугольника через радиус описанной окружности и любую сторону:
P = 2(a + √4R2 — a2) = 2(b + √4R2 — b2)
5. Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:
P = 2(a + √Do2 — a2) = 2(b + √Do2 — b2)
Площадь прямоугольника
Определение.
Площадью прямоугольника называется пространство ограниченный сторонами прямоугольника, то есть в пределах периметра прямоугольника.
Формулы определения площади прямоугольника
1. Формула площади прямоугольника через две стороны:
S = a · b
2. Формула площади прямоугольника через периметр и любую сторону:
| S = | Pa — 2a2 | = | Pb — 2b2 |
| 2 | 2 |
3. Формула площади прямоугольника через диагональ и любую сторону:
S = a√d2 — a2 = b√d2 — b2
4. Формула площади прямоугольника через диагональ и синус острого угла между диагоналями:
5. Формула площади прямоугольника через радиус описанной окружности и любую сторону:
S = a√4R2 — a2 = b√4R2 — b2
6. Формула площади прямоугольника через диаметр описанной окружности и любую сторону:
S = a√Do2 — a2 = b√Do2 — b2
Окружность описанная вокруг прямоугольника
Определение.
Окружностью описанной вокруг прямоугольника называется круг проходящий через четыре вершины прямоугольника, центр которого лежит на пересечении диагоналей прямоугольника.
Формулы определения радиуса окружности описанной вокруг прямоугольника
1. Формула радиуса окружности описанной вокруг прямоугольника через две стороны:
2. Формула радиуса окружности описанной вокруг прямоугольника через периметр квадрата и любую сторону:
| R = | √P2 — 4Pa + 8a2 | = | √P2 — 4Pb + 8b2 |
| 4 | 4 |
3. Формула радиуса окружности описанной вокруг прямоугольника через площадь квадрата:
| R = | √S2 + a4 | = | √S2 + b4 |
| 2a | 2b |
4. Формула радиуса окружности описанной вокруг прямоугольника через диагональ квадрата:
5. Формула радиуса окружности описанной вокруг прямоугольника через диаметр описанной окружности:
6. Формула радиуса окружности описанной вокруг прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
7. Формула радиуса окружности описанной вокруг прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
8. Формула радиуса окружности описанной вокруг прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:
Угол между стороной и диагональю прямоугольника
Формулы определения угла между стороной и диагональю
1. Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:
2. Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:
Угол между диагоналями прямоугольника
Формулы определения угла между диагоналями прямоугольника
1. Формула определения угла между диагоналями прямоугольника через угол между стороной и диагональю:
β = 2α
2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ:
Длина прямоугольника

4.6
Средняя оценка: 4.6
Всего получено оценок: 89.
4.6
Средняя оценка: 4.6
Всего получено оценок: 89.
В этой статье мы поговорим о длине прямоугольника. Как определить, какая из сторон является длиной и зачем их разделять. Разберем три способа нахождения длины прямоугольника и решим небольшую задачу.
Опыт работы учителем математики — более 33 лет.
Что такое длина прямоугольника
Довольно часто люди путают местами длину и ширину прямоугольника, как правило, это не критично, но в результате значительно уменьшается наглядность, а от этого страдает качество решения.
Прямоугольник это частный случай параллелограмма. Параллелограмм, каждый угол которого равен 90 градусам, называется прямоугольником. Для наглядного изображения лучше будет, если нижней опорой прямоугольника будет служить длина. Так сложилось, что такой рисунок больше всего напоминает рисунки в учебнике, а потому ученику будет проще разобраться в теме.
Три способа найти длину прямоугольника
Если разделить фигуру на две части диагональю, то можно заметить, что прямоугольник поделится ею на два прямоугольных треугольника. Из этого разделения и вытекают все формулы длины прямоугольника.
-
Через теорему Пифагора
Если известна длина диагонали (обозначим ее буквой d) и длина прямоугольника (примем значение за букву a). Тогда корень квадратный из разности квадратов диагонали и длины будет равен ширине прямоугольника.
Чтобы было понятнее, напишем решение в виде нескольких формул.
Согласно теореме Пифагора – квадрат гипотенузы равен сумме квадратов катетов. Гипотенуза – это сторона, противоположная прямому углу, две другие стороны зовутся катетами. В нашем случае гипотенуза это диагональ.
Значит: d2=a2+b2 . Из этого выражения выразим квадрат ширины (значение «b»):b2=d2-a2
Для того, чтобы определить значение b, нужно взять корень квадратный из обеих сторон получившегося выражения: b=(d2-a2)(-1)
В случае необходимости, можно поменять местами а и b, тогда получится формула длины.
-
Через площадь
Рассмотрим еще один способ найти длину прямоугольника – через площадь.Площадь прямоугольника равна произведению длины и ширины. То есть, используя уже знакомые обозначения S=a*b. Выразим из этой формулы значение ширины: b=S/b.
Так же, как и в первом методе, можно поменять местами а и b, чтобы получить формулу для длины: a=S/b.
-
Тригонометрическая функция
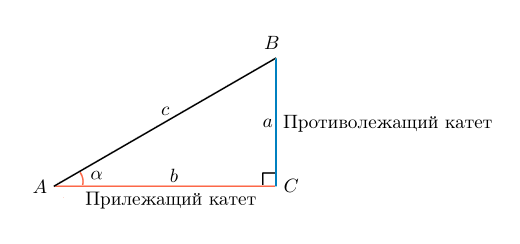
Один из самых быстрых, но при этом немного сложных способов нахождения длины – воспользоваться тригонометрической функцией.
Если имеется прямоугольный треугольник, то соответственно имеются отношения, известные как синус и косинус.
Выберем угол между длиной и диагональю. Обозначим его α. Тогда sin α равен отношению катета, противоположного углу α к гипотенузе: Sin α = a/c
Значение синуса любого угла можно найти в таблицах Брадиса или с помощью калькулятора. Для удобства можно воспользоваться онлайн-версией, которая найдет значение отношения автоматически.
Но в формуле нет значения b, которое соответствует длине, а, значит, воспользуемся основным тригонометрическим тождеством. Косинус – это отношение стороны, прилежащей к углу, к гипотенузе: cos a=b/c
Значит можно найти длину, умножив косинус на гипотенузу: b=cos α*c
Задача
- Найти длину прямоугольника, если известно, что его ширина равна 3, а диагональ 5.
Воспользуемся теоремой Пифагора и найдем b. Длина равна корню квадратному из разности квадрата диагонали и квадрата ширины.
5^2=25
3^2=9
25-9=16
Корень квадратный из 16 равен 4.
Значение b=4
Что мы узнали?
Мы рассмотрели, как правильно изображать прямоугольник для большей наглядности, рассмотрели как можно найти длину или ширину при различных условиях задачи и решили задачу средней сложности на нахождение длины прямоугольника через теорему Пифагора.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 89.
А какая ваша оценка?
Периметр прямоугольника
Периметр прямоугольника — это сумма
всех сторон прямоугольника.
Периметр прямоугольника можно рассчитать
через четыре стороны, через смежные стороны,
через диагональ, через площадь,
через радиус описанной окружности.
Самый простой способ найти периметр
прямоугольника, это сложить все стороны.
Также, исходя из свойства прямоугольника, — «противоположные
стороны равны и параллельны», можно сказать, что периметр
численно равен удвоенной сумме ширины и высоты — двух
смежных сторон прямоугольника.
Кроме этих двух способов периметр прямоугольника
можно найти через другие величины. Например, через
площадь прямоугольника, диагональ прямоугольника, и так далее.
В прямоугольник невозможно вписать окружность,
поэтому выразить периметр через вписанную
окружность не получится.
Единицы измерения периметра прямоугольника:
км, м, дм, см, мм.
Формулы периметра прямоугольника
- Периметр прямоугольника через четыре стороны
Полупериметр
Полупериметр — это половина периметра.
Обозначается латинской буквой p.
Чтобы найти полупериметр нужно разделить
периметр на два, или домножить периметр на 0.5.
[ p = frac
= P cdot 0.5 ]
Полупериметр применяется в некоторых формулах
нахождения разных величин прямоугольника. Вместо того,
чтобы вычислять периметр, в таких формулах
удобней вычислять полупериметр.
Основные определения и величины
Длина прямоугольника — это длинная сторона
/ наибольшая сторона прямоугольника.
Обозначается латинской буквой a.
Ширина прямоугольника — это широкая сторона
/ наименьшая сторона прямоугольника.
Обозначается латинской буквой b.
Сторона прямоугольника — это ширина или длина прямоугольника,
в зависимости от численного значения длины стороны.
Обозначается латинской буквой a или b.
Диагональ прямоугольника — это отрезок, соединяющий
противоположные стороны прямоугольника.
Обозначается латинской буквой c или d.
Средняя линия прямоугольника — это отрезок, соединяющий
наименьшие параллельные стороны прямоугольника друг с
другом, причем делящий их пополам на равные отрезки.
Обозначается латинской буквой l.
Радиус описанной окружности прямоугольника — это отрезок,
соединяющий центр описанной около треугольника
окружности и произвольную точку на окружности.
Обозначается латинской буквой R.
Высота прямоугольника — это любая сторона прямоугольника,
а также любой отрезок в прямоугольнике, образующий угол в 90 градусов.
Как вычислить площадь и периметр прямоугольника
В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.
Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.
Количество просмотров этой статьи: 15 252.
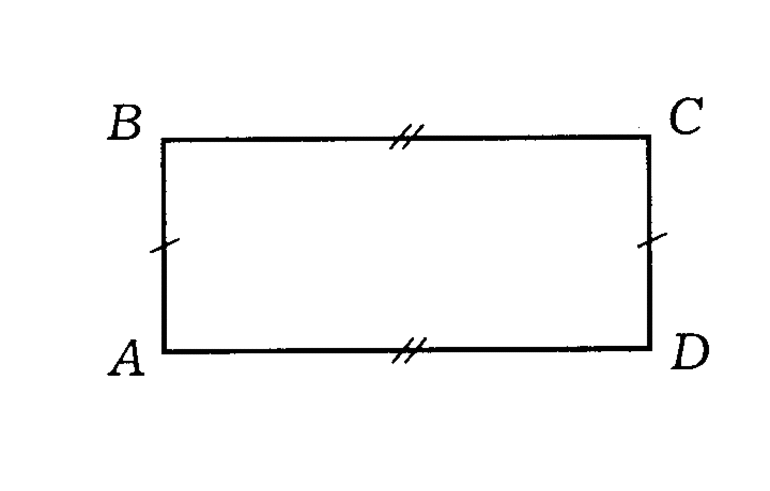
Прямоугольник — это четырехугольник (двумерная фигура) с четырьмя прямыми углами. Параллельные стороны прямоугольника равны. [1] X Источник информации Прямоугольник, у которого все стороны равны, называется квадратом. Все квадраты являются прямоугольниками, но не все прямоугольники — квадраты. Периметр фигуры равен сумме значений ее сторон. [2] X Источник информации Площадь фигуры равна произведению ее длины на ширину. [3] X Источник информации
Как найти периметр прямоугольника
Прямоугольник — это четырехугольник, у которого все четыре угла прямые, то есть, составляют 90 градусов. Частным случаем прямоугольника могут быть квадрат или ромб.
Периметр прямоугольника — это сумма длин всех его ребер.
Основные свойства прямоугольника:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- противоположные стороны фигуры равны и параллельны друг другу;
- сумма всех углов равна 360 градусов;
- диагонали прямоугольника равны по длине и точкой пересечения делятся пополам;
- диагонали делят фигуру на два одинаковых прямоугольных треугольника;
- по теореме Пифагора, квадрат диагонали прямоугольника равен сумме квадратов двух его соседних ребер;
- стороны рассматриваемого четырехугольника также являются его высотами;
- точка пересечения диагоналей — это центр прямоугольника и также центр вписанной окружности;
- диагональ этого четырехугольника — это диаметр описанной окружности;
- вокруг него всегда можно описать окружность.
Варианты нахождения периметра прямоугольника
По сторонам
Если нам известны все стороны прямоугольника (или две смежные), мы можем использовать следующую формулу для нахождения суммы длин всех ребер:
где (a) и (b) — это две соседние стороны фигуры.
По любой стороне и площади
Зная значение любого из ребер четырехугольника и его площадь, мы можем найти значение второго и периметр фигуры.
Так как площадь прямоугольника — это произведение двух его смежных сторон ((S=atimes b)) , чтобы найти неизвестную сторону, нужно поделить площадь на известную величину: (b=frac Sa) .
Получается, что формула для расчета (P) рассматриваемой фигуры будет выглядеть следующим образом:
По любой стороне и диагонали
В случае, если мы знаем длину одного из ребер и диагональ данного четырехугольника, мы можем найти вторую сторону с помощью теоремы Пифагора.
где (d) — диагональ прямоугольника, а (b) — неизвестная сторона.
Чтобы рассчитать сумму длин всех сторон, нужно воспользоваться формулой:
По любой стороне и радиусу описанной окружности
Когда нам известна одна из сторон и радиус описанной окружности вокруг прямоугольника, мы можем узнать его неизвестное ребро. Из свойств прямоугольника помним, что точка пересечения диагоналей фигуры — это центр описанной окружности. Это значит, что 1/2 диагонали — это радиус этой окружности. Таким образом, по теореме Пифагора мы можем узнать неизвестную сторону прямоугольника:
где (R) — радиус описанной окружности.
Тогда формула для расчета P будет выглядеть так:
Примеры решения задач
Задача 1
Известно, что стороны прямоугольника равны 5 см и 7 см. Найти его периметр.
Решение:
Применяем самую первую формулу для расчета:
Задача 2
Мы знаем, что площадь четырехугольника с прямыми углами составляет 24 (см^2) , одна из его сторон равна 6 см. Вычислить Р фигуры.
Решение:
Берем формулу (P=2(frac Sa+a)) и подставляем известные значения:
Задача 3
Дан прямоугольник со стороной 3 см и диагональю 5 см. Нужно высчитать P данной фигуры.
Решение:
Вспоминаем формулу для расчета (P=2(a+sqrt)) и вставляем известные величины:
Задача 4
Вокруг прямоугольника с ребром 3 см описали окружность с радиусом 5 см. Определить P заданной фигуры.
Решение:
В этом случае для расчета суммы длин всех сторон применяем формулу (P=2(a+sqrt)) . Используем известные значения и получаем:
Периметр прямоугольника
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое периметр прямоугольника и по каким формулам его можно посчитать.
Тема в общем-то простая, каждый из нас изучал ее еще в начальных классах. Тем не менее с возрастом кто-то мог что-нибудь и подзабыть.
Но для начала предлагаем освежить теоретическую базу и вспомнить, что такое прямоугольник.
Что такое прямоугольник и что такое периметр
Прямоугольник – это геометрическая фигура, которая представляет собой четырехугольник, а конкретно параллелограмм (фигура, у которой противоположные стороны равны и параллельны). Но параллелограмм не обычный, а с особенностями. У него все стороны пересекаются друг с другом под прямым углом.
Выглядит прямоугольник соответственно:
А частным случаем прямоугольника является квадрат:
У такого прямоугольника стороны не только пересекаются под прямым углом, но и равны между собой.
Как и многие термины в математике, жир слово пришло к нам из Древней Греции. Дословно оно означает «περιμετρέο» — «окружность» или «измерять вокруг». Таким образом,
Периметр – это совокупная длина границ любой геометрической фигуры. Этим словом обозначают как сами границы, так и их математическое значение.
С этим словом мы часто встречаемся в повседневной жизни. Например, когда нужно поставить забор на дачном участке, то его устанавливают по периметру участка. И мы понимаем, что речь идет о границах.
Также, солдаты или полицейские часто стоят в оцеплении «по периметру» какой-то территории. А кулинары часто украшают торт фруктами или кремовыми цветами также «по периметру».
Как найти периметр прямоугольника
Возьмем для примера такой прямоугольник:
Исходя из общего определения, чтобы посчитать периметр прямоугольника, надо просто сложить все его стороны.
Периметр в математике обозначается латинской буквой «Р». И соответственно формула выглядит так:
С учетом равенства сторон, формулы можно существенно упростить:
или
Предположим, что у нас длина прямоугольника равна 4 сантиметрам, а ширина 2. Тогда периметр этой геометрической фигуры составит:
И тут появляется важное замечание. Периметр измеряется в тех же величинах, что и длины сторон прямоугольника. Это могут быть миллиметры, сантиметры, метры, километры и так далее.
В случае с квадратом, который, напомним, является частным случаем прямоугольника, посчитать периметр еще проще. Благодаря тому, что у него все стороны равны (назовем их условно «а»), формула выглядит так:
или
Опять же приведем конкретный пример. Если возьмем квадрат со стороной 4 сантиметра, то его периметр составит P = 4 * 4 = 16 сантиметров.
Другие формулы для расчета периметра прямоугольника
Иногда школьникам предлагают такую задачу – нужно вычислить периметр прямоугольника, зная его площадь и длину одной стороны.
Тут надо знать, как вычисляется сама площадь. Для этого надо просто перемножить длины двух сторон:
Соответственно, мы можем определить длину недостающей нам стороны. Для этого надо просто разделить площадь на другую сторону:
Таким образом, мы у нас будут значения обеих сторон прямоугольника. А уже после периметр вычисляется по стандартной формуле.
Бывают и более сложные задачи по нахождению периметра прямоугольники, например, как в приведенном ниже видео:
Вместо заключения
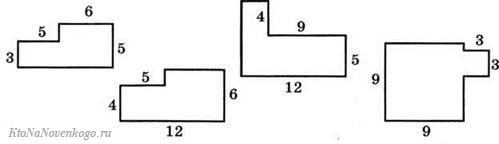
Зная длины сторон, можно вычислять и периметры более сложных прямоугольных фигур. Вот таких:
Страшно выглядят они только на первый взгляд. А на деле, надо просто провести недостающую линию и разделить каждую из фигур на два прямоугольника. Далее вычисляем их по отдельности и складываем друг с другом. Как результат – общий периметр фигуры.
Вот и все, что мы хотели сегодня рассказать.
Общие сведения
Фигуру с четырьмя прямыми углами, то есть равными 90 градусов, называют прямоугольником. Он состоит из четырёх отрезков, каждый из которых соединяется с двумя другими. Впервые упоминание о прямоугольнике встречается в манускриптах Древнего Египта. Но подробные признаки фигуры в III веке до н. э. дал математик Евклид.
В евклидовой геометрии достаточным условием для прямоугольника является существование трёх прямых углов в замкнутой фигуре. Если этот признак выполняется, оставшийся будет прямой в силу правила о сумме углов в простейших многоугольниках: если она не равняется 360 градусам, тело не может называться прямоугольным.
Современное правило, позволяющее отнести фигуру к прямоугольному объекту — параллелограмм называется прямоугольником, когда его 4 угла прямые. Исходя из этого определения, сюда относятся:
- квадрат;
- ромб.
Эти фигуры являются частным видом не только параллелограмма, но и прямоугольника. Для них действуют одинаковые правила и формулы. Единственно, для производных четырёхугольников существует ряд упрощений.
Углы многоугольника называют вершинами, а прямые линии, соединяющие их — гранями или сторонами. Для обозначения первых используют большие буквы латинского алфавита, чаще всего — А, B, C, D. Проставляют их по часовой стрелке начиная с нижнего левого угла. Соответственно, отрезки, соединяющие вершины, подписывают так: AB, BC, CD, AD.
Грани фигуры формируют ширину и длину. Эти названия условны для квадрата и ромба, так как их 4 стороны между собой равны.
В классической прямоугольной фигуре нижнюю грань принимают за ширину, а боковую считают длиной. Узнать их можно, просто измерив размеры или рассчитав по формулам.
В повседневности термины «длина» и «ширина» фактически обозначают пространственные оси координат, расположенные параллельно поверхности земли. За первую принимают более длинную сторону фигуры, вне зависимости от её пространственного расположения. Другими словами, это «размер по оси X» или «размер по оси Y», поэтому понятия о длине и ширине — довольно абстрактные.
Свойства и линии
Из-за того, что прямоугольник — это параллелограмм, все свойства последнего справедливы и к нему. В первую очередь для него характерно, что противоположные стороны являются параллельными, то есть лежат на непересекающихся прямых. Отсюда следует, что фигуры отличаются друг от друга только размерами двух граней.
К основным свойствам прямоугольника относят:
- противолежащие стороны имеют равную длину: AB = CD, BC = AD;
- все углы равны 90 градусов;
- отрезки, обозначающие ширину и длину, всегда перпендикулярные друг другу: AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB;
- сумма любых двух углов фигуры равняется 180 градусов, соответственно всех четырёх — 360;
- в четырёхугольном теле можно провести 2 диагонали, длины которых будут совпадать по величине: AB = BC;
- сумма квадратов диагональных отрезков равняется удвоенной сумме квадратов сторон фигуры: AC2 + BD2 = 2 (AB2 + BC2);
- построенная диагональ разделяет прямоугольник на 2 одинаковые фигуры — прямоугольные треугольники;
- точка пересечения прямых линий, соединяющая попарно противоположные углы, является центром фигуры и описанной окружности;
- диагонали в месте пересечения разделяются на 4 равных отрезка;
- в многоугольник, у которого длина не равна ширине, вписать окружность нельзя, поэтому её можно построить только для частных случаев прямоугольника.
На свойстве, что сложенные квадраты диагоналей можно найти как сумму квадратов всех его сторон, построено решение многих геометрических задач. Нелишним будет доказательство теоремы. Пусть имеется прямоугольник, у которого линии AC и BD — диагонали. Если изобразить многоугольник на рисунке и построить отрезки, можно увидеть, что каждая диагональ делит фигуру на 2 треугольника: ABC и BDC.
Используя теорему косинусов, можно записать: AC2 = AB2 + BC2 — 2 * AB * BC * cos (ABC); BD2 = CD2 + BC2 — 2 * CD * BC * cos (BCD). После сложения полученных выражений получится запись: AC2 + BD2 = AB2 + BC2 — 2 * AB * BC * cos (ABC) + CD2 + BC2 — 2 * CD * BC * cos (BCD).
Так как по свойству прямоугольной фигуры противоположные стороны равны, уравнение примет вид: AC2 + BD2 = 2AB2 + 2BC2 — 2 * AB * BC * cos (ABC) — 2 * AB * BC * cos (BCD). Учитывая, что сумма двух углов равняется 1800, полученное выражение можно переписать так: AC2 + BD 2 = 2 (AB 2 + BC 2). Что и следовало доказать.
Формулы нахождения длины
Существует несколько способов, позволяющих найти длину. Как лучше это сделать и какой алгоритм использовать, зависит от известных данных и личных предпочтений решающего. Как показывает практика, найти величину достаточно просто, если есть значение ширины и ещё одного из параметров многоугольника.
Найти длину (BC) прямоугольника можно следующим образом:
- Зная площадь и ширину. Так как первая величина находится из произведения сторон S = AB * BC, длина будет равняться отношению размера замкнутой плоскости к ширине: BC = S/AB.
- По известному периметру и примыкающей стороне. Периметр прямоугольника равен сумме всех его граней: P = AB + BC + CD + AD. Так как противолежащие стороны равны, равенство можно переписать так: P = 2AB + 2BC. Отсюда следует, что BC = (P — 2AB)/2.
- Если известна диагональ и ширина. Отрезок, соединяющий противолежащие вершины, делит многоугольник на 2 прямоугольных треугольника, поэтому можно воспользоваться теоремой Пифагора: a = √ ( b2 + c2), где: a — гипотенуза (диагональ); b, с — катеты (ширина и длина). Отсюда: b = √ (c2 — a2) = ВС = √ CA2 — AB 2.
- Используя формулу радиуса описанной окружности: R = √ (AB2 — BC2)/2. Для квадрата или ромба формула выглядит проще: R = a / √2 = d / 2, где d — диаметр описанного круга.
При решении задач может случиться, что исходные данные не позволяют напрямую воспользоваться формулами для нахождения длины. В этом случае приходится использовать переходные выражения.
Диагональ прямоугольника можно вычислить через радиус описанной окружности d = 2 R или используя синус угла: d = a / sin (a), то есть найти из отношения прилегающей функции к ширине. Исходя из этого, можно вывести ещё одну формулу для поиска длины: BC = CA * cos (a).
Площадь фигуры можно найти не только как произведение сторон, но и зная размер диагонали с величиной синуса острого угла: S = d2 * sin (b) / 2, где b — угол между диагоналями. Приведённых формул будет достаточно для нахождения длины прямоугольника. При этом следует отметить важное свойство фигуры — высота многоугольника является шириной. Это свойство необходимо знать, так как в примерах нередко даётся размер не стороны, а именно высоты.
Решение примеров
Несмотря на то что формулы довольно простые, запомнить их простой зубрёжкой сложно. Чтобы материал закрепился, нужно научиться их применять на практике. Если понять принцип нахождения длины, многие из этих выражений можно будет вывести самостоятельно.
Вот некоторые задачи, рассчитанные на учащихся седьмых классов, рекомендуемые к самостоятельной проработке:
- Определить длину прямоугольного многоугольника, у которого длина в 4 раза больше ширины. Периметр тела равен 20 см. Для решения задачи нужно принять сторону фигуры за х. Тогда длина будет составлять 4х. Согласно формуле, периметр равен: P = 2AB + 2 BC = 2* x + 2 * 4x. После подстановки значения P и выражения неизвестного, должно получиться следующее равенство: x = 20 / 10 = 2. Отсюда следует, что искомая длина равняется: BC = 4 * x = 4 * 2 = 8 см. Задача решена.
- Длина прямоугольной фигуры больше её ширины на 2. Если ширина увеличится на 3 см, а длина на 8, площадь фигуры возрастёт в 3 раза. Найти длину. Чтобы решить задачу, нужно рассуждать следующим образом: пусть x ширина для первого состояния фигуры. Значит, длина этой фигуры будет x + 2. Соответственно, площадь равна: S = x * (x + 2). После трансформации ширина изменилась до значения x + 3, а длина — х + 2 + 8 = х + 10. Площадь новой фигуры равна: S = (х + 3) * (х + 10). После раскрытия скобок получится уравнение: 2 * х2 — 7* х — 30 = 0. После его решения должно получиться, что x = 6 см. Отсюда длина будет равняться: 6 + 2 = 8 см.
- Определить длину и ширину прямоугольника ABCD, в который вписаны 3 круга, если радиус каждой описанной окружности равен 5 см. Для решения примера нужно вспомнить, что ширина многоугольника равна двум радиусам круга или его диаметру. Значит, AB = 2 * 5 = 10 см. Соответственно, длина будет составлять 3 диаметра или 6 радиусов: BC = 6 * 5 = 30 см. Ответ найден.
В процессе изучения материала совсем не зазорно пользоваться так называемыми онлайн-калькуляторами. Это сайты, предлагающие своим пользователям рассчитать различные математические величины по исходным данным. Их интересность не только в том, что можно получить готовый ответ, но и в появлении возможности просмотреть подробное решение. Это как раз и позволит устранить пробелы в знании на стадии обучения.