Как найти координаты вектора в базисе
Решение:
Записываем матрицу перехода А:
и находим ее определитель
<>0
Видим, что ранг матрицы С равен трем. Из теоремы о базисном миноре векторы f1 , f2 , f3 линейно независимы, а поэтому могут быть приняты в качестве базиса пространства R 3 .
Находим обратную матрицу А -1 .
Транспонированная матрица:
Обратная матрица А -1
Находим координаты вектора х относительно нового базиса.
Пример №1 . Даны векторы a<1;2;1>, b<2;-2;1>, c <1;-2;0>и d <0;3;1>. Установить, что векторы a , b , c образуют базис, и найти координаты вектора d в этом базисе.
Решение:
Соотношение, записанное для векторов d = αa + βb + γc, справедливо для каждой из проекций:
α*1 + β*2 + γ*1 = 0
α*2 — β*2 — γ*2 = 3
α*1 + β*1 + γ0 = 1 т.е. получена алгебраическая система трёх уравнений с тремя неизвестными. Решение системы удобнее вычислять методом Крамера или методом обратной матрицы:
α = 1/2; β = 1/2; γ = -3/2
следовательно, и вектор d имеет разложение в базисе a, b, c :
d = 1/2a + 1/2b — 3/2c
Пример №2 . Даны векторы 


Пример №3 . Даны два линейных преобразования:
х’1 = a11x1 + a12x2 + a13x3, х»1 = b11x’1 + b12x’2 + b13x’3,
х’2 = a21x1 + a22x2 + a23x3, х»2 = b21x’1 + b22x’2 + b23x’3,
х’3 = a31x1 + a32x2 + a33x3, х»3 = b31x’1 + b32x’2 + b33x’3,
Средствами матричного исчисления найти преобразование, выражающее х»1, x»2, x»3 через х1, х2, х3.
х’1 = 4x1 + 3x2 + 5x3, х»1 = — x’1 + 3x’2 — 2x’3,
х’2 = 6x1 + 7x2 + x3, х»2 = — 4x’1 + x’2 + 2x’3,
х’3 = 9x1 + x2 + 8x3, х»3 = 3x’1 — 4x’2 + 5x’3,
Решение. Используя калькулятор, получаем:
Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B.
Вычислим определитель матрицы А:
∆ = 4*(7*8 — 1*1) — 6*(3*8 — 1*5) + 9*(3*1 — 7*5) = -182
Определитель матрицы А равен detA=-182
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1 : A -1 ·A·X = A -1 ·B, тогда получим E·X = A -1 ·B, или X = A -1 ·B.
Найдем обратную матрицу A -1 .
| A -1 = -1/182 |
|
Матрицу Х ищем по формуле:
| X = A -1 ·B = -1/182 |
|
* | = |
|
Пример №4 . В декартовой прямой системе координат даны вершины пирамиды A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1). Найдите:
а) длину ребра AB;
б) косинус угла между векторами AB и AC ;
в) уравнение ребра AB;
г) уравнение грани ABC;
д) уравнение высоты, опущенной из вершины D на грань ABC;
е) координаты векторов e 1= AB , e 2= AC , e 3= AD и докажите, что они образуют линейную независимую систему;
ж) координаты вектора MN , где M и N – середины ребер AD и DC соответственно;
з) разложение вектора MN по базису ( e 1, e 2, e 3)
Решение. Пункты (а-д) решаются через онлайн калькулятор.
Задание 1 . Разложить вектор d =(8;-5) по векторам a =(1;-2) и b =(2;3).
Решение. Векторы a и b образуют базис на плоскости, так как они не коллинеарны (
Следовательно, вектор d = α a +β b , где α и β – коэффициенты, которые надо найти.
Таким образом, имеем равенство
8i-5j=α(i-2j)+β(2i+3j)=(α+2β)i+ (-2α+3β)j.
В координатной форме это равенство примет вид 
Решим полученную систему уравнений.
Векторное пространство: размерность и базис, разложение вектора по базису
В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.
Введем некоторые определения.
Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.
Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:
e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )
Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.
Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.
Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.
Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.
Переставив местами в исходной системе другие векторы, получим еще один базис.
Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.
Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.
Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.
Рассмотрим применение данной теории на конкретных примерах.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 )
Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.
Решение
Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.
A = 3 2 3 — 2 1 — 1 1 2 — 2 A = 3 — 2 1 2 1 2 3 — 1 — 2 = 3 · 1 · ( — 2 ) + ( — 2 ) · 2 · 3 + 1 · 2 · ( — 1 ) — 1 · 1 · 3 — ( — 2 ) · 2 · ( — 2 ) — 3 · 2 · ( — 1 ) = = — 25 ≠ 0 ⇒ R a n k ( A ) = 3
Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.
Ответ: указанные векторы являются базисом векторного пространства.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 ) d = ( 0 , 1 , 2 )
Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.
Решение
Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , — 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , — 1 , — 2 ) является базисом.
Ответ: указанная система векторов не является базисом.
Исходные данные: векторы
a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )
Могут ли они являться базисом четырехмерного пространства?
Решение
Cоставим матрицу, используя в качестве строк координаты заданных векторов
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
По методу Гаусса определим ранг матрицы:
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
1 2 3 3 0 1 0 2 0 1 — 1 1 0 1 — 2 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 — 2 — 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4
Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.
Ответ: заданные векторы являются базисом четырехмерного пространства.
Исходные данные: векторы
a ( 1 ) = ( 1 , 2 , — 1 , — 2 ) a ( 2 ) = ( 0 , 2 , 1 , — 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )
Составляют ли они базис пространства размерностью 4?
Решение
Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.
Ответ: нет, не составляют.
Разложение вектора по базису
Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.
Таким образом, мы пришли к формулировке важнейшей теоремы:
Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.
Докажем эту теорему:
зададим базис n -мерного векторного пространства — e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :
x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n — некоторые числа.
Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:
Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:
1 — x 1 ) · e ( 1 ) + ( x
2 — x 2 ) · e ( 2 ) + . . . ( x
Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x
2 — x 2 ) , . . . , ( x
n — x n ) будут равны нулю. Из чего справедливым будет: x 1 = x
n . И это доказывает единственный вариант разложения вектора по базису.
При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .
Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.
Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .
Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.
Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x
Вектор x → будет представлен следующим образом:
2 · e ( 2 ) + . . . + x
Запишем это выражение в координатной форме:
( x 1 , x 2 , . . . , x n ) = x
1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x
2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x
n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x
2 e 1 ( 2 ) + . . . + x
2 e 2 ( 2 ) + + . . . + x
n e 2 ( n ) , . . . , x
2 e n ( 2 ) + . . . + x
Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x
n e 2 n ⋮ x n = x
Матрица этой системы будет иметь следующий вид:
e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )
Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x
n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .
Применим рассмотренную теорию на конкретном примере.
Исходные данные: в базисе трехмерного пространства заданы векторы
e ( 1 ) = ( 1 , — 1 , 1 ) e ( 2 ) = ( 3 , 2 , — 5 ) e ( 3 ) = ( 2 , 1 , — 3 ) x = ( 6 , 2 , — 7 )
Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.
Решение
Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .
Используем метод Гаусса:
A = 1 — 1 1 3 2 — 5 2 1 — 3
1 — 1 1 0 5 — 8 0 3 — 5
1 — 1 1 0 5 — 8 0 0 — 1 5
R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.
Пусть в базисе вектор x → имеет координаты x
3 . Связь этих координат определяется уравнением:
3 e 1 ( 3 ) x 2 = x
3 e 2 ( 3 ) x 3 = x
Применим значения согласно условиям задачи:
Решим систему уравнений методом Крамера:
∆ = 1 3 2 — 1 2 1 1 — 5 — 3 = — 1 ∆ x
1 = 6 3 2 2 2 1 — 7 — 5 — 3 = — 1 , x
1 ∆ = — 1 — 1 = 1 ∆ x
2 = 1 6 2 — 1 2 1 1 — 7 — 3 = — 1 , x
2 ∆ = — 1 — 1 = 1 ∆ x
3 = 1 3 6 — 1 2 2 1 — 5 — 7 = — 1 , x
Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x
Ответ: x = ( 1 , 1 , 1 )
Связь между базисами
Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:
c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
Указанные системы являются также базисами заданного пространства.
n ( 1 ) — координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:
1 ( 1 ) e 1 ( 1 ) + c
2 ( 1 ) e 1 ( 2 ) + . . . + c
n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c
1 ( 1 ) e 2 ( 1 ) + c
2 ( 1 ) e 2 ( 2 ) + . . . + c
n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c
1 ( 1 ) e n ( 1 ) + c
2 ( 1 ) e n ( 2 ) + . . . + c
В виде матрицы систему можно отобразить так:
( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c
n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Сделаем по аналогии такую же запись для вектора c ( 2 ) :
( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c
n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
И, далее действуя по тому же принципу, получаем:
( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c
n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Матричные равенства объединим в одно выражение:
c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c
n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )
Оно и будет определять связь векторов двух различных базисов.
Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :
e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e
n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )
Дадим следующие определения:
n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )
к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .
n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )
к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .
Онлайн калькулятор. Разложение вектора по базису.
Этот онлайн калькулятор позволит вам очень просто разложить вектор по базисным векторам.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач и закрепить пройденый материал.
Калькулятор для разложения вектора по базисным векторам
Выберите размерность пространства
Количество координат в векторе:
Введите значение базисных векторов:
Введите значение вектора, который необходимо разложить по базису:
Инструкция использования калькулятора для разложение вектора по базисным векторам
- Для того чтобы разложить вектор по базисным векторам онлайн:
- выберите необходимую вам размерность пространства (количество координат в векторе);
- введите значения базисных векторов;
- введите значения вектора который нужно разложить по базису;
- Нажмите кнопку «Разложить вектор по базису» и вы получите детальное решение задачи.
Ввод данных в калькулятор для разложение вектора по базисным векторам
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора разложение вектора по базисным векторам
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Теория. Разложение вектора по базису
Чтобы разложить, вектор b по базисным векторам a1 , . an , необходимо найти коэффициенты x 1, . xn , при которых линейная комбинация векторов a1 , . an равна вектору b .
Коэффициенты x 1, . xn будут координатами вектора b в базисе a1 , . an .
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
http://zaochnik.com/spravochnik/matematika/vektory/vektornoe-prostranstvo/
http://ru.onlinemschool.com/math/assistance/vector/basis_expansion/
Координаты вектора в данном базисе.
Базисом
векторного пространства
называется такая упорядоченная линейно
независимая система векторов, что любой
вектор пространства можно представить
в виде линейной комбинации векторов
этой системы.
В трехмерном
векторном пространстве базис состоит
из трех векторов, который обычно
обозначается так: {е1,
е2,
е3 }.
Базис называется
ортонормированным, если длины всех
базисных векторов равны единицы, и
базисные векторы попарно перпендикулярны.
Ортонормированный базис обычно
обозначается так: {i,
j,
k
}.
Координатами
вектора m
в базисе
{е1,
е2,
е3 }
называются
коэффициенты разложения вектора m
по векторам базиса, т.е. если m
= хе1
+ уе2
+ zе3,
то числа х, у, z
— координаты вектора m.
В этом случае будем записывать m(х,
у, z).
Имеет место
теорема
о координатах линейной комбинации:
если вектор m=
x
а + y
b
и
а(а1,а2,а3),
b(b1,b2,b3)
m(m1,m2,m3),
то
m1
=x a1
+ y b1,
m2
=x a2
+ y b2,
m3
=x a3
+ y b3.
1.24.
Даны векторы а(2,
3, -1),
b
(0,1,4), с(1,0,-3).
Найти координаты векторов: а) 2а
— b — 2с,
б)
а — b
— 3с,
в)
а + 2
b +3
с), г) а
— b
– с,
д)
( а + b),
е)
(а —
2 b + с).
ОТВЕТ.
а) (2,5,0), б) (-1,2,4), в) (5,5,-2), г) (1,2,-2), д) (1,1,3),
е) (1,,-4)
ПРИМЕР 1.7
Даны векторы
а(1,1,2),
b (-2,
3 5), с(-4,1,1),
d
(0, -1, 3) Можно ли вектор d
представить
в виде линейной комбинации векторов а,
b, с ?
Если да, то найти коэффициенты этой
линейной комбинации.
РЕШЕНИЕ
Выясним,
существуют ли такие числи х, у, z,
что
d
= х
а + у
b + z
с. (1)
По теореме о
координатах линейной комбинации векторов
из равенства (1) получаем выражение для
первой координаты вектора d
через первые
координаты векторов а,
b, с, и
аналогичные выражения для вторых и
третьих координат
0 = х — 2у — 4 z
(2)
-1 = х + 3у + z
(3)
3 = 2х + 5у + z
(4)
Выясним, имеет ли
эта система решение. Из (2) следует, что
х
= 2у + 4z
(5)
Затем, подставляя
(5) в (3) и (4), получаем:
5у
+ 5z
= -1 (6)
9у
+ 9z
= 3 (7)
Система, состоящая
из уравнений (2), (3), (4), равносильна
системе, состоящей из уравнений (5), (6),
(7) . Ясно, что последняя система не имеет
решений, следовательно, и данная система
не имеет решений,. Поэтому вектор d
нельзя
представить
в виде линейной комбинации векторов а,
b, с.
■
1.25.
Определить, какие из данных троек
векторов линейно зависимы:
а) а(-3,0,
2), b
(2, 1, -4), с(11,
-2, -2); б) а(1,
0, 7), b
(-1, 2, 4), с(3,
2, 1);
в) а(5,
-1,4), b
(3,-5, 2), с(-1,-13,
-2).
ОТВЕТ..
а), с) линейно зависимы.
1.26.
Представить вектор d
как линейную комбинацию векторов а,
b, с:
1)
а(2,3,1),
b (5,
7, 0), с(3,
-2, 4), d
(4, 12, -3);
2) а(5,
-2, 0),
b (0,
-3, 4), с(-6,
0, 1), d
(25, -22, 16);
3)
а(3, 5, 6),
b (2,
-7, 1), с(12,
0, 6), d
(0, 20, 18).
ОТВЕТ.
1) d
= а + b + с,
2) d
= 5а
+ 4 b,
3) d
= 4а
– с.
1.27.
Можно ли вектор d
(1,1,1) представить в виде линейной
комбинации векторов а(1,-1,0),
b (2,2,1),
с(0,-4,-1)?
ОТВЕТ..
Нет.
1.28.
Даны векторы а(х,
3, 4),
b (-1,
5, у). Существуют
ли такие числа х и у, для которых система
векторов {а,
b } линейно
зависима ?
ОТВЕТ.
Да, х = —
,
у =
.
ПРИМЕР 1.8
В параллелепипеде
АВСDА1В1С1D1
К – середина ребра АА1,
точка М лежит на ребре ВС и ВМ =
ВС, О = А1С1
В1D1.
Найти координаты вектора
в базисе {,
,
}
.
РЕШЕНИЕ
Так как координаты
вектора в данном базисе это коэффициенты
разложения этого вектора по векторам
базиса, то данную задачу можно
сформулировать так: выразить вектор
через векторы
,
,
,
поэтому
будем действовать так же, как при решении
ПРИМЕРА 1.3.
1)
=
+
=
+
= 2
+
,
т.е.
= 2
+
. (1).
2) Выразим вектор
через базисные векторы.
=
+
= —
+
.
(2)
3) Выразим вектор
через базисные векторы.
=
+
=
= —
–
(3)
4) Подставим (2) и
(3) в (1), получим
= 2(—
+
)
+
(-
–
) = 2
–
–
.
Следовательно,
первая координата вектора
равна 2, вторая координата равна —
,
третья координата равна —
,
т.е.
(2, —,
—
).
ОТВЕТ.
(2, —,
—
).
1.29.
АВСD – тетраэдр. М и К – точки пересечения
медиан граней ВСD и АDС, N
– середина АВ, Р
ВС и ВР :
РС = 1 : 2.
Найти координаты векторов
,
в базисе {,
,
}
.
ОТВЕТ.
(
,
,
),
(
,
,
0),
(
,0, —
),
(-
,
,
).
1.30.
АВСD – тетраэдр. N
и К середины ребер ВС и АС. Найти
координаты векторов
и
в базисе {}
.
ОТВЕТ.
(-1,2,-2),
(2,-4,2).
1.31.
В тетраэдре АВСD М- середина ВС, а N
– точка пересечения медиан грани АDС.
Найти координаты векторов
и
в базисе {,
,
}.
ОТВЕТ.
(-1,-1,2),
(-
,
,
).
1.32.
В тетраэдре АВСD N
— середина ВС, а М и К – точки пересечения
медиан граней ВСD и АВD. Найти координаты
векторов
и
в базисе {,
,
}.
ОТВЕТ.
(-
,
1,
),
(-1,
,
).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
оксана николаевна кузнецова
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Вектор в произвольном линейном пространстве — это некоторый элемент этого пространства.
Замечание 1
Базисом трёхмерного пространства называют некоторые линейно независимые вектора $a, b$ и $c$, если любой вектор $d$ может быть выражен в виде линейной комбинации этих векторов, то есть существуют некоторые вещественные коэффициенты $λ, μ$ и $ν$, причём такие, что будет соблюдаться условие $d= λ cdot a + μcdot b + ν cdot c left( 1 right)$.
Числа $λ, μ$ и $ν$ называются координатами рассматриваемого вектора относительно некоторого базиса $a, b$ и $c$.
В контексте плоскости базисом будет два независимых вектора, лежащих в этой плоскости, а не три, как в объёмном мире.
Любой вектор $d$ имеет лишь единственное разложение по базису векторов, то есть его координаты задаются однозначно через используемый базис.
Определение 1
Аффинными координатами некоторой точки $M$ в пространстве называются координаты точки относительно базиса пространства $a, b$ и $c$ и некоторой точки $O$, которую принимают за начало координат.
Декартова система координат является примером аффиной системы координат, причём базисные вектора в ней принято обозначать не буквами $a, b$ и $c$, а $i, j$ и $k$, представляющими собой направленные ортогональные между собой отрезки, причём длина каждого равна единице.
Для декартовой системы координат формула разложения выглядит так:
$d = X cdot vec{i} + Y cdot vec{j} + Z cdot vec{k}$
Здесь $X, Y$ и $Z$ — координаты вектора, а $ i, j$ и $k$ — базис.
Через базис декартовой системы координат выражается скалярное произведение векторов, заданных в этом пространстве. Для этого их координаты записываются через специальную матрицу.
Пример 1
Докажите, что вектора, $a_1…a_4$, перечисленные ниже, являются базисом пространства $mathbb{R^4}$.
$a_1 = (1; 2; -1: -2)$;
$a_2 = (2; 3 0; -1)$;
$a_3 = (1; 2; 1; 4)$;
$a_4 = (1; 3; -1; 0)$
Решение:
Размерность данного пространства равна 4, а это значит, что для проверки того, являются ли эти вектора базисом, нужно доказать их линейную независимость, то есть доказать, что ранг матрицы, составленной из координат этих векторов как из строчек, равен количеству строк.
Составленная матрица имеет вид:
$A = begin{pmatrix} 1 & 2 & -1 & -2 \ 2 & 3 & 0 & -1 \ 1 & 2 & 1 & 4 \ 1 & 3 & -1 & 0 \ end{pmatrix}$
Преобразуем её к треугольной, для краткости описания выполняемых операций строчки будем записывать (n), здесь $n$ — номер строчки.
1) (4) — (1); (3) — (1); (2) — (1) $cdot 2$:
$begin{pmatrix} 1 & 2 & -1 & -2 \ 0 & -1 & 2 & 3 \ 0 & 0 & 2 & 6 \ 0 & 1 & 0 & 2 \ end{pmatrix}$
2) (4) + (2):
$begin{pmatrix} 1 & 2 & -1 & -2 \ 0 & -1 & 2 & 3 \ 0 & 0 & 2 & 6 \ 0 & 0 & 2 & 5 \ end{pmatrix}$
3) (4) — (3):
$begin{pmatrix} 1 & 2 & -1 & -2 \ 0 & -1 & 2 & 3 \ 0 & 0 & 2 & 6 \ 0 & 0 & 0 & -1 \ end{pmatrix}$
Приведённая матрица имеет ранг 4, а значит данные вектора образуют базис этого пространства.
«Разложение вектора по базису векторов: формулировка с примерами решения» 👇
Пример 2
Пусть вектор $vec{k}$ можно разложить с использованием базиса $vec{a}$ и $vec{b}$ по формуле
$vec{k}= 5cdot vec{a} – 3 cdot vec{b}$. Каковы его координаты в соответствии с этим базисом?
Решение:
$vec{a}$ и $vec{b}$ — единичные вектора данного двумерного пространства, а это значит, что коэффициенты при них в заданном равенстве и являются координатами в этом базисе:
$vec{k} = (5; — 3)_{{a; b}}$.
Пример 3
Дан базис из трёх векторов $(1; 1; 3), ( -3; 4; 9), (2; -2; 4)$ и вектор $vec{k}=(8; -9; 6)$. Разложите данный вектор по заданному базису.
Решение:
Воспользуемся формулировкой разложения $(1)$:
$k_1 cdot (1; 1; 3) + k_2 cdot ( -3; 4; 9) + k_3 cdot (2; -2; 4) = (8; -9; 6)$;
Для того чтобы узнать координаты в данном базисе, составим расширенную матрицу, действия со строчками будем записывать как в предыдущем примере:
$begin{array}{ccc|c} 1 & -3 & 2 & 8 \ -1 & 4 & -2 & -9 \ 3 & 9 & 4 & 6 \ end{array}$
1) (2) — (1); (3) — (1) $cdot 3$:
$begin{array}{ccc|c} 1 & -3 & 2 & 8 \ 0 & 1 & 0 & -1 \ 0 & 18 & -2 & -18 \ end{array}$;
2) (1) + (2) $cdot 3$; (3) — (2) $cdot 18$:
$begin{array}{ccc|c} 1 & 0 & 2 & 5 \ 0 & 1 & 0 & -1 \ 0 & 0 & -2 & 0 \ end{array}$;
3) (3) : (-2):
$begin{array}{ccc|c} 1 & 0 & 2 & 5 \ 0 & 1 & 0 & -1 \ 0 & 0 & 1 & 0 \ end{array}$;
4) (1) — (3) $cdot 2$:
$begin{array}{ccc|c} 1 & 0 & 0 & 5 \ 0 & 1 & 0 & -1 \ 0 & 0 & 1 & 0 \ end{array}$;
Координатами вектора $vec{k}$ в заданном базисе будут $(5; — 1; 0)$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Базис векторов и линейные действия над векторами аналитическим путём (теория и решение задач)
Базис – это неопределённое количество векторов в векторном пространстве, и абсолютно любой из этих векторов может создавать линейную комбинацию.
Помощь в написании работы
Базис векторов
Система линейно независимых векторов пространства, за которыми можно разложить произвольный вектор – это и есть базис векторов или этого пространства.
Так, согласно доказательству (3), произвольные три некомпланарные векторы ,
,
, образуют в трёхмерном пространстве базис, по которому, согласно формуле (2) можно единственным образом разложить произвольный вектор
пространства. Векторы
,
,
, которые образуют базис называются базисными.
Будем считать, что базисные векторы ,
,
сведены к точке
.
Числ , про которые упоминалось в разделах “линейно зависимая и линейно независимые системы векторов”, называют координатами вектора в заданном базисе, и пишут:
.
Аналогично, на плоскости базис образуют какие-то два неколлинеарные векторы, а любой некомпланарный с ними может быть разложен по этому базису.
Базисным вектором на прямой линии может быть любой ненулевой вектор.Согласно свойствам линейных операций над векторами, следует, что при сложении и вычитании векторов в данном базисе прибавляются и отнимаются их соответствующие координаты, а при умножении вектора на число умножаются не это число координаты вектора, то есть:
.
.
.
Векторы равны, когда у них одинаковые соответствующие координаты.
Линейные действия над векторами аналитическим путём
Если раньше линейные действия над векторами осуществлялись графически, то теперь эти операции можно выполнять аналитически, не пользуясь рисунком. Давайте вспомним и сформулируем линейные действия:
Чтобы прибавлять (отнимать) два вектора, необходимо прибавить (отнять) их соответствующие координаты, то есть:
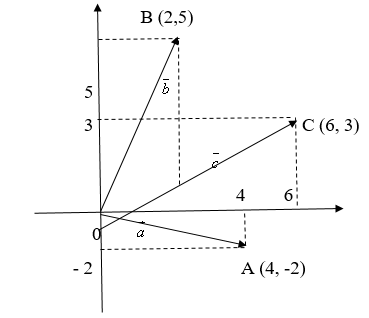
Приведём пример:
Найти сумму векторов и
, заданных на плоскости
.
Решение:
Согласно правилу 1 у нас получается:
= (6, 3).
Построим эти векторы: .
Рис. 3
Мы видим, что четырёхугольник OABC – параллелограмм. Координаты вектора мы сначала получили путём вычислений (аналитически), без помощи рисунка. Рисунок только подтверждает правило параллелограмма при прибавлении векторов, поэтому дальше рисунками будем пользоваться для наглядности.
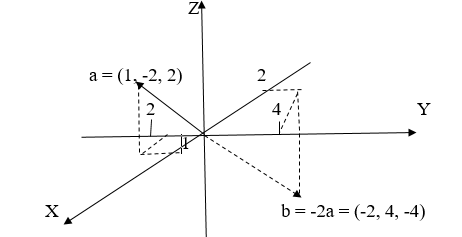
Чтобы умножить вектор на число, необходимо каждую из его координат умножить на это число:
Дан вектор Найти
Решение:
Согласна правилу 2 у нас получается:
Геометрическое изображение смотрите на рис. 4.
Рис. 4
Два вектора равны, если у них равны соответствующие координаты:
.
Теперь вы понимаете, как получить координаты вектора не только графическим путём, но и аналитическим. В дальнейшем у вас не возникнет сложностей по этому поводу.
Как найти базис вектора, пример
В некотором базисе заданы своими координатами векторы и
Разложить вектор
по базису, который образовался из векторов
и
Решение:
Разложение вектора по базису
и
имеет такой вид:
где числа и
– неизвестные. Чтобы их найти, подставим в последнее равенство координаты векторов
и
, а тогда воспользуемся свойствами 1 и 2:
Согласно свойству 3 про равенство векторов, получим систему уравнений:
Первое равенство умножаем на 1, а второе на (- 2) и в итоге у на получается:
.
Значит, ответ у нас выходит:
Разложение векторов по векторам базиса
Краткая теория
Вектор
называется линейной комбинацией векторов
векторного пространства
,
если он равен сумме произведений этих векторов на произвольные действительные
числа:
где
– какие угодно действительные числа
Векторы
векторного пространства
называются линейно зависимыми, если существуют
такие числа
,
не равные одновременно нулю, что
В противном случае векторы
называются линейно независимыми.
Из приведенных выше определений следует, что векторы
линейно независимы, если последнее равенство
справедливо лишь при
,
и линейно зависимы, если равенство выполняется, когда хотя бы одно из чисел
отлично от нуля.
Можно показать, что если векторы
линейно зависимы, то
по крайней мере один из них линейно выражается через все остальные. Верно и
обратное утверждение о том, что если один из векторов выражается через
остальные, что все эти векторы в совокупности линейно зависимые.
Примеров линейно независимых векторов являются два неколлениарных на плоскости или три некомпланарных в
трехмерном пространстве, т.е. определитель, составленный из координат этих
векторов должен быть не равен нулю.
Пример решения задачи
Задача
Даны векторы
и
в
некотором базисе. Показать, что векторы
образуют
базис, и найти координаты вектора
в
этом базисе.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Составим из координат векторов определитель и
вычислим его:
Определитель не равен нулю, следовательно, система
векторов является линейно-независимой и образует базис трехмерного
пространства.
Вектор
единственным образом разлагается по векторам
этого базиса.
Приравнивая соответствующие координаты векторов,
получаем следующую систему 3-х линейных уравнений:
Решим систему уравнений
методом Крамера:
Ответ:
Координаты вектора
в базисе векторов
или