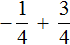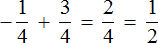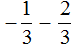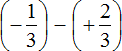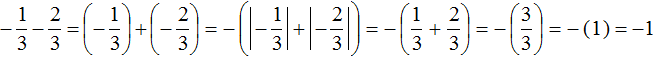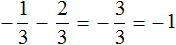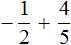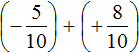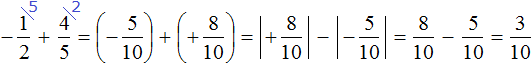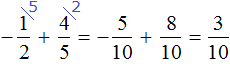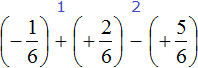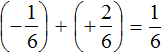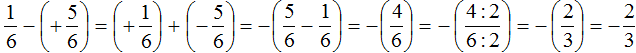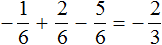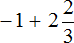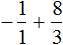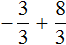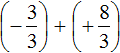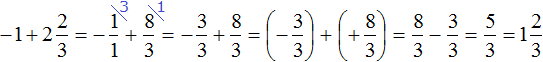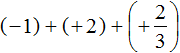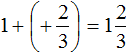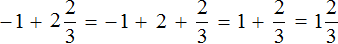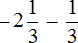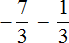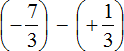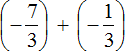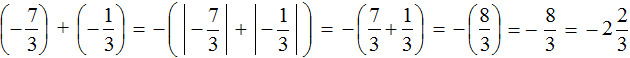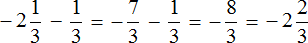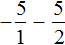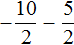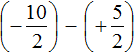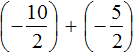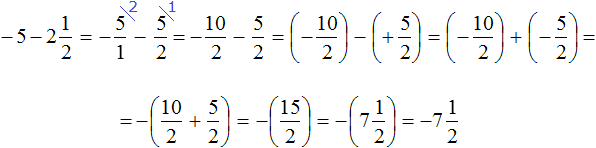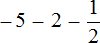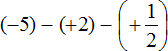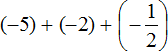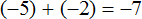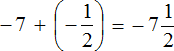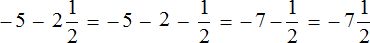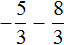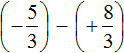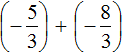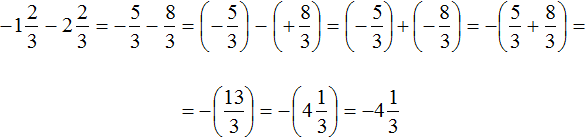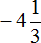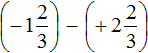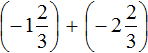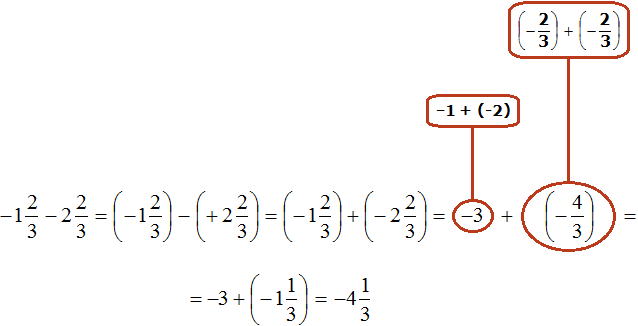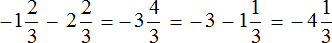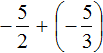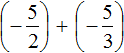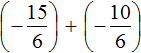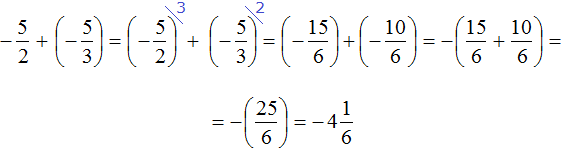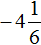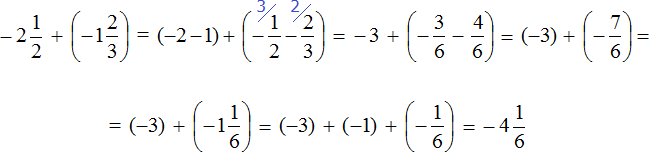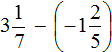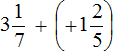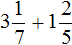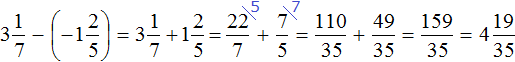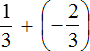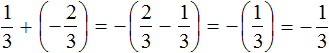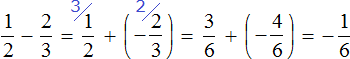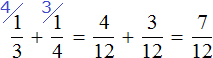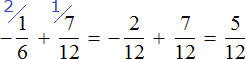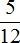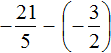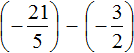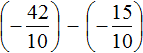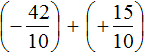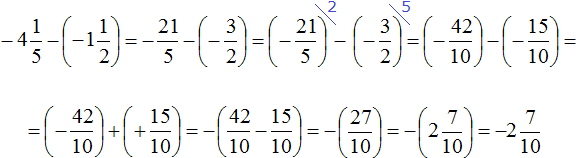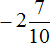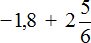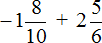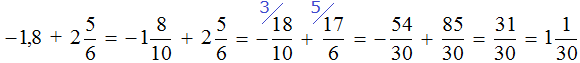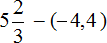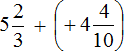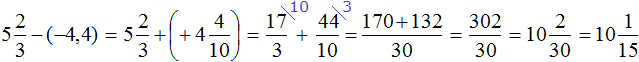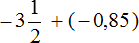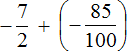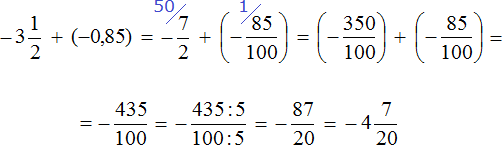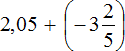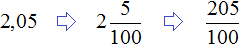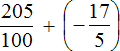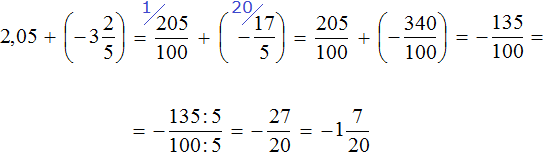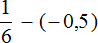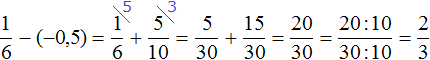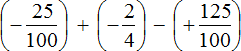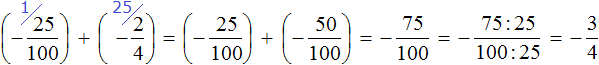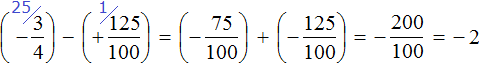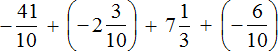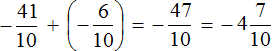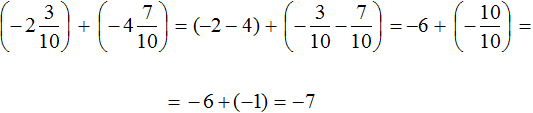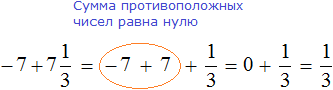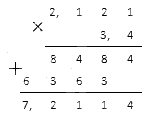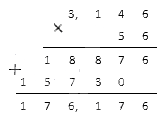Содержание
- Рациональные приёмы вычислений на уроках математики
- «Мозг хорошо устроенный ценится больше, чем мозг хорошо наполненный.»
- Сложение и вычитание рациональных чисел
Рациональные приёмы вычислений на уроках математики
Разделы: Математика
Класс: 4
Ключевые слова: математика
«Мозг хорошо устроенный ценится больше,
чем мозг хорошо наполненный.»
Умения рационально производить вычисления характеризуют довольно высокий уровень математического развития. Знакомство и применение рациональных способов вычислений развивает вариативность мышления, показывает ценность знаний, которые при этом используются. Эти умения чрезвычайно сложны, формируются они медленно и за время обучения в начальной школе далеко не у всех детей могут быть достаточно сформированы.
Говорят, если хотите научиться плавать, вы должны войти в воду, а если хотите уметь решать задачи, то должны начать их решать. Но для начала надо освоить азы арифметики. Научиться считать быстро. Считать в уме можно только при большом желании и систематической тренировки. И тогда перед вами откроется совсем другая математика: живая, полезная, понятная.
Скажите, пожалуйста, как рациональнее сложить 1+ 7, 4 * 8? Какие законы применили?
27 + 46+13? 27 – 19 – 7? Какие свойства, законы? Т.е основы рациональных приёмов вычислений основаны на чём?
Методика преподавания математики в начальных классах раскрывает основы рациональных приёмов вычислений, связанных с выполнением разных математических действий с натуральными числами.
Рациональные приёмы сложения основываются
1. Коммуникативный закон сложения а +в =в +а
2. Ассоциативный закон сложения а+в+с = а+ (в+с)
на коммуникативном и ассоциативном приёмах сложения, а так же свойствах изменения суммы. Рассмотрим некоторые из них.
Свойства сложения.
1.1
а+в+с =У, то (а – к) +с+в = У –к
38+24+15 = 77, то 36+ 24+ 15 = ?
а+в+с=У, то (а+ к) +в +с = У+к
38 + 24+15 = 77, то 40+ 24 + 15 =?
1.2.
а+ в =С , то (а +к ) + (в – к) = С
56 + 27 = 83, то (56 + 4) + (27 – 4) = ?
Какие ещё рациональные приёмы сложения можно применить на уроке математики?
Округление одного из слагаемых; поразрядного сложения; приём группировки вокруг одного и того же «корневого» числа.
Рассмотрим эти приёмы:
13 + 49 + 76 + 61 = (поразрядное сложение)
38 + 59 = 38 + (…округление слагаемого)
26 + 24 + 23 +25 + 24 = (группировка вокруг одного и того же «корневого» числа
Все приёмы рациональных вычислений, связанных с вычитанием, основываются на законах вычитания.
Если уменьшаемое увеличить или уменьшить на число, то соответственно разность увеличится или уменьшится на это же самое число
а – в = С, то (а +к) — в = С +к
74 – 28 = 46, то 77 – 28 = 49
а-в = С , то (а – к ) — в = С-к
74 – 28 = 46, то 71 – 28 = 43
Если вычитаемое увеличить или уменьшить на несколько единиц, то разность измениться в противоположную сторону.
Если уменьшаемое и вычитаемое уменьшить или увеличить на одно и тоже число, то разность не измениться.
Найди верные равенства.
229 – 36 = (229 – 9 ) – ( 36 – 6)
174 – 58 = (174 – 4) – ( 58 – 4)
358 – 39 = ( 358 – 8 ) – (39 – 
617 – 48 = ( 617 – 7 ) – (48 – 
Для рациональных вычислений используют частичные приёмы умножения и деления.
Приём замены множителя или делителя на произведение.
75 * 8 = 75 * 2*2*2=
960 : 15 = 960 : 3 : 5 =
Приём умножения на 9, 99,999, 11 …
87 * 99 = 87 * 100- 87 = 8700 – 87 = 8613
87 * 11 = 87 *10 + 87 = 870+ 87 = 957
Успешное применение различных приёмов зависит от умения подмечать особенности чисел и их сочетаний. Например, познакомив детей в первом классе с натуральным рядом чисел и имея его перед глазами, легко закрепить состав числа.
0 1 2 3 4 5 6 7
Отработав, таким образом, состав чисел в пределах 10 и познакомившись с переместительным законом сложения, дети легко справляются с заданием найти сумму чисел в пределах 10, а в дальнейшем, используя переместительное и сочетательное свойство сложения, легко можно найти сумму других чисел. Например:
48 +14 +22 +36 =120
Существуют приёмы на знаниях некоторых свойств чисел или результатов действий. Легко находить сумму последовательных нечётных чисел, начиная с 1.
Она равна произведению количества слагаемых на самого себя. (проверить)
Рационализация может осуществляться за счет возможности выполнять некоторые арифметические действия. Для этого очень важно научить детей внимательно рассматривать условия задания, суметь подметить все его особенности. Такие задания, как поставь нужный знак действия16 … 17 = 33 ( рассуждать), далее подобные задания усложняются. 8…6…33 = 15
Сравни, не вычисляя
51 : 3 … 30 : 3 + 21 :5
636 :6 … 600 : 6+ 30 : 6+ 6 :6
Задания могут даваться в занимательной форме: Математический лабиринт, составь слово, найди пару , расшифруй пословицу и т.д.
Используй рациональные приёмы вычисления, разгадай слово
Какие приёмы использовали?
Важно показать ученикам красоту и изящество устных вычислений, используя разнообразные вычислительные приёмы, помогающие значительно облегчить процесс вычисления.
СЧЁТ НА ПАЛЬЦАХ: способ быстрого умножения чисел первого десятка на 9. Допустим нам надо умножить 7 на 9. Повернём ладошки к себе, загнём седьмой палец, число пальцев слева от загнутого пальца – это число десятков, а число – справа, количество единиц.
Все задания, которые рассматривались, воспитывают интерес к математике, развивают их математические способности. Такую работу можно продолжать на математическом кружке.
Источник
Сложение и вычитание рациональных чисел
В данном уроке рассматривается сложение и вычитание рациональных чисел. Тема относится к категории сложных. Здесь необходимо использовать весь арсенал полученных ранее знаний.
Правила сложения и вычитания целых чисел справедливы и для рациональных чисел. Напомним, что рациональными называют числа, которые могут быть представлены в виде дроби , где a – это числитель дроби, b – знаменатель дроби. При этом, b не должно быть нулём.
В данном уроке дроби и смешанные числа мы всё чаще будем называть одним общим словосочетанием — рациональные числа.
Пример 1. Найти значение выражения:
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении, является знаком операции и не относится к дроби . У этой дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы запишем его для наглядности:
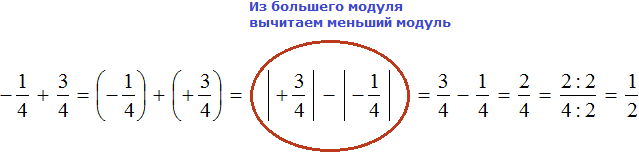
Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того рационального числа, модуль которого больше. А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих дробей до их вычисления:
Модуль рационального числа больше, чем модуль рационального числа . Поэтому мы из вычли 

Некоторые примитивные действия, такие как заключение чисел в скобки и проставление модулей, можно пропустить. Данный пример вполне можно записать покороче:
Пример 2. Найти значение выражения:
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус, стоящий между рациональными числами 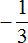
Заменим вычитание сложением. Напомним, что для этого нужно к уменьшаемому прибавить число, противоположное вычитаемому:
Получили сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус:
Запишем решение данного примера покороче:
Примечание. Заключать в скобки каждое рациональное число вовсе необязательно. Делается это для удобства, чтобы хорошо видеть какие знаки имеют рациональные числа.
Пример 3. Найти значение выражения:
В этом выражении у дробей разные знаменатели. Чтобы облегчить себе задачу, приведём эти дроби к общему знаменателю. Не будем подробно останавливаться на том как это сделать. Если испытываете с этим затруднения, обязательно повторите урок действия с дробями.
После приведения дробей к общему знаменателю выражение примет следующий вид:
Заключим каждое рациональное число в скобки вместе своими знаками:
Это сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший модуль, и перед полученным ответом ставим знак того рационального числа, модуль которого больше:
Запишем решение данного примера покороче:
Пример 4. Найти значение выражения
Заключим каждое рациональное число в скобки вместе со своими знаками:
Вычислим данное выражение в следующем порядке: слóжим рациональные числа 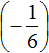
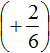
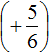
Первое действие:
Второе действие:
Таким образом, значение выражения равно
Пример 5. Найти значение выражения:
Представим целое число −1 в виде дроби 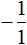

Приведём данные дроби к общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
Заключим каждое рациональное число в скобки вместе со своими знаками:
Получили сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший модуль, и перед полученным ответом ставим знак того рационального числа, модуль которого больше:
Есть и второй способ решения. Он заключается в том, чтобы сложить отдельно целые части.
Итак, вернёмся к изначальному выражению:
Заключим каждое число в скобки. Для этого смешанное число 
Вычислим целые части:
В главном выражении вместо (−1) + (+2) запишем полученную единицу:
Полученное выражение 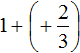
Запишем решение этим способом покороче:
Пример 6. Найти значение выражения
Переведём смешанное число 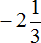
Заключим каждое рациональное число в скобки вместе со своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Запишем решение данного примера покороче:
Пример 7. Найти значение выражение
Представим целое число −5 в виде дроби 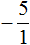

Приведём данные дроби к общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
Заключим каждое рациональное число в скобки вместе со своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Таким образом, значение выражения 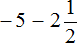
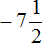
Решим данный пример вторым способом. Вернемся к изначальному выражению:
Запишем смешанное число 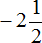
Заключим каждое рациональное число в скобки вместе своими знаками:
Заменим вычитание сложением там, где это можно:
Вычислим целые части:
В главном выражении вместо 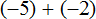
Выражение 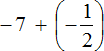
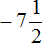

Запишем это решение покороче:
Пример 8. Найти значение выражения
Переведём смешанные числа в неправильные дроби:
Заключим каждое рациональное число в скобки вместе своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Таким образом, значение выражения равно
Данный пример можно решить и вторым способом. Он заключается в том, чтобы сложить целые и дробные части по отдельности. Вернёмся к изначальному выражению:
Заключим каждое рациональное число в скобки вместе со своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус. Но в этот раз слóжим по отдельности целые части (−1 и −2), и дробные 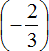
Запишем это решение покороче:
Пример 9. Найти выражения выражения
Переведём смешанные числа в неправильные дроби:
Заключим рациональное число 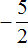
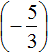
Приведём данные дроби в общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Таким образом, значение выражения 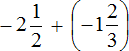
Теперь попробуем решить этот же пример вторым способом, а именно сложением целых и дробных частей по отдельности.
В этот раз, в целях получения короткого решения, попробуем пропустить некоторые действия, такие как: запись смешанного числа в развёрнутом виде и замена вычитания сложением:
Обратите внимание, что дробные части были приведены к общему знаменателю.
Пример 10. Найти значение выражения
Заменим вычитание сложением:
В получившемся выражении нет отрицательных чисел, которые являются основной причиной допущения ошибок. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вычитаемым, а также убрать скобки:
Получилось простейшее выражение, которое вычисляется легко. Вычислим его любым удобным для нас способом:
Пример 11. Найти значение выражения
Это сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:
Пример 12. Найти значение выражения
Выражение состоит из нескольких рациональных чисел. Согласно порядку действий, в первую очередь необходимо выполнить действия в скобках.
Сначала вычислим выражение 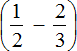
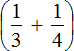
Первое действие:
Второе действие:
Третье действие:
Ответ: значение выражения 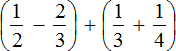
Пример 13. Найти значение выражения
Переведём смешанные числа в неправильные дроби:
Заключим рациональное число 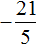
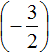
Приведём данные дроби в общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
Заменим вычитание сложением:
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:
Таким образом, значение выражения 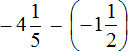
Рассмотрим сложение и вычитание десятичных дробей, которые тоже относятся к рациональным числам и которые могут быть как положительными, так и отрицательными.
Пример 14. Найти значение выражения −3,2 + 4,3
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении, является знаком операции и не относится к десятичной дроби 4,3. У этой десятичной дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы его запишем для наглядности:
Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того рационального числа, модуль которого больше. А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих десятичных дробей до их вычисления:
Модуль числа 4,3 больше, чем модуль числа −3,2 поэтому мы из 4,3 вычли 3,2. Получили ответ 1,1. Ответ положителен, поскольку перед ответом должен стоять знак того рационального числа, модуль которого больше. А модуль числа 4,3 больше, чем модуль числа −3,2
Таким образом, значение выражения −3,2 + (+4,3) равно 1,1
Этот пример можно записать покороче:
Пример 15. Найти значение выражения 3,5 + (−8,3)
Это сложение рациональных чисел с разными знаками. Как и в прошлом примере из большего модуля вычитаем меньший и перед ответом ставим знак того рационального числа, модуль которого больше:
3,5 + (−8,3) = −(|−8,3| − |3,5|) = −(8,3 − 3,5) = −(4,8) = −4,8
Таким образом, значение выражения 3,5 + (−8,3) равно −4,8
Этот пример можно записать покороче:
Пример 16. Найти значение выражения −7,2 + (−3,11)
Это сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус.
Запись с модулями можно пропустить, чтобы не загромождать выражение:
−7,2 + (−3,11) = −7,20 + (−3,11) = −(7,20 + 3,11) = −(10,31) = −10,31
Таким образом, значение выражения −7,2 + (−3,11) равно −10,31
Этот пример можно записать покороче:
Пример 17. Найти значение выражения −0,48 + (−2,7)
Это сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:
−0,48 + (−2,7) = (−0,48) + (−2,70) = −(0,48 + 2,70) = −(3,18) = −3,18
Пример 18. Найти значение выражения −4,9 − 5,9
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус который располагается между рациональными числами −4,9 и 5,9 является знаком операции и не относится к числу 5,9. У этого рационального числа свой знак плюса, который невидим по причине того, что он не записывается. Но мы запишем его для наглядности:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус:
(−4,9) + (−5,9) = −(4,9 + 5,9) = −(10,8) = −10,8
Таким образом, значение выражения −4,9 − 5,9 равно −10,8
Запишем решение этого примера покороче:
Пример 19. Найти значение выражения 7 − 9,3
Заключим в скобки каждое число вместе со своими знаками
Заменим вычитание сложением
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед ответом поставим знак того числа, модуль которого больше:
(+7) + (−9,3) = −(9,3 − 7) = −(2,3) = −2,3
Таким образом, значение выражения 7 − 9,3 равно −2,3
Запишем решение этого примера покороче:
Пример 20. Найти значение выражения −0,25 − (−1,2)
Заменим вычитание сложением:
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед ответом поставим знак того числа, модуль которого больше:
−0,25 + (+1,2) = 1,2 − 0,25 = 0,95
Запишем решение этого примера покороче:
Пример 21. Найти значение выражения −3,5 + (4,1 − 7,1)
Выполним действия в скобках, затем слóжим полученный ответ с числом −3,5
Первое действие:
4,1 − 7,1 = (+4,1) − (+7,1) = (+4,1) + (−7,1) = −(7,1 − 4,1) = −(3,0) = −3,0
Второе действие:
−3,5 + (−3,0) = −(3,5 + 3,0) = −(6,5) = −6,5
Ответ: значение выражения −3,5 + (4,1 − 7,1) равно −6,5.
Пример 22. Найти значение выражения (3,5 − 2,9) − (3,7 − 9,1)
Выполним действия в скобках. Затем из числа, которое получилось в результате выполнения первых скобок, вычтем число, которое получилось в результате выполнения вторых скобок:
Первое действие:
3,5 − 2,9 = (+3,5) − (+2,9) = (+3,5) + (−2,9) = 3,5 − 2,9 = 0,6
Второе действие:
3,7 − 9,1 = (+3,7) − (+9,1) = (+3,7) + (−9,1) = −(9,1 − 3,7) = −(5,4) = −5,4
Третье действие
0,6 − (−5,4) = (+0,6) + (+5,4) = 0,6 + 5,4 = 6,0 = 6
Ответ: значение выражения (3,5 − 2,9) − (3,7 − 9,1) равно 6.
Пример 23. Найти значение выражения −3,8 + 17,15 − 6,2 − 6,15
Заключим в скобки каждое рациональное число вместе со своими знаками
Заменим вычитание сложением там, где это можно:
Выражение состоит из нескольких слагаемых. Согласно сочетательному закону сложения, если выражение состоит из нескольких слагаемых, то сумма не будет зависеть от порядка действий. Это значит, что слагаемые можно складывать в любом порядке.
Не будем изобретать велосипед, а слóжим все слагаемые слева направо в порядке их следования:
Первое действие:
(−3,8) + (+17,15) = 17,15 − 3,80 = 13,35
Второе действие:
13,35 + (−6,2) = 13,35 − −6,20 = 7,15
Третье действие:
7,15 + (−6,15) = 7,15 − 6,15 = 1,00 = 1
Ответ: значение выражения −3,8 + 17,15 − 6,2 − 6,15 равно 1.
Пример 24. Найти значение выражения
Переведём десятичную дробь −1,8 в смешанное число. Остальное перепишем без изменения:
Далее вычисляем данное выражение, применяя ранее изученные правила:
Пример 25. Найти значение выражения
Заменим вычитание сложением. Попутно переведём десятичную дробь (−4,4) в неправильную дробь
В получившемся выражении нет отрицательных чисел. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вторым числом, и убрать скобки. Тогда получим простое выражение на сложение, которое решается легко
Пример 26. Найти значение выражения
Переведём смешанное число 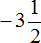
Получили сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус:
Пример 27. Найти значение выражения
Переведём обе дроби в неправильные дроби. Чтобы перевести десятичную дробь 2,05 в неправильную дробь, можно перевести ее сначала в смешанное число, а затем в неправильную дробь:
После перевода обеих дробей в неправильные дроби, получим следующее выражение:
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль и перед полученным ответом поставим знак того числа, модуль которого больше:
Пример 28. Найти значение выражения
Заменим вычитание сложением. Далее переведём десятичную дробь в обыкновенную дробь. Затем вычислим получившееся выражение, применяя ранее изученные правила:
Пример 29. Найти значение выражения
Переведём десятичные дроби −0,25 и −1,25 в обыкновенные дроби, остальное перепишем без изменения. Получим следующее выражение:
Можно сначала заменить вычитание сложением там, где это можно и сложить рациональные числа одно за другим.
Есть и второй вариант: сначала сложить рациональные числа 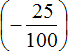
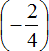
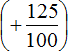
Первое действие:
Второе действие:
Ответ: значение выражения 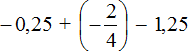
Пример 30. Найти значение выражения
Переведём десятичные дроби в обыкновенные. Остальное перепишем без изменения:
Получили сумму из нескольких слагаемых. Если сумма состоит из нескольких слагаемых, то выражение можно вычислять в любом порядке. Это следует из сочетательного закона сложения.
Поэтому мы можем организовать наиболее удобный для нас вариант. В первую очередь можно сложить первое и последнее слагаемое, а именно рациональные числа 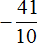
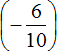
Первое действие:
Полученное число можно сложить со вторым слагаемым, а именно с рациональным числом 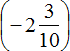
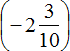
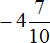
Второе действие:
Ну и слóжим полученное число −7 с последним слагаемым, а именно с рациональным числом 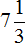
Третье действие:
Ответ: значение выражения 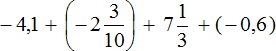
Источник
Что значит найти значения сумм рациональным способом?
49 + 87 + 62 + 51 + 38 + 13.
На этой странице находится ответ на вопрос Что значит найти значения сумм рациональным способом?, из категории
Математика, соответствующий программе для 1 — 4 классов. Чтобы посмотреть
другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов
подберите похожие вопросы и ответы в категории Математика. Ответ, полностью
соответствующий критериям вашего поиска, можно найти с помощью простого
интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе.
Обратите внимание на варианты ответов других пользователей, которые можно не
только просмотреть, но и прокомментировать.
Как вычислить рационально 70 + 3 + 10? Что значит «рационально «?
В моем понимание рационально, то есть быстрее и разумно что-то сделать.
Например, 197+231+103+69=? и возникает вопрос «Что делать?». Нет вопроса не возникает просто можно все по порядку сложить, но это очень долго, трудоемко и можно допустить ошибки в вычислениях. Если обратить внимание на пары чисел, что их очень просто и быстро сложить для этого поменяем местами слагаемые, тогда получится 197+103+231+69=300+300=600. А то приходилось бы складывать по порядку 197+231+103+69=428+103+69=531+69=600, но получаем такой же результат.
В примере 70+3+10 надо числа «3» и «10» поменять местами для более удобного сложения.
Тогда получится 70+10+3 и в данном случае практически нельзя допустить ошибки.
Рациональные приёмы вычислений на уроках математики
Умения рационально производить вычисления характеризуют довольно высокий уровень математического развития. Знакомство и применение рациональных способов вычислений развивает вариативность мышления, показывает ценность знаний, которые при этом используются. Эти умения чрезвычайно сложны, формируются они медленно и за время обучения в начальной школе далеко не у всех детей могут быть достаточно сформированы.
Говорят, если хотите научиться плавать, вы должны войти в воду, а если хотите уметь решать задачи, то должны начать их решать. Но для начала надо освоить азы арифметики. Научиться считать быстро. Считать в уме можно только при большом желании и систематической тренировки. И тогда перед вами откроется совсем другая математика: живая, полезная, понятная.
Скажите, пожалуйста, как рациональнее сложить 1+ 7, 4 * 8? Какие законы применили?
27 + 46+13? 27 – 19 – 7? Какие свойства, законы? Т.е основы рациональных приёмов вычислений основаны на чём?
Методика преподавания математики в начальных классах раскрывает основы рациональных приёмов вычислений, связанных с выполнением разных математических действий с натуральными числами.
Рациональные приёмы сложения основываются
1. Коммуникативный закон сложения а +в =в +а
2. Ассоциативный закон сложения а+в+с = а+ (в+с)
на коммуникативном и ассоциативном приёмах сложения, а так же свойствах изменения суммы. Рассмотрим некоторые из них.
Свойства сложения.
1.1
а+в+с =У, то (а – к) +с+в = У –к
38+24+15 = 77, то 36+ 24+ 15 = ?
а+в+с=У, то (а+ к) +в +с = У+к
38 + 24+15 = 77, то 40+ 24 + 15 =?
1.2.
а+ в =С , то (а +к ) + (в – к) = С
56 + 27 = 83, то (56 + 4) + (27 – 4) = ?
Какие ещё рациональные приёмы сложения можно применить на уроке математики?
Округление одного из слагаемых; поразрядного сложения; приём группировки вокруг одного и того же «корневого» числа.
Рассмотрим эти приёмы:
13 + 49 + 76 + 61 = (поразрядное сложение)
38 + 59 = 38 + (…округление слагаемого)
26 + 24 + 23 +25 + 24 = (группировка вокруг одного и того же «корневого» числа
Все приёмы рациональных вычислений, связанных с вычитанием, основываются на законах вычитания.
Если уменьшаемое увеличить или уменьшить на число, то соответственно разность увеличится или уменьшится на это же самое число
а – в = С, то (а +к) — в = С +к
74 – 28 = 46, то 77 – 28 = 49
а-в = С , то (а – к ) — в = С-к
74 – 28 = 46, то 71 – 28 = 43
Если вычитаемое увеличить или уменьшить на несколько единиц, то разность измениться в противоположную сторону.
Если уменьшаемое и вычитаемое уменьшить или увеличить на одно и тоже число, то разность не измениться.
Найди верные равенства.
229 – 36 = (229 – 9 ) – ( 36 – 6)
174 – 58 = (174 – 4) – ( 58 – 4)
358 – 39 = ( 358 – 8 ) – (39 – 
617 – 48 = ( 617 – 7 ) – (48 – 
Для рациональных вычислений используют частичные приёмы умножения и деления.
Приём замены множителя или делителя на произведение.
75 * 8 = 75 * 2*2*2=
960 : 15 = 960 : 3 : 5 =
Приём умножения на 9, 99,999, 11 …
87 * 99 = 87 * 100- 87 = 8700 – 87 = 8613
87 * 11 = 87 *10 + 87 = 870+ 87 = 957
Успешное применение различных приёмов зависит от умения подмечать особенности чисел и их сочетаний. Например, познакомив детей в первом классе с натуральным рядом чисел и имея его перед глазами, легко закрепить состав числа.
0 1 2 3 4 5 6 7
Отработав, таким образом, состав чисел в пределах 10 и познакомившись с переместительным законом сложения, дети легко справляются с заданием найти сумму чисел в пределах 10, а в дальнейшем, используя переместительное и сочетательное свойство сложения, легко можно найти сумму других чисел. Например:
48 +14 +22 +36 =120
Существуют приёмы на знаниях некоторых свойств чисел или результатов действий. Легко находить сумму последовательных нечётных чисел, начиная с 1.
Она равна произведению количества слагаемых на самого себя. (проверить)
Рационализация может осуществляться за счет возможности выполнять некоторые арифметические действия. Для этого очень важно научить детей внимательно рассматривать условия задания, суметь подметить все его особенности. Такие задания, как поставь нужный знак действия16 … 17 = 33 ( рассуждать), далее подобные задания усложняются. 8…6…33 = 15
Сравни, не вычисляя
51 : 3 … 30 : 3 + 21 :5
636 :6 … 600 : 6+ 30 : 6+ 6 :6
Задания могут даваться в занимательной форме: Математический лабиринт, составь слово, найди пару , расшифруй пословицу и т.д.
Используй рациональные приёмы вычисления, разгадай слово
Какие приёмы использовали?
Важно показать ученикам красоту и изящество устных вычислений, используя разнообразные вычислительные приёмы, помогающие значительно облегчить процесс вычисления.
СЧЁТ НА ПАЛЬЦАХ: способ быстрого умножения чисел первого десятка на 9. Допустим нам надо умножить 7 на 9. Повернём ладошки к себе, загнём седьмой палец, число пальцев слева от загнутого пальца – это число десятков, а число – справа, количество единиц.
Все задания, которые рассматривались, воспитывают интерес к математике, развивают их математические способности. Такую работу можно продолжать на математическом кружке.
Действия с рациональными числами: правила, примеры, решения
Ниже рассмотрим правила основных математических действий над рациональными числами: сложение, вычитание, умножение и деление. Разберем теорию на практических примерах.
Действие сложения рациональных чисел
Рациональные числа содержат натуральные, тогда смысл действия сложения рациональных чисел сопоставим со смыслом сложения натуральных. Например, сумму рациональных чисел, записанную как 5 + 1 4 возможно описать следующим образом: к 5 целым предметам добавили четверть такого предмета, после чего полученное количество рассматривается совместно.
Сформулируем правила сложения рациональных чисел:
Сложение нуля с отличным от него рациональным числом
Прибавление нуля к любому числу дает то же число. Данное правило возможно записать в виде равенства: a + 0 = a (для любого рационального числа а). Используя переместительное свойство сложения, получим также верное равенство: 0 + a = a .
Пара простых примеров: сумма рационального числа 2 , 1 и числа 0 равно 2 , 1 и: 6 4 5 + 0 = 6 4 5 .
Сложение противоположных рациональных чисел
Сумма противоположных чисел равна нулю.
Данное правило можно записать в виде: a + ( — a ) = 0 (для любого рационального числа a ).
К примеру, числа 45 , 13 и — 45 , 13 являются противоположными, т.е. их сумма равно нулю: 45 , 13 + ( — 45 , 13 ) = 0 .
Сложение положительных рациональных чисел
В виде обыкновенной дроби возможно представить любое положительное рациональное число и использовать далее схему сложения обыкновенных дробей.
Необходимо произвести сложение рациональных чисел: 0 , 6 и 5 9 .
Решение
Выполним перевод десятичной дроби в обыкновенную и тогда: 0 , 6 + 5 9 = 6 10 + 5 9 .
Осуществим сложение дробей с разными знаменателями:
6 10 + 5 9 = 54 90 + 50 90 = 104 90 = 1 7 45
Ответ: 0 , 6 + 5 9 = 1 7 45 .
Рациональные числа, которые подвергают действию сложения, возможно записать в виде конечных десятичных дробей или в виде смешанных чисел и, таким образом, осуществить сложение десятичных дробей и смешанных чисел соответственно.
Сложение рациональных чисел с разными знаками
Для того, чтобы осуществить сложение рациональных чисел с разными знаками, необходимо из бОльшего модуля слагаемых вычесть меньший и перед полученным результатом поставить знак того числа, модуль которого больше.
Необходимо осуществить сложение рациональных чисел с разными знаками 8 , 2 и — 2 3 4 .
Решение
Согласно исходным данным, необходимо произвести сложение положительного числа с отрицательным. Придерживаясь вышеуказанного правила, определим модули заданных чисел: | 8 , 2 | = 8 , 2 и | — 2 3 4 | = 2 3 4 . Проведя сравнение модулей — рациональных чисел, получим: 8 , 2 > 2 3 4 и соответственно поймем, какое число из заданных станет уменьшаемым, а какое — вычитаемым. Произведем вычитание смешанных чисел, т.е.: 8 , 2 — 2 3 4 = 8 2 10 — 2 3 4 = 5 9 20 .
Полученному результату присваивается знак плюс, т.к. бОльшее из слагаемых по модулю – положительное число. Ответ: 8 , 2 + ( — 2 3 4 ) = 5 9 20 .
Сложение отрицательных рациональных чисел
Для того, чтобы произвести сложение отрицательных рациональных чисел, необходимо сложить модули заданных слагаемых, затем полученному результату присвоить знак минус.
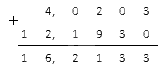
Необходимо произвести сложение чисел: — 4 , 0203 и — 12 , 193 .
Решение
Модули заданных чисел соответственно равны: 4 , 0203 и 12 , 193 . Сложим их:
Полученному результату присваиваем знак минус: — 16 , 2133 .
Ответ: ( — 4 , 0203 ) + ( — 12 , 193 ) = — 16 , 2133 .
Действие вычитания рациональных чисел
Вычитание – действие, обратное сложению, в котором мы находим неизвестное слагаемое по сумме и известному слагаемому. Тогда из равенства c + b = a следует, что a — b = c и a — c = b . И наоборот: из равенств a — b = c и a — c = b следует, что c + b = a .
При вычитании из бОльшего положительного рационального числа мы либо производим вычитание обыкновенных дробей, либо, если это уместно, вычитание десятичных дробей или смешанных.
Необходимо вычислить разность рациональных чисел: 4 , ( 36 ) – 1 5 .
Решение
Сначала переведем периодическую десятичную дробь в обыкновенную: 4 , ( 36 ) = 4 + ( 0 , 36 + 0 , 0036 + … ) = 4 + 0 , 36 1 — 0 , 01 = 4 + 36 99 = 4 + 4 11 = 4 4 11
Далее переходим к действию вычитания обыкновенной дроби из смешанного числа: 4 , ( 36 ) — 1 5 = 4 4 11 — 1 5 = 4 + 4 11 — 1 5 = 4 + 20 55 — 11 55 = 4 + 9 55 = 4 9 55
Ответ: 4 , ( 36 ) — 1 5 = 4 9 55
В прочих случаях вычитание рациональных чисел необходимо заменить сложением: к уменьшаемому прибавить число, противоположное вычитаемому: a – b = a + ( — b ) .
Указанное равенство можно доказать, опираясь на свойства действий с рациональными числами. Они дают возможность записать цепочку равенств: ( a + ( — b ) ) + b = a + ( ( — b ) + b ) = a + 0 = a . Отсюда в силу смысла действия вычитания следует, что сумма a + ( — b ) есть разность чисел a и b .
Необходимо из рационального числа 2 7 вычесть рациональное число 5 3 7
Решение
Согласно последнему указанному правилу используем для дальнейших действий число, противоположное вычитаемому, т.е. — 5 3 7 . Тогда: 2 7 — 5 3 7 = 2 7 + — 5 3 7
Далее произведем сложение рациональных чисел с разными знаками: 2 7 + — 5 3 7 = — 5 3 7 — 2 7 = — 5 3 7 — 2 7 = — 5 1 7
Ответ: 2 7 + — 5 3 7 = — 5 1 7
Действие умножения рациональных чисел
Общее понятие числа расширяется от натуральных чисел к целым, так же как от целых к рациональным. Все действия с целыми числами имеют те же свойства, что и действия с натуральными. В таком случае, и действия с рациональными числами также должны характеризоваться всеми свойствами действий с целыми числами. Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.
Умножение на нуль
Произведение любого рационального числа a на нуль есть нуль.
Используя переместительное свойство умножения, получим: 0 · а = 0 .
К примеру, умножение рационального числа 7 13 на 0 даст 0 . Перемножив отрицательное рациональное число — 7 1 8 и нуль, также получим нуль. В частном случае, произведение нуля на нуль есть нуль: 0 · 0 = 0 .
Умножение на единицу
Умножение любого рационального числа a на 1 дает число a .
Т.е. a · 1 = a или 1 · a = a (для любого рационального a ). Единица здесь является нейтральным числом по умножению.
К примеру, умножение рационального числа 5 , 46 на 1 даст в итоге число 5 , 46 .
Умножение взаимообратных чисел
Если множители есть взаимообратные числа, то результатом их произведения будет единица. Т.е. : а · а — 1 = 1 .
К примеру, результатом произведения чисел 5 6 и 6 5 будет единица.
Умножение положительных рациональных чисел
В общих случаях умножение положительных рациональных чисел сводится к умножению обыкновенных дробей. Первым действием множители представляются в виде обыкновенных дробей, если заданные числа таковыми не являются.
Необходимо вычислить произведение положительных рациональных чисел 0 , 5 и 6 25 .
Решение
Представим заданную десятичную дробь в виде обыкновенной 0 , 5 = 5 10 = 1 2 .
Далее произведем умножение обыкновенных дробей: 1 2 · 6 25 = 6 50 = 3 25 .
Ответ: 0 , 5 · 6 25 = 3 25
Можно также работать и с конечными десятичными дробями. Удобнее будет в данном случае не переходить к действиям над обыкновенными дробями.
Необходимо вычислить произведение рациональных чисел 2 , 121 и 3 , 4 .
Решение
Перемножим десятичные дроби столбиком:
Ответ: 2 , 121 · 3 , 4 = 7 , 2114
В частных случаях нахождение произведения рациональных чисел представляет собой умножение натуральных чисел, умножение натурального числа на обыкновенную или десятичную дробь.
Умножение рациональных чисел с разными знаками
Чтобы найти произведение рациональных чисел с разными знаками, необходимо перемножить модули множителей и полученному результату присвоить знак минус.
Необходимо найти произведение чисел: — 3 3 8 и 2 1 2
Решение
Согласно вышеуказанному правилу получим: — 3 3 8 · 2 1 2 = — 3 3 8 · 2 1 2 = — 3 3 8 · 2 1 2
Заменим смешанные дроби неправильными и найдем искомое произведение: — 3 3 8 · 2 1 2 = — 27 8 · 5 2 = — 135 16 = — 8 7 16
Ответ: — 3 3 8 · 2 1 2 = — 8 7 16
Умножение отрицательных рациональных чисел
Для того, чтобы найти произведение отрицательных рациональных чисел, необходимо перемножить модули множителей.
Необходимо найти произведение отрицательных рациональных чисел — 3 , 146 и — 56 .
Решение: модули заданных чисел соответственно равны 3 , 146 и 56 .
Перемножим их столбиком:
Полученный результат и будет являться искомым произведением.
Ответ: ( — 3 , 146 ) · ( — 56 ) = 176 , 176
Деление рациональных чисел
Деление – действие, обратно умножению, в ходе которого мы находим неизвестный множитель по заданному произведению и известному множителю. Смысл действия деления можно записать так: из равенства b · c = a следует, что a : b = c и a : c = b . И наоборот: из равенств a : b = c и a : c = b следует, что b · c = a .
На множестве рациональных чисел деление не считается самостоятельным действием, поскольку оно производится через действие умножения. Собственно, этот смысл заложен в правило деления рациональных чисел.
Разделить число а на число b , отличное от нуля – то же самое, что умножить число a на число, обратное делителю. Т.е., на множестве рациональных чисел верно равенство: a : b = a · b — 1 .
Указанное равенство доказывается просто: на основе свойств действий с рациональными числами справедливой будет цепочка равенств ( a · b — 1 ) · b = a · ( b — 1 · b ) = a · 1 = a , которая и доказывает равенство a : b = a · b — 1 .
Таким образом, деление рационального числа на другое рациональное число, отличное от нуля, сводится к действию умножения рациональных чисел.
Необходимо выполнить действие деления 3 1 3 : — 1 1 6
Решение
Определим число, обратное заданному делителю. Запишем заданный делитель в виде неправильной дроби: — 1 1 6 = — 7 6 .
Число, обратное этой дроби, будет: — 6 7 . Теперь, согласно вышеуказанному правилу, произведем действие умножения рациональных чисел: 3 1 3 — 1 1 6 = 3 1 3 · — 6 7 = 10 3 · ( — 6 7 ) = — ( 10 3 · 6 7 ) = — 20 7 = — 2 6 7
Содержание
- Рациональные приёмы вычислений на уроках математики
- «Мозг хорошо устроенный ценится больше, чем мозг хорошо наполненный.»
- Алгебра
- Понятие рационального выражения
- Сокращение рациональных выражений
- Представление дроби в виде суммы дробей
- Преобразование рациональных выражений
Рациональные приёмы вычислений на уроках математики
Разделы: Математика
Класс: 4
Ключевые слова: математика
«Мозг хорошо устроенный ценится больше,
чем мозг хорошо наполненный.»
Умения рационально производить вычисления характеризуют довольно высокий уровень математического развития. Знакомство и применение рациональных способов вычислений развивает вариативность мышления, показывает ценность знаний, которые при этом используются. Эти умения чрезвычайно сложны, формируются они медленно и за время обучения в начальной школе далеко не у всех детей могут быть достаточно сформированы.
Говорят, если хотите научиться плавать, вы должны войти в воду, а если хотите уметь решать задачи, то должны начать их решать. Но для начала надо освоить азы арифметики. Научиться считать быстро. Считать в уме можно только при большом желании и систематической тренировки. И тогда перед вами откроется совсем другая математика: живая, полезная, понятная.
Скажите, пожалуйста, как рациональнее сложить 1+ 7, 4 * 8? Какие законы применили?
27 + 46+13? 27 – 19 – 7? Какие свойства, законы? Т.е основы рациональных приёмов вычислений основаны на чём?
Методика преподавания математики в начальных классах раскрывает основы рациональных приёмов вычислений, связанных с выполнением разных математических действий с натуральными числами.
Рациональные приёмы сложения основываются
1. Коммуникативный закон сложения а +в =в +а
2. Ассоциативный закон сложения а+в+с = а+ (в+с)
на коммуникативном и ассоциативном приёмах сложения, а так же свойствах изменения суммы. Рассмотрим некоторые из них.
Свойства сложения.
1.1
а+в+с =У, то (а – к) +с+в = У –к
38+24+15 = 77, то 36+ 24+ 15 = ?
а+в+с=У, то (а+ к) +в +с = У+к
38 + 24+15 = 77, то 40+ 24 + 15 =?
1.2.
а+ в =С , то (а +к ) + (в – к) = С
56 + 27 = 83, то (56 + 4) + (27 – 4) = ?
Какие ещё рациональные приёмы сложения можно применить на уроке математики?
Округление одного из слагаемых; поразрядного сложения; приём группировки вокруг одного и того же «корневого» числа.
Рассмотрим эти приёмы:
13 + 49 + 76 + 61 = (поразрядное сложение)
38 + 59 = 38 + (…округление слагаемого)
26 + 24 + 23 +25 + 24 = (группировка вокруг одного и того же «корневого» числа
Все приёмы рациональных вычислений, связанных с вычитанием, основываются на законах вычитания.
Если уменьшаемое увеличить или уменьшить на число, то соответственно разность увеличится или уменьшится на это же самое число
а – в = С, то (а +к) — в = С +к
74 – 28 = 46, то 77 – 28 = 49
а-в = С , то (а – к ) — в = С-к
74 – 28 = 46, то 71 – 28 = 43
Если вычитаемое увеличить или уменьшить на несколько единиц, то разность измениться в противоположную сторону.
Если уменьшаемое и вычитаемое уменьшить или увеличить на одно и тоже число, то разность не измениться.
Найди верные равенства.
229 – 36 = (229 – 9 ) – ( 36 – 6)
174 – 58 = (174 – 4) – ( 58 – 4)
358 – 39 = ( 358 – 8 ) – (39 – 
617 – 48 = ( 617 – 7 ) – (48 – 
Для рациональных вычислений используют частичные приёмы умножения и деления.
Приём замены множителя или делителя на произведение.
75 * 8 = 75 * 2*2*2=
960 : 15 = 960 : 3 : 5 =
Приём умножения на 9, 99,999, 11 …
87 * 99 = 87 * 100- 87 = 8700 – 87 = 8613
87 * 11 = 87 *10 + 87 = 870+ 87 = 957
Успешное применение различных приёмов зависит от умения подмечать особенности чисел и их сочетаний. Например, познакомив детей в первом классе с натуральным рядом чисел и имея его перед глазами, легко закрепить состав числа.
0 1 2 3 4 5 6 7
Отработав, таким образом, состав чисел в пределах 10 и познакомившись с переместительным законом сложения, дети легко справляются с заданием найти сумму чисел в пределах 10, а в дальнейшем, используя переместительное и сочетательное свойство сложения, легко можно найти сумму других чисел. Например:
48 +14 +22 +36 =120
Существуют приёмы на знаниях некоторых свойств чисел или результатов действий. Легко находить сумму последовательных нечётных чисел, начиная с 1.
Она равна произведению количества слагаемых на самого себя. (проверить)
Рационализация может осуществляться за счет возможности выполнять некоторые арифметические действия. Для этого очень важно научить детей внимательно рассматривать условия задания, суметь подметить все его особенности. Такие задания, как поставь нужный знак действия16 … 17 = 33 ( рассуждать), далее подобные задания усложняются. 8…6…33 = 15
Сравни, не вычисляя
51 : 3 … 30 : 3 + 21 :5
636 :6 … 600 : 6+ 30 : 6+ 6 :6
Задания могут даваться в занимательной форме: Математический лабиринт, составь слово, найди пару , расшифруй пословицу и т.д.
Используй рациональные приёмы вычисления, разгадай слово
Какие приёмы использовали?
Важно показать ученикам красоту и изящество устных вычислений, используя разнообразные вычислительные приёмы, помогающие значительно облегчить процесс вычисления.
СЧЁТ НА ПАЛЬЦАХ: способ быстрого умножения чисел первого десятка на 9. Допустим нам надо умножить 7 на 9. Повернём ладошки к себе, загнём седьмой палец, число пальцев слева от загнутого пальца – это число десятков, а число – справа, количество единиц.
Все задания, которые рассматривались, воспитывают интерес к математике, развивают их математические способности. Такую работу можно продолжать на математическом кружке.
Источник
Алгебра
Именная карта банка для детей
с крутым дизайном, +200 бонусов
Закажи свою собственную карту банка и получи бонусы
План урока:
Понятие рационального выражения
В 5 и 6 классе мы уже изучали дроби и действия над ними. В 7 классе рассматривались рациональные числа, которые, по сути, и являются дробями. Однако до этого мы изучали только так называемые числовые дроби, у которых в числителе и знаменателе стоят какие-то числа либо выражения с числами, но не переменные величины.
Следующие дроби являются числовыми:
Однако нередко в алгебре приходится иметь дело и с дробями, которые содержат переменные. В качестве примера подобных выражений можно привести:
Так как деление на ноль является недопустимой операцией в алгебре, то некоторые дроби могут не иметь смысла. Так, дробь
бессмысленна, так как ее знаменатель 21 – 3•7 равен нулю.
Если дробь содержит переменные величины, то ее значение зависит от этих переменных. Так, дробь
при у = 4 принимает значение, равное 9. Если же у = 3, то эта дробь окажется бессмысленной.
Значения переменных величин, при которых дробь сохраняет свой смысл, называют допустимыми значениями переменных.
Пример. Укажите множество допустимых значений величин х и у для дроби
Решение. Недопустим только случай, при котором в знаменателе находится ноль, то есть когда выполняется равенство
или равносильное ему равенство
Следовательно, допустимыми значениями являются все такие пары (х; у), что х ≠ у.
Пример. Каковы допустимые значения величин а и b в дроби
Решение. В данной записи есть три дробных черты, а значит, и три знаменателя:
Ни один из знаменателей не должен равняться нулю, поэтому
Перенесем в последнем неравенстве 2-ое слагаемое вправо, изменив знак (правила преобразований выражений со знаком ≠ точно такие же, как и у равенств):
По свойству пропорции имеем:
Итак, допустимыми являются все значения a и b, при которых а ≠ 0, b≠ 0, a≠b.
Пример. Найдите множество допустимых значений х для дроби
Ясно, что знаменатель должен отличаться от нуля:
Чтобы найти, при каких значениях неизвестной величины знаменатель обращается в ноль, надо решить уравнение
Представим полином в левой части как произведение, применив формулу квадрата разности:
Получаем, что исходная дробь сохраняет смысл при любых х, отличных от – 5 и 5.
Порою дроби, содержащие переменные, могут встречаться в тождествах.
Пример. Докажите тождество
Решение. У дроби в левой части знаменатель всегда положителен, поэтому все допустимыми являются все значения c. Согласно свойству операции деления, делимое равно произведению делителя и частного, поэтому для доказательства тождества надо лишь показать справедливость равенства
(с 3 – 2с 2 + с – 2) = (с – 2)(с 2 + 1)
Раскроем скобки в правой части:
(с – 2)(с 2 + 1) = с 3 – 2с 2 + с – 2
Получили одинаковое выражение и для левой, и для правой части тождества, следовательно, оно верное.
Теперь сформулируем понятие рационального выражения.
Среди рациональных выражений выделяют целые и дробные выражения.
Приведем примеры целых рациональных выражений:
А вот несколько примеров дробных рациональных выражений:
Стоит заметить, что дробь и дробное выражение – это два разных понятия. Для иллюстрации приведем два примера:
- – это дробь, но целое, а не дробное выражение;
- (х + 7):t – это дробное выражение, но не дробь.
Отдельно отметим, что дробь равна нулю тогда, когда ее числитель равен нулю, а знаменатель нет. Если же и знаменатель равен нулю, то получается недопустимое действие – деление на ноль, поэтому дробь не будет иметь смысла.
Пример. Найдите все корни уравнения
Решение. На первый взгляд уравнение кажется сложным, особенно из-за знаменателя. Однако он здесь почти не играет роли. В левой части находится дробь, значит, нулю равен ее знаменатель:
х – 1 = 0 или х + 2 = 0
Получили два корня. Осталось убедиться, что при этих значениях х дробь не становится бессмысленной, то есть ее знаменатель не обращается в ноль. При х = 1 имеем знаменатель
2•1 4 – 3•1 3 + 5•1 – 4 = 2 – 3 + 5 – 4 = 0
поэтому число 1 НЕ является корнем уравнения. Теперь проверим знаменатель при х = – 2:
2•(– 2) 4 – 3•( – 2) 3 + 5•( – 2) – 4 =
= 32 + 24 – 10 – 4 = 42
Получается, что единственное корень уравнения – это ( – 2).
Сокращение рациональных выражений
Узнав, какие выражения являются рациональными, мы приступим к изучению их преобразований. Напомним главное свойство дроби:
Оно означает, что числитель и знаменатель можно умножить на произвольное число (кроме нуля), то значение дроби останется прежним:
Это правило остается верным и в том случае, когда вместо чисел используются переменные величины.
Например, возможны такие преобразования рациональных выражений:
Например, пусть надо привести дробь
к знаменателю 6а 2 b 2 .
На что именно надо умножитель знаменатель, что получился одночлен 6а 2 b 2 ? Очевидно, что
6а 2 b 2 = 2а 2 b•3b
Поэтому выражения над и под дробной чертой надо умножить на 3b:
Использованный нами множитель 3b называют дополнительным множителем.
Обратная операция, при которой из знаменателя и числителя убирают совпадающие множители, называется сокращением дроби:
Это тождество означает, что дроби можно сокращать, убирая общий множитель, например:
Аналогичные действия можно совершать не только с числовыми дробями, но и с дробными выражениями:
В последнем примере мы вынесли общие множители за скобки (2х и 7у), чтобы над и под чертой появилась одинаковая сумма х + 3у, которую можно сократить.
Однако при сокращении дробей важно учитывать область ее допустимых значений, ведь из-за изменения знаменателя она может измениться. Например, пусть требуется построить график функции
В числителе стоит разность квадратов, которую можно разложить на множители:
Казалось бы, мы получили линейную функцию
чей график нам известен – это прямая. Но она определена при всех возможных х, в то время как исходная дробь бессмысленна при х = 2, ведь тогда знаменатель становится равен нулю. Поэтому график функции будет выглядеть как прямая, однако одна из ее точек, с координатами (2; 4), будет «выколотой» точкой, и исключенной:
Данный рисунок означает, что графиком функции – прямая линия, кроме точки (2; 4)
Выколотая точка на графике изображается маленьким незакрашенным кружочком.
Следующее важное свойство дроби связано со знаком минус. Знак, стоящий перед дробью, можно перенести либо в знаменатель, либо в числитель:
Также напомним, что можно поменять местами уменьшаемое и вычитаемое в скобках, если изменить перед ней знак:
Применение этих правил позволяет упрощать некоторые дроби, например:
Более сложный пример:
Рассмотрим такое понятие, как однородный многочлен. Так называют тот полином, у которого все одночлены имеют одинаковую степень.
Подробнее о степени одночлена можно узнать в этом уроке. Если коротко, то степень одночлена – эта сумма степеней у всех переменных, входящих в его буквенную часть. Например, у следующих мономов степень равна 4:
- 3х 4 (у единственной переменной степень равна 4);
- 8х 3 у (степень у х равна 3, а степень у равна 1, 3 + 1 = 4);
- 5х 2 у 2 (степени у обеих переменных равны 2, 2 + 2 = 4);
- 10у 4 (в буквенной части только переменная у, чья степень равна 4).
Соответственно, многочлен 3х 4 + 8х 3 у + 5х 2 у 2 + 10у 4 , составленный из всех этих мономов, будет однородным. Примерами однородных полиномов также являются:
- z 6 + v 6 – 2z 2 v 4 (здесь степени мономов равны 6);
- a 2 – ab (степень одночленов равна 2).
В отношении однородных полиномов, состоящих из двух переменных, можно применять особый прием. Достаточно поделить его на одну из переменных в степени полинома, и получится выражение, зависящее только от одной дроби. Поясним это на примере. Пусть надо вычислить значение отношения
если известно другое отношение:
В исходной дроби представляет собой отношение двух однородных полиномов третьей степени. Поэтому поделим их на y 3 (можно было делить и на х 3 ). При этом значение дроби не изменится, ведь мы делим числитель и знаменатель на одинаковый моном:
Получили выражение, которое зависит только от отношения
Попытаемся найти эту величину из условия
Отсюда следует, что
Теперь подставим найденное отношение в формулу(1):
До этого мы рассматривали примеры дробных выражений, состоящие из полиномов с целыми коэффициентами. Если же используются дробные числа, то от них всегда можно избавиться, домножив дробь на какое-нибудь число.
Например, дана дробь
Коэффициенты при у и у 2 дробные. Избавимся от них. Для этого используем дополнительный множитель 12:
Далее рассмотрим сложение и вычитание дробных выражений. Проще всего эту операцию проводить в том случае, когда у дробей совпадают знаменатели. В такой ситуации используются уже нам известные правила:
Сложим две величины:
В их знаменателе стоит одинаковый полином, а потому операция будет выглядеть так:
Здесь мы в числителе использовали формулу квадрата разности.
Теперь вычтем из выражения
У них совпадают знаменатели, поэтому проблем с вычитанием не возникает:
Заметим, что обычно у дробных выражения стараются сокращать до тех пор, пока не получится несократимая дробь.
Если у дробей различные знаменатели, то приводят к общему знаменателю, домножая их на какой-нибудь дополнительный множитель.
Рассмотрим следующий пример:
Знаменатели дробей разные, однако, обе дроби можно привести к знаменателю 24х 2 у 3 . Почему именно к нему? Дело в том, у коэффициентов мономов 6х 2 у и 8ху 3 наименьшим общим кратным (НОК) является число 24 (о НОК можно узнать из этого урока). Добавим к этому коэффициенту переменные из одночленов с наибольшими показателями (х 2 и у 3 ) и получим моном 24х 2 у 3 . Итак,домножим первую дробь на 4у 2 , а вторую – на 3х:
Есть и более простой способ найти общий знаменатель, для этого достаточно просто перемножить знаменатели дробей-слагаемых. Однако дальнейшие преобразования будут более долгими. Решим таким путем тот же пример:
В числителе возможно вынесение общего множителя 2ху за скобки:
Видно, что конечный результат операции не изменился.
Если в знаменателях складываемых дробей стоят многочлены, то стоит попробовать разложить их на множители. За счет этого порою удается найти более простой общий знаменатель.
Пусть надо сложить выражения
Вынесем в знаменателях за скобки множители х и у:
В знаменателях есть похожие множители, (3х – у) и (у – 3х). Чтобы они оказались одинаковыми, надо поменять местами вычитаемое и уменьшаемое в одних скобках. Для этого перед ними надо добавить знак «минус»:
Общим множителем этих дробей является произведение ху(3х – у):
Осталось разложить числитель, где стоит разность квадратов:
Следующий важный навык, который может потребоваться при работе с рациональными выражениями – это выделение целой части из дроби.
Продемонстрируем эту операцию на примере
Перепишем дробь, поменяв порядок слагаемых в числителе:
И в знаменателе, и в числителе есть сумма х 2 + 1. Теперь можно произвести выделение целой части:
В справедливости данного преобразования можно убедиться, выполнив его «в обратную сторону»:
Любой многочлен можно сделать дробью, если приписать ему числитель, равный 1. Пусть надо упростить формулу
Заменим 2х – 1 на дробь и произведем вычитание:
Упростить далее эту дробь довольно сложно, но всё же возможно. Для этого надо заменить одночлен (– 3х 2 ) на разность (– х 2 – 2х 2 ), а 14х на сумму (6х+8х). Посмотрим, что получится в результате:
Складывать можно и более двух дробей. Пусть надо упростить сумму
Будем складывать слагаемые последовательно, то есть сначала сложим два первых слагаемых, потом к результату добавим третье, а далее и 4-ое слагаемое:
Представление дроби в виде суммы дробей
Сумму двух дробей можно представить в виде несократимой дроби единственным образом, например:
Однако у обратной задачи, разложения одной дроби на сумму нескольких других, есть бесконечной множество решений:
То же самое верно в отношении дробных выражений. Например,
можно разложить так:
С другой стороны, это же выражение можно представить в следующем виде:
Для раскладывания дроби на сумму дробей можно воспользоваться методом неопределенных коэффициентов, предложенным Рене Декартом в 1637 году. Покажем, как его использовать, на примере. Пусть надо представить в виде суммы двух дробей отношение
Заметим, что знаменатель х 2 – 4 можно записать как произведение полиномов первой степени (х – 2)(х + 2):
Это означает, что исходное выражение можно представить как сумму дробей со знаменателями (х – 2) и (х + 2). Обозначим числители в этих дробях как неизвестные величины aи b (они и носят название неопределенных коэффициентов). Тогда можно записать, что
Задача сводится к тому, чтобы найти a и b. Для этого преобразуем сумму дробей:
Полученная дробь должна равняться исходной дроби:
У правой и левой части равны знаменатели, а значит, должны равняться и числители:
(a + b)x + (2a– 2b) = 2x + 6
Это тождество может быть верным только тогда, когда справа и слева равны коэффициенты перед переменной х, а также свободные члены, поэтому можно записать систему:
Решив эту систему, мы сможем найти значения a и b. Используем метод подстановки, выразив а из первого уравнения:
Подставим эту формулу во второе уравнение:
Далее находим a:
а = 2 – b = 2 – (– 2,5) = 2 + 2,5 = 4,5
Итак, получили, что a = 4,5 и b = – 2,5. Это значит, исходную дробь можно разложить следующим образом:
Теперь рассмотрим, как производится умножение и деление дробных выражений. Эти действия аналогичны операциям с обычными числами, которые уже изучались в 5 классе. Напомним две основные формулы:
Пусть требуется перемножить величины
Эта операция осуществляется так:
Теперь посмотрим, как выполняется деление:
Деление заменяется умножением на дробь, обратную делителю:
Для упрощения выражений часто используют формулы сокращенного умножения:
При возведении дроби в степень надо отдельно возводить в степени знаменатель и числитель:
Вообще для любого натурального числа nбудет верным тождество:
Пусть надо возвести в 4-ую степень дробь
Выглядеть это будет так:
Преобразование рациональных выражений
Если у дроби в знаменателе и числителе записаны полиномы, то ее называют рациональной дробью. В виде рациональной дроби можно записать любое рациональное выражение.
Пусть надо записать в виде рациональной дроби выражение
Сначала выполним вычитание в скобках, а потом и деление:
Обратим внимание, что выражение
(2а + 1) 2 – (2а – 1) 2
представляет собой не что иное, как разность квадратов, для которой можно применить формулу сокращенного умножения:
(2а + 1) 2 – (2а – 1) 2 = (2а + 1 + 2а – 1)( 2а + 1 – (2а – 1)) =
= (2а + 1 + 2а – 1)( 2а + 1 – 2а + 1).
Используя это, продолжим работать с дробью:
Однако иногда удобнее не производить вычисления в скобках, а использовать распределительный закон умножения:
Пусть требуется упростить произведение:
Сначала раскроем скобки:
Часто проблемы возникают с так называемыми «многоэтажными» дробями. Так называют дроби, у которых в числителе и знаменателе стоят другие дробные выражения. Выглядят они внушительно, однако правила работы с ними такие же, как и с другими выражениями. Каждая дробная черта просто означает операцию деления.
Пусть требуется выполнить преобразование дробного рационального выражения
Сначала представим эту дробь как операцию деления:
Теперь в каждой из скобок произведем сложение:
Источник
Рациональный способ вычисления — это значит, найти искомую величину за меньшее число действий. Особенно часто таким способом приходится пользоваться в математике.
Простой пример. Нужно вычислить сумму всех натуральных чисел от 1 до 100. Можно просто складывать все числа подряд и найти эту сумму. Но это будет не рационально. Рациональный способ вычисления этой суммы предложил великий Карл Гаусс. Он сложил числа парами так, чтобы сумма в каждой паре были равны. 1 и 100, 2 и 99, 3 и 98, и т.д. Сумма каждой пары равна 101 и таких пар пятьдесят (последняя пара 50 и 51. Значит всю сумму можно вычислить так: (1+100)*100/2 =5050. Это рациональный способ.
Гаусс пошел дальше и вывел формулу вычисления суммы любого количества чисел в любой последовательности. Sn = (a1+an)*n/2, где a1- первый член последовательности, аn — последний член последовательности, n — количество членов последовательности.
Вообще рациональным можно назвать вычисление по любым формулам. Так как формулы дают универсальный способ расчета. Пример. Даны радиус окружности, нужно найти пройденный путь, если тело совершает 20 оборотов. Можно рассчитать длину окружности и затем умножить его на 20. Если представить все это в виде формулы, то мы сразу получим результат.