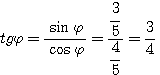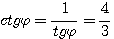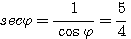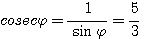Как найти значение оставшихся тригонометрических функций

ВИДЕО УРОК

Выражение всех тригонометрических функций через одну из них с помощью основных
тригонометрических тождеств.

Основные тригонометрические тождества позволяют определить по значению
одной из тригонометрических функций значения всех остальных.

ПРИМЕР:

Известно, что

sin x =
–³/₅,

причём

π < х <  ^3π/₂.

Найти

cos x,
tg x, ctg x.

РЕШЕНИЕ:

Из формулы

sin² α
+ cos² α = 1

получаем

cos² х  = 1 – sin² х.

подставив вместо  sin
х  его
значение, получим:

Итак,

cos² х
= ¹⁶/₂₅

значит,

либо  cos х = ⁴/₅

либо  cos х = –⁴/₅.

По условию:

π < х <  ^3π/₂,

то есть аргумент  х  принадлежит 
третьей четверти. Но в третьей четверти косинус отрицателен. Значит, из
двух указанных выше возможностей выбираем одну:

cos х
= –⁴/₅.

Зная  sin x  и  cos
х, находим  tg x  и  ctg x:

ctg x = ⁴/₃.

ОТВЕТ:

cos х = –⁴/₅,

tg x
= ³/₄,

ctg x
= ⁴/₃.

ПРИМЕР:

Дано:

sin α = ²⁰/₂₉.

Вычислить значения остальных
тригонометрических функций острого угла  α.

РЕШЕНИЕ:

Из формулы:

sin² α + соs² α = 1

имеем:

соs² α = 1 – sin² α

Подставляя вместо  sin² α  его численное значение  ²⁰/₂₉, получаем:

Следовательно:

соs α = ²¹/₂₉

Для нахождения 
tg α 
воспользуемся формулой

Получим:

tg α = ²⁰/₂₉ : ²¹/₂₉ = ²⁰/₂₁.

Отсюда, пользуясь формулой

tg α ∙ сtg α = 1,

Имеем:

ОТВЕТ:

соs α = ²¹/₂₉,

tg α = ²⁰/₂₁,

сtg α = ²¹/₂₀.

ПРИМЕР:

Определить значения тригонометрических функций угла  α, если

tg α = ³/₄

и  180° < α < 270°.

РЕШЕНИЕ:

По формуле

Находим

По формуле

Находим

Учитывая, что  sec α < 0  при 

180° < α < 270°

получим

–sec α = ⁵/₄

откуда

sec α = –⁵/₄

По формуле

Находим

сos α = – ⁴/₅.

Значения  sin α  найдём из
формулы

|sin α| = ³/₅.

Учитывая, что  sin α < 0  при 

180° < α < 270°

находим

sin α = –³/₅.

ОТВЕТ:

sin α = –³/₅,

соs α = –⁴/₅,

сtg α = ⁴/₃.

ПРИМЕР:

Известно, что

ctg x = –⁵/₁₂,

причём

^π/₂ < х < π.

Найти

sin х, cos x,
tg x.

РЕШЕНИЕ:

Из формулы

1 + ctg² α = cosec² α

находим

подставив
вместо  ctg x  его значение, получим:

Итак,

sin² х = ¹⁴⁴/₁₆₉

значит,

либо  sin х = ¹²/₁₃

либо  sin х = –¹²/₁₃.

По условию:

^π/₂ < х < π,

то есть аргумент  х  принадлежит 
второй четверти. Но во второй четверти синус положителен. Значит, из
двух указанных выше возможностей выбираем одну:

sin х = ¹²/₁₃.

Для отыскания значения  cos x  воспользуемся
формулой:

Из этой формулы находим

cos x
= ctg x ∙ sin х =

= –⁵/₁₂ ∙ ¹²/₁₃ = –⁵/₁₃.

Осталось вычислить
значение  tg x. Из равенства

находим

tg x = –¹²/₅.

ОТВЕТ:

sin х = ¹²/₁₃,

cos х = –⁵/₁₃,

tg x = –¹²/₅.

ПРИМЕР:

Дано:

сtg α = ⁴⁵/₂₈.

Вычислить остальные тригонометрические функции
острого угла  α.

РЕШЕНИЕ:

Записываем значение  tg α  как
величину, обратную  сtg α:

tg α = ²⁸/₄₅.

на основании формулы

имеем:

Возведя обе части этого
равенства в квадрат, получим:

Прибавим к обеим частям
этого равенства по единице:

Учитывая, что

sin² α + cos² α = 1,

находим:

откуда

sin α = ²⁸/₅₃.

Из формулы

Имеем, что

соs α = сtg α ∙ sin α.

В применению к данному случаю получим:

ОТВЕТ:

sin х = ²⁸/₅₃,

cos х = ⁴⁵/₅₃,

tg x = ²⁸/₄₅.

Вычисление
значений тригонометрических функций острого угла по значению одной из них надо
производить каждый раз, как было показано выше на примерах, пользуясь основными
формулами:

которые
надо твёрдо заучить.

Соотношения
между тригонометрическими функциями одного аргумента.

Если
преобразовать основные тригонометрические тождества, не предавая определённого
значения заданной функции, то можно вывести некоторые соотношения между
тригонометрическими функциями одного аргумента. Можно получить
выражения любой из тригонометрических функций через все остальные с помощью
следующих формул:

 Формулы,
приведённые в таблице, позволяют по значению одной из тригонометрических
функций находить значения всех остальных.

Во всех формулах, в
которых входят функции  tg α  или  sес α,
исключается значение

α = (2k + 1) ^π/₂,

где  k – любое целое
число, так как при этих и только при этих значениях  α  функции  tg α  или  sес α  не определены, то
есть не существуют. Во всех формулах, в которые входят функции  ctg α  или  cosес α, исключаются значения 

α = kπ,

где  k – любое целое
число, так как при этих и только при этих значениях  α  функции  ctg α  или  cosес α  не определены (не
существуют).

В тех формулах, в
которые входят радикалы, в общем случае перед радикалом следует становить
двойной знак  ±. Выбор определенного знака может быть произведён, если
дано дополнительное условие.

Пусть, например,

Если угол 
α 
находится в интервале от  0  до  π (или от  2kπ  до  2kπ + π, где  k – любое целое число), то

а если угол 
α 
находится в интервале от  π  до  2π (или от  π + 2kπ  до  2π + 2kπ, где  k – любое целое число), то

Таким образом,
выбор знака перед радикалом зависит от того промежутка, в котором
находится  α.

ПРИМЕР:

Дано:

соs α = ²/₇.

Вычислить значения остальных
тригонометрических функций острого угла  α.

РЕШЕНИЕ:

Из формулы:

sin² α + соs² α = 1

имеем:

ОТВЕТ:

ПРИМЕР:

Выразить значения
тригонометрических функций острого угла   
через  cos α.

РЕШЕНИЕ:

Из формулы:

sin² α +
cos² α = 1

находим:

Из формулы:

имеем:

и, следовательно

Подобного
рода задачи можно решать в общем виде и составить формулы, выражающие любую из
тригонометрических функций через все остальные.

ПРИМЕР:

Выразить  cos α  через все остальные тригонометрические функции
угла  α.

РЕШЕНИЕ:

Из тождества:

sin² α +
cos² α = 1

находим:

Далее из равенства

sec² α = 1 + tg² α

находим:

откуда

Заменив в полученном
равенстве

находим:

Так как

то последнее равенство примет вид:

Итак

ПРИМЕР:

Вывести выражения
тригонометрических функций острого угла   
через  tg α.

РЕШЕНИЕ:

Из формулы:

имеем:

Прибавляя к обеим частям
этих равенств по единице, получим:

или,
так как

ответы

ваш ответ

похожие темы

похожие вопросы 5

Внимание! Эти формулы работают только если аргументы у тригонометрических функций одинаковые, т.е.

(sin^2⁡ 776^° +cos^2⁡ 776^° =1)
(tg, 3xcdot ctg, 3x=1)

Но:

(sin^2⁡x+cos^2⁡3x≠1)
(tg, xcdot ctg, y≠1)

Все формулы связи тригонометрических функций учить не надо, потому что они достаточно легко получаются друг из друга несложными преобразованиями (подробности в этих видео). Кроме того, при частом использовании они постепенно запоминаются сами.

Примеры применения формул связи

Зачем нужны формулы связи? Они позволяют найти все тригонометрические функции угла, если известна лишь одна из них, а также дают возможность упрощать выражения, доказывать тождества, решать тригонометрические уравнения, заменяя одну функцию другой и так далее.

Пример. Найдите (5sin⁡,α), если (cos,⁡α=frac{2sqrt{6}}{5}) и (α∈(frac{3π}{2};2π)). 
Решение. Нам известен косинус, найти надо синус. А что связывает синус и косинус? Основное тригонометрическое тождество:

(sin^2α+cos^2⁡α=1).

Подставим вместо косинуса его значение:

(sin^2⁡α+)((frac{2sqrt{6}}{5}))(^2=1)
(sin^2⁡α+)(frac{4cdot 6}{25})(=1)
(sin^2⁡α+)(frac{24}{25})(=1)
(sin^2⁡α=1-)(frac{24}{25})
(sin^2⁡α=)(frac{1}{25})
(sin⁡α=±)(frac{1}{5})

Внимание! Последняя строчка – место, где теряется огромное количество баллов на ЕГЭ! Это одна из самых популярных ошибок – забыть отрицательный корень. Пожалуйста, раз и навсегда запомните, что у неполного квадратного уравнения вида (x^2=a) (при (a>0)) два корня (x_1=sqrt{a})  и (x_2=-sqrt{a}). Пусть двойка над иксом (та которая «квадрат») будет вам вечным маяком, сигнализирующим: «тут ДВА корня! Два! Не забудь!»

Вернемся к задаче. Получилось, что синус может иметь значение (frac{1}{5}), а может (-)(frac{1}{5}). И какое значение нам надо выбрать — с минусом или плюсом? Тут нам на помощь приходит информация, что (α∈(frac{3π}{2};2π)). Давайте нарисуем числовую окружность и отметим отрезок ((frac{3π}{2};2π)).

Обратите внимание – в этой четверти синус принимает только отрицательные значения (можно провести перпендикуляры до оси синусов и убедиться, что это так).

Значит, в нашем случае (sin,⁡α=-frac{1}{5}) т.е. (5sin,⁡α=5cdot(-frac{1}{5})=-1).

Ответ: (-1).

Пример.Найдите (tg,α), если (cos,⁡α=)(frac{sqrt{10}}{10}) и (α∈(frac{3π}{2};2π)). 
Решение. Есть 2 пути решения этой задачи:

— напрямую вычислить тангенс через формулу (tg^2α+1=)(frac{1}{cos^2⁡α});
— сначала с помощью тождества (sin^2⁡α+cos^2⁡α=1) найти (sin⁡,α), а потом через формулу (tg,α=)(frac{sin⁡,α}{cos⁡,α}) получить тангенс.

В учебниках обычно идут первым путем, поэтому мы пойдем вторым.

Вычисляем синус:

(sin^2⁡α+)((frac{sqrt{10}}{10})^2)(=1)
(sin^2⁡α+)(frac{10}{100})(=1)
(sin^2⁡α+)(frac{1}{10})(=1)
(sin^2⁡α=1-)(frac{1}{10})
(sin^2⁡α=)(frac{9}{10});
(sin⁡,α=±)(frac{3}{sqrt{10}})

Опять (α∈(frac{3π}{2};2π)), значит в итоге синус может быть только отрицательным. То есть, (sin⁡,α=-)(frac{3}{sqrt{10}}).
А теперь вычисляем тангенс: (tg,α=-)(frac{3}{sqrt{10}})(:)(frac{sqrt{10}}{10})(=)(-frac{3}{sqrt{10}}cdotfrac{10}{sqrt{10}})(=-)(frac{30}{10})(=-3).

Ответ: (-3).

Пример. Известно, что (tg,α=-frac{3}{4}) и (frac{π}{2}<α<π). Найдите значения трех других тригонометрических функций угла (α).
Решение. Проще всего из тангенса найти котангенс:

(ctg, α=)(frac{1}{tg, α})
(ctg,α=1:(-frac{3}{4})=1cdot(-frac{4}{3})=-frac{4}{3}).

Теперь вычислим косинус по упомянутой выше формуле:

(tg^2 α+1=)(frac{1}{cos^2⁡α})
((-)(frac{3}{4}))(^2+1=)(frac{1}{cos^2⁡α})
(frac{9}{16})(+1=)(frac{1}{cos^2⁡α})
(frac{9+16}{16})(=)(frac{1}{cos^2⁡α})
(frac{25}{16})(=)(frac{1}{cos^2⁡α})
(cos^2⁡α=)(frac{16}{25})
(cos⁡α=±)(frac{4}{5})

Опять перед нами стоит выбор плюс или минус. Отметим отрезок ((frac{π}{2};π)) на тригонометрической окружности и посмотрим какие значения принимает косинус в этой четверти, чтобы определится со знаком.

Очевидно, что косинус отрицателен в этой четверти, а значит (cos,⁡α=-)(frac{4}{5}).

Осталось найти синус:

(sin^2⁡α+cos^2⁡α=1)
(sin^2⁡α+(-)(frac{4}{5})()^2=1)
(sin^2⁡α+)(frac{16}{25})(=1)
(sin^2⁡α=1-)(frac{16}{25})
(sin^2⁡α=)(frac{9}{25})
(sin,⁡α=±)(frac{3}{5})

Опять используем круг, чтобы определить знак.

Получается, что (sin,⁡α=)(frac{3}{5}).

Ответ: (ctg,α=-)(frac{4}{3});   (cos,⁡α=-)(frac{4}{5});    (sin,α=)(frac{3}{5}).

Пример (ЕГЭ). Найдите (tg^2 α), если (5 sin^2⁡α+13 cos^2⁡α=6).
Решение. Давайте пойдем от того, что известно. В равенстве (5 sin^2⁡α+13 cos^2⁡α=6) синус заменим на косинус:

(5(1-cos^2⁡α)+13 cos^2⁡α=6)
(5-5 cos^2⁡α+13 cos^2⁡α=6)
(5+8 cos^2⁡α=6)
(8 cos^2⁡α=1)
(cos^2⁡α=)(frac{1}{8})

Поняли почему именно синус заменили на косинус, а не наоборот? И почему не надо извлекать корень, досчитывая до «чистого» косинуса? Потому что для нахождения (tg^2α) хорошо подходит формула (tg^2α+1=)(frac{1}{cos^2⁡α}) :

(tg^2 α+1=1:)(frac{1}{8})
(tg^2 α+1=1cdot)(frac{8}{1})
(tg^2 α+1=8)
(tg^2 α=7)

Ответ: (7).

Теперь еще одна задача из ЕГЭ, для наглядности мы ее решение оформили картинкой.

Пример. Упростите выражение (frac{1}{sin^2 α})(-ctg^2 α-cos^2 β).
Решение.

Пример. Докажите тождество (frac{cos^4⁡α-sin^4⁡α}{(1-sin⁡α)(1+sin⁡α)})(+2tg^2 α=)(frac{1}{cos^2 α}).
Решение.

Левая часть полностью идентична правой, то есть тождество доказано.

Как доказать все формулы связи