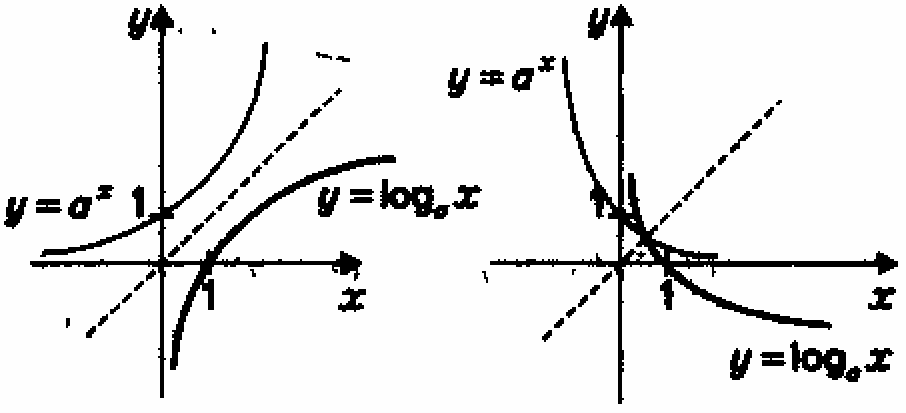Как найти значение логарифмической функции по точкам

Сообщения без ответов | Активные темы

Автор	Сообщение
	Заголовок сообщения: График функции в логарифмическом масштабе Добавлено: 20 авг 2018, 23:47
Начинающий Зарегистрирован: 20 авг 2018, 23:28 Сообщений: 6 Cпасибо сказано: 2 Спасибо получено: 0 раз в 0 сообщении Очков репутации: 1	Не знаю, в каком разделе форума можно задать мой вопрос, а правила нарушать не хочется. Мне нужно узнать функцию, график которой в логарифмической системе координат представляет собой прямую линию. Есть две точки A и B, координаты которых (x,y) известны В логарифмической системе координат эти точки лежат на одной прямой Нужна формула, по которой, зная координату X, можно вычислить координату Y любой точки на этом графике. Наверно это очень простая задача, но я математику учил более полвека назад и, увы, не сильно в этом преуспевал. Буду очень благодарен за помощь или подсказку, куда обратиться с этим вопросом Последний раз редактировалось Andy 21 авг 2018, 08:47, всего редактировалось 1 раз. Название темы исправлено модератором.
Вернуться к началу

FEBUS	Заголовок сообщения: Re: Где спросить про логарифмическую функцию? Добавлено: 21 авг 2018, 00:13
	Не ясно, что вам нужно. В ЛСК уравнение прямой [math]Y=kX+B[/math] или [math]lg{y}=klg{x}+lg{b}[/math]. В Декартовой СК это [math]y=bx^{k}.[/math]
Вернуться к началу

Deda	Заголовок сообщения: Re: Где спросить про логарифмическую функцию? Добавлено: 21 авг 2018, 00:45
	Извиняюсь, если объяснил невнятно Хотел загрузить картинку с графиком, но не грузится. На ссылки вроде запретов нет, вот загрузил график на сторонний сайт http://prntscr.com/kkyuoj Координаты (значения по X и Y) точек A и B известны Мне нужно, зная значение Y произвольной точки на этом графике, вычислить координату X этой точки Например на графике по моей ссылке предположим (условно) Ax=8, Ay=5.3, Bx=820, By=0.75 Как узнать для произвольной точки значение Nx, если известно, что например Ny=2? По графику видно, что приблизительно Nx=110. Но как это вычислить точно? Не пинайте за дилетантский вопрос
Вернуться к началу

FEBUS	Заголовок сообщения: Re: Где спросить про логарифмическую функцию? Добавлено: 21 авг 2018, 01:42
	Из системы находим [math]a[/math] и [math]k[/math] [math]left{!begin{aligned} & lg{y_{A}}=lg{a}+klg{x_{A} } \ & lg{y_{B}}=lg{a}+klg{x_{B} } end{aligned}right.[/math] Или [math]left{!begin{aligned} & y_{A}=ax_{A} ^{k} \ & y_{B}=ax^{k}_{A} end{aligned}right.[/math] Затем находим [math]x_{N}[/math] из уравнения [math]lg{y_{N}}=lg{a}+klg{x_{N}}[/math].
Вернуться к началу

Deda	Заголовок сообщения: Re: Где спросить про логарифмическую функцию? Добавлено: 21 авг 2018, 10:36
	Booker48 писал(а): Deda писал(а): Например на графике по моей ссылке предположим (условно) Ax=8, Ay=5.3, Bx=820, By=0.75 Нееее… Это вы координаты даёте нелогарифмические. Логарифмическими для A будут (0.25, 1.7). Для B — (1.9, 0.87). Тогда [math]y = 10^{3.0125}x^{-0.83}[/math] Так у меня и есть нелогарифмические, а самые обычные координаты! И результат мне тоже нужен обычный, а не логарифмический! Попробую объяснить еще раз. Есть самые обычные две точки с самыми обычными координатами. Просто именно в логарифмической системе координат (на логарифмической сетке!) график, описывающий нужную мне функцию, выглядит как прямая! Больше ничего логарифмического тут нет! Andy Выше давал приблизительные координаты точек A и B — A(8, 5.3), B(820, 0.75) Именно такие координаты и являются исходными данными! FEBUS Спасибо за формулы, попробую разобраться и проверить. Только в результате мне нужна обычная координата X, а не ее логарифм и т.д.
Вернуться к началу

Booker48	Заголовок сообщения: Re: График функции в логарифмическом масштабе Добавлено: 21 авг 2018, 12:06
	Deda писал(а): Выше давал приблизительные координаты точек A и B — A(8, 5.3), B(820, 0.75) Именно такие координаты и являются исходными данными! Только на картинке у А приблизительно (18; 5.3). Тут такое дело. Если вы по картинке определяете координаты точек концов отрезка (по логарифмической шкале, на глазок), то вам на глазок придётся и координаты абсциссы для Y=2 определять. Хотите приемлемой точности — нужно на логарифмической шкале обычной линейкой измерить линейные координаты точек, а затем пересчитывать по формулам, которые приведены выше. FEBUS предлагает решать систему, я — составить уравнение прямой, что, в сущности равносильно.
Вернуться к началу

Логарифмическая функция

Определение логарифма

log_а в = х или а^х = в.

Например:

Необходимо запомнить следующие соотношения:

1) log _а 1 = 0; 2) log _а а = 1; 3) log _а а ^т;

5) если 0< а < 1, то log _а в < 0 при в > 1 и log _а
в > 0 при 0 < в < 1.

Например: 1) log ₅ 1=0, т.к. 5⁰ =1;

2) Log₇ 7=1, т.к. 7¹ =7;

3) Log₃ 3 ⁴=4, т.к. log₃ 3 ⁴= 4 log₃
3;

4) а>1, а=2, в > 1, в=16, то Log₂ 16 =4,

0 < в < 1, в = ,
то Log₂ =
-4< 0;

5) 0< а <1, а=,
в >1, в=27, то Log
27=-3

0< в <1, в = ,
а =, то log=3.

Поскольку логарифм определен для
положительных чисел, а, значит, для натуральных
чисел N, то его определение можно сформулировать
следующим образом:

Логарифм числа N по основанию а (обозначает log_aN)
называется показатель степени, в которую надо
возвести число а, чтобы получить число N, т.е b=log_aN,
если a^b=N.

По определению логарифма справедливо
равенство

,

из которого на основе свойств показательной
функции устанавливаются основные свойства
логарифмов (здесь М, N и k – положительные числа):

,

,

,

Эти свойства позволяют сводить умножение и
деление чисел (представленных в виде степеней
некоторого числа, принятого за основание) к
сложению и вычитанию показателей степеней, а
возведение в степень и извлечение корня – к
умножению и делению на показатель степени,
поэтому применение логарифмов упрощает и
сокращает сложные вычисления.

При выполнении преобразований логарифмических
выражений часто используют свойства степеней:

а ^m+n= а ^m+ аⁿ; а ^m-n
= ; (а ^m)
ⁿ = а ^mn = (а ⁿ ) ^m.

Из определения следует, что а ^{log а в} ₌
в — это равенство называется основным
логарифмическим тождеством.

Например:

1. Логарифм произведения двух положительных чисел
   равен сумме логарифмов этих чисел:



Например:

2. Если а,b,c-положительные числа, причем а не равно
   1, то справедливо равенство



Например:

3. Если a и b- положительные числа, причем а не равно
   1, то для любого числа r справедливо равенство .
4. Если а,b и с – положительные числа, то

Если основанием логарифма является число
е=2,71828…, то логарифм называется натуральным и
обозначается ln x = log _e x.

При нашей десятичной системе счисления самым
удобным основанием является число 10. Логарифм
по основанию 10 называется десятичным логарифмом
и обозначается lg:

Функция , ее свойства

Мы ввели понятие логарифма положительного
числа по положительному и отличному от 1
основанию а. Для любого положительного числа
можно найти логарифм по заданному основанию. Но
тогда следует подумать и о функции вида

,

о ее графике и свойствах. Этим мы и займемся .

Рассмотрим одновременно две функции:
показательную

у = а^х и логарифмическую у = log_aх.
Пусть точка (b;с) принадлежит графику функции у = а^х;
это значит, что справедливо равенство с = a^b.
Перепишем это равенство “на языке логарифмов”: . Последнее
равенство означает, что точка (с; b) принадлежит
графику функции .

Итак, если точка (b;с) принадлежит графику
функции у = а^x, то точка (с; b) принадлежит
графику функции у = log_ax.

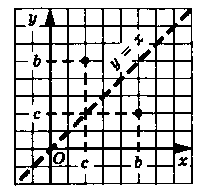
В связи с тем, что точки координатной плоскости
хОу с координатами (b;с) и (с;b) симметричны
относительно прямой у=х (рис. 1).

рис.1.

Таким образом, справедливо следующее
утверждение.

График функции у = log_a х симметричен
графику функции у = а^x относительно прямой у
= х.

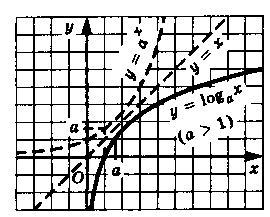
На рис.2 схематически изображены графики
функций у = а^x и у = log_aх в случае, когда
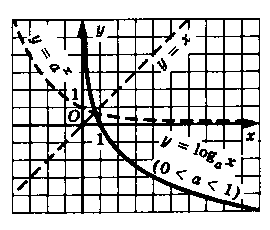
a>1; на рис.3 схематически изображены графики
функций у = а^x и у = log_aх в случае, когда 0
< a < 1.

рис.2.

рис.3.

График функции у = log_aх называют
логарифмической кривой, хотя на самом деле
нового названия можно было не придумывать. Ведь
это та же экспонента, что служит графиком
показательной функции, только по-другому
расположенная на координатной плоскости.

Если значение основания а указано, то график
логарифмической функции можно построить по
точкам. Пусть, например, нужно построить график
функции у=Iog₂х. Составляя таблицу
контрольных точек, будем руководствоваться
соотношением Iog₂2^r = r. Поэтому в
таблицу в качестве значений аргумента х мы
включим числа, являющиеся степенями числа 2.

Имеем:

log2 = log22-2 = -2,log2 = log22-1 = -1,

log21 = log220 = 0, log22 = log221 = 1,

log24 = log222 = 2, log28 = log223 = 3.

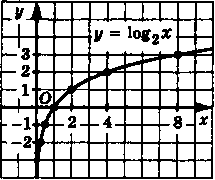
рис.4.

Сведем полученные результаты в таблицу:

Построив на координатной плоскости точки (;-2), (;-1), (1;0), (2;1), (4;2), (8;3), проводим
через них логарифмическую кривую (рис. 4).

Свойства функции у = log_ax, a > 1.

Необходимую информацию извлекаем из
геометрической модели, представленной на рис. 2.

1) D(f) = (0; +);

2) не является ни четной, ни нечетной;

3) возрастает на (0; + );

4) не ограничена сверху, не ограничена снизу;

5) не имеет ни наибольшего, ни наименьшего
значений;

6) непрерывна;

7) Е(f) = (-; +);

выпукла вверх.

Замечание. Сравните график функции у = log_ax,
изображенный на рис.2, и график функции у = х^r
(0 < r < 1). Не правда ли, они похожи (при х > а)? На
самом деле между ними есть принципиальная
разница: график функции у = х^r “набирает
обороты” быстрее. Иными словами, для достаточно
больших значений х ордината графика степенной
функции у=х^r ( при 0<r<1 и уж тем более при r
>= 1) значительно больше соответствующей
ординаты графика логарифмической функции с
любым основанием, большим, чем 1. В курсе
математического анализа доказано, что при а>1 и
r>0 выполняется равенство

.

Свойства функции у = log_ax, 0 < a < 1.

Необходимую информацию извлекаем из
геометрической модели, представленной на рис.3.

1) D(f) = (0; +);

2) не является ни четной, ни нечетной;

3) убывает на (0; + );

4) не ограничена сверху, не ограничена снизу;

5) нет ни наибольшего, ни наименьшего значений;

6) непрерывна;

7) E(f) = (-;+);

выпукла вниз.

Отметим, что ось у является вертикальной
асимптотой графика логарифмической функции и в
случае, когда a>1, ив случае, когда 0<a<1.

Краткое содержание темы

Пример 1. Построить графики функций.

А) б) в)

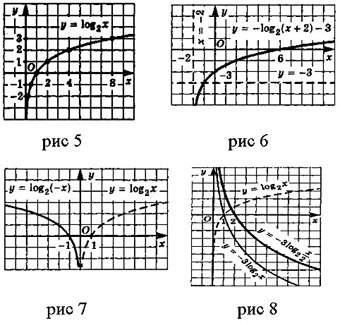
Решение. В этом примере нужно выполнить
различные преобразования графика функции (см рис 5)

а) перейдем к вспомогательной системе
координат с началом в точке (-2;-3) (пунктирные
прямые х=-2 и у=-3 на рис 6) 2Привяжем” график
функции к
новой системе координат – это и будет требуемый
график (рис 6)

б) Напомним, что график функции симметричен графику
функции
относительно оси у. Учтя это, строим график
функции , а
затем, подвергнув его преобразованию симметрии
относительно оси у, получаем график функции рис 7.

в) Построение графика функции осуществим в несколько
шагов.

1. Построим график функции (пунктирная линия на рисунке
2. Осуществим растяжение построенного графика от
   оси х с коэффициентом 3 и симметрию
   “растянутого” графика относительно оси х.
   Получим график функции
   (тонкая линия на рис 8).
3. Осуществим сжатие построенного графика к оси у
   с коэффициентом (т.е растяжение графика от оси у с
   коэффициентом 2). Получим график функции (жирная линия на
   рис 8).

Пример 2.Найдем область определения функции .

Область определения логарифмической функции — множество R₊.
Поэтому заданная функция определена только для
тех х, при которых , т.е. при .
Следовательно, областью определения заданной
функции является интервал (-;0,8).

Пример 3. Найдем область определения функции .

Как и в предыдущем примере, функция f определена
для всех тех х, при которых . Решая это квадратное
неравенство, получаем что D(f) – объединение
интервалов (-; -1) и
(4;).

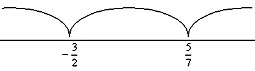
Пример 4. Найдем область определения функции.

Решая методом интервалов неравенство

находим (рис 145), что

Задания для самостоятельной работы
студентов

Задание 1.

Найдите значение логарифмической функции у=log₂x
в указанных точках:

Задание 2.

В одной системе координат изобразите графики
функций:

Задание 3.

Сравните числа:

Задание 4.

Постройте график функции.

  Функции с логарифмами (наибольшее и наименьшее значение). В этой статье речь пойдёт о задачах на нахождение  наибольшего и наименьшего значения функции. Рассмотрим задачи с логарифмами. Задания связанные с исследованием функции разнообразны. Кроме логарифмических функций рассматриваются: функции с числом е, с тригонометрическими функциями, дробно-рациональные функции и прочие.

В любом случае рекомендую ещё раз просмотреть теорию изложенную в статье «Исследование функций. Это нужно знать». Если вы этот материал поняли и имеете хороший навык нахождения производных, то любую задачу в этой теме решите без труда.

Напомню алгоритм нахождения наибольшего или наименьшего значения функции на заданном отрезке:

1. Вычисляем производную.

2. Приравниваем её к нулю и решаем уравнение.

3. Определяем принадлежат ли полученные корни (нули производной) данному отрезку. Отмечаем те, которые принадлежат.

4. Вычисляем значения функции на границах отрезка и в точках (полученных в предыдущем пункте) принадлежащих данному отрезку.

*В некоторых случаях удобно обойтись без п.4. Достаточно определить убывание (возрастание) функции чтобы найти точку максимума (минимума) и далее вычислить наименьшее (наибольшее) значение.

Найдите наименьшее значение функции у=5х–ln (х+5)⁵  на отрезке [–4,5;0].

Необходимо вычислить значение функции на концах интервала, и в точках экстремума, если таковые имеются на данном интервале, и выбрать наименьшее из них.

Вычисляем производную, приравниваем её к нулю, решаем уравнение.

Производная функции:

Найдем нули производной:

*Дробь равна нулю тогда, когда числитель равен нулю.

Точка  х= – 4  принадлежит заданному интервалу. 

Таким образом, вычисляем значение функции в точках: – 4,5; – 4; 0.

Значения с логарифмами, которые мы получили, вычислить (или проанализировать) можно. НО! На это уйдет драгоценное время

Вычислять их не обязательно. Почему? Мы знаем, что ответом должно быть либо, целое число, либо конечная десятичная дробь. А значения с логарифмами:  – 22,5 – ln 0,5⁵  и   – ln3125  такого ответа не дадут.

Кроме того, убедится в том, что в точке х=–4 функция приобретает минимальное значение, можно определив знаки производной на интервалах от (– 5:– 4) и (– 4;+∞). 

Теперь информация для тех, у кого с производной и пониманием того, как решать подобные задачи, нет вообще никаких трудностей. Как можно обойтись без вычисления производной и без лишних расчётов?

Итак, если учесть, что ответом должно быть целое число, либо конечная десятичная дробь, то такое значение мы можем получить только тогда, когда х будет являться целым числом, либо целым с конечной десятичной дробью и при этом под знаком логарифма в скобках у нас получится единица или число е. В противном случае, мы не сможем получить оговоренное значение. А это возможно только при  х = – 4.

Значит именно в этой точке значение функции будет наименьшим, вычислим его:

Ответ: – 20

Решить самостоятельно:  

Найдите наименьшее значение функции у=3х– ln (х+3)³ на отрезке [–2,5;0].

Посмотреть решение

Найдите наибольшее значение функции у=ln (х+5)⁵–5х  на отрезке [–4,5;0].

Посмотреть решение

Найдите наибольшее значение функции у=х²–13х+11∙lnх+12 на отрезке [13/14; 15/14]. 

Чтобы найти наименьшее значение функции на отрезке, необходимо вычислить значение функции на его концах, и в точках экстремума, если таковые имеются на данном интервале.

Вычислим производную, приравниваем её к нулю, решим полученное уравнение:

Решив квадратное уравнение,  получим

Точка  х = 1, принадлежит заданному интервалу.

Точка  х = 22/4 ему не принадлежит.

Таким образом, вычисляем значение функции в точках:

Мы знаем, что ответом является целое число либо конечная десятичная дробь, значит наибольшее значение функции равно 0. В первом и третьем случае такое значение мы не получим, так как натуральный логарифм данных дробей  такого результата не даст.

Кроме того, убедится в том, что в точке х = 1 функция приобретает максимальное значение, можно определив знаки производной на интервалах от (0:1) и (1;+∞). 

Как решить такой тип задач без вычисления производной?

Если учесть, что ответом должно быть целое число, либо конечная десятичная дробь, то это условие обеспечивается только тогда, когда х будет являться целым числом, либо целым с конечной десятичной дробью и при этом под знаком логарифма у нас будет единица или число е.

Это возможно только при  х = 1. Значит в точке х=1 (или 14/14) значение функции будет наибольшим, вычислим его:

Ответ: 0

Решите самостоятельно:

Найдите наибольшее значение функции  у = 2х²–13х+9∙lnх+8 на отрезке [13/14; 15/14]. 

Посмотреть решение

Отмечу, что способ решения таких заданий без нахождения производных, можно использовать только для экономии времени при вычислении задания на самом экзамене. И только в том случае, когда вы отлично понимаете, как решать такие задачи через нахождение производной (по алгоритму) и хорошо умеете это делать. Бесспорно, что при решении без вычисления производной должен быть некоторый опыт в аналитике.

«Хитрых» приёмов, которые порой помогают в конкретных заданиях множество, и все их не запомнить. Важно понимать принципы решения, свойства. Если же вы возложите свои надежды на какой-то приём, то он может просто не сработать по простой причине: вы его забудете или вам попадёт такой тип задания,  который вы видите впервые.

В данной рубрике продолжим рассматривать задачи, не пропустите! 

На этом всё. Успехов Вам!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.