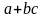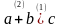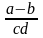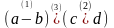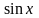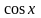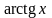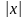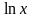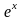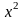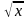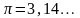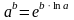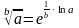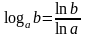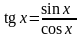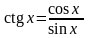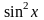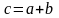Арифметические выражения в Pascal
Арифметические выражения формируются из переменных, констант, функций, знаков операций и круглых скобок. В арифметических выражениях используются следующие арифметические операции:
|
Выражение |
Тип данных |
Тип результата |
Операция |
Пример |
|
A+B |
Real Integer Real, Integer |
Real Integer Real |
Сложение |
|
|
A—B |
Real Integer Real, Integer |
Real Integer Real |
Вычитание |
|
|
A*B |
Real Integer Real, Integer |
Real Integer Real |
Умножение |
|
|
A/B |
Real Integer Real, Integer |
Real Real Real |
Деление |
|
|
A div B |
Integer |
Integer |
Целочисленное деление |
11 div 5 Þ2 10 div 3Þ3 2 div 3Þ0 |
|
A mod B |
Integer |
Integer |
Деление с остатком |
11 mod 5Þ1 10 mod 3Þ1 14 mod 5Þ4 |
Приоритет операций в порядке убывания: /, *, div, mod, -, +
Для изменения приоритета операций используются круглые скобки.
Например:
(A+B)/(A-B)
Математические функции в Pascal
|
Функция |
Назначение |
Тип результата |
|
Abs(X) Arctan(X) Sin(X) Cos(X) Exp(X) Ln(X) Sqr(X) Sqrt(X) Frac(X) Int(X) Round(X) Trunc(X) |
Абсолютное значение аргумента Арктангенс аргумента Синус аргумента Косинус аргумента ex Натуральный логарифм Квадрат аргумента Квадратный корень аргумента Возвращает число, равное дробной части числа Возвращает число, равное целой части числа Возвращает число, равное целой части числа Возвращает число, равное целой части числа |
Совпадает с типом Х Вещественный Вещественный Вещественный Вещественный Вещественный Совпадает с типом Х Вещественный Вещественный Вещественный LongInt LongInt |
Пример программы с использованием арифметических выражений
Program p2;
Const
X=-2;
A=732;
B=3.4;
Var
Z,Y:Real;
BEGIN
Y:=1/(1-1/Sqrt(A+B));
Z:=Arctan(X)/(1-ABS(X));
Write(‘Ý=’,Y,’ Z=’,Z);
END.
Условные выражения и операции отношения в Pascal
Операции отношения выполняют сравнение двух операндов и определяют, истинно значение выражения или ложно. Они используются для управления циклами и в условных операторах.
Операции отношения
|
Выражение |
Операция |
Результат |
|
A=B A<>B A>B A<B A>=B A<=B |
Равно Не равно Больше Меньше Больше или равно Меньше или равно |
True, если A= B True, если A <>B True, если A >B True, если A <B True, если A>= B True, если A<= B |
Операции расположены в порядке убывания приоритета.
Например
Выражение Результат
12>=12 True
56>10 True
11<=6 False
Логические выражения и операции в Pascal
Результатом выполнения логического выражения является логическое значение True или False.
Имеется одна унарная логическая операция not (отрицание) и две бинарные операции and (логическое умножение) и or (логическое сложение).
Таблица истинности
|
Выражение |
Значение А |
Значение В |
Результат |
|
Not A |
True False |
False True |
|
|
A and B |
True True False False |
True False True False |
True False False False |
|
A or B |
True True False False |
True False True False |
True True True False |
Pascal. Урок 2
Арифметические выражения
Рассмотрим подробно арифметические выражения, т.к. именно с их помощью выполняются все вычисления в программе.
Результатом арифметического выражения является целое или вещественное значение. Выражение задает порядок действий над элементами данных и состоит из:
- операндов (констант, переменных, функций);
- знаков операций;
- круглых скобок.
Арифметические операции
Операции определяют действия, которые надо выполнить над операндами. В отличие от традиционной математической записи обязательно указывать все знаки операций.
Например, в выражении (х+у) *5-10 операндами являются переменные х и у, а также константы 5 и 10; а +, * — знаки арифметических операций сложения и умножения соответственно. Символ операции умножения — * (звездочка) должен присутствовать в явном виде. Если все объекты, входящие в выражение, определены в момент их использования (в нашем примере — это переменные х и у), то значение выражения считается определенным.
В простейшем случае выражение может состоять из одной переменной или константы. Круглые скобки ставятся так же, как и в обычных математических выражениях для управления порядком выполнения операций.
Операции DIV и MOD
Целочисленное деление div (от division, деление) отличается от обычной операции деления тем, что возвращает целую часть частного, а дробная часть отбрасывается — 13 div 3 = 4, а не 4,(3). Результат div всегда равен нулю, если делимое меньше делителя.
Например:
11 div 5 = 2
10 div 3 = 3
2 div 3 = 0
123 div 4 = 30
17 div (-5) = -3
-17 div 5 = -3
-17 div (-5) = 3
Взятие остатка от деления mod (от modulus, мера) вычисляет остаток, полученный при выполнении целочисленного деления.
Например:
10 mod 5 = 0
11 mod 5 = 1
10 mod 3 = 1
14 mod 5 = 4
17 mod (- 5) = — 2
-17 mod 5 = -2
-17 mod (-5) = 2
Аргументы операций div и mod — целые числа. Взаимосвязь между операциями div и mod проста. Для а>0 и b>0 справедливо:
a mod b = a – (a div b)*b
(a div b)*b + (a mod b) = a
Обратите внимание — операцию mod можно использовать, чтобы узнать, кратно ли целое а целому b. А именно, а кратно b тогда и только тогда, когда а mod b = 0.
Приоритет операций
| Операция | Приоритет | Вид операции |
| not, @ | Первый (высший) | Унарная операция |
| *, /, div, mod, and, shl, shr | Второй | Операции типа умножения |
| +, —, or, xor | Третий | Операции типа сложения |
| =, , ,=, in | Четвертый | Операции отношения |
Обратите внимание — операции с равным приоритетом выполняются слева направо. Выражение, заключенное в скобки, перед выполнением вычисляется как отдельный операнд. При наличии вложенных скобок вычисления выполняются, начиная с самых внутренних. В тексте программы необходимо проверять парность расстановки скобок: число открывающих скобок должно быть равно числу закрывающих скобок.
Арифметические процедуры и функции
| Стандартная функция | Выполняемое действие | Тип | |
| аргумента | результата | ||
| abs (x) | |x| | real | real |
| integer | integer | ||
| sqr (x) | x2 | real | real |
| integer | integer | ||
| sqrt (x) | x1/2 | real | real |
| integer | real | ||
| exp (x) | ex | real | real |
| integer | real | ||
| ln (x) | ln (x) | real | real |
| integer | real | ||
| sin (x) | sin (x) | real | real |
| integer | real | ||
| cos (x) | cos (x) | real | real |
| integer | real | ||
| arctan (x) | arctg (x) | real | real |
| integer | real | ||
| pi | число Π | — | real |
Вызов стандартной функции осуществляется путем указания в нужном месте программы имени функции (аbs, ln, ехр и др.) и ее аргумента, заключенного в круглые скобки. После вычисления значения функции ее вызов заменяется результатом, и расчет содержащего ее выражения продолжается дальше.
Следует знать:
- аргумент прямых тригонометрических функций sin и соs задается в радианах.
Для преобразования значения угла из радианной меры в градусную необходимо умножить величину угла на число 180/рi.
Для перевода значения угла из градусной меры в радианную необходимо умножить величину угла на число pi/180. - результат функции агсtаn получается в радианах;
- функция random ( N ) возвращает случайное число х, удовлетворяющее условию 0<=х. Тип аргумента и результата — word. В том случае, если нам необходимы целые случайные числа из диапазона A<=х<=B, мы можем получить их, используя выражение A+random (B-A+1).
Если параметр диапазон не указан, то random возвращает число х в диапазоне 0<=х<1. Тип результата — rеаl. В том случае, если нам необходимы вещественные случайные числа из другого диапазона: A < х< B, мы можем задать его при помощи A+B*random.
Перед первым обращением к функции random необходимо с помощью вызова процедуры randomize инициализировать программный генератор случайных чисел. В противном случае при каждом запуске программы датчик будет выдавать одни и те же числа. Эту особенность можно использовать при отладке программы; - процедура dec(х,n) уменьшает значение целочисленной переменной х на n .
Например, х:=10; dec (х, 2); {результат: 8} .
При отсутствии необязательного параметра n процедура принимает вид deс(х) , а значение х уменьшается на единицу; - процедура inc(х,n) увеличивает значение целочисленной переменной х на n.
Например, х:=10; inc(х,3); {результат: 13}.
При отсутствии необязательного параметра n процедура принимает вид inс (х), а значение х увеличивается на единицу; - функция frас(х) вычисляет дробную часть х.
Аргумент и результат — rеаl.
Например write (frас(0.25*11) :4:2); {результат 0.75}; - функция int (х) вычисляет целую часть х.
Аргумент и результат — rеа1.
Например, write(int(422.117) :4:2) ; {результат 422.00}.
Таким образом, х=int (х) +frас (х). - функция преобразования типа trunc(х) возвращает ближайшее целое число, меньше или равное вещественному х, для х>=0 , и больше или равное х, для х<=0 (от truncate, усекать). Таким образом, выполняется отбрасывание десятичных знаков после точки.
Аргумент — rеаl , результат — longint.
Например:
trunc ( 6.7); {результат: 6},
trunc;(-1.6); {результат:-1}. - Функция преобразования типа round(х) возвращает значение х, округленное до ближайшего целого числа (от round, круглый).
Аргумент — rеаl, результат — longint.
Например:
round (6.7); {результат:7},
round(-1.6); {результат:-2}. - Вычисление степени числа выполняется в Тurbо Раsсаl с использованием свойств логарифмов:
c=ab => Ln(c)= b*Ln(a) => c=eb*Ln(a) => c:=exp(b*Ln(a));
Таким образом, нельзя возвести в степень отрицательное число. Для этого можно использовать операторы циклов. - Для вычисления логарифма с основанием а используем:
Loga(x)=Ln(x)/Ln(a); - В Тurbо Раsсаl определены только три тригонометрические функции: sin, соs, аrсtg. Для вычисления остальных тригонометрических функций необходимо использовать известные соотношения:
tg(x)=sin(x)/cos(x);
ctg(x)=cos(x)/sin(x);
csc(x)=1/sin(x);
§5. Арифметические выражения
Арифметические выражения состоят из операций и операндов. В языке программирования Pascal существует шесть операций: сложение (обозначается знаком «+»), вычитание (обозначается знаком «-»), умножение (обозначается знаком «*»), деление (обозначается знаком «/»), деление нацело (обозначается словом «div») и взятие остатка от деления нацело (обозначается словом «mod»). Слова div и mod являются служебными зарезервированными.
Важным понятием в арифметике является понятие операнда. Операндами называются те объекты, над которыми выполняется арифметическая операция. В математике различные операции могут иметь разное количество операндов, но все арифметические имеют два операнда. Операндом для операции может являться как одиночное число или имя переменной, так и целое арифметическое выражение. Рассмотрим выражение (2+2)*2. У операции сложения операндами являются два числа `2`, а у операции умножения правый операнд – это число `2`, а левый – это выражение в скобках `(2+2)`. Прежде чем выполнять операцию, необходимо вычислить оба её операнда.
Приоритет операций в Паскале точно такой же, как и в математике. Сначала выполняются операции умножения, деления, div и mod (это тоже операции деления), а потом операции сложения и вычитания. Операции одного приоритета выполняются слева направо. Для изменения порядка действий можно использовать круглые скобки. Операции в скобках имеют более высокий приоритет, чем операции вне скобок. Так при вычислении выражения 2+2*2 получается число `6`, потому что операция умножения имеет более высокий приоритет, чем сложение, и, следовательно, выполняется первой. Если же записать выражение (2+2)*2, то при вычислении получается число `8`, потому что сложение в скобках выполняется раньше умножения.
Рассмотрим, как определить тип результата при вычислении арифметического выражения. Операции сложения, вычитания и умножения выдают целый результат, если оба их операнда целые, и вещественный, если хотя бы один из операндов – вещественный. Операция деления «/» всегда выдаёт вещественный результат. Даже если мы `4` делили на `2`, всё равно в итоге получается нецелое число. На первый взгляд это кажется странным, но в отличие от математики в программировании каждое число кроме значения ещё имеет тип, и если типы у чисел не совпадают, то они НЕ считаются равными. Нужно уяснить, что `bb(1!=1.0)`. Это несложно понять, если помнить, что раз числа `1` и `1.0` имеют различные типы, то будут представлены совершенно разными последовательностями битов. Операции div и mod всегда выдают целый результат и, в отличие от всех остальных арифметических операций, могут иметь только целые операнды. Попытка применить данные операции к вещественным числам приведёт к тому, что программа просто не будет работать.
Давайте подробнее познакомимся с двумя последними операциями. Операция a div b выдаёт целую часть от деления числа a на число b. То есть 5 div 2 = 2, а 3 div 7 = 0. Операция a mod b выдаёт остаток от деления a на b по следующему закону:
a mod b = a – ((a div b) * b)
Приведём примеры выполнения этих их операций для всех возможных знаков операндов:
5 div 3 = 1; 5 mod 3 = 2;
-5 div 3 = -1; -5 mod 3 = -2;
5 div -3 = -1; 5 mod -3 = 2;
-5 div -3 = 1; -5 mod -3 = -2;
Операндами в арифметическом выражении также могут быть стандартные математические функции, которые приведены в таблице ниже.
| Функция | Комментарий | Тип аргумента | Тип результата |
| abs(x) | $$ │x│$$ — модуль $$ x$$ | integer, real | совпадает с типом аргумента |
| sqr(x) | $$ {x}^{2}$$ | integer, real | совпадает с типом aргумента |
| sqrt(x) | `sqrt x`$$ $$ — корень квадратный из $$ x$$ | integer, real | real |
| Pi | `3.1415926535897932385` | нет | real |
| sin(x) | $$ mathrm{sin}x$$ | integer, real | real |
| cos(x) | $$ mathrm{cos}x$$ | integer, real | real |
| arctan(x) | `»arctg»x` | integer, real | real |
| trunc(x) | отсекание дробной части $$ x$$ | real | integer |
| round(x) | округление $$ x$$ до ближайшего целого. Половины округляются в сторону увеличения модуля. | real | integer |
Необходимо отметить, что функциям sin и cos угол следует подавать в радианах, а не в градусах! Также функция arctan возвращает результат в радианах.
С помощью операций
формируются арифметические и логические
выражения, которые состоят из операций
и операндов, над которыми выполняются
операции.
При записи арифметических выражений
используются арифметические операции,
среди которых сначала выполняются
умножение и деление, а потом сложение
и вычитание. Порядок выполнения операций
можно изменить с помощью круглых скобок.
Пример. Примеры
записи арифметических выражений
приведены в таблице 3.
Таблица 3
|
Математическая запись |
Запись на Паскале |
|
|
|
|
|
|
При записи логических выражений
используются операции сравнения и
логические операции. Операции
сравнения сравнивают значения левого
и правого операндов, в результате чего
логическое выражение становится истинным
или ложным. Несколько логических
выражений могут быть связаны с помощью
логических операций.
Пример.
(11 div 2 = 5) and
(2*2 <> 4)
false
(11 div 2 = 5) or
(2*2 <> 4)
true
not(11 mod 2 = 0)
true
(2 <= 3) xor
(11 mod 2 = 1)
false
1.6. Стандартные функции в языке Pascal
В языке Pascal используются
следующие математические функции
(таблица 4):
Таблица 4
|
Математическая запись |
Запись на Паскале |
|
|
sin(x) |
|
|
cos(x) |
|
|
arctan(x) |
|
|
abs(x) |
|
|
ln(x) |
|
|
exp(x) |
|
|
sqr(x) |
|
|
sqrt(x) |
|
Константа |
pi |
В языке Pascal можно
использовать следующие математические
выражения (таблица
5):
Таблица 5
|
Математическая запись |
Запись на Паскале |
|
|
exp(bln(a)) |
|
|
exp(ln(a)/b) |
|
|
ln(b)/ln(a) |
|
|
ln(x)/ln(10) |
|
|
sin(x)/cos(x) |
|
|
cos(x)/sin(x) |
|
|
sin(sqr(x)) |
|
|
sqr(sin(x)) |
Среди стандартных функций в языке
Pascal также наиболее
часто применяются:
-
round
(округление числа). -
trunc
(целая часть числа). -
frac
(дробная часть числа). -
random
(случайное число). -
odd
(проверка нечётности). -
ord
(порядковый номер аргумента). -
chr
(символ с заданным порядковым номером). -
pred
(предшествующее значение аргумента). -
succ
(последующее значение аргумента).
Пример.
round(3.7)
4
trunc(3.7)
3
frac(3.7)
0.7
random(10)
7
odd(3)
true
ord(’A’)
63
chr(63)
’A’
pred(’B’)
’A’
succ(’B’)
’C’
1.7. Операторы языка Pascal
В языке Pascal используются
следующие операторы:
-
Составной
оператор begin…end
(начало…конец). -
Оператор
присваивания …:=…
(…присвоить…). -
Операторы
ввода:
-
read(…)
(считывать); -
readln(…)
(считывать до новой строки).
-
Операторы
вывода:
-
write(…)
(записывать); -
writeln(…)
(записывать до новой строки).
-
Оператор
безусловного перехода goto…
(перейти к…). -
Оператор
условного перехода (условный оператор)
if…then…else…
(если…то…иначе…). -
Оператор
варианта (оператор выбора) case…of…else…end
(в случае…из…иначе…конец). -
Оператор
цикла с предусловием while…do…
(пока…делать…). -
Оператор
цикла с постусловием repeat…until…
(повторять…до тех пор, пока…). -
Операторы
цикла с параметром:
-
for…:=…to…do…
(для…от…до…делать…); -
for…:=…downto…do…
(для…от…вниз до…делать…).
-
Оператор
присоединения with…do…
(с…делать…).
Задача 1.
Условие
задачи.
Вычислить
(составить
блок-схему алгоритма и программу для
решения задачи).
Блок-схема.
-
Программа.
Объяснение программы.
Program
z1;Программа по имени z1
Var
Раздел описания переменных
a,b,c:real;
Переменные a,
b,
c
– вещественного типа (т.е.
эти переменные – дробные числа)Begin
Начало раздела операторов (или начало
составного оператора)writeln(‘Введи
a,b’);Вывод пояснительного текста ‘Введи
a,b’read(a,b);
Ввод значений переменных a
и bc:=a+b;
Переменной c
присваивается значение выражения
a+bwriteln(‘c=’,c:10:3);
Вывод пояснительного текста ‘c=’
и значения переменной c,
имеющей в числе 10 позиций, в т.ч. 3 цифры
после запятойEnd.
Конец раздела операторов и программы
Экран
пользователя.Введи а,b
3|__|5
c=|__|
|__|
|__|
|__|
|__|
8.000
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Оператор присваивания
Оператор присваивания является одним из основных операторов любого языка программирования.
Оператор присваивания предназначен для присваивания переменной значения выражения.
Формат оператора присваивания:
<переменная>:=<выражение>
В операторе присваивания слева от знака присваивания «:=» записывается переменная, а справа – выражение, численное значение которого присваивается этой переменной.
Выполнение оператора присваивания приведет к вычислению выражения и присваиванию значения выражения переменной.
Обязательным является требование, чтобы выражение и переменная были совместимы по присваиванию.
Например, оператор присваивания
y:=x+h/2;
означает, что переменной y присваивается число, полученное в результате вычисления выражения x+h/2 при известных числовых значениях переменных x и h .
Следует обратить внимание, что всем переменным в правой части оператора присваивания ранее уже были присвоены значения предыдущими операторами, например,
x:=0; h:=1;
Рассмотрим пример
t:=t+1;
Здесь переменной t присваивается значение, которое до этого момента имела переменная t, плюс 1. Если переменная t имела до выполнения этого оператора значение равное 7, то после исполнения оператора t:=t+1 значение переменной будет равно 8.
Арифметические выражения
Арифметические выражения строятся из арифметических констант, переменных, функций и операций над ними.
Правила записи и смысл арифметических выражений в Паскале почти не отличаются от обычной математической записи.
В арифметических выражениях используются следующие операции и соответствующие знаки:
| Операция | Знак операции |
| Сложение | + |
| Вычитание | — |
| Умножение | * |
| Деление | / |
| Деление целых чисел | div |
| Остаток от деления целых чисел | mod |
Операции +, -, *, / имеют очевидный смысл. Результатом операции div будет целое значение, равное целой части результата деления первого числа на второе. Результатом операции mod будет целое значение, равное остатку от деления (но не дробной части).
Примеры арифметических операций:
Vara,b,c:integer;
Begin
a:=10; b:=3;
c:=a mod b; {с равно 1 – равно остатку, но не дробной части}
c:= a div b; {с равно 3 – равно целой части }
b:=a+b; {b равно числу 13}
End.
Арифметические операции выполняются в порядке старшинства: сначала вычисление функции, затем умножение, деление, сложение, вычитание.
Если последовательность выполнения операций не определяется их старшинством, действия выполняются слева направо. Желаемый порядок выполнения операций всегда может быть задан соответствующим образом расставленными круглыми скобками. Допускается ставить лишние круглые скобки, если это упрощает чтение формулы.
Рассмотрим арифметическое выражение
-a*x*x+b/x*c+y-c*n/(a-b)
В таблице приведен порядок выполнения операций:
| № | Операция | № | Операция |
| 1 | a*x | 7 | -a*x*x+b/x*c+y |
| 2 | a*x*x | 8 | c*n |
| 3 | -a*x*x | 9 | (a-b) |
| 4 | b/x | 10 | c*n/(a-b) |
| 5 | b/x*c | 11 | -a*x*x+b/x*c+y-c*n/(a-b) |
| 6 | -a*x*x+b/x*c |
ЗАМЕЧАНИЕ. Все данные, входящие в арифметическое выражение, должны быть одного типа.
Исключение составляют только константы и переменные целого типа (integer), которые разрешается использовать в выражениях вещественного типа (real). Если в выражении используются данные целого и вещественного типа, результат операции будет вещественного типа. В других случаях необходимо выполнять преобразование данных.
Пример. Пусть переменные x и y описаны следующим образом:
varx:integer;
y:real;
Рассмотрим оператор y:= x+2, в котором используются переменные целого, вещественного типов и константа. Результат операции будет вещественного типа, поэтому оператор y:=x+2; является допустимым, хотя справа от присваивания стоит целая переменная и константа;
Следующие операторы являются ошибочными:
x:=y+2 {несовместимость типов: переменной целого типа x присваивается значение переменной вещественного типа y}
x:=y/x {несовместимость типов: операция деления всегда возвращает значение вещественного типа}
Для обеспечения совместимости типов необходимо выполнять преобразования данных. Для преобразования Real в Integer имеются две функции:
Round() – округляет Real до ближайшего целого;
Trunc() – усекает Real путем отбрасывания дробной части.
Правильная запись рассматриваемых операторов: x:=y+2; и x:=y/x; имеет вид:
x:=round(y)+2;
x:=round(y/x);
x:=trunc(y)+2;
x:=trunc(y/x);
Программируя арифметические выражения, нужно иметь в виду следующие основные правила:
- Два знака арифметических операций нельзя писать рядом. Например, следующие записи будут неправильными:
+–a –b — следует писать +(–a) –b
a*–b — следует писать a*(–b)
- Знак умножения опускать нельзя, например, при записи произведения: a*b и 2*n, запись ab и 2n будет неправильной, так как ab воспринимается как идентификатор, а запись 2n не является идентификатором, потому что начинается с цифры.
- В арифметических выражениях допускается использовать только круглые скобки. Количество открывающих круглых скобок должно соответствовать количеству закрывающих круглых скобок. Применение фигурных и квадратных скобок запрещается, так как они имеют особое значение.
- Все данные, входящие в выражения должны быть одного типа. Если в выражении используются данные целого и вещественного типа, результат операции будет вещественного типа.
В арифметических выражениях могут использоваться различные элементарные функции. В языке Турбо Паскаль существуют стандартные функции. Пользователь может не знать, как вычисляется стандартная функция, ему достаточно правильно записать имя функции и ее аргумент. Наиболее часто используемые стандартные функции приведены в таблице:
| Функция | Назначение |
| Abs(x) | Абсолютное значение аргумента x |
| Sqr(x) | Вычисляет квадрат аргумента x |
| Sqrt(x) | Вычисляет квадратный корень аргумента x |
| Exp(x) | Возвращает экспоненту аргумента ex (степень числа e=2,72) |
| Ln(x) | Вычисляет натуральный логарифм аргумента x |
| Pi | Значение числа p=3.1415926 |
| Frac(x) | Дробная часть числа x |
| Int(x) | Целая часть числа x |
| Sin(x) | Синус аргумента x (угол в радианах) |
| Cos(x) | Косинус аргумента x (угол в радианах) |
| Arctan(x) | Арктангенс аргумента x (угол в радианах) |
| Randomize | Инициализация генератора случайных чисел |
| Random(x) | Если x отсутствует, то значением функции является случайное число типа real из диапазона 0<=…<Если задается значение x, то значением функции будет случайное число из диапазона 0< <x. |
В языке Турбо Паскаль нет операции возведения в степень. При необходимости ее использования можно воспользоваться следующей зависимостью:
x n = exp(n*ln(x));
Примеры записи простых арифметических выражений и операторов присваивания приведены в таблице:
| Обычная математическая запись | Запись на Турбо Паскале |
| |
x/(y*z) или x/y/z |
| |
y*x/z |
| |
(x+a)/(y+b) |
| |
1/(m*sqrt(a+b)) |
| |
x1:=(-b+sqrt(b*b-4*a*c))/(2*a) |
| |
y:=sin(x) |
| |
sqr((x+y-z)/2/a) |
Типичные ошибки в записи выражений:
4x+1 Пропущен знак умножения между 4 и x
a+sinx Аргумент x функции sinx не заключен в скобки
((a+b)/sqr(c*7) не хватает закрывающей скобки
ЗАДАЧА2. Вычислить корни квадратного уравнения
a∙x 2 +b∙x + c =0
по известным формулам
Предположим, что дискриминант этого уравнения больше нуля и уравнение имеет только действительные корни. Программа нахождения корней уравнения приведена ниже.
Program a2;
Var {раздел объявления переменных}
X1:real; {1-й корень уравнения}
X2:real; {2-й корень уравнения}
D:integer; {дискриминант уравнения}
A:integer; {коэффициент a}
B:integer; {коэффициент b}
C:integer; {коэффициент c}
Begin
Write(‘Введите коэффициенты a,b,c:’);
Readln(a,b,c); {чтение с клавиатуры коэффициентов}
D:=sqrt(b*b-4*a*c); {вычисление дискриминанта}
X1:=(-b+d)/(2*a); {вычисление 1-го корня уравнения}
X2:=(-b-d)/(2*a); {вычисление 2-го корня уравнения}
Write(‘Корни уравнения равны: ’, x1:8:2, x2:8:2);
End.
Результаты работы программы:
Введите коэффициенты a,b,c:2 –6 4
Корни уравнения равны: 2.00 1.00