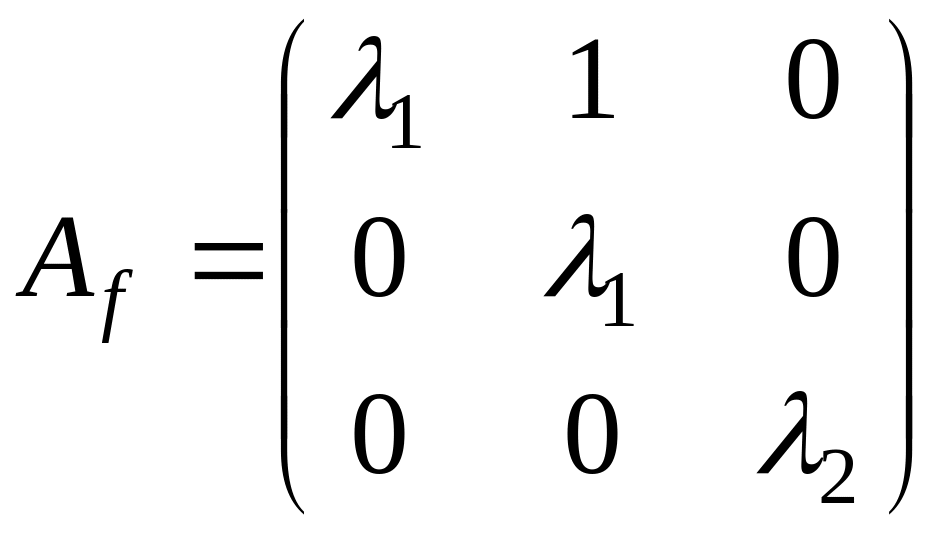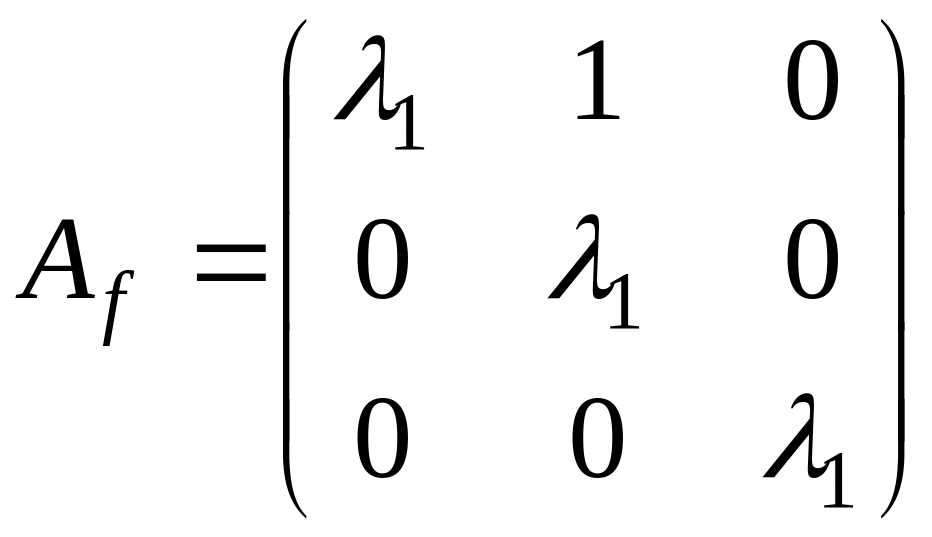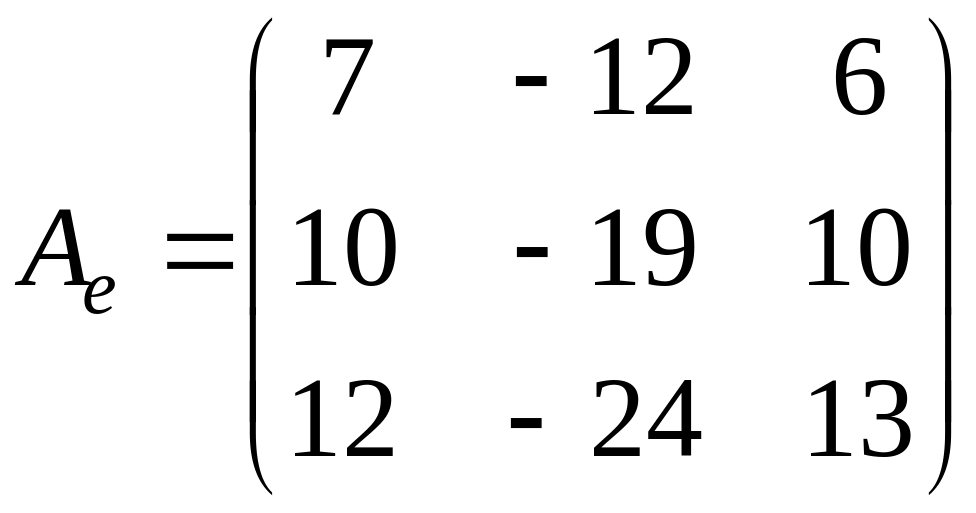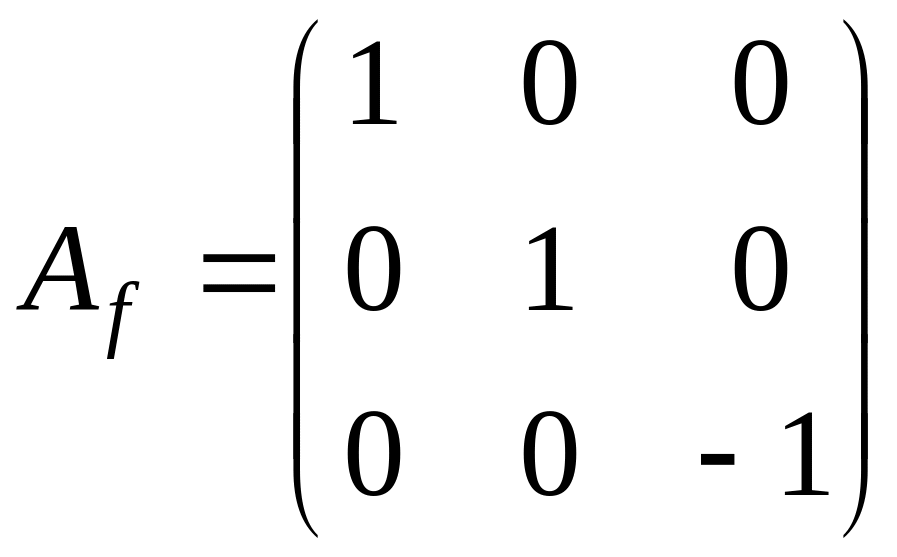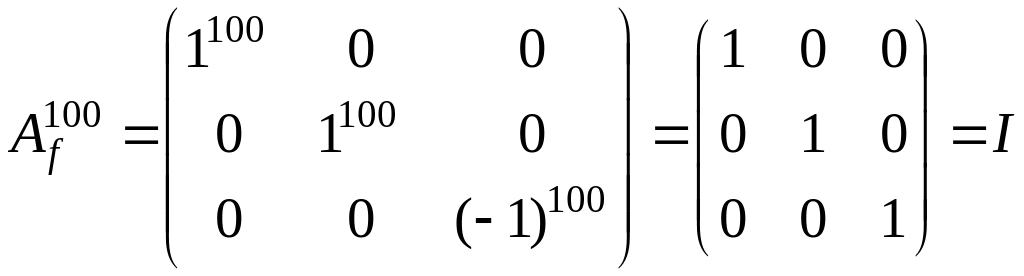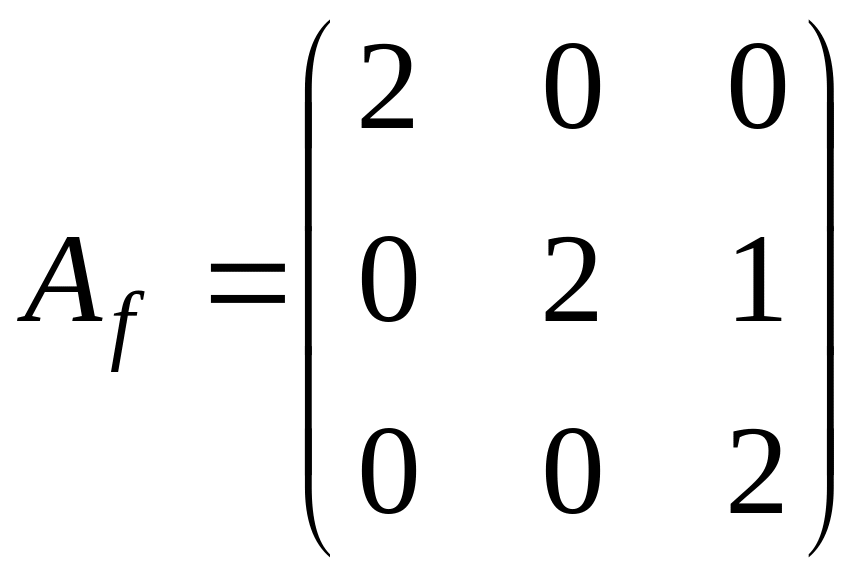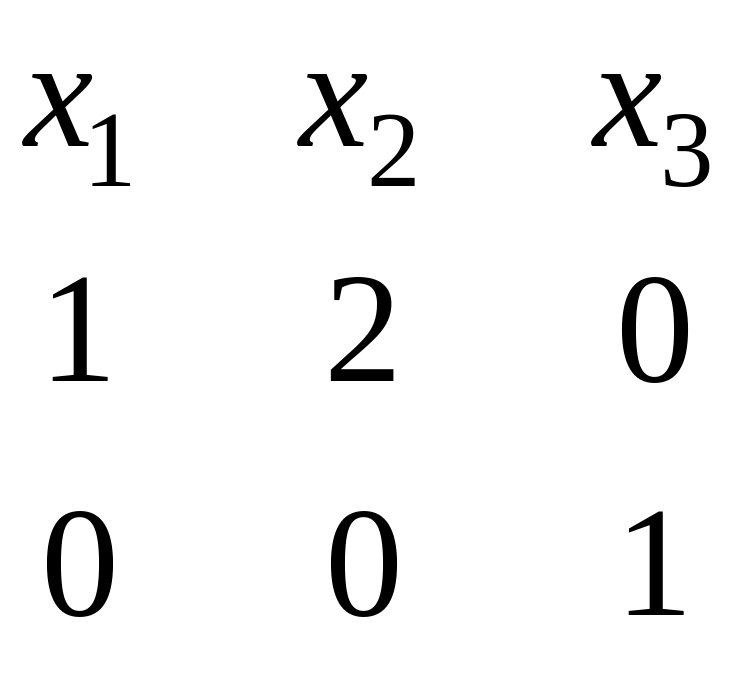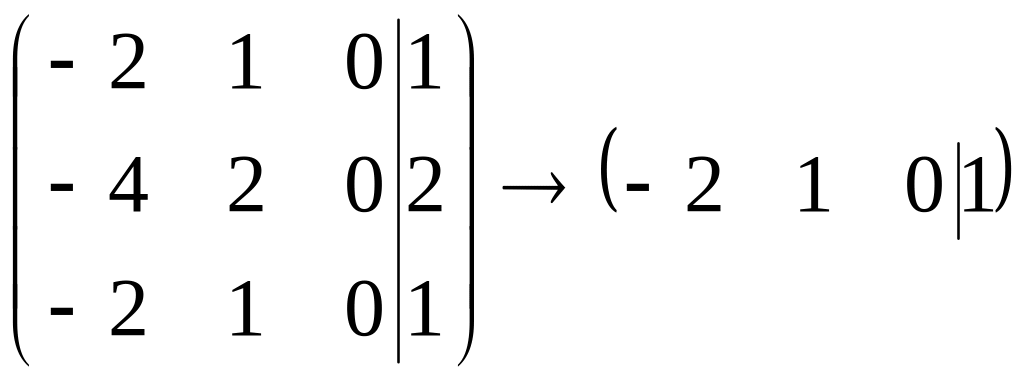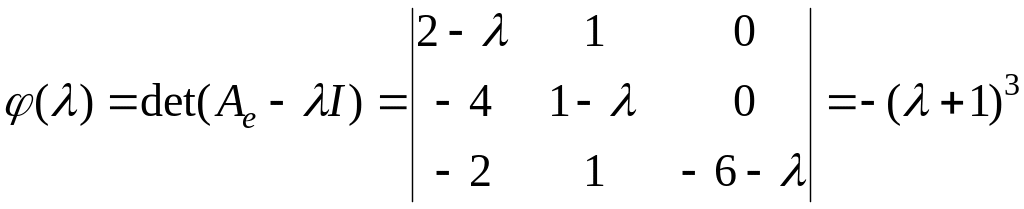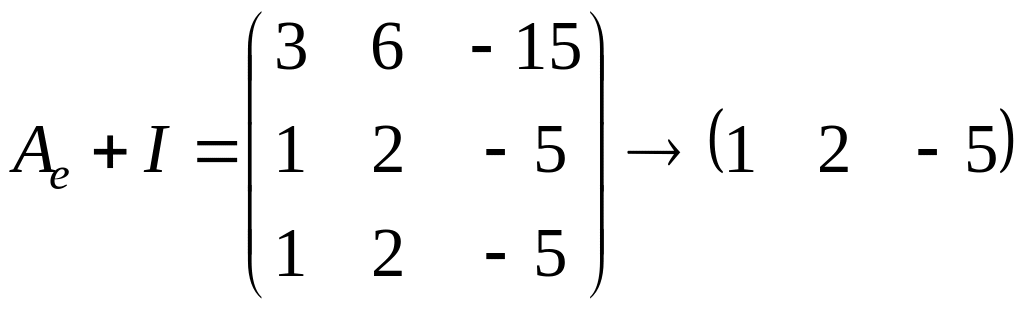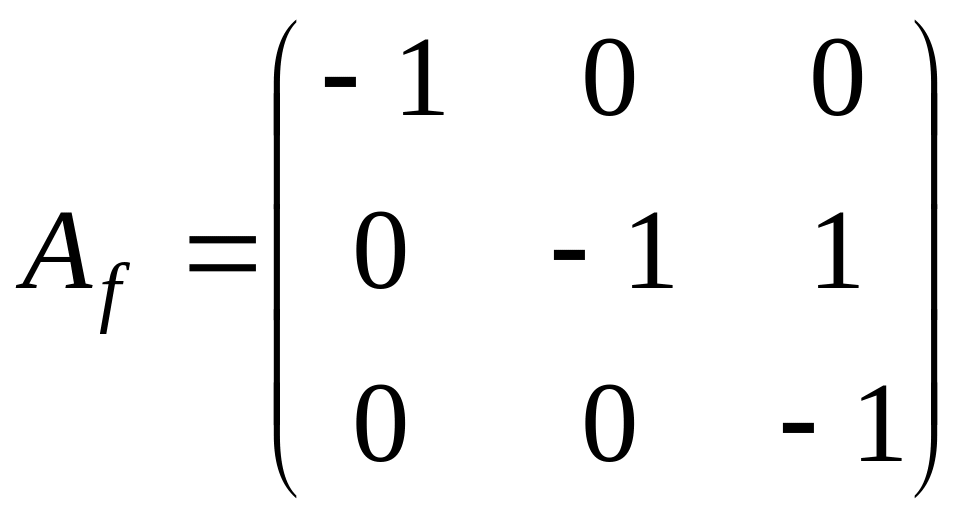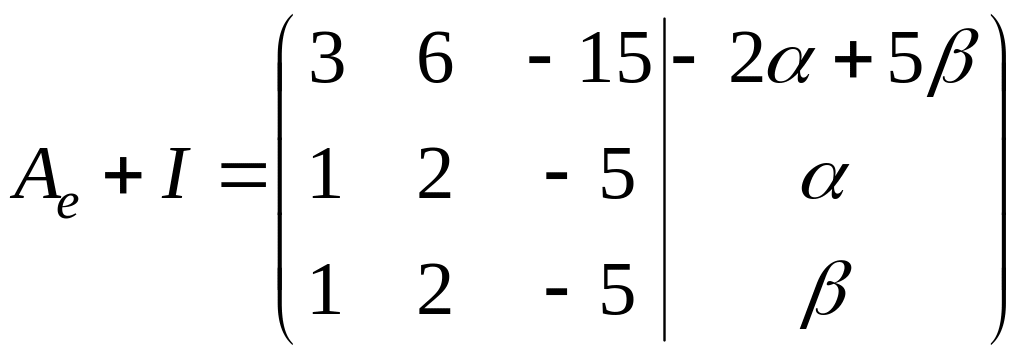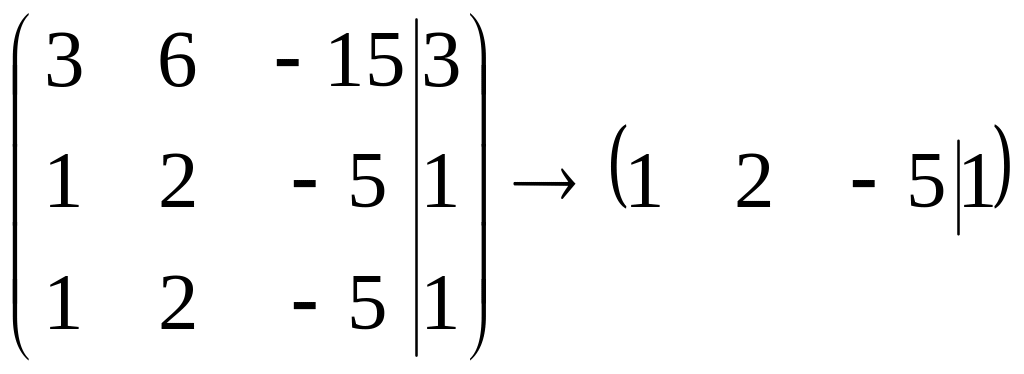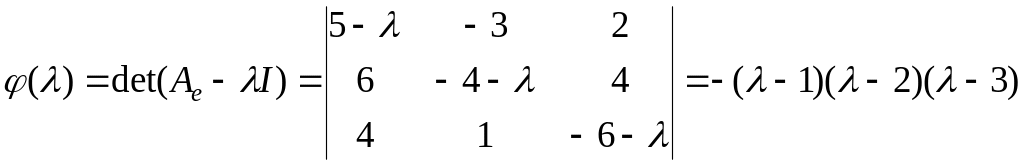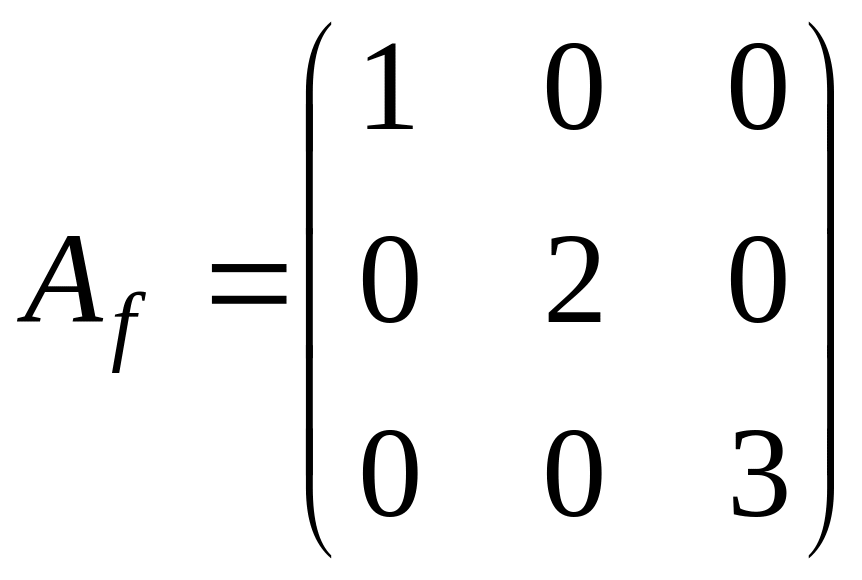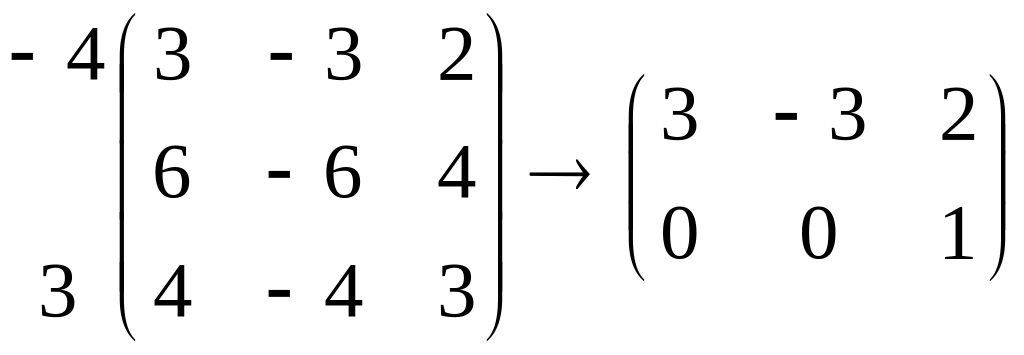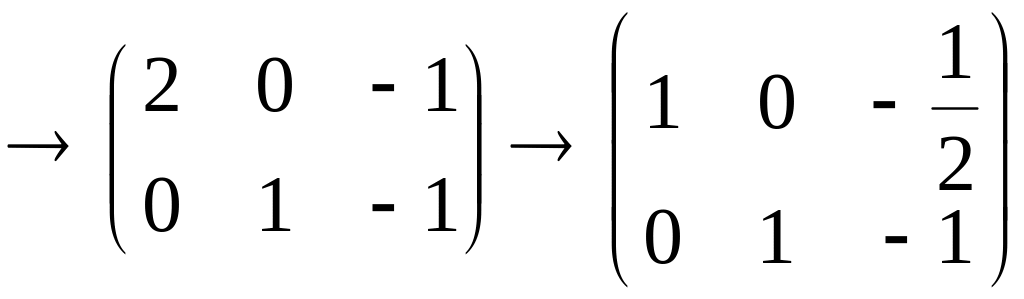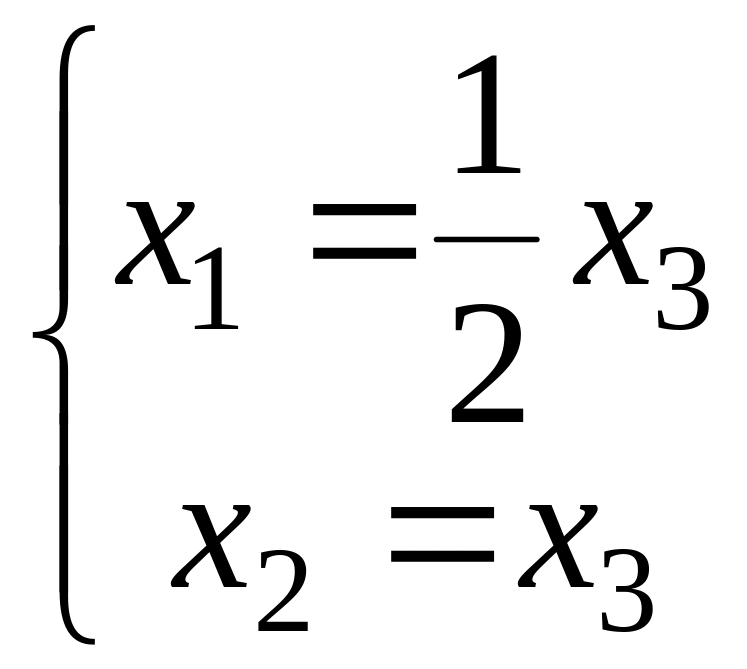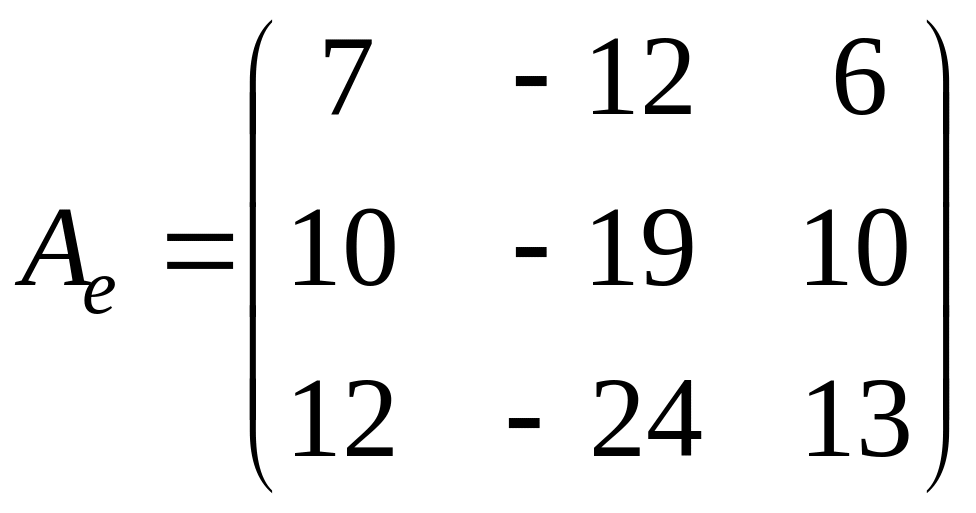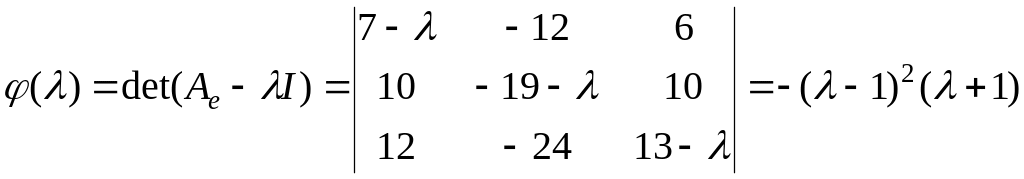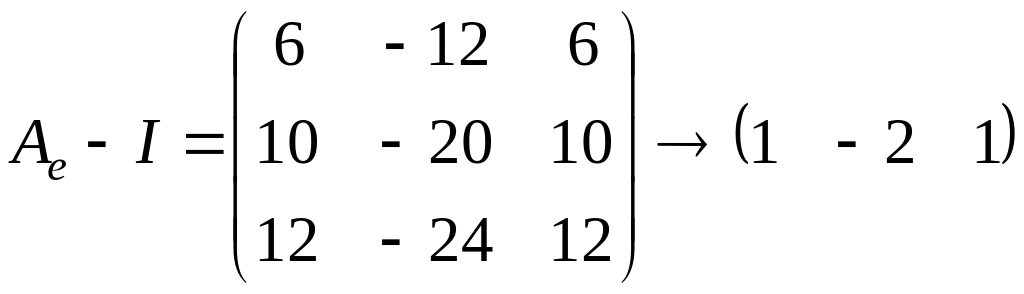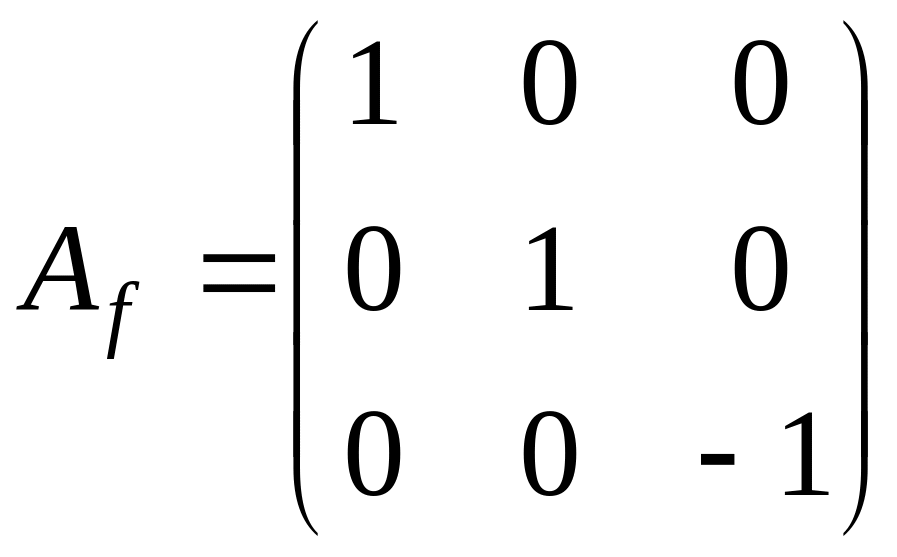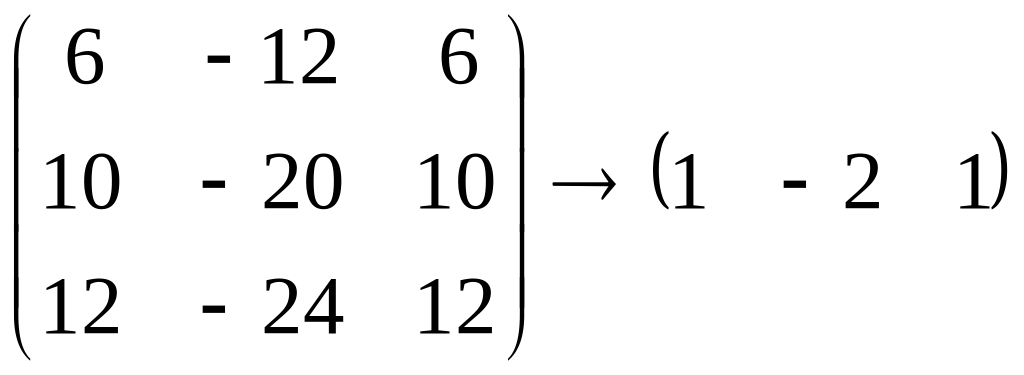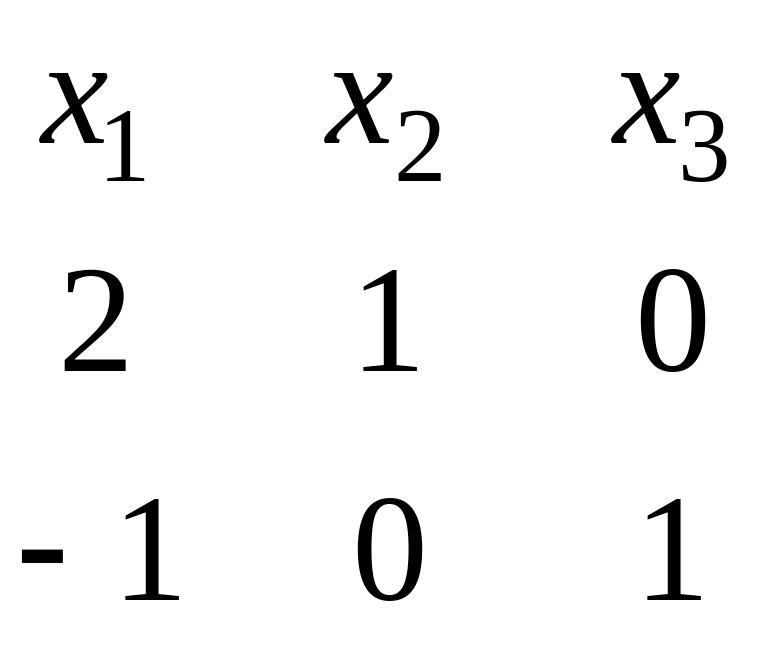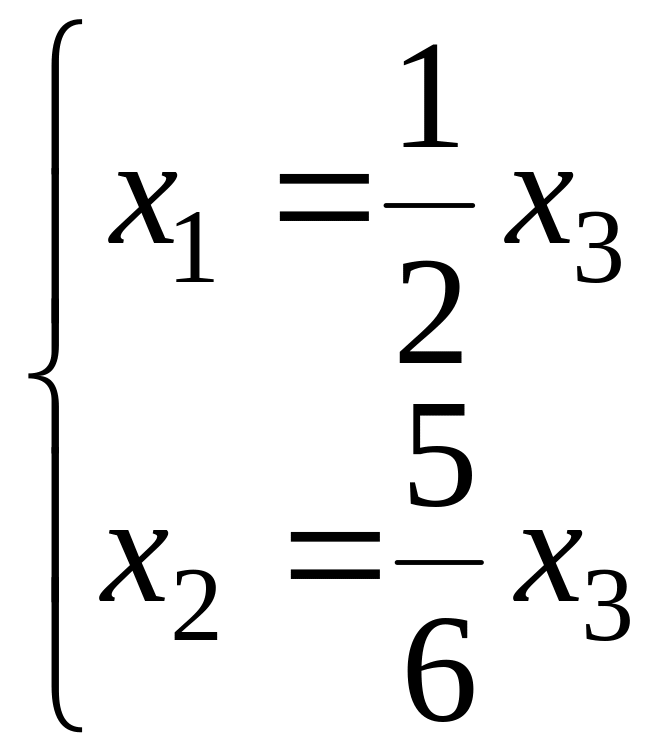Как найти жорданова форма матрицы онлайн - Avtoru.top

Пусть дана матрица
3-го порядка. Надо найти жорданову форму
и жорданов базис.

Пусть
характеристический многочлен матрицы

имеет вид

,
где

Тогда
жорданова форма матрицы имеет вид

.

Пусть
характеристический многочлен матрицы

имеет вид

где

.
Возможны два случая:

а)

,
поэтому

и, следовательно,

,
поэтому жорданова форма содержит две
жордановы клетки с собственным значением

;

б)

,
поэтому

и, следовательно, жорданова форма
содержит одну жорданову клетку с
собственным значением

Пусть
характеристический многочлен матрицы

имеет вид

Возможны два
случая:

а)

,
поэтому

и, следовательно, жорданова форма
содержит две жордановы клетки с
собственным значением

;

б)

,
поэтому

и, следовательно, жорданова форма
содержит одну жорданову клетку с
собственным значением

Задача.
Дана матрица

.
Найти

.

Р е ш е
н и е.

Найдем характеристический многочлен
матрицы:

Жорданова
форма матрицы

имеет вид

.

Найдем

Для
нахождения

воспользуемся формулой

,
где

– матрица перехода от базиса

к базису

.
Очевидно, что

поэтому

Пример
1. Найти жорданову форму и жорданов
базис матрицы оператора

Р е ш е
н и е.

Вычислим

следовательно,
собственное значение

,

Найдем
геометрическую кратность собственного
значения

.
Для этого посчитаем ранг матрицы

Следовательно,

поэтому
жорданова форма имеет вид

или

.

Найдем собственный вектор

,
соответствующий собственному значению

.
Так как он удовлетворяет условию

то
решим систему

Следовательно,
координаты собственного вектора

удовлетворяют уравнению

Заметим, что коэффициент при

равен 0, поэтому

может принимать любые значения.
Отбрасывать

нельзя !!!

Для
нахождения ФСР построим таблицу

Векторы

,

образуют фундаментальную систему
решений в собственном подпространстве

,
поэтому любой собственный вектор,
отвечающий собственному значению

,
линейно через них выражается и,
следовательно, имеет вид

.
Так как

,

,
то должен быть один присоединенный
вектор, который будет являться решением
системы

.
Подберем коэффициенты

таким образом, чтобы система

была совместна. Так как

то для
совместности системы необходимо, чтобы
выполнялось условие

.
Возьмем

,
тогда

,
и координаты присоединенного вектора
являются решением системы

то есть
удовлетворяют уравнению

или

.

Возьмем

Таким образом, у нас есть собственный
вектор

,
присоединенный к нему

и нужен еще один собственный вектор,
отвечающий собственному значению

.
Можно взять или вектор

,
или

,
или любой другой, отличный от

,
отвечающий собственному значению

.
Эти три вектора и будут образовывать
жорданов базис.

Пример 2. Найти жорданову
форму и жорданов базис матрицы оператора

Р е ш е
н и е.

Вычислим

следовательно,
собственное значение

,

Найдем
геометрическую кратность собственного
значения

.
Для этого посчитаем ранг матрицы

Следовательно,

поэтому
жорданова форма имеет вид

или

.

Найдем собственный вектор

,
соответствующий собственному значению

.
Так как он удовлетворяет условию

то
решим систему

Очевидно,
что координаты собственного вектора

удовлетворяют уравнению

или

.

Для
нахождения ФСР построим таблицу

Векторы

,

образуют фундаментальную систему
решений в собственном подпространстве

,
поэтому любой собственный вектор,
отвечающий собственному значению

,
линейно через них выражается
и, следовательно, имеет вид

Так как

,
то должен быть один присоединенный
вектор, который будет являться решением
системы

.
Подберем коэффициенты

таким образом, чтобы система

была совместна. Так как

то для
совместности системы необходимо, чтобы
выполнялось условие

.
Возьмем

,
тогда

и координаты присоединенного вектора
являются решением системы

то есть
удовлетворяют уравнению

или

.

Возьмем

Таким образом, у нас есть собственный
вектор

,
присоединенный к нему

и нужен еще один собственный вектор,
отвечающий собственному значению

.
Можно взять или вектор

,
или

,
или любой другой, отличный от

,
отвечающий собственному значению

.
Эти три вектора и будут образовывать
жорданов базис.

Пример 3. Найти жорданову
форму и жорданов базис матрицы оператора

Р е ш е
н и е.

Вычислим

Таким образом, получили три собственных
значения

,

,

.
Так как алгебраическая кратность каждого
из них равна 1, то жорданова форма имеет
следующий вид

Найдем собственный вектор

,
соответствующий собственному значению

.
Очевидно, что он является решением
уравнения

и, следовательно, его координаты
удовлетворяют системе

то есть

,
поэтому можем взять

.

Вычислим собственный вектор

,
соответствующий собственному значению

.
Очевидно, что он удовлетворяет уравнению

,
а его координаты – системе

откуда
следует, что

,
поэтому можем взять

.

Найдем собственный вектор

,
соответствующий собственному значению

.
Так как он является решением уравнения

,
то его координаты удовлетворяют системе

и,
следовательно,

,
поэтому можем взять

.

Векторы

образуют жорданов базис матрицы.

Пример 4. Найти жорданову
форму и жорданов базис матрицы оператора

Р е ш е
н и е.

Вычислим

Таким образом, получили два собственных
значения

,

.
Так как алгебраическая кратность

равна 2, нужно вычислить геометрическую
кратность

собственного значения

.
Для этого посчитаем ранг матрицы

Очевидно, что

,
поэтому

и, следовательно, жорданова форма имеет
следующий вид

Найдем собственные векторы

,
соответствующие собственному значению

.
Очевидно, что они являются решением
уравнения

,
а их координаты

– решением системы

и,
следовательно, удовлетворяют уравнению

или

.

Для
нахождения ФСР построим таблицу

Векторы

образуют фундаментальную систему
решений в собственном подпространстве

Так
как

,
то нужно выбрать любые два линейно
независимых вектора из этой линейной
комбинации. Возьмем

,

Найдем собственный вектор

,
соответствующий собственному значению

.
Очевидно, что он удовлетворяет уравнению

,
а его координаты

– системе

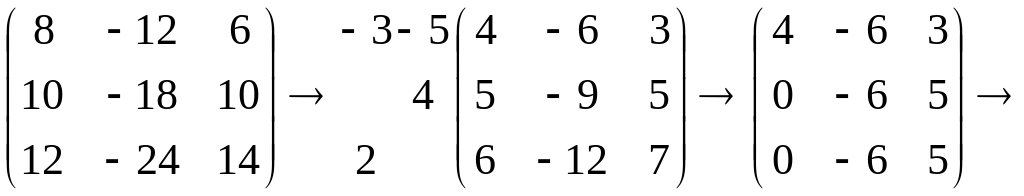
то есть

,
поэтому можем взять

.

Векторы

образуют жорданов базис матрицы.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Жорданова форма матрицы

Рассматривается задача упрощения квадратной матрицы при помощи преобразования подобия. Наиболее простой вид квадратной матрицы — диагональный. Для диагональных матриц легко решаются многие типовые задачи линейной алгебры, например, обращение матриц, решение системы уравнений, нахождение многочлена от матрицы и т.п. Однако, как показано ранее, не всякая квадратная матрица подобна диагональной. Поэтому возникает необходимость приведения матрицы к такому виду, пусть даже не диагональному, чтобы при решении типовых задач линейной алгебры не возникало значительных трудностей.

Элементарные делители матрицы

Пусть — числовая квадратная матрица n-го порядка. Характеристическая матрица (A-lambda E) приводится (элементарными преобразованиями) к нормальному диагональному виду $operatorname{diag} Bigl(e_1(lambda), ldots,e_n(lambda)Bigr)$ , где e_i(lambda) — инвариантные множители матрицы (A-lambda E) . Характеристический многочлен согласно свойству 2 можно представить в виде (7.25):

$Delta_{A}(lambda)=(-1)^ncdot e_1(lambda)cdot e_2(lambda)cdotldotscdot e_n(lambda).$

Разложим каждый из многочленов e_i(lambda) на линейные множители:

$begin{aligned} e_1(lambda)&= (lambda-lambda_1)^{a_1}cdot (lambda-lambda_2)^{a_2}cdotldotscdot (lambda-lambda_k)^{a_k},\[2pt] e_2(lambda)&= (lambda-lambda_1)^{b_1}cdot (lambda-lambda_2)^{b_2}cdotldotscdot (lambda-lambda_k)^{b_k},\ &cdotscdotscdotscdotscdots\ e_{n-1}(lambda)&= (lambda-lambda_1)^{ell_1}cdot (lambda-lambda_2)^{ell_2}cdotldotscdot (lambda-lambda_k)^{ell_k},\[2pt] e_n(lambda)&= (lambda-lambda_1)^{m_1}cdot (lambda-lambda_2)^{m_2}cdotldotscdot (lambda-lambda_k)^{m_k}. end{aligned}$

(7.33)

Здесь lambda_1,lambda_2,ldots,lambda_k — различные собственные значения матрицы ; показатели степеней, удовлетворяют неравенствам 0leqslant a_ileqslant b_ileqslantldots leqslantell_ileqslant m_i (i=1,ldots,k) так как каждый последующий инвариантный множитель делится на предыдущий. Некоторые из множителей (lambda-lambda_i)^j в (7.33) могут иметь нулевую степень, т.е. быть равными единице. Исключение составляют множители $(lambda-lambda_i)^{m_i}$ минимального многочлена (7.29) ( $mu_{A}(lambda)=e_n(lambda)$ по свойству 6) , для которых согласно свойству 4 все показатели степеней больше или равны единицы (m_igeqslant1,~ i=1,ldots,k) .

Учитывая, что характеристический многочлен (7.24) равен произведению инвариантных множителей (с коэффициентом (-1)^n ):

$Delta_{A}(lambda)= (-1)^ncdot (lambda-lambda_1)^{n_1}cdot (lambda-lambda_2)^{n_2}cdotldotscdot (lambda-lambda_k)^{n_k}= (-1)^ncdot e_1(lambda)cdot e_2(lambda)cdot ldotscdot e_n(lambda),$

получаем, что a_i+b_i+ldots+ell_i+m_i=n_i~(i=1,ldots,k) и n_1+n_2+ldots+ n_k=n , т.е. сумма степеней всех инвариантных множителей равна порядку квадратной матрицы .

Каждый отличный от единицы многочлен вида (lambda-lambda)^j , указанный в | разложениях (7.33) инвариантных множителей, называется элементарным делителем характеристической матрицы (A-lambda E) (или просто элементарным делителем матрицы ).

По формулам (7.33) можно составить таблицу элементарных делителей:

$begin{matrix}(lambda-lambda_1)^{m_1},&(lambda-lambda_1)^{ell_1}, &ldots,,&(lambda-lambda_1)^{b_1},&(lambda-lambda_1)^{a_1},\[4pt] (lambda-lambda_2)^{m_2}, &(lambda-lambda_2)^{ell_2},&ldots,,&(lambda-lambda_2)^{b_2},& (lambda-lambda_2)^{a_2}, \ vdots&vdots&cdots&vdots&vdots\[4pt] (lambda-lambda_k)^{m_k}, &(lambda-lambda_k)^{ell_k}, &ldots,,&(lambda-lambda_k)^{b_k},&(lambda-lambda_k)^{a_k}. end{matrix}$

(7.34)

Составление таблицы элементарных делителей по таблице инвариантных множителей

Для составления таблицы (7.34) элементарных делителей по таблице (7.33) инвариантных множителей нужно:

а) в первый столбец таблицы (7.34) записать элементарные делители последнего инвариантного множителя e_n(lambda) из таблицы (7.33);

б) во второй столбец (7.34) записать элементарные делители предпоследнего инвариантного множителя $e_{n-1}(lambda)$ из таблицы (7.33) так, чтобы в i-й строке (7.34) были степени одного и того же двучлена (lambda-lambda_i) , и т.д. 18 последний столбец (7.34) записать элементарные делители первого инвариантного множителя e_1(lambda) из таблицы (7.33) так, чтобы в i-й строке (7.34) были степени одного и того же двучлена (lambda-lambda_i) .

Элементы, тождественно равные единице, не являются элементарными делителями и в таблицу (7.34) не заносятся. Поэтому в каждой строке таблицы может быть разное количество элементарных делителей, точнее, в каждом последующем столбце количество делителей не больше, чем в предыдущем. В каждой строке таблицы (7.34) стоят делители (lambda-lambda_i)^j , относящиеся к одному собственному значению . Поскольку собственные значения lambda_1,ldots,lambda_k могут быть упорядочены по-разному, то и строки таблицы (7.34) можно переставлять. Это не будет в дальнейшем иметь существенного значения.

Составление таблицы инвариантных множителей по таблице элементарных делителей

По таблице (7.34) элементарных делителей можно восстановить таблицу (7.33) инвариантных множителей. Для этого нужно:

а) перемножая элементарные делители первого столбца таблицы (7.34), получить последний инвариантный множитель e_n(lambda) в таблице (7.33);

б) перемножая элементарные делители второго столбца таблицы (7.34), получить предпоследний инвариантный множитель $e_{n-1}(lambda)$ в таблице (7.33) и т.д. Исчерпав столбцы таблицы (7.34), дописываем недостающие инвариантные множители, полагая их равными единице (количество инвариантных множителей равно сумме степеней всех элементарных делителей, т.е. порядку матрицы).

Заметим, что, составляя таблицу (7.33) по таблице (7.34), можно переставлять строки таблицы (7.34), так как это не приведет к изменению таблицы (7.33). Столбцы таблицы (7.34) переставлять нельзя.

Согласно теореме об инвариантных множителях, эквивалентные характеристические матрицы (A-lambda E) и (B-lambda E) имеют одинаковые инвариантные множители (7.33). Тогда они имеют и одинаковые элементарные делители (7.34). Следовательно, критерий подобия числовых матриц можно сформулировать следующим образом.

Теорема 7.8 (критерий подобия матриц). Числовые матрицы подобны тогда и только тогда, когда они имеют одинаковые элементарные делители.

Таким образом, нахождение подобных матриц связано с умением составлять матрицы, элементарные делители которых совпадают с заданной таблицей (7.34).

Жордановы клетки и матрицы

Квадратную матрицу (r-го порядка) вида

$J_{r}(lambda_0)= begin{pmatrix}lambda_0&1&0&cdots&0\ 0&lambda_0&1&cdots&0\ vdots&vdots&vdots&ddots&vdots\ 0&0&0&cdots&1\ 0&0&0&cdots&lambda_0 end{pmatrix}$

(7.35)

называют жордановой клеткой r-го порядка, соответствующей собственному значению lambda_0 . Все элементы на главной диагонали этой верхней треугольной матрицы равны , элементы над главной диагональю равны единице, а остальные элементы равны нулю.

Найдем элементарные делители жордановой клетки. Для этого составим характеристическую матрицу

$J_{r}(lambda_0)-lambda E= begin{pmatrix}lambda_0-lambda&1&0&cdots&0\ 0&lambda_0-lambda&1&cdots&0\ vdots&vdots&vdots&ddots&vdots\ 0&0&0&cdots&1\ 0&0&0&cdots&lambda_0-lambda end{pmatrix}$

и найдем наибольшие общие делители d_i(lambda) миноров i-го порядка. Среди ненулевых миноров первого порядка есть минор, равный единице $(M_{{}_2}^{{}^1}=1)$ . Рассматривая его как многочлен нулевой степени, заключаем, что наибольший общий делитель миноров первого порядка должен быть также многочленом нулевой степени, т.е. d_1(lambda)=1 . Среди миноров второго порядка также имеется минор, равный единице: $M_{{}_{2,3}}^{{}^{1,2}}=begin{vmatrix}1&0\ lambda_0-lambda&1 end{vmatrix}$ , следовательно, d_2(lambda)=1 и т.д. Минор (r-l)-гo порядка $M_{{}_{2,3,ldots,r}}^{{}^{1,2,ldots,r-1}}$ имеет нижний треугольный вид с единичными элементами на главной диагонали, т.е. $M_{{}_{2,3,ldots,r}}^{{}^{1,2,ldots,r-1}}=1$ . Поэтому $d_{r-1}(lambda)=1$ . Минор r-го порядка, т.е. определитель характеристической матрицы, равен (lambda_0-lambda)^r , поэтому d_r(lambda)=(lambda-lambda_0)^r . По формулам (7.11) находим инвариантные множители:

$e_1(lambda)=e_2(lambda)=ldots=e_{r-1}(lambda)=1,quad e_r(lambda)=(lambda-lambda_0)^r.$

Следовательно, жорданова клетка (7.35) имеет всего один элементарный делитель (lambda-lambda_0)^r . Поэтому характеристическая матрица приводится к нормальному диагональному виду (7.9):

$Bigl(J_A(lambda_0)-lambda EBigr)sim operatorname{diag} underbrace{Bigl(1,ldots,1, (lambda-lambda_0)^rBigr)}_{r}.$

(7.36)

Заметим, что характеристический многочлен $Delta_{J_A(lambda_0)}= (lambda-lambda_0)^r$ имеет единственный корень кратности , т.е. — собственное значение матрицы (7.35).

Рассмотрим теперь блочно-диагональную матрицу

$J=operatorname{diag}Bigl(J_{r_1}(lambda_1),J_{r_2}(lambda_2)Bigr)= begin{pmatrix}J_{r_1}(lambda_1)!!&vline!!&O\hline O!!&vline!!& J_{r_2}(lambda_2) end{pmatrix}!,$

(7.37)

где $J_{r_1}(lambda_1)$ и $J_{r_2}(lambda_2)$ — жордановы клетки, а — нулевые матрицы соответствующих размеров. Для определенности считаем, что r_1geqslant r_2 . Характеристическая матрица (J-lambda E) также имеет блочно-диагональный вид. С помощью элементарных преобразований каждого блока матрица , учитывая (7.36), приводится к диагональному виду

$(J-lambda E)sim operatorname{diag} underbrace{left(1,ldots,1,(lambda-lambda_1)^{r_1}right.}_{r_1}, underbrace{left.{1,ldots,1,(lambda-lambda_2)^{r_2}}right)}_{r_2}$

Если lambda_1ne lambda_2 , то $d_1(lambda)=ldots=d_{r_1+r_2-1}(lambda)=1,~ d_{r_1+r_2}(lambda)=(lambda-lambda_1)^{r_1}cdot (lambda-lambda_2)^{r_2}$ .

Тогда $e_1(lambda)=ldots=e_{r_1+r_2-1}(lambda)=1,~ e_{r_1+r_2}(lambda)=(lambda-lambda_1)^{r_1}cdot (lambda-lambda_2)^{r_2}$ .

Следовательно, матрица (7.37) имеет два элементарных делителя $(lambda-lambda_1)^{r_1}$ и $(lambda-lambda_2)^{r_2}$ .

Если lambda_1=lambda_2 , то $d_1(lambda)=ldots=d_{r_1+r_2-2}(lambda)=1,~ d_{r_1+r_2-1}(lambda)=(lambda-lambda_1)^{r_2},~ d_{r_1+r_2}(lambda)= (lambda-lambda_2)^{r_1+r_2}$ .

Тогда $e_1(lambda)=ldots=e_{r_1+r_2-2}(lambda)=1,~ e_{r_1+r_2-1}(lambda)=(lambda-lambda_1)^{r_2},~ e_{r_1+r_2}(lambda)=(lambda-lambda_2)^{r_1}$ .

Следовательно, матрица (7.37) имеет два элементарных делителя $(lambda-lambda_1)^{r_1}$ и $(lambda-lambda_2)^{r_2}$ .

Таким образом, элементарные делители блочно-диагональной матрицы (7.37) получаются объединением элементарных делителей каждого блока.

Определение жордановой матрицы

Жордановой матрицей называют блочно-диагональную матрицу, на диагонали которой стоят жордановы клетки:

$J=operatorname{diag}Bigl(J_{r_1}(lambda_1),, J_{r_2}(lambda_2),,ldots,, J_{r_k}(lambda_k)Bigr)= begin{pmatrix} J_{r_1}(lambda_1)!!&vline!!&O!!& vline!!&cdots!!&vline!!&O\[4pt]hline O!!&vline!!& J_{r_2}(lambda_2)!!&vline!!& cdots!!&vline!!&O\[4pt]hline vdots!!&vline!!& vdots!!& vline!!&ddots!!&vline!!& vdots\[4pt]hline O!!&vline!!& O!!&vline!!& cdots!!&vline!!& J_{r_k}(lambda_k) end{pmatrix}!.$

(7.38)

Здесь — нулевые матрицы соответствующих размеров. Среди собственных значений lambda_1,lambda_2, ldots,lambda_k могут быть равные, размеры r_1,r_2,ldots, r_k жордановых клеток (всех или некоторых) тоже могут совпадать. Жорданова матрица — почти диагональная. На ее главной диагонали стоят собственные значения, некоторые элементы над главной диагональю равны единице, остальные элементы нулевые. Про матрицу (7.38) говорят, что она имеет нормальную жорданову форму (или просто жорданову форму).

Элементарные делители жордановой матрицы (7.38) $(lambda- lambda_1)^{r_1},,(lambda-lambda_2)^{r_2},,ldots,, (lambda-lambda_k)^{r_k}$ получаются в результате объединения элементарных делителей жордановых клеток.

Составление жордановой матрицы по таблице элементарных делителей

Чтобы составить по таблице (7.34) элементарных делителей соответствующую жорданову матрицу, нужно:

а) для первой строки $(lambda-lambda_1)^{m_1},, (lambda-lambda_1)^{ell_1},,ldots,, (lambda-lambda_1)^{b_1},,(lambda-lambda_1)^{a_1}$ элементарных делителей в (7.34) записать жордановы клетки

$J_{m_1}(lambda_1),quad J_{ell_1}(lambda_1),quad ldots,quad J_{b_1}(lambda_1),quad J_{a_1}(lambda_1);$

б) для второй строки $(lambda-lambda_2)^{m_2},, (lambda-lambda_2)^{ell_2},,ldots,, (lambda-lambda_2)^{b_2},,(lambda-lambda_1)^{a_2}$ элементарных делителей в (7.34) записать жордановы клетки

$J_{m_2}(lambda_2),quad J_{ell_2}(lambda_2),quad ldots,quad J_{b_2}(lambda_2),quad J_{a_2}(lambda_2)$

и т.д. Получив полный набор жордановых клеток (количество которых совпадает с количеством элементарных делителей в таблице (7.34)), составить из них блочно-диагональную матрицу вида (7.38). Порядок, в котором нужно располагать жордановы клетки на диагонали, строго не регламентирован. Поэтому для одной и той же таблицы (7.34) можно получить разные жордановы матрицы, отличающиеся только перестановкой жордановых клеток.

Составление таблицы элементарных делителей по жордановой матрице

Чтобы по жордановой матрице (7.38) составить таблицу (7.34) ее элементарных делителей, нужно:

а) выбрать в жордановой матрице все жордановы клетки, соответствующие собственному значению lambda_1 ; составить для каждой клетки элементарный делитель, а затем записать эти элементарные делители в порядке убывания степеней в первую строку таблицы (7.34), например, для жордановых клеток

$J_{m_1}(lambda_1),quad J_{ell_1}(lambda_1),quad ldots,quad J_{b_1}(lambda_1),quad J_{a_1}(lambda_1)$ , где m_1geqslantell_1geqslantldots geqslant b_1geqslant a_1geqslant1 ,

записать строку $(lambda-lambda_1)^{m_1},, (lambda-lambda_1)^{ell_1},,ldots,, (lambda-lambda_1)^{b_1},,(lambda-lambda_1)^{a_1}$ элементарных делителей;

б) выбрать в жордановой матрице все жордановы клетки, соответствующие собственному значению lambda_2 , составить для каждой клетки элементарный делитель, а затем записать эти элементарные делители в порядке убывания степеней во вторую строку таблицы (7.34) и т.д., пока не исчерпаются все собственные значения данной жордановой матрицы. Порядок, в котором выбираются собственные значения жордановой матрицы, точно не устанавливается. Поэтому для одной жордановой матрицы можно получить разные таблицы элементарных делителей, которые будут отличаться только перестановкой строк. Ранее отмечалось, что перестановка строк таблицы (7.34) не влияет на составление таблицы (7.33) инвариантных множителей.

Замечания 7.6

1. Диагональная матрица имеет жорданову форму, в которой все жордановы клетки первого порядка:

$operatorname{diag}(lambda_1,, lambda_2,,ldots,, lambda_n)= operatorname{diag} Bigl(J_1(lambda_1),,J_1(lambda_2),,ldots,,J_{1}(lambda_1)Bigr).$

2. Хотя жорданова матрица в общем случае не диагональная, для нее достаточно просто решаются типовые задачи линейной алгебры. Например, для неоднородной системы уравнений Jx=b с невырожденной матрицей J=J_n(lambda_0) можно сразу записать решение:

$x_n=frac{b_n}{lambda_0},,quad x_{n-1}=frac{b_{n-1}-x_n}{lambda_0},,quadldots,,quad x_1=frac{b_1-x_2}{lambda_0},.$

3. Для решения тех или иных задач линейной алгебры используются различные простые виды квадратных матриц, которые обычно называют нормальными, или каноническими формами, например, первая и вторая естественные формы матрицы, вещественная жорданова форма. Матрицу (7.38) называют также канонической формой.

Пример 7.13. Найти элементарные делители и инвариантные множители жордановых матриц

$A=begin{pmatrix}1!!&vline!!&0!!&vline!!&0&0\hline 0!!&vline!!&2!!&vline!!&0&0\hline 0!!&vline!!&0!!&vline!!&3&1\ 0!!&vline!!&0!!&vline!!&0&3 end{pmatrix}!,quad B=begin{pmatrix} 1&1!!&vline!!&0!!&vline!!&0\ 0&1!!&vline!!&0!!&vline!!&0\hline 0&0!!&vline!!&1!!&vline!!&0\hline 0&0!!&vline!!&0!!&vline!!&2 end{pmatrix}!,quad C= begin{pmatrix}1&1!!&vline!!&0&0\ 0&1!!&vline!!&0&0\hline 0&0!!&vline!!&1&1\ 0&0!!&vline!!&0&1 end{pmatrix}!.$

Решение. Матрица $A=operatorname{diag} Bigl(J_1(1),,J_1(2),, J_2(3)Bigr)$ состоит из трех жордановых клеток с разными собственными значениями lambda_1=1, lambda_2=2, lambda_3=3 . Для каждого собственного значения запишем жорданову клетку и соответствующий элементарный делитель:

$begin{array}{lllll}lambda_1=1&quad Rightarrow&quad J_1(1)&quad Rightarrow& quad (lambda-1);\[2pt] lambda_2=2&quad Rightarrow&quad J_1(2)&quad Rightarrow& quad (lambda-2);\[2pt] lambda_3=3&quad Rightarrow&quad J_2(3)&quad Rightarrow& quad (lambda-3)^2. end{array}$

Получили таблицу элементарных делителей, которая состоит из одного столбца. По этой таблице составляем инвариантные множители (количество которых равно порядку матрицы ). Записываем последний инвариантный множитель e_4(lambda)=(lambda-3)^2(lambda-1)(lambda-2) , перемножая элементарные делители первого столбца. Поскольку исчерпаны все элементарные делители (второго столбца в таблице нет), то остальные инвариантные множители полагаем равными единице: e_3(lambda)= e_2(lambda)= e_1(lambda)=1 .

Матрица $B=operatorname{diag} Bigl(J_2(1),, J_1(1),,J_1(2)Bigr)$ состоит из трех жордановых клеток, соответствующих двум разным собственным значениям lambda_1=1, lambda_2=2 .

Для каждого собственного значения записываем соответствующие жордановы клетки и элементарные делители:

$begin{array}{lllll}lambda_1=1&quad Rightarrow& quad J_2(1),,J_1(1)&quad Rightarrow&quad (lambda-1)^2,,(lambda-1);\[2pt] lambda_2=2&quad Rightarrow& quad J_1(2)&quad Rightarrow&quad (lambda-2). end{array}$

Получили таблицу элементарных делителей, которая состоит из двух столбцов. По этой таблице составляем инвариантные множители (количество которых равно порядку матрицы ). Записываем последний инвариантный множитель e_4(lambda)=(lambda-1)^2(lambda-2) , перемножая элементарные делители первого столбца. Записываем предпоследний инвариантный множитель e_3(lambda)=lambda-1 по второму столбцу таблицы. Поскольку исчерпаны все элементарные делители (третьего столбца в таблице нет), то остальные инвариантные множители полагаем равными единице: e_2(lambda)=e_1(lambda)=1 .

Матрица $C=operatorname{diag}Bigl(J_2(1),,J_2(1)Bigr)$ состоит из двух одинаковых жордановых клеток, соответствующих одному собственному значению lambda_1=1 . Для этого собственного значения записываем жордановы клетки и соответствующие элементарные делители:

lambda_1=1qquad Rightarrowqquad J_2(1),,J_2(1)qquad Rightarrowqquad (lambda-1)^2,,(lambda-1)^2.

Получили таблицу элементарных делителей, которая состоит из двух столбцов. По этой таблице составляем инвариантные множители (количество которых равно порядку матрицы ). Записываем последний инвариантный множитель e_4(lambda)=(lambda-1)^2 по первому столбцу таблицы. Записываем предпоследний инвариантный множитель e_3(lambda)=(lambda-1)^2 по второму столбцу таблицы. Поскольку исчерпаны все элементарные делители (третьего столбца в таблице нет), то остальные инвариантные множители полагаем равными единице: e_2(lambda)=e_1(lambda)=1 .

Пример 7.14. По инвариантным множителям найти жорданову матрицу:

а) матрица Acolon~ e_1(lambda)= e_2(lambda)=e_3(lambda)=1,~ e_4(lambda)=(lambda-1)(lambda-2)(lambda-3)(lambda-4) ;

б) матрица Bcolon~ e_1(lambda)=e_2(lambda)=1,~ e_3(lambda)=(lambda-1),~ e_4(lambda)=(lambda-1)^3 ;

в) матрица Ccolon~ e_1(lambda)=1,~ e_2(lambda)=(lambda-1),~ e_3(lambda)=(lambda-1),~ e_4(lambda)=(lambda-1)^2 .

Решение. Для матрицы составляем таблицу (7.34) элементарных делителей. В первый столбец таблицы записываем элементарные делители последнего инвариантного множителя:

(lambda-1),quad (lambda-2),quad (lambda-3),quad (lambda-4).

Остальные элементарные делители равны единице и в таблицу не заносятся. Составляем по таблице элементарных делителей жорданову матрицу. Для каждого элементарного делителя записываем соответствующую жорданову клетку: J_1(1), J_1(2), J_1(3), $J_1(4)phantom{,}$ . Располагая эти клетки на главной диагонали блочной матрицы, получаем искомую жорданову матрицу:

$A=begin{pmatrix} 1!!&vline!!& 0!!&vline!!&0!!&vline!!&0\hline 0!!&vline!!& 2!!&vline!!&0!!&vline!!&0\hline 0!!&vline!!& 0!!&vline!!&3!!&vline!!&0\hline 0!!&vline!!& 0!!&vline!!&0!!&vline!!&4 end{pmatrix}!.$

Для матрицы составляем таблицу (7.34) элементарных делителей. В первый столбец таблицы записываем единственный элементарный делитель последнего инвариантного множителя e_4(lambda) , во второй столбец — предпоследнего инвариантного множителя e_3(lambda):

(lambda-1)^3,qquad (lambda-1).

Инвариантные множители e_1(lambda)=e_2(lambda)=1 не содержат элементарных делителей, отличных от единицы, и поэтому в таблицу не записываются. Составляем по таблице элементарных делителей жорданову матрицу. Для каждого элементарного делителя записываем соответствующую жорданову клетку: J_3(1),~J_1(1) . Располагая эти клетки на главной диагонали блочной матрицы, получаем искомую жорданову матрицу:

$B=begin{pmatrix}1&1&0!!&vline!!&0\ 0&1&1!!&vline!!&0\ 0&0&1!!&vline!!&0\hline 0&0&1!!&vline!!&0 end{pmatrix}!.$

Для матрицы составляем таблицу (7.34) элементарных делителей. В первый столбец таблицы записываем единственный элементарный делитель последнего инвариантного множителя e_3(lambda) , второй столбец — предпоследнего инвариантного множителя , в третий столбец — e_2(lambda):

(lambda-1)^2,qquad (lambda-1),qquad (lambda-1).

Инвариантный множитель e_1(lambda)=1 не содержит элементарных делителей, отличных от единицы, и поэтому в таблицу не записывается. Составляем по таблице элементарных делителей жорданову матрицу. Для каждого элементарного делителя записываем соответствующую жорданову клетку: J_2(1),J_1(1),J_1(1) . Располагая эти клетки на главной диагонали блочной матрицы, получаем искомую жорданову матрицу:

$C=begin{pmatrix} 1&1!!&vline!!&0!!&vline!!&0\ 0&1!!&vline!!&0!!&vline!!&0\hline 0&0!!&vline!!&1!!&vline!!&0\hline 0&0!!&vline!!&0!!&vline!!&1 end{pmatrix}!.$

Теорема 7.9 о приведении матрицы к нормальной жордановой форме. Любая квадратная матрица подобна жордановой матрице. Две жордановы матрицы подобны тогда и только тогда, когда они составлены из одинаковых жордановых клеток и отличаются друг от друга лишь расположением клеток на главной диагонали, другими словами, любую квадратную матрицу при помощи преобразования подобия можно привести к нормальной жордановой форме и притом единственной (с точностью до перестановок жордановых клеток).

В самом деле, для любой квадратной матрицы можно найти элементарные делители, т.е. составить таблицу (7.34). По элементарным делителям можно составить соответствующую жорданову матрицу J_A . При этом матрицы и J_A будут иметь одинаковые элементарные делители, что является критерием их подобия. Значит, найдется невырожденная преобразующая матрица такая, что $J_A=S^{-1}Lambda S$ . Заметим, что жорданова форма J_A матрицы определяется по ее элементарным делителям единственным образом с точностью до перестановок жордановых клеток.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	— twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{»}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Radians}	mathrm{Degrees}	square!	(	)	%	mathrm{clear}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	—
pi	e	x^{square}	0	.	bold{=}	+

Subscribe to verify your answer

Number Line

Examples

gauss:jordan:begin{pmatrix}1 & 2 \3 & 4end{pmatrix}
gauss:jordan:begin{pmatrix}1 & 2 & 3 \4 & 5 & 6 \7 & 8 & 9end{pmatrix}
gauss:jordan:begin{pmatrix}1 & 3 & 5 & 9 \1 & 3 & 1 & 7 \4 & 3 & 9 & 7 \5 & 2 & 0 & 9end{pmatrix}

Description

Reduce matrix to Gauss Jordan (RREF) form step-by-step

matrix-gauss-jordan-calculator

Нахождение собственных чисел и собственных векторов

Данный калькулятор поможет найти собственные числа и векторы, используя характеристическое уравнение.

Больше:

Выводить десятичную дробь

Оставляйте лишние ячейки пустыми для ввода неквадратных матриц.
Элементы матриц — десятичные (конечные и периодические) дроби: 1/3, 3,14, -1,3(56) или 1,2e-4; либо арифметические выражения: 2/3+3*(10-4), (1+x)/y^2, 2^0,5 (=2), 2^(1/3), 2^n, sin(phi), cos(3,142rad), a_1 или (root of x^5-x-1 near 1,2).
- decimal (finite and periodic) fractions:
  
  1/3, 3,14, -1,3(56) или 1,2e-4
- 2/3+3*(10-4), (1+x)/y^2, 2^0,5 (=2), 2^(1/3), 2^n, sin(phi), cos(3,142rad), a_1 или (root of x^5-x-1 near 1,2)
- matrix literals:
  
  {{1,3},{4,5}}
- operators:
  
  +, -, *, /, , !, ^, ^{*}, ,, ;, ≠, =, ⩾, ⩽, > и <
- functions:
  
  sqrt, cbrt, exp, log, abs, conjugate, min, max, gcd, rank, adjugate, inverse, determinant, transpose, pseudoinverse, cos, sin, tan, cot, cosh, sinh, tanh, coth, arccos, arcsin, arctan, arccot, arcosh, arsinh, artanh и arcoth
- units:
  
  rad, deg
- special symbols:
  - pi, e, i — mathematical constants
  - k, n — integers
  - I or E — identity matrix
  - X, Y — matrix symbols
Используйте ↵ Ввод, Пробел, ←↑↓→, Backspace и Delete для перемещения по ячейкам, Ctrl⌘ Cmd+C/Ctrl⌘ Cmd+V — для копирования матриц.
Перетаскивайте матрицы из результата (drag-and-drop), или даже из текстового редактора.
За теорией о матрицах и операциях над ними обращайтесь к страничке на Википедии.

Примеры

Найти собственные векторы ({{-26,-33,-25},{31,42,23},{-11,-15,-4}})

Источник

Для любой невырожденной квадратной матрицы (т.е. такой определитель которой отличен от нуля), существует
обратная матрица,
такая, что её произведение на исходную матрицу равно единичной:

A∙A⁻¹
= A⁻¹∙A
= E

Наш калькулятор поддерживает два различных способа вычисления обратной матрицы: по методу Гаусса-Жордана и при помощи построения алгебраических дополнений к исходной матрице.

Для нахождения обратной матрицы по методу Гаусса-Жордана, к исходной матрице справа дописывают единичную матрицу:

( A | E )

Затем, с помощью элементарных преобразований приводят исходную матрицу к единичной, выполняя теже самые операции и над единичной матрицей, записанной справа. В результате таких действий исходная матрица приводится к единичной, а единичная к обратной:

( A | E) → ( E | A⁻¹ )

Метод довольно простой, удобный и не очень трудоемкий.

Для нахождения обратной матрицы при помощи метода алгебраических дополнений используют следующую формулу:

где
| A |
— определитель матрицы
A,
A_{i j}
— алгебраическое дополнение элемента
a_{i j}
матрицы
A.

По определению:

A_{i j} = (-1) ^i+j M_{i j}

где
M_{i j}
— минор элемента
a_{i j}
матрицы
A.

По определению — минор элемента
a_{i j}
матрицы
A
— это определитель, полученный путем вычеркивания
i
строки,
j
столбца матрицы
A.

Таким образом, метод алгебраических дополнений для вычисления обратной матрицы порядка
n
является достаточно трудоемким, поскольку помимо определителя исходной матрицы, нужно вычислить
n²
определителей
n—1
порядка.

Источник

Жорданова форма матрицы

Элементарные делители матрицы

Составление таблицы элементарных делителей по таблице инвариантных множителей

Составление таблицы инвариантных множителей по таблице элементарных делителей

Жордановы клетки и матрицы

Определение жордановой матрицы

Составление жордановой матрицы по таблице элементарных делителей

Составление таблицы элементарных делителей по жордановой матрице

Number Line

Нахождение собственных чисел и собственных векторов

Не пропустите также: