1. По результатам проведенных измерений
построить проходящий через начало
координат график зависимости квадрата
периода колебаний
от массыm,предварительно рассчитав
,
для каждого значения m.Выбрав одну из полученных в эксперименте
точек, лежащую на усредненной прямой,
рассчитать коэффициент жесткости
пружины по формуле
.
2. Оценить погрешность полученного
результата. В предположении, что ошибка
в определении числа колебаний
отсутствовала, эту погрешность можно
рассчитать по формуле
Ошибка определения времени 10 колебаний
определяется как
.
Систематическую погрешность определения
времени
,
связанную с конечной скоростью реакции
человека, можно принять равной
0,1 с(приборной
ошибкой в нашем случае можно пренебречь
по сравнению с этой величиной).
Случайную ошибку
следует рассчитать по методу Стьюдента:
Для числа колебаний n=4и доверительной вероятностиP=0,95=3,2Окончательный
результат записать в таблицу 2. Сравнить
полученное значение коэффициента
жесткости пружины с результатом,
полученным ранее.
Контрольные вопросы
1. Какие деформации называются упругими?
Сформулируйте закон Гука.
2. Какие колебания называются свободными?
3. Какой функцией описываются гармонические
колебания?
4. Составьте дифференциальное уравнение
колебаний груза на пружине. Какой вид
имеет решение этого уравнения?
5. Получите формулу для периода колебаний
пружинного маятника.
6. Чем можно объяснить различие
в значениях
коэффициента жесткости, полученных
разными методами?
СПИСОК ЛИТЕРАТУРЫ
1. Детлаф А.А., Яворский Б.М. Курс физики.—М.:
Высш. шк., 1989.
2. Савельев И.В. Курс физики.—М.:
Наука, 1989—Т. 2.
3. Большова К.М., Пустовалов Г.Е. Краткий
курс общей физики.-М: Изд.МГУ, 1982.
Работа 5
ИЗУЧЕНИЕ СВОБОДНЫХ
КОЛЕБАНИЙ
ФИЗИЧЕСКОГО
МАЯТНИКА
Цель работы. Определение момента
инерции физического маятника по периоду
его малых колебаний и приведенной длине.
Введение
Математическим маятником называется
идеализированная система, состоящая
из невесомой нерастяжимой нити, на
которой подвешена масса, сосредоточенная
в одной точке. Достаточно хорошим
приближением к математическому маятнику
служит небольшой тяжелый шарик,
подвешенный на длинной тонкой нити.
Если колеблющееся тело нельзя представить
как материальную точку, маятник называется
физическим. Всегда можно подобрать
математический маятник, синхронный
данному физическому, т. е. такой
математический маятник, период колебаний
которого равен периоду колебаний
физического маятника. Длина такого
математического маятника называется
приведенной длиной физического маятника.
Выведем формулу периода колебаний
физического маятника. На рис. 3 точка О—
след горизонтальной оси вращения, точка
В — центр масс физического маятника.
Следует отметить, что в однородном поле
сил тяжести центр инерции тела и его
центр масс совпадают.
При отклонении маятника от положения
равновесия на угол возникает вращательный момент, стремящийся
вернуть маятник в положение равновесия.
Этот момент равен
(1)
где m—масса
физического маятника,
d—расстояние
от оси вращения до центра масс маятника,—угловое
отклонение тела, отсчитываемое от
положения равновесия. Ограничимся
рассмотрением малых колебаний. При
малыхугловое перемещение можно рассматривать
как вектор, лежащий на оси вращения,
направление которого связано с
направлением поворота тела из положения
равновесия в заданное правилом правого
винта.
При малых углах можно принятьесли
выражено в радианах, и записать формулу
(1) следующим образом
(1à)
Учитывая, что векторы
и
антипараллельны, следует величинам
проекций вращающего момента и углового
перемещения на ось вращения приписать
противоположные знаки. Тогда формула
(1а) примет вид
(2)
Используем основной закон динамики
вращательного движения тела относительно
неподвижной оси, записав его в проекциях
на ось вращения:
(3)
где J — момент
инерции тела относительно оси вращения,
а—угловое
ускорение, причем
Подставляя
в формулу (3) момент силы из формулы (2),
получим уравнение движения маятника
(4)
Решение полученного дифференциального
уравнения второго порядка с постоянными
коэффициентами можно записать в виде
(5)
ãäå
à
è
постоянные,
определяемые начальными условиями.
Величины
и
называют соответственно амплитудой и
фазой колебания, а0
начальной фазой.
Уравнение (5) является уравнением
гармонического колебательного движения,
а величина0циклической собственной частотой
колебания. По истечении времени
фаза получает приращение,
а тело возвращается в исходное положение
с сохранением направления движения.
ВеличинаTназывается
периодом колебания. Таким образом,
период колебания физического маятника
определяется формулой
(6)
Известно, что период колебаний
математического маятника записывается
в виде
Сравнивая эту формулу с формулой (6),
делаем вывод, что математический маятник
будет иметь тот же период колебаний,
что и данный физический, если длина
математического маятника
(7)
Это и есть формула приведенной длины
физического маятника.
Дано:
m=400 г=0.4 кг.m=400,г = 0.4,кг.
Найти:
k−?k-?
Решение:
По графику зависимости смещения от времени на рис. 18 найдём период колебаний заданного пружинного маятника:
T=1 с.T=1,с.
Период колебаний пружинного маятника вычислим по формуле:
T=2πmk,T=2pisqrt{dfrac{m}{k}},
где mm — масса груза маятника, kk — коэффициент упругости пружины.
Возведём в квадрат обе части последнего уравнения и найдём жёсткость пружины маятника k:k:
T2=4π2mk;T^2=4pi^2dfrac{m}{k};
k=4π2mT2.k=dfrac{4pi^2m}{T^2}.
Подставим численные значения физических величин и вычислим жёсткость пружины маятника k:k:
k=4⋅3.142⋅0.412=15.8Нм≈16Нм.k=dfrac{4cdot 3.14^2cdot 0.4}{1^2}=15.8dfrac{Н}{м}approx 16dfrac{Н}{м}.
Ответ: k=16Нм.k= 16dfrac{Н}{м}.
Внимание! Администрация сайта rosuchebnik.ru не несет ответственности за содержание методических разработок, а также за соответствие разработки ФГОС.
Цель урока: проверить справедливость закона Гука для пружины динамометра и измерить коэффициент жесткости этой пружины, рассчитать погрешность измерения величины.
Задачи урока:
- образовательные: умение обрабатывать и объяснять результаты измерений и делать выводы Закрепление экспериментальных умений и навыков
- воспитательные: вовлечение учащихся в активную практическую деятельность, совершенствование навыки общения.
- развивающие: владение основными приемами, используемыми в физике – измерение, эксперимент
Тип урока: урок обучения умениям и навыкам
Оборудование: штатив с муфтой и зажимом, винтовая пружина, набор грузиков известной массы (по 100 г, погрешность Δm = 0,002 кг), линейка с миллиметровыми делениями.
Ход работы
I. Организационный момент.
II. Актуализация знаний.
- Что такое деформация?
- Сформулировать закон Гука
- Что такое жесткость и в каких единицах она измеряется.
- Дайте понятие об абсолютной и относительной погрешности.
- Причины, приводящие к появлению погрешностей.
- Погрешности, возникающие при измерениях.
- Как чертят графики результатов эксперимента.
Возможные ответы учащихся:
- Деформация – изменение взаимного положения частиц тела, связанное с их перемещением относительно друг друга. Деформация представляет собой результат изменения межатомных расстояний и перегруппировки блоков атомов. Деформации разделяют на обратимые (упругие) и необратимые (пластические, ползучести). Упругие деформации исчезают после окончания действия приложенных сил, а необратимые — остаются. В основе упругих деформаций лежат обратимые смещения атомов металлов от положения равновесия; в основе пластических — необратимые перемещения атомов на значительные расстояния от исходных положений равновесия.
- Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации».
Fупр = –kx
- Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Обозначают k. Единица измерения Н/м. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как:
k = Fупр/x
- Абсолютной погрешностью приближенного значения называется модуль разности точного и приближенного значений.
∆х = |х – хср|
- Относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения.
ε = ∆х/х
- Измерения никогда не могут быть выполнены абсолютно точно. Результат любого измерения приближенный и характеризуется погрешностью – отклонением измеренного значения физической величины от ее истинного значения. К причинам, приводящим к появлению погрешностей, относятся:
– ограниченная точность изготовления средств измерения.
– изменение внешних условий (изменение температуры, колебание напряжения)
– действия экспериментатора (запаздывание с включением секундомера, различное положение глаза…).
– приближенный характер законов, используемых для нахождения измеряемых Величин
- Погрешности, возникающие при измерениях, делятся на систематические и случайные. Систематические погрешности – это погрешности, соответствующие отклонению измеренного значения от истинного значения физической величины всегда в одну сторону (повышения или занижения). При повторных измерениях погрешность остается прежней. Причины возникновения систематических погрешностей:
– несоответствие средств измерения эталону;
– неправильная установка измерительных приборов (наклон, неуравновешенность);
– несовпадение начальных показателей приборов с нулем и игнорирование поправок, которые в связи с этим возникают;
– несоответствие измеряемого объекта с предположением о его свойствах.
Случайные погрешности – это погрешности, которые непредсказуемым образом меняют свое численное значение. Такие погрешности вызываются большим числом неконтролируемых причин, влияющих на процесс измерения (неровности на поверхности объекта, дуновение ветра, скачки напряжения и т.д.). Влияние случайных погрешностей может быть уменьшено при многократном повторении опыта.
Погрешности средств измерений. Эти погрешности называют еще инструментальными или приборными. Они обусловлены конструкцией измерительного прибора, точностью его изготовления и градуировки.
При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле Fупр = kx
Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины kср.
III. Порядок выполнения работы
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указателем и крючком см. рис.).
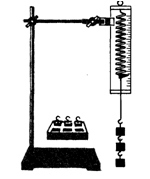
2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.
3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.
4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.
5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины.
По результатам измерений заполните таблицу:
|
№ опыта |
m, кг |
Fупр = mg, Н |
׀х׀, · 10–3 м |
kср, Н/м |
|
1 |
0,1 |
1 |
||
|
2 |
0,2 |
2 |
||
|
3 |
0,3 |
3 |
||
|
4 |
0,4 |
4 |
6. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины kcp.
Вычисление погрешностей прямых измерений.
Вариант 1. Расчет случайной погрешности.
1. Вычислите жесткость пружины в каждом из опытов:
2. kср = (k1 + k2 + k3 + k4)/4 ∆k = ׀k – k ср׀, ∆kср = (∆k1 + ∆k2 + ∆k3 + ∆k4)/4
Результаты занести в таблицу.
3. Вычислить относительную погрешность ε = ∆kср/kср · 100%
4. Заполните таблицу:
|
№ опыта |
Fупр, Н |
׀х׀, · 10–3 м |
k, Н/м |
kср, Н/м |
Δk, Н/м |
Δkср, Н/м |
|
1 |
1 |
|||||
|
2 |
2 |
|||||
|
3 |
3 |
|||||
|
4 |
4 |
5. Запишите ответ в виде: k = kср ± ∆kср, ε =…%, подставив в эту формулу числовые значения найденных величин.
Вариант 2. Расчет инструментальной погрешности.
1. k = mg/х Для вычисления относительной погрешности используем формулу 1 стр. 344 учебника.
ε = ∆А/А + ∆В/В + ∆С/С = εm + εg + εx.
∆m = 0,01 • 10–3 кг; ∆g = 0,2 кг · м/с·с; ∆x =1 мм
2. Рассчитайте наибольшую относительную погрешность, с которой найдено значение kср (из опыта с одним грузом).
ε = εm + εg + εx = ∆m/m + ∆g/g + ∆x/x
3. Найдите ∆kср = kср • ε
4. Заполните таблицу:
|
№ опыта |
Fупр, Н |
∆x, · 10–3 м |
∆m, кг |
∆g, кг · м/с·с |
kср, Н/м |
Δk, Н/м |
ε |
|
1 |
1 |
5. Запишите ответ в виде: k = kср ± ∆kср, =…%,подставив в эту формулу числовые значения найденных величин.
Вариант 3. Расчет методом оценки погрешности косвенных измерений
1. Для вычисления погрешности следует использовать опыт, который мы получили во время проведения опыта № 4, потому что ему соответствует наименьшая относительная погрешность измерений. Вычислите пределы Fmin и Fmax, в которых находится истинное значение F, считая, что Fmin = F – ΔF, Fmax = F + ΔF.
2. Примите ΔF = 4Δm·g, где Δm – погрешность во время изготовления грузиков (для оценки можно считать, что Δm = 0,005 кг):
xmin = x – ∆x xmax = x + ∆x, где Δх = 0,5 мм.
3. Пользуясь методом оценки погрешности косвенных измерений, вычислите:
kmax = Fmax/xmin kmin = Fmin/xmax
4. Вычислите среднее значение kcp и абсолютную погрешность измерения Δk по формулам:
kср = (kmax + kmin)/2 Δk = (kmax – kmin)/2
5. Вычислите относительную погрешность измерений:
ε = ∆kср/kср · 100%
6. Заполните таблицу:
|
Fmin, H |
Fmax, H |
xmin, м |
xmax, м |
kmin, Н/м |
kmax, Н/м |
kср, Н/м |
Δk, Н/м |
εk |
7. Запишите в тетради для лабораторных работ результат в виде k = kcp ± Δk, ε = …% подставив в эту формулу числовые значения найденных величин.
Запишите в тетради для лабораторных вывод по проделанной работе.
IV. Рефлексия
Попробуйте составить синквейн о понятии «урок – практикум». Синквейн (в переводе с франц.– пять строк): Первая строка – одно существительное (суть, название темы);
Вторая строка – описание свойств-признаков темы в двух словах (двумя прилагательными);
Третья строка – описание действия (функций) в рамках темы тремя глаголами;
Четвертая строка – фраза (словосочетание) из четырех слов, показывающая отношение к теме;
Пятая строка – синоним из одного слова (существительное), который повторяет суть темы (к первому существительному).
|
Пример: Строки |
Ответы |
|
Слово-существительное |
Атмосфера |
|
Два прилагательных |
Воздушная, тяжелая |
|
Три глагола |
Простирается, давит, сжимает |
|
Словосочетание из четырех слов, |
Сильно давит на тела |
|
Синоним-существительное |
Оболочка |
V. Подведение итогов урока.
Лабораторная работа № 2 «Измерение жесткости пружины»
Цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести
уравновешивающей силу упругости на основе закона Гука:
В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости Fупр от модуля удлинения |x|. При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины k
ср.
Результат измерения обычно записывается в виде выражения k = = kcp±Δk, где Δk — наибольшая абсолютная погрешность измерения. Из курса алгебры (VII класс) известно, что относительная погрешность (εk) равна отношению абсолютной погрешности Δk к значению величины k:
откуда Δk — εkk. Существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются. В данной работе
Поэтому
Средства измерения: 1) набор грузов, масса каждого равна m0 = 0,100 кг, а погрешность Δm0 = 0,002 кг; 2) линейка с миллиметровыми делениями.
Материалы: 1) штатив с муфтами и лапкой; 2) спиральная пружина.
Порядок выполнения работы
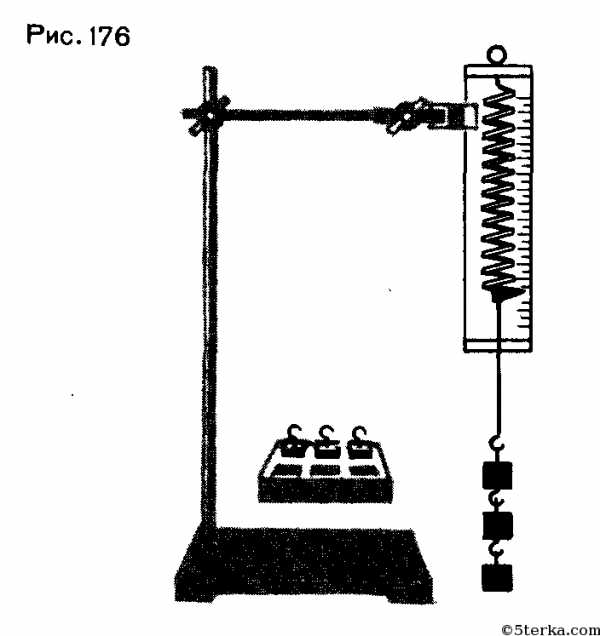
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указате-лем и крючком — рис. 176).
2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.
3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.
4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.
5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины. По результатам измерений заполните таблицу:
|
Номер опыта |
m, кг |
mg1, Н |
|х|, м |
6. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины kcp.
7. Рассчитайте наибольшую относительную погрешность, с которой найдено значение kср (из опыта с одним грузом). В формуле (1)
так как погрешность при измерении удлинения Δx=1 мм, то
8. Найдите
и запишите ответ в виде:
1 Принять g≈10 м/с2.
Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации».
Закон Гука
Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как:
где F — приложенная к пружине сила, а х — изменение длины пружины под ее действием. Средства измерения: набор грузов, масса каждого равна m0 = (0,1±0,002) кг.
Линейка с миллиметровыми делениями (Δх = ±0,5 мм). Порядок выполнения работы описан в учебнике и комментариев не требует.
|
№ опыта |
масса, кг |
удлинение |х|, |
К, Н/м |
|
|
м |
||||
|
1 |
0,1 |
1 |
0,036 |
27,78 |
|
2 |
0,2 |
2 |
0,074 |
27,03 |
|
3 |
0,3 |
3 |
0,112 |
26,79 |
|
4 |
0,4 |
4 |
0,155 |
25,81 |
* Ускорение свободного падения примем равным 10 м/с2.
Вычисления:
Вычисление погрешности измерения:
εх максимально когда х — наименьшее, т.е., в нашем случае, для опыта с одним грузом
Можно записать результат измерений как:
или округляя:
т.к. в нашем случае отклонения вычисленных R1; R2; R3; R4 от R
ср велики из-за разности условий опытов принимаем
5terka.com
Лабораторная работа «Определение жесткости пружины»
Лабораторная работа
«Определение жесткости пружины»
Цель работы: Определение коэффициента жесткости пружины. Проверка справедливости закона Гука .Оценка погрешности измерений.
Порядок выполнения работы.
Базовый уровень
Оборудование: штатив с муфтой и лапкой, набор грузов по 100 г, пружинный динамометр, линейка.
-
Укрепите пружину в штативе и измерьте длину пружины L0 в отсутствие внешнего воздействия (F=0Н). Результаты измерений запишите в таблицу.
-
Подвесьте к пружине груз весом 1 Н и определите ее длину L1 в этом случае.
-
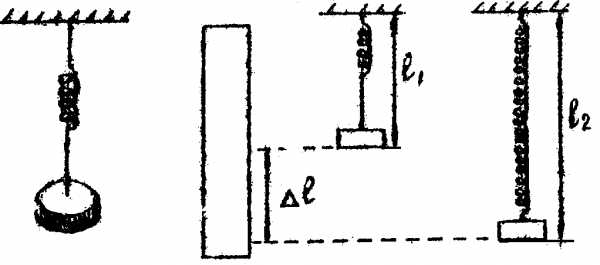
Найдите деформацию (удлинение) пружины по формуле l=L0-L1 .Результаты измерений занесите в таблицу.
-
Аналогично найдите удлинение пружины при подвешивании грузов весом 2 Н и 3 Н . Результаты измерений занесите в таблицу.
-
Вычислите среднее арифметическое значение kср.по формуле kср=(k1+k2+k3)/3
-
F,Н
l,м
k,Н/м
kср, Н/м
6. Начертите график зависимости l (F).
Продвинутый уровень
Оборудование: штатив с муфтой и лапкой, набор грузов по 100 г, пружина, линейка.
-
Укрепите пружину в штативе и измерьте длину пружины L0 в отсутствие внешнего воздействия (F=0Н). Результаты измерений запишите в таблицу.
-
Подвесьте к пружине груз весом 1 Н и определите ее длину L1 в этом случае.
-
Найдите деформацию (удлинение) пружины по формуле l=L0-L1 .Результаты измерений занесите в таблицу.
-
Аналогично найдите удлинение пружины при подвешивании грузов весом 2 Н и 3 Н . Результаты измерений занесите в таблицу.
-
Вычислите среднее арифметическое значение kср.по формуле kср=(k1+k2+k3)/3
-
Оцените погрешность ∆k методом средней ошибки. Для этого вычислите модуль разности │kср-ki│=∆ki для каждого измерения
-
Полученный результат запишите в виде k=kср±∆k
-
F,Н
l,м
k,Н/м
kср, Н/м
∆k,Н/м
∆kср, Н/м
Углубленный уровень
Оборудование: штатив с муфтой и лапкой, набор грузов по 100 г, пружина, линейка.
-
Укрепите пружину в штативе и измерьте длину пружины L0 в отсутствие внешнего воздействия (F=0Н). Результаты измерений запишите в таблицу.
-
Подвесьте к пружине груз весом 1 Н и определите ее длину L1 в этом случае.
-
Найдите деформацию (удлинение) пружины по формуле l=L0-L1 .Результаты измерений занесите в таблицу.
-
Аналогично найдите удлинение пружины при подвешивании грузов весом 2 Н и 3 Н . Результаты измерений занесите в таблицу.
-
Вычислите среднее арифметическое значение kср.по формуле kср=(k1+k2+k3)/3
-
Вычислите относительные погрешности и абсолютную погрешность измерений ∆k по формулам
εF=(∆F0+Fи) / Fmax
εl=(∆l0+lи) / lmax
εk=εF+εl
∆k= εk* kср
-
Полученный результат запишите в виде k=kср±∆k
-
Начертите график зависимости l (F).Сформулируйте геометрический смысл жесткости.
-
F,Н
l,м
k,Н/м
kср, Н/м
εF
εl
εk
∆k
infourok.ru
Лабораторная работа №2 — решебник по физике за 10 класс Мякишев, Буховцев, Сотский
§84. Электрический заряд и элементарные частицы. Закон сохранения заряда (стр. 277-281)
§85. Закон Кулона. Единица электрического заряда (стр. 282-285)
Вопросы к параграфу:
1;
2;
3;
4;
§86. Пример решения задач по теме «Закон Кулона» (стр. 286-289)
Задачи для самостоятельного решения:
1;
2;
3;
4;
5;
§87. Близкодействие и действие на расстоянии (стр. 290-291)
Вопросы к параграфу:
1;
2;
§88. Электрическое поле (стр. 292-294)
Вопросы к параграфу:
1;
2;
3;
§89. Напряжённость электрического поля. Силовые линии (стр. 295-297)
Вопросы к параграфу:
1;
2;
3;
§90. Поле точечного заряда и заряженного шара. Принцип суперпозиции полей (стр. 298-299)
Вопросы к параграфу:
1;
2;
3;
4;
§91. Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» (стр. 300-302)
Задачи для самостоятельного решения:
1;
2;
3;
§92. Проводники и диэлектрики в электростатическом поле (стр. 303-307)
Вопросы к параграфу:
1;
2;
3;
4;
Задания ЕГЭ:
A1;
A2;
§93. Потенциальная энергия заряженного тела в однородном электростатическом поле (стр. 308-310)
Вопросы к параграфу:
1;
2;
A1;
§94. Потенциал электростатического поля и разность потенциалов (стр. 311-313)
Вопросы к параграфу:
1;
2;
3;
§95. Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности (стр. 314-316)
Вопросы к параграфу:
1;
2;
3;
4;
5;
§96. Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» (стр. 317-320)
Задачи для самостоятельного решения:
1;
2;
3;
4;
5;
6;
7;
§97. Электроёмкость. Единицы электроёмкости. Конденсатор (стр. 321-324)
§98. Энергия заряженного конденсатора. Применение конденсаторов (стр. 325-326)
Вопросы к параграфу:
1;
2;
Задания ЕГЭ:
A1;
A2;
§99. Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора» (стр. 327-330)
Задачи для самостоятельного решения:
1;
2;
3;
4;
5;
gdzplus.me
Определение жёсткости пружины
Лабораторная работа № 1.
«Определение жёсткости пружины».
Цель: Определить жёсткость пружины с помощью графика зависимости силы упругости от удлинения. Сделать вывод о характере этой зависимости.
Оборудование: штатив, динамометр, 3 груза, линейка.
Ход работы.
Подвесьте груз к пружине динамометра, измерьте силу упругости и удлинение пружины.
Затем к первому грузу прикрепите второй. Повторите измерения.
Ко второму грузу прикрепите третий. Снова повторите измерения.
Результаты занесите в таблицу:
|
Сила упругости Fупр, Н |
Удлинение Δl, м |
Постройте график зависимости силы упругости от удлинения пружины:
Fупр, Н
3,0
2,0
1,0
0 0,02 0,04 0,06 0,08 Δl, м
По графику найдите средние значения силы упругости и удлинения. Рассчитайте среднее значение коэффициента упругости:
Сделайте вывод.
Лабораторная работа № 1
DOC / 26 Кб
xn--j1ahfl.xn--p1ai
Лабораторная работа 4. Определение коэффициента упругости пружины (4 ч)
Цель
– определить коэффициент упругости
пружины двумя способами: 1) используя
зависимость периода упругих колебаний
от массы; 2) по закону Гука.
Приборы
и материалы:
пружина, площадка для грузов, набор
грузов, секундомер, линейка.
Описание установки
Установка
(рис. 4.1, 4.2) представляет собой пружину,
верхний конец которой жестко соединен
с кронштейном. К кронштейну прикреплена
измерительная линейка. К нижнему концу
пружины подвешивается площадка, на
которую можно помещать различный набор
грузов.
Рис. 4.1 Рис. 4.2
Задание 1. Определение коэффициента упругости пружины по закону Гука
1. Записать формулу
для определения коэффициента упругости
по закону Гука.
2. Продумать и
записать порядок выполнения работы
(рис. 4.2).
3.
Составить таблицу для значений измеряемых
величин и произвести необходимые
измерения.
Задание 2. Определение коэффициента упругости пружины из зависимости периода упругих колебаний от массы груза
1.
Навесить на пружину груз в 100 г, при этом
общая масса будет равна
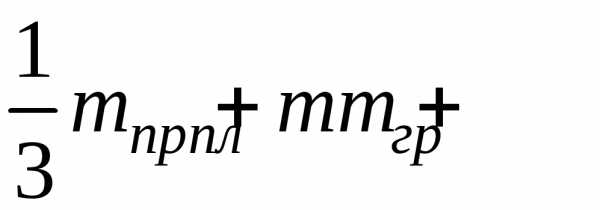
(4.1)
где
mnp
– масса
пружины,
mгр
– масса
груза,
тпл
– масса
площадки.
2.
Слегка оттянуть пружину и отпустить.
Система придет в колебательное движение.
По секундомеру определить время t,
в течение которого происходит 20–30
полных колебаний системы. Опыт повторить
не менее трех раз и найти среднее значение
< t >.
Из полученных данных определить средний
период < T
> по формуле
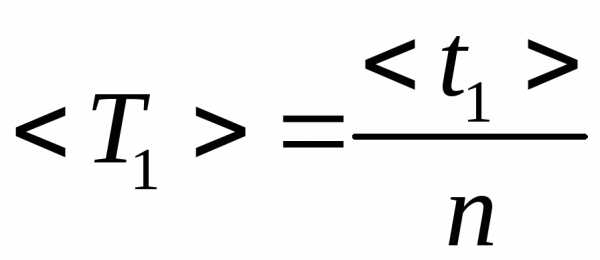
3.
Добавляя грузы по 100 г, аналогично
определить <
T2
>,< T3
>.
4. Полученные данные
занести в табл. 4.1.
5.
Для каждого значения периода <
T > определить
коэффициент упругости пружины K1
, K2
, K3
из формулы
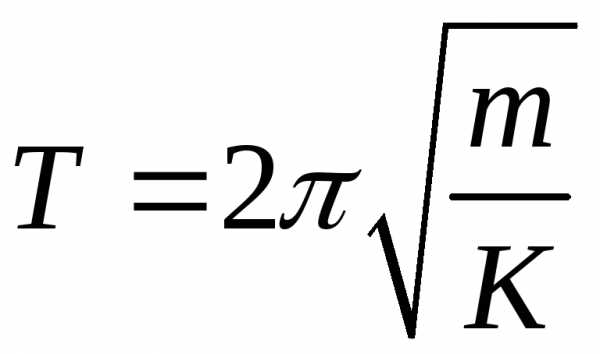
откуда
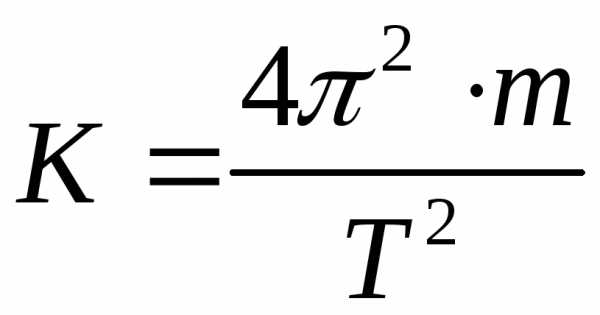
Найти
среднее значение <
K >.
6. Сравнить значения
коэффициента упругости, полученные при
выполнении заданий 1 и 2.
7. Сделать выводы.
Таблица 4.1
Измеряемые и расчетные величины для определения коэффициента упругости к
|
Номер измерений i |
Масса колеблющейся системы |
Число n |
Время колебаний |
Средний период колебаний < T > |
Коэффициент упругости |
||
|
t |
< |
||||||
|
K |
< |
||||||
|
1 |
|||||||
|
2 |
|||||||
|
3 |
Контрольные вопросы
1. Дайте определение
гармонического колебания.
2.
Дайте определение кинематических
характеристик гармонического колебания:
амплитуды, периода, частоты, фазы
колебания.
3.
Запишите уравнения смещения, скорости
и ускорения при колебательном движении,
их максимальные значения.
4. Получите формулу
периода упругих колебаний.
5. Объясните
физический смысл коэффициента упругости.
Литература
[5, § 141, 142].
Лабораторная работа 5. Определение силы земного притяжения с помощью математического маятника (4 ч)
Цель
– экспериментально определить модуль
ускорения силы земного тяготения в
данном географическом месте.
Приборы
и материалы:
маятник на нити изменяемой длины, шкалы
с подвижным угольником и двумя барабанами,
секундомер.
studfiles.net
Лабораторная работа по физике для 7 класса «Измерение коэффициента жесткости пружины»
Лабораторная работа.
Определение коэффициента жесткости пружины.
Цель работы: используя экспериментальную зависимость силы упругости от абсолютного удлинения, вычислить коэффициент жёсткости пружины.
Оборудование: штатив, линейка, пружина, грузы массой по 100 г.
Теория. Под деформацией понимают изменение объема или формы тела под действием внешних сил. При изменении расстояния между частицами вещества (атомами, молекулами, ионами) изменяются силы взаимодействия между ними. При увеличении расстояния растут силы притяжения, а при уменьшении – силы отталкивания, которые стремятся вернуть тело в исходное состояния. Поэтому силы упругости имеют электромагнитную природу. Сила упругости всегда направлена к положению равновесия и стремится вернуть тело в исходное состояние. Сила упругости прямо пропорциональна абсолютному удлинению тела.
Закон Гука: Сила упругости, возникающая при деформации тела, прямо пропорциональна его удлинению (сжатию) и направлена противоположно перемещению частиц тела при деформации, Fупр = кΔх, где k – коэффициент
жесткости [k] = Н/м, Δх = ΔL – модуль удлинения тела.
Коэффициент жесткости зависит от формы и размеров тела,
а также от материала. Он численно равен силе упругости
при удлинении (сжатии) тела на 1 м.
Порядок выполнения работы.
1. Закрепить динамометр в штативе.
2. Измерить линейкой первоначальную длину пружины L0.
3. Подвесить груз массой 100 г.
4. Измерить линейкой длину деформированной пружины L. Определить погрешность измерения длины: ΔƖ= 0,5дел*С1, где С1 – цена деления линейки.
5. Вычислить удлинение пружины Δх = ΔL = L – L0.
6. На покоящийся относительно пружины груз действуют две компенсирующие друг друга силы: тяжести и упругости Fт = Fупр (смотри верхний рисунок)
7. Вычислить силу упругости по формуле, Fупр=mg. Определить погрешность измерения силы: ΔF= 0,5дел*С2, где С2 – цена деления динамометра.
8. Подвесить груз массой 200 г и повторить опыт по пунктам 4-6.
9. Подвесить груз массой 300 г и повторить опыт по пунктам 4-6.
10. Результаты занести в таблицу.
11. Вычислите коэффициент жесткости пружины для каждого измерения К= Fупр / Δx и запишите в таблицу эти значения. Определите среднее значение Кср
12. Определите абсолютную погрешность измерения Δ к = (ΔF/ Fупр + ΔƖ / L) * к измеренное, где ΔF – погрешность измерения силы, ΔƖ – погрешность измерения длины.
13. Выбрать систему координат и построить график зависимости силы упругости Fупр от удлинения пружины ΔL.
Таблица измерения
п/п
Начальная длина, L0, м
Конечная длина, L, м
Абсолютное удлинение Δx1 =ΔL = L – L0, м
Сила упругости, Fупр, Н
Коэффициент жёсткости, К, Н/м
1
2
3
14. Сделайте вывод. Полученный в результате опытов коэффициент жесткости пружины можно записать: к = кср измеренное (у каждого ученика свой коэффициент) ± Δ к (для всех разная погрешность).
infourok.ru
Лабораторная работа по физике «Измерение жесткости пружины»
МОУ «Гимназия №6» Физический практикум 10 класс
Лабораторная работа №3
Измерение жесткости пружины
Цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести 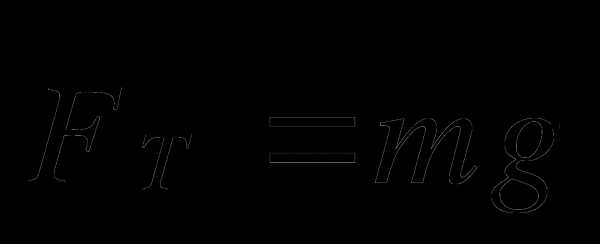
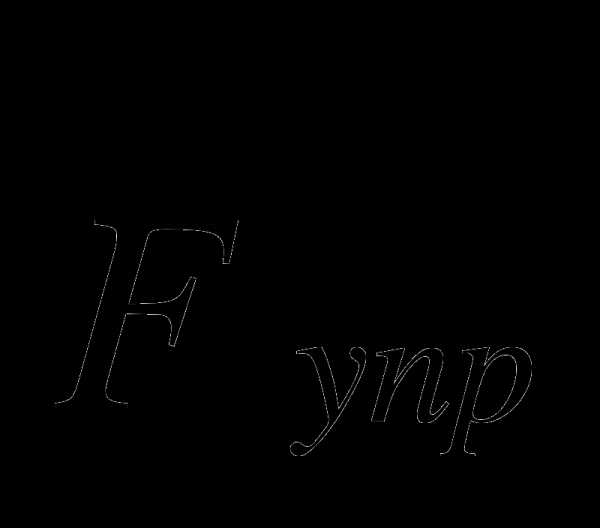
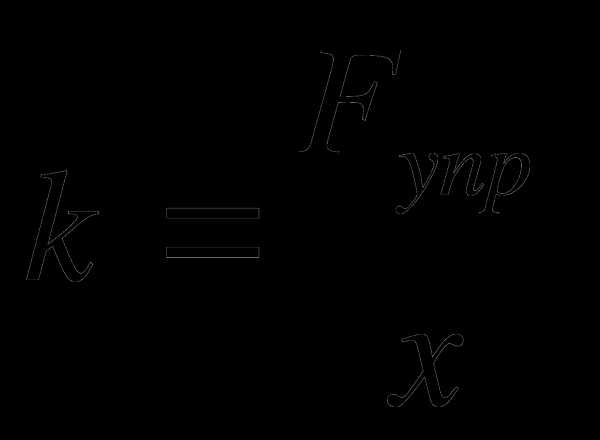



Результат измерения обычно записывается в виде выражения , где 


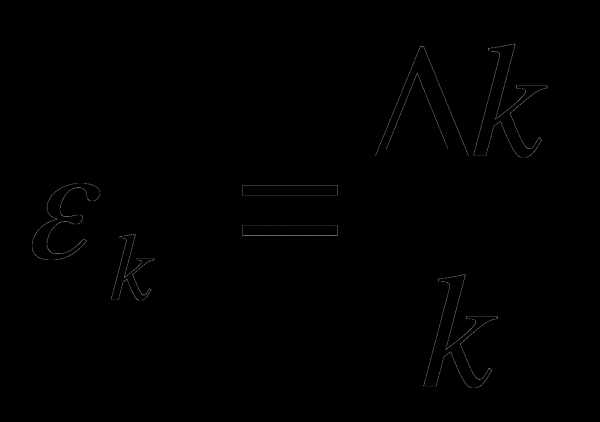

В данной работе 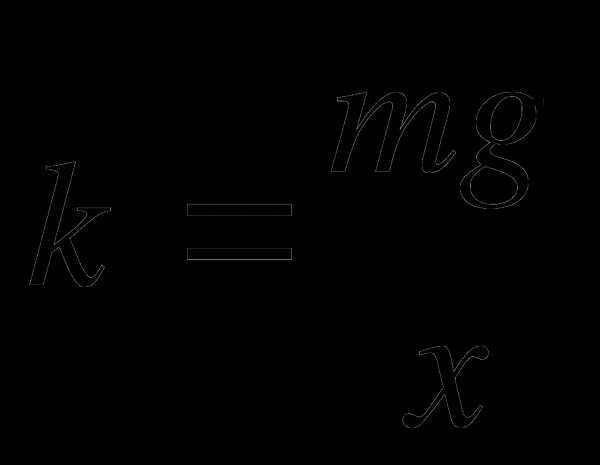
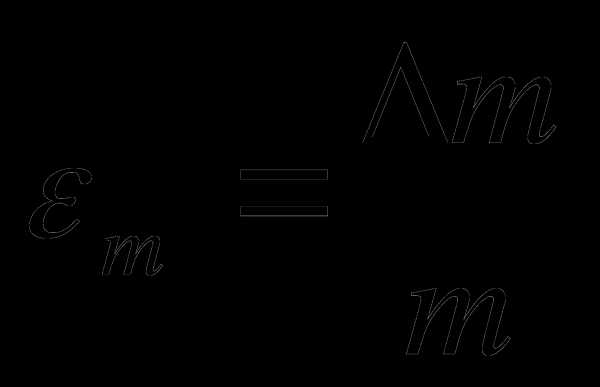
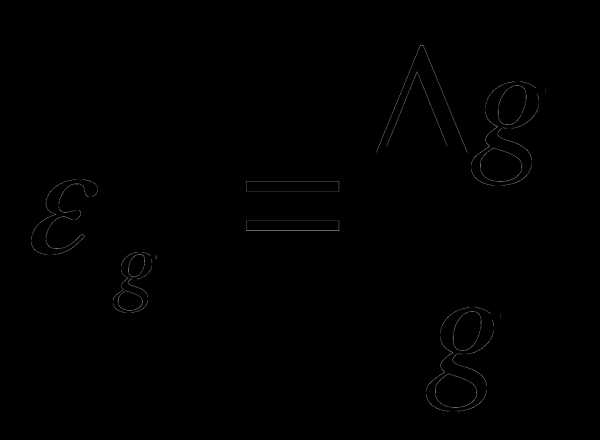
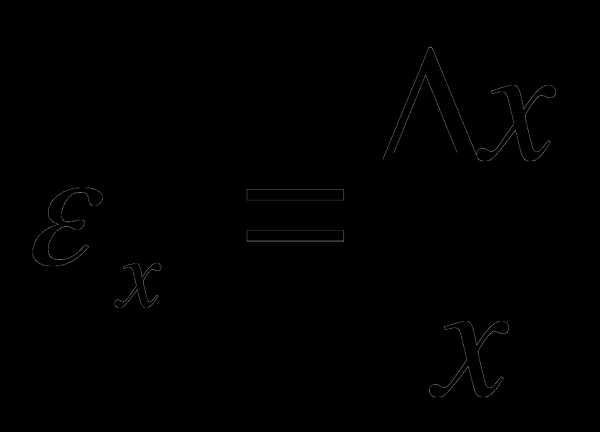
Средства измерения:
-
набор грузов, масса каждого равна m0=0,100 кг, а погрешность
=0,002 кг;
-
линейка с миллиметровыми делениями. Погрешность
=1 мм;
-
абсолютная погрешность
=0,02
.
Материалы:
-
спиральная пружина;
-
штатив с муфтой и лапкой.
Ход работы:
-
Закрепите на штативе конец спиральной пружины.
-
Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.
-
Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.
-
Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.
-
К первому грузу добавьте второй, третий и т.д. грузы, записывая каждый раз удлинение x пружины. По результатам измерений заполните таблицу:
-
По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины
.
-
Рассчитайте наибольшую относительную погрешность, с которой найдено значение
(из опыта с одном грузом).
-
Найдите
и запишите ответ в виде: .
infourok.ru
No related posts.
Сила упругости и закон Гука
Для начала определим основные термины, которые будут использоваться в данной статье. Известно, если воздействовать на тело извне, оно либо приобретет ускорение, либо деформируется. Деформация — это изменение размеров или формы тела под влиянием внешних сил. Если объект полностью восстанавливается после прекращения нагрузки, то такая деформация считается упругой; если же тело остается в измененном состоянии (например, согнутом, растянутом, сжатым и т. д. ), то деформация пластическая.
Примерами пластических деформаций являются:
- лепка из глины;
- погнутая алюминиевая ложка.
В свою очередь, упругими деформациями будут считаться:
- резинка (можно растянуть ее, после чего она вернется в исходное состояние);
- пружина (после сжатия снова распрямляется).
В результате упругой деформации тела (в частности, пружины) в нем возникает сила упругости, равная по модулю приложенной силе, но направленная в противоположную сторону. Сила упругости для пружины будет пропорциональна ее удлинению. Математически это можно записать таким образом:
F = — k·x;
где F — сила упругости, x — расстояние, на которое изменилась длина тела в результате растяжения, k — необходимый для нас коэффициент жесткости. Указанная выше формула также является частным случаем закона Гука для тонкого растяжимого стержня. В общей форме этот закон формулируется так: «Деформация, возникшая в упругом теле, будет пропорциональна силе, которая приложена к данному телу». Он справедлив только в тех случаях, когда речь идет о малых деформациях (растяжение или сжатие намного меньше длины исходного тела).
Формулы периода и частоты колебаний пружинного маятника
При проектировании и вычислении основных показателей также уделяется довольно много внимания частоте и периоду колебания. Косинус – периодическая функция, в которой применяется значение, неизменяемое через определенный промежуток времени. Именно этот показатель называют период колебаний пружинного маятника. Для обозначения этого показателя применяется буква Т, также часто используется понятие, характеризующее значение, обратное периоду колебания (v). В большинстве случаев при расчетах применяется формула T=1/v.
Период колебаний вычисляется по несколько усложненной формуле. Она следующая: T=2п√m/k. Для определения частоты колебания используется формула: v=1/2п√k/m.
Рассматриваемая циклическая частота колебаний пружинного маятника зависит от следующих моментов:
- Масса груза, который прикреплен к пружине. Этот показатель считается наиболее важным, так как оказывает влияние на самые различные параметры. От массы зависит сила инерции, скорость и многие другие показатели. Кроме этого, масса груза – величина, с измерением которой не возникает проблем из-за наличия специального измерительного оборудования.
- Коэффициент упругости. Для каждой пружины этот показатель существенно отличается. Коэффициент упругости указывается для определения основных параметров пружины. Зависит этот параметр от количества витков, длины изделия, расстояние между витками, их диаметра и многого другого. Определяется он самым различным образом, зачастую при применении специального оборудования.
Не стоит забывать о том, что при сильном растяжении пружины закон Гука прекращает действовать. При этом период пружинного колебания начинает зависеть от амплитуды.
Для измерения периода применяется всемирная единица времени, в большинстве случаев секунды. В большинстве случаев амплитуда колебаний вычисляется при решении самых различных задач. Для упрощения процесса проводится построение упрощенной схемы, на которой отображаются основные силы.
Определение коэффициента жесткости
Коэффициент жесткости (он также имеет названия коэффициента упругости или пропорциональности) чаще всего записывается буквой k, но иногда можно встретить обозначение D или c. Численно жесткость будет равна величине силы, которая растягивает пружину на единицу длины (в случае СИ — на 1 метр). Формула для нахождения коэффициента упругости выводится из частного случая закона Гука:
k = F/x.
Чем больше величина жесткости, тем больше будет сопротивление тела к его деформации. Также коэффициент Гука показывает, насколько устойчиво тело к действию внешней нагрузки. Зависит этот параметр от геометрических параметров (диаметра проволоки, числа витков и диаметра намотки от оси проволоки) и от материала, из которого она изготовлена.
Единица измерения жесткости в СИ — Н/м.
Физические характеристики пружин
Цилиндрические пружины характеризуются рядом параметров, сочетание которых обуславливает их жесткость — способность сопротивляться деформации:
- материал; пружины чаще всего изготавливают из стальной проволоки, причем сталь в них применялася особая, ее характеризует среднее или высокое содержание углерода, низкое содержание других примесей (низколегированный сплав) и особая термообработка (закалка), придающая материалу дополнительную упругость;
- диаметр проволоки; чем он меньше, тем эластичнее пружина, но тем меньше ее способность запасать энергию; пружины сжатия изготавливают, как правило, из более толстой проволоки, чем пружины растяжения;
- форма сечения проволоки; не всегда проволока, из которой намотана пружина, имеет круглое сечение; уплощенное сечение имеют пружины сжатия, чтобы при максимальном сокращении длины (виток «садится» на соседний виток) конструкция была более устойчивой;
- длина и диаметр пружины; длину пружины следует отличать от длины проволоки, из которой она намотана; эти два параметра согласуются через количество витков и диаметр пружины, который, в свою очередь, не следует путать с диаметром проволоки.
Готовые работы на аналогичную тему
Курсовая работа Жесткость пружины, формула 450 ₽ Реферат Жесткость пружины, формула 250 ₽ Контрольная работа Жесткость пружины, формула 230 ₽
Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость
Существуют и другие физические характеристики, влияющие на работоспособность пружин. Например, при повышении температуры металл становится менее упругим, а при существенном ее понижении может стать хрупким. При интенсивной эксплуатации пружина со временем теряет часть упругости по причине постепенного разрушения связей между атомами кристаллической решетки.
Расчет жесткости системы
Встречаются более сложные задачи, в которых необходим расчет общей жесткости. В таких заданиях пружины соединены последовательно или параллельно.
Последовательное соединение системы пружин
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
1/k = 1/k1 + 1/k2 + … + 1/ki,
где k — общая жесткость системы, k1, k2, …, ki — отдельные жесткости каждого элемента, i — общее количество всех пружин, задействованных в системе.
Параллельное соединение системы пружин
В случае когда пружины соединены параллельно, величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
k = k1 + k2 + … + ki.
Измерение жесткости пружины опытным путем — в этом видео.
Вычисление коэффициента жесткости опытным методом
С помощью несложного опыта можно самостоятельно рассчитать, чему будет равен коэффициент Гука. Для проведения эксперимента понадобятся:
- линейка;
- пружина;
- груз с известной массой.
Последовательность действий для опыта такова:
- Необходимо закрепить пружину вертикально, подвесив ее к любой удобной опоре. Нижний край должен остаться свободным.
- При помощи линейки измеряется ее длина и записывается как величина x1.
- На свободный конец нужно подвесить груз с известной массой m.
- Длина пружины измеряется в нагруженном состоянии. Обозначается величиной x2.
- Подсчитывается абсолютное удлинение: x = x2-x1. Для того чтобы получить результат в международной системе единиц, лучше сразу перевести его из сантиметров или миллиметров в метры.
- Сила, которая вызвала деформацию, — это сила тяжести тела. Формула для ее расчета — F = mg, где m — это масса используемого в эксперименте груза (переводится в кг), а g — величина свободного ускорения, равная приблизительно 9,8.
- После проведенных расчетов остается найти только сам коэффициент жесткости, формула которого была указана выше: k = F/x.
Формула определения жесткости
Изучаемая современными школьниками формула, как найти коэффициент жесткости пружины, представляет собой соотношение силы и величины, показывающей изменение длины пружины в зависимости от величины данного воздействия (или
Читать также: Как сварить алюминий дома
равной ему по модулю силы упругости). Выглядит эта формула так: F = –kx. Из этой формулы коэффициент жесткости упругого элемента равен отношению силы упругости к изменению его длины. В международной системе единиц физических величин СИ он измеряется в ньютонах на метр (Н/м).
Другой вариант записи формулы: коэффициент Юнга
Деформация растяжения/сжатия в физике также может описываться несколько видоизмененным законом Гука. Формула включает значения относительной деформации (отношения изменения длины к ее начальному значению) и напряжения (отношения силы к площади поперечного сечения детали). Относительная деформация и напряжение по этой формуле пропорциональны, а коэффициент пропорциональности – величина, обратная модулю Юнга.
Модуль Юнга интересен тем, что определяется исключительно свойствами материала, и никак не зависит ни от формы детали, ни от ее размеров.
К примеру, модуль Юнга для ста
ли примерно равен единице с одиннадцатью нулями (единица измерения – Н/кв. м).
Смысл понятия коэффициент жесткости
Коэффициент жесткости – коэффициент пропорциональности из закона Гука. Еще он с полным правом называется коэффициентом упругости.
Фактически он показывает величину силы, которая должна быть приложена к упругому элементу, чтобы изменить его длину на единицу (в используемой системе измерений).
Значение этого параметра зависит от нескольких факторов, которыми характеризуется пружина:
- Материала, используемого при ее изготовлении.
- Формы и конструктивных особенностей.
- Геометрических размеров.
По этому показателю можно сд
елать вывод, насколько изделие устойчиво к воздействию нагрузок, то есть каким будет его сопротивление при приложении внешнего воздействия.
Особенности расчета пружин
Показывающая, как найти жесткость пружины, формула, наверное, одна из наиболее используемых современными конструкторами. Ведь применение эти упругие детали находят практически везде, то есть требуется просчитывать их поведение и выбирать те из них, которые будут идеально справляться с возложенными обязанностями.
Закон Гука весьма упрощенно показывает зависимость деформации упругой детали от прилагаемого усилия, инженерами используются более точные формулы расчета коэффициента жесткости, учитывающие все особенности происходящего процесса.
- Цилиндрическую витую пружину современная инженерия рассматривает как спираль из проволоки с круглым сечением, а ее деформация под воздействием существующих в системе сил представляется совокупностью элементарных сдвигов.
- При деформации изгиба в качестве деформации рассматривается прогиб стержня, расположенного концами на опорах.
Примеры задач на нахождение жесткости
Задача 1
На пружину длиной 10 см действует сила F = 100 Н. Длина растянутой пружины составила 14 см. Найти коэффициент жесткости.
- Рассчитываем длину абсолютного удлинения: x = 14—10 = 4 см = 0,04 м.
- По формуле находим коэффициент жесткости: k = F/x = 100 / 0,04 = 2500 Н/м.
Ответ: жесткость пружины составит 2500 Н/м.
Задача 2
Груз массой 10 кг при подвешивании на пружину растянул ее на 4 см. Рассчитать, на какую длину растянет ее другой груз массой 25 кг.
- Найдем силу тяжести, деформирующей пружину: F = mg = 10 · 9.8 = 98 Н.
- Определим коэффициент упругости: k = F/x = 98 / 0.04 = 2450 Н/м.
- Рассчитаем, с какой силой действует второй груз: F = mg = 25 · 9.8 = 245 Н.
- По закону Гука запишем формулу для абсолютного удлинения: x = F/k.
- Для второго случая подсчитаем длину растяжения: x = 245 / 2450 = 0,1 м.
Ответ: во втором случае пружина растянется на 10 см.




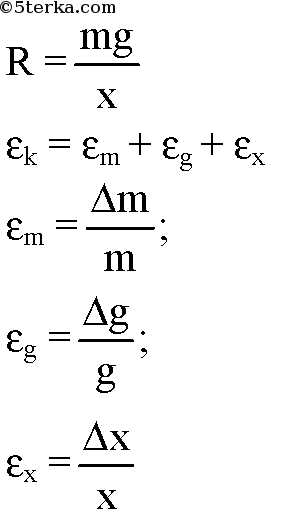
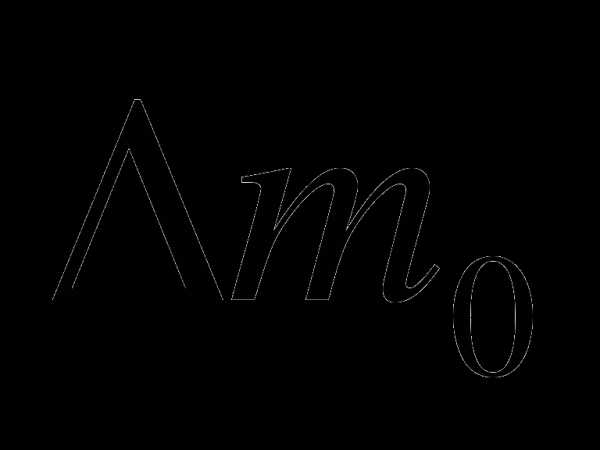 =0,002 кг;
=0,002 кг; =1 мм;
=1 мм;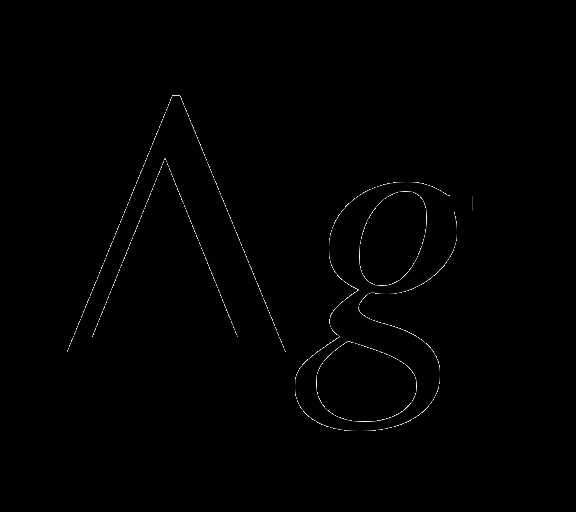 =0,02
=0,02 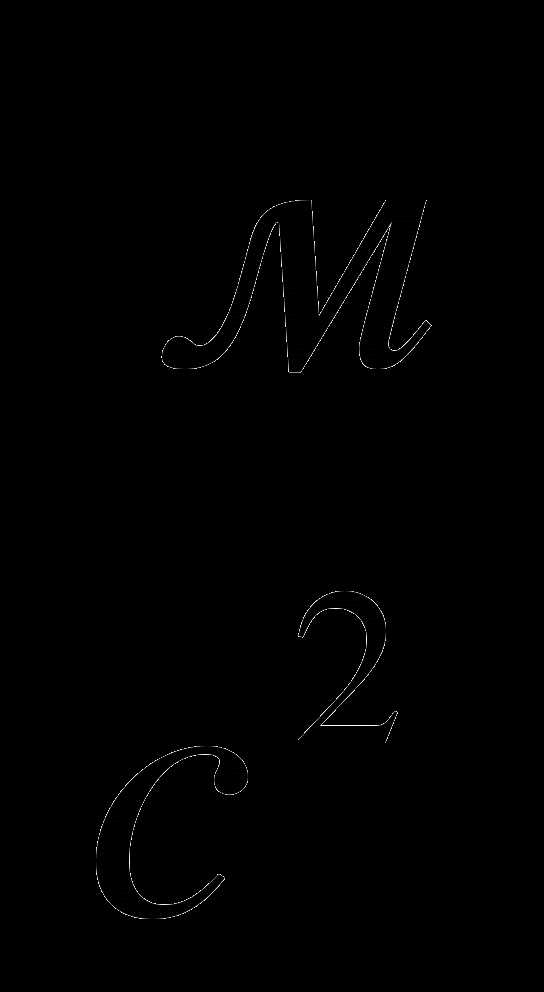 .
.