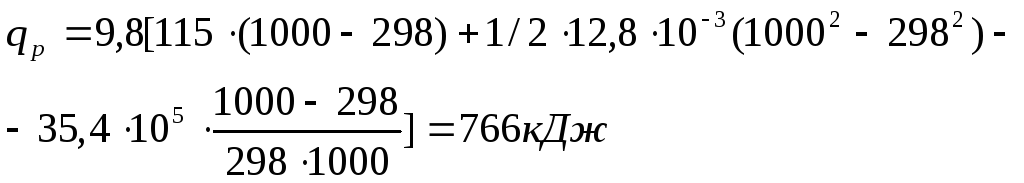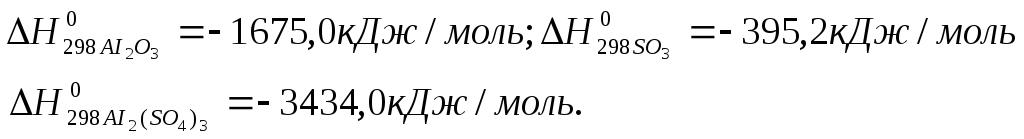Различают
истинную и среднюю теплоемкости. Истинная
теплоемкость равна количеству тепла,
которое нужно подвести к телу, чтобы
увеличить его температуру на дифференциально
малую величину. Она определяется
соотношением:
Средняя
теплоемкость в интервале температур
от Т1
до Т2
равна количеству тепла, которое нужно
подвести к телу, чтобы повысить его
температуру на 1 градус:
Взаимосвязь
истинной и средней теплоемкостей
выражается уравнением:
Зависимость
теплоемкости от температуры в интервале
температур 298 – Т для практических
расчетов выражают обычно эмпирическими
уравнениями в виде средних рядов:
где:
а0,
а1,
а2
и а-2
– коэффициенты, зависящие от природы
вещества.
Количество
тепла в процессах при постоянных V
и P,
затраченное на нагревание n-моль
вещества от Т1
до Т2
определяется из соотношений:
Учитывая
зависимость теплоемкости от температуры,
можно записать:
(1-3)
Пример 2:
Определить
количество тепла, поглощенное при
нагревании 1 кг
(корунда) от 298 до 1000 К, если эмпирические
коэффициенты в уравнении мольной
теплоемкости Ср
в интервале температур 298-1000К равны
Дж/моль*К: а0
– 115, а1
– 12.8 * 10-3
, а-2
– 35.4 .105.
Решение:
Запишем
уравнение зависимости теплоемкости от
температуры на основании данных задачи:
находим
число моль корунда:
По
уравнению (1-3) определяем количество
теплоты:
1.3. Закон Гесса
Закон
Гесса лежит в основе термохимии.
Термохимия занимается изучением тепловых
эффектов химических реакций. Тепловым
эффектом химической реакции называется
количество энергии, которое система
выделяет или поглощает в виде теплоты
при полном необратимом протекании
реакции при постоянстве температуры и
давления или температуры и объема.
Условия знаков в термохимии иные, чем
в термодинамике, те есть теплота, которая
выделяется в ходе реакции, считается
положительной (экзотермическая реакция),
и наоборот, теплота, которая поглощается
в ходе реакции (подводится), считается
отрицательной (эндотермическая реакция).
Поэтому в термохимии тепловые эффекты
обозначаются Q
и учитывается, что Q
= -q.
Закон
Гесса вытекает непосредственно из
первого закона термодинамики. Он
читается:
Тепловой
эффект химической реакции зависит
только от вида и состояния исходных
веществ и конечных продуктов, но не
зависит от пути перехода при условии,
если объем и температура или давление
и температура в ходе реакции остаются
постоянными.
Действительно,
при P=const:
qp=∆H=-Qp
; при V=const:
qv=∆U=-Qv
. Связь между Qp
и Qv
выражается уравнением:
Qp
= Qv
— ∆nRT
Где
∆n
– изменение числа моль газообразных
участников реакции.
Для практических
расчетов широко используется следствия
из закона Гесса. Их пять.
Первое
следствие. Теплота образования соединения
из исходных веществ не зависит от
способа, каким это соединение получено.
Второе
следствие. Тепловой эффект разложения
какого-либо соединения равен по абсолютной
величине и противоположен по знаку
тепловому эффекту его образования.
Третье
следствие. Если совершаются две реакции,
приводящие из различных начальных
состояний к одинаковым конечным, то
разница между их тепловыми эффектами
представляет собой тепловой эффект
перехода из одного начального состояния
в другое; если совершаются две реакции,
приводящие из одинаковых начальных к
различным конечным состояниям, то
разница между их тепловыми эффектами
представляет собой тепловой эффект
перехода из одного конечного состояния
в другое.
Четвертое
следствие. Тепловой эффект реакции
равен разности между суммой теплот
образования конечных продуктов и суммой
теплот образования исходных веществ с
учетом соответствующих стехиометрических
коэффициентов:
Для
расчета теплот образования выбрано
стандартное состояние и приняты условия
нормировки энтальпии. В соответствии
с международным соглашением за стандартное
состояние принято состояние при давлении
1 атм. (1,013.105
н/м2)
и температуре 298К. Условия нормировки:
для каждого элемента в модификации,
наиболее устойчивой в стандартном
состоянии, абсолютное значение стандартной
энтальпии равно нулю:
Тогда энтальпия сложного вещества
определится тепловым эффектом с обратным
знаком реакции его образования из
элементов в стандартном состоянии.
Пятое
следствие. Тепловой эффект реакции
равен разности между суммой теплот
сгорания исходных веществ и суммой
теплот сгорания конечных продуктов с
учетом соответствующих стехиометрических
коэффициентов.
Теплотой
сгорания называется тепловой эффект
реакции полного сгорания одного моль
данного соединения до образования
высших окислов.
Пример 3:
Пользуясь
стандартными теплотами образования
соединений при 298К и 1,013*105
н/м2
, вычислить тепловой эффект реакции при
Р=const
и V=const:
Стандартные
теплоты образования веществ следующие:
Решение:
В соответствии с
четвертым следствием из закона Гесса:
Для
расчета ∆Ux
воспользуемся уравнением:
∆Ux=
∆Hx-∆nRT
∆Ux=
— 573,4 + 3.8,314
.10-3
.298
= -566,0кДж
Пример 4:
Пользуясь
стандартными теплотами сгорания,
вычислить тепловой эффект реакции:
если теплоты
сгорания веществ следующие:
Решение:
Согласно
пятому следствию из закона Гесса,
тепловой эффект реакции равен:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
72,2% бесплатных материалов
968 руб. средняя цена курсовой работы
353 руб. средняя цена домашнего задания
116 руб. средняя цена решённой задачи
161 руб. средняя цена лабораторной работы
174 руб. средняя цена реферата
177 руб. средняя цена доклада
1626 руб. средняя цена ВКР
665 руб. средняя цена диссертации
596 руб. средняя цена НИР
358 руб. средняя цена отчёта по практике
276 руб. средняя цена ответов (шпаргалок)
202 руб. средняя цена лекций
232 руб. средняя цена семинаров
280 руб. средняя цена рабочей тетради
187 руб. средняя цена презентации
67 руб. средняя цена перевода
143 руб. средняя цена изложения
150 руб. средняя цена сочинения
308 руб. средняя цена статьи
Гарантия возврата средств


Зависимость теплоемкости от температуры
- Эксперименты показали, что при повышении температуры газа вибрационное движение атомов в молекуле усиливается, и требуется больше энергии. Поэтому, чем выше температура, тем больше тепла придется потратить на нагрев газа на G. следовательно, теплоемкость газа Рис. 3.2 . Функция температуры, а не константа value. In в общем случае удельная теплоемкость температуры/может быть выражена следующим уравнением с =c₀₀h-а! B-BH-LR B- (3.19). Где находится удельная теплоемкость при 0°C?
Поскольку влияние на величину термина температуры выше первой температуры очень мало, то в технических расчетах часто берут линейную зависимость теплоемкости от температуры и выражают ее формулой С -=c₀ х-а/. (3.20 утра)) На рисунке 3.2 показан график зависимости теплоемкости от температуры. Кривая строится по формуле (3.19), а прямая-по формуле (3.20).
Если с течением времени изменяется температура окружающей среды или коэффициент теплообмена а.
Людмила Фирмаль
В дальнейшем будем использовать только формулу (3.20), то есть линейную зависимость теплоемкости от температуры. Из-за того, что теплоемкость зависит от температуры, расход тепла в случае одного и того же повышения температуры будет меняться. Чем выше начальная температура нагрева, тем больше тепла должно быть потреблено для того же повышения температуры. Это хорошо видно на рисунке.
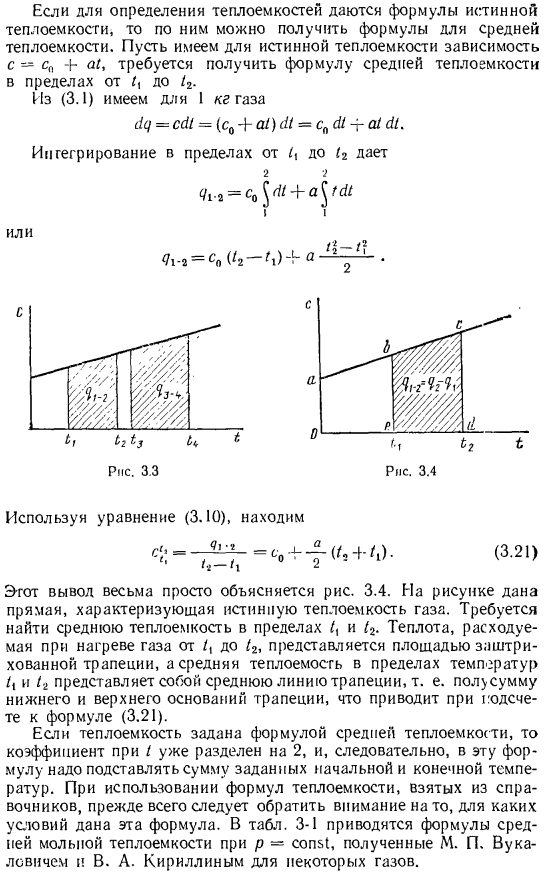
- Трапециевидная заштрихованная область представляет собой расход тепла между нагреванием газа до / ОТ / и 1g-I равен~ / равному. Если дана истинная формула теплоемкости для определения удельной теплоемкости, то из них можно получить формулу для средней удельной теплоемкости. Для истинной теплоемкости предположим, что нужно получить формулу для средней теплоемкости в диапазоне от I до 1 г, так как существует зависимость c-c» 4-a1″. (3.1) до 1 кг газа =сЛ=(с₀+о/)А=с₀4-а/ л Интеграция с меня, чтобы дать Или Рисунок 3.3 рисунок 3.4 (3.21) Используя формулу(3.10)、 Этот вывод объясняется довольно просто цифрой.
Приведена диаграмма Прямая линия, характеризующая истинную теплоемкость газа. Необходимо найти среднюю теплоемкость в I, и/₂. Теплота, потребляемая при нагревании газа от/до/, представлена площадью штрихованной трапеции, а средняя теплоемкость в диапазоне температур 1 г представляет собой сумму трапециевидной средней линии, то есть дна трапеции и половины верхнего дна, и уравнения (3.21). Если удельная теплоемкость задается формулой средней удельной теплоемкости, то коэффициент I уже делится на 2, поэтому в эту формулу необходимо подставить сумму заданных начальных и конечных температур.
Однако чаще известны лишь температура жидкости, омывающей стенку, и коэффициент теплообмена на ее поверхности.
Людмила Фирмаль
При использовании формулы теплоемкости, полученной из эталона, в первую очередь необходимо обратить внимание на условия, при которых эта формула находится given. In стол. 3-1, приведена формула для средней молярной теплоемкости при р = const (для некоторых газов это М. П. Вука-ловец и В. А. Кирилин. 28、97 + 0.002566 / 28.78 + 0.001117 / 29.56 + 0.003404 / 29.06 + 0.002818 / 28.09 + 0.002412 / 32.85+ 0.00544 / 36.05 + 0.0203 / + 0.00000642 / * В таблице приведены последние экспериментальные данные по теплоемкости, полученные спектроскопически. Потому что обработка этих данных в виде выражения дает очень сложный результат.
Расчет теплопотребления с учетом этих данных выглядит следующим образом (рис. 3.4): Если вы знаете только среднюю теплоемкость в диапазоне от 0 до GS, вам нужно найти потребление тепла для нагрева газа от I до ( ₂ ).Поэтому вам нужно найти площадь трапеции LcMr. Эта область представляет собой тепло, затрачиваемое на нагрев газа от 0°до 0°, и тепло, затрачиваемое на нагрев того же газа от 0 ° до/ / C. Таким образом, площадь трапеции ba1eB определяет тепло. от₍к。. Так… Яг-я — н-8-OassU-ЛП. Да. Но… пл. С/гсйО=/?,=с ’,’ / ₄ ; пл. OaBeO = ХХ = с ‘*. Тепло, необходимое для нагрева газа от I до ₂ 7. ; = с ’-/» .- «’ ■ / !•(3.22) В этом выражении/, и / 2 Тепло capacity.
Смотрите также:
- Решение задач по теплотехнике
Зависимость теплоемкости от температуры
По этой ссылке вы найдёте полный курс лекций по математике:
В практике тепловых расчетов широкое применение получила следующая приближенная зависимость истинной удельной теплоемкости от температуры: где а — экспериментальное значение истинной теплоемкости при температуре О °С; b> d> е — постоянные коэффициенты, зависящие от природы рабочего тела, определяемые на основании экспериментальных данных.
Для менее точных расчетов зависимости истинной удельной теплоемкости от температуры применяется уравнение второй степени: Для двухатомных газов часто ограничиваются первыми двумя членами уравнения (3.13): В табл. 3.1 приведены температурные зависимости истинных мольных теплоемкостей при постоянном давлении для некоторых газов. Зная зависимость с = /(f), можно аналитически определить теплоту или удельную теплоту, исходя из определений «»Я?. Q = JCdt, g-Jcdt. Таблица 3.1 Газ „ х кДж
Мольная теплоемкость С„, ——=т Р кмоль•К Азот 28,97 + 0,002566* Водород 28,78 + 0,001117* Кислород 29,56 + 0,003404* Окись углерода 29,06 + 0,002818* Воздух 29,09 + 0,002412* Водяной пар 32,85 + 0,00544* Углекислота 36,05 + 0,0203* — 0,00000642*2 Однако в практических расчетах используется более простой способ, при котором удельная теплота определяется через среднюю удельную теплоемкость процесса ст: В справочной литературе в основном приводятся коэффициенты для истинной удельной или мольной теплоемкости.
Зная их, можно самостоятельно получить выражение для средних теплоемкостей.
На примере линейной зависимости истинной удельной теплоемкости в форме (3.15) для конечного участка процесса 1—2 будем иметь С учетом того что cm = q/{t2 — средняя удельная теплоемкость в зависимости от коэффициентов а и b будет иметь вид Обычно в справочной литературе приведены численные значения средних удельных теплоемкостей от нулевой до фиксированной температуры t. В данном случае средняя удельная теплоемкость в интервале температур от tx до t2 Зависимость с = f(t) может быть дана как функция эмпирической температуры f, так и абсолютной температуры Т.
Зависимость истинной удельной теплоемкости от абсолютной температуры с = f(T) можно получить на примере формулы (3.15). Так как t = Т — 273,15, то с = а + b • (Т — 273,15). Обозначив через а’ — а — Ь* 273,15, получим с = а’ + ЬТ. Тогда в процессе нагрева от Тх до Т2 количество сообщенной ТРТ удельной теплоты может быть подсчитано по уравнению д=[а’+|(Г2 + Т1)](Т2-Т1), а средняя удельная теплоемкость запишется в виде Ряд экспериментальных исследований показал, что с понижением температуры теплоемкость водорода быстро уменьшается и уже при Т = 60 К его мольная теплоемкость становится равной теплоемкости идеального одноатомного газа.
Явление падения теплоемкости с понижением
температуры находится в полном соответствии с положениями молекулярно-кинети-ческой теории теплоемкости. При низких абсолютных температурах прекращаются и вращательные движения молекул, и колебательные движения атомов внутри молекул, а остаются лишь три степени свободы поступательного движения, свойственные молекуле идеального одноатомного газа.
Результатом этого и является приближение теплоемкости всех газов при низких температурах к значению теплоемкости идеального одноатомного газа. В 1906 г. Нернст высказал предположение о том, что при последующем понижении температуры и приближении ее к абсолютному нулю должно прекратиться и поступательное движение молекул и тогда любой газ приобретает свойства твердых тел. Проводя опыты над рядом твердых тел вблизи абсолютного нуля, Нернст показал, что теплоемкости твердых тел стремятся к нулю при Т 0 К, а для всех твердых тел при температуре Т — 0 К теплоемкости равны нулю.
Возможно вам будут полезны данные страницы:
Иными словами, при Т = 0 К частицы вещества (молекулы) превращаются в жесткую систему, лишенную тепловых движений. Из этого следует, что эмпирическая зависимость теплоемкости от температуры в виде уравнения (3.18) является справедливой только в области высоких температур и совершенно недействительна в области низких абсолютных температур. Истинный характер изменения теплоемкости от температуры показан на рис. 3.2.