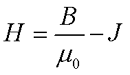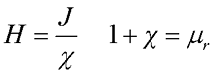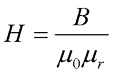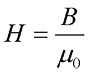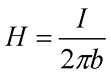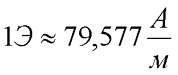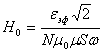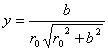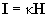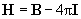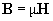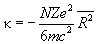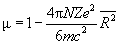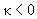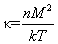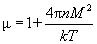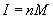Магнитное поле играет очень большую роль в электротехнике и электронике. Без магнитного поля не функционировали бы герконы, электромагнитные реле, соленоиды, катушки индуктивности, дроссели, трансформаторы, двигатели, динамики, генераторы электрической энергии да и вообще много чего.
Природа магнетизма
Согласно одной из легенд, когда-то давным-давно жил в Греции пастух по имени Магнес. И вот шел он как-то со своим стадом овец, присел на камень и обнаружил, что конец его посоха, сделанный из железа, стал притягиваться к этому камню. С тех пор стали называть этот камень магнетит в честь Магнеса. Этот камень представляет из себя оксид железа.
Если такой камень положить на деревянную доску на воду или подвесить на нитке, то он всегда выстраивался в определенном положении. Один его конец всегда показывал на СЕВЕР, а другой — на ЮГ.
Этим свойством камня пользовались древние цивилизации. Поэтому, это был своего рода первый компас. Потом уже стали обтачивать такой камень и делать из разные фигурки. Например, так выглядел китайский древний компас, ложка которого была сделана из того самого магнетита. Ручка у этой ложки всегда показывала на ЮГ.
Ну а далее дело шло за практичностью и маленькими габаритами. Из магнетита вытачивали маленькие стрелки, которые подвешивали на тонкую иглу посередине. Так стали появляться первые малогабаритные компасы.
Древние цивилизации, конечно, не знали еще что такое север и юг. Поэтому, одну сторону магнетита они назвали северным полюсом (North), а противоположный конец — южным (South). Названия на английском очень легко запомнить, если кто смотрел американский мультфильм «Южный парк», он же Сауз (South) парк).
Магнитные линии и магнитный поток
Вокруг магнита экспериментальным путем были обнаружены магнитные силовые линии. Эти магнитные линии создают так называемое магнитное поле.
Как вы могли заметить на рисунке, концентрация магнитных силовых линий на самых краях магнита намного больше, чем в его середине. Это говорит о том, что магнитное поле является более сильным именно на краях магнита, а в его середине практически равна нулю. Направлением магнитных силовых линий считается направление от севера к югу.
Ошибочно считать, что магнитные силовые линии начинают свое движение от северного полюса и заканчивают свой век на южном. Это не так. Магнитные линии — они замкнуты и непрерывны. В магните это будет выглядеть примерно так.
Если приблизить два разноименных полюса, то произойдет притягивание магнитов
Если же приблизить одноименными полюсами, то произойдет их отталкивание
Итак, ниже важные свойства магнитных силовых линий.
- Магнитные линии не поддаются гравитации.
- Никогда не пересекаются между собой.
- Всегда образуют замкнутые петли.
- Имеют определенное направление с севера на юг.
- Чем больше концентрация силовых линий, тем сильнее магнитное поле.
- Слабая концентрация силовых линий указывает на слабое магнитное поле.
Магнитные силовые линии, которые образуют магнитное поле, называют также магнитным потоком.
Итак, давайте рассмотрим два рисунка и ответим себе на вопрос, где плотность магнитного потока будет больше? На рисунке «а» или на рисунке «б»?
Видим, что на рисунке «а» мало силовых магнитных линий, а на рисунке «б» их концентрация намного больше. Отсюда можно сделать вывод, что плотность магнитного потока на рисунке «б» больше, чем на рисунке «а».
В физике формула магнитного потока записывается как
где
Ф — магнитный поток, Вебер
В — плотность магнитного потока, Тесла
а — угол между перпендикуляром n (чаще его зовут нормалью) и плоскостью S, в градусах
S — площадь, через которую проходит магнитный поток, м2
Что же такое 1 Вебер? Один вебер — это магнитный поток, который создается полем индукцией 1 Тесла через площадку 1м2 расположенной перпендикулярно направлению магнитного поля.
Напряженность магнитного поля
Формула напряженности
Слышали ли вы когда-нибудь такое выражение: «напряженность между ними все росла и росла». То есть по сути напряженность — это что-то невидимое, какая-то сдерживающая сила, энергия. Здесь почти все то же самое. Напряженностью магнитного поля также часто называют силой магнитного поля. Напряженность магнитного поля напрямую зависит от плотности магнитного потока и выражается формулой
где
H — напряженность магнитного поля, Ампер/метр
B — плотность магнитного потока, Тесла
μ0 — магнитная постоянная = 4π × 10-7 Генри/метр или если написать по человечески 1,2566 × 10-6 Генри/метр.
PS.
Эта формула работает только тогда, когда между витками катушки находится воздух, либо вакуум. Более крутая формула выглядит вот так.
где
μ — это относительная магнитная проницаемость.
У разных веществ она разная
Напряженность магнитного поля проводника с током
Итак, имеем какой-либо проводник, по которому течет электрический ток.
Для того, чтобы вычислить напряженность магнитного поля на каком-то расстоянии от проводника при условии, что проводник находится в воздушном пространстве либо в вакууме, достаточно воспользоваться формулой
где
H — напряженность магнитного поля, Ампер/метр
I — сила тока, текущая через проводник, Ампер
r — расстояние до точки, в которой измеряется напряженность, метр
Магнитное поле проводника с током
Оказывается, если через какой-либо проводник пропустить электрический ток, то вокруг проводника образуется магнитное поле.
Здесь можно вспомнить знаменитое правило буравчика, но для наглядности я лучше буду использовать правило самореза, так как почти все хоть раз в жизни ввинчивали либо болт, либо саморез.
Ввинчиваем по часовой стрелке — саморез идет вниз. В нашем случае он показывает направление электрического тока. Движение наших рук показывает направление линий магнитного поля. Все то же самое, когда мы начинаем откручивать саморез. Он начинает вылазить вверх, то есть в нашем случае показывает направление электрического тока, а наша рука в этом время рисует в воздухе направление линий магнитного поля.
Также часто в учебниках физики можно увидеть, что направление электрического тока от нас рисуют кружочком с крестиком, а к нам — кружочком с точкой. В этом случае опять представляем себе саморез и уже в голове увидим направление магнитного поля.
Как думаете, что будет если мы сделаем вот такую петельку из провода? Что изменится в этом случае?
Давайте же рассмотрим этот случай более подробно. Так в этой плоскости оба проводника создают магнитное поле, то по идее они должны отталкиваться друг от друга. Но если они хорошо закреплены, то начинается самое интересное. Давайте рассмотрим вид сверху, как это выглядит.
Как вы можете заметить, в области, где суммируются магнитные силовые линии плотность магнитного потока прям зашкаливает.
Соленоид
А что если сделать много-много таких петелек? Взять какую-нибудь круглую бобину, намотать на нее провод и потом убрать бобину. У нас должно получится что-то типа этого.
Если подать постоянное напряжение на такую катушку, магнитные силовые линии будут выглядеть вот так.
Вы только посмотрите, какая бешеная плотность магнитного потока внутри такой катушки! Получается, что от каждой петельки магнитное поле суммируется, что в итоге дает такую плотность магнитного потока. Такую катушку также называют катушкой индуктивности или соленоидом.
Вот также схема, показывающая как магнитные силовые линии складываются в соленоиде.
Плотность магнитного потока зависит от того, какая сила тока проходит через соленоид. Чтобы увеличить плотность магнитного потока, достаточно поверх витков намотать еще больше витков и вставить сердечник из специального материала — феррита.
Если в электрических цепях есть такое понятие, как ЭДС — электродвижущая сила, то и в магнитных цепях есть свой аналог — МДС — магнитодвижущая сила. Магнитодвижущая сила выражается в виде тока, протекающего через катушку из N витков и выражается в Амперах-витках.
где
I — это сила тока в катушке, Амперы
N — количество витков катушки, штуки)
Также советую посмотреть очень простое и интересное видео про магнитное поле.
Похожие статьи по теме «магнитное поле»
Катушка индуктивности
Трансформатор
Электромагнитное реле
В этой статье мы собираемся обсудить 9 фактов, связанных с магнитным полем и расстоянием.
Перейдем к соотношению между магнитное поле и расстояние. По сути, возникает очень важный закон, известный как закон обратных квадратов. Магнитные монополи и диполи показывают ту же зависимость между магнитным полем и расстоянием, что и напряженность магнитного поля обычно увеличивается, когда расстояние между полем и источником уменьшается.
Будь то магнитный монополь или диполь, магнитное поле всегда изменяется обратно пропорционально кубу расстояния. Предположим, что магнитное поле равно B, а расстояние равно R, тогда соотношение между ними таково: B ∝ 1/R³ Очень просто мы можем описать это с помощью примера.
Возьмем магнит. Его поле на расстоянии 1 м равно B. Таким образом, его магнитное поле на расстоянии 3 м составляет 1/27 от предыдущего значения B. Следовательно, значение магнитного поля на расстоянии 3 м упадет до B/27 [поскольку значение магнитного поля убывает как куб расстояния]. Для некоторых специальных магнитов магнитное поле спадает быстрее, чем это, но для большинства магнитов магнитное поле изменяется обратно пропорционально кубу расстояния.
Как расстояние влияет на магнитную силу?
Простыми словами можно сказать, что если приблизить друг к другу два одинаковых полюса двух магнитов, то сила отталкивания между ними будет становиться все сильнее. Точно так же сила притяжения между двумя полюсами станет сильнее, если два противоположных полюса двух магнитов приблизить друг к другу.
В чем причина этого? Причина в том, что магнитная сила изменяется обратно пропорционально расстоянию между двумя магнитами. Всякий раз, когда они приближаются друг к другу, магнитная сила становится очень сильной, поскольку расстояние меньше. И наоборот, всякий раз, когда они находятся далеко друг от друга, магнитная сила становится очень меньше по мере увеличения расстояния.
Магнитная сила очень похожа на кулоновскую силу. Мы знаем, что в случае кулоновской силы сила изменяется обратно пропорционально квадрату расстояния, точно так же магнитная сила также изменяется обратно пропорционально квадрату расстояния. Если F — магнитная сила, а R — расстояние от источника, то F ∝ 1/R².
Магнитная сила станет F1 ∝ 1/(2R)², когда расстояние между двумя магнитами станет вдвое больше предыдущего значения, т. е. здесь можно сделать вывод о 2R.
⇒F1 ∝ 1/4R²
Это означает, что магнитная сила стала в 3/2 раза меньше предыдущего значения. Когда расстояние между двумя магнитами станет в три раза больше предыдущего расстояния R, то есть 1R, магнитная сила станет F3∝ XNUMX/(XNUMXR)².
⇒F2 ∝ 1/9R²
Это означает, что магнитная сила стала на 1/9 меньше предыдущей.
Если расстояние стало в пять раз больше предыдущего значения R, т. е. 5R, магнитная сила станет F3 ∝ 1/(5R)².
⇒ F3 ∝ 1/25R²
Это означает, что магнитная сила стала на 1/25 меньше предыдущей.
Какая связь между магнитным полем и расстоянием?
Между магнитным полем и расстоянием существует обратная зависимость. Итак, всякий раз, когда мы уходим далеко от магнита, неизбежно происходит изменение магнитного эффекта или, точнее, магнитного поля, оно уменьшается. Точно так же, когда мы приближаемся к магниту, магнитное поле увеличивается.
Если взять в качестве примера провод, то сила магнитного поля будет падать с увеличением расстояния. В этой статье мы приведем несколько примеров того, как магнитные поля меняются с расстоянием для разных проводников с током. Они есть-
- Бесконечно длинный провод
- соленоид
- тороид
- Круговая петля или катушка с током
1. Бесконечно длинный провод
В случае бесконечно длинного провода с током, если магнит находится на расстоянии R от длинного провода с током, то B = µ₀I/2πR, где µ0 — магнитная проницаемость в свободном пространстве, значение которой равно 4π x 10⁻⁷ Hm. что магнитное поле для бесконечно длинного провода с током обратно пропорционально расстоянию R, B ∝ 1/R.
2. Соленоид
В случае длинного соленоида с током напряженность магнитного поля не зависит от расстояния соленоида от оси. Это зависит только от тока, протекающего через соленоид (I), и количества витков (N) вокруг соленоида. Магнитное поле, B = µ0нИ. Это означает, что магнитное поле B пропорционально току I, B = µ0nI, где n= N/L, L — длина соленоида.
Мы использовали для вычисления значения магнитного поля соленоида с помощью закона замыкания Ампера, т. е. ∲B.dl = µ0NI
Или B∲dl = µ0NI
Или BL = µ0NI, где ∲dl = L = длина соленоида
Или B = µ0NI/L = мк0nI, где n=N/L
3. Тороид
В случае тороида, поскольку количество витков вокруг тороида, находящихся снаружи, равно нулю, следовательно, математическая формула для магнитного поля принимает вид B = µ0nI = 0. Точно так же количество витков внутри тороида также равно нулю, следовательно, магнитное поле тороида внутри него также равно нулю. Расстояние и в этом случае не влияет на поле.
4. Круговая петля или катушка с током
Магнитное поле круглой катушки с током зависит от расстояния катушки от оси (x), а также от значения радиуса круглой катушки (R). Математическое выражение магнитного поля B: B = µ0NI/2 x R²/(√(R + x))³
Как рассчитать магнитное поле на расстоянии?
Сначала мы можем взять пример с тороидом. Мы уже знаем, что с помощью закона Ампера можно вычислить величину магнитного поля тороида внутри и вне его. Согласно закону цепи Ампера ∲B.dl = µ0NI
Или B∲dl = µ0NI
Или B.(2πR) = µ0NI
Или B = µ0NI/2πR, где ∲dl = 2πR, а R — радиус тороида. Внутри тороида и вне тороида число витков равно нулю, следовательно, магнитное поле также равно нулю.
Для длинного соленоида значение магнитного поля соленоида мы рассчитывали с помощью закона замыкания Ампера, т. е. ∲B.dl = µ0NI
Или B∲dl = µ0NI
Или BL = µ0NI, где ∲dl = L = длина соленоида
Или B = µ0NI/L = мк0nI где n(количество витков на единицу длины соленоида)=N/L ,L — длина соленоида N — число витков соленоида.
Магнитное поле обратно пропорционально расстоянию?
Здесь мы обсудим, почему, как и когда магнитное поле становится обратно пропорциональным расстоянию. Здесь будут получены случаи, когда магнитное поле обратно пропорционально расстоянию.
Мы должны взять здесь пример бесконечно длинного провода с током. Представим себе амперную петлю, т. е. круг вокруг провода. Радиус окружности равен R, а расстояние между воображаемой окружностью и бесконечно длинным проводом равно r. Мы рассчитаем магнитное поле для двух областей. В одном случае r > R, а в другом r < R.
Случай I
(г>р)
Согласно закону цепи Ампера, ∲B.dl = µ0I
Здесь B∲dl= µ0I
Или B.(2πr) = µ0где ∲dl = 2πr
Или B = µ0I/2πr, где I — ток в контуре. Следовательно, B ∝ 1/r (r > R) означает, что магнитное поле обратно пропорционально расстоянию r.
Случай II
( г < р )
Здесь амперианская петля взята внутрь. Следовательно, значение вложенного тока стало Ien. следовательно, яen = I.(πr²/πR²)= Ir²/R²
Согласно закону цепи ампера ∲B.dl = µ0Ien
Или B.(2πr) = µ0.Ir²/R²
Или B = µ0.Ir/2πR² (r
В этом случае магнитное поле B пропорционально расстоянию r, т. е. B ∝ r.
Насколько магнитное поле уменьшается с расстоянием?
Мы возьмем здесь пример катушки с током, радиус которой равен R, чтобы показать, насколько магнитное поле уменьшается с расстоянием. магнитное поле этой катушки с током равно B = µ0NI/2 x R²/(√(R² + x²))³, где x — расстояние между катушкой и точкой, магнитное поле которой будет рассчитываться.
Если расстояние x равно нулю, то магнитное поле становится равным B = µ0NI/2R т. е. магнитное поле обратно пропорционально расстоянию R в центре катушки. Теперь, используя эту формулу, мы сможем показать, насколько магнитное поле уменьшается с расстоянием. B ∝ 1/R, когда расстояние R становится вдвое больше предыдущего значения, равного 2R, тогда магнитное поле B становится равным ½ своего предыдущего значения, равного B/2.
Точно так же, когда R в четыре раза превышает предыдущее значение, равное 4R, тогда магнитное поле B становится на 4/XNUMX своего предыдущего значения, равного B/XNUMX.
Если расстояние R станет половиной своего предыдущего значения, равного R/2, то магнитное поле B станет вдвое больше своего предыдущего значения, равного 2B, а если расстояние R станет одной трети своего предыдущего значения, равного R/3, то магнитное поле B становится в три раза больше своего предыдущего значения, равного 3B.
Как изменится магнитное поле при увеличении расстояния между катушками?
Возьмем пару катушек. Один между ними неподвижен, а другой движется. Магнитный поток, связанный с неподвижной катушкой, будет уменьшаться, если расстояние между подвижной катушкой и неподвижной катушкой увеличивается. Точно так же магнитный поток, который связан с неподвижной катушкой, будет увеличиваться, если расстояние между движущейся катушкой и неподвижной катушкой уменьшается.
Как мы знаем, магнитный поток Φ = BA, где B — магнитное поле катушки. Следовательно, Φ ∝ B. Это означает, что когда расстояние между двумя катушками увеличивается, магнитное поле также уменьшается, тогда как магнитное поле увеличивается, когда расстояние между двумя катушками уменьшается.
Этот магнитный поток Φ также связан с взаимной индуктивностью M пары катушек. Φ= MI, где I — ток, протекающий через катушки. Таким образом, когда расстояние между двумя катушками увеличивается, взаимная индуктивность уменьшается, а когда расстояние между двумя катушками уменьшается, взаимная индуктивность увеличивается, поскольку взаимная индуктивность пропорциональна магнитному потоку.
Как найти ток с магнитным полем и расстоянием?
Возьмем один пример бесконечно длинного проводника с током. Математическое выражение магнитного поля: B = µ0I/2πR. Значение тока, протекающего через этот проводник, можно рассчитать по этой математической формуле.
I = 2πR.B/µ0.
Рассчитаем текущее значение математической задачи.
Напряженность магнитного поля бесконечно длинного провода равна 4 х 10-4 Т. Чему будет равна сила тока, если это поле перпендикулярно расстоянию 0.08 м?[ µ0= 4π х 10-7 Тм/А].
Ответ
В = 4 х 10-4 T
R = 0.08 м
µ0= 4π х 10-7 Тм/А
я =?
ток, I = 2πR.B/µ₀ = (2 x π x 0.08 x 4 x 10-4)/4π х 10-7
= 160 А
Таким образом, мы можем рассчитать значение тока, используя математические выражения магнитных полей соленоидов, тороидов, токов, несущих круговые петли и т. д.
Заключение
В этой статье мы обсудили связь между магнитным полем и расстоянием, а также связь между магнитной силой и расстоянием. Кроме того, также обсуждается, насколько магнитное поле изменяется с расстоянием.
Всем доброго времени суток. В прошлой статье я рассказывал о основной характеристике магнитного поля – магнитной индукции, однако приведённые расчётные формулы соответствуют магнитному полю в вакууме. Что в практической деятельности встречается довольно редко. Когда проводники с током находятся в какой–либо среде, даже в воздухе, магнитное поле, которое они создают, претерпевает некоторые, а иногда и существенные изменения. Какие изменения происходят с магнитным полем, и от чего это зависит, я расскажу в данной статье.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Как связана индукция и напряженность магнитного поля?
Магнетиком называется вещество, которое под действием магнитного поля способно намагничиваться (или как говорят физики приобретать магнитный момент). Магнетиками являются практически все вещества. Намагничивание веществ объясняется тем, что в веществах присутствуют свои собственные микроскопические магнитные поля, которые создаются вращением электронов по своим орбитам. Когда внешнее магнитное поле отсутствует, то микроскопические поля расположены произвольным образом, а под воздействием внешнего магнитного поля соответствующим образом ориентируются.
Для характеристики намагничивания различных веществ используют так называемый вектор намагничивания J.
Таким образом, под действием внешнего магнитного поля с магнитной индукцией В0, магнетик намагничивается и создает свое магнитное поле с магнитной индукцией В’. В итоге общая индукция В будет состоять из двух слагаемых
Тут возникает проблема вычисления магнитной индукции намагниченного вещества В’, для решения которой необходимо считать электронные микротоки всего вещества, что практически нереально.
Альтернативой данного решения есть ввод вспомогательных параметров, а именно напряженность магнитного поля Н и магнитная восприимчивость χ. Напряженность связывает магнитную индукцию В и намагничивание вещества J следующим выражением
где В – магнитная индукция,
μ0 – магнитная постоянная, μ0 = 4π*10-7 Гн/м.
В то же время вектор намагничивания J связан с напряженность магнитного поля В параметром, характеризующим магнитные свойства вещества и называемым магнитной восприимчивостью χ
где J – вектор намагничивания вещества,
μr – относительная магнитная проницаемость вещества.
Однако наиболее часто для характеристики магнитных свойств веществ используют относительную магнитную проницаемость μr.
Таким образом, связь между напряженностью и магнитной индукцией будет иметь следующий вид
где μ0 – магнитная постоянная, μ0 = 4π*10-7 Гн/м,
μr – относительная магнитная проницаемость вещества.
Так как намагничивание вакуума равна нулю (J = 0), то напряженность магнитного поля в вакууме будет равна
Отсюда можно вывести выражения напряженности для магнитного поля, создаваемого прямым проводом с током:
где I – ток протекающий по проводнику,
b – расстояние от центра провода до точки, в которой считается напряженность магнитного поля.
Как видно из данного выражения единицей измерения напряженности является ампер на метр (А/м) или эрстед (Э)
Таким образом, магнитная индукция В и напряженность Н являются основными характеристиками магнитного поля, а магнитная проницаемость μr – магнитной характеристикой вещества.
Намагничивание ферромагнетиков
В зависимости от магнитных свойств, то есть способности намагничиваться под действием внешнего магнитного поля, все вещества делятся на несколько классов. Которые характеризуются разной величиной относительной магнитной проницаемости μr и магнитной восприимчивости χ. Большинство веществ являются диамагнетиками (χ = -10-8 … -10-7 и μr < 1) и парамагнетиками (χ = 10-7 … 10-6 и μr > 1), несколько реже встречаются ферромагнетики (χ = 103 … 105 и μr >> 1). Кроме данных классов магнетиков существует ещё несколько классов магнетиков: антиферромагнетики, ферримагнетики и другие, однако их свойства проявляются только при определённых условиях.
Особый интерес в радиоэлектронике ферромагнитные вещества. Основным отличием данного класса веществ является нелинейная зависимость намагничивания, в отличие от пара- и диамагнетиков, имеющих линейную зависимость намагничивания J от напряженности Н магнитного поля.
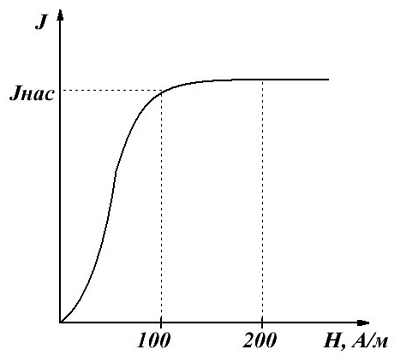
Зависимость намагничивания J ферромагнетика от напряженности Н магнитного поля.
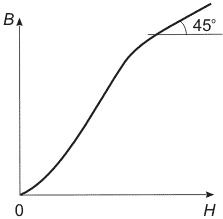
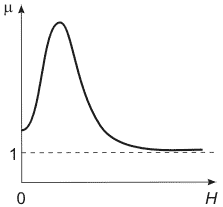
На данном графике показана основная кривая намагничивания ферромагнетика. Изначально намагниченность J, в отсутствие магнитного поля (Н = 0), равна нулю. По мере возрастания напряженности намагничивание ферромагнетика проходит довольно интенсивно, вследствие того что его магнитная восприимчивость и проницаемость очень велика. Однако по достижении напряженности магнитного поля порядка H ≈ 100 А/м увеличение намагниченности прекращается, так как достигается точка насыщения JНАС. Данное явление называется магнитным насыщением. В данном режиме магнитная проницаемость ферромагнетиков сильно падает и при дальнейшем увеличении напряженности магнитного поля стремится к единице.
Гистерезис ферромагнетиков
Еще одной особенностью ферромагнетиков является наличие петли гистерезиса, которая является основополагающим свойством ферромагнетиков.
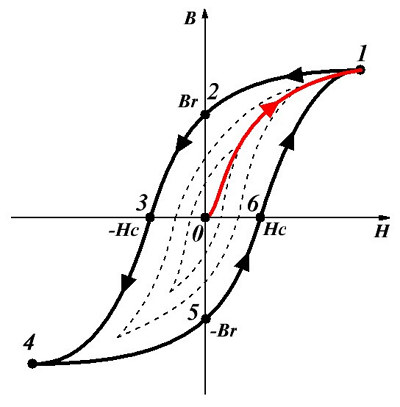
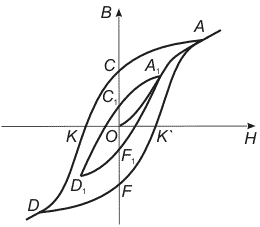
Петля гистерезиса ферромагнетика.
Для понимания процесса намагничивания ферромагнетика изобразим зависимость индукции В от напряженности Н магнитного поля, где красным цветом выделим основную кривую намагничивания. Данная зависимость довольно неопределенна, так как зависит от предыдущего намагничивания ферромагнетика.
Возьмём образец ферромагнитного вещества, которое не подвергалось намагничиванию (точка 0) и поместим его в магнитное поле, напряженность Н которого начнем увеличивать, то есть зависимость будет соответствовать кривой 0 – 1, пока не будет достигнуто магнитное насыщение (точка 1). Дальнейшее увеличение напряженности не имеет смысла, потому как намагниченность J практически не увеличивается, а магнитная индукция увеличивается пропорционально напряженности Н. Если же начинать уменьшать напряженность, то зависимость В(Н) будет соответствовать кривой 1 – 2 – 3, при этом когда напряженность магнитного поля упадёт до нуля (точка 2), то магнитная индукция не упадёт до нуля, а будет равна некоторому значению Br, которое называется остаточной индукцией, а намагничивание будет иметь значение Jr, называемое остаточным намагничиванием.
Для того чтобы снять остаточное намагничивание и уменьшить остаточную индукцию Br до нуля, необходимо создать магнитное поле, противоположное полю, вызвавшему намагничивание, причем напряженность размагничивающего поля должна составлять Нс, называемая коэрцитивной силой. При дальнейшем росте напряженности магнитного поля, которое противоположно первоначальному полю, происходит насыщение ферромагнетика (точка 4).
Таким образом, при действии на ферромагнетик переменного магнитного поля зависимость индукции от напряженности будет соответствовать кривой 1 – 2 – 3 – 4 – 5 – 6 – 1, которая называется петлёй гистерезиса. Таких петель для ферромагнетика может быть множество (пунктирные кривые), называемые частными циклами. Однако, если при максимальных значениях напряженности магнитного поля происходит насыщение, то получается максимальная петля гистерезиса (сплошная кривая).
Так как магнитная проницаемость μr ферромагнетиков имеет довольно сложную зависимость от напряженности магнитного поля, поэтому нормируются два параметра магнитной проницаемости:
μн – начальная магнитная проницаемость соответствует напряженности Н = 0;
μmax – максимальная магнитная проницаемость достигается в магнитном поле при приближении магнитного насыщения.
Таким образом, у ферромагнетиков величины Br, Нс и μн (μmax) являются основными характеристиками, влияющими на выбор вещества в конкретном случае.
(3)
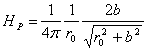
Для исследования зависимости напряженности
магнитного поля прямолинейного тока от расстояния до проводника применяется
следующий метод. Прямоугольная, вытянутая по вертикали рамка ABCD
(рис.3) присоединяется к генератору переменной ЭДС. По рамке течет переменный
ток, изменяющийся с течением времени t, следующим образом:
,
где 
— амплитудное
(максимальное) значение тока в цепи; 
— угловая частота
переменного тока.
Вокруг проводника
создается переменное магнитное поле напряженностью
,
где 
— амплитудное
значение напряженности.
Маленькая плоская катушка- это индукционный
датчик (ИД), содержащий N витков, помещается в точку Р
поля так, чтобы ее центр совпал с этой точкой. По законам электромагнитной
индукции в катушке возникает ЭДС
;
где Ф- магнитный поток, пронизывающий каждый поток
катушки. Известно, что
,
где 
— магнитная
постоянная; 
— магнитная проницаемость среды, в
которой создано магнитное поле, в нашем случае 
,
т.к. поле создано в воздухе; S- площадь измерительной
катушки ИД. Поэтому можно записать
(4)
Обозначив
, (5)
получим
(6)
Равенство (5) показывает, что 
пропорционально
. Следовательно, рассчитав , можно рассчитать значение в любой точке поля. Т.к. 
(здесь 
-действующее
значение ЭДС), то
(7)
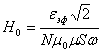
Схема установки
Рис.3
Расчетные формулы
где d-ширина
участка АВ рамки.
Формула погрешности
=
Таблица измерений
|
|
|
|
|
|
|
|
H |
|
1 |
0.01 |
0.01 |
0.001 |
0.110 |
0.005 |
95 |
11* |
|
3 |
0.02 |
0.072 |
48 |
7.0* |
|||
|
5 |
0.03 |
0.054 |
32 |
5.2* |
|||
|
7 |
0.04 |
0.046 |
24 |
4.5* |
|||
|
9 |
0.05 |
0.032 |
19 |
3.1* |
|||
|
11 |
0.06 |
0.026 |
15 |
2.5* |
|||
|
13 |
0.07 |
0.023 |
13 |
2.2* |
|||
|
15 |
0.08 |
0.020 |
11 |
1.9* |
|||
|
17 |
0.09 |
0.018 |
9 |
1.8* |
|||
|
19 |
0.10 |
0.017 |
8 |
1.7* |
|||
|
21 |
0.11 |
0.016 |
7 |
1.5* |
|||
|
23 |
0.12 |
0.016 |
6 |
1.5* |
|||
|
25 |
0.13 |
0.015 |
6 |
1.4* |
|||
|
27 |
0.14 |
0.014 |
5 |
1.4* |
|||
|
29 |
0.15 |
0.014 |
4 |
1.3* |
Атомно-силовой микроскоп может использоваться для исследования магнитных полей на поверхности образца. Такие методики объединяются под названием МСМ (магнитно-силовая микроскопия). В них используются специальные кантилеверы, которые покрыты магнитной пленкой. При взаимодействии с магнитным полем образца такой кантилевер отклоняется. Могут существовать следующие типы кантилеверов: диамагнитные, парамагнитные [1], суперпарамагнитные [2] и ферромагнитные (магнитожесткие [3] и магнитомягкие [4]).
Здесь мы кратко напомним об этих трех типах магнетиков, рассмотрев диамагнетизм, парамагнетизм и ферромагнетизм на феноменологическом уровне. Заинтересованных же отошлем к более серьезной литературе, например, [5, 6, 7].
Магнитные свойства вещества описываются вектором намагниченности
. Его связь с напряженностью магнитного поля
задается формулой [8,9]:
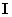
(1)
где
– магнитная восприимчивость вещества. В свою очередь, напряженность магнитного поля связана с вектором магнитной индукции
и вектором намагничивания следующим образом:
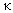
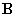
(2)
Подставляя (1) в (2), получим:
(3)
где
– магнитная проницаемость вещества. Таким образом, магнитные свойства вещества описываются одним независимым параметром –
или
.
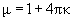
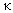
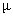
Диа- и парамагнетизм.
Атомы многих веществ не имеют постоянных магнитных моментов, или, вернее, все спиновые и орбитальные магнитные моменты внутри атома уравновешены так, что суммарный магнитный момент равен нулю. Если наложить магнитное поле, то внутри атома будут генерироваться слабые дополнительные токи. В соответствии с законом Ленца они будут индицироваться так, чтобы уменьшить магнитное поле, и наведенный магнитный момент атомов направлен навстречу магнитному полю. Таков механизм диамагнетизма.
Магнитная восприимчивость и магнитная проницаемость для диамагнетиков:
(4)
(5)
где
– число атомов в единице объема,
– число электронов в атоме,
и
– заряд и масса электрона,
– скорость света,
– средний квадрат расстояния электрона до ядра. Энергия теплового движения слишком мала, чтобы изменить внутреннее (квантованное) состояние атома. Поэтому для диамагнетиков
и
не должны зависеть от температуры. Обратим внимание, что
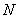
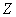
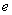
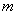
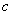
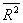
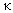
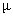
и, тем самым,
.
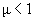
К диамагнетикам относятся, например, кислород, алюминий, платина, хлористое железо –
, благородные газы и т.д.
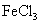
Однако существуют такие вещества, атомы которых обладают магнитным моментом, спиновым или орбитальным. Таким образом, кроме диамагнитного эффекта (а он всегда присутствует) есть возможность выстраивания индивидуальных атомных моментов в одном направлении. Магнитные моменты ориентируются в направлении магнитного поля, усиливая его.
Парамагнетизм, вообще говоря, довольно слаб, потому что выстраивающие силы относительно малы по сравнению с силами теплового движения, которые стараются разрушить упорядочивание. Отсюда следует, что парамагнетизм особо чувствителен к температуре. Эффект парамагнетизма тем сильнее, чем ниже температура.
Пусть
– магнитный момент атома,
– магнитная индукция,
– число атомов в единице объема,
– константа Больцмана,
– температура. Тогда для парамагнетиков в слабых полях –
, когда зависимость вектора намагничивания от напряженности магнитного поля линейна, магнитная восприимчивость и магнитная проницаемость равны:
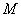
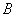
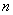
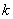
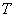
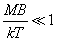
(6)
(7)
Обратно пропорциональная зависимость восприимчивости от абсолютной температуры (6) носит название закона Кюри. Заметим, что для парамагнетиков
и, тем самым,
.
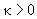
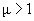
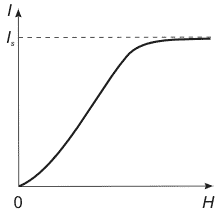
В сильных полях намагничивание приходит в состояние насыщение, когда все магнитные моменты устанавливаются параллельно полю:
(8)
Так как диамагнетизм проявляется во всех веществах, он частично или полностью компенсирует парамагнетизм за счет противоположного по знаку вклада в восприимчивость. Поэтому для материалов с атомами, имеющими магнитный момент, можно говорить лишь о преобладании диа- или парамагнитных свойств в веществе, причем их баланс зависит от температуры. К парамагнетикам относятся, например, азот, углекислота, вода, серебро, висмут и т.д.
Ферромагнетизм.
В ферромагнетиках эффект упорядочения магнитных моментов проявляется во много раз сильнее, чем в диа- и парамагнетиках. Ферромагнетизм определяется коллективным взаимодействием атомных магнитных моментов, находящимися в состоянии с нарушенной симметрией (фазовый переход второго рода) и образующих магнитные домены. Ферромагнетиками называются тела, которые могут обладать спонтанной намагниченностью, то есть намагничены уже в отсутствие магнитного поля. Типичными представителями ферромагнетиков являются переходные металлы: железо, кобальт, никель и многие их сплавы. Ферромагнетизмом обладают некоторые редкоземельные элементы (гадолиний, тербий, диспрозий, гольмий, эрбий, туллий).
Характерной особенностью ферромагнетиков является сложная нелинейная зависимость между
и
или между
и
. Характер этой зависимости представлен на рис. 1 и 2.
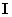
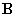
Рис. 1. Зависимость намагничивания от
напряженности магнитного поля.
Рис. 2. Зависимость магнитной индукции от
напряженности магнитного поля.
По мере возрастания
намагниченность
сначала быстро увеличивается, а затем приходит к насыщению и остается практически постоянной:
(насыщение), то есть кривая
переходит в горизонтальную прямую. Магнитная индукция
также растет с увеличением поля
, а в состоянии насыщения
, то есть кривая
переходит в прямую, наклоненную под углом
(если
и
откладывать на осях координат в одинаковом масштабе).
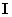
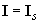
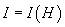
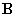
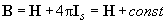
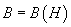
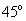
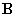
Магнитная восприимчивость
и магнитная проницаемость
уже зависят не только от свойств вещества и температуры, как у диа- и парамагнетиков, а являются функциями напряженности поля
и, более того, определяется его историей.
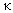
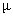
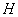
Восприимчивость и проницаемость сначала возрастают с
, затем проходят через максимум, и, наконец, в сильных полях, когда достигнуто насыщение,
стремится к единице (рис.3), а
– к нулю.
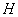
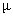
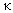
Рис. 3. Зависимость магнитной восприимчивости от напряженности магнитного поля.
Значения
в максимуме у большинства ферромагнетиков при обычных температурах составляют многие сотни и тысячи единиц.
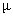
Вторая характерная особенность ферромагнетиков состоит в том, что для них зависимость
от
или
от
не однозначна, а определяется предшествующей историей намагничивания ферромагнитного образца. Это явление называется магнитным гистерезисом. Изображенная на рисунке 4 замкнутая кривая
называется петлей гистерезиса, а кривая
– предельной (наибольшей) петлей гистерезиса.
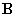
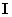
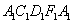
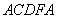
Рис. 4. Петля гистерезиса.
При
индукция
не обращается в нуль, а изображается отрезком
. Ему соответствует остаточное намагничивание
. С наличием такого остаточного намагничивания связано существование постоянных магнитов. Для того, чтобы размагнитить образец, надо довести кривую размагничивания до точки
или
. Этим точкам соответствует магнитное поле
. Оно называется коэрцитивной силой ферромагнетика. Значения остаточного намагничивания и коэрцитивной силы для разных ферромагнетиков меняются в широких пределах. Для мягкого железа петля гистерезиса узкая (коэрцитивная сила мала), для стали и всех материалов, идущих на изготовление магнитов, – широкая (коэрцитивная сила велика). Например, для кобальта и его сплавов, которые используются для покрытия магнитожестких кантилеверов, характерная величина коэрцитивной силы составляет 400 эрстед. С другой стороны, магнитное поле зонда в целом ряде случаев может оказаться слишком большим, что может приводить к искажению или даже разрушению исследуемой магнитной структуры. Для этих целей используют зонды с покрытием
–
. Совершенно такой же характер имеет петля гистерезиса, когда по вертикальной оси откладывается не индукция
, а намагничивание
.
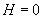
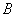
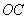
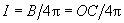
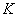
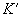
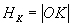
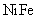
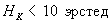
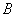
Выводы.
- Вещества по их поведению в магнитном поле подразделяют на три основных типа: диамагнитные, парамагнитные и ферромагнитные.
- Диамагнитные свойства проявляют все вещества. Суть эффекта – в возникновении индуцированных внутриатомных токов, которые уменьшают индукцию магнитного поля в веществе. Магнитная восприимчивость диамагнетиков отрицательна.
- Парамагнитные свойства могут проявлять вещества с атомами, имеющими магнитный момент. Магнитная восприимчивость при этом положительна и уменьшается с ростом температуры.
- Ферромагнетизм является очень сильным коллективным эффектом. Причем магнитная восприимчивость и проницаемость вещества становится неоднозначными функциями поля и зависят от его истории. Характерные ферромагнитные явления – спонтанная намагниченность и гистерезис намагниченности. Коэрцитивная сила магнитожестких кантилеверов (с кобальтовым покрытием) составляет порядка 400 эрстед, а магнитомягких (с покрытием
) – менее 10 эрстед.
Литература.
- O. Teschke, M.U. Kleinke, M.E.R. Dotto et al, J. Appl. Phys. 94, 1 (2003).
- P.F. Hopkins, J. Moreland, S.S. Malhotra et al, J. Appl. Phys. 79, 6448 (1996).
- H.J. Mamin, D. Rugar, P. Gruetter et al, Bull. Am. Phys. Soc. 35, 420 (1990).
- P. Grutter, D. Rugar, H.J. Mamin et al, Appl. Phys. Lett. 57, 1820 (1990).
- Тикадзуми С. Физика ферромагнетизма. I часть. – М.: Мир, 1987. – 302 с.;
Тикадзуми С. Физика ферромагнетизма. II часть. – М.: Мир, 1987. – 420 с. - Уайт Р.М. Квантовая теория магнетизма. – М.: Мир, 1972.
- Дорфман Я.Г. Диамагнетизм и химическая связь. – М.: Физматгиз, 1961.
- Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике: Физика сплошных сред. – М.: Мир, 1977. – 300 с.
- Сивухин Д.В. Курс общей физики: Электричество. – М.: Наука, 1983. – 687 с.