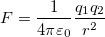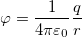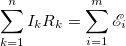Электрический заряд
q — заряд
n — число частиц
e — заряд электрона
Найти
- q
- n
- e
Известно, что:
=
Вычислить ‘q‘
Закон Кулона
F — сила
k — коэффициент пропорциональности
q1, q2 — заряды
r — расстояние
Найти
- F
- k
- q1
- q2
- r
Известно, что:
=
Вычислить ‘F‘
Постоянная Кулона
k — коэффициент пропорциональности
ε_0 — электрическая постоянная
Найти
- k
- π
- ε_0
Известно, что:
=
Вычислить ‘k‘
Относительная диэлектрическая проницаемость
ε — диэлектрическая постоянная (проницаемость)
F_вак — сила в вакууме
F_окр — сила в окружающей среде
Найти
- ε
- F_вак
- F_окр
Известно, что:
=
Вычислить ‘ε‘
Электрическое поле
E — электрическое поле
F — сила
q — заряд
Найти
- E
- F
- q
Известно, что:
=
Вычислить ‘E‘
Электрическое поле точечного заряда в вакууме
E — электрическое поле
k — коэффициент пропорциональности
q_0 — заряд
r — расстояние
Найти
- E
- k
- q_0
- r
Известно, что:
=
Вычислить ‘E‘
Электрическое поле точечного заряда в окружающей среде
E — электрическое поле
k — коэффициент пропорциональности
q — заряд
ε — диэлектрическая постоянная (проницаемость)
r — расстояние
Найти
- E_окр
- k
- q_0
- ε
- r
Известно, что:
=
Вычислить ‘E_окр‘
Электрическое поле вне заряженной сферы
E — электрическое поле
k — коэффициент пропорциональности
σ — плотность поверхностного заряда
R — радиус
r — расстояние
Найти
- E
- k
- σ4
- π
- R
- r
Известно, что:
=
Вычислить ‘E‘
Электрическое поле вне заряженной сферы
E — электрическое поле
k — коэффициент пропорциональности
q — заряд
r — расстояние
Найти
- E
- k
- q
- r
Известно, что:
=
Вычислить ‘E‘
Электрическое поле бесконечной заряженной плоскости
E — электрическое поле
k — коэффициент пропорциональности
σ — плотность поверхностного заряда
Найти
- E
- k2
- π
- σ
Известно, что:
=
Вычислить ‘E‘
Электрическое поле бесконечной заряженной плоскости
E — электрическое поле
σ — плотность поверхностного заряда
ε_0 — электрическая постоянная
Найти
- E
- σ
- ε_0
Известно, что:
=
Вычислить ‘E‘
Электрическое поле конденсатора
E — электрическое поле
k — коэффициент пропорциональности
σ — плотность поверхностного заряда
Найти
- E
- k
- π
- σ
Известно, что:
=
Вычислить ‘E‘
Работа в электрическом поле
A — работа
F — сила
Δd — расстояние
Найти
- A
- F
- Δ_d
Известно, что:
=
Вычислить ‘A‘
Потенциальная энергия системы двух точечных зарядов
W — потенциальная энергия
k — коэффициент пропорциональности
q0, q — заряды
ε — диэлектрическая постоянная (проницаемость)
r — расстояние
Найти
- W
- k
- q0
- q
- ε
- r
Известно, что:
=
Вычислить ‘W‘
Работа в электрическом поле — разность потенциальных энергий
A — работа
W1 — начальная потенциальная энергия
W2 — конечная потенциальная энергия
Найти
- A
- W1
- W2
Известно, что:
=
Вычислить ‘A‘
Потенциал электростатического поля
φ — потенциал
W — потенциальная энергия
q — заряд
Найти
- φ
- W
- q
Известно, что:
=
Вычислить ‘φ‘
Напряжение — разность потенциалов
U — напряжение
φ1 — начальный потенциал
φ2 — конечный потенциал
Найти
- U
- φ1
- φ2
Известно, что:
=
Вычислить ‘U‘
Работа переноса заряда
A — работа
q — заряд
U — напряжение
Найти
- A
- q
- U
Известно, что:
=
Вычислить ‘A‘
Потенциал электростатического поля вокруг точечного заряда
φ — потенциал
k — коэффициент пропорциональности
q_0 — заряд
ε — диэлектрическая постоянная (проницаемость)
r — расстояние
Найти
- φ
- k
- q0
- ε
- r
Известно, что:
=
Вычислить ‘φ‘
Напряжённость электростатического поля
E — электрическое поле
U — напряжение
Δd — расстояние
Найти
- E
- U
- Δ_d
Известно, что:
=
Вычислить ‘E‘
Результирующее электрическое поле
E — результирующее электрическое поле
E0 — внешнее электрическое поле
E1 — внутреннее электрическое поле
Найти
- E
- E0
- E1
Известно, что:
=
Вычислить ‘E‘
Электрический момент
p — электрический момент
q — заряд
l — расстояние
Найти
- p
- q
- l
Известно, что:
=
Вычислить ‘p‘
Электрическая ёмкость
C — электрическая ёмкость
q — заряд
φ — потенциал
Найти
- C
- q
- φ
Известно, что:
=
Вычислить ‘C‘
Электрическая ёмкость шара
C — электрическая ёмкость
ε — диэлектрическая постоянная (проницаемость)
R — радиус
k — коэффициент пропорциональности
Найти
- C
- ε
- R
- k
Известно, что:
=
Вычислить ‘C‘
Электрическая ёмкость двух проводников
C — электрическая ёмкость
q — заряд
U — напряжение
Найти
- C
- q
- U
Известно, что:
=
Вычислить ‘C‘
Электрическая ёмкость плоского конденсатора
C — электрическая ёмкость
ε — диэлектрическая постоянная (проницаемость)
ε0 — электрическая постоянная
S — площадь
d — расстояние между плас
Найти
- C
- ε
- ε0
- S
- d
Известно, что:
=
Вычислить ‘C‘
Электрическая ёмкость сферического конденсатора
C — электрическая ёмкость
ε — диэлектрическая постоянная (проницаемость)
ε0 — электрическая постоянная
R1 — радиус внутренней сферы
R2 — радиу
Найти
- C
- π
- ε
- ε0
- R1
- R2
Известно, что:
=
Вычислить ‘C‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
q — заряд
E1 — напряженность электрического поля, создаваемого пластиной конденсатора
d — расстояние между пластин
Найти
- W
- q
- E1
- d
Известно, что:
=
Вычислить ‘W‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
q — заряд
E — электрическое поле
d — расстояние между пластинами
Найти
- W
- q
- E
- d
Известно, что:
=
Вычислить ‘W‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
q — заряд
U — напряжение
Найти
- W
- q
- U
Известно, что:
=
Вычислить ‘W‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
C — электрическая ёмкость
U — напряжение
Найти
- W
- C
- U
Известно, что:
=
Вычислить ‘W‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
q — заряд
C — электрическая ёмкость
Найти
- W
- q
- C
Известно, что:
=
Вычислить ‘W‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
ε — диэлектрическая постоянная (проницаемость)
ε0 — электрическая постоянная
E — электрическое поле
V — объём
Найти
- W
- ε
- ε0
- E
- V
Известно, что:
=
Вычислить ‘W‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
ε — диэлектрическая постоянная (проницаемость)
ε0 — электрическая постоянная
E — электрическое поле
S — площадь
d —
Найти
- W
- ε
- ε0
- E
- S
- d
Известно, что:
=
Вычислить ‘W‘
Плотность энергии электрического поля
ω_p — плотность энергии электрического поля
W — потенциальная энергия
V — объём
Найти
- ω_p
- W
- V
Известно, что:
=
Вычислить ‘ω_p‘
Плотность энергии электрического поля
ω_p — плотность энергии электрического поля
ε0 — электрическая постоянная
ε — диэлектрическая постоянная (проницаемость)
E — электрическое п
Найти
- ω_p
- ε0
- ε
- E
Известно, что:
=
Вычислить ‘ω_p‘
Так же как гравитационная масса тела в механике Ньютона, заряд в электродинамике относится к фундаментальным, основным понятиям.
Это физическая величина, означающая свойство некоторых частиц или тел вовлекаться в электромагнитные взаимодействия. В физике электрический заряд принято обозначать q, реже Q.
Из установленных экспериментальных фактов следуют следующие выводы:
- в природе есть два типа электрических зарядов, условно «позитивные» (+) и «негативные» (-);
- заряды передаются от одного тела к другому (допустим в случае прямого соприкосновения двух объектов). Поэтому электрический заряд, в отличие от массы тела, не является постоянной характеристикой конкретного тела. Одно и то же тело в разных условиях может иметь разные заряды.
- Одинаковые заряды отталкиваются, противоположные – притягиваются. То есть «+» отталкивает «+», «-» отталкивает «-». Но «+» притягивает «-» и наоборот.
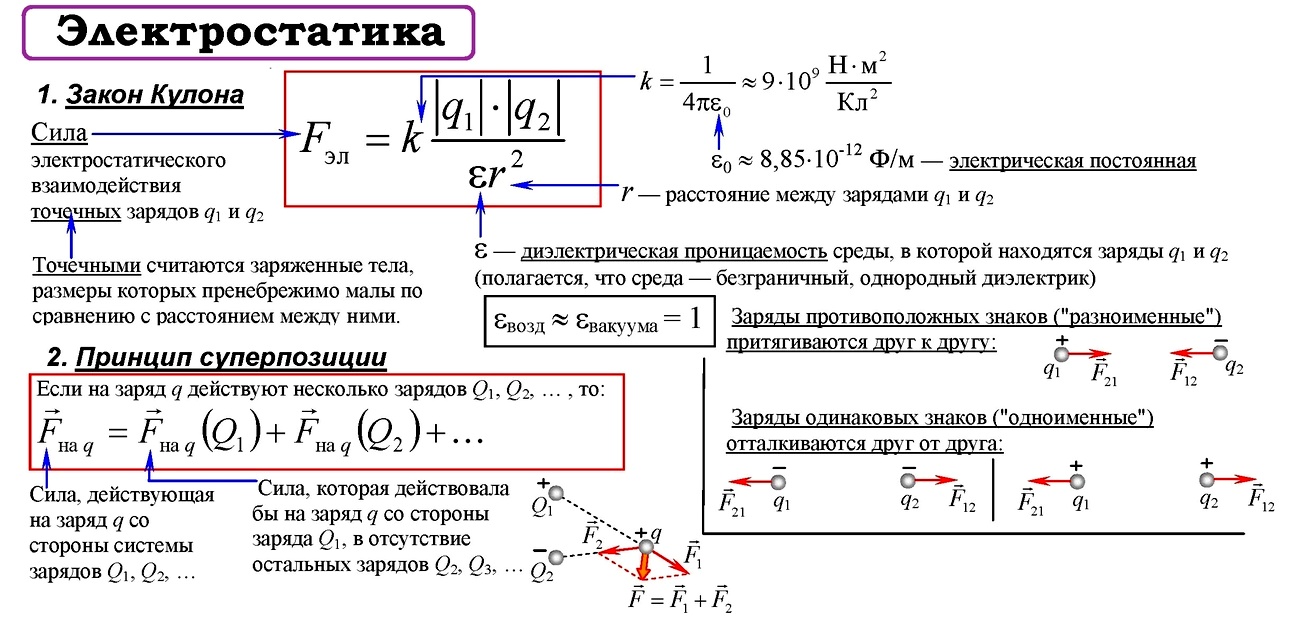
Закон Кулона
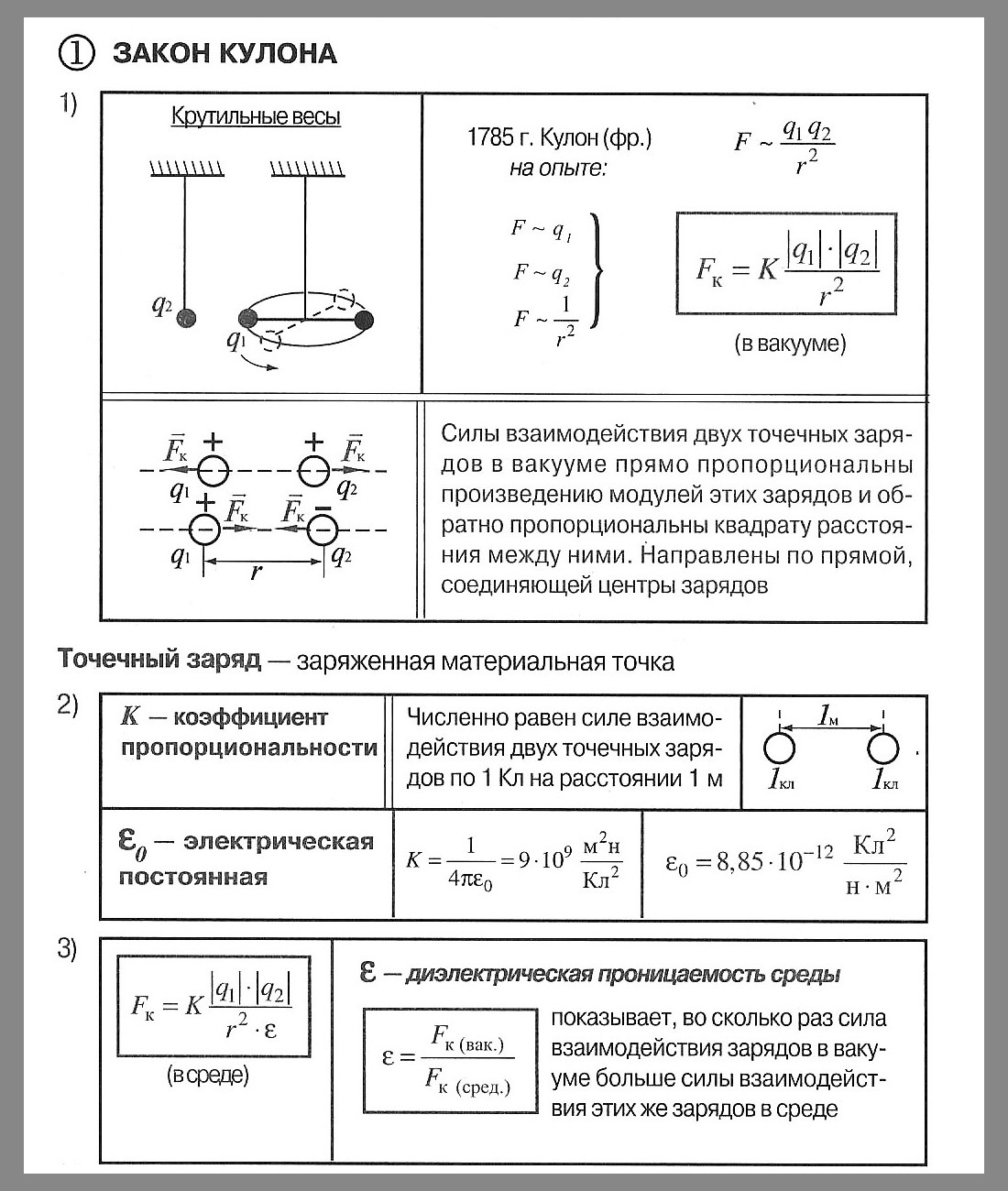
К одним из основных законов природы относится установленный экспериментально закон сохранения заряда (более известный как «Закон Кулона»).
В замкнутой системе алгебраическая сумма зарядов сохраняется:
q1+q2+q3+…+qn=constq_1 + q_2 + q_3 + … + q_n = const
Этот закон также значит, что в изолированной системе не могут происходить процессы появления или исчезновения зарядов только одного знака. То есть заряды рождаются и умирают парами («+» с «-»).
В современной науке, носителями заряда являются элементарные частицы. Все тела во Вселенной состоят из атомов. Но атомы в свою очередь состоят из таких элементарных частиц. Положительно заряженных протонов, отрицательных электронов и частиц без заряда — нейтронов. Протоны и нейтроны входят в состав ядра атома (поэтому оно позитивно заряжено), а электроны в состав оболочки (негативно заряженная). В нейтральном атоме заряд ядра равняется заряду всех электронов в оболочке. Заряд протона и электрона одинаковые по значению.
Экспериментально показано, что заряд может передаваться от одного тела к другому только целыми порциями или дискретно:
q=±ne(n=0,1,2,…),q = ± ne (n = 0, 1, 2, …),
ee – заряд электрона.
Измерение величины заряда
Стандартным методом обнаружения и измерения заряда, является прибор — электрометр. Он состоит из металлического стержня и стрелки, вращающейся вокруг горизонтальной оси. Стержень и стрелка изолированны от металлического корпуса прибора. Когда заряженное тело касается стержня прибора, электрические заряды одного знака перетекают по стержню и стрелке. Силы электростатического отталкивания поворачивают стрелку на некоторый угол. По величине угла можно судить о заряде, который был передан стержню электрометра.
На практике часто используют понятие точечного заряда. Точечным зарядом называют заряженное тело, размерами которого можно пренебречь.
Сила взаимодействия 2 зарядов
Сила взаимодействия неподвижных зарядов прямо пропорциональна модулю зарядов и обратно пропорциональна расстоянию между этими зарядами.
F=k∣q1∣⋅∣q2∣r2F = k frac{| q_1| cdot | q_2|}{r^2}
Закон Кулона хорошо согласуется когда заряды точечные, т.е когда размер заряженных тел гораздо меньше расстоянию между ними. Величина коэффициента kk зависит от выбора системы единиц.
В Международной системе СИ, принятой в большинстве стран:
k=14πε0k = frac {1} {4 pi varepsilon_0}
Также в СИ за 1 единицу заряда принят кулон (обозначается Кл). Кулон — это заряд, который проходит за время 1 с (одна секунда) через поперечное сечение проводника при силе тока 1А (один ампер).
Тест по теме «Электрический заряд. Закон Кулона»
Электричество Основные формулы
1. Электростатика
1.1 Закон Кулона
q1, q2 — величины точечных зарядов,
r — расстояние между зарядами.
1.2 Напряженность поля уединенного точечного заряда
q — величина уединенного точечного заряда,
r — расстояние от заряда.
1.3 Потенциал точки в поле точечного заряда
q — величина уединенного точечного заряда,
r — расстояние от заряда.
1.4 Потенциальная энергия заряда в электростатическом поле
φ — потенциал,
q1 — величина заряда.
1.5 Потенциальная энергия заряда q1 в поле точечного заряда
q — величина уединенного точечного заряда, который создает поле,
r — расстояние между зарядами.
1.6 Теорема Гаусса
N — поток вектора напряженности электрического поля через замкнутую поверхность,
q — полный заряд, находящийся внутри замкнутой поверхности.
1.7 Напряженность электрического поля вблизи от поверхности проводника
σ — поверхностная плотность заряда.
1.8 Емкость плоского кондесатора
q — заряд конденсатора,
U — модуль разности потенциалов между обкладками.
1.9 Энергия плоского кондесатора
q — заряд конденсатора,
U — модуль разности потенциалов между обкладками.
2. Постоянный электрический ток
2.1 Закон Ома для участка однородной цепи
U — напряжение на концах участка,
R — сопротивление участка цепи.
2.2 Закон Ома для замкнутой цепи с источником тока
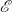
r — внутреннее сопротивление источника ЭДС.
2.3 Работа постоянного тока
U — напряжение на концах участка цепи,
t — время, за которое совершается работа.
2.4 Закон Джоуля-Ленца
Q — теплота,
R — сопротивление проводника,
t — время, за которое выделяется теплота.
2.5 Полная мощность, развиваемая источником тока
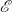
R — сопротивление цепи,
r — внутреннее сопротивление источника тока.
2.6 Полезная мощность
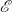
R — сопротивление цепи,
r — внутреннее сопротивление источника тока.
2.7 Коэффициент полезного действия источника тока
R — сопротивление цепи,
r — внутреннее сопротивление источника тока.
2.8 Первое правило Кирхгофа
n — число проводников, сходящихся в узле;
Ik — сила тока в k-м проводнике.
2.9 Второе правило Кирхгофа
n — число неразветвленных участков в контуре;
m — число ЭДС в контуре.
Содержание
- 1 Как найти заряд q?
- 2 Чему равна Q в физике?
- 3 Как найти T по физике?
- 4 Что означает Q в формуле Q QM?
- 5 Как найти электрический заряд?
- 6 Чему равна Q?
- 7 Как найти количество теплоты Q?
- 8 Как найти диаметр по физике?
- 9 Как найти начальную скорость в физике?
- 10 Как найти u0 в физике?
- 11 Как найти n в физике формула?
- 12 Как найти площадь по физике?
- 13 Что за формула Q CM t2 t1?
Формула нахождения заряда
В соответствии с ней, нужно перемножить силу тока на время его прохождения по проводнику. Количество заряда можно узнать через формулу +-ne, где n служит целым числом, а е равно значению = -1,6*10^-19 Кулон. Обратите внимание!
Чему равна Q в физике?
В физике q — символ электрического заряда, а Q — количества теплоты. В механике Q обозначает объёмный расход жидкости. В механике и радиотехнике Q обозначает добротность. В теоретической механике q обозначает обобщённые координаты.
Как найти T по физике?
Время обозначается как t. Единица измерения времени – с (секунды). Самая простая формула при равномерном прямолинейном движении. Время, необходимое для прохождения пути равняется частному от деления пути на скорость равномерного прямолинейного движения: t = S / v.
Что означает Q в формуле Q QM?
Удельная теплота сгорания – физическая величина, показывающая количество теплоты, выделяющееся при полном сгорании 1 кг вещества.
Как найти электрический заряд?
Электрический заряд, прошедший по участку цепи, можно определить, измерив силу тока и время его прохождения: q = I ⋅ t . Используя это соотношение и подставляя его в формулу A = U ⋅ q , получим формулу для нахождения работы электрического тока: A = U ⋅ I ⋅ t .
Чему равна Q?
Электроны несут отрицательный заряд. Количество электронов в атоме равно числу протонов в ядре, поэтому в целом атом нейтрален. Заряд любого тела: q = ±Ne , где е = 1,6*10 -19 Кл — элементарный или минимально возможный заряд (заряд электрона), N — число избыточных или недостающих электронов.
Как найти количество теплоты Q?
Чтобы рассчитать количество теплоты, необходимое для нагревания вещества (или выделяемое им при охлаждении), следует удельную теплоёмкость вещества умножить на его массу и на разность между конечной и начальной температурой вещества.
Как найти диаметр по физике?
Существует формула для расчета длины окружности: l=2пR, где l-длина окружности, 2- константа, п — число, равное 3,14; R — радиус окружности. Зная, что диаметр — это двойной радиус, вышеуказанную формулу можно записать в виде: l=пD, где D — диаметр. Выразить из данной формулы диаметр окружности: D=l/п.
Как найти начальную скорость в физике?
Если известны пройденное расстояние, время и ускорение, для определения начальной скорости можно использовать следующее соотношение:
- Vi = (d / t) — [(a * t) / 2]
- В эту формулу входят следующие величины: Vi — начальная скорость d — пройденное расстояние a — ускорение t — время
Как найти u0 в физике?
Сопротивление проводника прямо пропорционально напряжению на его концах и обратно пропорционально величине силы тока, протекающего через него. Формула для нахождения сопротивления по закону Ома, если известны сила тока и напряжение: R = U I {R= dfrac{U}{I}} R=IU, где R — сопротивление, U — напряжение, I — сила тока.
Как найти n в физике формула?
N = A/t, где N — мощность, A — работа, t — время выполненной работы.
Как найти площадь по физике?
Чтобы определить площадь тела, используют формулы: площадь прямоугольника S можно рассчитать, умножив длину прямоугольника на ширину прямоугольника. S = l 1 ⋅ l 2 . Площадь треугольника S = ah 2 , где a — сторона, h — высота, проведённая к данной стороне.
Что за формула Q CM t2 t1?
Q=cm( ) — формула для расчета количества теплоты, выделенной при изменении температуры тела с t1 на t2. Здесь C — удельная теплоемкость тела — данные о удельной теплоемкости тела можно найти в таблице удельных теплоемкостей, а m — масса тела.
ЭЛЕКТРОСТАТИКА
Теория и формулы (кратко и сжато)
Электростатика – раздел электродинамики, изучающий покоящиеся электрически заряженные тела. Существует два вида электрических зарядов: положительные (стекло о шелк) и отрицательные (эбонит о шерсть).
Элементарный заряд – минимальный заряд (е = 1,6∙10-19 Кл)
Заряд любого тела кратен целому числу элементарных зарядов: q = N∙е
Электризация тел – перераспределение заряда между телами. Способы электризации: трение, касание, влияние.
Закон сохранения электрического заряда – в замкнутой системе алгебраическая сумма зарядов всех частиц остается неизменной. q1 + q 2 + q 3 + …..+ qn = const
Пробный заряд – точечный положительный заряд.
Закон Кулона
Закон Кулона (установлен опытным путем в 1785 году) Сила взаимодействия двух неподвижных точечных зарядов в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорционально квадрату расстояния между ними.
Электрическое поле
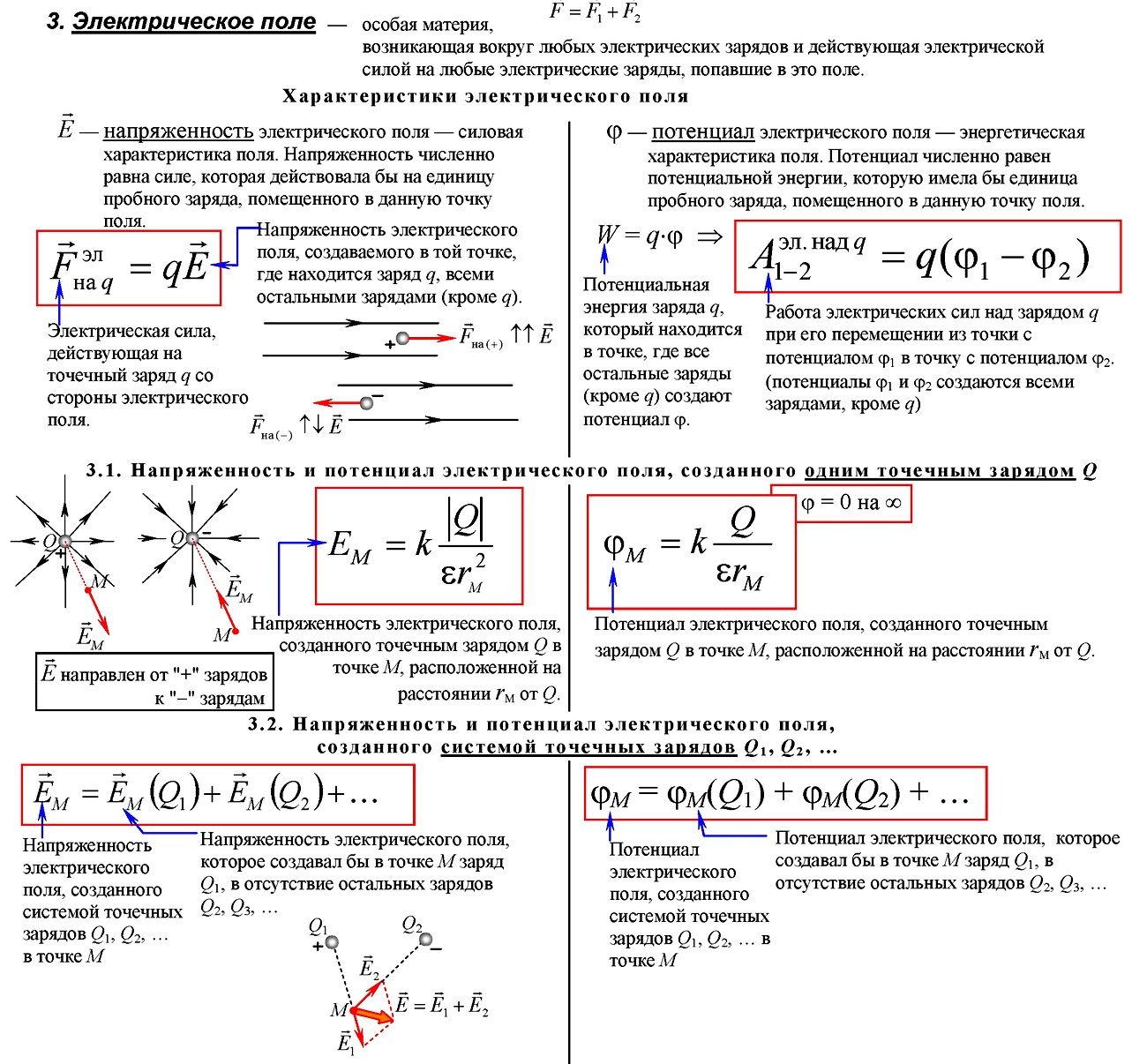
Электрическое поле – вид материи, осуществляющий взаимодействие между электрическими зарядами, возникает вокруг зарядов, действует только на заряды
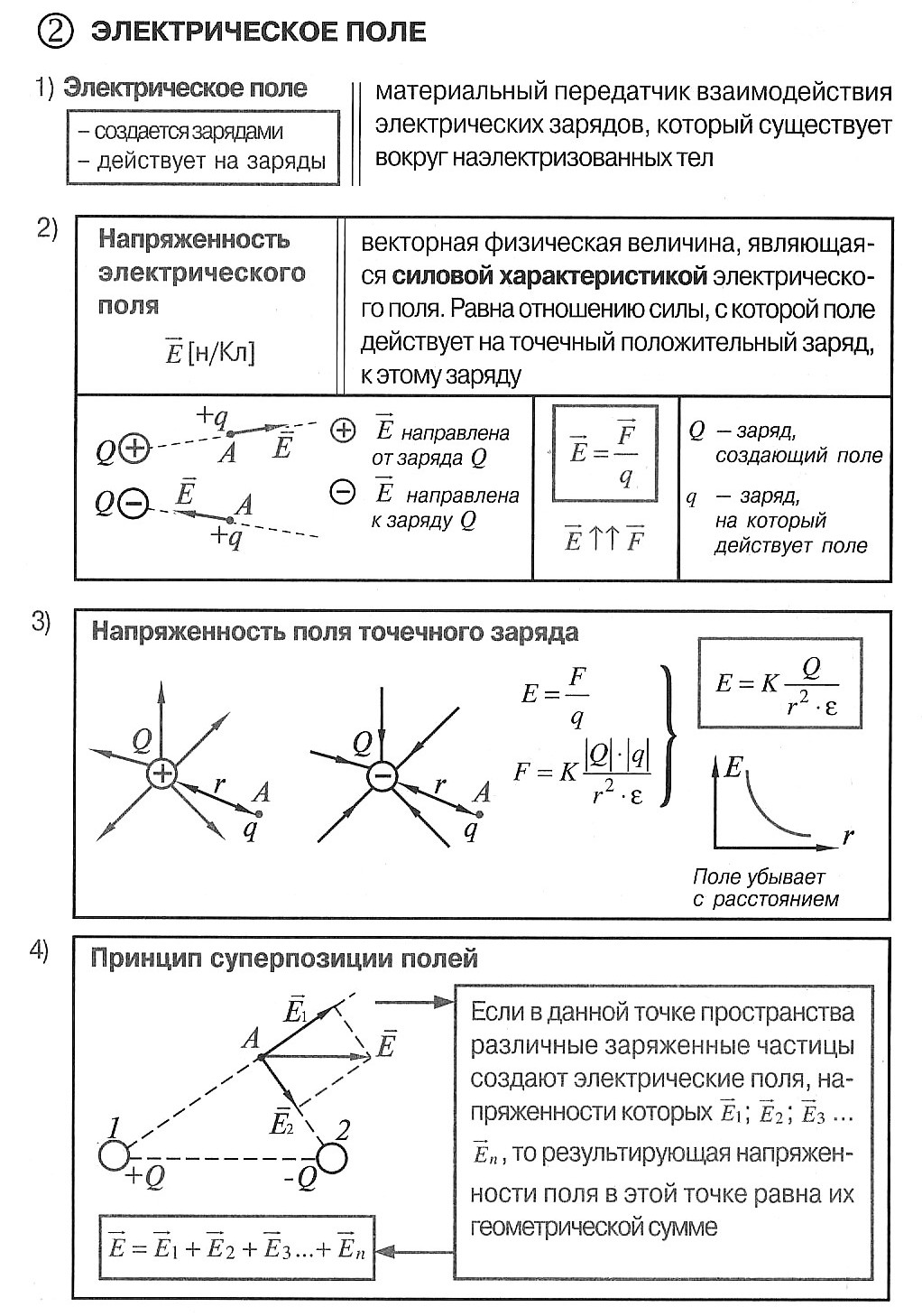
Силовые линии напряженности электрического поля – непрерывные линии, касательные к которым в каждой точке, через которые они проходят, совпадают с вектором напряженности.
Свойства силовых линий:
- не замкнуты;
- не пересекаются;
- непрерывны;
- направление совпадает с направлением вектора напряжённости;
- начало на + q или в бесконечности, конец на – q или в бесконечности;
- гуще вблизи зарядов (где больше напряжённость).
- перпендикулярны поверхности проводника
Разность потенциалов или напряжение (Δφ или U) — это разность потенциалов в начальной и конечной точках траектории заряда Δφ = φ1 – φ2
Чем меньше меняется потенциал на отрезке пути, тем меньше напряженность поля.
Напряженность электрического поля направлена в сторону уменьшения потенциала.
Электроемкость
Электроемкость С — характеризует способность проводника накапливать электрический заряд на своей поверхности.
- — не зависит от электрического заряда и напряжения.
- — зависит от геометрических размеров проводников, их формы, взаимного расположения, электрических свойств среды между проводниками.
Проводники и диэлектрики
Конденсаторы
Конденсатор — электротехническое устройство, служащее для быстрого накопления электрического заряда и быстрой отдачи его в цепь (два проводника, разделенных слоем диэлектрика ).
Скачать таблицы по теме «Электростатика»
Конспект уроков по теме «Электростатика. Теория и формулы» + шпаргалка.
Еще конспекты для 10-11 классов: