Как найти закономерность в хаосе

Колмогоровская сложность и наши поиски смысла

Что математика может рассказать нам о поиске порядка в хаосе жизни

Была ли встреча с самым дорогим вам человеком случайной, или виной тому была какая-то скрытая причина? А что насчёт странного вчерашнего сна – это были только случайные метания синапсов мозга, или он раскрыл что-то глубокое по поводу вашего подсознания? Возможно, сон пытался рассказать вам что-то о вашем будущем. Возможно, что и нет. Имеет ли тот факт, что ваш близкий родственник заболел опасной разновидностью рака, какой-то глубокий смысл, или же это просто последствия случайных мутаций ДНК?

В нашей жизни мы часто задумываемся над закономерностями происходящих вокруг нас событий. Мы задаёмся вопросом, случайны ли наши жизни, или у них есть какой-то смысл, уникально истинный и глубокий. Я, как математик, часто обращаюсь к числам и теоремам за идеями по поводу подобных вопросов. И так получилось, что я кое-что узнал о поиске смысла в закономерностях жизни благодаря одной из самых глубоких теорем математической логики. Эта теорема, проще говоря, демонстрирует, что в принципе невозможно узнать, является ли объяснение закономерности наиболее глубоким или интересным из всех объяснений. Точно так же, как в жизни, поиск смысла в математике ничем не ограничен.

Небольшая прелюдия. Рассмотрим следующие три строки символов.

1. 100100100100100100100100100100100100100100100100100100100100100100100

2. 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

3. 38386274868783254735796801834682918987459817087106701409581980418.

Как мы можем их описать? Например, мы легко можем это сделать, просто записав их – так, как мы только что и проделали. Однако сразу ясно, что первые две строчки можно описать и короче. Первая – это просто последовательность повторяющихся «100». Вторая – список первых нескольких простых чисел. А что насчёт третьей? Её можно описать, просто выведя всю строку. Но есть ли для неё лучшее, более короткое описание?

В начале 1960-х американский подросток Грегори Хайтин, всемирно известный русский [и советский] математик Андрей Николаевич Колмогоров, и пионер информатики Рэй Соломонов независимо друг от друга сформулировали способ измерения сложности последовательностей символов. Их идеи стали называть теорией сложности Колмогорова или алгоритмической теорией информации. Они постулируют, что сложность строки определяется длиной наикратчайшей компьютерной программы, способной её выдать. То есть, возьмём строчку, и поищем самую короткую компьютерную программу, которая её выдаёт. Программа – один из видов описания строки. Если кратчайшая из таких программ окажется очень короткой, тогда в строке есть простая закономерность, и она не очень сложная. Мы говорим, что в такой строке мало алгоритмическое содержание. И наоборот, если для выдачи строки требуется длинная программа, тогда строка сложная, и её алгоритмическое содержание больше. Для любой строки необходимо искать кратчайшую программу, выдающую такую строку. Длина такой программы называется Колмогоровской сложностью строки.

Давайте вернёмся к трём первым строчкам. Первые две строки можно описать при помощи относительно коротких компьютерных программ:

1. Вывести “100” 30 раз.

2. Вывести первые 25 простых чисел.

Колмогоровская сложность первой строки меньше Колмогоровской сложности второй строки, поскольку первая программа короче второй. Что насчёт третьей? У этой строчки нет очевидных закономерностей. Тем не менее, можно написать дурацкую программу, выводящую эту последовательность:

3. Вывести “38386274868783254735796801834682918987459817087106701409581980418”

Такая программа справляется с задачей, но неудовлетворительно. Возможно, существует программа короче, демонстрирующая наличие закономерности в этой строке. Когда кратчайшей программой, выдающей строку, оказывается программа «вывести строку», мы говорим, что эта строка очень сложна, и известных закономерностей не содержит. Строка без закономерностей называется случайной. Но хотя мы закономерности не увидели, она может существовать. В математике, как и в жизни, мы сталкиваемся со множеством закономерностей, кажущихся случайными.

Мы могли бы попытаться использовать удивительные возможности современных компьютеров, чтобы найти закономерность и кратчайшую программу. Разве не было бы замечательно, если бы существовал компьютер, способный просто вычислить Колмогоровскую сложность любой строки? Такой компьютер принимал бы на вход строку, и выводил бы длину кратчайшей программы, способной выдать эту строку. Конечно же, со всеми этими новомодными штучками вроде ИИ, глубинного обучения, больших данных, квантовых вычислений, и т.п., должно быть легко создать такой компьютер.

Увы, такой компьютер создать невозможно! Пусть современные компьютеры и весьма мощны, эта задача невыполнима. Таково содержание одной из глубочайших теорем математической логики. Теорема, по сути, говорит, что Колмогоровскую сложность строки невозможно вычислить. Не существует механического устройства, определяющего размер наименьшей программы, выдающей заданную строку. Дело не в том, что наш текущий уровень компьютерных технологий не дотягивает до задачи, или что мы недостаточно умны для того, чтобы написать такой алгоритм. Было доказано, что сама идея описание и вычисления демонстрирует, что компьютер в принципе не в состоянии выполнить такую задачу для любой строки. И если компьютер, возможно, способен на поиски определённых закономерностей в строке, он не способен найти наилучшую закономерность. Мы, возможно, и найдём короткую программу, выводящую определённую последовательность, но всегда может существовать ещё более короткая. Мы никогда об этом не узнаем.

Само доказательство невычислимости Колмогоровской сложности для последовательности довольно формальное. Но это доказательство от противного, и мы можем примерно представить себе, как оно работает, рассмотрев пару небольших и милых парадоксов.

Парадокс интересных чисел связан с утверждением, что все натуральные числа интересные. 1 – это первое число, и это интересно. 2 – первое чётное число. 3 – первое нечётное простое число. 4 – интересное число, потому что 4 = 2 × 2 и 4 = 2+2. В таком роде можно продолжать дальше, и находить интересные свойства многих чисел. В какой-то момент мы можем встретить число без интересных свойств. И мы можем назвать это число первым неинтересным номером – но это само по себе уже интересное свойство. В итоге неинтересные числа тоже оказываются интересными!

Идеи, содержащиеся в Колмогоровском доказательстве, похожи на идеи парадокса Берри, касающегося описания больших чисел. Заметим, что чем больше слов мы используем, тем большее число мы можем описать. К примеру, трем словами можно описать «триллион триллионов», а пятью – » триллион триллионов триллионов триллионов триллионов», куда как более крупное число. Теперь рассмотрим число, описываемое следующей фразой:

Самое маленькое число, которое нельзя описать меньше, чем пятнадцатью словами [The smallest number that cannot be described in less than 15 words]

Для описания числа требуется 15, 16 или даже больше слов. Его нельзя описать 12, 13 или 14 словами. Однако, вот в чём проблема: приведённая выше фраза описывает это число при помощи 10 слов [по-английски – 12 слов / прим. перев.]. Наше описание числа противоречит описанию числа – вот вам и парадокс.

В парадоксе интересных чисел и в парадоксе Берри мы приходим к противоречиям, предполагая существование точного способа описания чего-либо. Точно так же, доказательство невычислимости Колмогоровской сложности вытекает из того, что если бы оно было вычислимым, мы пришли бы к противоречию.

То, что Колмогоровская сложность невычислима – это результат из чистой математики, и мы не должны путать этот идеальный мир с куда как более сложной и беспорядочной реальностью. Однако существуют некоторые общие моменты, связанные с Колмогоровской сложностью, которые мы можем привнести в реальный мир.

Много раз мы сталкивались с тем, что казалось нам совершенно хаотичным. Случайность нервирует нас, и мы ищем закономерности, частично устраняющие хаос. Если мы находим закономерность, остаётся неясным, является ли она лучшей закономерностью, объясняющей наши наблюдения. Мы можем задаться вопросом – существует ли более глубокая закономерность, дающая лучшее объяснение. Теория Колмогоровской сложности учит нас тому, что на базовом уровне не существует гарантированного способа определить наилучшую закономерность. Мы просто никогда не узнаем о том, является ли найденная нами закономерность наилучшей.

Но именно это и делает поиск бесконечно интересным. По определению нечто является интересным, если требует дополнительных размышлений. Очевидный и полностью понятный факт не требует дальнейших размышлений. То, что шестью семь будет сорок два – совершенно понятно и неинтересно. Только когда мы не уверены по поводу идей, нам нужно подтверждать их и размышлять о них. Поиск улучшенных закономерностей всегда будет интересным.

Реальный мир добавляет сложности. Если в мире строк и компьютерных программ ошибок нет, в реальном мире можно совершить ошибку. Мы легко узнаем, выводит ли какая-то определённая программа строку, или нет. И хотя мы, вероятно, не сможем определить оптимальную программу для вывода определённой строки, мы сможем определить, выводит ли она требуемую строку. А реальный мир, в отличие от этого, гораздо более сложный. Нам может показаться, что мы видим последовательность, когда её, на самом деле, нет.

Наше понимание наших поисков смысла начинает оформляться. Мы презираем случайности и обожаем закономерности. Мы биологически запрограммированы находить закономерности, объясняющие то, что мы видим. Но мы не можем быть уверены, что найденная нами закономерность будет правильной. Даже если бы мы каким-то образом могли гарантировать отсутствие ошибки, и достигли бы совершенства, подобного компьютерному, где-то всё равно всегда может находиться ещё более глубокая истина. Это напряжение подпитывает нашу любовь к литературе, театру и кино. Когда мы читаем роман или смотрим пьесу, автор или режиссёр представляет нам последовательность событий с общей темой, закономерностью или моралью. Литература, пьесы и кино предлагают нам великолепный способ убежать от обычно непонятного и бессмысленного хаоса, встречающегося нам в окружающем мире. Очень хорошая литература идёт дальше, и оставляет нам возможности многих интерпретаций. Мы лицом к лицу встречаемся с невычислимостью Колмогоровской сложности.

Это напряжение также определяет, как мы проживаем наши жизни. Путешествуя сквозь якобы случайные события, мы ищем закономерности и структуру. Жизнь полна взлётов и падений. Есть радость влюблённости, веселого времяпрепровождения с детьми, ощущения великих достижений по окончанию сложной работы. Есть боль разрушающихся отношений, агония неудачи после активных попыток выполнить задачу, трагедия смерти любимого. Мы пытаемся искать во всём этом смысл. Мы презираем чувство полной случайности и идею, что мы просто следуем хаотичным, незамысловатым законам физики. Мы хотим знать, нет ли в окружающем мире какого-то смысла, цели, значимости. Нам нужна волшебная история жизни, и мы рассказываем себе истории.

Иногда эти истории просто ложны. Иногда мы обманываем себя и окружающих. А иногда мы правильно определяем закономерности. Но даже когда история правдива, она не обязательно будет наилучшей. Мы никогда не будем уверены, что в глубине не лежит ещё более базовая и точная история. Старея и впадая в тоску, мы приобретаем определённые идеи по поводу Вселенной, недоступные нам раньше. Мы находим улучшенные закономерности. Возможно, мы начинаем видеть вещи яснее. Или нет. Мы никогда не узнаем. Но мы знаем, что поиски гарантированно не закончатся.

Нозон Яновски – доктор наук в математике, работает в Образовательном центре городского университета Нью-Йорка, профессор информатики в Бруклинском колледже того же университета.

Кто из нас не мечтал о путешествиях во времени? Например, о путешествии в прошлое – чтобы спасти кого-то от фатальной ошибки, собрать доказательства нераскрытых преступлений и увидеть наконец, как жили наши далекие предки в африканской саванне. Эта тема настолько популярна, что в Голливуде от нее откажется разве что ленивый. Исследователи, однако, утверждают, что мир не ведет себя аккуратно и упорядоченно. Если бы это было так, идентичные события всегда приводили бы к одним и тем же «побочным эффектам», а будущее было бы полностью предсказуемым и предрешенным. К счастью, теория хаоса утверждает обратное и полная случайность – тоже не про нас. Мы существуем где-то посередине, в мире, который часто кажется случайным, но на самом деле подчиняется определенным правилам и законам. Согласно теории хаоса малейшие изменения могут привести к радикальным последствиям в будущем – в другом месте и в другое время.

Теория хаоса гласит, что небольшие изменения приводят к большим последствиям.

Теория хаоса

В 1970-х годах американский математик и метеоролог Эдвард Лоренц не только открыл хаос (что было событием случайным) но также определил его ключевой механизм, отметив странное свойство – повторение (построение траектории с течением времени) любых двух близлежащих точек приводит к их разделению.
По сути, хаос – это наука о неожиданностях, о нелинейности и непредсказуемости.

В то время как большинство наук имеют дело с предположительно предсказуемыми явлениями, такими как гравитация, электричество или химические реакции, теория хаоса являет собой фактическую невозможность предсказания или контроля, например турбулентности, погоды, экономики, состояния мозга и так далее.

Эти явления часто описываются с помощью фрактальной математики, которая отражает бесконечную сложность природы. Так, многие природные объекты обладают фрактальными свойствами, включая облака, деревья и реки, однако многие привычные нам системы демонстрируют сложное, хаотичное поведение.

Признание хаотической, фрактальной природы нашего мира может подарить нам его новое понимание. Хаос – это не просто беспорядок, а скорее удивительный переход между порядком и беспорядком.

Принципы хаоса

Один из принципов хаоса предложенных Лоренцом – тот самый эффект бабочки. Если бабочка хлопает крыльями в России, то где-то в Нью-Мексико начинается ураган. Да, звучит как полная бессмыслица, но с научной точки зрения такая связь может быть реальна. И если бы бабочка не взмахнула крыльями в нужной точке пространства/времени, урагана бы не произошло.

Еще один принцип теории хаоса заключается в том, что небольшие изменения могут резко изменить результаты. В конечном итоге этот принцип олицетворяет течение нашей жизни и все, что с ней происходит. Кто знает, какими будут долгосрочные последствия обучения миллионов детей хаосу и фракталам?

Фракталы – это бесконечно сложные паттерны, которые создаются путем многократного повторения простого процесса в непрерывном цикле обратной связи. Движимые рекурсией, фракталы представляют собой образы динамических систем – картины Хаоса. Геометрически они существуют между нашими привычными измерениями.

Важно понимать, что закономерности внутри хаоса скрыты, так как крайне чувствительны к любым, даже самым маленьким изменениям. Это означает, что похожие, но не идентичные ситуации могут привести к совершенно разным результатам. Но есть еще кое-что интересное: в хаотичном мире последствия могут быть совершенно несоразмерны причинам. И хотя правила детерминированы, в долгосрочной перспективе будущее непредсказуемо.

Это интересно: Можно ли верить прогнозам погоды?

Поскольку хаос чувствителен к небольшим изменениям, существует бесконечное множество способов и правил, которым необходимо следовать. Понимание этих процессов позволяет узнать подробности о настоящем и прошлом, чтобы в конечном итоге определить, как и по каким законам будут развиваться происходящие в мире события. Теория хаоса утверждает, что небольшие изменения чреваты последствиями, точно предсказать которые невозможно.

Точно так же мы не можем перепроектировать некоторую часть информации о прошлом, просто зная текущие и даже будущие ситуации. При этом путешествие во времени не помогает восстановить прошлую информацию, так как даже при движении назад во времени хаотическая система все еще в игре и приводит к непредсказуемым последствиям. И хотя эффект бабочки является классической поэтической метафорой, иллюстрирующей теорию хаоса, его динамика проявляется в реальности, включая рост популяции тигров и вращение лун Плутона. Чудеса.

Не забудьте подписаться на наш канал в Яндекс.Дзен – там регулярно выходят статьи, которых нет на сайте

Существует ли эффект бабочки?

Итак, поскольку мы не можем знать все начальные условия сложной системы в достаточной (т.е. совершенной) детализации, надеяться предсказать конечную судьбу этой самой системы тоже не выйдет. Однако результаты исследования в области квантовой физики, проведенное исследователями из Лос-Аламосской Национальной лаборатории, показали, что так называемый эффект бабочки можно преодолеть в квантовом мире и «расшифровать» потерянную информацию, по существу обратив время вспять.

Безусловно, эффект бабочки» отлично «смотрится» в теориях о путешествиях во времени, однако результаты исследования, опубликованного в журнале Physical Review Letters, показали, что никаких доказательств эффекта бабочки в квантовой механике не существует.

Как пишут авторы научной работы, мысленный эксперимент по «расшифровке» информации (после обращения времени вспять), «как ожидается, приведет к тому же эффекту бабочки, что и в знаменитом рассказе Рэя Брэдбери «И грянул гром» – главный герой отправляется в прошлое и случайно наступает на бабочку. Вернувшись в свой век он понимает, что мир полностью изменился.

Больше по теме: Компьютерная симуляция доказала – «эффекта бабочки» не существует

Исследователи также выяснили, что квантовая система эффективно правит и даже восстанавливает информацию, зашифрованную в прошлом – для этого не нужен ни хаос, ни эффект бабочки. С помощью компьютерного моделирования авторы работы обнаружили, что во время путешествий во времени мир остается прежним, а значит изменений в законах квантовой механики попросту не будет.

Путешествие во времени неизбежно меняет прошлое из-за существования путешественника, – отмечают исследователи. Более того, понятие хаоса в классической физике и в квантовой механике необходимо рассматривать по-разному.

Нельзя не отметить и результаты еще одного интересного исследования, согласно которым на квантовом уровне путешествия во времени возможны. Подробнее о результатах можно прочитать здесь. И, конечно, подписывайтесь на наш новостной канал в Telegram – так вы всегда будете в курсе последних событий из мира науки и высоких технологий!

Область математики График аттрактора Лоренца для значений r = 28, σ = 10, b = 8/3 Анимация двухстержневого маятника при промежуточной энергии, демонстрирующая хаотическое поведение. Запуск маятника из немного другого начального состояния приведет к совершенно другой траектории. Двухстержневой маятник — одна из простейших динамических систем с хаотическими решениями.

Теория хаоса — это раздел математики, сосредоточенный на изучении хаоса — состояний динамических систем, чьи явно случайные состояния беспорядка и нерегулярности часто регулируются детерминированными законами, которые очень чувствительны к начальным условиям. Теория хаоса — это междисциплинарная теория, утверждающая, что в пределах очевидной случайности сложных хаотических систем существуют лежащие в основе закономерности, взаимосвязанность, постоянные петли обратной связи, повторение, самоподобие, фракталы и самоорганизация. эффект бабочки, лежащий в основе принципа хаоса, описывает, как небольшое изменение в одном состоянии детерминированной нелинейной системы может привести к большим различиям в более позднем состоянии. (это означает, что существует чувствительная зависимость от начальных условий). Метафора этого поведения состоит в том, что бабочка, машущая крыльями в Китае, может вызвать ураган в Техасе.

Небольшие различия в начальных условиях, например, из-за ошибок в измерениях или из-за округления Ошибки в численных вычислениях могут привести к сильно различающимся результатам для таких динамических систем, что делает долгосрочное прогнозирование их поведения в целом невозможным. Это может произойти, даже если эти системы детерминированы, что означает, что их будущее поведение следует уникальной эволюции и полностью определяется их начальными условиями, без участия случайных элементов. Другими словами, детерминированная природа этих систем не делает их предсказуемыми. Такое поведение известно как детерминированный хаос или просто хаос . Эдвард Лоренц резюмировал эту теорию следующим образом:

Хаос: когда настоящее определяет будущее, но приблизительное настоящее не определяет его приблизительно.

Хаотическое поведение существует во многих природных системах, включая поток жидкости, нарушения сердечного ритма, погода и климат. Это также происходит спонтанно в некоторых системах с искусственными компонентами, таких как фондовый рынок и дорожное движение. Это поведение можно изучить с помощью анализа хаотической математической модели или с помощью аналитических методов, таких как графики повторения и карты Пуанкаре. Теория хаоса находит применение в различных дисциплинах, включая метеорологию, антропологию, социологию, физику, экологию, информатика, инженерия, экономика, биология, экология, пандемия антикризисное управление и философия. Теория легла в основу таких областей исследований, как сложные динамические системы, теория края хаоса и процессы самосборки.

Содержание

• 1 Введение
• 2 Хаотическая динамика
  • 2.1 Хаос как спонтанное нарушение топологической суперсимметрии
  • 2.2 Чувствительность к начальным условиям
  • 2.3 Непериодичность
  • 2.4 Топологическое перемешивание
  • 2.5 Топологическая транзитивность
  • 2.6 Плотность периодических орбит
  • 2.7 Странные аттракторы
  • 2.8 Минимальная сложность хаотической системы
  • 2.9 Бесконечномерные отображения
  • 2.10 Рывковые системы
• 3 Спонтанный порядок
• 4 История
• 5 Приложения
  • 5.1 Криптография
  • 5.2 Робототехника
  • 5.3 Биология
  • 5.4 Другие области
• 6 См. Также
• 7 Ссылки
• 8 Дополнительная литература
  • 8.1 Статьи
  • 8.2 Учебники
  • 8.3 Полутехнические и популярные работы
• 9 Внешние ссылки

Введение

Теория хаоса касается детерминированных систем, поведение которых в принципе можно предсказать. Хаотические системы какое-то время предсказуемы, а затем «кажутся» случайными. Время, в течение которого поведение хаотической системы может быть эффективно предсказано, зависит от трех вещей: насколько неопределенности можно допустить в прогнозе, насколько точно ее текущее состояние может быть измерено, и временного масштаба, зависящего от динамики системы., называется Ляпуновское время. Некоторые примеры времен Ляпунова: хаотические электрические цепи, около 1 миллисекунды; погодные системы, несколько дней (бездоказательно); внутренняя солнечная система — от 4 до 5 миллионов лет. В хаотических системах неопределенность прогноза увеличивается экспоненциально с истекшим временем. Следовательно, математически удвоение времени прогноза более чем возводит в квадрат пропорциональную неопределенность прогноза. Это означает, что на практике осмысленный прогноз не может быть сделан на интервале, превышающем время Ляпунова более чем в два или три раза. Когда невозможно сделать осмысленные прогнозы, система кажется случайной.

Хаотическая динамика

Карта, определяемая x → 4 x (1 — x) и y → (x + y) mod 1 отображает чувствительность к начальным положениям x. Здесь две серии значений x и y заметно расходятся со временем от крошечной начальной разницы.

В обычном использовании «хаос» означает «состояние беспорядка». Однако в теории хаоса этот термин определяется более точно. Хотя общепринятого математического определения хаоса не существует, обычно используемое определение, первоначально сформулированное Робертом Л. Девани, гласит, что для классификации динамической системы как хаотической она должна обладать следующими свойствами:

1. она должна быть чувствительным к начальным условиям,
2. он должен быть топологически транзитивным,
3. он должен иметь плотные периодические орбиты.

В некоторых случаях последние два свойства выше имеют было показано, что фактически подразумевает чувствительность к начальным условиям. В случае дискретного времени это верно для всех непрерывных отображений в метрических пространствах. В этих случаях, хотя это часто является наиболее значимым с практической точки зрения свойством, в определении нет необходимости указывать «чувствительность к начальным условиям».

Если внимание ограничено интервалами, второе свойство подразумевает два других. Альтернативное и, как правило, более слабое определение хаоса использует только первые два свойства из приведенного выше списка.

Хаос как спонтанное нарушение топологической суперсимметрии

В динамических системах с непрерывным временем хаос — это явление спонтанного нарушения топологической суперсимметрии, которое является внутренним свойством операторов эволюции всех стохастических и детерминированных (частных) дифференциальных уравнений. Эта картина динамического хаоса работает не только для детерминированных моделей, но и для моделей с внешним шумом, что является важным обобщением с физической точки зрения, поскольку в действительности все динамические системы испытывают влияние их стохастической среды. На этом рисунке дальнодействующее динамическое поведение, связанное с хаотической динамикой (например, эффект бабочки ), является следствием теоремы Голдстоуна — в приложении к спонтанному нарушению топологической суперсимметрии.

Чувствительность к начальным условиям

Уравнения Лоренца, используемые для создания графиков для переменной y. Начальные условия для x и z оставались такими же, но условия для y были изменены между 1.001, 1.0001 и 1.00001 . Значения для

ρ { displaystyle rho}

,

σ { displaystyle sigma}

и

β { displaystyle beta}

были 45.92, 16и 4 соответственно. Как видно из графика, даже малейшая разница в начальных значениях вызывает значительные изменения примерно через 12 секунд эволюции в трех случаях. Это пример чувствительной зависимости от начальных условий.

Чувствительность к начальным условиям означает, что каждая точка в хаотической системе произвольно близко аппроксимируется другими точками, которые имеют существенно разные будущие пути или траектории. Таким образом, произвольно небольшое изменение или возмущение текущей траектории может привести к значительно иному поведению в будущем.

Чувствительность к начальным условиям широко известна как «эффект бабочки », так называемый, потому что названия статьи, данной Эдвардом Лоренцем в 1972 году Американской ассоциации содействия развитию науки в Вашингтоне, округ Колумбия, под названием «Предсказуемость: хлопают ли крылья бабочки в Бразилии» вызвать Торнадо в Техасе ?. Хлопающее крыло представляет собой небольшое изменение начального состояния системы, которое вызывает цепочку событий, препятствующих предсказуемости крупномасштабных явлений. Если бы бабочка не махала крыльями, траектория всей системы могла бы быть совершенно иной.

Следствием чувствительности к начальным условиям является то, что если мы начнем с ограниченного количества информации о системе (как это обычно бывает на практике), то по прошествии определенного времени система больше не будет предсказуемой.. Это наиболее распространено в случае погоды, которая обычно предсказуема только на неделю вперед. Это не означает, что нельзя утверждать что-либо о событиях далекого будущего — только то, что существуют некоторые ограничения для системы. Например, мы знаем с помощью погоды, что температура на Земле естественным образом не достигнет 100 ° C или упадет до -130 ° C (в течение текущей геологической эры ), но это не означает, что мы можем предсказать в какой день будет самая жаркая температура в году.

Говоря более математическим языком, показатель Ляпунова измеряет чувствительность к начальным условиям в виде скорости экспоненциального отклонения от возмущенных начальных условий. Более конкретно, учитывая две начальные траектории в фазовом пространстве, которые бесконечно близки, с начальным разделением δ Z 0 { displaystyle delta mathbf {Z} _ {0 }}, две траектории расходятся со скоростью, заданной как

| δ Z (t) | ≈ e λ t | δ Z 0 |, { displaystyle | delta mathbf {Z} (t) | приблизительно e ^ { lambda t} | delta mathbf {Z} _ {0} |,}

где t { displaystyle t}— время, а λ { displaystyle lambda}— показатель Ляпунова. Скорость разделения зависит от ориентации исходного вектора разделения, поэтому может существовать целый спектр показателей Ляпунова. Число показателей Ляпунова равно количеству измерений фазового пространства, хотя принято относиться к самому большому из них. Например, наиболее часто используется максимальный показатель Ляпунова (MLE), поскольку он определяет общую предсказуемость системы. Положительный MLE обычно считается признаком того, что система хаотична.

В дополнение к вышеупомянутому свойству также существуют другие свойства, связанные с чувствительностью начальных условий. К ним относятся, например, теоретико-измерительное смешивание (как обсуждается в эргодической теории) и свойства K-системы.

Не- периодичность

Хаотическая система может иметь последовательности значений для развивающейся переменной, которые в точности повторяются, обеспечивая периодическое поведение, начиная с любой точки этой последовательности. Однако такие периодические последовательности скорее отталкивают, чем привлекают, а это означает, что если развивающаяся переменная находится вне последовательности, даже если она близка, она не войдет в последовательность и фактически будет отклоняться от нее. Таким образом, для почти для всех начальных условий переменная эволюционирует хаотически с непериодическим поведением.

Топологическое смешение

Шесть итераций набора состояний

[x, y] { displaystyle [x, y]}

, прошедших через логистическую карту. Первая итерация (синий цвет) — это начальное условие, которое по сути образует круг. Анимация показывает с первой по шестую итерацию круговых начальных условий. Видно, что смешивание происходит по мере продвижения итераций. Шестая итерация показывает, что точки практически полностью разбросаны в фазовом пространстве. Если бы мы продвинулись дальше в итерациях, перемешивание было бы однородным и необратимым. Логистическая карта имеет уравнение

x k + 1 = 4 x k (1 — x k) { displaystyle x_ {k + 1} = 4x_ {k} (1-x_ {k})}

. Чтобы расширить пространство состояний логистической карты до двух измерений, второе состояние,

y { displaystyle y}

, было создано как

yk + 1 = xk + yk { displaystyle y_ {k + 1} = x_ {k} + y_ {k}}

, если

xk + yk < 1 {displaystyle x_{k}+y_{k}<1}

и

yk + 1 = xk + yk — 1 { displaystyle y_ {k + 1} = x_ {k} + y_ {k} -1}

в противном случае. Карта, определяемая x → 4 x (1 — x) и y → ( x + y) mod 1 также отображает топологическое смешение. Здесь синяя область преобразуется динамикой сначала в фиолетовую область, затем в розовую и красную области и, в конечном итоге, в облако вертикальных линий, разбросанных по пространству.

Топологическое смешение (или более слабое условие топологической транзитивности) означает, что система со временем развивается так, что любая заданная область или открытый набор ее фазового пространства в конечном итоге перекрывается с любой другой заданной областью. Эта математическая концепция «смешивания» соответствует стандартной интуиции, а смешивание цветных красителей или жидкостей является примером хаотической системы.

Топологическое смешение часто не упоминается в популярных описаниях хаоса, которые приравнивают хаос только к чувствительности к начальным условиям. Однако чувствительная зависимость только от начальных условий не дает хаоса. Например, рассмотрим простую динамическую систему, полученную путем многократного удвоения начального значения. Эта система повсюду чувствительно зависит от начальных условий, так как любая пара близлежащих точек со временем оказывается далеко разнесенной. Однако в этом примере нет топологического перемешивания и, следовательно, нет хаоса. В самом деле, его поведение чрезвычайно простое: все точки, кроме 0, стремятся к положительной или отрицательной бесконечности.

Топологическая транзитивность

Отображение f: X → X { displaystyle f: X to X}называется топологически транзитивным, если для любой пары из открытых множеств U, V ⊂ X { displaystyle U, V subset X}, существует k>0 { displaystyle k>0}, чтобы fk (U) ∩ V ≠ ∅ { displaystyle f ^ {k} (U) cap V neq emptyset}. Топологическая транзитивность — это более слабая версия топологического смешивания. Интуитивно, если карта топологически транзитивна, то для данной точки x и области V существует точка y около x, орбита которой проходит через V. Это означает, что невозможно разложить систему на два открытых множества.

Важной родственной теоремой является теорема Биркгофа о транзитивности. Легко видеть, что существование плотной орбиты влечет топологическую транзитивность. off Теорема транзитивности утверждает, что если X является счетным, полным метрическим пространством, то топологическая транзитивность влечет существование плотного множества точек в X, которые имеют плотные орбиты.

Плотность периодических орбит

Для хаотической системы наличие плотных периодических орбит означает, что к каждой точке в пространстве приближается произвольно близко по периодическим орбитам. Одномерное логистическое отображение , определяемое как x → 4 x (1 — x), является одной из простейших систем с плотностью периодических орбит. Например, 5–5 8 { displaystyle { tfrac {5 — { sqrt {5}}} {8}}}→ 5 + 5 8 { displaystyle { tfrac {5 + { sqrt {5}}} {8}}}→ 5 — 5 8 { displaystyle { tfrac {5 — { sqrt {5}}} {8}}}(или приблизительно 0,3454915 → 0.9045085 → 0.3454915) является (нестабильной) орбитой периода 2, и аналогичные орбиты существуют для периодов 4, 8, 16 и т. Д. (Действительно, для всех периодов, указанных в теореме Шарковского ).

теорема Шарковского является На основе доказательства Ли и Йорка (1975), что любая непрерывная одномерная система, которая демонстрирует регулярный цикл с периодом три, также будет иметь регулярные циклы любой другой длины, а также полностью хаотические орбиты.

Странные аттракторы

Аттрактор Лоренца демонстрирует хаотическое поведение. Эти два графика демонстрируют чувствительную зависимость от начальных условий в области фазового пространства, занимаемой аттрактором.

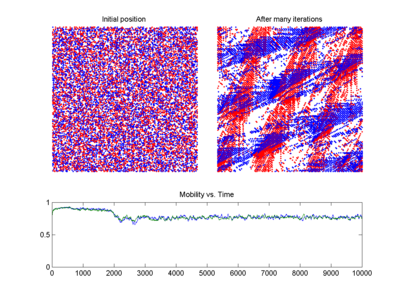
Некоторые динамические системы, такие как одномерные логистическая карта, определенная как x → 4 x (1 — x), хаотична каждые где, но во многих случаях хаотическое поведение обнаруживается только в подмножестве фазового пространства. Наибольший интерес возникают случаи, когда хаотическое поведение имеет место на аттракторе , поскольку тогда большой набор начальных условий приводит к орбитам, сходящимся к этой хаотической области.

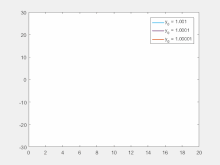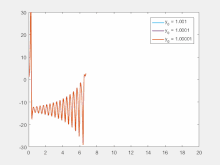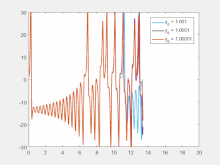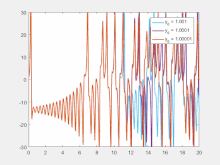
Простой способ Визуализировать хаотический аттрактор — это начать с точки в области притяжения аттрактора, а затем просто построить его следующую орбиту. Из-за условия топологической транзитивности это, вероятно, даст картину всего конечного аттрактора, и действительно, обе орбиты, показанные на рисунке справа, дают картину общей формы аттрактора Лоренца. Этот аттрактор является результатом простой трехмерной модели погодной системы Лоренца. Аттрактор Лоренца, возможно, является одной из самых известных диаграмм хаотической системы, вероятно, потому, что он не только один из первых, но и один из самых сложных и, как таковой, дает начало очень интересной схеме, которая с учетом немного воображения, похоже на крылья бабочки.

В отличие от аттракторов с неподвижной точкой и предельных циклов, аттракторы, возникающие из хаотических систем, известные как странные аттракторы, имеют большую детализацию и сложность. Странные аттракторы встречаются как в непрерывных динамических системах (таких как система Лоренца), так и в некоторых дискретных системах (таких как отображение Энона ). Другие дискретные динамические системы имеют отталкивающую структуру, называемую множеством Джулиа, которая формируется на границе между бассейнами притяжения неподвижных точек. Наборы Julia можно рассматривать как странные отпугиватели. Как странные аттракторы, так и множества Жюлиа обычно имеют фрактальную структуру , и для них можно вычислить фрактальную размерность.

Минимальная сложность хаотической системы

Бифуркационная диаграмма логистической карты x → r x (1 — x). Каждый вертикальный слой показывает аттрактор для определенного значения r. На диаграмме отображается удвоение периода по мере увеличения r, что в конечном итоге приводит к хаосу.

Дискретные хаотические системы, такие как логистическая карта, могут проявлять странные аттракторы независимо от их размерности. Универсальность одномерных карт с параболическими максимумами и константами Фейгенбаума δ = 4.664201… { displaystyle delta = 4.664201…},α = 2.502907… { displaystyle alpha = 2.502907…}хорошо виден с картой, предложенной в качестве игрушечной модели для дискретной лазерной динамики: x → G x (1 — tanh (x)) { displaystyle x rightarrow Gx (1- mathrm {tanh} (x))}, где x { displaystyle x}обозначает амплитуду электрического поля, G { displaystyle G}— коэффициент усиления лазера как параметр бифуркации. Постепенное увеличение G { displaystyle G}на интервале [0, ∞) { displaystyle [0, infty)}изменяет динамику с обычной на хаотическая с качественно такой же бифуркационной диаграммой , что и для логистической карты.

Напротив, для непрерывных динамических систем теорема Пуанкаре – Бендиксона показывает, что странный аттрактор может возникать только в трех или более измерениях. Конечномерные линейные системы никогда не бывают хаотичными; чтобы динамическая система отображала хаотическое поведение, она должна быть либо нелинейной, либо бесконечномерной.

Теорема Пуанкаре – Бендиксона утверждает, что двумерное дифференциальное уравнение имеет очень регулярное поведение. Аттрактор Лоренца, обсуждаемый ниже, генерируется системой трех дифференциальных уравнений, таких как:

d x d t = σ y — σ x, d y d t = ρ x — x z — y, d z d t = x y — β z. { displaystyle { begin {align} { frac { mathrm {d} x} { mathrm {d} t}} = sigma y- sigma x, \ { frac { mathrm {d} y} { mathrm {d} t}} = rho x-xz-y, \ { frac { mathrm {d} z} { mathrm {d} t}} = xy- beta z. end {align}}}

где x { displaystyle x}, y { displaystyle y}и z { displaystyle z}составляют состояние системы, t { displaystyle t}— время, а σ { displaystyle sigma}, ρ { displaystyle rho}, β { displaystyle beta}— системные параметры. Пять членов в правой части линейны, а два — квадратичны; всего семь сроков. Другой хорошо известный хаотический аттрактор порождается уравнениями Рёсслера, которые имеют только один нелинейный член из семи. Спротт нашел трехмерную систему, состоящую всего из пяти членов, в которой был только один нелинейный член, который демонстрирует хаос для определенных значений параметров. Чжан и Хайдель показали, что, по крайней мере, для диссипативных и консервативных квадратичных систем, трехмерные квадратичные системы только с тремя или четырьмя членами в правой части не могут демонстрировать хаотическое поведение. Причина в том, что решения таких систем асимптотичны по отношению к двумерной поверхности и, следовательно, решения имеют хорошее поведение.

В то время как теорема Пуанкаре – Бендиксона показывает, что непрерывнаядинамическая система на евклидовой плоскости не может быть хаотической, двумерные непрерывные системы с неевклидовой геометрией могут демонстрировать хаотичное поведение. Как это ни удивительно, хаос может возникать и в линейных системах, если они бесконечны. Теория линейного хаоса разработана в области математического анализа, известный как функциональный анализ.

Бесконечные карты

Прямое обобщение дискретных карт основано на интеграле свертки, который опосредует взаимодействие между пространственно распределенными карты: ψ n + 1 (r →, t) знак равно ∫ К (r → — r →, t) е [ψ n (r →, t)] dr →, { displaystyle psi _ {n +1} ({ vec { r}}, t) = int K ({ vec {r}} — { vec {r}} ^ {,}, t) f [ psi _ {n} ({ vec {r}} ^ {,}, t)] d { vec {r}} ^ {,}},

где ядро ​​K (r → — r →, t) { displaystyle K ({ vec {r }} — { vec {r}} ^ {,}, t)}— пропагатор, полученный как функция Грина системы физических систем, f [ψ n (r →, t)] { displaystyle f [ psi _ {n} ({ vec {r}}, t)]}может быть логистической картой, как ψ → G ψ [1 — tanh ⁡ (ψ) ] { displaystyle psi rightarrow G psi [1- tanh ( psi)]}или сложная карта. Для примеров сложных карт набор Джулии f [ψ] = ψ 2 { displaystyle f [ psi] = psi ^ {2}}или Карта Икеда ψ N + 1 знак равно A + B ψ nei (| ψ N | 2 + C) { displaystyle psi _ {n + 1} = A + B psi _ {n} e ^ {i (| psi _ {n} | ^ {2} + C)}}может служить. Когда возникают проблемы с распространением волн на расстоянии L = ct { displaystyle L = ct}с длиной волны λ = 2 π / k { displaystyle lambda = 2 pi / k }ядром K { displaystyle K}может иметь форму функции Грина для уравнения Шредингера :.

K (r → — r →, L) = ik exp ⁡ [ik L] 2 π L exp ⁡ [ik | г → — г →, | 2 2 L] { Displaystyle К ({ vec {r}} — { vec {r}} ^ {,}, L) = { frac {ik exp [ikL]} {2 pi L}} exp [{ frac {ik | { vec {r}} — { vec {r}} ^ {,} | ^ {2}} {2L}}]}.

Системы рывков

В физике, рывок — это третья производная от положения по времени. Таким образом, дифференциальные уравнения вида

J (x…, X ¨, x ˙, x) = 0 { displaystyle J left ({ overset {…} {x}}, { ddot { x}}, { dot {x}}, x right) = 0}

иногда используют уравнениями рывка. Было показано, что уравнение определено в системе трех обыкновенных нелинейных дифференциальных уравнений первого порядка. Это мотивирует математический интерес к рывковым системам. Системы, включающие четвертую или более производную, называются системы гипердергивания.

Поведение системы рывковковывается уравнением рывка, а для некоторых уравнений рывка простые электронные схемы могут моделировать решения. Эти схемы известны как схемы рывков.

Одно из самых интересных свойств рывковых схем — возможность хаотического поведения. Фактически, некоторые хорошо известные хаотические системы, как аттрактор Лоренца и отображение Лоренца и отображениелера, условно описываются как система трех дифференциальных уравнений первого порядка, которые можно объединить в одно (хотя и довольно сложное) уравнение рывка. Нелинейные рывковые системы — это в некотором смысле минимально сложные, демонстрирующие хаотическое поведение; не существует хаотической системы, включающей только обыкновенные дифференциальные уравнения первого порядка (система, приводящая к уравнению только второго порядка).

Пример уравнения рывка с нелинейностью величиной x { displaystyle x}:

d 3 xdt 3 + A d 2 xdt 2 + dxdt — | х | + 1 = 0. { displaystyle { frac { mathrm {d} ^ {3} x} { mathrm {d} t ^ {3}}} + A { frac { mathrm {d} ^ {2 } x} { mathrm {d} t ^ {2}}} + { frac { mathrm {d} x} { mathrm {d} t}} — | х | + 1 = 0.}

Здесь A — регулируемый параметр. Это уравнение имеет хаотическое решение для A = 3/5 и может быть реализовано с помощью следующей схемы рывка; Желаемая нелинейность обеспечивается двумя диодами:

В приведенной выше схеме все резисторы имеют одинаковое значение, кроме RA = R / A = 5 R / 3 { displaystyle R_ {A} = R / A = 5R / 3}, и все конденсаторы одинакового размера. Доминирующая частота: 1/2 π R C { displaystyle 1/2 pi RC}. Выходной сигнал операционного усилителя 0 будет соответствовать переменной x, выходной сигнал 1 соответствует первой производной x, а выходной сигнал 2 соответствует второй производной.

Подобные схемы требуют только одного диода или вообще не требуют диодов.

См. Также хорошо известную схему Чуа, основу для хаотических генераторов истинных случайных чисел. Простота построения схемы сделала ее повсеместным реальным примером хаотической системы.

Спонтанный порядок

При правильных условиях хаос спонтанно превращается в последовательность шагов. В модели Курамото четырех условий достаточно, чтобы произвести синхронизацию в хаотической системе. Примеры включают связанные колебания маятников Кристиана Гюйгенса ‘, светлячков, нейронов, резонанс Лондонского моста, Миллениум и большие массивы Джозефсоновские перекрестки.

История

Папоротник Барнсли создан с помощью игры в хаос. Естественные формы (папоротники, облака, горы и т. Д.) Можно воссоздать с помощью итеративной системы функций (IFS).

Ранним сторонником теории хаоса был Анри Пуанкаре. В 1880-х годах, изученная задача трех тел, он обнаружил, что могут быть непериодические орбиты, но не постоянно увеличивающиеся и не приближающиеся к фиксированной точке. В 1898 году Жак Адамар опубликовал влиятельное исследование хаотического движения частиц, скользящей без трения по постоянной отрицательной кривизны, под названием «бильярд Адамара ». Адамару удалось показать, что все траектории нестабильны, в том, что все траектории частиц экспоненциально расходятся друг от друга, с положительной экспонентой Ляпунова.

Теория хаоса началась в области эргодической теории. Более поздние исследования, также по теме нелинейных дифференциальных уравнений, проводились Джорджем Дэвидом Биркгофом, Андреем Николаевичем Колмогоровым, Мэри Люси Картрайт и Джон Эденсор Литтлвуд и Стивен Смейл. За исключением Смейла, все эти исследования были вдохновлены физикой: проблема трех тел в случае Биркгофа, турбулентность и астрономические проблемы в случае Колмогорова и радиотехника в случае Картрайта и Литтлвуда. Хотя хаотическое движение планет не наблюдалось, экспериментаторы сталкивались с турбулентностью в движении жидкости и непериодическими колебаниями в радиосхемах без теории, объясняющей то, что они видели.

Несмотря на первоначальные открытия в первой половине двадцатого века, теория хаоса формализовалась как таковая только после середины века, когда некоторым ученым впервые стало очевидно, что линейная теория, преобладающая Теория систем в то время века просто не могла получить наблюдаемое поведение некоторых экспериментов, подобных экспериментов с логистической картой . То, что приписывалось неточности измерения и простому «шуму », рассматривалось теоретиками хаоса как полноценный компонент изучаемых систем.

Основным катализатором теории развития хаоса был электронный компьютер. Большая часть математики теории хаоса включает в себя повторяющуюся итерацию простых математических формул, что было бы непрактично выполнять вручную. Электронные компьютеры сделали эти повторяющиеся процессы практичными, а рисунки и изображения сделали возможным визуализацию эти системы. Будучи аспирантом лаборатории Тихиро Хаяси в университете Киото, Ёсисуке Уэда экспериментировал с аналоговыми компьютерами и 27 ноября 1961 года заметил то, что он назвал «случайным переходным феноменом». Однако его советник не согласился с его выводами в то время и не разрешил ему сообщить о своих выводах до 1970 года.

Турбулентность в концевом вихре от самолета крыло. Исследователи критической точки зрения, за пределами которой создается турбулентность, важны для теории хаоса, что было проанализировано, например, советским физиком Львом Ландау, который разработал теорию Ландау-Хопфа. турбулентность. Дэвид Руэлль и Флорис Такенс позже предсказали, в отличие от Ландау, что турбулентность жидкости может развиваться через странный аттрактор, основная концепция хаоса теории.

Эдвард Лоренц был одним из первых пионеров теории. Его интерес к хаосу возник случайно благодаря его работе над прогнозом погоды в 1961 году. Лоренц использовал простой цифровой компьютер, Royal McBee LGP-30, чтобы запрограммировать его погодное моделирование. Он хотел снова увидеть последовательность данных и, чтобы найти время, начал моделирование в середине его хода. Он сделал это, распечатав данные, соответствующие условиям в середине исходного моделирования. К его удивлению, погода, которую машина начала предсказывать, полностью отличалась от предыдущего расчета. Лоренц отследил это до компьютерной распечатки. Компьютер работал с 6-значной точностью, но в распечатке переменные округлялись до 3-значного числа, поэтому такое значение, как 0,506127, напечатано как 0,506. Это различие крошечное, и в то время считалось, что оно не должно иметь практического эффекта. Однако Лоренц обнаружил, что небольшие изменения начальных условий приводят к большим изменениям в долгосрочных результатах. Открытие Лоренца, давшее название аттракторам Лоренца, показало, что даже подробное атмосферное моделирование, как правило, не может дать точных долгосрочных прогнозов погоды.

В 1963 году Бенуа Мандельброт обнаружил повторяющиеся закономерности во всех масштабах в данных о ценах на хлопок. Заранее он изучил теорию информации и пришел к выводу, что шум имеет структуру, подобную множеству Кантора : на любой шкале соотношение периодов, содержащих шум, к периодам без ошибок было постоянным — таким образом, ошибки были неизбежно и должно быть запланировано с учетом избыточности. Мандельброт описал как «эффект Ноя» (при котором могут происходить внезапные прерывистые изменения), так и «эффект Джозефа» (при котором значение может сохраняться в течение некоторого времени, но затем внезапно измениться). Это поставило под сомнение идею о том, что изменения в цене были нормально распределенными. В 1967 году он опубликовал статью «Какова длина побережья Британии? Статистическое самоподобие и дробное измерение », в котором показано, что длина береговой линии изменяется в зависимости от масштаба измерительного прибора, похожа на себя во всех масштабах и бесконечна по длине для бесконечно малого измерительного прибора. Утверждая, что клубок шпагата выглядит как точка при взгляде издалека (0-мерный), шар при взгляде достаточно близко (3-мерный) или изогнутая прядь (1-мерный), он утверждал, что размеры объект относителен к наблюдателю и может быть дробным. Объект, неоднородность которого постоянна в разных масштабах («самоподобие»), — это фрактал (примеры включают губку Менгера, прокладку Серпинского и кривая Коха или снежинка, которая бесконечно длинна, но охватывает конечное пространство и имеет фрактальную размерность примерно 1,2619). В 1982 году Мандельброт опубликовал Фрактальную геометрию природы, ставшую классикой теории хаоса. Биологические системы, такие как ветвление кровеносной и бронхиальной систем, оказались подходящими для фрактальной модели.

В декабре 1977 года Нью-Йоркская академия наук организовала первый симпозиум по хаосу, на котором присутствовали Дэвид Рюэлль, Роберт Мэй, Джеймс А. Йорк (создатель термина «хаос» в математике), Роберт Шоу и метеоролог Эдвард Лоренц. В следующем году Пьер Кулле и Чарльз Трессер опубликовали «Iterations d’endomorphismes et groupe de renormalisation», а статья Митчелла Фейгенбаума «Количественная универсальность для одного класса нелинейных преобразований» наконец появилась в журнале, спустя 3 дня. лет отказов рефери. Так, Фейгенбаум (1975) и Кулле и Трессер (1978) открыли универсальность в хаосе, что позволило применить теорию хаоса к множеству различных явлений.

В 1979 году Альберт Дж. Либхабер во время симпозиума, организованного в Аспене Пьером Хоэнбергом, представил свое экспериментальное наблюдение каскада бифуркаций . что приводит к хаосу и турбулентности в системах конвекции Рэлея – Бенара. Он был удостоен премии Вольфа по физике в 1986 году вместе с Митчеллом Дж. Фейгенбаумом за их вдохновляющие достижения.

В 1986 году Нью-Йоркская академия наук со- совместно с Национальным институтом психического здоровья и Управлением военно-морских исследований организовала первую важную конференцию по хаосу в биологии и медицине. Там Бернардо Хуберман представил математическую модель среди шизофреников. Это привело к обновлению физиологии в 1980-х годах посредством применения теории хаоса, например, в исследовании патологических сердечных циклов.

В 1987 г. Пер Бак, Чао Тан и Курт Визенфельд опубликовали статью в Physical Review Letters, впервые описывающая самоорганизованная критичность ( SOC), считается одним из механизмов возникновения сложности в природе.

Наряду в основном лабораторными подходами, такими как песочная куча Бак-Танга-Визенфельда, многие другие были объединены на крупномасштабные природные или социальные системы, которые, как известно (или предположительно), демонстрируют масштабно-инвариантное поведение. Эти подходы не всегда приветствовались (по крайней мере, использовались) специалисты по изучаемым предметам, SOC, тем не менее, стал надежным кандидатом для объяснения ряда природных явлений, включая землетрясений (которые задолго до этого были обнаружены) SOC, известный как источник масштабно-инвариантного поведения, например, закон Гутенберга-Рихтера, описывающий статистическое распределение размеров землетрясений, и закон Омори, описывающий частоту афтершоков.), солнечные вспышки, колебания в экономических системах, таких как финансовые рынки (ссылки на SOC распространены в эконофизике ), формирование ландшафта, лесные пожары, оползни, эпидемии и биологическая эволюция (где использовался SOC, например, как динамический механизм, лежащий в основе теории «прерывистое равновесие » выдвинуто Найлсом Элдриджем и Стивеном Джеем Гулдом ). Из-за последствий безмасштабного распределения размеров событий, некоторые исследователи предполагают рассматривать как пример SOC, — это возникновение войн. Эти исследования SOC включают в себя попытки моделирования (разработка новых моделей или адаптацию использования к специфике данной системы), так и обширный анализ данных для определения существующих и / или характеристик естественных масштабов.

В том же году Джеймс Глейк опубликовал Хаос: создание новой науки, который стал бестселлером и представил общие принципы теории хаоса, а также его история для широкой публики, хотя в его истории недооценивается важный советский вклад. Первоначально несколько человек превратилась в трансдисциплинарную и институциональную дисциплину, главным образом под названием нелинейный системный анализ. Ссылаясь на концепцию Томаса Куна о смене парадигмы , изложенную в Структура научных революций (1962), многие «хаологи» (как некоторые описывали себя) утверждал, что эта новая теория была примером такого сдвига, и этот тезис поддержал Глейк.

Доступность более дешевых и мощных компьютеров расширяет область теории хаоса. В настоящее время теория хаоса продолжает активную область исследований, включающую различные различные дисциплин, таких как математика, топология, физика, системы социальных, моделирование населения, биология, метеорология, астрофизика, теория информации, вычислительная нейробиология, пандемия антикризисное управление и т. Д.

Приложения

A конус текстильный оболочка, внешне похожие на Правило 30, клеточный автомат с хаотическим поведением.

Хотя она применима к множеству других ситуаций. Некоторые области, которыми сегодня приносит пользу теория хаоса: геология, математика, микробиология, биология, информатика, экономика, инженерия, финансы, алгоритмическая торговля, метеорология, философия, антропология, физика, политика, динамика населения, психология и робототехника. Несколько категорий ниже с примерами, это ни в коем случае не исчерпывающий список, появляются новые приложения.

Криптография

Теория хаоса много лет использовалась в криптографии. Используется несколько десятилетий хаос и последняя нелинейная динамика при разработке сотен криптографических примитивов. Эти алгоритмы включают в себя алгоритмы шифрования изображений , хэш-функции, безопасные генераторы псевдослучайных чисел, потоковые шифры, водяные знаки и стеганография. Большинство этих алгоритмов основаны на одномодальных хаотических картах, и большая часть этих алгоритмов использует параметры управления и начальное состояние хаотических карт в качестве своих ключей. С более широкой точки зрения, без общности, сходство между хаотическими картами и криптографическими системами является основной мотивацией для разработки криптографических алгоритмов на основе хаоса. Один тип шифрования, секретный ключ или симметричный ключ, основан на рассредоточении и путанице, что хорошо моделируется теорией хаоса. Другой тип вычислений, ДНК-вычисление, в сочетании с теорией хаоса, предлагает способ шифрования изображений и другой информации. Доказано, что многие из криптографических алгоритмов DNA-Chaos либо небезопасны, либо применяемая техника считается неэффективной.

Робототехника

Робототехника — еще одна область, которая недавно извлекла выгоду из хаоса теория. Вместо того, чтобы роботы действовали методом проб и ошибок для поведения с окружающей средой, для построения прогнозной модели была применена теория хаоса. Хаотическую динамику демонстрируют пассивные ходящие двуногие роботы.

Биология

Более ста лет биологи отслеживают популяции разных видов с помощью модели населения. Большинство моделей являются непрерывными, но недавно ученые смогли реализовать хаотические модели в определенных популяциях. Например, исследование моделей канадской рыси показало, что рост популяции характеризовался хаотическим поведением. Хаос также можно найти в экологических системах, таких как гидрология. Хотя у хаотической гидрологической модели есть свои недостатки, еще предстоит многому научиться, глядя на данные через призму теории хаоса. Другое биологическое применение можно найти в кардиотокографии. Наблюдение за плодами — это тонкий баланс между получением точной информации и максимально неинвазивным вмешательством. Более точные модели предупреждающих знаков гипоксии плода можно получить с помощью хаотического моделирования.

Другие области

В химии прогнозирование растворимости газа имеет важное значение для производства полимеров, но модели, использующие оптимизацию роя частиц (PSO), как правило, сходятся не в том направлении. Улучшенная версия PSO была создана путем введения хаоса, который предотвращает застревание моделирования. В небесной механике, особенно при наблюдении за астероидами, применение теории хаоса позволяет лучше предсказывать, когда эти объекты приблизятся к Земле и другим планетам. Четыре из пяти спутников Плутона вращаются хаотично. В квантовой физике и электротехнике изучение больших массивов джозефсоновских контактов значительно выиграло от теории хаоса. Ближе к дому угольные шахты всегда были опасными местами, где частые утечки природного газа приводят к гибели многих людей. До недавнего времени не было надежного способа предсказать, когда они произойдут. Но эти утечки газа имеют хаотические тенденции, которые при правильном моделировании можно довольно точно предсказать.

Теория хаоса может применяться вне естественных наук, но исторически почти все такие исследования страдали от недостаточной воспроизводимости; плохая внешняя валидность; и / или невнимание к перекрестной проверке, что приводит к плохой точности прогноза (если даже предпринималась попытка прогнозирования вне выборки). Гласс, Манделл и Зельц обнаружили, что ни одно исследование ЭЭГ еще не показало наличие странных аттракторов или других признаков хаотического поведения.

Исследователи продолжали применять теорию хаоса к психологии. Например, при моделировании группового поведения, в котором разнородные члены могут вести себя так, как будто они в разной степени разделяют то, что в теории Уилфреда Биона является основным предположением, исследователи обнаружили, что групповая динамика является результатом индивидуальной динамика членов: каждый человек воспроизводит групповую динамику в разном масштабе, и хаотическое поведение группы отражается в каждом члене.

Редингтон и Рейдборд (1992) попытались продемонстрировать, что человеческое сердце может отображать хаотические черты. Они наблюдали за изменениями в интервалах между ударами сердца для одного пациента психотерапевта, когда она проходила периоды различной эмоциональной интенсивности во время сеанса терапии. По общему признанию, результаты были неубедительными. Не только были неоднозначности в различных графиках, которые авторы создали, чтобы якобы показать доказательства хаотической динамики (спектральный анализ, фазовая траектория и графики автокорреляции), но и когда они пытались вычислить показатель Ляпунова как более определенное подтверждение хаотического поведения, авторы обнаружили, что они не могут надежно сделать это.

В своей статье 1995 года Меткалф и Аллен утверждали, что они обнаружили в поведении животных образец удвоения периода, ведущего к хаосу. Авторы исследовали хорошо известную реакцию, называемую полидипсией, вызванной расписанием, при которой животное, лишенное пищи в течение определенного периода времени, будет пить необычное количество воды, когда пищу, наконец, принесут. Действующим здесь контрольным параметром (r) была продолжительность интервала между кормлениями после возобновления. Авторы тщательно протестировали большое количество животных и включили множество повторений, и они спланировали свой эксперимент так, чтобы исключить вероятность того, что изменения в образцах ответов были вызваны разными начальными точками для r.

Временные ряды и графики первых задержек лучше всего подтверждают сделанные утверждения, показывая довольно четкий переход от периодичности к нерегулярности по мере увеличения времени кормления. С другой стороны, различные графики фазовых траекторий и спектральный анализ недостаточно хорошо согласуются с другими графиками или с общей теорией, чтобы неумолимо вести к хаотическому диагнозу. Например, фазовые траектории не показывают определенной прогрессии в сторону все большей и большей сложности (и от периодичности); процесс кажется довольно запутанным. Кроме того, там, где Меткалф и Аллен видели периоды два и шесть на своих спектральных графиках, есть место для альтернативных интерпретаций. Вся эта двусмысленность требует некоторого извилистого апостериорного объяснения, чтобы показать, что результаты соответствуют хаотической модели.

Адаптировав модель профориентации к хаотической интерпретации взаимоотношений между сотрудниками и рынком труда, Аниундсон и Брайт обнаружили, что лучшие предложения можно сделать людям, которые борются с карьерными решениями. Современные организации все чаще рассматриваются как открытые сложные адаптивные системы с фундаментальными естественными нелинейными структурами, подверженные внутренним и внешним силам, которые могут способствовать хаосу. Например, тимбилдинг и групповое развитие все чаще исследуются как изначально непредсказуемая система, поскольку неопределенность различных людей, встречающихся впервые, делает траекторию команды непознаваемой. 108>

Некоторые говорят, что метафора хаоса, используемая в вербальных теориях, основанная на математических моделях и психологических аспектах человеческого поведения, дает полезные сведения для описания сложности небольших рабочих групп, выходящие за рамки самой метафоры.

Это так. Возможно, что экономические модели также могут быть улучшены за счет применения теории хаоса, но прогнозирование состояния экономической системы и того, какие факторы влияют на нее больше всего, является чрезвычайно сложной задачей. Экономические и финансовые системы в корне отличаются от систем классического естествознания, поскольку первые по своей природе являются стохастическими по своей природе, так как они являются результатом взаимодействия людей, и, таким образом, чисто детерминированные модели вряд ли обеспечат точное представление данных. Эмпирическая литература, которая проверяет хаос в экономике и финансах, дает очень неоднозначные результаты, отчасти из-за путаницы между конкретными тестами на хаос и более общими тестами на нелинейные отношения.

Прогнозирование трафика может выиграть от применения хаоса. теория. Более точные прогнозы того, когда возникнет трафик, позволят принять меры по его рассредоточению до того, как это произойдет. Сочетание принципов теории хаоса с несколькими другими методами привело к более точной модели краткосрочного прогнозирования (см. График модели трафика BML справа).

Теория хаоса была применена к окружающей воде данные цикла (также известные как гидрологические данные), такие как осадки и сток. Эти исследования дали противоречивые результаты, потому что методы обнаружения хаотической сигнатуры часто относительно субъективны. Ранние исследования имели тенденцию «преуспевать» в обнаружении хаоса, тогда как последующие исследования и метаанализ ставили эти исследования под сомнение и давали объяснения, почему эти наборы данных вряд ли будут иметь хаотическую динамику низкой размерности.

См. Также

Примеры хаотических систем

Другие связанные темы

Люди

Список литературы

Дополнительная литература

Статьи

• Шарковский, АН (1964). «Сосуществование циклов непрерывного отображения линии в себя». Украинская математика. J. 16 : 61–71.
• Li, T.Y. ; Yorke, J.A. (1975). «Третий период подразумевает хаос» (PDF). Американский математический ежемесячник. 82(10): 985–92. Bibcode : 1975AmMM… 82..985L. CiteSeerX 10.1.1.329.5038. DOI : 10.2307 / 2318254. JSTOR 2318254.
• Алемансур, Хамед; Миандоаб, Эхсан Маани; Пишкенари, Хоссейн Неджат (март 2017 г.). «Влияние размера на хаотическое поведение нанорезонаторов». Коммуникации в нелинейной науке и численном моделировании. 44 : 495–505. Bibcode : 2017CNSNS..44..495A. doi : 10.1016 / j.cns.2016.09.010.
• Кратчфилд ; Такер; Моррисон; Дж. Д. Фермер ; Packard ; N.H.; Шоу ; Р.С. (декабрь 1986 г.). «Хаос». Scientific American. 255 (6): 38–49 (библиография с.136). Bibcode : 1986SciAm.255d..38T. doi : 10.1038 / scientificamerican1286-46.Онлайн-версия (Примечание: цитируемые тома и страницы для онлайн-текста отличаются от цитируемых здесь. Цитата здесь взята из фотокопии, что согласуется с другими цитатами, найденными в Интернете, которые не отражают просмотры статей. Интернет-контент идентичен печатному тексту. Варианты цитирования зависят от страны публикации).
• Kolyada, SF (2004). «Чувствительность Ли-Йорка и другие концепции хаоса». Украинская математика. Дж. 56 (8): 1242–57. DOI : 10.1007 / s11253-005-0055-4. S2CID 207251437.
• Day, R.H.; Павлов, О.В. (2004). «Вычисление экономического хаоса». Вычислительная экономика. 23 (4): 289–301. doi : 10.1023 / B: CSEM.0000026787.81469.1f. SSRN 806124.
• Strelioff, C.; Хюблер А. (2006). «Среднесрочное предсказание хаоса» (PDF). Phys. Rev. Lett. 96 (4): 044101. Bibcode : 2006PhRvL..96d4101S. doi : 10.1103 / PhysRevLett.96.044101. PMID 16486826. 044101. Архивировано из оригинала (PDF) 26 апреля 2013 г.
• Hübler, A.; Фостер, G.; Фелпс, К. (2007). «Управление хаосом: нестандартное мышление» (PDF). Сложность. 12 (3): 10–13. Bibcode : 2007Cmplx..12c..10H. DOI : 10.1002 / cplx.20159. Архивировано с оригинального (PDF) 30.10.2012. Проверено 17 июля 2011 г.
• Motter, Adilson E.; Кэмпбелл, Дэвид К. (2013). «Хаос в 50». Физика сегодня. 66 (5): 27. arXiv : 1306.5777. Bibcode : 2013PhT…. 66e..27M. doi : 10.1063 / PT.3.1977.

Учебники

• Alligood, K.T.; Зауэр, Т.; Йорк, Дж. (1997). Хаос: введение в динамические системы. Springer-Verlag. ISBN 978-0-387-94677-1. CS1 maint: ref = harv (ссылка )
• Бейкер, Г.Л. (1996). Хаос, рассеяние and Statistical Mechanics. Cambridge University Press. ISBN 978-0-521-39511-3.
• Badii, R.; Politi A. (1997). Сложность: иерархические структуры и масштабирование в физике. Cambridge University Press. ISBN 978-0-521-66385-4.
• Bunde; Havlin, Shlomo, eds. (1996). Фракталы и неупорядоченные системы. Springer. ISBN 978-3642848704.и Bunde; Havlin, Shlomo, eds. (1994). Fractals in Science. Springer. ISBN 978-3-540-56220-7.
• Collet, Pierre, и Eckmann, Jean-Pierre (1980). Итерированные карты на интервале как Dynamical Systems. Birkhauser. ISBN 978-0-8176-4926-5. CS1 maint: несколько имен: список авторов (ссылка )
• Девани, Роберт Л. (2003). Введение в хаотические динамические системы (2-е изд.). Westview Press. ISBN 978-0- 8133-4085-2. CS1 maint: ref = harv (ссылка )
• Робинсон, Кларк (1995). Динамические системы: устойчивость, символическая динамика и хаос. CRC Press. ISBN 0-8493-8493-1. CS1 maint: ref = harv (ссылка )
• Фельдман, Д.П. (2012). Хаос и Фракталы: элементарное введение. Oxford University Press. ISBN 978-0-19-956644-0.
• Gollub, JP; Baker, GL (1996). Chaotic динамика. Cambridge University Press. ISBN 978-0-521-47685-0.
• Гукенхаймер, Джон ; Холмс, Филип (1983). Нелинейные колебания, динамические системы и бифуркации векторных полей. Springer-Verlag. ISBN 978-0-387-90819-9.
• Гулик, Денни (1992). Встречи с хаосом. Макгро-Хилл. ISBN 978-0-07-025203-5.
• Гуцвиллер, Мартин (1990). Хаос в классической и квантовой механике. Springer-Verlag. ISBN 978-0-387-97173-5.
• Гувер, Уильям Грэм (2001) [1999]. Обратимость времени, компьютерное моделирование и хаос. World Scientific. ISBN 978-981-02-4073-8.
• Каутц, Ричард (2011). Хаос: наука о П. изменяемое случайное движение. Издательство Оксфордского университета. ISBN 978-0-19-959458-0.
• Киль, Л. Дуглас; Эллиотт, Юэл В. (1997). Теория хаоса в социальных науках. Издательство «Персей». ISBN 978-0-472-08472-2.
• Мун, Фрэнсис (1990). Хаотическая и фрактальная динамика. Springer-Verlag. ISBN 978-0-471-54571-2.
• Отт, Эдвард (2002). Хаос в динамических системах. Издательство Кембриджского университета. ISBN 978-0-521-01084-9.
• Строгац, Стивен (2000). Нелинейная динамика и хаос. Издательство «Персей». ISBN 978-0-7382-0453-6.
• Спротт, Джулиен Клинтон (2003). Хаос и анализ временных рядов. Издательство Оксфордского университета. ISBN 978-0-19-850840-3. CS1 maint: ref = harv (ссылка )
• Tél, Tamás; Gruiz, Márton (2006) Хаотическая динамика: введение, основанное на классической механике. Cambridge University Press. ISBN 978-0-521-83912-9.
• Teschl, Gerald ( 2012). Обыкновенные дифференциальные уравнения и динамические системы. Провиденс : Американское математическое общество. ISBN 978-0-8218- 8328-0.
• Thompson JM, Stewart HB (2001). Nonlinear Dynamics And Chaos. John Wiley and Sons Ltd. ISBN 978-0-471-87645-8.
• ; Reilly (1992). Экспериментальный подход к нелинейной динамике и хаосу. American Journal of Physics. 61 . Addison-Wesley. P. 958. Bibcode : 1993AmJPh..61..958T. doi : 10.1119 / 1.17380. ISBN 978-0-201-55441-0.
• Уиггинс, Стивен (2003). Введение в прикладные динамические системы и хаос. Спрингер. ISBN 978-0-387-00177-7.
• Заславс ky, Джордж М. (2005). Гамильтонов хаос и дробная динамика. Издательство Оксфордского университета. ISBN 978-0-19-852604-9.

Политехнические и популярные работы

• , Хаос в природе, World Scientific Publishing Company, 2012, ISBN 978-981-4374-42-2.
• Авраам, Ральф; и другие. (2000). Abraham, Ralph H.; Уэда, Ёсисуке (ред.). Авангард Хаоса: Воспоминания о первых днях теории Хаоса. Всемирная научная серия по нелинейным наукам, серия A. 39 . World Scientific. Bibcode : 2000cagm.book….. A. DOI : 10.1142 / 4510. ISBN 978-981-238-647-2. CS1 maint: ref = harv (ссылка )
• (2000). Фракталы везде. Морган Кауфманн. ISBN 978-0-12-079069-2.
• Берд, Ричард Дж. (2003). Хаос и жизнь: сложность и порядок в эволюции и Мысль. Columbia University Press. ISBN 978-0-231-12662-5.
• Джон Бриггс и Дэвид Пит, Turbulent Mirror:: Иллюстрированное руководство по теории хаоса and the Science of Wholeness, Harper Perennial 1990, 224 pp.
• Джон Бриггс и Дэвид Пит, Семь жизненных уроков хаоса: духовная мудрость от науки изменений, Harper Perennial 2000, 224 стр.
• Cunningham, Лоуренс А. (1994). «От случайных блужданий к хаотическим сбоям: линейная генеалогия гипотезы эффективного рынка капитала». George Washington Law Review. 62 : 546.
• Предраг Цвитанович, Универсальность в хаосе, Адам Хилгер 1989, 648 стр.
• Леон Гласс и Майкл С. Макки, От часов к хаосу: ритмы жизни, Принстон University Press 1988, 272 стр.
• Джеймс Глейк, Хаос: Создание новой науки, Нью-Йорк: Пингвин, 1988. 368 стр.
• Джон Гриббин. Глубокая простота. Penguin Press Science. Penguin Books.
• Л. Дуглас Киль, Юэл Эллиотт (редактор), Теория хаоса в социальных науках: основы и приложения, University of Michigan Press, 1997, 360 стр.
• Арвинд Кумар, Хаос, Фракталы и самоорганизация; Новые взгляды на сложность природы, Национальный книжный фонд, 2003 г.
• Ханс Лауверьер, Фракталы, издательство Принстонского университета, 1991 г.
• Эдвард Лоренц, Сущность хаоса, Вашингтонский университет, 1996 г.
• Маршалл, Алан (2002). Единство природы — целостность и дезинтеграция в экологии и науке. DOI : 10.1142 / 9781860949548. ISBN 9781860949548.
• Дэвид Пик и Майкл Фрейм, Хаос под контролем: искусство и наука сложности, Фриман, 1994.
• Хайнц-Отто Пайтген и Дитмар Saupe (ред.), The Science of Fractal Images, Springer 1988, 312 стр.
• Клиффорд А. Пиковер, Computers, Pattern, Chaos, and Beauty: Graphics from the Unseen World, St Martins Pr 1991.
• Клиффорд А. Пиковер, Хаос в стране чудес: Визуальные приключения во фрактальном мире, St Martins Pr, 1994.
• Илья Пригожин и Изабель Стендерс, Order Out of Chaos, Bantam 1984.
• Peitgen, Heinz-Otto; Рихтер, Питер Х. (1986). Красота фракталов. DOI : 10.1007 / 978-3-642-61717-1. ISBN 978-3-642-61719-5.
• Дэвид Рюэлль, Chance and Chaos, Princeton University Press, 1993.
• Иварс Петерсон, Часы Ньютона: Хаос в Солнечной системе, Фримен, 1993.
• Ян Роулстон; Джон Норбери (2013). Невидимый во время бури: роль математики в понимании погоды. Издательство Принстонского университета. ISBN 978-0691152721.
• Руэлль, Д. (1989). Хаотическая эволюция и странные аттракторы. DOI : 10.1017 / CBO9780511608773. ISBN 9780521362726.
• Манфред Шредер, Фракталы, хаос и степенные законы, Фримен, 1991.
• Смит, Питер (1998). Объясняя хаос. DOI : 10.1017 / CBO9780511554544. ISBN 9780511554544.
• Ян Стюарт, «Играет ли Бог в кости ?: Математика хаоса», издательство Blackwell Publishers, 1990.
• Стивен Строгац, Синхронизация: новая наука стихийного порядка, Hyperion, 2003.
• Йошисуке Уэда, The Road To Chaos, Aerial Pr, 1993.
• М. Митчелл Уолдроп, Сложность: зарождающаяся наука на грани порядка и хаоса, Саймон и Шустер, 1992.
• Антонио Савая, Анализ финансовых временных рядов: Хаос и нейродинамический подход, Ламберт, 2012.

Внешние ссылки

Викискладе есть средства массовой информации, связанные с теорией хаоса.

• , энциклопедией математики, EMS Press, 2001 [1994]
• Nonlinear Dynamics Research Group с анимацией во Flash
• Группа Хаоса в Университете Мэриленда
• Гипертексток Хаоса. Введение в хаос и фракталы
• ChaosBook.org Учебник для продвинутых выпускников по хаосу (без фракталов)
• Общество теории хаоса в психологии и науках о жизни
• Группа исследований нелинейной динамики в CSDC, Флоренс Италия
• Интерактивный эксперимент с хаотическим маятником в реальном времени, позволяет пользователям взаимодействовать и брать образцы данных из реального работающего хаотического маятника с демпфированием
• Нелинейная динамика: как наука понимает хаос, доклад, представленный Санни Ауянг, 1998.
• Нелинейная динамика. Модели бифуркации и хаоса Элмера Дж. Винса
• Хаос Глейка (отрывок)
• Группа системного анализа, моделирования и прогнозирования в Оксфордском университете
• Страница об уравнении Макки-Гласса
• Высокие беспокойства — Математика хаоса (2008) Документальный фильм BBC, режиссер Дэвид Мэлоун
• Теория эволюции хаоса — статья, опубликованная в Newscientist, демонстрирующая сходство эволюции и нелинейных систем, включая фрактальную природу жизни и хаоса.
• Джос Лейс, Этьен Гиз и Орельен Альварес, Хаос, математическое приключение. Девять фильмов о динамических системах, эффекте бабочки и теории хаоса, предназначенных для широкой аудитории.
• «Теория хаоса», обсуждение BBC Radio 4 со Сьюзан Гринфилд, Дэвидом Папино и Нилом Джонсоном («В наше время», 16 мая, 2002)