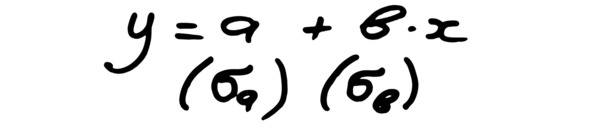1. Парная линейная регрессия
1.1. Оформление отчёта
Отчёт о работе оформляется в виде рабочей книги Excel. Саму работу мы тоже выполняем в этой же рабочей книги. Каждое отдельное задание оформляем на новом рабочем листе. Подробности оформления отчёта описаны в работе [1].
Отчёт начинаем, как обычно, с титульного листа. Это первый лист рабочей книги. На титульном листе нужно указать название министерства, ВУЗа, кафедры. Далее идёт тип и название документа. Конечно, нужно указать номер студенческой группы, а также фамилию и инициалы студента. В нижней части титульного листа располагают название города и год.
На втором листе размещают оглавление работы. В нашем случае это название разделов и ссылка на соответствующий лист рабочей книги.
На третьей странице отчёта укажите номер зачетки. Это будут настройки генератора случайных чисел для имитационного моделирования.
Задание. Создайте новый документ Excel и сохраните, выбрав уникальное информативное имя файла.
1.2. Общий план работы
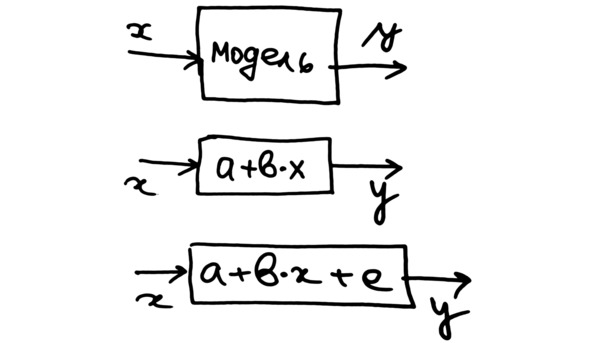
В первой работе мы будем знакомиться с парной линейной регрессией. Напомним, что регрессия — это построение зависимости в среднем по большому количеству точек (исходных данных). Слово «парная» означает, что у нас всего «пара» переменных — «икс» и «игрек». Слово «линейная» указывает, что мы будем строить линейное уравнение, то есть уравнение прямой линии. В линейном уравнении «икс» участвует в первой степени
В качестве исходных данных мы будем использовать результаты имитационного моделирования. Это позволит работать с такими данными, которые заведомо содержат интересующие нас закономерности.
Мы сгенерируем два столбца, в которых будет находиться одна независимая переменная «икс» и одна зависимая переменная «игрек». В этих данных будет заложена линейная взаимосвязь на фоне случайных отклонений — случайный разброс точек вокруг прямой линии.
«Икс» называют независимой переменной — independent variable. Предполагается, что «икс» может меняться как угодно и что он ни от чего в нашей модели не зависит. Другими словами, «икс» — это вход модели.
Изменение «икса» объясняет поведение «игрека». Поэтому «икс» ещё называют «объясняющей» переменной.
«Игрек» выступает в роли зависимой переменной — dependent variable. Он зависит от «икса». Хотя бы частично.
Для моделирования мы используем генератор случайных чисел из надстройки «Анализ данных». Попутно заметим, что полученные случайные числа будут записаны как числовые значения. Они не будут меняться со временем. В других ситуациях нам как раз будет нужно, чтобы случайные числа менялись — тогда мы будем вызывать функцию RAND.
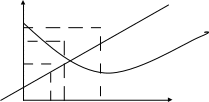
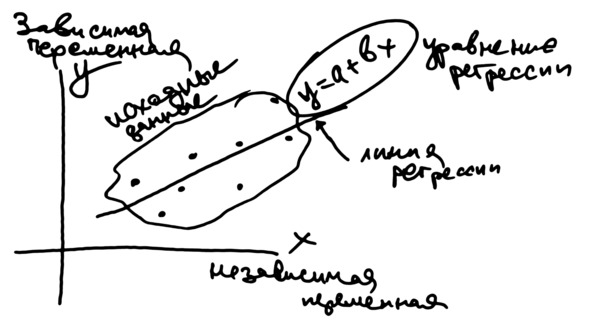
Далее мы рассмотрим методику построения линейной модели, которая описывает наши данные в среднем. Это означает, что на графике линия должна проходить в среднем — по местам сгущения точек.
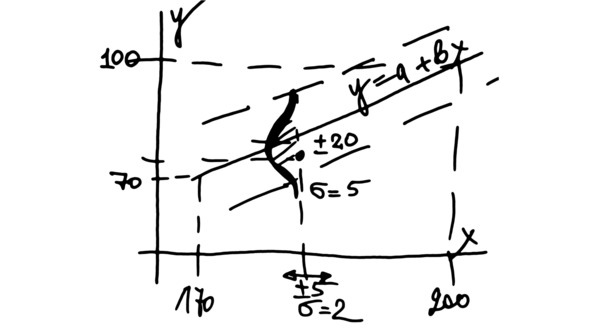
Кроме уравнения такой линии, нам понадобится определить возможную неопределённость (погрешность) полученных коэффициентов.
Окончательное уравнение должно содержать как коэффициенты, так и их погрешность. Случайную ошибку обычно описывают с помощью «сигмы». Это стандартное отклонение, или среднеее квадратическое отклонение (СКО). Для каждого коэффициента указываем его сигму — под коэффициентом в скобках, см. рис.
Рис. Коэффициенты и их сигмы
Для оценки коэффициентов и их «сигм» в данной работе используем три способа:
— надстройку «Анализ данных»;
— функцию ЛИНЕЙН — LINEST;
— формулы Excel.
Затем нам нужно будет провести интерпретацию полученного уравнения. Мы сформулируем смысл уравнения регрессии в виде высказывания, понятного обычному пользователю.
1.3. Надстройка
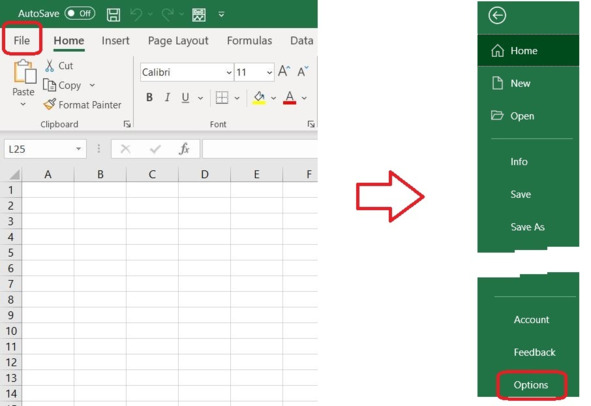
Чтобы включить надстройку «Анализ данных», вызовите File — Options.
Рис. Меню «Файл»
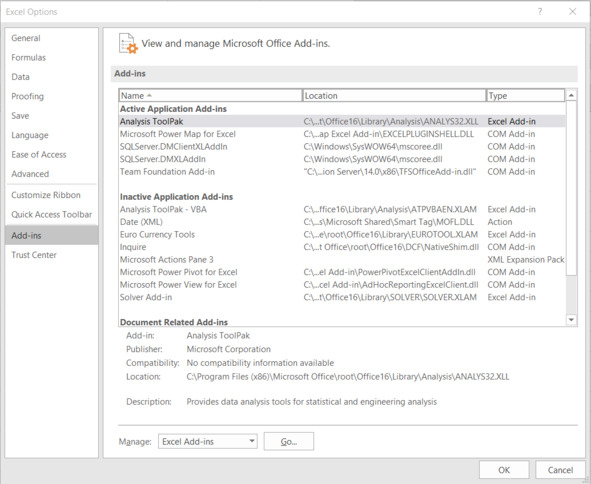
В диалоговом окне Excel Options выбираем: Add-ins — Manage — Excel Add-ins — Go, см. рис.
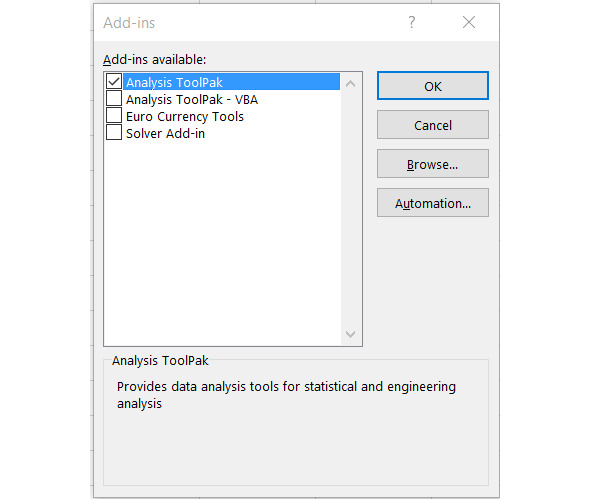
Ставим галочку рядом пунктом AnalysisToolpak — Пакет анализа, см. рис.
Рис. Меню «Надстройки»
Рис. Включение надстройки «Анализ данных»
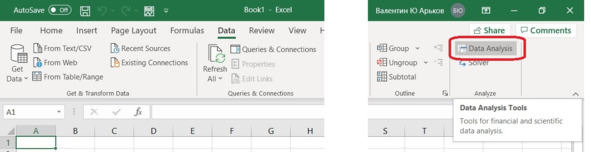
Если надстройка активирована, можно будет найти кнопку Data Analysis в разделе меню Data — Analysis, см. рис.
Рис. Надстройка в разделе «Анализ»
1.4. Исходные данные
Сгенерируем исходные данные. Наши переменные будут расположены по столбцам.
В данной работе мы сформируем по 100 значений в каждом столбце. Это не слишком много и не слишком мало. С одной стороны, графики будут достаточно наглядными. С другой стороны, рисунки не будут слишком основательно заполнены точками.
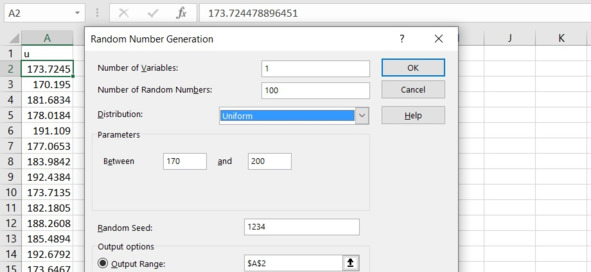
Первый столбец — переменная u. Сгенерируйте столбец случайных чисел с равномерным распределением от 170 до 200. Начальное состояние генератора — четыре последние цифры номера зачетки, см. рис.
Рис. Настройки генератора
Далее нам нужно сгенерировать два столбца случайных чисел e1 и e2 со стандартным нормальным распределением. У такого распределения среднее значение MEAN равно нулю, а стандартное отклонение STANDARD DEVIATION равно единице. Сразу задаём генерирование двух столбцов — число переменных равно двум. Начальное состояние генератора — четыре последних цифры номера зачетки плюс 5.
Разные настройки генератора позволят создать независимые случайные числа в разных колонках.
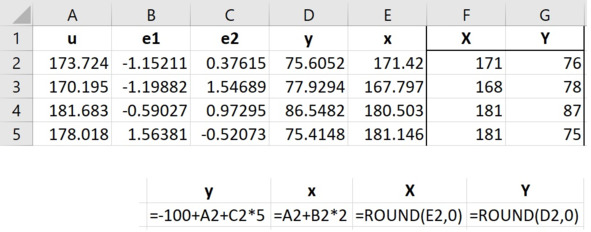
В следующем столбце y введём формулу, как показано на рисунке.
Рис. Формулы по столбцам
В следующем столбце сформируем x. Добавим к значениям u из первого столбца случайный разброс e1.
Наконец, округлим два последних столбца x и y до целых значений с помощью функции ROUND. Эти два столбца X и Y будут имитировать результаты измерений. Когда мы что-то измеряем, всегда появляются случайные погрешности измерений, пускай даже небольшие и незаметные. К тому же, такие параметры тела, как рост и вес, немного меняются даже в течение суток.
Наши «иксы» — это значения роста человека в сантиметрах. «Игреки» — это значения веса в килограммах. Мы закладываем в нашу выборку зависимость веса от роста. Затем добавляем в данные случайный разброс.
Рис. Линейная модель
Рис. Зашумлённые наблюдения
Рис. Постановка задачи
Рис. Имитационное моделирование
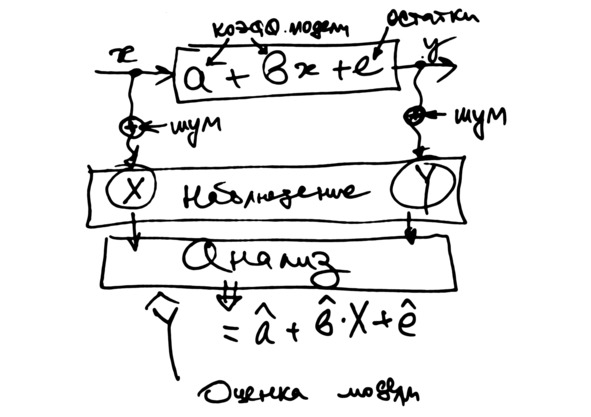
На схеме показано, как добавляются случайные погрешности измерений к значениям иксов и игреков. Таким образом, при анализе реальных данных наши числа всегда содержат случайный шум. Это зашумлённые данные.
Результаты эконометрического анализа — это ОЦЕНКИ коэффициентов уравнения. Мы говорим «оценки», чтобы подчеркнуть, что полученные значения коэффициентов отличаются от истинных, правильных, точных значений. К тому же, они изменяются, если взять другой набор таких же данных — другую выборку.
Кроме коэффициентов уравнения, нас будут интересовать ПРОНОЗ значений завипсимой переменной — игрека. Задавая значения икса, мы пронозируем возможное значение игрека. Оно тоже будет меняться; это будет случайная погрешность. Так что пронозы тоже являются оценками.
Оценки коэффициентов и пронозы зависимой переменной обозначены символом, который называют «крышка», или «крышечка». Обозначение читается так: «икс с крышкой», «игрек с крышкой», см. рис.
Рис. Условные обозначения
Мы подробно обсуждаем такие «очевидные» вещи, о которых почему-то не пишут в учебниках. Это вроде как «все знают». Хотя выясняется, что это знают только преподаватели, а вот студенты должны об этом узнать каким-то волшебным образом, ведь «это же настолько элементарно».
Один преподаватель так и сказал: «Ну я же это вам уже рассказывал». Студенты возразили: «Нет, вы нам это не рассказывали». Преподаватель просто возмутился: «Ну не вам, значит другим. Я это уже сколько раз рассказывал. Каждый год кому-нибудь обязательно рассказываю. Одним объясняю, а другие не понимают!»
Вот поэтому приходится составлять учебное пособие — для изучения учебника. Учебное пособие (по определению) должно помогать в учёбе. Слово «пособить» означает «помочь». Но пособие не может заменить учебник. Так что студентам не помешает открыть пару учебников по нашему предмету, а потом вернуться к нашему пособию и продолжить изучение материала.
Символ «крышка» — это пример того, что называется УСЛОВНЫЕ ОБОЗНАЧЕНИЯ. Это означает, что авторы о чём-то «условились», то есть «договорились». Это соглашение, доворённость о том, что и как будет в тексте и в формулах обозначено. Следите за условными обозначениями в формулах.
Чтобы всё окончательно запутать, в книгах по эконометрике и в программных продуктах используют разные условные обозначения. А ещё эти обозначения не всегда подробно объясняют и расшифровывают. Так что следите за смыслом.
1.5. Диаграмма разброса
Построим диаграмму разброса Y (X). В русском варианте пакета Excel он называется «точечный график».
Выбираем ячейку для вывода графика.
Вызываем Insert — Charts — Scatter — Scatter.
Рис. Выбор диаграммы разброса
Щёлкните по графику правой кнопкой мыши и выберите Select Data (Выбрать данные).
В диалоговом окне выберите Legend Entries / Series (Легенда графика либо ряды данных) — Add (Добавить).
Рис. Выбор данных для графика
Рис. Выбор рядов данных
Рис. Выбор диапазона ячеек
В меню Edit Series (Редактирование ряда данных) установите следующие настройки:
Series Name (Название ряда) — Исходные данные
Series X values (Ряд X) — нажмите кнопку, выделите колонку значений X и нажмите кнопку в окне Edir Series (Редактирование ряда)
Series Y values (Ряд Y) — выделите колонку значений Y
Рис. Источник данных
Обратите внимание на изменение в диалоговом окне Select Data Source (Выберите источник данных). В списке рядов данных Legend Entries (Series) появился ряд «Исходные данные». В разделе Horizontal (Category) Axis Labels (Метки горизонтальной оси) выводятся значения переменной X.
После нажатия OK появится окно графика.
Рис. Настройки график по умолчанию
Можно видеть настройки графика по умолчанию: заголовок графика — имя ряда данных, масштаб по осям начинается от нуля. Названия осей отсутствуют.
Настройте оформление графика:
Измените заголовок, сделав двойной щелчок по заголовку.
Настройте масштаб по осям. Укажите на ось, щёлкните правой кнопкой по горизонтальной оси и выберите в контекстном меню Format Axis (Форматирование оси). Можно также дважды щёлкнуть осилевой кнопкой мыши.
В правой части окна Excel появится окно Format Axis. Выберите масштаб по оси так, чтобы занять всё поле графика исходными данными, но оставить место по краям графика: Axis Options (Настройка осей) — Bounds (Граничные значения) — Minimum (Минимум) / Maximum (Максимум).
Рис. Настройка графика
Аналогично настройте масштаб по вертикальной оси.
Рис. Масштаб по оси
Настройте маркеры для точек на графике. Щёлкните по любому из маркеров. Появится меню Format Data Series (Форматировать ряд данных). Выберите Marker (Маркер) — Marker Options (Настройка маркера) — Built-in (Встроенный) — Type (Тип) и Size (Размер).
Рис. Тип маркера
Настройте заливку маркера:
Format Data Series (Форматировать ряд данных). Выберите Marker (Маркер) — Fill (Заливка) — Solid Fill (Сплошная заливка) и Color (Цвет), а также Border (Обрамление) — No line (Без обрамления).
Рис. Диаграммма с маркерами
Установите названия осей.
Щёлкните по графику. В верхнем меню появится раздел Chart Tools (Инструменты диаграмм) — Design (Конструктор).
Выберите Add Chart Element (Добавить элемент диаграммы) — Axis Titles (Заголовки осей) — Primary horizontal (Основной заголовок горизонтальной оси).
Рис. Вставка заголовков осей
Введите информативное название оси, указав параметр и единицы измерения. Для редактирования заголовка щёлкните по нему левой кнопной мыши.
Аналогично введите заголовок вертикальной оси.
Для нас это упражнение по оформлению документов / документов / отчётов. Графики, заголовки, единицы измерения и прочее — всё должно быть понятно не только автору, но и читателю. Да и сам составитель документа через неделю может и не вспомнить, что он выводил на очередной график. Так что лучше чётко указать, кто есть кто.
Рис. Оформленный график
1.6. Регрессионный анализ
Мы будем проводить регрессионный анализ тремя способами:
— надстройка;
— функция;
— формулы.
Эти способы получения оценок коэффициентов уравнения регрессии в общих чертах рассмотрены в работе [2].
В дополнение к описанным приёмам нам предстоит получить оценки с. к. о. для оценок коэффициентов уравнения. С.к.о., или среднее квадратичное отклонение, или стандартное отклонение, или просто «сигма», характеризует возможный разброс оценок. Если взять другую выборку, мы полчим немного другие оценки, очень похожие, но всё-таки разные.
Для понимания материала желательно освежить в памяти понятия распределения и сигмы. Эти вещи рассматриваются в курсе «Бизнес-аналитика и статистика».
1.6.1. Надстройка
Вызываем надстройку «Анализ данных»: Data — Data Analysis. Выбираем в диалоговом окне раздел Регрессия — Regression.
На текущем листе будут выведены многочисленные результаты регрессионного анализа. Сейчас нас будут интересовать коэффициенты и их стандартные отклонения (сигмы). Их можно найти в таблице с коэффициентами уравнения регрессии.
Постройте регрессию Y на Х.
Запустите надстройку Анализ данных:
Data (Данные) — Data Analysis (Анализ данных) — Regression (Регрессия)
Рис. Вызов модуля регрессионного анализа
Выберите факторную и результативную переменные.
Input (Исходные данные) — Input Y Range (Диапазон исходных данных по Y)
Input (Исходные данные) — Input X Range (Диапазон исходных данных по X)
Confidence Level (Доверительная вероятность) = 95%
Output Options (Параметры вывода результатов) — New Worksheet (Вывод результатов на новую страницу рабочей книги Excel)
Residuals (Остатки) — Line Fit Plots (Графики линейной регрессии)
Рис. Параметры регрессионного анализа
После нажатия OK будет сформирована новая страница с результатами регрессионного анализа.
Переименуйте листы рабочей книги, дважды щёлкнув по соответствующей вкладке.
Рис. Результаты анализа
Настройте оформление графика.
Установите приемлемые размеры графика.
Настройте заголовок графика и названия осей, дважды щёлкнув по соответствующим надписям.
Установите масштаб по осям. Всё поле графика должно быть занято данными. При этом точки не должны оказаться на границе или за пределами графика.
Настройте маркеры для исходных данных.
Настройте вывод на график линии регрессии.
Format Data Series (Формат вывода данных на график) — Series Options (Настройки вывода для ряда данных) — Fill & Line (Заливка и линии) — Marker (Маркер) — None (Без маркера)
Line (Линия) — Solid Line (Сплошная линия)
Color (Цвет линии)
Width (Толщина линии)
Удалите легенду (условные обозначения) с графика
Рис. Легенда для диаграммы
Рис. Окончательное оформление графика
Рис. Коэффициенты и их сигмы (с. к. о.)
В таблице приводятся следующие оценки:
— Coefficients (Коэффициенты)
— Standard Error (Стандартные ошибки коэффициентов)
— Intercept (Свободный член уравнения)
— X Variable 1 (Коэффициент регрессии при первой переменной X)
Запишите результаты регрессионного анализа в следующем виде:
Рис. Оценки и их ошибки
Количество значащих разрядов должно быть не меньше, чем в исходных данных. Значащие разряды относятся к представлению числа с плавающей точкой, а не к знакам после десятичной запятой, см. рис.
Рис. Три значащих разряда
Напомним, что такое «число с плавающей точкой». Это особая компьютерная запись числа. Часто встречается при выводе чисел на экран. Такое число состоит из мантиссы (значащей части) и показателя степени, см. рис.
Рис. Число с плавающей точкой
Выражение «плавающая точка» имеет свой смысл. При записи дробных чисел точка в западных странах и запятая в России разделяет целую и дробную части числа. Слово «плавающая» означает, что положение этого разделителя «плавает», то есть его можно сдвинуть влево или вправо — достаточно умножать на десять в какой-нибудь степени.
Обратим внимание, что на рисунке во всех числах имеется всего три значащих разряда. Это количество десятичных знаков в мантиссе.
Вторая часть записи — показатель степени. Между мантиссой и показателем находится английская буква Е. Это первая буква английского слова EXPONENT, которое переводится как «показатель степени». Русское слово «экспонента» звучит похоже, но означает «возведение числа Эйлера е ≈ 2,718… в какую-нибудь степень».
Перед нами очередная ловушка для переводчика. Есть такое выражение — «ложные друзья переводчика». Это иностранные слова, которые звучат точно так же, как и русские слова, но имеют другое значение.
Просмотрите статью Floating-point arithmetic в Википедии.
Посмотрите перевод слова exponent в Переводчике Яндекса.
Посмотрите значение слова экспонента и выражения экспоненциальная функция в Вики-Словаре.
В нашем примере значения роста содержат три значащих разряда, значения веса — два. Поэтому следует оставить хотя бы три значащих разряда.
Если при округлении последний разряд оказался равным нулю, записываем ноль. Это явно указывает читателю, сколько мы оставили значащих разрядов.
Рис. Коэффициенты и с. к. о. — три значащих разряда
Запишите уравнеие регрессии с указанием названия переменных.
Рис. Уравнение регрессии
Проведём интепретацию уравнения регрессии. Объясним простыми словами, что означает коэффициент 0,920 при переменной «Рост». Напомним, что в нашем примере вес измеряется в килограммах, а рост — в сантиметрах.
Чтобы число было приятнее для глаза, умножим его на десять. Вот что у нас теперь получается:
При увеличении роста в анализируемой выборке на 10 сантиметров вес увеличивается в среднем на 9,2 килограмма.
Проведите интерпретацию своего уравнения регрессии в таком же стиле.
1.6.2. Функция LINEST
Функция LINEST / ЛИНЕЙН позволяет получить оценку параметров линейного уравнения с помощью метода наименьших квадратов (МНК). Прежде всего, это коэффициенты линейного уравнения. В уравнении может быть один «игрек» и один или более «иксов». Другими словами, это модель с одним входом и несколькими выходами.
Само название функции, скорее всего, является сокращением от выражения Linear Estimates (линейные оценки) или Linear Model Estimate (оценка линейной модели).
Данная функция позволяет получить не только оценки коэффициентов уравнения регрессии. Здесь есть и дополнительные возможности, см. рис.
Рис. Параметры функции LINEST
При указании значения TRUE для аргумента stats функция выводит дополнительные статистические показатели.
В справке по данной функции приводится порядок вывода результатов. В первой строке имеем оценки коэффициентов. Во второй строке выводятся стандартные ошибки для наших коэффициентов Standard Errors (SE).
Конец ознакомительного фрагмента.
Содержание
- Решение задач по эконометрике
- Корреляционно-регрессионный метод анализа
- Непараметрические показатели связи
- Гетероскедастичность случайной составляющей
- Автокорреляция
- Эконометрические методы проведения экспертных исследований
- Классификация эконометрических моделей и методов
- Введение
- I. Основная часть
- Параметрическая идентификация парной линейной эконометрической модели
- Критерий Фишера
- Параметрическая идентификация парной нелинейной регрессии
- Прогнозирование спроса на продукцию предприятия. Использование в MS Excel функции «Тенденция»
Решение задач по эконометрике
Корреляционно-регрессионный метод анализа
- Уравнение парной линейной регрессии (см. также уравнение парной линейной регрессии матричным методом);
При регрессионном анализе необходимо найти уравнение линейной парной регрессии. Исходные данные представляют собой значения X (признак-фактор) и значения Y (признак-результат).
Для этого указывается количество строк . Второй вариант ввода данных — вставить их из Excel (X — первый столбец,Y — второй столбец). Пример. Для зависимой переменной, если указан процент (например, 105%), то значение рассчитывается от среднего значения X. - Уравнение нелинейной регрессии: экспоненциальная y = a*e bx ,степенная y = a x b , равносторонняя гипербола y = b/x + a , логарифмическая y = b ln(x) + a , показательная y = a*b x . Если необходимо найти полиномиальное уравнение второго порядка (парабола), то можно воспользоваться сервисом Аналитическое выравнивание;
Далее выбирается вид регрессии, зависимая переменная и уровень значимости α. - Дисперсионный анализ. Разложение дисперсий для анализа влияния анализируемого признака (см. также Однофакторный дисперсионный анализ);
- Уравнение множественной регрессии. Дополнительно с помощью другого онлайн-калькулятора Матрица парных коэффициентов корреляции находятся уравнения множественной регрессии в стандартизованном и натуральном масштабе.
- Расчет коэффициента детерминации;
- Метод статистических уравнений зависимостей;
- Система одновременных уравнений:
. Необходимое и достаточное условия идентификации.
Непараметрические показатели связи
Гетероскедастичность случайной составляющей
Автокорреляция
- Автокорреляция уровней временного ряда. Проверка на автокорреляцию с построением коррелограммы;
Эконометрические методы проведения экспертных исследований
- Метод средних оценок.
- Метод медиан рангов.
- Коэффициент конкордации.
- Коэффициент контингенции.
- Критерий Манна-Уитни
- Методом дисперсионного анализа проверить нулевую гипотезу о влиянии фактора на качество объекта.
Полученное решение оформляется в формате Word . Сразу после решения следует ссылка на скачивание шаблона в Excel, что дает возможность проверить все полученные показатели. Если в задании требуется решение в Excel , то можно воспользоваться статистическими функциями в Excel.
Источник
Классификация эконометрических моделей и методов
| Доступные действия |
|
- Прокомментировать файл
МОСКОВСКИЙ ГУМАНИТАРНО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Кафедра общегуманитарных дисциплин
Специальность: Бухгалтерский учет, анализ и аудит.
Учебная дисциплина: «Эконометрика»
студентки 3 курса группа ББ-341
факультет экономики и управления
Тимофеевой Татьяны Евгеньевны
Снастин Александр Анатольевич
I. Основная часть
Параметрическая идентификация парной линейной эконометрической модели
Параметрическая идентификация парной нелинейной регрессии
Прогнозирование спроса на продукцию предприятия. Использование в MS Excel функции «Тенденция»
Введение
Классификация эконометрических моделей и методов.
Эконометрика — это наука, лежащая на стыке между статистикой и математикой, она разрабатывает экономические модели для цели параметрической идентификации, прогнозирования (анализа временных рядов).
Классификация эконометрических моделей и методов.
Эконометрические модели (ЭМ)
| Эконометрические модели параметрической идентификации | Эконометрические модели для цели прогнозирования | Система эконометрических моделей |
(установление параметров (есть ли тренд) (комплексная модели) оценка)
y — зависимая переменная (отклик), прибыль, например. x — независимая переменная (регрессор), какова численность персонала, например. На основании наблюдений оцениваются a и b (определение параметров моделей или регрессионные коэффициенты).
| № п/п | y | x |
| 1 | 11 | 1 |
| 2 | 13 | 2 |
| 3 | 14 | 3 |
| 4 | 12 | 4 |
| 5 | 17 | 5 |
| 6 | 16,7 | 6 |
| 7 | 17,8 | 7 |
На основании наблюдений оценивается a и b (определение параметров моделей или регрессионные коэффициенты).
Параметрическая идентификация занимается оценкой эконометрических моделей, в которых имеется один или несколько x и один y. Для целей установления влияния одних параметров работы предприятия на другие.
Если x в первой степени и нет корней, ни степеней, нет 1/x, то модель линейная.
y=ax b — степенная функция;
y=ab x — показательная функция;
y=a1/x — парабола односторонняя.
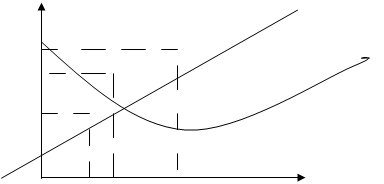
Выбираем наиболее надежную модель. После построения по одним и тем же эксперт данным одной линейной и нескольких нелинейных моделей над каждой из полученных моделей производим две проверки.
1 — на надежность модели или статистическую значимость. Fкр — или критерий Фишера. Табличное F и расчетное F. Если Fp > Fтабл. — то модель статистически значима.
2 — Отобрав из моделей все значимые модели, среди них находим самую точную, у которой минимальная средняя ошибка аппроксимации.
Эконометрические модели для прогнозов исследуют поведение одного параметра работы предприятия во времени.
I. Основная часть
Параметрическая идентификация парной линейной эконометрической модели
По семи областям региона известны значения двух признаков за 2007г.
Расходы на покупку продовольственных товаров в общих расходах,%, у
среднедневная заработная плата одного работающего, руб., х
1 68,8 45,1 2 61,2 59 3 59,9 57,2 4 56,7 61,8 5 55 58,8 6 54,3 47,2 7 49,3 55,2

(y-ŷ) /y 1 68,80 45,10 3102,88 2034,01 61,33 11,8286862 55,87562 0,108648 2 61, 20 59,00 3610,80 3481,00 56,46 2,0326612 22,46760 0,077451 3 59,90 57, 20 3426,28 3271,84 57,09 0,6331612 7,89610 0,046912 4 56,70 61,80 3504,06 3819,24 55,48 5,7874612 1,48840 0,021517 5 55,00 58,80 3234,00 3457,44 56,53 1,8379612 2,34090 0,027820 6 54,30 47, 20 2562,96 2227,84 60,59 7,3131612 39,56410 0,115840 7 49,30 55, 20 2721,36 3047,04 57,79 0,0091612 72,08010 0,172210 Итого 405, 20 384,30 22162,34 21338,41 405,27 29,4422535 201,7128 0,570398 Средн. з 57,89 54,90 3166,05 3048,34 57,90 4, 2060362 28,81612 0,081485


Исходные данные x и y могут быть двух типов:
а) рассматриваем одно предприятие, то наблюдения берутся через равностоящие промежутки времени (1 в квартал);
б) если каждое наблюдение — это отдельное предприятие, то данные берутся на одну и ту же дату, например, на 01.01.07
у — расходы на продовольственные товары в процентах; траты, например, на еду.

(Гаусс) x² — (x) ²
х — среднедневная заработная плата, в руб.
у = а + b х — линейная парная регрессионная ЭМ.
=-0.35 a=y — b x =76,88
b = (3166,049-57,88571*54,9) / (3048,344-54,9) = — 0,35
а = 57,88571 — ( — 0,35) *54,9 = 77,10071
ŷ (игрек с крышечкой) = 76,88-0,35х -это модельное значение y, которое получается путем подстановки в y = a + b x, конкретное значение a и b коэффициенты, а также x из конкретной строчки.
Критерий Фишера

n — количество наблюдений;
m — количество регрессоров (x1)
Допустим, 0,7. Fкрит не может быть меньше единицы, поэтому, если мы получим значение П
2,95 2,79 2,61 2,40
Когда m=1, выбираем 1 столбец.
k2=n-m=7-1=6 — т.е.6-я строка — берем табличное значение Фишера
Влияние х на у — умеренное и отрицательное
ŷ — модельное значение.
| F расч. = | 28,648: 1 | = 0,92 |
| 200,50: 5 |
А = 1/7 * 398,15 * 100% = 8,1% Fтабл
Нарушается данная модель, поэтому данное уравнение статистически не значимо.
Так как расчетное значение меньше табличного — незначимая модель.
1 Σ (y — ŷ) *100%
N y
A= 1/7*0,563494* 100% = 8,04991% 8,0%
Считаем, что модель точная, если средняя ошибка аппроксимации менее 10%.
Параметрическая идентификация парной нелинейной регрессии
Модель у = а * х b — степенная функция
Чтобы применить известную формулу, необходимо логарифмировать нелинейную модель.
log у = log a + b log x
Y=C+b*X -линейная модель.



С = 1,7605 — ( — 0,298) * 1,7370 = 2,278
Возврат к исходной модели
Ŷ=10 с *x b =10 2.278 *x -0.298
| №п/п | У | X | Y | X | Y*X | У | I (y-ŷ) /yI | |
| 1 | 68,80 | 45,10 | 1,8376 | 1,6542 | 3,039758 | 2,736378 | 60,9614643 | 0,113932 |
| 2 | 61, 20 | 59,00 | 1,7868 | 1,7709 | 3,164244 | 3,136087 | 56,2711901 | 0,080536 |
| 3 | 59,90 | 57, 20 | 1,7774 | 1,7574 | 3,123603 | 3,088455 | 56,7931534 | 0,051867 |
| 4 | 56,70 | 61,80 | 1,7536 | 1,7910 | 3,140698 | 3, 207681 | 55,4990353 | 0,021181 |
| 5 | 55,00 | 58,80 | 1,7404 | 1,7694 | 3,079464 | 3,130776 | 56,3281590 | 0,024148 |
| 6 | 54,30 | 47, 20 | 1,7348 | 1,6739 | 2,903882 | 2,801941 | 60,1402577 | 0,107555 |
| 7 | 49,30 | 55, 20 | 1,6928 | 1,7419 | 2,948688 | 3,034216 | 57,3987130 | 0,164274 |
| Итого | 405, 20 | 384,30 | 12,3234 | 12,1587 | 21,40034 | 21,13553 | 403,391973 | 0,563493 |
| Средняя | 57,88571 | 54,90 | 1,760486 | 1,736957 | 3,057191 | 3,019362 | 57,62742 | 0,080499 |
Входим в EXCEL через «Пуск»-программы. Заносим данные в таблицу. В «Сервис» — «Анализ данных» — «Регрессия» — ОК
Если в меню «Сервис» отсутствует строка «Анализ данных», то ее необходимо установить через «Сервис» — «Настройки» — «Пакет анализа данных»
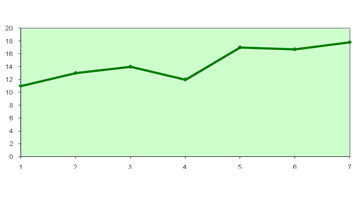
Прогнозирование спроса на продукцию предприятия. Использование в MS Excel функции «Тенденция»
A — спрос на товар. B — время, дни
1 11 1 2 14 2 3 13 3 4 15 4 5 17 5 6 17,9
Шаг 1. Подготовка исходных данных
Шаг 2. Продлеваем временную ось, ставим на 6,7 вперед; имеем право прогнозировать на 1/3 от данных.
Шаг 3. Выделим диапазон A6: A7 под будущий прогноз.
Шаг 4. Вставка функция
Полный алфавитный перечень Тенденция
Известные значения x (курсор В1: В5)
Выделяем с 1 по 5
| Новый x | В6: В7 |
| Известный y | А1: А5 |
| Const | 1 |
| Ок |
Шаг 5. ставим курсор в строку формул за последнюю скобку

диапазон у готово.
Если каждое последующее значение нашего временной оси будет отличаться не на несколько процентов, а в несколько раз, тогда нужно использовать не функцию «Тенденция», а функцию «Рост».
Источник
9
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ
АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ТЮМЕНСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
МЕЖДУНАРОДНЫЙ
ИНСТИТУТ ФИНАНСОВ, УПРАВЛЕНИЯ И БИЗНЕСА
Параметрическая идентификация парной
линейной эконометрической модели
(реферат по эконометрике)
Автор работы: 25э04
А. Н. Суслов
Тюмень
2011
Содержание
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСУДАРСТВЕННОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ТЮМЕНСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
МЕЖДУНАРОДНЫЙ
ИНСТИТУТ ФИНАНСОВ, УПРАВЛЕНИЯ И БИЗНЕСА
Введение
I.
Основная часть
Параметрическая
идентификация парной линейной
эконометрической модели
Критерий
Фишера
Параметрическая
идентификация парной нелинейной
регрессии
Прогнозирование
спроса на продукцию предприятия.
Использование в MS Excel функции «Тенденция»
Приложение
Введение
Классификация
эконометрических моделей и методов.
Эконометрика — это
наука, лежащая на стыке между статистикой
и математикой, она разрабатывает
экономические модели для цели
параметрической идентификации,
прогнозирования (анализа временных
рядов).
Классификация
эконометрических моделей и методов.
-
Эконометрические
модели (ЭМ)
|
Эконометрические |
Эконометрические |
Система |
(установление параметров
(есть ли тренд) (комплексная модели)
оценка)
y=a+b+x y=a+b*t
y=a+b1x1-b2x2
y —
зависимая переменная (отклик), прибыль,
например. x — независимая
переменная (регрессор), какова численность
персонала, например. На основании
наблюдений оцениваются a
и b (определение параметров
моделей или регрессионные коэффициенты).
-
№ п/п
y
x
1
11
1
2
13
2
3
14
3
4
12
4
5
17
5
6
16,7
6
7
17,8
7
На основании наблюдений
оценивается a и b
(определение параметров моделей или
регрессионные коэффициенты).
Параметрическая
идентификация занимается оценкой
эконометрических моделей, в которых
имеется один или несколько x
и один y. Для целей
установления влияния одних параметров
работы предприятия на другие.
Если x
в первой степени и нет корней, ни степеней,
нет 1/x, то модель линейная.
y=axb
— степенная функция;
y=abx
— показательная функция;
y=a1/x
— парабола односторонняя.
Y
-прибыль — линейная модель
— степенная функция
x
– численность
Выбираем наиболее
надежную модель. После построения по
одним и тем же эксперт данным одной
линейной и нескольких нелинейных моделей
над каждой из полученных моделей
производим две проверки.
1 — на надежность модели
или статистическую значимость. Fкр
— или критерий Фишера. Табличное F
и расчетное F. Если Fp
> Fтабл. — то
модель статистически значима.
2 — Отобрав из моделей
все значимые модели, среди них находим
самую точную, у которой минимальная
средняя ошибка аппроксимации.
Эконометрические
модели для прогнозов исследуют поведение
одного параметра работы предприятия
во времени.
I. Основная часть Параметрическая идентификация парной линейной эконометрической модели
По семи областям
региона известны значения двух признаков
за 2007г.
|
Район |
Расходы на |
среднедневная |
|
1 |
68,8 |
45,1 |
|
2 |
61,2 |
59 |
|
3 |
59,9 |
57,2 |
|
4 |
56,7 |
61,8 |
|
5 |
55 |
58,8 |
|
6 |
54,3 |
47,2 |
|
7 |
49,3 |
55,2 |
|
№п/п |
Y |
x |
ух |
Х2 |
ŷ |
|
(у — ŷ) 2 |
(y-ŷ) |
|
1 |
68,80 |
45,10 |
3102,88 |
2034,01 |
61,33 |
11,8286862 |
55,87562 |
0,108648 |
|
2 |
61, 20 |
59,00 |
3610,80 |
3481,00 |
56,46 |
2,0326612 |
22,46760 |
0,077451 |
|
3 |
59,90 |
57, 20 |
3426,28 |
3271,84 |
57,09 |
0,6331612 |
7,89610 |
0,046912 |
|
4 |
56,70 |
61,80 |
3504,06 |
3819,24 |
55,48 |
5,7874612 |
1,48840 |
0,021517 |
|
5 |
55,00 |
58,80 |
3234,00 |
3457,44 |
56,53 |
1,8379612 |
2,34090 |
0,027820 |
|
6 |
54,30 |
47, 20 |
2562,96 |
2227,84 |
60,59 |
7,3131612 |
39,56410 |
0,115840 |
|
7 |
49,30 |
55, 20 |
2721,36 |
3047,04 |
57,79 |
0,0091612 |
72,08010 |
0,172210 |
|
Итого |
405, 20 |
384,30 |
22162,34 |
21338,41 |
405,27 |
29,4422535 |
201,7128 |
0,570398 |
|
Средн. з |
57,89 |
54,90 |
3166,05 |
3048,34 |
57,90 |
4, 2060362 |
28,81612 |
0,081485 |
y
x
yx
x2
Исходные данные x
и y могут быть двух типов:
а) рассматриваем одно
предприятие, то наблюдения берутся
через равностоящие промежутки времени
(1 в квартал);
б) если каждое наблюдение
— это отдельное предприятие, то данные
берутся на одну и ту же дату, например,
на 01.01.07
у — расходы на
продовольственные товары в процентах;
траты, например, на еду.
|
b = |
y x-yx |
(Гаусс) |
|
x² — (x) ² |
х — среднедневная
заработная плата, в руб.
у = а + b
х — линейная парная регрессионная ЭМ.
=-0.35 a=y
— b x =76,88
b =
(3166,049-57,88571*54,9) / (3048,344-54,9) = — 0,35
а = 57,88571 — ( — 0,35) *54,9 =
77,10071
ŷ = а+bх
ŷ = 77,10071-0,35х
ŷ (игрек с крышечкой)
= 76,88-0,35х -это модельное значение y,
которое получается путем подстановки
в y = a + b
x, конкретное значение a
и b коэффициенты, а также
x из конкретной строчки.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Валентин Юльевич Арьков
Введение в эконометрику. Учебное пособие
© Валентин Юльевич Арьков, 2021
ISBN 978-5-0053-9438-5
Создано в интеллектуальной издательской системе Ridero
Введение
Эконометрика – это построение математических моделей экономических систем по фактическим данным с помощью статистических методов. Это значит, что требуется проводить анализ больших объемов реальных данных. На сегодняшний день такую деятельность часто называют «Наука о данных».
Основные идеи и методы эконометрики изучают в рамках предмета «Математическая статистика». Конечно, при построении моделей здесь нужно учитывать специфику именно экономических процессов.
С другой стороны, математическими моделями также занимается предмет «Математическая экономика». В рамках этой дисциплины рассматривают математические модели – в том числе и как иллюстрацию экономической теории. Иногда эконометрику рассматривают как раздел экономики или математической экономики.
Эконометрика во многом опирается на основной раздел статистики под названием РЕГРЕССИЯ. Это построение линии (и уравнения этой линии) В СРЕДНЕМ по точкам. В эконометрике рассматривается построение парной и множественной, линейной и нелинейной регрессии (без привязки ко времени), а также регрессионных моделей временных рядов. Кроме того, эконометрические модели могут иметь несколько входов и несколько выходов – это системы эконометрических уравнений.
В настоящее время многие пакеты прикладных программ позволяют проводить эконометрические исследования. Для практического знакомства с технологиями эконометрики мы будем использовать электронные таблицы MS Excel. Можно также обратиться к любым другим табличным редакторам, в том числе, к бесплатным.
1. Парная линейная регрессия
1.1. Оформление отчёта
Отчёт о работе оформляется в виде рабочей книги Excel. Саму работу мы тоже выполняем в этой же рабочей книги. Каждое отдельное задание оформляем на новом рабочем листе. Подробности оформления отчёта описаны в работе [1].
Отчёт начинаем, как обычно, с титульного листа. Это первый лист рабочей книги. На титульном листе нужно указать название министерства, ВУЗа, кафедры. Далее идёт тип и название документа. Конечно, нужно указать номер студенческой группы, а также фамилию и инициалы студента. В нижней части титульного листа располагают название города и год.
На втором листе размещают оглавление работы. В нашем случае это название разделов и ссылка на соответствующий лист рабочей книги.
На третьей странице отчёта укажите номер зачетки. Это будут настройки генератора случайных чисел для имитационного моделирования.
Задание. Создайте новый документ Excel и сохраните, выбрав уникальное информативное имя файла.
1.2. Общий план работы
В первой работе мы будем знакомиться с парной линейной регрессией. Напомним, что регрессия – это построение зависимости в среднем по большому количеству точек (исходных данных). Слово «парная» означает, что у нас всего «пара» переменных – «икс» и «игрек». Слово «линейная» указывает, что мы будем строить линейное уравнение, то есть уравнение прямой линии. В линейном уравнении «икс» участвует в первой степени
В качестве исходных данных мы будем использовать результаты имитационного моделирования. Это позволит работать с такими данными, которые заведомо содержат интересующие нас закономерности.
Мы сгенерируем два столбца, в которых будет находиться одна независимая переменная «икс» и одна зависимая переменная «игрек». В этих данных будет заложена линейная взаимосвязь на фоне случайных отклонений – случайный разброс точек вокруг прямой линии.
«Икс» называют независимой переменной – independent variable. Предполагается, что «икс» может меняться как угодно и что он ни от чего в нашей модели не зависит. Другими словами, «икс» – это вход модели.
Изменение «икса» объясняет поведение «игрека». Поэтому «икс» ещё называют «объясняющей» переменной.
«Игрек» выступает в роли зависимой переменной – dependent variable. Он зависит от «икса». Хотя бы частично.
Для моделирования мы используем генератор случайных чисел из надстройки «Анализ данных». Попутно заметим, что полученные случайные числа будут записаны как числовые значения. Они не будут меняться со временем. В других ситуациях нам как раз будет нужно, чтобы случайные числа менялись – тогда мы будем вызывать функцию RAND.
Далее мы рассмотрим методику построения линейной модели, которая описывает наши данные в среднем. Это означает, что на графике линия должна проходить в среднем – по местам сгущения точек.
Кроме уравнения такой линии, нам понадобится определить возможную неопределённость (погрешность) полученных коэффициентов.
Окончательное уравнение должно содержать как коэффициенты, так и их погрешность. Случайную ошибку обычно описывают с помощью «сигмы». Это стандартное отклонение, или среднеее квадратическое отклонение (СКО). Для каждого коэффициента указываем его сигму – под коэффициентом в скобках, см. рис.
Рис. Коэффициенты и их сигмы
Для оценки коэффициентов и их «сигм» в данной работе используем три способа:
– надстройку «Анализ данных»;
– функцию ЛИНЕЙН – LINEST;
– формулы Excel.
Затем нам нужно будет провести интерпретацию полученного уравнения. Мы сформулируем смысл уравнения регрессии в виде высказывания, понятного обычному пользователю.
1.3. Надстройка
Чтобы включить надстройку «Анализ данных», вызовите File – Options.
Рис. Меню «Файл»
В диалоговом окне Excel Options выбираем: Add-ins – Manage – Excel Add-ins – Go, см. рис.
Ставим галочку рядом пунктом AnalysisToolpak – Пакет анализа, см. рис.
Рис. Меню «Надстройки»
Рис. Включение надстройки «Анализ данных»
Если надстройка активирована, можно будет найти кнопку Data Analysis в разделе меню Data – Analysis, см. рис.
Рис. Надстройка в разделе «Анализ»
1.4. Исходные данные
Сгенерируем исходные данные. Наши переменные будут расположены по столбцам.
В данной работе мы сформируем по 100 значений в каждом столбце. Это не слишком много и не слишком мало. С одной стороны, графики будут достаточно наглядными. С другой стороны, рисунки не будут слишком основательно заполнены точками.
Первый столбец – переменная u. Сгенерируйте столбец случайных чисел с равномерным распределением от 170 до 200. Начальное состояние генератора – четыре последние цифры номера зачетки, см. рис.
Рис. Настройки генератора
Далее нам нужно сгенерировать два столбца случайных чисел e1 и e2 со стандартным нормальным распределением. У такого распределения среднее значение MEAN равно нулю, а стандартное отклонение STANDARD DEVIATION равно единице. Сразу задаём генерирование двух столбцов – число переменных равно двум. Начальное состояние генератора – четыре последних цифры номера зачетки плюс 5.
Разные настройки генератора позволят создать независимые случайные числа в разных колонках.
В следующем столбце y введём формулу, как показано на рисунке.
Рис. Формулы по столбцам
В следующем столбце сформируем x. Добавим к значениям u из первого столбца случайный разброс e1.
Наконец, округлим два последних столбца x и y до целых значений с помощью функции ROUND. Эти два столбца X и Y будут имитировать результаты измерений. Когда мы что-то измеряем, всегда появляются случайные погрешности измерений, пускай даже небольшие и незаметные. К тому же, такие параметры тела, как рост и вес, немного меняются даже в течение суток.
Наши «иксы» – это значения роста человека в сантиметрах. «Игреки» – это значения веса в килограммах. Мы закладываем в нашу выборку зависимость веса от роста. Затем добавляем в данные случайный разброс.
Рис. Линейная модель
Рис. Зашумлённые наблюдения
Рис. Постановка задачи
Рис. Имитационное моделирование
На схеме показано, как добавляются случайные погрешности измерений к значениям иксов и игреков. Таким образом, при анализе реальных данных наши числа всегда содержат случайный шум. Это зашумлённые данные.
Результаты эконометрического анализа – это ОЦЕНКИ коэффициентов уравнения. Мы говорим «оценки», чтобы подчеркнуть, что полученные значения коэффициентов отличаются от истинных, правильных, точных значений. К тому же, они изменяются, если взять другой набор таких же данных – другую выборку.
Кроме коэффициентов уравнения, нас будут интересовать ПРОНОЗ значений завипсимой переменной – игрека. Задавая значения икса, мы пронозируем возможное значение игрека. Оно тоже будет меняться; это будет случайная погрешность. Так что пронозы тоже являются оценками.
Оценки коэффициентов и пронозы зависимой переменной обозначены символом, который называют «крышка», или «крышечка». Обозначение читается так: «икс с крышкой», «игрек с крышкой», см. рис.
Рис. Условные обозначения
Мы подробно обсуждаем такие «очевидные» вещи, о которых почему-то не пишут в учебниках. Это вроде как «все знают». Хотя выясняется, что это знают только преподаватели, а вот студенты должны об этом узнать каким-то волшебным образом, ведь «это же настолько элементарно».
Один преподаватель так и сказал: «Ну я же это вам уже рассказывал». Студенты возразили: «Нет, вы нам это не рассказывали». Преподаватель просто возмутился: «Ну не вам, значит другим. Я это уже сколько раз рассказывал. Каждый год кому-нибудь обязательно рассказываю. Одним объясняю, а другие не понимают!»
Вот поэтому приходится составлять учебное пособие – для изучения учебника. Учебное пособие (по определению) должно помогать в учёбе. Слово «пособить» означает «помочь». Но пособие не может заменить учебник. Так что студентам не помешает открыть пару учебников по нашему предмету, а потом вернуться к нашему пособию и продолжить изучение материала.
Символ «крышка» – это пример того, что называется УСЛОВНЫЕ ОБОЗНАЧЕНИЯ. Это означает, что авторы о чём-то «условились», то есть «договорились». Это соглашение, доворённость о том, что и как будет в тексте и в формулах обозначено. Следите за условными обозначениями в формулах.
Чтобы всё окончательно запутать, в книгах по эконометрике и в программных продуктах используют разные условные обозначения. А ещё эти обозначения не всегда подробно объясняют и расшифровывают. Так что следите за смыслом.
Индекс корреляции
Опять воюю с excel’ем Считаю индекс корреляции вручную и на excel’е, вручную результат 0.659, эксель выдает 0.8732 (там, на самом деле, R^2=0,7626, я беру корень из этого числа).
Исходная статистика:
1 16,6
2 13,3
3 21,7
4 4,5
5 2,2
6 0,6
7 1,8
Уравнение регрессии:
y=40,99914*exp(-0,5411*x)
значения y(с крышечкой) при подстановке в уравнение икса:
23,86591024
13,89252729
8,086945468
4,70747227
2,740255299
1,595123385
0,928533416
Ищу по формуле R=(1-сумм(y-y(с крышечкой))^2/сумм(y-y(среднее))^2)^0.5
сумм(y-y(с крышечкой))^2=240,544
сумм(y-y(среднее))^2=425,674
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Чему равен коэффициент корреляции между (Х + 5) и (-2У), если значение коэффициента корреляции Х и У равно 0.5
Есть задача 1. Чему равен коэффициент корреляции между (Х + 5) и (-2У), если значение коэффициента.
Коэффициент корреляции
Случайные величины x1,x2,x3,x4,x5 независимы и имеют одинаковую дисперсию σ^2. Найти.
найти коэффициент корреляции
Пусть Х — равномерно распределенная на интервале (0,1) случайная величина. Случайная величнина.
Найти коэффициент корреляции
1) Известно, что с.в. U=4-9x, V=8+3y, коэффициент корреляции x и y = 1. Найти коэффициент.
Похоже, опять с логарифмами путаница. Учитесь проверять свои расчёты самостоятельно.
Регрессионный анализ — это статистический метод исследования, позволяющий показать зависимость того или иного параметра от одной либо нескольких независимых переменных. В докомпьютерную эру его применение было достаточно затруднительно, особенно если речь шла о больших объемах данных. Сегодня, узнав как построить регрессию в Excel, можно решать сложные статистические задачи буквально за пару минут. Ниже представлены конкретные примеры из области экономики.
Виды регрессии
Само это понятие было введено в математику Фрэнсисом Гальтоном в 1886 году. Регрессия бывает:
- линейной;
- параболической;
- степенной;
- экспоненциальной;
- гиперболической;
- показательной;
- логарифмической.
Пример 1
Рассмотрим задачу определения зависимости количества уволившихся членов коллектива от средней зарплаты на 6 промышленных предприятиях.
Задача. На шести предприятиях проанализировали среднемесячную заработную плату и количество сотрудников, которые уволились по собственному желанию. В табличной форме имеем:
Для задачи определения зависимости количества уволившихся работников от средней зарплаты на 6 предприятиях модель регрессии имеет вид уравнения Y = а0 + а1x1 +…+аkxk, где хi — влияющие переменные, ai — коэффициенты регрессии, a k — число факторов.
Для данной задачи Y — это показатель уволившихся сотрудников, а влияющий фактор — зарплата, которую обозначаем X.
Использование возможностей табличного процессора «Эксель»
Анализу регрессии в Excel должно предшествовать применение к имеющимся табличным данным встроенных функций. Однако для этих целей лучше воспользоваться очень полезной надстройкой «Пакет анализа». Для его активации нужно:
- с вкладки «Файл» перейти в раздел «Параметры»;
- в открывшемся окне выбрать строку «Надстройки»;
- щелкнуть по кнопке «Перейти», расположенной внизу, справа от строки «Управление»;
- поставить галочку рядом с названием «Пакет анализа» и подтвердить свои действия, нажав «Ок».
Если все сделано правильно, в правой части вкладки «Данные», расположенном над рабочим листом «Эксель», появится нужная кнопка.
Линейная регрессия в Excel
Теперь, когда под рукой есть все необходимые виртуальные инструменты для осуществления эконометрических расчетов, можем приступить к решению нашей задачи. Для этого:
- щелкаем по кнопке «Анализ данных»;
- в открывшемся окне нажимаем на кнопку «Регрессия»;
- в появившуюся вкладку вводим диапазон значений для Y (количество уволившихся работников) и для X (их зарплаты);
- подтверждаем свои действия нажатием кнопки «Ok».
В результате программа автоматически заполнит новый лист табличного процессора данными анализа регрессии. Обратите внимание! В Excel есть возможность самостоятельно задать место, которое вы предпочитаете для этой цели. Например, это может быть тот же лист, где находятся значения Y и X, или даже новая книга, специально предназначенная для хранения подобных данных.
Анализ результатов регрессии для R-квадрата
В Excel данные полученные в ходе обработки данных рассматриваемого примера имеют вид:
Прежде всего, следует обратить внимание на значение R-квадрата. Он представляет собой коэффициент детерминации. В данном примере R-квадрат = 0,755 (75,5%), т. е. расчетные параметры модели объясняют зависимость между рассматриваемыми параметрами на 75,5 %. Чем выше значение коэффициента детерминации, тем выбранная модель считается более применимой для конкретной задачи. Считается, что она корректно описывает реальную ситуацию при значении R-квадрата выше 0,8. Если R-квадрата 2 (RI) представляет собой числовую характеристику доли общего разброса и показывает, разброс какой части экспериментальных данных, т.е. значений зависимой переменной соответствует уравнению линейной регрессии. В рассматриваемой задаче эта величина равна 84,8%, т. е. статистические данные с высокой степенью точности описываются полученным УР.
F-статистика, называемая также критерием Фишера, используется для оценки значимости линейной зависимости, опровергая или подтверждая гипотезу о ее существовании.
Значение t-статистики (критерий Стьюдента) помогает оценивать значимость коэффициента при неизвестной либо свободного члена линейной зависимости. Если значение t-критерия > tкр, то гипотеза о незначимости свободного члена линейного уравнения отвергается.
В рассматриваемой задаче для свободного члена посредством инструментов «Эксель» было получено, что t=169,20903, а p=2,89Е-12, т. е. имеем нулевую вероятность того, что будет отвергнута верная гипотеза о незначимости свободного члена. Для коэффициента при неизвестной t=5,79405, а p=0,001158. Иными словами вероятность того, что будет отвергнута верная гипотеза о незначимости коэффициента при неизвестной, равна 0,12%.
Таким образом, можно утверждать, что полученное уравнение линейной регрессии адекватно.
Задача о целесообразности покупки пакета акций
Множественная регрессия в Excel выполняется с использованием все того же инструмента «Анализ данных». Рассмотрим конкретную прикладную задачу.
Руководство компания «NNN» должно принять решение о целесообразности покупки 20 % пакета акций АО «MMM». Стоимость пакета (СП) составляет 70 млн американских долларов. Специалистами «NNN» собраны данные об аналогичных сделках. Было принято решение оценивать стоимость пакета акций по таким параметрам, выраженным в миллионах американских долларов, как:
- кредиторская задолженность (VK);
- объем годового оборота (VO);
- дебиторская задолженность (VD);
- стоимость основных фондов (СОФ).
Кроме того, используется параметр задолженность предприятия по зарплате (V3 П) в тысячах американских долларов.
Решение средствами табличного процессора Excel
Прежде всего, необходимо составить таблицу исходных данных. Она имеет следующий вид:
- вызывают окно «Анализ данных»;
- выбирают раздел «Регрессия»;
- в окошко «Входной интервал Y» вводят диапазон значений зависимых переменных из столбца G;
- щелкают по иконке с красной стрелкой справа от окна «Входной интервал X» и выделяют на листе диапазон всех значений из столбцов B,C, D, F.
Отмечают пункт «Новый рабочий лист» и нажимают «Ok».
Получают анализ регрессии для данной задачи.
Изучение результатов и выводы
«Собираем» из округленных данных, представленных выше на листе табличного процессора Excel, уравнение регрессии:
СП = 0,103*СОФ + 0,541*VO – 0,031*VK +0,405*VD +0,691*VZP – 265,844.
В более привычном математическом виде его можно записать, как:
y = 0,103*x1 + 0,541*x2 – 0,031*x3 +0,405*x4 +0,691*x5 – 265,844
Данные для АО «MMM» представлены в таблице:





































 . Необходимое и достаточное условия идентификации.
. Необходимое и достаточное условия идентификации.