ЛЕКЦИЯ 2
ВЗАИМНАЯ ИНФОРМАЦИЯ.
ЦЕЛЬ ЛЕКЦИИ: На
основе понятия условной энтропии дать
определение взаимной информации,
рассмотреть свойства и представить
вывод формулы для вычисления среднего
количества взаимной информации.
Измеряй все,
доступное измерению, и делай недоступное
измерению доступным. Галилео Галилей
В предыдущей лекции
приведено определение условной энтропии
как величины, показывающей, какова в
среднем неопределенность выбора значения
некоторой величины у,
когда известно значение х.
[1]
или H(x,y)
= H(x) + Hx
(y)
Условная энтропия
удовлетворяет следующим условиям.:
0 ≤Hx(y)
≤ H(y),
Hx(y)
= 0, когда
по реализации ансамбля X
можно точно
установить реализацию ансамбля Y;
Hx(y)
= H(y),
когда ансамбли
Х
и У
независимы
и знание реализации X
не прибавляет информации об Y;
H(y)
> Hx(y)
– общий
случай, когда знание реализации
X
снижает первоначальную неопределенность
Y.
Взаимная
информация.
В технике передачи
сообщений интерес представляет
возможность получения информации о
передаваемых сообщениях по символам,
наблюдаемым на выходе канала. Представим
математически операции, выполняемые
передатчиком и приемником. Передатчик
и приемник назовем дискретными
преобразователями. На вход преобразователя
поступает последовательность входных
символов некоторого ансамбля Х,
а на выходе получается последовательность
выходных символов, представленная
ансамблем У.
Преобразователь может обладать внутренней
памятью. Выходной символ в этом случае
будет зависеть не только от данного
входного символа, но и от всех предыдущих.
Задача заключается в том, чтобы
количественно определить информацию
о символах х
входного ансамбля Х,
содержащуюся в выходных символах у
ансамбля У
на выходе канала, в том числе с учетом
указанной статистической зависимости.
Введем обозначение
взаимной информации I(x,y).
В соответствии со свойством 5 энтропии,
можем записать соотношение
I(x,y)=H(x)
– H(x,y),
[2]
которое будет
определять меру взаимной информации
для любых пар (x,y)
ансамблей Х
и У.
В выражении [2] Н(х)
– априорная энтропия, Н(x,y)
– остаточная энтропия после получения
сведений об ансамбле Х.
Тогда I(x,y)
будет характеризовать полную информацию,
содержащуюся в ансамбле У
об ансамбле Х.
Проиллюстрируем
графически энтропию системы и информацию
Рис. 1 Графическое
отображение взаимной информации.
Верхние раздельные
овалы — при отсутствии связи между
ансамблями переменных Х
и У;
Нижние совмещенные
овалы — при наличии статистической связи
между ансамблями Х
и У.
Рассмотрим ансамбли
Х
и У,
характеризующие систему. Энтропию
ансамбля Х
изобразим овалом с площадью Н(Х):
чем больше энтропия, тем больше площадь.
Энтропия ансамбля У
— второй овал
с площадью Н(У).
Если ансамбли статистически независимы,
т.е. связь между ними отсутствует, овалы
не пересекаются. Полная энтропия системы
равна сумме энтропий, т. е. сумме площадей.
Если же между
ансамблями возникает статистическая
связь (корреляция), то овалы на схеме
пересекаются. Возникшая взаимная
информация I(Х,У)
и есть количественная мера этого
пересечения. Энтропия уменьшается на
величину этой информации:
Н(Х,У) = Н(Х) +
Н(У) — I(Х,Y)
[3]
Чем больше взаимная
информация, тем теснее связь, тем меньше
энтропия Н(Х,У).
Из свойства 5
энтропии следует
H(X,Y)
= H(X) + HX(Y)
H(X,Y)
= H(Y) + HY(X)
[4]
а также
H(X)
+ HX(Y)
= H(Y) + HY(X)
H(X)
–HX(Y)
= H(Y) – HY(X)
[5]
Сравнив [5] и [2],
отметим, что выражение [5] характеризует
взаимное равенство информации об
ансамбле Х,
если известен ансамбль У,
и обратно, знание об ансамбле У,
если известен ансамбль Х.
I(X,Y)
– называется средней взаимной информацией,
содержащейся в ансамблях Х
и У.
Свойства взаимной
информации.
-
I(X,Y)
= I(Y,X).
Взаимная информация симметрична. -
I(X,Y)
≥ 0.
Взаимная информация всегда положительна.
3.
I(X,Y)
= 0 тогда
и только тогда, когда ансамбли
Х
и У
независимы.
-
I(X,Y)
= H(X)
– HX(Y)
= H(Y)
– HY(X)
= H(X)
+ H(Y)
– H(X,Y),
т. е. в случае наступления совместного
события H(X)
+ H(Y)
= H(X,Y)
взаимная информация отсутствует. -
I(X,Y)
≤ min{H(X),H(Y)}.
Взаимная
информация не может быть больше
информации о каждом ансамбле в
отдельности. -
I(X,Y)
≤ min {log |X|, log|Y|}.
Логарифмическая
мера каждого из ансамблей в отдельности
больше или равна взаимной информации.
7. Взаимная
информация I(X,Y)
имеет максимум (является выпуклой
функцией распределения вероятностей).
В общем случае
свойство 4 определяет взаимную информацию
через энтропию объединенной системы
H(X,Y)
и энтропию отдельных ее частей H(X)
и H(Y)
рис.1.
I(X,Y)
= H(X) + H(Y) – H(X,Y)
[6]
Выразим полную
взаимную информацию через вероятности
состояний системы. Для этого запишем
значения энтропии отдельных систем
через математическое ожидание:
H(X)=M[—log
P(X)], H(Y)=M[—log
P(Y)], H(X,Y)=M[—log
P(X,Y)]
[7]
Тогда выражение
[6] примет вид
I(X,Y)
=M[ — logP(X) – logP(Y) + log(X,Y)].
Преобразовав,
получим
[8]
Выражение
[8] преобразуем с использованием свойства
математического
ожидания,
заключающегося в следующем. Для ансамбля
случайных величин Х
можно
определить функцию φ(х)
по всем значениям х.
Тем самым устанавливается отображение
Х
на множество вещественных значений х.
Ансамбль
У=
[у=φ(х)]
представляет
собой набор множества значений случайных
величин. Для вычисления математического
ожидания величины у
необязательно знать распределение
вероятностей py(y)
для у.
Если распределение px(x)
по ансамблю Х
известно,
то
Тогда,
если p(xi)
вероятность реализации любого из m
элементов
ансамбля Х,
а p(yj)
вероятность реализации любого из n
элементов ансамбля У,
то выражение количества взаимной
информации будет иметь вид
[9]
Данная
формула позволяет определить полное
количество взаимной информации об
ансамбле Х
по принятому на выходе канала ансамблю
У.
Количество взаимной информации измеряется
в битах.
Марковская
модель источника.
Рассмотрим
случайные последовательности из
произвольного числа событий. Если
элементы случайной последовательности
– вещественные числа, то такие
последовательности называются случайными
процессами.
Номер
элемента в последовательности трактуется
как момент времени, в который появилось
данное значение. В общем случае множество
значений времени может быть непрерывным
или дискретным, множество значений
случайной последовательности может
быть также непрерывным или дискретным
Случайный
процесс х1,
x2,
…
со значениями xi
, алфавита Х,
(i
= 1, 2, …)
задан, если для любых n
указан способ вычисления совместных
распределений вероятностей p(x1
,…x
n).
Проще всего задать случайный процесс,
предположив, что его значения в различные
моменты времени независимы и одинаково
распределены.
где
p(xi)
– вероятность появления
xi
в момент i.
Для описания такого процесса достаточно
указать вероятности p(x)
для всех x
(всего IХI
– 1
вероятностей). Для описания более сложных
моделей процессов следует опираться
на свойство стационарности, позволяющее
упростить математические выкладки.
Процесс называется стационарным, если
для любых n
и t
имеет
место равенство
p(x1,
…, x
n)
= p(
x
1+ t x
n+ t),
причем
xi
= x1+
t,
i
= 1, …n.
Случайный процесс стационарен, если
вероятность любой последовательности
не изменится при ее сдвиге во времени.
Числовые характеристики, в частности
математическое ожидание, стационарных
процессов не зависят от времени.
Рассматривая стационарные процессы,
мы можем вычислять независящие от
времени информационные характеристики
случайных процессов. Пример стационарного
процесса – процесс, значения которого
независимы и одинаково распределены.
Рассмотрим далее
сигнал, представляющий собой некоторую
последовательность символов,
создаваемую дискретным
источником сообщений.
К. Шеннон так
определяет дискретный источник сообщений:
“ Можно считать, что дискретный источник
создает сообщение символ за символом.
Он будет выбирать последовательные
символы с некоторыми вероятностями,
зависящими, вообще говоря, как от
предыдущих выборов, так и от конкретного
рассматриваемого символа. Физическая
система или математическая модель
системы, которая создает такую
последовательность символов, определяемую
некоторой заданной совокупностью
вероятностей, называется вероятностным
процессом. Поэтому можно считать, что
дискретный источник представляется
некоторым вероятностным процессом.
Обратно, любой вероятностный процесс,
который создает дискретную последовательность
символов, выбираемых из некоторого
конечного множества, может рассматриваться
как дискретный источник”.
Статистическая
структура такого процесса и статистические
свойства источника вполне определяются
одномерными p
( i
), двумерными
p
( i,
j
) вероятностями
появления элементов сообщений на выходе
источника. Как указывалось, если между
последовательными элементами сообщения
отсутствует статистическая связь, то
статистическая структура сообщения
полностью определяется совокупностью
одномерных вероятностей. Появление
того или иного элемента сообщения на
выходе источника можно рассматривать
как определенное событие, характеризующееся
своей вероятностью появления. Для
совокупности событий вместе с их
априорными вероятностями появления
существует понятие ансамбля.
Примерами
дискретного источника могут служить:
-
Печатные тексты
на различных языках. -
Непрерывные
источники сообщений, которые превращены
в дискретные с помощью некоторого
процесса квантования (квантованная
речь, телевизионный сигнал.
3. Математические
случаи, когда просто определяется
абстрактно некоторый вероятностный
процесс, который порождает последовательность
символов.
Подобные источники
создают представляют собой вероятностные
процессы, известные как дискретные
Марковские процессы. В общем случае
результат может быть описан следующим
образом. Существует конечное число
возможных “состояний” системы :
S1,S2,.
. . ,Sn.
Кроме того, имеется совокупность
переходных вероятностей pi(j),
т. е. вероятностей того, что система,
находящаяся в cостоянии
Si
, перейдет затем в состояние Sj.
Чтобы использовать этот Марковский
процесс в качестве источника сообщений,
нужно только предположить, что при
каждом переходе из одного состояния в
другое создается одна буква. Состояния
будут соответствовать “остатку влияния”
предшествовавших букв. В графическом
примере “состоянием” является узловая
точка схемы, а переходные вероятности
и создаваемые при этом буквы указаны
около соответствующих линий.
Такой источник из
четырех букв A,
B,
C,
В , имеющих,
соответственно, переходные вероятности
0,1; 0,4; 0,3; 0,2, возвращаясь в узловую точку
после
создания очередной
буквы, может формировать как конечные,
так и бесконечную последовательности.
На дискретный
источник можно распространить такие
характеристики случайного сигнала, как
эргодичность и стационарность. Полагая
источник эргодическим, можно “…
отождествлять средние значения вдоль
некоторой последовательности со средним
значением по ансамблю возможных
последовательностей ( причем вероятность
расхождения равна нулю)”. Например,
относительная частота буквы А
в частной бесконечной последовательности
будет с вероятностью единица равняться
ее относительной частоте по ансамблю
последовательностей.
Простейшей
моделью источника, порождающего зависимые
сообщения, является Марковский источник.
Случайный процесс называют цепью
Маркова
связности
s,
если для любых n
и для любых x
= (x1,
…, xn)
алфавита X
справедливы
соотношения
p(x)
= p(x1
, …,x
s )p(x
s+ 1/
x
1,
… , x
s)p(xs+2/x2,
…,xs+1)…p(xn/xn-s,…,x
n-1).
Марковским
процессом связности s
называется такой процесс, для которого
при n
> s
p(xn
,…,
xn-1)
= p(xn
/x
n—s
,…,
xn-1),
т. е. условная вероятность текущего
значения при известных s
предшествующих не зависит от всех других
предшествующих значений.
Описание
Марковского процесса задается начальным
распределением вероятностей на
последовательностях из первых s
значений
и условными вероятностями p(xn
/xn—s
,…,xn-1)
для всевозможных последовательностей.
Если указанные условные вероятности
не изменяются при сдвиге последовательностей
во времени, Марковская цепь называется
однородной.
Однородная Марковская цепь связности
s
= 1
называется простой цепью Маркова. Для
ее описания достаточно указать
распределение вероятностей p(x1)
величины х,
принадлежащей множеству
Х
и
условные вероятности
πij
= P(xt
= j / xt-1
= i), i,j = 0,1,…,M-1,
называемые
переходными вероятностями цепи Маркова.
Переходные
вероятности удобно записывать в виде
квадратной матрицы размерности МхМ
называемой
матрицей переходных вероятностей. Эта
матрица – стохастическая (неотрицательная,
сумма элементов каждой строки равна
1).
Если
pt
— стохастический вектор, компоненты
которого – вероятности состояний цепи
Маркова в момент времени t,
т.е. pt=[pt(0),…,pt(M-1)],
где pt(i)
есть вероятность состояния i
в момент времени t
(I
= 0,1,…,M-1),
то из формулы полной вероятности следует
или в
матричной форме
pt+1
= ptΠ.
[ 10 ]
Для
произвольного числа шагов n
получим
,
т. е.
вероятности перехода за n
шагов
могут быть вычислены как элементы
матрицы. Предположим, что существует
стохастический вектор удовлетворяющий
уравнению
p
= pΠ. [
2 ]
Предположим,
р1
= р.
Тогда, воспользовавшись выражением
[1], получим р2
=
р
и, наконец, p
t
= p
при всех t.
Таким образом, Марковская цепь стационарна,
если в качестве начального распределения
выбрано решение уравнения [ 2 ].
Стохастический
вектор р,
удовлетворяющий уравнению [ 2 ], называется
стационарным
распределением
для цепи Маркова, задаваемой матрицей
переходных вероятностей Π. Финальным
распределением вероятностей называют
вектор
[
3 ]
Величина
p∞
не зависит от начального распределения
и от времени, т. е. является стационарным
распределением. Цепи, определяемые
выражением [ 3 ], называют эргодическими.
Если все элементы матрицы Π положительны
и не равны нулю, соответствующая
Марковская цепь эргодична. Чтобы
сформулировать необходимое и достаточное
условие эргодичности, введем несколько
определений.
Состояние
цепи i
достижимо
из
состояния j,
если для некоторого n
вероятность перехода из состояния j
в состояние
i
за n
шагов положительна. Множество состояний
называется замкнутым,
если никакое состояние вне С
не
может быть достигнуто из состояния,
входящего в С.
Цепь
называется
неприводимой,
если в ней нет никаких замкнутых множеств
кроме множества всех состояний. Цепь
Маркова неприводима тогда и только
тогда, когда состояния достижимы друг
из друга. Состояние i
называется периодическим, если существует
такое t
> 1,
что вероятность перехода из
i
в
i
за
n
шагов равна нулю при всех n
не кратных t.
Цепь, не содержащая периодических
состояний, называется непериодической.
Непериодическая неприводимая цепь
Маркова эргодична.
ЛИТЕРАТУРА.
1.
Шеннон К. Работы по теории информации
и кибернетике. М.: изд. “ИЛ”, 1963 г., стр.
249 – 259.
8
Соседние файлы в папке Лекции
- #
- #
16.04.2013264.19 Кб37Лекция 15 Стандарт MPEG -2
- #
- #
16.04.2013223.74 Кб37Лекция 16 Стандарт MPEG -4
- #
- #
- #
- #
- #
- #
- #
Время на прочтение
10 мин
Количество просмотров 3.8K
В части 1 мы познакомились с понятием энтропии.
В этой части я рассказываю про Взаимную Информацию (Mutual Information) – концепцию, которая открывает двери в помехоустойчивое кодирование, алгоритмы сжатия, а также даёт новый взгляд на задачи регрессии и Machine Learning.
Это необходимая компонента, чтобы в следующей части перейти к задачам ML как к задачам извлечения взаимной информации между факторами и прогнозируемой величиной. Один из способов объяснения успешности ML моделей заключается в том, что они создают естественное бутылочное горлышко, ограниченное автоподстраиваемым значением бит информации, через которое пропускается (дистиллируется) информация о входных данных. Но про это – в следующей части.
Здесь будет три важных картинки:
-
первая – про визуализацию энтропий двух случайных величин и их взаимную информацию;
-
вторая – про понимание самой концепции зависимости двух случайных величин и про то, что нулевая корреляция не значит независимость;
-
и третья – про то, что пропускная способность информационного канала имеет простую геометрическую интерпретацию через меру выпуклости функции энтропии.
Также мы докажем упрощённый вариант теоремы Шаннона-Хартли о максимальной пропускной способности канала с шумом.
Материал довольно сложный, изложен неподробно и больше похож на заметки для лектора. Подразумевается, что вы будете самостоятельно изучать непонятные моменты или писать мне вопросы, чтобы я раскрыл их понятнее и подробнее.
2. Mutual Information
Когда есть две зависимые величины, можно говорить о том, сколько информации об одной содержится в другой. Последние задачи в части 1 по сути были про это – про Взаимную Информацию двух случайных величин.
Рассмотрим, для примера, пару= (вес_человека, рост_человека). Для простоты будем считать, что это целые числа в килограммах и сантиметрах с конечным числом возможных значений. Теоретически, мы могли бы собрать данные 7 млрд. людей и построить двумерное распределение для пары
— распределение двух зависимых случайных величин. Можно построить отдельно распределение только веса
(забыв про рост), и распределение роста
(забыв о существовании веса). Эти два распределения называются маржинальными распределениями для совместного распределения на плоскости
Эти маржинальные распределения естественно в данном контексте называть априорными распределениями — они соответствуют нашему знанию о весе и росте, когда мы ничего не знаем про человека.
Ясно, что информация о росте человека заставит нас пересмотреть распределение веса, например, сообщение «рост = 2 метра 10 см» сместит распределение веса в область больших значений. Новое распределение веса после получения сообщения естественно назвать апостериорным. Соответственно, можно записать формулу информации, полученной в этом сообщении, как разность энтропий априорного и апостериорного распределений:
Здесь снаружи фигурных скобок я пишу индекс, по которому нужно «бежать» внутри фигурных скобок, чтобы получить список, а если индексов два, то матрицу.
Важно отметить, что никто не гарантирует, что эта величина будет положительная. Возможно такое совместное распределение при котором условное распределение
имеет большую энтропию (неопределенность), нежели маржинальное распределение
. Но в среднем для зависимых случайных величин значение
положительно, а именно, мат. ожидание этой величины положительно:
Эту величину естественно назвать информацией о величине в величине
. Оказывается, она симметрична относительно перестановки в паре
.
Опр. 2.1: Взаимная информация двух случайных величин – это
или
или
Это три эквивалентных определения. — это энтропия дискретного распределения, у которого значения не числа, а пары чисел
. Эквивалентность докажем ниже.
Есть визуализация того, чему равно значение MI:
Энтропиям случайных величин соответствуют круги – зелёный и красноватый, их площади равны и
, а коричневая площадь их пересечения как раз равна
Энтропия как мера
Эта визуализация, с одной стороны, не более чем визуализация, подчёркивающая, что энтропия – это неотрицательная величина, и чтотоже неотрицательная величина, которая меньше либо равна обеих энтропий
и
. Но, с другой стороны, есть интересные результаты, что можно построить пространство с мерой, в котором случайная величина соответствует подмножеству, объединение подмножеств соответствует прямому произведению случайных величин (то есть объединение в пару), а мера подмножеств и есть энтропия соответствующих случайных величин.
Кстати, в применении к ML картинка с зеленым и красным кругами выглядит так
Нам даны факторы (factors) и нужно спрогнозировать сигнал (target). Например, нужно спрогнозировать температуру воздуха завтра в 12:00 в центре Лондона с точностью до 0.5°C. В качестве факторов могут выступать данные про температуру в Лондоне и его окрестностях за последние 10 лет, текущая дата, текущие значения температуры, давления, влажности, ветра, а также положение Луны и другие данные. Типичная ситуация, когда количество бит информации в факторах огромно, а спрогнозировать нужно мало энтропийную величину. Весь объем данных в факторах можно назвать случайной величиной w, а target величиной h. У этих случайных величин есть взаимная информация и суть задачи прогноза как раз в том, чтобы найти эту информацию в факторах.
Распишем подробнее первое выражение:
Для независимых случайных величин
так как по определению независимости для любого
а значит для независимых случайных величин взаимная информация равна 0.
Оказывается, в обратную сторону тоже верно, то есть утверждение эквивалентно независимости случайных величин. А вот для корреляции двух случайных величин аналогичное утверждение было бы неверным.
Чтобы увидеть эквивалентность определений MI, удобно ввести обозначения:
-
— вероятности того, что рост и вес равны.
-
— вероятности того, что рост равен(маржинальное распределение роста).
-
— вероятности того, что вес равен(маржинальное распределение веса).
Будем считать, что все эти числа не равны 0.
Во-первых, заметим, что
Далее делаем подстановки и простые преобразования и получаем эквивалентность первого и третьего определения:
Рассмотрение случая, когда какие-то из вероятностей равны нулю оставим учебникам.
Задача 2.1: Приведите пример случайных величин, для которых корреляция равна нулю, а не равна нулю.
Задача 2.2: Две случайные величины много раз измерили и нанесли точки на плоскость. Какие картинки соответствуют зависимым случайным величинам, а какие – независимым?
Для каких из них корреляция x и y равна 0?
На каких из 12 картинок эти две величины зависимы?
Зависимые: 3-й, 4-й, 5-й, 8-й, 11-й, 12-й.
Корреляция равна нулю для всех, кроме 4-го, 5-го, 8-го и 12-го.
Задача 2.3: Посчитайте MI(w=»число делится на a=6″, h=»число делится на b=15″). Предполагается, что мы берём одно из натуральных чисел случайно и все числа равновероятны. Чтобы не мучаться с понятием равномерного распределения на натуральных числах, считайте, что мы случайно берём число из множества {1, …, 30}. Докажите, что если взять взаимопростые числа a и b, то MI=0.
Ответ
Мы знаем маржинальные распределения: и
Кроме того, мы знаем что вероятность делится и на 6, и на 15 равна 1/30. Из этого выводится матрица совместных вероятностей:
Используем формулу и получаем
MI=0.0311278
Задача 2.4: Докажите, что есть ещё одно эквивалентное определение
то есть MI – это то, насколько код Хаффмана для потока пар построенный в предположении независимости случайных величин (то есть в предположении, что совместное распределение равно произведению маржинальных), будет менее эффективен, чем код Хаффмана, построенный на настоящем совместном распределении. Измеряется в сэкономленных битах на символ (символ – измерение пары
).
Мы до сих пор жили в области дискретных распределений. Переход к непрерывным величинам получается просто.
Вспомним про задачу 1.7. Давайте предположим, что у нас есть вещественные случайные величины , но мы их дискретизировали — первую на корзинки размера
, а вторую — на корзинки размера
. Подставив в выражение
вместо H приближенную формулу (см. задачу 1.7)
для энтропий дискретизированного непрерывного распределения, мы получим, что из первого слагаемого вылезет из второго слагаемого —
а из третьего вычитаемого —
и эти три кусочка сократятся.
Таким образом, взаимную информацию непрерывных величин естественно определить как предел MI дискретизированных случайных величин при стремлении к корзинкам нулевого размера.
Опр. 2.2: Взаимная информация двух непрерывных случайных величин равна
Здесь мы пользуемся H из определения 1.6 части 1.
Задача 2.5: Оцените для какой-либо имеющейся у вас задачи прогноза чего-либо. Посчитайте
, насколько близко это отношение к 1?
Задача оценки MI двух случайных величин по множеству их измерений по сути сводится к задаче расчета матрицы совместного распределения для дискретизированных значений этих случайных величин. Чем больше корзинок в дискретизации, тем меньше неточность, связанная с этой дискретизацией, но тем меньше статистики для точной оценки
.
Оценка MI по наблюдаемым измерениям — отдельная большая тема, и мы к ней ещё вернёмся в задаче 3.1.
Задача 2.6: Докажите, что для любой строго монотонной функции верно, что
Ответ
Опр. 2.6: Информационный канал — это цепь Маркова длины 2, задающая зависимость между между двумя зависящими случайными величинами, одна из которых называется input, а другая — output. Часто под информационным каналом имеют в виду лишь матрицу переходных вероятностей: без фиксирования значения входного распределения. Распределение на входе будем обозначать как вектор
а распределение значений на выходе как вектор
Для дискретных распределений мы для каждого из M возможных входов имеем распределение на N возможных значениях выхода, то есть мы по сути имеем матрицу из M столбцов и N строчек, в которой все числа неотрицательные, а сумма чисел в каждом столбце равна 1.
Такие матрицы называются стохастическими матрицами, а точнее левыми стохастическими матрицами (left stochastic matrix).
Про левые и правые стохастические матрицы
У левых стохастических матриц сумма чисел в каждом столбце равна 1, а у правых – в каждой строчке. Бывают ещё дважды стохастические матрицы, в которых и столбцы и строчки суммируются в 1. Я выбрал вариант, когда вектор вероятностей значений на входе рассматривается как столбец, и чтобы получить вектор вероятностей значений на выходе нужно проделать обычное матричное умножение .
В англоязычной литературе вектор вероятностей принято рассматривать как строчку, матрицу переходов транспонировать (и она станет правой стохастической) и умножать на матрицу слева: . Я боюсь, это будет многим непривычно , поэтому выбрал вариант столбцов и левых стохастических матриц перехода.
Таким образом, информационный канал суть левая стохастическая матрица T. Задавая распределение на входе, вы получаете распределение
на выходе, просто умножая матрицу
на вектор
:
Пропускной способностью информационного канала
называется максимальное значение
, достижимое на некотором распределении
на входе.
Информационный канал для передачи бит, в котором 1 из-за помех превращается в 0 с вероятностью а 0 превращается в 1 c вероятностью
задается матрицей
Задача 2.7: Пусть есть информационный канал с помехами, в котором 1 превращается в 0 с вероятностью а 0 превращается в 1 c вероятностью
Чему равно значение
при условии, что на вход поступает случайный бит с распределением
? На каком распределении на входе достигается максимум
и чему он равен, то есть какая пропускная способность у этого канала?
Ответ:
Здесь удобно воспользоваться формулой
Имеем:
-
Распределение на входе:
-
Распределение на выходе:
-
Совместное распределение, то есть распределение на парах (вход, выход):
-
И два условных распределения:
-
Если воспользоваться формулой MI, то получим:
А эта формула не что иное как мера выпуклости функции (aka JSD, см. ниже) на отрезке
, а именно, это значение этой функции на выпуклой сумме абсцисс концов этого отрезка минус выпуклая сумма значений этой функции на концах отрезка (ординат отрезка).
На рисунке показана функция . Отрезок KL делится точкой A в пропорции
. Длина отрезка AB и есть значение MI.
Максимальная длина отрезка достигается в такой точке, в которой производная равна углу наклона отрезка.
Обобщая задачу 2.7 на многомерный случай, получаем:
Утверждение 2.1: Пропускная способность канала определяется мерой выпуклости функции в симплексе, который является образом стохастического преобразования, задаваемым информационным каналом, а именно, максимальным значением разницы
от афинной (aka выпуклой) суммы вершин симплекса, вершины которого задаются столбцами стохастической матрицы, и афинной суммы значений функции
на вершинах симплекса. Максимум берётся по всем возможным весам, задающих афинную сумму. В определении ниже веса – это
, а вершины симплекса – это
.
Интересно, что на значение пропускной способности канала можно посмотреть как на некоторую меру объема, заключённого в симплексе, задаваемом множеством условных распределений как вершинами.
Опр. 2.4: Пусть есть несколько распределений на одном и том же множестве значений. Дивергенция Шаннона-Джейсона (Jensen–Shannon Divergence, JSD) этого набора c весами
вычисляется как
для
то есть
Чем сильнее распределения отличаются друг от друга, тем больше JSD. Максимум
и есть пропускная способность канала
Задача 2.8: Пусть есть две зависимые нормальные величины , с дисперсиями
и
соответственно, и пусть первая получается из второй добавлением независимого нормального шума c дисперсией
:
Тогда
Чему равна взаимная информация
?
Ответ
Энтропии величин и
равны
Энтропия пары вещественных случайных величин равна
Последнее равно после сумме энтропий двумерного распределения пары (энтропия пары независимых равна сумме их энтропий). А энтропия пары
равна энтропии пары
потому что линейное преобразование вектора случайных величин c помощью матрицы
даёт вектор с той же энтропией +
(докажите это!), а детерминант нашего линейного преобразование равен 1.
Пояснение про матрицу: здесь матрица – это матрица соответствующая массиву
:
и её детерминант равен 1. Значение детерминанта равно множителю, во сколько раз изменяется объём кубика в
-мерном пространстве (у нас
). Слагаемое
всплывает здесь по той же самой причине, по которой всплывает слагаемое
в формуле энтропии в задаче 1.7 дискретизированной вещественной случайной величины. Конец пояснения.
В итоге по формуле мы получаем
Замечание 1: Когда дисперсия (мощность) шума равна дисперсии (мощности) сигнала
каждое измерение
содержит 0.5 бита информации о значении
Замечание 2: Собственно, этот результат и есть теорема Шаннона-Хартли в упрощённом виде.
Задача 2.9: Пусть есть две зависимые величины , где
имеет экспоненциальное распределение с параметром
, а
. Чему равна взаимная информация
? Другими словами, сколько информации сохраняется при округлении экспоненциальной случайной величины до какого-то знака. Сравните
и
Ответ
Задача на понимание. Из первой случайной величины однозначно определяется значение второй. Значит информация MI равна просто энтропии второй величины, а распределение второй случайной величины есть геометрическая прогрессия с , у которой энтропия равна
(см. задачу 1.4).
Задача 2.10: Пусть есть две зависимые величины , где
имеет бета-распределение с параметрами
, а
сэмплируется из биномиального распределения с параметрами
. Чему равна взаимная информация
? Другими словами, сколько бит информации про истинный CTR рекламного объявления можно извлечь в среднем из статистики кликов на k показах.
Задача 2.11: Две зависимые величины получаются следующим образом – сначала сэмплируется случайная величина
из экспоненциального распределения со средним
, а потом сэмплируются две пуассоновские случайные величины
с параметром
. Чему равна взаимная информация
? Одна из возможных интерпретаций этой задачи такая: чему равна взаимная информация между числом продаж в одну неделю и числом продаж в другую неделю некого неизвестного нам товара.
Последние задачи являются примером того, как зависимости случайных величин можно моделировать с помощью графических вероятностных моделей, в частности, байесовских сетей.
Задача 2.12: Случайная величина получается из независимых случайных величин
с распределением
по формуле
Константные веса вам неизвестны, но априорное знание о них, это то, что они независимо были сэмплированы из
. Вы решаете задачу вычисления оценок весов
классическим методом регрессии и строите прогноз
Как будет расти квадратичная ошибка и значение
с ростом размера обучающего пула? Проанализируйте ответ для случая
.
-
Часть 3 – ML & Mutual Information. Основы ML в контексте теории информации.
(по
столбцам) образ-т правильный
приём
полную
группу событий
Вероятности, стоящие на главной
диагонали выражают правильный приём. Вероятности, которые стоят по столбцам,
образуют полную группу событий.
Пример: Влияние помех в канале связи
описывается канальной матрицей. Требуется вычислить потери при передачи
сигналов, если вероятность появления сигналов следующая:
p(x1) = 0.7 p(x2)
= 0.2 p(x3) = 0.1
H(y / x) = -[0.7 * (0.98
log 0.98 + 2*0.01 log 0.01) + 0.2 * (0.15 log 0.15 + 0.75 log 0.75 + 0.1 log
0.1) + 0.1 * (0.3 log 0.3 + 0.2 log 0.2 + 0.5 log 0.5)] = 0.463 бит/символ .
Энтропия и
информация
Пусть
имеется система X с энтропией H(x). После получении информации о
состоянии системы; система полностью определилась, т.е энтропия равна нулю,
следовательно, информация, получаемая в результате выяснения состояния системы x равна уменьшению энтропии.
Ix = H(x) – 0 = H(x)
Количество
информации приобретённое при полном выяснении состояния системы равна энтропии.
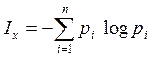
— называют частной информацией о
системе или информацией от отдельного сообщения.
Для
системы с равновозможными состояниями
Полная
информация
Пример: На шахматной доске в одной из клеток
поставлена фигура. Вероятность нахождения фигуры на любой клетке одинакова.
Определить информацию, получаемую от сообщения о нахождении фигуры в какой-либо
клетке.
Ix = log 64 = 6 бит
Пример 2: Определить частную информацию от
сообщения о нахождении фигуры в одной из четырёх клеток.
P = 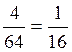
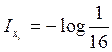
Пример 3: Определить частную информацию,
содержащаяся в сообщении случайного лица о своём дне рожденье.
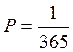
вероятность полученного сообщения; 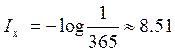
Пример 4: Определить полную информацию от
сообщения о дне рождения случайного лица.
x1 – день рожденье
x2 – не день рожденье
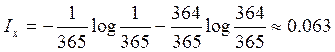
Пример 5: По цели может быть произведено n выстрелов. Вероятность поражения цели
при каждом выстреле p. После k-ого
выстрела (1£ к á n) производятся разведка, сообщение
поражена или не поражена цель. Определить к при условии, чтобы
количество информации, доставляемая разведкой была максимальной.
xk – система (цель после к-ого выстрела) имеет два
состояния:
x1 – цель поражена;
x2 – промах
p1 = 1 – (1 — p)k p2
= (1 — p)k
Информация будет максимальна, когда p1 = p2, следовательно
1 – (1 — p)k = (1 — p)k , k
=
p = 0.2; к = 3
Взаимная
информация
Имеется две системы: X и
Y. Они взаимосвязаны. Необходимо
определить, какое количество информации по системе X
даст наблюдение за системой Y. Такую информацию определяют, как
уменьшение энтропии системы X в результате получения сведений о
системе Y.
Iy®x = H(x) – H(x / y)
Iy®x = Ix®y = Ix«y
1) Если системы X и
Y независимы, то
H(x / y) = H(x) и Iy®x
= 0 — информации не будет
2)
Система полностью зависимы
H(x / y) = H(y / x) = 0 Iy®x = H(x)
= H(y)
Выражения для взаимной информации
можно получить через взаимную энтропию
H(x / y) = H(x, y) – H(y) Iy®x = H(x) + H(y) – H(x, y)
Формула для расчёта взаимной информации
H(x) = M[ — log p(x)], H(y) = M[ — log p(y)]
H(x, y) = M[ — log p(x, y)]
Iy®x = M[ — log p(x) – log p(y) + log p(x,
y)]
Сумма равна единице
Этих
сведений достаточно, чтобы определить взаим-
ную
информацию, создавшуюся в системе
Пример: Найти полную взаимную информацию,
содержащуюся в системах X и Y.
Если задача на матрицы совместных вероятностей.
|
|
x1 |
x2 |
x3 |
rj |
|
y1 |
0.1 |
0.2 |
0 |
0.3 |
|
y2 |
0 |
0.3 |
0 |
0.3 |
|
y3 |
0 |
0.2 |
0.2 |
0.4 |
|
pi |
0.1 |
0.7 |
0.2 |

Икс { displaystyle X}
Y { displaystyle Y}
ЧАС ( Икс , Y ) { Displaystyle mathrm {H} (X, Y)}
ЧАС ( Икс ) { Displaystyle mathrm {H} (X)}
ЧАС ( Икс ∣ Y ) { Displaystyle mathrm {H} (X середина Y)}
ЧАС ( Y ) { Displaystyle mathrm {H} (Y)}
ЧАС ( Y ∣ Икс ) { displaystyle mathrm {H} (Y mid X)}
я ( Икс ; Y ) { displaystyle operatorname {I} (X; Y)}
В теории вероятностей и теории информации, то взаимная информация ( MI) два случайных величин является мерой взаимной зависимости между двумя переменными. Более конкретно, оно квантифицирует « количество информации » (в единицах, такие как Shannons ( биты ), нац или Hartleys ), полученный около одной случайной величины, наблюдая за другую случайную величину. Концепция взаимной информации тесно связана с концепцией энтропии случайной величины, фундаментальным понятием в теории информации, которое количественно определяет ожидаемое «количество информации», содержащееся в случайной величине.
Не ограничиваясь действительными случайными величинами и линейной зависимостью, такой как коэффициент корреляции, MI является более общим и определяет, насколько совместное распределение пары отличается от произведения предельных распределений и. MI является ожидаемым значением в точечно взаимной информации (PMI). ( Икс , Y ) { displaystyle (X, Y)}


Величина была определена и проанализирована Клодом Шенноном в его знаменательной статье « Математическая теория коммуникации », хотя он не называл это «взаимной информацией». Этот термин был введен позже Робертом Фано. Взаимная информация также известна как получение информации.
СОДЕРЖАНИЕ
- 1 Определение
- 2 В терминах PMF для дискретных распределений
- 3 С точки зрения PDF для непрерывных распределений
- 4 Мотивация
- 5 Отношение к другим величинам
- 5.1 Неотрицательность
- 5.2 Симметрия
- 5.3 Связь с условной и совместной энтропией
- 5.4 Связь с расхождением Кульбака – Лейблера
- 5.5 Байесовская оценка взаимной информации
- 5.6 Допущения независимости
- 6 вариаций
- 6.1 Метрическая система
- 6.2 Условная взаимная информация
- 6.3 Информация о взаимодействии
- 6.3.1 Многомерная статистическая независимость
- 6.3.2 Приложения
- 6.4 Направленная информация
- 6.5 Нормализованные варианты
- 6.6 Взвешенные варианты
- 6.7 Скорректированная взаимная информация
- 6.8 Абсолютная взаимная информация
- 6.9 Линейная корреляция
- 6.10 Для дискретных данных
- 7 приложений
- 8 См. Также
- 9 Примечания
- 10 Ссылки
Определение
Позвольте быть пара случайных величин со значениями в пространстве. Если их совместное распределение равно и предельные распределения равны и, взаимная информация определяется как ( Икс , Y ) { displaystyle (X, Y)}



я ( Икс ; Y ) знак равно D K L ( п ( Икс , Y ) ‖ п Икс ⊗ п Y ) { Displaystyle I (X; Y) = D _ { mathrm {KL}} (P _ {(X, Y)} | P_ {X} otimes P_ {Y})}
где — расходимость Кульбака – Лейблера. D K L { Displaystyle D _ { mathrm {KL}}}
Обратите внимание, что в собственности дивергенции Кульбака-Лейблера, что равно нулю именно тогда, когда совместное распределение совпадает с произведением маргиналов, т.е. когда и являются независимыми (и, следовательно, наблюдения ничего не говорит вам о). В общем случае неотрицательно, это мера стоимости кодирования как пары независимых случайных величин, хотя на самом деле это не так. я ( Икс ; Y ) { Displaystyle I (X; Y)}





В терминах PMF для дискретных распределений
Взаимная информация двух совместно дискретных случайных величин и вычисляется как двойная сумма: Икс { displaystyle X}
я ( Икс ; Y ) знак равно ∑ у ∈ Y ∑ Икс ∈ Икс п ( Икс , Y ) ( Икс , у ) бревно ( п ( Икс , Y ) ( Икс , у ) п Икс ( Икс ) п Y ( у ) ) , { displaystyle operatorname {I} (X; Y) = sum _ {y in { mathcal {Y}}} sum _ {x in { mathcal {X}}} {p _ {(X, Y)} (x, y) log left ({ frac {p _ {(X, Y)} (x, y)} {p_ {X} (x) , p_ {Y} (y)}} Правильно)},} |
( Уравнение 1) |
где есть совместная вероятность массовый функция из и, и, и являются предельными вероятностями массовых функций и соответственно. п ( Икс , Y ) { displaystyle p _ {(X, Y)}}





С точки зрения PDF-файлов для непрерывных распределений
В случае совместно непрерывных случайных величин двойная сумма заменяется двойным интегралом :
я ( Икс ; Y ) знак равно ∫ Y ∫ Икс п ( Икс , Y ) ( Икс , у ) бревно ( п ( Икс , Y ) ( Икс , у ) п Икс ( Икс ) п Y ( у ) ) d Икс d у , { displaystyle operatorname {I} (X; Y) = int _ { mathcal {Y}} int _ { mathcal {X}} {p _ {(X, Y)} (x, y) log { left ({ frac {p _ {(X, Y)} (x, y)} {p_ {X} (x) , p_ {Y} (y)}} right)}} ; dx , dy,} |
( Уравнение 2) |
где теперь совместная вероятность плотность функция и, и, и являются функциями маргинальных плотностей вероятности и соответственно. п ( Икс , Y ) { displaystyle p _ {(X, Y)}}





Если используется логическая база 2, единицами взаимной информации являются биты.
Мотивация
Наглядно, взаимной информации измеряет информацию, и доля: Он измеряет, сколько зная одну из этих переменных уменьшает неопределенность относительно другой. Например, если и независимы, то знание не дает никакой информации о и наоборот, поэтому их взаимная информация равна нулю. С другой стороны, if является детерминированной функцией и является детерминированной функцией, тогда вся информация, передаваемая с помощью, совместно используется: знание определяет ценность и наоборот. В результате, в этом случае взаимной информации является таким же, как неопределенность, содержащейся в (или) один, а именно энтропии из (или). Более того, эта взаимная информация совпадает с энтропией и энтропией. (Очень частный случай, когда и являются одной и той же случайной величиной.) Икс { displaystyle X}




















Взаимная информация является мерой присущей зависимости, выраженной в совместном распределении по и по отношению к предельному распределению и при предположении о независимости. Таким образом, взаимная информация измеряет зависимость в следующем смысле: тогда и только тогда, когда и являются независимыми случайными величинами. Это легко увидеть в одном направлении: если и независимы, то, следовательно: Икс { displaystyle X}








- бревно ( п ( Икс , Y ) ( Икс , у ) п Икс ( Икс ) п Y ( у ) ) знак равно бревно 1 знак равно 0. { displaystyle log { left ({ frac {p _ {(X, Y)} (x, y)} {p_ {X} (x) , p_ {Y} (y)}} right)} = log 1 = 0.}
Более того, взаимная информация неотрицательна (т.е. см. Ниже) и симметрична (т.е. см. Ниже). я ( Икс ; Y ) ≥ 0 { Displaystyle OperatorName {I} (X; Y) geq 0}
Отношение к другим величинам
Неотрицательность
Используя неравенство Дженсена об определении взаимной информации, мы можем показать, что она неотрицательна, т. Е. я ( Икс ; Y ) { displaystyle operatorname {I} (X; Y)}
- я ( Икс ; Y ) ≥ 0 { Displaystyle OperatorName {I} (X; Y) geq 0}
Симметрия
- я ( Икс ; Y ) знак равно я ( Y ; Икс ) { Displaystyle OperatorName {I} (X; Y) = OperatorName {I} (Y; X)}
Отношение к условной и совместной энтропии
Взаимная информация может быть эквивалентно выражена как:
- я ( Икс ; Y ) ≡ ЧАС ( Икс ) — ЧАС ( Икс ∣ Y ) ≡ ЧАС ( Y ) — ЧАС ( Y ∣ Икс ) ≡ ЧАС ( Икс ) + ЧАС ( Y ) — ЧАС ( Икс , Y ) ≡ ЧАС ( Икс , Y ) — ЧАС ( Икс ∣ Y ) — ЧАС ( Y ∣ Икс ) { displaystyle { begin {align} operatorname {I} (X; Y) amp; {} Equiv mathrm {H} (X) — mathrm {H} (X mid Y) \ amp; {} Equiv mathrm {H} (Y) — mathrm {H} (Y mid X) \ amp; {} Equiv mathrm {H} (X) + mathrm {H} (Y) — mathrm {H } (X, Y) \ amp; {} Equiv mathrm {H} (X, Y) — mathrm {H} (X mid Y) — mathrm {H} (Y mid X) end { выровнено}}}
где и являются предельные энтропии, и являются условные энтропии, и является совместной энтропии из и. ЧАС ( Икс ) { Displaystyle mathrm {H} (X)}





Обратите внимание на аналогию с объединением, различием и пересечением двух множеств: в этом отношении все приведенные выше формулы очевидны из диаграммы Венна, приведенной в начале статьи.
С точки зрения канала связи, в котором выход является зашумленной версией входа, эти отношения суммированы на рисунке: Y { displaystyle Y}
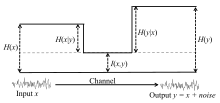
Поскольку не отрицательно, следовательно,. Здесь мы даем подробный вывод для случая совместно дискретных случайных величин: я ( Икс ; Y ) { displaystyle operatorname {I} (X; Y)}

- я ( Икс ; Y ) знак равно ∑ Икс ∈ Икс , у ∈ Y п ( Икс , Y ) ( Икс , у ) бревно п ( Икс , Y ) ( Икс , у ) п Икс ( Икс ) п Y ( у ) знак равно ∑ Икс ∈ Икс , у ∈ Y п ( Икс , Y ) ( Икс , у ) бревно п ( Икс , Y ) ( Икс , у ) п Икс ( Икс ) — ∑ Икс ∈ Икс , у ∈ Y п ( Икс , Y ) ( Икс , у ) бревно п Y ( у ) знак равно ∑ Икс ∈ Икс , у ∈ Y п Икс ( Икс ) п Y ∣ Икс знак равно Икс ( у ) бревно п Y ∣ Икс знак равно Икс ( у ) — ∑ Икс ∈ Икс , у ∈ Y п ( Икс , Y ) ( Икс , у ) бревно п Y ( у ) знак равно ∑ Икс ∈ Икс п Икс ( Икс ) ( ∑ у ∈ Y п Y ∣ Икс знак равно Икс ( у ) бревно п Y ∣ Икс знак равно Икс ( у ) ) — ∑ у ∈ Y ( ∑ Икс п ( Икс , Y ) ( Икс , у ) ) бревно п Y ( у ) знак равно — ∑ Икс ∈ Икс п ( Икс ) ЧАС ( Y ∣ Икс знак равно Икс ) — ∑ у ∈ Y п Y ( у ) бревно п Y ( у ) знак равно — ЧАС ( Y ∣ Икс ) + ЧАС ( Y ) знак равно ЧАС ( Y ) — ЧАС ( Y ∣ Икс ) . { displaystyle { begin {align} operatorname {I} (X; Y) amp; {} = sum _ {x in { mathcal {X}}, y in { mathcal {Y}}} p_ {(X, Y)} (x, y) log { frac {p _ {(X, Y)} (x, y)} {p_ {X} (x) p_ {Y} (y)}} amp; {} = sum _ {x in { mathcal {X}}, y in { mathcal {Y}}} p _ {(X, Y)} (x, y) log { frac { p _ {(X, Y)} (x, y)} {p_ {X} (x)}} — sum _ {x in { mathcal {X}}, y in { mathcal {Y}} } p _ {(X, Y)} (x, y) log p_ {Y} (y) \ amp; {} = sum _ {x in { mathcal {X}}, y in { mathcal {Y}}} p_ {X} (x) p_ {Y mid X = x} (y) log p_ {Y mid X = x} (y) — sum _ {x in { mathcal { mathcal { X}}, y in { mathcal {Y}}} p _ {(X, Y)} (x, y) log p_ {Y} (y) \ amp; {} = sum _ {x in { mathcal {X}}} p_ {X} (x) left ( sum _ {y in { mathcal {Y}}} p_ {Y mid X = x} (y) log p_ {Y) mid X = x} (y) right) — sum _ {y in { mathcal {Y}}} left ( sum _ {x} p _ {(X, Y)} (x, y) right) log p_ {Y} (y) \ amp; {} = — sum _ {x in { mathcal {X}}} p (x) mathrm {H} (Y mid X = x) — sum _ {y in { mathcal {Y}}} p_ {Y} (y) log p_ {Y} (y) \ amp; {} = — mathrm {H} (Y mid X) + mathrm {H} (Y) \ amp; {} = mathrm {H} (Y) — mathrm {H} (Y mid X). \ конец {выровнено}}}
Доказательства остальных тождеств, приведенных выше, аналогичны. Доказательство общего случая (не только дискретного) аналогично, с интегралами вместо сумм.
Наглядно, если энтропия рассматривается как мера неопределенности относительно случайной величины, то есть мера того, что вовсе не говорит о. Это «величина неопределенности, остающаяся примерно после того, как известна», и, таким образом, правая часть второго из этих равенств может быть прочитана как «величина неопределенности, минус величина неопределенности, которая остается после того, как известна», что эквивалентно «степени неопределенности, устраняемой знанием ». Это подтверждает интуитивное значение взаимной информации как количества информации (то есть уменьшения неопределенности), которую знание одной переменной дает о другой. ЧАС ( Y ) { Displaystyle mathrm {H} (Y)}









Обратите внимание, что в дискретном случае и поэтому. Таким образом, можно сформулировать основной принцип, согласно которому переменная содержит, по крайней мере, столько же информации о себе, сколько может предоставить любая другая переменная. ЧАС ( Y ∣ Y ) знак равно 0 { Displaystyle mathrm {H} (Y середина Y) = 0}

Связь с расходимостью Кульбака – Лейблера
Для совместного дискретного или непрерывного совместно пара, взаимная информация является Кульбак-Либлер дивергенция от произведения маргинальных распределений,, из совместного распределения, то есть, ( Икс , Y ) { displaystyle (X, Y)}

я ( Икс ; Y ) знак равно D KL ( п ( Икс , Y ) ∥ п Икс п Y ) { displaystyle operatorname {I} (X; Y) = D _ { text {KL}} left (p _ {(X, Y)} parallel p_ {X} p_ {Y} right)}
Кроме того, пусть будет условной функцией массы или плотности. Тогда у нас есть тождество п Икс ∣ Y знак равно у ( Икс ) знак равно п ( Икс , Y ) ( Икс , у ) / п Y ( у ) { displaystyle p_ {X mid Y = y} (x) = p _ {(X, Y)} (x, y) / p_ {Y} (y)}
я ( Икс ; Y ) знак равно E Y [ D KL ( п Икс ∣ Y ∥ п Икс ) ] { displaystyle operatorname {I} (X; Y) = mathbb {E} _ {Y} left [D _ { text {KL}} ! left (p_ {X mid Y} parallel p_ { X} right) right]}
Доказательство для совместно дискретных случайных величин выглядит следующим образом:
- я ( Икс ; Y ) знак равно ∑ у ∈ Y ∑ Икс ∈ Икс п ( Икс , Y ) ( Икс , у ) бревно ( п ( Икс , Y ) ( Икс , у ) п Икс ( Икс ) п Y ( у ) ) знак равно ∑ у ∈ Y ∑ Икс ∈ Икс п Икс ∣ Y знак равно у ( Икс ) п Y ( у ) бревно п Икс ∣ Y знак равно у ( Икс ) п Y ( у ) п Икс ( Икс ) п Y ( у ) знак равно ∑ у ∈ Y п Y ( у ) ∑ Икс ∈ Икс п Икс ∣ Y знак равно у ( Икс ) бревно п Икс ∣ Y знак равно у ( Икс ) п Икс ( Икс ) знак равно ∑ у ∈ Y п Y ( у ) D KL ( п Икс ∣ Y знак равно у ∥ п Икс ) знак равно E Y [ D KL ( п Икс ∣ Y ∥ п Икс ) ] . { displaystyle { begin {align} operatorname {I} (X; Y) amp; = sum _ {y in { mathcal {Y}}} sum _ {x in { mathcal {X}} } {p _ {(X, Y)} (x, y) log left ({ frac {p _ {(X, Y)} (x, y)} {p_ {X} (x) , p_ { Y} (y)}} right)} \ amp; = sum _ {y in { mathcal {Y}}} sum _ {x in { mathcal {X}}} p_ {X mid Y = y} (x) p_ {Y} (y) log { frac {p_ {X mid Y = y} (x) p_ {Y} (y)} {p_ {X} (x) p_ { Y} (y)}} \ amp; = sum _ {y in { mathcal {Y}}} p_ {Y} (y) sum _ {x in { mathcal {X}}} p_ { X mid Y = y} (x) log { frac {p_ {X mid Y = y} (x)} {p_ {X} (x)}} \ amp; = sum _ {y in { mathcal {Y}}} p_ {Y} (y) ; D _ { text {KL}} ! left (p_ {X mid Y = y} parallel p_ {X} right) \ amp; = mathbb {E} _ {Y} left [D _ { text {KL}} ! left (p_ {X mid Y} parallel p_ {X} right) right]. end { выровнено}}}
Аналогичным образом это тождество может быть установлено для совместно непрерывных случайных величин.
Обратите внимание, что здесь дивергенция Кульбака – Лейблера включает интегрирование только по значениям случайной величины, а выражение по- прежнему обозначает случайную величину, поскольку оно является случайным. Таким образом, взаимная информация также может быть понята как ожидание в Кульбаке-Лейблере расходимости однофакторного распределения из от условного распределения в дали: чем больше разные распределения и в среднем, тем больше информации усиление. Икс { displaystyle X}









Байесовская оценка взаимной информации
Если доступны выборки из совместного распределения, можно использовать байесовский подход для оценки взаимной информации этого распределения. Первой такой работой, которая также показала, как выполнять байесовскую оценку многих других теоретико-информационных свойств, помимо взаимной информации, была. Последующие исследователи переработали и расширили этот анализ. См. Недавнюю статью, основанную на предыдущем, специально разработанном для оценки взаимной информации как таковой. Кроме того, недавно в. Y { displaystyle Y}
Допущения независимости
Формулировка взаимной информации о расхождении Кульбака-Лейблера основана на том, что каждый заинтересован в сравнении с полностью факторизованным внешним продуктом. Во многих задачах, таких как факторизация неотрицательной матрицы, интересуют менее экстремальные факторизации; в частности, кто-то желает сравнить с приближением матрицы низкого ранга по некоторой неизвестной переменной ; то есть, в какой степени можно было п ( Икс , у ) { Displaystyle р (х, у)}


- п ( Икс , у ) ≈ ∑ ш п ′ ( Икс , ш ) п ′ ′ ( ш , у ) { Displaystyle р (х, у) приблизительно сумма _ {ш} р ^ { простое число} (х, ш) п ^ { простое простое число} (ш, у)}
С другой стороны, может быть интересно узнать, сколько еще информации переносит его факторизация. В таком случае избыточная информация, которую полное распределение переносит через матричную факторизацию, дается дивергенцией Кульбака-Лейблера п ( Икс , у ) { Displaystyle р (х, у)}
- я L р M А знак равно ∑ у ∈ Y ∑ Икс ∈ Икс п ( Икс , у ) бревно ( п ( Икс , у ) ∑ ш п ′ ( Икс , ш ) п ′ ′ ( ш , у ) ) , { displaystyle operatorname {I} _ {LRMA} = sum _ {y in { mathcal {Y}}} sum _ {x in { mathcal {X}}} {p (x, y) log { left ({ frac {p (x, y)} { sum _ {w} p ^ { prime} (x, w) p ^ { prime prime} (w, y)}}) Правильно)}},}
Традиционное определение взаимной информации восстанавливается в крайнем случае, когда процесс имеет только одно значение. W { displaystyle W}
Вариации
Было предложено несколько вариантов взаимной информации для удовлетворения различных потребностей. Среди них — нормализованные варианты и обобщения для более чем двух переменных.
Метрическая
Многие приложения требуют метрики, то есть меры расстояния между парами точек. Количество
- d ( Икс , Y ) знак равно ЧАС ( Икс , Y ) — я ( Икс ; Y ) знак равно ЧАС ( Икс ) + ЧАС ( Y ) — 2 я ( Икс ; Y ) знак равно ЧАС ( Икс ∣ Y ) + ЧАС ( Y ∣ Икс ) { Displaystyle { begin {выровнен} d (X, Y) amp; = mathrm {H} (X, Y) — operatorname {I} (X; Y) \ amp; = mathrm {H} (X) + mathrm {H} (Y) -2 operatorname {I} (X; Y) \ amp; = mathrm {H} (X mid Y) + mathrm {H} (Y mid X) end {выровнено}}}
удовлетворяет свойствам метрики ( неравенство треугольника, неотрицательность, неразличимость и симметрия). Этот показатель расстояния также известен как изменение информации.
Если это дискретные случайные величины, тогда все члены энтропии неотрицательны, поэтому можно определить нормализованное расстояние Икс , Y { displaystyle X, Y}
- D ( Икс , Y ) знак равно d ( Икс , Y ) ЧАС ( Икс , Y ) ≤ 1. { Displaystyle D (X, Y) = { frac {d (X, Y)} { mathrm {H} (X, Y)}} leq 1.}
Метрика — универсальная метрика, в том смысле, что если какое-либо другое расстояние измеряет место и близко, то он также будет судить о них близко. D { displaystyle D}


Добавление определений показывает, что
- D ( Икс , Y ) знак равно 1 — я ( Икс ; Y ) ЧАС ( Икс , Y ) . { displaystyle D (X, Y) = 1 — { frac { operatorname {I} (X; Y)} { mathrm {H} (X, Y)}}.}
В теоретико-множественной интерпретации информации (см. Рисунок для условной энтропии ) это фактически расстояние Жаккара между и. Икс { displaystyle X}
Наконец-то,
- D ′ ( Икс , Y ) знак равно 1 — я ( Икс ; Y ) Максимум { ЧАС ( Икс ) , ЧАС ( Y ) } { displaystyle D ^ { prime} (X, Y) = 1 — { frac { operatorname {I} (X; Y)} { max left { mathrm {H} (X), mathrm {H} (Y) right }}}}
также является метрикой.
Условная взаимная информация
Основная статья: Условная взаимная информация
Иногда полезно выразить взаимную информацию двух случайных величин, обусловленную третьей.
я ( Икс ; Y | Z ) знак равно E Z [ D K L ( п ( Икс , Y ) | Z ‖ п Икс | Z ⊗ п Y | Z ) ] { displaystyle operatorname {I} (X; Y | Z) = mathbb {E} _ {Z} [D _ { mathrm {KL}} (P _ {(X, Y) | Z} | P_ {X | Z} время P_ {Y | Z})]}
Для совместно дискретных случайных величин это принимает вид
- я ( Икс ; Y | Z ) знак равно ∑ z ∈ Z ∑ у ∈ Y ∑ Икс ∈ Икс п Z ( z ) п Икс , Y | Z ( Икс , у | z ) бревно [ п Икс , Y | Z ( Икс , у | z ) п Икс | Z ( Икс | z ) п Y | Z ( у | z ) ] , { displaystyle operatorname {I} (X; Y | Z) = sum _ {z in { mathcal {Z}}} sum _ {y in { mathcal {Y}}} sum _ { х in { mathcal {X}}} {p_ {Z} (z) , p_ {X, Y | Z} (x, y | z) log left [{ frac {p_ {X, Y | Z} (x, y | z)} {p_ {X | Z} , (x | z) p_ {Y | Z} (y | z)}} right]},}
который можно упростить как
- я ( Икс ; Y | Z ) знак равно ∑ z ∈ Z ∑ у ∈ Y ∑ Икс ∈ Икс п Икс , Y , Z ( Икс , у , z ) бревно п Икс , Y , Z ( Икс , у , z ) п Z ( z ) п Икс , Z ( Икс , z ) п Y , Z ( у , z ) . { displaystyle operatorname {I} (X; Y | Z) = sum _ {z in { mathcal {Z}}} sum _ {y in { mathcal {Y}}} sum _ { x in { mathcal {X}}} p_ {X, Y, Z} (x, y, z) log { frac {p_ {X, Y, Z} (x, y, z) p_ {Z) } (z)} {p_ {X, Z} (x, z) p_ {Y, Z} (y, z)}}.}.}
Для совместно непрерывных случайных величин это принимает вид
- я ( Икс ; Y | Z ) знак равно ∫ Z ∫ Y ∫ Икс п Z ( z ) п Икс , Y | Z ( Икс , у | z ) бревно [ п Икс , Y | Z ( Икс , у | z ) п Икс | Z ( Икс | z ) п Y | Z ( у | z ) ] d Икс d у d z , { displaystyle operatorname {I} (X; Y | Z) = int _ { mathcal {Z}} int _ { mathcal {Y}} int _ { mathcal {X}} {p_ {Z } (z) , p_ {X, Y | Z} (x, y | z) log left [{ frac {p_ {X, Y | Z} (x, y | z)} {p_ {X | Z} , (x | z) p_ {Y | Z} (y | z)}} right]} dxdydz,}
который можно упростить как
- я ( Икс ; Y | Z ) знак равно ∫ Z ∫ Y ∫ Икс п Икс , Y , Z ( Икс , у , z ) бревно п Икс , Y , Z ( Икс , у , z ) п Z ( z ) п Икс , Z ( Икс , z ) п Y , Z ( у , z ) d Икс d у d z . { displaystyle operatorname {I} (X; Y | Z) = int _ { mathcal {Z}} int _ { mathcal {Y}} int _ { mathcal {X}} p_ {X, Y, Z} (x, y, z) log { frac {p_ {X, Y, Z} (x, y, z) p_ {Z} (z)} {p_ {X, Z} (x, z) p_ {Y, Z} (y, z)}} dxdydz.}
Использование третьей случайной величины может увеличивать или уменьшать взаимную информацию, но всегда верно, что
- я ( Икс ; Y | Z ) ≥ 0 { Displaystyle OperatorName {I} (X; Y | Z) geq 0}
для дискретных, совместно распределенных случайных величин. Этот результат был использован в качестве основного строительного блока для доказательства других неравенств в теории информации. Икс , Y , Z { displaystyle X, Y, Z}
Информация о взаимодействии
Основная статья: Информация о взаимодействии
Было предложено несколько обобщений взаимной информации для более чем двух случайных величин, таких как полная корреляция (или мультиинформационная) и двойная полная корреляция. Выражение и изучение многомерной взаимной информации более высокой степени было достигнуто в двух, казалось бы, независимых работах: МакГилл (1954), который назвал эти функции «информацией о взаимодействии», и Ху Куо Тинг (1962). Информация о взаимодействии определяется для одной переменной следующим образом:
- я ( Икс 1 ) знак равно ЧАС ( Икс 1 ) { Displaystyle OperatorName {I} (X_ {1}) = mathrm {H} (X_ {1})}
и для п gt; 1 , { displaystyle ngt; 1,}
- я ( Икс 1 ; . . . ; Икс п ) знак равно я ( Икс 1 ; . . . ; Икс п — 1 ) — я ( Икс 1 ; . . . ; Икс п — 1 ∣ Икс п ) . { displaystyle operatorname {I} (X_ {1}; ,… ,; X_ {n}) = operatorname {I} (X_ {1}; ,… ,; X_ {n -1}) — operatorname {I} (X_ {1}; ,… ,; X_ {n-1} mid X_ {n}).}
Некоторые авторы меняют порядок членов в правой части предыдущего уравнения, которое меняет знак, когда количество случайных величин нечетное. (И в этом случае выражение с одной переменной становится отрицательным значением энтропии.) Обратите внимание, что
- я ( Икс 1 ; … ; Икс п — 1 ∣ Икс п ) знак равно E Икс п [ D K L ( п ( Икс 1 , … , Икс п — 1 ) ∣ Икс п ‖ п Икс 1 ∣ Икс п ⊗ ⋯ ⊗ п Икс п — 1 ∣ Икс п ) ] . { displaystyle I (X_ {1}; ldots; X_ {n-1} mid X_ {n}) = mathbb {E} _ {X_ {n}} [D _ { mathrm {KL}} (P_ {(X_ {1}, ldots, X_ {n-1}) mid X_ {n}} | P_ {X_ {1} mid X_ {n}} otimes cdots otimes P_ {X_ {n -1} mid X_ {n}})].}
Многомерная статистическая независимость
Многомерные функции взаимной информации обобщают случай парной независимости, который утверждает, что если и только если, на произвольные многочисленные переменные. n переменных взаимно независимы тогда и только тогда, когда функции взаимной информации обращаются в нуль при (теорема 2). В этом смысле можно использовать как уточненный критерий статистической независимости. Икс 1 , Икс 2 { Displaystyle X_ {1}, X_ {2}}




Приложения
Для 3 переменных Brenner et al. применили многомерную взаимную информацию к нейронному кодированию и назвали его отрицательность «синергизмом», а Watkinson et al. применил это к генетической экспрессии. Для произвольных k переменных Tapia et al. применили многомерную взаимную информацию к экспрессии генов). Он может быть нулевым, положительным или отрицательным. Позитивность соответствует отношениям, обобщающим попарные корреляции, нулевое значение соответствует уточненному понятию независимости, а отрицательность обнаруживает многомерные «возникающие» отношения и кластеризованные точки данных).
Одна многомерная схема обобщения, которая максимизирует взаимную информацию между совместным распределением и другими целевыми переменными, оказывается полезной при выборе признаков.
Взаимная информация также используется в области обработки сигналов как мера сходства между двумя сигналами. Например, показатель FMI — это показатель эффективности слияния изображений, который использует взаимную информацию для измерения количества информации, которую слитое изображение содержит об исходных изображениях. Код Matlab для этой метрики можно найти по адресу. Доступен пакет python для вычисления всей многомерной взаимной информации, условной взаимной информации, совместных энтропий, общих корреляций, информационного расстояния в наборе данных из n переменных.
Направленная информация
Направленная информация,, измеряет количество информации, которое вытекает из процесса к, где обозначает вектор и обозначает. Термин направленная информация был введен Джеймсом Мэсси и определяется как я ( Икс п → Y п ) { displaystyle operatorname {I} left (X ^ {n} to Y ^ {n} right)}






- я ( Икс п → Y п ) знак равно ∑ я знак равно 1 п я ( Икс я ; Y я ∣ Y я — 1 ) { displaystyle operatorname {I} left (X ^ {n} to Y ^ {n} right) = sum _ {i = 1} ^ {n} operatorname {I} left (X ^ { i}; Y_ {i} mid Y ^ {i-1} right)}
.
Обратите внимание, что если, направленная информация становится взаимной информацией. Направленная информация имеет множество применений в задачах, где причинно-следственная связь играет важную роль, таких как пропускная способность канала с обратной связью. п знак равно 1 { displaystyle n = 1}
Нормализованные варианты
Нормализованные варианты взаимной информации представлены коэффициентами ограничения, коэффициента неопределенности или квалификации:
- C Икс Y знак равно я ( Икс ; Y ) ЧАС ( Y ) а также C Y Икс знак равно я ( Икс ; Y ) ЧАС ( Икс ) . { displaystyle C_ {XY} = { frac { operatorname {I} (X; Y)} { mathrm {H} (Y)}} ~~~~ { t_dv {and}} ~~~~ C_ {YX} = { frac { operatorname {I} (X; Y)} { mathrm {H} (X)}}.}.
Два коэффициента имеют значение в диапазоне [0, 1], но не обязательно равны. В некоторых случаях может потребоваться симметричная мера, например следующая мера избыточности :
- р знак равно я ( Икс ; Y ) ЧАС ( Икс ) + ЧАС ( Y ) { Displaystyle R = { гидроразрыва { OperatorName {I} (X; Y)} { mathrm {H} (X) + mathrm {H} (Y)}}}
который достигает минимум нуля, когда переменные независимы, и максимальное значение
- р Максимум знак равно мин { ЧАС ( Икс ) , ЧАС ( Y ) } ЧАС ( Икс ) + ЧАС ( Y ) { displaystyle R _ { max} = { frac { min left { mathrm {H} (X), mathrm {H} (Y) right }} { mathrm {H} (X) + mathrm {H} (Y)}}}
когда одна переменная становится полностью избыточной при знании другой. См. Также Резервирование (теория информации).
Другой симметричной мерой является симметричная неопределенность ( Witten amp; Frank 2005), определяемая формулой
- U ( Икс , Y ) знак равно 2 р знак равно 2 я ( Икс ; Y ) ЧАС ( Икс ) + ЧАС ( Y ) { Displaystyle U (X, Y) = 2R = 2 { frac { operatorname {I} (X; Y)} { mathrm {H} (X) + mathrm {H} (Y)}}}
который представляет собой среднее гармоническое значение двух коэффициентов неопределенности. C Икс Y , C Y Икс { displaystyle C_ {XY}, C_ {YX}}
Если мы рассматриваем взаимную информацию как частный случай полной корреляции или двойной полной корреляции, нормализованная версия, соответственно,
- я ( Икс ; Y ) мин [ ЧАС ( Икс ) , ЧАС ( Y ) ] { displaystyle { frac { operatorname {I} (X; Y)} { min left [ mathrm {H} (X), mathrm {H} (Y) right]}}}
а также я ( Икс ; Y ) ЧАС ( Икс , Y ) . { displaystyle { frac { operatorname {I} (X; Y)} { mathrm {H} (X, Y)}} ;.}
Эта нормализованная версия, также известная как Коэффициент качества информации (IQR), которая определяет количество информации переменной на основе другой переменной в сравнении с общей неопределенностью:
- я Q р ( Икс , Y ) знак равно E [ я ( Икс ; Y ) ] знак равно я ( Икс ; Y ) ЧАС ( Икс , Y ) знак равно ∑ Икс ∈ Икс ∑ у ∈ Y п ( Икс , у ) бревно п ( Икс ) п ( у ) ∑ Икс ∈ Икс ∑ у ∈ Y п ( Икс , у ) бревно п ( Икс , у ) — 1 { displaystyle IQR (X, Y) = operatorname {E} [ operatorname {I} (X; Y)] = { frac { operatorname {I} (X; Y)} { mathrm {H} ( X, Y)}} = { frac { sum _ {x in X} sum _ {y in Y} p (x, y) log {p (x) p (y)}} { sum _ {x in X} sum _ {y in Y} p (x, y) log {p (x, y)}}} — 1}
Существует нормализация, которая происходит из первого представления о взаимной информации как о аналоге ковариации (таким образом, энтропия Шеннона аналогична дисперсии ). Затем вычисляется нормализованная взаимная информация по аналогии с коэффициентом корреляции Пирсона,
- я ( Икс ; Y ) ЧАС ( Икс ) ЧАС ( Y ) . { displaystyle { frac { operatorname {I} (X; Y)} { sqrt { mathrm {H} (X) mathrm {H} (Y)}}} ;.}
Взвешенные варианты
В традиционной формулировке взаимной информации,
- я ( Икс ; Y ) знак равно ∑ у ∈ Y ∑ Икс ∈ Икс п ( Икс , у ) бревно п ( Икс , у ) п ( Икс ) п ( у ) , { Displaystyle OperatorName {I} (X; Y) = sum _ {y in Y} sum _ {x in X} p (x, y) log { frac {p (x, y) } {p (x) , p (y)}},}
каждое событие или объект, указанные в, взвешиваются по соответствующей вероятности. Это предполагает, что все объекты или события эквивалентны, за исключением вероятности их возникновения. Однако в некоторых приложениях может случиться так, что одни объекты или события более значимы, чем другие, или что определенные шаблоны ассоциации более семантически важны, чем другие. ( Икс , у ) { Displaystyle (х, у)}
Например, детерминированное отображение можно рассматривать как более сильное, чем детерминированное отображение, хотя эти отношения дадут ту же взаимную информацию. Это связано с тем, что взаимная информация вообще не чувствительна к какому-либо внутреннему порядку в значениях переменных ( Cronbach 1954, Coombs, Dawes amp; Tversky 1970, Lockhead 1970) и, следовательно, не чувствительна вообще к форме реляционного отображения между связанные переменные. Если желательно, чтобы первое отношение, показывающее согласие по всем значениям переменных, было более сильным, чем более позднее, можно использовать следующую взвешенную взаимную информацию ( Guiasu 1977). { ( 1 , 1 ) , ( 2 , 2 ) , ( 3 , 3 ) } { Displaystyle {(1,1), (2,2), (3,3) }}
- я ( Икс ; Y ) знак равно ∑ у ∈ Y ∑ Икс ∈ Икс ш ( Икс , у ) п ( Икс , у ) бревно п ( Икс , у ) п ( Икс ) п ( у ) , { displaystyle operatorname {I} (X; Y) = sum _ {y in Y} sum _ {x in X} w (x, y) p (x, y) log { frac { p (x, y)} {p (x) , p (y)}},}
который придает вес вероятности одновременного появления каждого значения переменной. Это допускает, что определенные вероятности могут иметь большее или меньшее значение, чем другие, тем самым позволяя количественную оценку соответствующих холистических факторов или факторов Прэгнанца. В приведенном выше примере использование больших относительных весов для, и будет иметь эффект оценки большей информативности отношения, чем отношения, что может быть желательно в некоторых случаях распознавания образов и т.п. Эта взвешенная взаимная информация является формой взвешенной KL-дивергенции, которая, как известно, принимает отрицательные значения для некоторых входных данных, и есть примеры, когда взвешенная взаимная информация также принимает отрицательные значения. ш ( Икс , у ) { Displaystyle ш (х, у)}





Скорректированная взаимная информация
Основная статья: скорректированная взаимная информация
Распределение вероятностей можно рассматривать как разбиение множества. Тогда можно спросить: если бы множество было разбито случайным образом, каким было бы распределение вероятностей? Какова ожидаемая ценность взаимной информации? Регулируется взаимной информации или AMI вычитает среднее значение МИ, так что АМИ равен нулю, когда два различных распределения являются случайными, и один, когда два распределения одинаковы. AMI определяется по аналогии со скорректированным индексом Rand двух разных разделов набора.
Абсолютная взаимная информация
Используя идеи колмогоровской сложности, можно рассматривать взаимную информацию двух последовательностей независимо от какого-либо распределения вероятностей:
- я K ( Икс ; Y ) знак равно K ( Икс ) — K ( Икс ∣ Y ) . { displaystyle operatorname {I} _ {K} (X; Y) = K (X) -K (X mid Y).}
Чтобы установить, что эта величина симметрична с точностью до логарифмического множителя (), требуется цепное правило для сложности Колмогорова ( Li amp; Vitányi 1997). Аппроксимация этой величины посредством сжатия может использоваться для определения меры расстояния для выполнения иерархической кластеризации последовательностей без знания какой-либо предметной области последовательностей ( Cilibrasi amp; Vitányi 2005). я K ( Икс ; Y ) ≈ я K ( Y ; Икс ) { Displaystyle OperatorName {I} _ {K} (X; Y) приблизительно OperatorName {I} _ {K} (Y; X)}
Линейная корреляция
В отличие от коэффициентов корреляции, таких как коэффициент корреляции момента продукта, взаимная информация содержит информацию обо всех зависимостях — линейных и нелинейных, — а не только о линейных зависимостях, как измеряет коэффициент корреляции. Однако в узком случае, когда совместное распределение для и является двумерным нормальным распределением (подразумевая, в частности, что оба предельных распределения нормально распределены), существует точная связь между коэффициентом корреляции и ( Гельфанд и Яглом, 1957). Икс { displaystyle X}


- я знак равно — 1 2 бревно ( 1 — ρ 2 ) { displaystyle operatorname {I} = — { frac {1} {2}} log left (1- rho ^ {2} right)}
Приведенное выше уравнение может быть получено следующим образом для двумерной гауссианы:
- ( Икс 1 Икс 2 ) ∼ N ( ( μ 1 μ 2 ) , Σ ) , Σ знак равно ( σ 1 2 ρ σ 1 σ 2 ρ σ 1 σ 2 σ 2 2 ) ЧАС ( Икс я ) знак равно 1 2 бревно ( 2 π е σ я 2 ) знак равно 1 2 + 1 2 бревно ( 2 π ) + бревно ( σ я ) , я ∈ { 1 , 2 } ЧАС ( Икс 1 , Икс 2 ) знак равно 1 2 бревно [ ( 2 π е ) 2 | Σ | ] знак равно 1 + бревно ( 2 π ) + бревно ( σ 1 σ 2 ) + 1 2 бревно ( 1 — ρ 2 ) { displaystyle { begin {align} { begin {pmatrix} X_ {1} \ X_ {2} end {pmatrix}} amp; sim { mathcal {N}} left ({ begin {pmatrix} mu _ {1} \ mu _ {2} end {pmatrix}}, Sigma right), qquad Sigma = { begin {pmatrix} sigma _ {1} ^ {2} amp; rho sigma _ {1} sigma _ {2} \ rho sigma _ {1} sigma _ {2} amp; sigma _ {2} ^ {2} end {pmatrix}} \ mathrm {H} (X_ {i}) amp; = { frac {1} {2}} log left (2 pi e sigma _ {i} ^ {2} right) = { frac {1} {2}} + { frac {1} {2}} log (2 pi) + log left ( sigma _ {i} right), quad i in {1,2 } \ mathrm {H} (X_ {1}, X_ {2}) amp; = { frac {1} {2}} log left [(2 pi e) ^ {2} | Sigma | right] = 1 + log (2 pi) + log left ( sigma _ {1} sigma _ {2} right) + { frac {1} {2}} log left (1 — rho ^ {2} right) \ конец {выровнено}}}
Следовательно,
- я ( Икс 1 ; Икс 2 ) знак равно ЧАС ( Икс 1 ) + ЧАС ( Икс 2 ) — ЧАС ( Икс 1 , Икс 2 ) знак равно — 1 2 бревно ( 1 — ρ 2 ) { displaystyle operatorname {I} left (X_ {1}; X_ {2} right) = mathrm {H} left (X_ {1} right) + mathrm {H} left (X_ { 2} right) — mathrm {H} left (X_ {1}, X_ {2} right) = — { frac {1} {2}} log left (1- rho ^ {2 }Правильно)}
Для дискретных данных
Когда и ограничены дискретным числом состояний, данные наблюдений суммируются в таблице непредвиденных обстоятельств с переменной строки (или) и переменной столбца (или). Взаимная информация — это одна из мер связи или корреляции между переменными строки и столбца. Другие меры ассоциации включают статистику критерия хи-квадрат Пирсона, статистику G-критерия и т. Д. Фактически, взаимная информация равна статистике G-критерия, деленной на, где — размер выборки. Икс { displaystyle X}






Приложения
Во многих приложениях требуется максимизировать взаимную информацию (таким образом, увеличивая зависимости), что часто эквивалентно минимизации условной энтропии. Примеры включают:
- В технологии поисковых машин взаимная информация между фразами и контекстами используется в качестве функции кластеризации k-средних для обнаружения семантических кластеров (концептов). Например, взаимная информация биграммы может быть вычислена как:
M я ( Икс , у ) знак равно бревно п Икс , Y ( Икс , у ) п Икс ( Икс ) п Y ( у ) ≈ бревно ж Икс Y B ж Икс U ж Y U { displaystyle MI (x, y) = log { frac {P_ {X, Y} (x, y)} {P_ {X} (x) P_ {Y} (y)}} приблизительно log { frac { frac {f_ {XY}} {B}} {{ frac {f_ {X}} {U}} { frac {f_ {Y}} {U}}}}}
- где — количество раз, когда биграмма xy появляется в корпусе, — это количество раз, когда униграмма x появляется в корпусе, B — общее количество биграмм, а U — общее количество униграмм. ж Икс Y { displaystyle f_ {XY}}
ж Икс { displaystyle f_ {X}}
- В области телекоммуникаций, то пропускная способность канала равна взаимной информацию, развернутой по всем распределениям ввода.
- Предложены процедуры дискриминирующего обучения скрытых марковских моделей на основе критерия максимальной взаимной информации (MMI).
- Предсказание вторичной структуры РНК на основе множественного выравнивания последовательностей.
- Прогноз филогенетического профилирования на основании попарного присутствия и исчезновения функционально связанных генов.
- Взаимная информация использовалась в качестве критерия для выбора функций и преобразования функций в машинном обучении. Его можно использовать для характеристики как релевантности, так и избыточности переменных, например выбора функции минимальной избыточности.
- Взаимная информация используется для определения сходства двух разных кластеров набора данных. Таким образом, он дает некоторые преимущества по сравнению с традиционным индексом Rand.
- Взаимная информация слов часто используется как функция значимости для вычисления словосочетаний в лингвистике корпуса. Это имеет дополнительную сложность, заключающуюся в том, что ни один экземпляр слова не является экземпляром двух разных слов; скорее, учитываются случаи, когда 2 слова встречаются рядом или в непосредственной близости; это немного усложняет расчет, поскольку ожидаемая вероятность того, что одно слово встретится в словах другого, возрастает. N { displaystyle N}
N { displaystyle N}
- Взаимная информация используется в медицинской визуализации для регистрации изображений. Учитывая эталонное изображение (например, сканирование мозга) и второе изображение, которое необходимо поместить в ту же систему координат, что и эталонное изображение, это изображение деформируется до тех пор, пока взаимная информация между ним и эталонным изображением не будет максимальной.
- Обнаружение фазовой синхронизации при анализе временных рядов
- В INFOMAX метода нейронной сети, и другого машинное обучение, в том числе INFOMAX на основе независимого компонентов анализа алгоритма
- Средняя взаимная информация в теореме внедрения задержки используется для определения параметра задержки внедрения.
- Взаимная информация между генами в данных экспрессии микрочипов используется алгоритмом ARACNE для реконструкции генных сетей.
- В статистической механике, парадокс Лошмидта может быть выражено в терминах взаимной информации. Лошмидт отметил, что невозможно определить физический закон, в котором отсутствует симметрия обращения времени (например, второй закон термодинамики ), только из физических законов, обладающих этой симметрией. Он отметил, что Н-теорема о Больцмане сделал предположение, что скорости частиц в газе были постоянно коррелированны, которые удаляют временную симметрию, присущую H-теорема. Можно показать, что если система описывается плотностью вероятности в фазовом пространстве, то из теоремы Лиувилля следует, что совместная информация (отрицательная от совместной энтропии) распределения остается постоянной во времени. Совместная информация равна взаимной информации плюс сумма всей маргинальной информации (отрицательной из предельных энтропий) для каждой координаты частицы. Предположение Больцмана сводится к игнорированию взаимной информации при вычислении энтропии, которая дает термодинамическую энтропию (деленную на постоянную Больцмана).
- Взаимная информация используется для изучения структуры байесовских сетей / динамических байесовских сетей, которая, как считается, объясняет причинную связь между случайными величинами, как показано на примере инструментария GlobalMIT: изучение глобально оптимальной динамической байесовской сети с критерием теста взаимной информации.
- Взаимная информация используется для количественной оценки информации, передаваемой во время процедуры обновления в алгоритме выборки Гиббса.
- Популярная функция стоимости в изучении дерева решений.
- Взаимная информация используется в космологии для проверки влияния крупномасштабной окружающей среды на свойства галактик в Галактическом зоопарке.
- Взаимная информация использовалась в солнечной физике для получения профиля солнечного дифференциального вращения, карты отклонения времени прохождения для солнечных пятен и диаграммы время-расстояние по измерениям спокойного Солнца.
- Используется в инвариантной кластеризации информации для автоматического обучения классификаторов нейронных сетей и сегментеров изображений без помеченных данных.
Смотрите также
- Точечная взаимная информация
- Квантовая взаимная информация
Примечания
- ^ Обложка, Томас М.; Томас, Джой А. (2005). Элементы теории информации (PDF). John Wiley amp; Sons, Ltd., стр. 13–55. ISBN 9780471748823.
- ^ Креер, JG (1957). «Вопрос терминологии». Сделки IRE по теории информации. 3 (3): 208. DOI : 10,1109 / TIT.1957.1057418.
- ^ a b c Крышка, TM; Томас, Дж. А. (1991). Элементы теории информации (ред. Вили). ISBN 978-0-471-24195-9.
- ^ Wolpert, DH; Вольф, Д.Р. (1995). «Оценочные функции вероятностных распределений по конечному набору выборок». Physical Review E. 52 (6): 6841–6854. Bibcode : 1995PhRvE..52.6841W. CiteSeerX 10.1.1.55.7122. DOI : 10.1103 / PhysRevE.52.6841. PMID 9964199. S2CID 9795679.
- ^ Хуттер, М. (2001). «Распространение взаимной информации». Достижения в системах обработки нейронной информации 2001.
- ^ Арчер, E.; Парк, И. М.; Подушка, J. (2013). «Байесовские и квазибайесовские оценки взаимной информации из дискретных данных». Энтропия. 15 (12): 1738–1755. Bibcode : 2013Entrp..15.1738A. CiteSeerX 10.1.1.294.4690. DOI : 10.3390 / e15051738.
- ^ Wolpert, DH; ДеДео, С. (2013). «Оценочные функции распределений, определенных в пространствах неизвестного размера». Энтропия. 15 (12): 4668–4699. arXiv : 1311.4548. Bibcode : 2013Entrp..15.4668W. DOI : 10.3390 / e15114668. S2CID 2737117.
- ^ Tomasz Jetka; Кароль Ниеналтовски; Томаш Винарский; Славомир Блонски; Михал Коморовский (2019), «Теоретико-информационный анализ многомерных сигнальных ответов отдельных клеток», PLOS Computational Biology, 15 (7): e1007132, arXiv : 1808.05581, Bibcode : 2019PLSCB..15E7132J, doi : 10.1371 / journal.pcbi. 1007132, PMC 6655862, PMID 31299056
- ^ Красков, Александр; Штегбауэр, Харальд; Andrzejak, Ralph G.; Грассбергер, Питер (2003). «Иерархическая кластеризация на основе взаимной информации». arXiv : q-bio / 0311039. Bibcode : 2003q.bio…. 11039K. Цитировать журнал требует
|journal=( помощь ) - Перейти ↑ McGill, W. (1954). «Многомерная передача информации». Психометрика. 19 (1): 97–116. DOI : 10.1007 / BF02289159. S2CID 126431489.
- ^ а б Ху, KT (1962). «Об объеме информации». Теория вероятн. Прил. 7 (4): 439–447. DOI : 10.1137 / 1107041.
- ^ a b Baudot, P.; Tapia, M.; Bennequin, D.; Гоайярд, Дж. М. (2019). «Анализ топологической информации». Энтропия. 21 (9). 869. arXiv : 1907.04242. Bibcode : 2019Entrp..21..869B. DOI : 10.3390 / e21090869. S2CID 195848308.
- ^ Бреннер, N.; Strong, S.; Koberle, R.; Bialek, W. (2000). «Синергия в нейронном коде». Neural Comput. 12 (7): 1531–1552. DOI : 10.1162 / 089976600300015259. PMID 10935917. S2CID 600528.
- ^ Watkinson, J.; Liang, K.; Ван, X.; Zheng, T.; Анастасиу, Д. (2009). «Вывод регулятивных взаимодействий генов из данных экспрессии с использованием трехсторонней взаимной информации». Чалл. Syst. Биол. Анна. NY Acad. Sci. 1158 (1): 302–313. Bibcode : 2009NYASA1158..302W. DOI : 10.1111 / j.1749-6632.2008.03757.x. PMID 19348651. S2CID 8846229.
- ^ а б Тапиа, М.; Baudot, P.; Формизано-Трезины, Ц.; Dufour, M.; Гоайярд, Дж. М. (2018). «Идентичность нейротрансмиттера и электрофизиологический фенотип генетически связаны в дофаминергических нейронах среднего мозга». Sci. Rep. 8 (1): 13637. Bibcode : 2018NatSR… 813637T. DOI : 10.1038 / s41598-018-31765-Z. PMC 6134142. PMID 30206240.
- ^ Кристофер Д. Мэннинг; Прабхакар Рагхаван; Хинрих Шютце (2008). Введение в поиск информации. Издательство Кембриджского университета. ISBN 978-0-521-86571-5.
- ^ Haghighat, MBA; Агаголзаде, А.; Сейедараби, Х. (2011). «Неопорный показатель слияния изображений, основанный на взаимной информации о характеристиках изображения». Компьютеры и электротехника. 37 (5): 744–756. DOI : 10.1016 / j.compeleceng.2011.07.012.
- ^ «Метрика Feature Mutual Information (FMI) для нереференсного слияния изображений — Обмен файлами — MATLAB Central». www.mathworks.com. Проверено 4 апреля 2018 года.
- ^ «InfoTopo: Анализ топологической информации. Глубокое статистическое обучение без учителя и с учителем — Обмен файлами — Github». github.com/pierrebaudot/infotopopy/. Проверено 26 сентября 2020 года.
- ^ Мэсси, Джеймс (1990). «Причинно-следственная связь, обратная связь и управляемая информация». Proc. 1990 г. Symp. на Инфо. Чт. и его применение, Waikiki, Гавайи, ноябрь 27-30, 1990. CiteSeerX 10.1.1.36.5688.
- ^ Пермутер, Хаим Генри; Вайсман, Цачи; Голдсмит, Андреа Дж. (Февраль 2009 г.). «Конечные каналы с инвариантной во времени детерминированной обратной связью». IEEE Transactions по теории информации. 55 (2): 644–662. arXiv : cs / 0608070. DOI : 10.1109 / TIT.2008.2009849. S2CID 13178.
- Перейти ↑ Coombs, Dawes amp; Tversky 1970.
- ^ a b Нажмите, WH; Теукольский, С.А.; Феттерлинг, штат Вашингтон; Фланнери, ВР (2007). «Раздел 14.7.3. Условная энтропия и взаимная информация». Числовые рецепты: искусство научных вычислений (3-е изд.). Нью-Йорк: Издательство Кембриджского университета. ISBN 978-0-521-88068-8.
- ^ Белый, Джим; Штейнгольд, Сэм; Фурнель, Конни. Метрики производительности для алгоритмов обнаружения групп (PDF). Интерфейс 2004 г.
- ^ Виджая, Деди Рахман; Сарно, Риянарто; Зулайка, Энни (2017). «Коэффициент качества информации как новый показатель для выбора материнского вейвлета». Хемометрика и интеллектуальные лабораторные системы. 160: 59–71. DOI : 10.1016 / j.chemolab.2016.11.012.
- ^ Штрел, Александр; Гош, Джойдип (2003). «Кластерные ансамбли — структура повторного использования знаний для объединения нескольких разделов» (PDF). Журнал исследований в области машинного обучения. 3: 583–617. DOI : 10.1162 / 153244303321897735.
- ^ Kvålseth, TO (1991). «Относительная мера полезной информации: некоторые комментарии». Информационные науки. 56 (1): 35–38. DOI : 10.1016 / 0020-0255 (91) 90022-м.
- Перейти ↑ Pocock, A. (2012). Выбор характеристик через совместное правдоподобие (PDF) (Диссертация).
- ^ a b Анализ естественного языка с использованием статистики взаимной информации Дэвида М. Магермана и Митчелла П. Маркуса
- ^ Хью Эверетт Теория Универсальной волновой функции, Thesis, Принстонский университет (1956, 1973), стр 1-140 (стр 30)
- ^ Эверетт, Хью (1957). «Формулировка относительного состояния квантовой механики». Обзоры современной физики. 29 (3): 454–462. Bibcode : 1957RvMP… 29..454E. DOI : 10,1103 / revmodphys.29.454. Архивировано из оригинала на 2011-10-27. Проверено 16 июля 2012.
- ^ GlobalMIT в Google Code
- ↑ Ли, Се Юн (2021). «Сэмплер Гиббса и вариационный вывод координатного восхождения: теоретико-множественный обзор». Коммуникации в статистике — теория и методы: 1–21. arXiv : 2008.01006. DOI : 10.1080 / 03610926.2021.1921214.
- ^ Ключи, Дастин; Холиков, Шукур; Певцов, Алексей А. (февраль 2015). «Применение методов взаимной информации во временной дистанционной гелиосейсмологии». Солнечная физика. 290 (3): 659–671. arXiv : 1501.05597. Bibcode : 2015SoPh..290..659K. DOI : 10.1007 / s11207-015-0650-у. S2CID 118472242.
- ^ Инвариантная кластеризация информации для неконтролируемой классификации изображений и сегментации Сюй Цзи, Жоао Энрикес и Андреа Ведальди
использованная литература
- Baudot, P.; Tapia, M.; Bennequin, D.; Гоайярд, Дж. М. (2019). «Анализ топологической информации». Энтропия. 21 (9). 869. arXiv : 1907.04242. Bibcode : 2019Entrp..21..869B. DOI : 10.3390 / e21090869. S2CID 195848308.
- Cilibrasi, R.; Витани, Пол (2005). «Кластеризация сжатием» (PDF). IEEE Transactions по теории информации. 51 (4): 1523–1545. arXiv : cs / 0312044. DOI : 10.1109 / TIT.2005.844059. Кирилл 911.
- Кронбах, LJ (1954). «О нерациональном применении информационных мер в психологии». В Quastler, Генри (ред.). Теория информации в психологии: проблемы и методы. Гленко, Иллинойс: Свободная пресса. С. 14–30.
- Кумбс, Швейцария; Dawes, RM; Тверски, А. (1970). Математическая психология: элементарное введение. Энглвуд Клиффс, Нью-Джерси: Прентис-Холл.
- Церковь, Кеннет Уорд; Хэнкс, Патрик (1989). «Нормы словесных ассоциаций, взаимная информация и лексикография». Труды 27-го ежегодного собрания Ассоциации компьютерной лингвистики: 76–83. DOI : 10.3115 / 981623.981633.
- Гельфанд И.М.; Яглом AM (1957). «Вычисление количества информации о случайной функции, содержащейся в другой такой функции». Переводы Американского математического общества. Серия 2. 12: 199–246. DOI : 10.1090 / trans2 / 012/09. ISBN 9780821817124. Английский перевод оригинала в Успехах математических наук 12 (1): 3-52.
- Гиасу, Сильвиу (1977). Теория информации с приложениями. Макгроу-Хилл, Нью-Йорк. ISBN 978-0-07-025109-0.
- Ли, Мин; Витани, Пол (февраль 1997 г.). Введение в колмогоровскую сложность и ее приложения. Нью-Йорк: Springer-Verlag. ISBN 978-0-387-94868-3.
- Локхед, GR (1970). «Идентификация и форма многомерного дискриминирующего пространства». Журнал экспериментальной психологии. 85 (1): 1–10. DOI : 10.1037 / h0029508. PMID 5458322.
- Дэвид Дж. К. Маккей. Теория информации, логический вывод и алгоритмы обучения Кембридж: Cambridge University Press, 2003. ISBN 0-521-64298-1 (доступно бесплатно в Интернете)
- Хагигхат, MBA; Агаголзаде, А.; Сейедараби, Х. (2011). «Неопорный показатель слияния изображений, основанный на взаимной информации о характеристиках изображения». Компьютеры и электротехника. 37 (5): 744–756. DOI : 10.1016 / j.compeleceng.2011.07.012.
- Афанасиос Папулис. Вероятность, случайные величины и случайные процессы, второе издание. Нью-Йорк: Макгроу-Хилл, 1984. (см. Главу 15.)
- Виттен, Ян Х. и Франк, Эйбе (2005). Data Mining: практические инструменты и методы машинного обучения. Морган Кауфманн, Амстердам. ISBN 978-0-12-374856-0.
- Пэн, HC; Лонг, Ф. и Динг, К. (2005). «Выбор функций на основе взаимной информации: критерии максимальной зависимости, максимальной релевантности и минимальной избыточности». IEEE Transactions по анализу шаблонов и машинному анализу. 27 (8): 1226–1238. CiteSeerX 10.1.1.63.5765. DOI : 10.1109 / tpami.2005.159. PMID 16119262. S2CID 206764015.
- Андре С. Рибейро; Стюарт А. Кауфман; Джейсон Ллойд-Прайс; Бьорн Самуэльссон и Джошуа Соолар (2008). «Взаимная информация в случайных булевых моделях регуляторных сетей». Physical Review E. 77 (1): 011901. arXiv : 0707.3642. Bibcode : 2008PhRvE..77a1901R. DOI : 10.1103 / physreve.77.011901. PMID 18351870. S2CID 15232112.
- Уэллс, WM III; Альт, P.; Atsumi, H.; Nakajima, S.; Кикинис, Р. (1996). «Мультимодальная регистрация объема путем максимизации взаимной информации» (PDF). Анализ медицинских изображений. 1 (1): 35–51. DOI : 10.1016 / S1361-8415 (01) 80004-9. PMID 9873920. Архивировано из оригинального (PDF) 06.09.2008. Проверено 5 августа 2010.
- Панди, Бисваджит; Саркар, Суман (2017). «Насколько галактика знает о своем крупномасштабном окружении ?: Теоретическая перспектива». Ежемесячные уведомления о письмах Королевского астрономического общества. 467 (1): L6. arXiv : 1611.00283. Полномочный код : 2017MNRAS.467L… 6P. DOI : 10.1093 / mnrasl / slw250. S2CID 119095496.






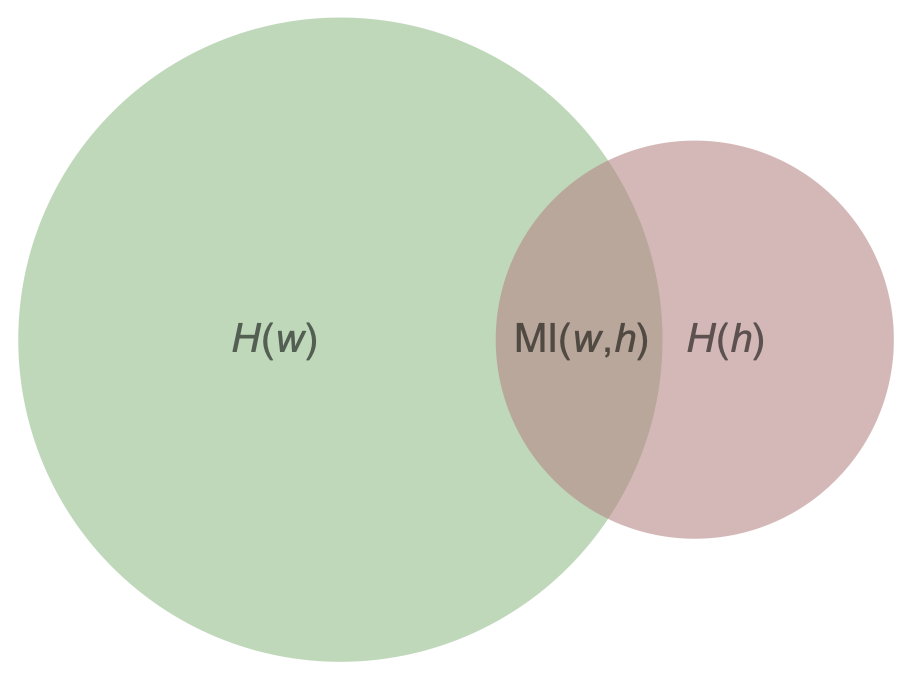

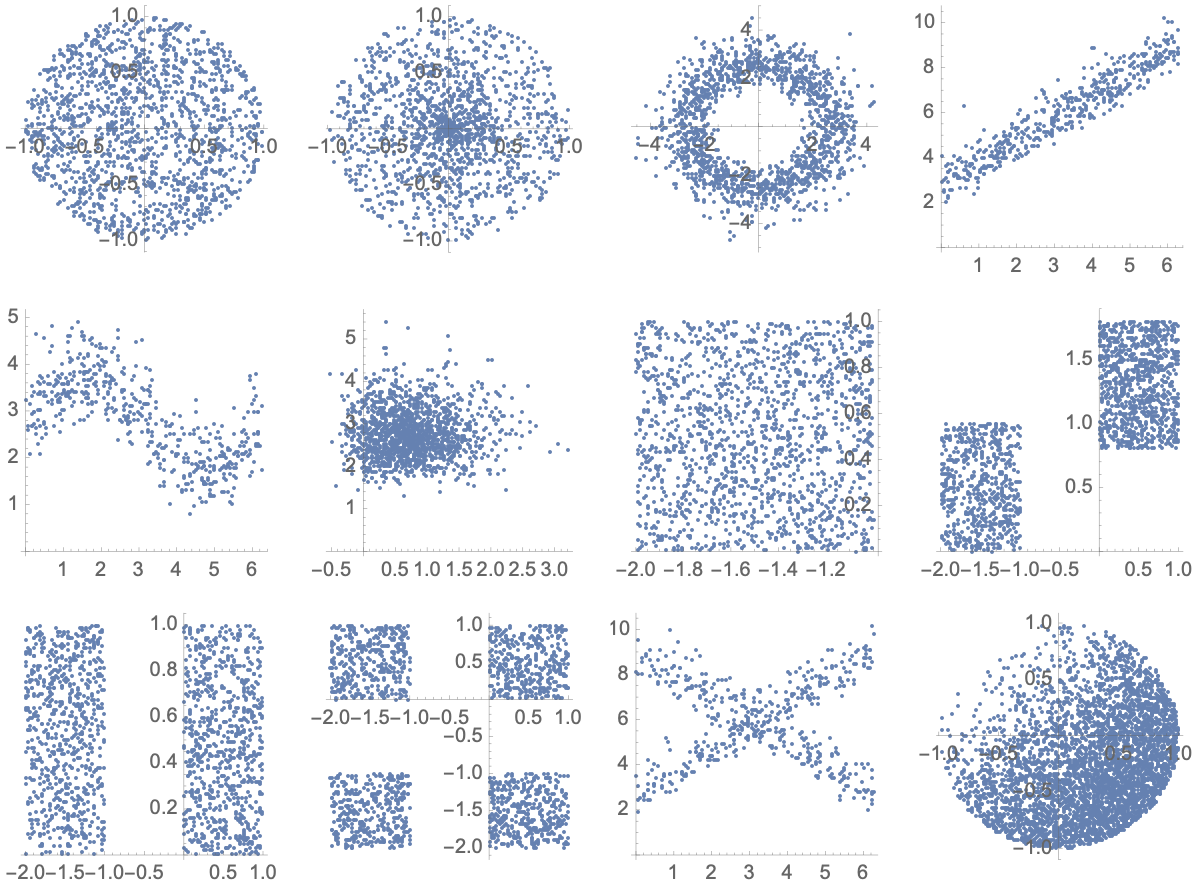

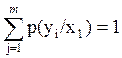
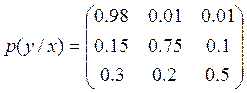
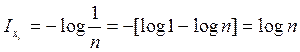
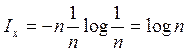
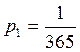
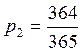
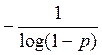
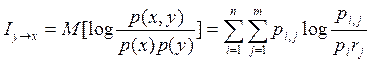
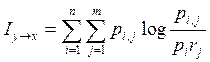
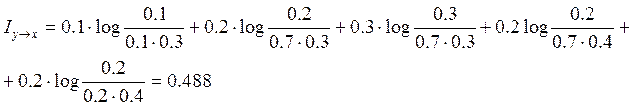











![{ displaystyle operatorname {I} (X; Y) = mathbb {E} _ {Y} left [D _ { text {KL}} ! left (p_ {X mid Y} parallel p_ { X} right) right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28338bdc75a2c5652cbb6a84e024d2b5ad74610c)
![{ displaystyle { begin {align} operatorname {I} (X; Y) amp; = sum _ {y in { mathcal {Y}}} sum _ {x in { mathcal {X}} } {p _ {(X, Y)} (x, y) log left ({ frac {p _ {(X, Y)} (x, y)} {p_ {X} (x) , p_ { Y} (y)}} right)} \ amp; = sum _ {y in { mathcal {Y}}} sum _ {x in { mathcal {X}}} p_ {X mid Y = y} (x) p_ {Y} (y) log { frac {p_ {X mid Y = y} (x) p_ {Y} (y)} {p_ {X} (x) p_ { Y} (y)}} \ amp; = sum _ {y in { mathcal {Y}}} p_ {Y} (y) sum _ {x in { mathcal {X}}} p_ { X mid Y = y} (x) log { frac {p_ {X mid Y = y} (x)} {p_ {X} (x)}} \ amp; = sum _ {y in { mathcal {Y}}} p_ {Y} (y) ; D _ { text {KL}} ! left (p_ {X mid Y = y} parallel p_ {X} right) \ amp; = mathbb {E} _ {Y} left [D _ { text {KL}} ! left (p_ {X mid Y} parallel p_ {X} right) right]. end { выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b644a60366facfab2ab84ca89da4068cc670ffea)








![{ displaystyle operatorname {I} (X; Y | Z) = mathbb {E} _ {Z} [D _ { mathrm {KL}} (P _ {(X, Y) | Z} | P_ {X | Z} время P_ {Y | Z})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3291764cf0532907067deb1d560302d1124f7de5)
![{ displaystyle operatorname {I} (X; Y | Z) = sum _ {z in { mathcal {Z}}} sum _ {y in { mathcal {Y}}} sum _ { х in { mathcal {X}}} {p_ {Z} (z) , p_ {X, Y | Z} (x, y | z) log left [{ frac {p_ {X, Y | Z} (x, y | z)} {p_ {X | Z} , (x | z) p_ {Y | Z} (y | z)}} right]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba63d00f0fc6c57b74ab192657205b9422267fbb)

![{ displaystyle operatorname {I} (X; Y | Z) = int _ { mathcal {Z}} int _ { mathcal {Y}} int _ { mathcal {X}} {p_ {Z } (z) , p_ {X, Y | Z} (x, y | z) log left [{ frac {p_ {X, Y | Z} (x, y | z)} {p_ {X | Z} , (x | z) p_ {Y | Z} (y | z)}} right]} dxdydz,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c398f8106e8dac1bba2a06eabee5230c14cf0a8f)





![{ displaystyle I (X_ {1}; ldots; X_ {n-1} mid X_ {n}) = mathbb {E} _ {X_ {n}} [D _ { mathrm {KL}} (P_ {(X_ {1}, ldots, X_ {n-1}) mid X_ {n}} | P_ {X_ {1} mid X_ {n}} otimes cdots otimes P_ {X_ {n -1} mid X_ {n}})].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b56fa053a5252fa20c65d8122fd32fa69ff2b0fd)
 .
.




![{ displaystyle { frac { operatorname {I} (X; Y)} { min left [ mathrm {H} (X), mathrm {H} (Y) right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/beff2776011750497c167aa722baea33effa6b6e) а также я ( Икс ; Y ) ЧАС ( Икс , Y ) . { displaystyle { frac { operatorname {I} (X; Y)} { mathrm {H} (X, Y)}} ;.}
а также я ( Икс ; Y ) ЧАС ( Икс , Y ) . { displaystyle { frac { operatorname {I} (X; Y)} { mathrm {H} (X, Y)}} ;.}
![{ displaystyle IQR (X, Y) = operatorname {E} [ operatorname {I} (X; Y)] = { frac { operatorname {I} (X; Y)} { mathrm {H} ( X, Y)}} = { frac { sum _ {x in X} sum _ {y in Y} p (x, y) log {p (x) p (y)}} { sum _ {x in X} sum _ {y in Y} p (x, y) log {p (x, y)}}} - 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6392ff4132d19d05ee2740cb15dee7abffa3df0c)







![{ displaystyle { begin {align} { begin {pmatrix} X_ {1} \ X_ {2} end {pmatrix}} amp; sim { mathcal {N}} left ({ begin {pmatrix} mu _ {1} \ mu _ {2} end {pmatrix}}, Sigma right), qquad Sigma = { begin {pmatrix} sigma _ {1} ^ {2} amp; rho sigma _ {1} sigma _ {2} \ rho sigma _ {1} sigma _ {2} amp; sigma _ {2} ^ {2} end {pmatrix}} \ mathrm {H} (X_ {i}) amp; = { frac {1} {2}} log left (2 pi e sigma _ {i} ^ {2} right) = { frac {1} {2}} + { frac {1} {2}} log (2 pi) + log left ( sigma _ {i} right), quad i in {1,2 } \ mathrm {H} (X_ {1}, X_ {2}) amp; = { frac {1} {2}} log left [(2 pi e) ^ {2} | Sigma | right] = 1 + log (2 pi) + log left ( sigma _ {1} sigma _ {2} right) + { frac {1} {2}} log left (1 - rho ^ {2} right) \ конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/548ed20f24c64370dcf1fc5c9b7067a2510b8e9a)



 ж Икс { displaystyle f_ {X}}
ж Икс { displaystyle f_ {X}}