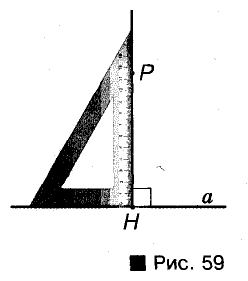
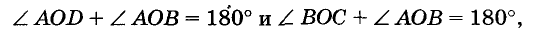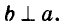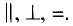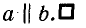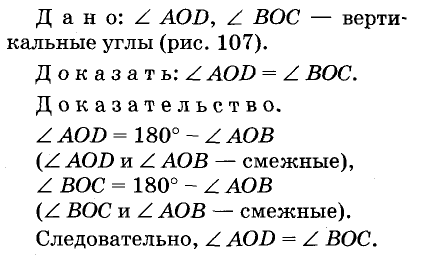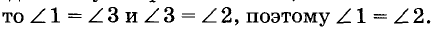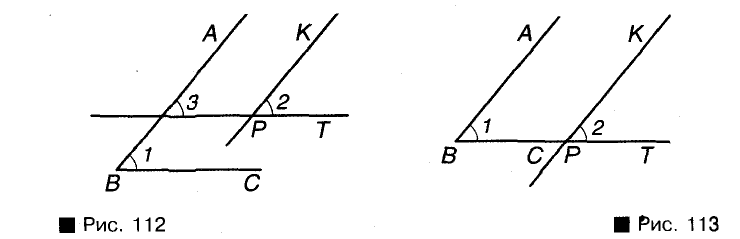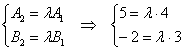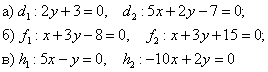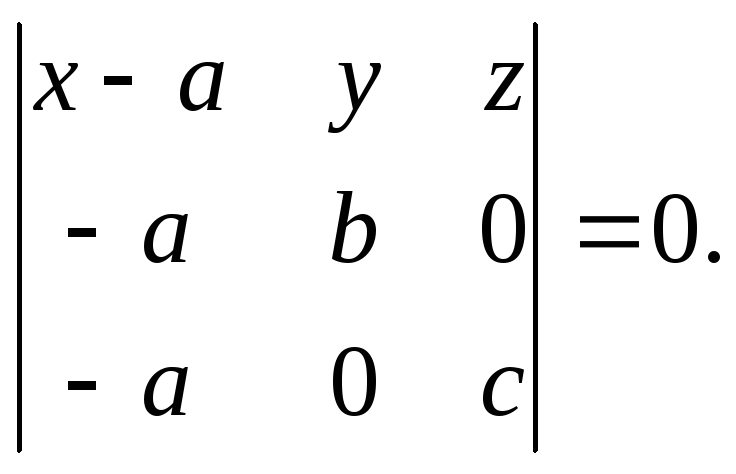Как найти взаимное расположение прямых на плоскости - Avtoru.top

Содержание:

Взаимное расположения прямых на плоскости:

Бывают два варианта взаимного расположения прямой и точки на плоскости: либо точка лежит на прямой в этом случае говорят, что прямая проходит через точку или точка не лежит на прямой иногда говорят, что точка не принадлежит прямой или прямая не проходит через точку.

Две прямые в плоскости могут пересекаться так как имеют общую точку или быть параллельными не имея общей точки. В пространстве может быть, когда две прямые не пересекаются, но они и не параллельны.

Определения

Два угла, на которые разбивается развернутый угол его внутренним лучом, называются смежными. Сумма мер двух: смежных углов равна 180°.

Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого угла Вертикальные углы равны.

Если две прямые пересекаются, они образуют четыре угла две пары вертикальных углов. Меньший из них — угол между данными прямыми.

Две прямые называются перпендикулярными, если они пересекаются под прямым углом. Отрезки или лучи называют перпендикулярными, если они лежат на перпендикулярных прямых Две прямые на плоскости называют параллельными, ест они не пересекаются.

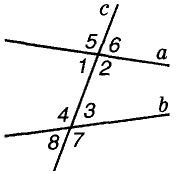
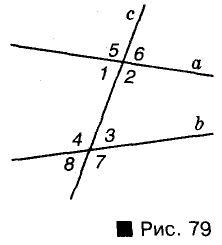
Прямая, пересекающая две другие прямые, называется и: секущей. С двумя данными прямыми она образует 8 углов, не которые пары этих углов имеют отдельные названия:

1 и 3, 2 и 4 — внутренние накрест лежащие;
1 и 4,2 и 3 — внутренние односторонние;
1 и 8, 2 и 7, 3 и 6, 4 и 5 — соответственные;
5 и 7, 6 и 8 — внешние накрест лежащие;
5 и 8, 6 и 7 — внешние односторонние.

Признак параллельности прямых:

Две прямые параллельны, если с секущей они образу ют равные внутренние накрест лежащие углы, или равные соответственные углы, или такие внутренние одно сторонние углы, сумма которых равна 180°.

Свойства параллельных прямых:

Секущая с двумя параллельными прямыми образуя равные внутренние накрест лежащие углы, равные ее ответственные углы, такие внутренние односторонние углы, сумма которых равна 180°.

Две прямые, параллельные третьей, параллельны.

Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой прямо» Две прямые, перпендикулярные к третьей, параллельны

Смежные и вертикальные углы

Два угла, на которые делится развернутый угол его внутренним лучом, называют смежными.

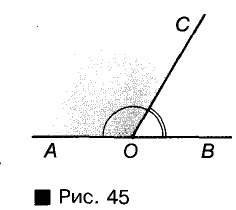
Одна сторона у смежных углов общая, а две другие — дополнительные лучи. Если точки А, О, В лежат на одной прямой, а С — произвольная точка, не принадлежащая прямой АВ, то углы АОС и СОВ — смежные (рис. 45).

Свойство смежных углов сформулируем в виде теоремы.

В математике теоремой называют каждое утверждение, истинность которого устанавливается путем логических рассуждений. Цепочку таких рассуждений называют доказательством.

В нашем учебнике теоремы напечатаны жирным шрифтом и пронумерованы.

Теорема: Сумма мер двух смежных углов равна 180°

Доказательство:

Объединение двух смежных углов является развернутым углом. Мера развернутого угла равна 180°. Значит, какими бы ни были смежные углы, сумма их мер равна 180°.

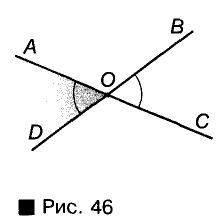
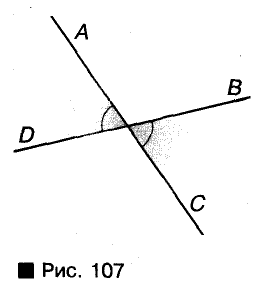
Два угла называются вертикальными, если стороны одного являются дополнительными лучами сторон другого. Например, если прямые АС и BD пересекаются в точке О, то углы AOD и ВОС — вертикальные (рис. 46). Каждый из них — смежный с углом АОВ. Углы АОВ и COD — тоже вертикальные.

Теорема: Вертикальные углы равны.

Доказательство:

Пусть AOD и ВОС — любые вертикальные углы (см. рис. 46). Каждый из них смежный с углом АОВ. По теореме о сумме смежных углов

отсюда

Правые части этих равенств одинаковые, поэтому Что и следовало доказать

Для любознательных:

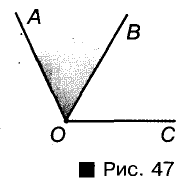
Слово смежные употребляют не только применительно к углам. Смежный—это имеющий общую границу с чем-то или прилегающий к чему-то, соседний. Можно говорить о смежных комнатах, смежных полях и т. п. Относительно углов это понятие имеет особый смысл. Не каждые два угла с общей стороной называют смежными. Например, на рисунке 47 углы АОВ и ВОС имеют общую сторону ОВ, но не являются смежными.

Смежные углы — это два угла, состоящие в определенном отношении. Один угол не может быть смежным. Когда говорим, что какой-то угол смежный, то обязательно должны уточнить: смежный с каким углом? Отношение смежности углов имеет такое свойство: если угол А смежный с углом B, то и угол В смежный с углом А.

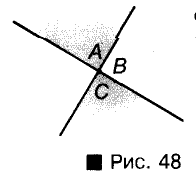
Пусть угол А смежный с углом В, а угол B смежный с углом

C. Что можно сказать об углах А и С? Они либо вертикальные, либо угол С — это тот же угол А (рис. 48).

Слово вертикальные также относится не только к углам. В основном вертикально расположенным считают продолговатый предмет, расположенный в направлении отвеса (перпендикулярно к горизонту).

Всегда верно свойство: если угол А вертикальный углу В, то и угол В вертикальный углу А.

Пример №1

Найдите меры смежных углов, если один из них на 50° больше другого.

Решение:

Пусть мера меньшего из смежных углов равна х, тогда мера большего угла х + 50°. По свойству смежных углов х + х + 50° = 180°, откуда х = 65°, а х + 50° = 115°.

Ответ. 65° и 115°.

Пример №2

Один из четырех углов, образованных пересечением двух прямых, вдвое больше другого. Найдите меру каждого из полученных углов.

Решение:

При пересечении двух прямых образуются вертикальные и смежные углы. Поскольку вертикальные углы равны, то они условие задачи не удовлетворяют. Делаем вывод: один из смежных углов вдвое больше другого, их меры х и 2х. По свойству смежных углов х + 2х = 180°, откуда х = 60°, а 2х = 120°. Соответствующие им вертикальные углы равны 60° и 120°.

Ответ. 60°, 120°, 60°, 120°.

Перпендикулярные и параллельные прямые

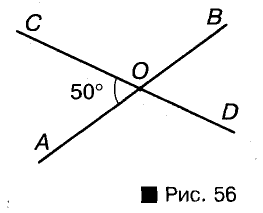
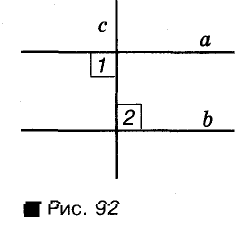
Вспомните, как могут располагаться на плоскости две прямые. Если они пересекаются, то образуют четыре угла — две пары вертикальных углов (речь идет об углах меньше развернутого). Меньший из них считается углом между данными прямыми. Например, на рисунке 56 прямые АВ И CD пересекаются под углом 50°. Говорят также, что угол между прямыми АВ и CD равен 50°. Если две прямые, пересекаясь, образуют четыре Прямых угла, говорят, что они пересекаются под прямым углом.

Две прямые, пересекающиеся под Прямым углом, называют перпендикулярными прямыми. Прямые а и б на рисунке 57 перпендикулярны одна Н другой. Записывают так: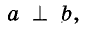или

Отрезки или лучи называют перпендикулярными, если они лежат на перпендикулярных прямых.

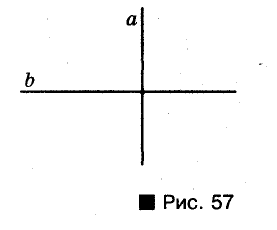
Если отрезок АВ лежит на прямой, перпендикулярной к прямой а, говорят, что отрезок АВ перпендикулярен к прямой а. Если при этом точка В принадлежит прямой о, то отрезок АВ называют перпендикуляром, проведенным из точки А к прямой а (рис. 58). Точку В называют основанием перпендикуляра, а длину Перпендикуляра АВ — расстоянием от точки А до прямой а.

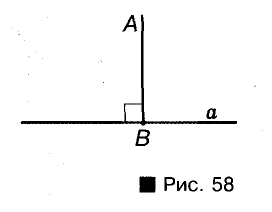
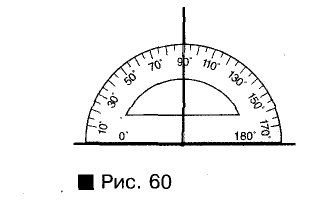
Через произвольную точку Р всегда можно провести прямую, перпендикулярную к данной прямой а. Это можно сделать с помощью угольника (рис. 59) или транспортира (рис. 60). Позже вы узнаете, как можно выполнить такое построение с помощью линейки и циркуля. Можно доказать, что существует только одна прямая, перпендикулярная к данной прямой и проходящая через данную точку.

Не каждые две прямые пересекаются. Особого внимания заслуживают прямые, которые не пересекаются и лежат в одной плоскости.

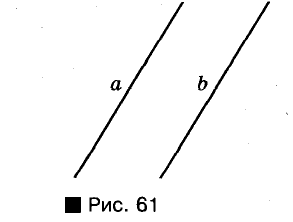
Две прямые на плоскости называются параллельными, если они не пересекаются (рис. 61). Если прямые а и b параллельные, пишут так: а || b.

Представление о параллельных прямых дают линии в тетради, линии нотного стана (рис. 62), ребра бруска.

Два отрезка или луча называют параллельными, если они лежат на параллельных прямых. Например, если ABCD — прямоугольник, то АВ || DC и ВС || AD.

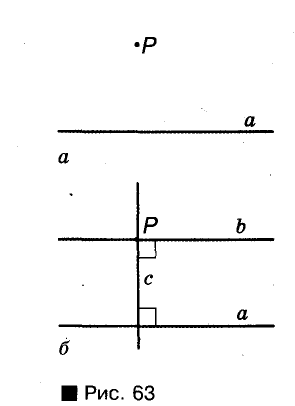
Через любую точку Р, не лежащую на прямой а, можно провести прямую, параллельную прямой а (рис. 63, а). Для этого можно через точку Р провести прямую с, перпендикулярную к прямой а, а потом прямую Ь, перпендикулярную к прямой с (рис. 63, б). При таком построении всегда b || а. Можно воспользоваться линейкой и угольником.

Для любознательных:

Можно доказать (попытайтесь!),что две прямые одной плоскости, перпендикулярные к третьей прямой, параллельны. То есть, если

Но если прямые а и b не принадлежат одной плоскости, то такое утверждение ошибочно. Например, если — куб, то

но прямые АВ и не параллельны (рис. 64).

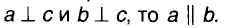
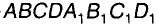
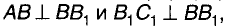
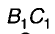
Слово параллельные происходит от греческого слова «параллелос», что в переводе означает «идущие рядом». Если говорить, что какая-либо прямая параллельна, то обязательно следует сказать, какой именно прямой она параллельна. Таким образом, параллельность прямых — это своеобразное отношение между двумя прямыми. Отношение параллельности прямых имеет такое свойство: если а || b, то и b || а. Другими отношениями являются перпендикулярность прямых, равенство углов и др. Символы этих отношений:

Позже вы узнаете о других отношениях между геометрическими объектами.

Как проводить параллельные прямые с помощью линейки и циркуля, вы узнаете позже.

Пример №3

Докажите, что биссектрисы смежных углов перпендикулярны

Решение:

Пример №4

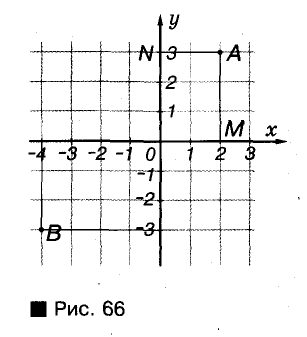
Обозначьте на координатной плоскости точки А (2; 3) и В (-4; -3). Найдите расстояния от этих точек до осей координат, если длина единичного отрезка равна 1 см.

Решение:

Из точек А и В опустим перпендикуляры на оси координат (рис. 66). Длина отрезка AM — расстояние от точки А до оси ОХ, а длина отрезка AN — расстояние от точки А до оси OY. По рисунку видим, что AM = 3 см, a AN = = 2 см.

Аналогично определяем, что расстояние от точки В до осей координат равно 3 см и 4 см.

Ответ. От точки А — 3 см и 2 см; От точки В — 3 см и 4 см.

Признаки параллельности прямых

Важную роль в исследовании параллельных прямых играют понятия секущей и некоторых пар углов.

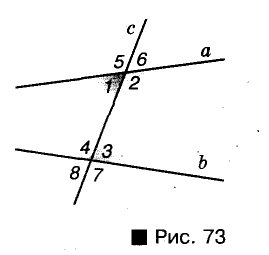
Пусть о и b — две произвольные прямые плоскости. Прямая с, пересекающая их, называется секущей прямых а и b (рис. 73).

Прямые а и b с их секущей с образуют 8 углов. На рисунке 73 они пронумерованы. Некоторые пары этих углов имеют специальные названия:

внутренние накрест лежащие углы: 1 и 3, 2 и 4;
внутренние односторонние углы: 1 и 4, 2 и 3;
соответственные углы: 1 и 8, 2 и 7, 3 и 6, 4 и 5.

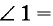
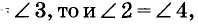
Обратите внимание! Если два каких-либо внутренних накрест лежащих угла равны, то также равны и внутренние накрест лежащие углы другой пары (рис. 74). Если, например, , потому что углы, смежные с равными, равны.

Случай, когда внутренние накрест лежащие углы равны, заслуживает особого внимания, поскольку именно при этом условии прямые а и b параллельны.

Теорема: (признак параллельности прямых).

Две прямые параллельны, если они с секущей образуют равные внутренние накрест лежащие углы.

Доказательство:

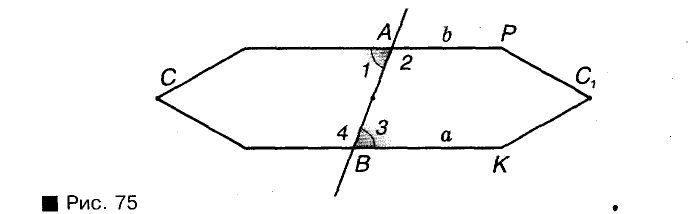
Пусть секущая АВ пересекает прямые а и b так, что образовавшиеся при этом внутренние накрест лежащие углы 1 и 3 равны. Тогда, как показано выше, углы 2 и 4 тоже равны. Допустим, что при таком условии прямые а и б пересекаются в какой-то отдаленной точке С. В результате образуется

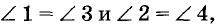
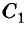
треугольник ABC (на рисунке 75 он изображен схематически в виде пятиугольника). Представим, что этот треугольник повернули вокруг точки О — середины отрезка АВ — так, что отрезок ОА занял положение ОВ. Тогда, поскольку луч АС совместится с лучом ВК, а луч ВС — с лучом АР. Так как лучи АС и ВС (по предположению) имеют общую точку С, то лучи ВК и АР тоже имеют какую-то общую точку .Это значит, что через две точки С и проведены две разные прямые. А этого не может быть.

Таким образом, если 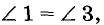то прямые а и 6 не могут пересекаться. А поскольку они лежат в одной плоскости и не пересекаются, то они параллельны: а || b. Что и требовалось доказать.

Обратите внимание на способ доказательства теоремы 3. Чтобы доказать, что прямые а и b параллельны, мы показывали, что они не могут пересекаться, то есть допускали противоречащее тому, что требовалось доказать. Такой способ рассуждения называют методом доказательства от противного.

На основе доказанной теоремы 3 нетрудно доказать и другие признаки параллельности прямых.

Теорема: Две прямые параллельны, если при пересечении с секущей они образуют внутренние односторонние углы, сумма которых равна 180°.

Доказательство:

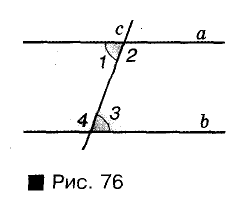
Пусть, например, на рисунке 76 сумма внутренних односторонних углов 1 и 4 равна 180°. Сумма смежных углов 3 и 4 тоже равна 180°. Поэтому 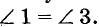. Это — внутренние накрест лежащие углы; если они равны, то прямые а и b параллельны.

Теорема: Две прямые параллельны, если при пересечении с секущей они образуют равные соответственные углы.

Доказательство:

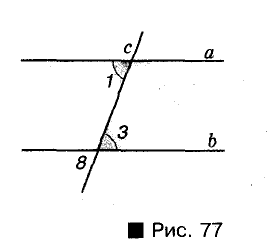
Пусть секущая с пересекает прямые а и b так, что образовавшиеся при этом соответственные углы 1 и 8 равны (рис. 77). Углы 8 и 3 равны, поскольку вертикальны.

Поэтому если

откуда следует, что

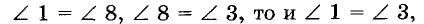
Заслуживает внимания такое следствие из теоремы 3.

Две прямые, перпендикулярные к третьей прямой, параллельны.

Ведь если каждая из прямых а и b перпендикулярна к с, то образовавшиеся при этом внутренние разносторонние углы равны, поскольку они прямые (рис. 78). Cледовательно, а и b параллельны.

Для любознательных:

Углы 5 и 7 (а также 6 и называют внешними накрест лежащими, а углы 5 и 8 (а также 6 и 7) — внешними односторонними углами (рис. 79).

Используя эти понятия, попробуйте сформулировать и доказать еще два признака параллельности прямых. Полезно также лучше понять сущность метода доказательства от противного. Если утверждение А противоречит утверждению В, то такие два утверждения называют противоречащими или противными друг другу. Из двух взаимно е противоречащих утверждений всегда одно верно, а другое ложно. Поэтому если убедимся, что утверждения А и В противоречат друг другу и, например, что утверждение В ложное, то можем быть уверены, что утверждение А верно.

Не следует путать противоречащие утверждения с противоположными. Например, когда речь идет о числовых выражениях и натуральных числах, то утверждения «выражение А положительное» и «выражение А отрицательное» или «число п простое» и «число л сложное» — противоположные, но не противоречащие, ведь каждое из них может быть неправильным. А вот утверждения «выражение А положительное» и «выражение А неположительное» или «число п простое» и «число п непростое» — взаимно противоречащие. Непростое означает составное или равное 1; неположительное — отрицательное или равное нолю.

Доказывая методом от противного, опровергать нужно не противоположное утверждение, а противоречащее данному. Опровергать что-либо — означает показать, что оно ошибочно.

Пример №5

Как построить параллельные прямые, пользуясь только линейкой и транспортиром?

Решение:

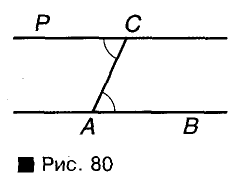
Начертим произвольный луч АВ и отложим равные углы ВАС и АСР, как показано на рисунке 80. Прямые АВ и СР параллельны, ведь углы ВАС и АСР внутренние накрест лежащие, и по построению они равны.

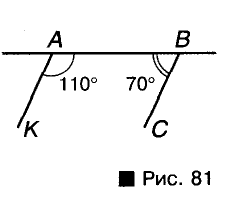
Через концы отрезка АВ с одной стороны от прямой АВ проведены лучи АК и ВС так, что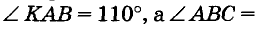70°. Параллельны ли эти лучи?

Прямую АВ можно считать секущей прямых АК и ВС (рис. 81).

Углы КАВ и ABC — внутренние односторонние. Поскольку их сумма 110° + 70° равна 180°, то прямые АК и ВС — параллельные (теорема 4). Поэтому и лучи АК и ВС — параллельные.

Ответ. Лучи АК и ВС параллельны.

Свойства параллельности прямых

Задача:

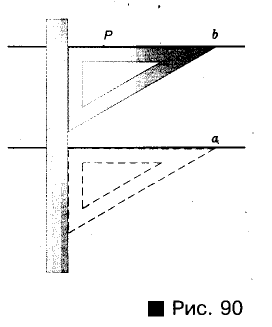
Даны прямая а и точка Р, не принадлежащая этой прямой. Проведите через точку Р прямую, параллельную прямой а.

Решение:

С помощью линейки и угольника построение можно выполнить, как показано на рисунке 90.

Можно ли через точку Р провести две разные прямые, параллельные прямой а? Геометры издавна считали истинным такое утверждение

Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.

Древнегреческий геометр Евклид это утверждение принял без доказательства. Его назвали аксиомой Евклида, потому что все утверждения, принимаемые без доказательств, называют аксиомами. (Подробнее об аксиомах и теоремах — в следующем параграфе.)

Не все ученые считают аксиому Евклида верной. Геометрию, в которой аксиому Евклида признают верной, называют евклидовой геометрией. Вы изучаете евклидову геометрию.

Теорема: (обратная теореме 3). Если прямые параллельны, то внутренние накрест лежащие углы, образованные ими с секущей, равны.

Доказательство:

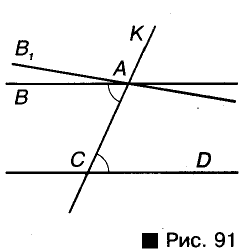
Пусть прямые АВ и CD параллельны, а КС — их секущая, проходящая через точку А (рис. 91). Докажем, что

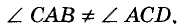
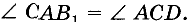
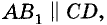
Допустим что Проведем прямую АВХ так, чтобы выполнялось равенство . По признаку параллельности прямых , а по условию АВ || CD. Получается, что через точку А проведены две разные прямые, параллельные прямой CD. Это противоречит аксиоме Евклида. Таким образом, сделанное нами допущение приводит к противоречию. Поэтому

Следствие:

Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой прямой.

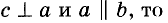
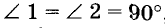
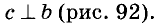
Действительно, если, , то естьСформулируйте и докажите теоремы. Рис. 92 обратные теоремам 4 и 5.

Теорема: Две прямые, параллельные третьей, параллельны.

Доказательство:

Пусть каждая из прямых а и b параллельна прямой с. Докажем, что а || b.

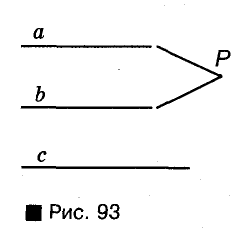
Допустим, что прямые а и b не параллельны (рис. 93), а пересекаются в некоторой точке Р. Получается, что через точку Р проходят две разные прямые а и Ь, параллельные с. Это противоречит аксиоме Евклида. Поскольку прямые а и b не могут пересекаться, они параллельны.

Примечание:

Доказательство теоремы верно и в случае, если прямая с лежит между а и b.

Для любознательных:

Последнюю теорему называют теоремой о транзитивности параллельности прямых (лат. transitivus — переходной), поскольку она утверждает, что параллельность двух пар параллельных прямых переходит на третью пару:

Чтобы это утверждение было верным всегда, договорились считать, что каждая прямая параллельна сама себе, то есть а || а. Ведь если

а || b и b || а, то а || а.

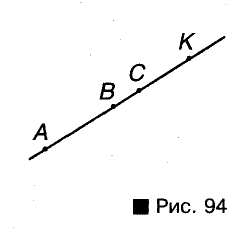
Отрезки одной прямой тоже считают параллельными. Например, если А, В, С, К — точки одной прямой, то каждый из отрезков АВ, АС, АК, ВС, ВК, СК параллелен любому из них (рис. 94). В целесообразности такой договоренности вы убедитесь позже, изучая параллельные переносы, параллельное проектирование и т. п. А в седьмом классе основное внимание будет обращаться на параллельность отрезков и лучей, не лежащих на одной прямой.

Существуют геометрии, в которых аксиома Евклида не считается верной. Их называют неевклидовыми геометриями. Такова, например, геометрия Лобачевского (см. с. 195).

Пример №6

Докажите, что прямые, перпендикулярные к непараллельным прямым, пересекаются.

Решение:

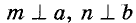
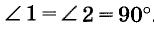
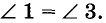
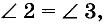
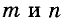
Пусть прямые а и b пересекаются, а прямые шип перпендикулярны к ним: (рис. 95). Тогда . Допустим, что m || п, то естьТогда и , откуда следует, что а || b. Это противоречит условию задачи. Значит, прямые не могут быть параллельными, они пересекаются.

Теоремы и аксиомы

Вы уже имеете представление о теоремах. Теорема — это утверждение, в истинности которого убеждаются с помощью логических рассуждений, доказательств.

Обычно теорема содержит условие (то, что дано) и заключение (что требуется доказать). Чтобы вычленить условйе и заключение теоремы, ее удобно подать в форме «Если… , то…». Например: «Если углы вертикальные, то они равны». Здесь слова перед запятой содержат условие теоремы, а после запятой — заключение.

Часто условие теоремы записывают после слова «дано», а заключение — после слова «доказать». Например, теорему о вертикальных углах можно оформить так.

Поменяв условие и заключение теоремы местами, получим новое утверждение (истинное или ложное). Если полученное таким способом утверждение истинное, его называют обратной теоремой.

Примеры:

«Если углы вертикальные, то они равны» — данная теорема. «Если углы равны, то они вертикальные» — обратное утверждение (ложное).
«Если соответственные утлы равны, то прямые параллельные» — данная теорема. «Если прямые параллельные, то соответственные углы равны» — обратная теорема. Важнейшие теоремы, в которых даются критерии чего- либо, называют признаками.

Доказывая теорему, ссылаются на другие истинные утверждения. Но в самом начале изучения геометрии еще никаких других истинных утверждений» нет. Поэтому некоторые Пермью утверждения обычно принимают без доказательств. Называют их аксиомами.

Некоторые аксиомы вам уже известны. Сформулируем их еще раз.

Какой бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, ей не принадлежащие.

Через любые две точки можно провести прямую, и только одну.
Из трех точек прямой одна и только одна лежит между двумя другими.
Каждый отрезок имеет определенную длину.
Каждый угол имеет определенную меру.
Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.

От теорем и аксиом следует отличать определения, в которых рйокрывается содержание понятия. Например: «Отрезком называется часть прямой, ограниченная двумя точками» — определение отрезка; «Острым углом называется угол, который «меньше прямого» — определение острого угла.

В определениях, аксиомах и теоремах — основное содержание геометрии. Их нужно знать, но формулировать (правильно!) можно и своими словами. Например, определение отрезка можно сформулировать так: «Отрезок — это часть прямой, ограниченная двумя ее точками», или так: «Часть прямой, ограниченная двумя ее точками, называется отрезком».

Для любознательных:

Слово аксиома греческого происхождения; сначала это слово обозначало: уважение, авторитет, неоспоримость; впоследствии словом «аксиома» начали называть утверждение, принимаемое без доказательства.

Слово теорема тоже греческого происхождения. Сначала теоремой называли зрелище, театральное представление. Первым геометрам доказанные ими теоремы казались довольно неожиданными, удивительными, словно интересные зрелища. И в самом деле удивительно: из немногих примитивных утверждений, принимаемых без доказательств, путем одних рассуждений человек может получить миллионы не очевидных следствий. Даже таких, которых в природе нигде не наблюдается. И таких, о существовании которых не догадывался ни один мыслитель.

Чтобы и вы поняли, какое удовлетворение ощущали первые геометры, открывая и доказывая все новые и новые свойства геометрических фигур с помощью одних лишь рассуждений, попробуйте ответить на один из таких вопросов.

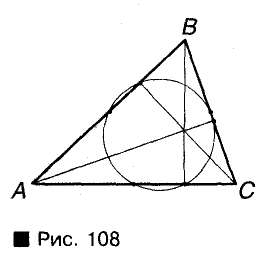
Посмотрите на рисунок 108. На нем выделены 6 точек: середины сторон треугольника ABC и основания его высот. Кажется, все эти точки лежат на одной окружности. Действительно ли это так? В каждом треугольнике? Кто первым обнаруживал подобные закономерности и обосновывал их, тот испытывал огромное удовлетворение, словно путешественник, пришедший первым туда, где еще никто не бывал, или спортсмен, побивший мировой рекорд.

Пример №7

Биссектрисы внутренних накрест лежащих углов, образованных секущей с двумя параллельными прямыми, параллельны. Докажите. Сформулируйте обратное утверждение.

Решение:

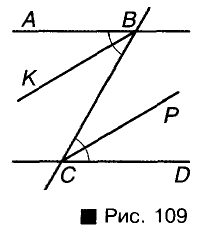
Пусть ВС — секущая прямых АВ и CD, углы ABC и BCD — внутренние накрест лежащие, а ВК и СР — их биссектрисы (рис. 109). Покажем, что если АВ || CD, то ВК || СР.

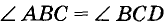
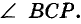
Если АВ || CD, то как внутренние накрест лежащие при параллельных прямых. Половины равных углов равны, поэтому Эти углы — внутренние накрест лежащие для прямых КВ и СР и секущей ВС. Поскольку эти углы равны, то прямые КВ и СР параллельны. А это и требовалось доказать.

Обратное утверждение: если биссектрисы внутренних накрест лежащих углов, образованных двумя прямыми с их секущей, параллельны, то параллельны и данные прямые.

Пример №8

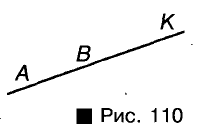
Два луча называют сонаправленными, если один из них является частью другого или если они параллельны и расположены по одну сторону от прямой, проходящей через их начала. Приведите примеры.

Решение:

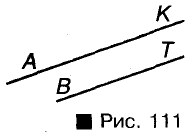
Лучи АК и ВК (рис. 110), а также лучи АК и ВТ (рис. 111).

Пример №9

Докажите, что углы с сонаправленными сторонами равны.

Решение:

Докажем, что если лучи ВА и РК, ВС и РТ сонаправленные, то углы 1 и 2 равны.

Если данные углы расположены, как показано на рисунке 112,

Если данные углы расположены, как показано на рисунке 113, то луч РТ составляет часть луча ВС. В этом случае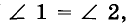, как соответственные углы при параллельных прямых ВА и РК.

Треугольник
Решение треугольников
Треугольники и окружность
Площадь треугольника
Длина дуги кривой
Геометрические фигуры и их свойства
Основные фигуры геометрии и их расположение в пространстве
Пространственные фигуры — виды, изображения, свойства

Источник

Взаимное расположение прямых на плоскости

Коллинеарные прямые

Две прямые называются коллинеарными, если они параллельны или совпадают.

Получим условие коллинеарности двух прямых l_1 и l_2 , заданных общими уравнениями:

l_1 colon ~ A_1x+B_1y+C_1=0; quad l_2 colon ~ A_2x+B_2y+C_2=0.

(3.19)

Необходимым и достаточным условием коллинеарности прямых (3.19) является условие коллинеарности их нормалей $vec{n}_1= A_1vec{i}+B_1vec{j}$ и $vec{n}_2= A_2vec{i}+B_2vec{j}$ . Следовательно, если прямые (3.19) коллинеарны, то $vec{n}_1 parallel vec{n}_2$ , т.е. существует такое число lambdane0 , что

$vec{n}_1=lambdacdotvec{n}_2 quad Leftrightarrow quad begin{cases}A_1=lambdacdot A_2,\B_1=lambdacdot B_2,end{cases}$ и наоборот.

Прямые совпадают, если помимо этих условий справедливо C_1=lambda C_2 . Тогда первое уравнение в (3.19) имеет вид lambda(A_2x+B_2y+C_2)=0 , т.е. равносильно второму, поскольку lambdane0 .

Таким образом, прямые (3.19) параллельны тогда и только тогда, когда соответствующие коэффициенты при неизвестных в их уравнениях пропорциональны, т.е. существует такое число lambdane0 , что A_1=lambda A_2,~B_1=lambda B_2 , но C_1nelambda C_2 . Прямые (3.19) совпадают тогда и только тогда, когда все соответствующие коэффициенты в их уравнениях пропорциональны:

A_1=lambdacdot A_2, quad B_1=lambdacdot B_2, quad C_1=lambdacdot C_2

Условия параллельности или совпадения прямых (3.19) можно записать в виде

$l_1parallel l_2~Leftrightarrow~frac{A_1}{A_2}=frac{B_1}{B_2}nefrac{C_1}{C_2}; quad l_1equiv l_2~Leftrightarrow~frac{A_1}{A_2}=frac{B_1}{B_2}=frac{C_1}{C_2}$

Условие коллинеарности двух прямых (3.19) можно записать в виде

$begin{vmatrix},A_1&B_1\A_2&B_2,end{vmatrix}=A_1cdot B_2-A_2cdot B_1=0.$

Семейство параллельных прямых и Линии уровня линейного трехчлена

Линии уровня линейного трехчлена

Линией уровня функции f(x,y) двух переменных называется геометрическое место точек координатной плоскости Oxy , в которых функция принимает постоянное значение, т.е. f(x,y)=operatorname{const} .

Для линейного трехчлена p(x,y)=Ax+By+C уравнение линии уровня p(x,y)=operatorname{const} имеет вид

Acdot x+Bcdot y+C=operatorname{const}.

(3.20)

При любом фиксированном значении постоянной уравнение (3.20) описывает прямую. Рассмотрим поведение семейства линий уровня, отличающихся значением постоянной. Поскольку коэффициенты и не изменяются, то у всех прямых (3.20) будет одна и та же нормаль vec{n}=Avec{i}+Bvec{j} . Следовательно, линии уровня линейного трехчлена p(x,y)=Ax+By+C представляют собой семейство параллельных прямых (рис.3.22). Поскольку нормаль совпадает с градиентом (см. пункт 3 замечаний 3.2), а градиент направлен в сторону наискорейшего возрастания функции, то при увеличении постоянной линии уровня (3.20) переносятся параллельно в направлении нормали.

Пересекающиеся прямые

Необходимым и достаточным условием пересечения двух прямых (3.19) является условие неколлинеарности их нормалей, или, что то же самое, условие непропорциональности коэффициентов при неизвестных:

$begin{vmatrix} A_1&B_1\ A_2&B_2 end{vmatrix}ne0 quad Leftrightarrowquad frac{A_1}{A_2}nefrac{B_1}{B_2},.$

(3.21)

При этом условии система уравнений $begin{cases} A_1cdot x+B_1cdot y+C_1=0,\[2pt] A_2cdot x+B_2cdot y+C_2=0end{cases}$ имеет единственное решение x_0,~y_0 , которое определяет точку M_0(x_0,y_0) пересечения прямых (3.19).

Угол между прямыми

Углом между двумя прямыми на плоскости называется угол между их направляющими векторами. По этому определению получаются не один угол, а два смежных угла, дополняющих друг друга до . В элементарной геометрии из двух смежных углов, как правило, выбирается меньший, т.е. величина varphi угла между двумя прямыми удовлетворяет условию $0leqslantvarphileqslantfrac{pi}{2}$ .

Угол между двумя прямыми и угол между их направляющими векторами

Если $vec{p}_1=a_1vec{i}+b_1vec{j}$ и $vec{p}_2=a_2vec{i}+b_2vec{j}$ направляющие векторы прямых l_1 и l_2 соответственно (рис.3.23,а), то величина varphi угла между этими прямыми вычисляется по формуле:

$cosvarphi=frac{langlevec{p}_1,vec{p}_2rangle}{|vec{p}_1|cdot|vec{p_2}|}=frac{a_1cdot a_2+b_1cdot b_2}{sqrt{a_1^2+b_1^2}cdot!sqrt{a_2^2+b_2^2}}.$

Чтобы получить величину varphi острого угла между прямыми, нужно правую часть взять по абсолютной величине:

$cosvarphi=frac{|langlevec{p}_1,vec{p}_2rangle|}{|vec{p}_1|cdot|vec{p_2}|}=frac{|a_1cdot a_2+b_1cdot b_2|}{sqrt{a_1^2+b_1^2}cdot!sqrt{a_2^2+b_2^2}},.$

Угол varphi между прямыми (3.19) можно вычислить как угол между их нормалями $vec{n}_1=A_1vec{i}+B_1vec{j}$ и $vec{n}_2=A_2vec{i}+B_2vec{j}$ :

$cosvarphi=frac{langlevec{n}_1,vec{n}_2rangle}{|vec{n}_1|cdot|vec{n_2}|}=frac{A_1cdot A_2+B_1cdot B_2}{sqrt{A_1^2+B_1^2}cdot!sqrt{A_2^2+B_2^2}}.$

(3.22)

Чтобы получить величину varphi острого угла между прямыми, нужно правую часть взять по абсолютной величине:

$cosvarphi=frac{|langlevec{n}_1,vec{n}_2rangle|}{|vec{n}_1|cdot|vec{n_2}|}=frac{|A_1cdot A_2+B_1cdot B_2|}{sqrt{A_1^2+B_1^2}cdot!sqrt{A_2^2+B_2^2}}.$

Необходимым и достаточным условием перпендикулярности прямых (3.19) является условие ортогональности их нормалей, т.е. равенства нулю скалярного произведения их нормалей $langlevec{n}_1, vec{n}_2 rangle=0$ :

A_1cdot A_2+B_1cdot B_2=0

По формуле (3.22) получаем острый угол varphi между прямыми (3.19), если A_1A_2+B_1B_2>0 (рис.3.23,а), и тупой в противном случае: A_1A_2+B_1B_2<0 (рис.3.23,6). Другими словами, по формуле (3.22) находится тот угол между прямыми, в котором лежат точки, принадлежащие разноименным полуплоскостям, опреляемым данными прямыми. На рис.3.23 положительные и отрицательные полуплоскости отмечены знаками плюс «+» или минус «–» соответственно.

Если прямые заданы уравнениями с угловыми коэффициентами:

$begin{aligned} l_1colon~ y=k_1cdot x+y_1, quad k_1=operatorname{tg}alpha_1,~alpha_1nefrac{pi}{2};\[3pt] l_2colon~ y=k_2cdot x+y_2, quad k_2=operatorname{tg}alpha_2,~alpha_2nefrac{pi}{2} end{aligned}$

то угол varphi между ними (один из смежных углов) находится по формуле

Острый и тупой углы между двумя прямыми

$operatorname{tg}alpha=operatorname{tg}(alpha_1-alpha_2)=frac{operatorname{tg}alpha_1-operatorname{tg}alpha_2}{1+operatorname{tg}alpha_1cdotoperatorname{tg}alpha_2}=frac{k_1-k_2}{1+k_1cdot k_2},.$

(3.23)

Если правая часть (3.23) положительна, то угол varphi острый (рис.3.24), в противном случае — тупой. Чтобы получить острый угол varphi , нужно правую часть (3.23) взять по абсолютной величине:

$operatorname{tg}varphi=left|frac{k_1-k_2}{1+k_1cdot k_2}right|.$

Если k_1=k_2 (условие параллельности прямых), то varphi=0 . Если k_1k_2+1=0 (условие перпендикулярности прямых), то правая часть (3.23) не определена (operatorname{tg}varphi=infty) . Тогда полагают, что $varphi=frac{pi}{2}$ .

Пример 3.11. Найти величину того угла, образованного прямыми l_1colon3x-y-3=0 и l_2colon x-2y+4=0 , внутри которого лежит точка M(5;2) .

Угол, образованный двумя прямыми, внутри которого лежит точка

Решение. По общим уравнениям прямых находим нормали $vec{n}_1=3vec{i}-vec{j}$ и $vec{n}_2=vec{i}-2vec{j}$ , а также величину varphi угла между нормалями, используя (3.22):

$cosvarphi=frac{3cdot1+(-1)(-2)}{sqrt{3^2+(-1)^2}cdot!sqrt{1^2+(-2)^2}}=frac{5}{5sqrt{2}}=frac{sqrt{2}}{2} quad Rightarrow quad varphi=arccosfrac{sqrt{2}}{2}=frac{pi}{4}.$

Подставляя координаты точки M(5;2) в левые части уравнений прямых, выясняем, каким полуплоскостям принадлежит эта точка. Для прямой l_1 , имеем 3cdot5-2-3>0 , значит точка лежит в положительной полуплоскости, определяемой прямой l_1 . Для прямой l_2 имеем 5-2cdot2+4>0 , значит, точка лежит также в положительной полуплоскости, определяемой прямой l_2 . Поскольку точка принадлежит одноименным полуплоскостям (положительным), то искомый угол — это угол psi , смежный найденному углу $varphi=frac{pi}{4}colonpsi=pi-varphi=pi-frac{pi}{4}=frac{3pi}{4}$ . Приведенные рассуждения кажутся ненужными, так как положение точки сразу же выясняется по рис.3.25. Однако, как это было ранее отмечено (см. ), при аналитическом решении изображения фигур не используются, поскольку записать вывод «по рисунку видно, что…» на алгоритмическом языке невозможно.

Пример 3.12. Составить уравнение прямой, проходящей через точку y_0=1 на оси ординат и образующей с прямой $y=frac{1}{2},x+1$ угол $varphi=frac{pi}{4}$ .

Уравнение прямой, проходящей через точку и образующей угол

Решение. Искомая прямая (с угловым коэффициентом ) образует с заданной прямой (с угловым коэффициентом $tfrac{1}{2}$ ) острый угол $varphi=frac{pi}{4},~operatorname{tg}varphi=1$ . По формуле (3.23), учитывая, что угол varphi острый, составляем уравнение и упрощаем его:

$1=left|frac{k-frac{1}{2}}{1+k,frac{1}{2}}right|! ~ Leftrightarrow ~ frac{k-frac{1}{2}}{1+k,frac{1}{2}}=pm1 ~ Leftrightarrow ~ !left[!begin{aligned}k-frac{1}{2}&=1+frac{1}{2},k,\k-frac{1}{2}&=-1-frac{1}{2},k.end{aligned}right.$

Отсюда находим два решения k_1=3 или $k_2=-frac{1}{3}$ . Следовательно, учитывая (3.18), поставленной задаче удовлетворяют две прямые (рис.3.26)

l_1colon,y=3x+1; или $l_2colon,y=-frac{1}{3},x+1.$

Заметим, что прямые l_1 и l_2 взаимно перпендикулярны, поскольку выполняется условие

$k_1k_2+1=3cdot!left(-frac{1}{3}right)+1=0.$

Пучки прямых на плоскости

Собственным пучком прямых на плоскости называется совокупность всех прямых плоскости, проходящих через фиксированную точку (центр пучка).

Собственный и несобственный пучок прямых

Несобственным пучком прямых называется совокупность прямых, параллельных фиксированной прямой (центром несобственного пучка прямых считается бесконечно удаленная точка плоскости).

Любые две прямые l_1 и l_2 определяют пучок прямых, содержащий заданные прямые l_1 и l_2 . Если прямые l_1 и l_2 пересекаются, то точка M_0 их пересечения является центром собственного пучка (рис.3.27,а). Если l_1 и l_2 параллельны, то они определяют несобственный пучок параллельных прямых (рис.3.27,6).

Пусть заданы уравнения двух прямых (3.19) l_1colon,A_1cdot x+B_1cdot y+C_1=0 и l_2colon,A_2cdot x+B_2cdot y+C_2=0 , линейной комбинацией этих уравнений называется уравнение

lambda_1cdot(A_1cdot x+B_1cdot y+C_1)+lambdacdot(A_2cdot x+B_2cdot y+C_2)=0.

(3.24)

где числа lambda_1,,lambda_2 — коэффициенты линейной комбинации. Его можно записать в форме

(lambda_1cdot A_1+lambda_2cdot A_2)cdot x+(lambda_1cdot B_1+lambda_2cdot B_2)cdot y+lambda_1cdot C_1+lambda_2cdot C_2=0.

(3.25)

Заметим, что линейная комбинация уравнений является уравнением первой степени для любых значений коэффициентов, кроме случая, когда оба коэффициента при неизвестных равны нулю, т.е. при lambda_1cdot A_1+lambda_2cdot A_2=0 и lambda_1cdot B_1+lambda_2cdot B_2=0 . Эти значения параметров и считаются недопустимыми.

Уравнение (3.24) называется уравнением пучка прямых, содержащего прямые A_1x+B_1y+C_1=0 и A_2x+B_2y+C_2=0 .

При любых допустимых значениях параметров lambda_1 и lambda_2 уравнение (3.24) задает прямую, принадлежащую пучку, и, наоборот, для любой прямой пучка найдутся такие значения параметров lambda_1,,lambda_2 , что уравнение (3.24) будет задавать эту прямую.

Действительно, уравнения прямых l_1 и l_2 получаются из (3.24) при lambda_1=1,~lambda_2=0 и при lambda_1=0,~lambda_2=1 соответственно.

Если прямые l_1 и l_2 параллельны, то существует такое число lambdane0 , что A_1=lambda A_2 и B_1=lambda B_2 . Тогда при любых допустимых значениях параметров lambda_1,,lambda_2 прямая (3.25) параллельна прямой l_2 , так как коэффициенты при неизвестных пропорциональны:

lambda_1cdot A_1+lambda_2cdot A_2=(lambda_1cdotlambda+lambda_2)cdot A_2, quad lambda_1cdot B_1+lambda_2cdot B_2=(lambda_1cdotlambda+lambda_2)cdot B_2.

Если прямые l_1 и l_2 пересекаются в точке M_0(x_0,y_0) , то любая прямая (3.24) проходит через точку пересечения прямых l_1 и l_2 , поскольку

$lambda_1cdotunderbrace{(A_1cdot x_0+B_1cdot y_0+C_1)}_{0}+lambda_2cdotunderbrace{(A_2cdot x_0+B_2cdot y_0+C_2)}_{0}=0$

при любых значениях lambda_1 и lambda_2 .

Осталось показать, что для любой точки $M^{ast}(x^{ast},y^{ast})$ плоскости существуют такие значения параметров lambda_1,,lambda_2 , при которых уравнение (3.24) задает прямую , проходящую через точку $M^{ast}(x^{ast},y^{ast})$ . В самом деле, подставим координаты точки $M^{ast}(x^{ast},y^{ast})$ в уравнение (3.24):

$lambda_1cdotunderbrace{(A_1cdot x^{ast}+B_1cdot y^{ast}+C_1)}_{ne0}+lambda_2cdotunderbrace{(A_2cdot x^{ast}+B_2cdot y^{ast}+C_2)}_{ne0}=0.$

Это означает, что прямая (3.24) проходит через точку $M^{ast}$ . Отсюда определяется отношение $frac{lambda_1}{lambda_2}=-frac{A_1x^{ast}+B_1y^{ast}+C_1}{A_2x^{ast}+B_2y^{ast}+C_2}$ , равное по абсолютной величине отношению расстояний от точки $M^{ast}$ до прямых l_1 и l_2 (см. пункт 5 замечаний 3.2). При таком выборе параметров lambda_1,,lambda_2 уравнение (3.24) будет задавать прямую, проходящую через точку $M^{ast}$ , т.е. прямую .

Пример 3.13. Составить уравнение прямой, проходящей через точку пересечения прямых 2x+y+4=0 и 3x-y-1=0 и через точку $M^{ast}(2;3)$ .

Решение. Искомая прямая входит в пучок прямых, задаваемый уравнением

lambda_1cdot(2x+y+4)+lambda_2cdot(3x-y-1)=0.

Подставляя координаты точки $M^{ast}(2;3)$ , получаем:

lambda_1cdot(2cdot2+3+4)+lambda_2cdot(3cdot2-3-1)=0 quad Leftrightarrow quad 11lambda_1+2lambda_2=0.

Возьмем, например, lambda_1=-2,~lambda_2=11 и подставим в уравнение пучка:

-2cdot(2x+y+4)+11cdot(3x-y-1)=0 quad Leftrightarrow quad 29x-13y-19=0.

Искомое уравнение получено.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

2.5.1. Взаимное расположение двух прямых

Рассмотрим две прямые, уравнения которых заданы в общем виде:

Тот случай, когда зал подпевает хором. Две прямые могут:

1) совпадать;

2) быть параллельными: ;

3) или пересекаться в единственной точке: .

Справка: – это математический знак пересечения.

Как определить взаимное расположение двух прямых?

Начнём с первого случая:

1) Две прямые совпадают, тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, то есть, существует такое число «лямбда», что выполняются равенства

Рассмотрим прямые и составим три уравнения из соответствующих коэффициентов: . Из каждого уравнения следует, что , следовательно, данные прямые совпадают.

И действительно, если все коэффициенты уравнения умножить на –1 (сменить знаки), и все коэффициенты уравнения сократить на 2, то получится одно и то же уравнение: – вспоминаем, что это «эталонный» вид общего уравнения прямой.

Второй случай, когда прямые параллельны:

2) Две прямые параллельны тогда и только тогда, когда их коэффициенты при переменных и пропорциональны: , но

В качестве примера рассмотрим прямые . Сначала проверяем пропорциональность соответствующих коэффициентов при переменных :

Однако совершенно очевидно, что .

Вывод:

И третий случай, когда прямые пересекаются:

3) Две прямые пересекаются, тогда и только тогда, когда их коэффициенты при переменных и НЕ пропорциональны, то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства

Так, оставим систему для прямых :

Из первого уравнения следует, что , а из второго уравнения: , значит, система несовместна (нет решений). Таким образом, коэффициенты при переменных не пропорциональны.

Вывод: прямые пересекаются

В практических задачах можно использовать только что рассмотренную схему решения, но существует и более «цивилизованная» упаковка:

Задача 74

Выяснить взаимное расположение прямых:

Решение основано на исследовании направляющих векторов прямых:

а) Из уравнений найдём направляющие векторы прямых: .

Вычислим определитель, составленный из координат данных векторов:
, значит, векторы не коллинеарны и прямые пересекаются.

Вопрос: всё ли вам понятно? Если нет, то используйте три ссылки выше. Ну а остальные перепрыгивают камень и следуют дальше, прямо к Кащею Бессмертному =)

б) Найдем направляющие векторы прямых :
– прямые имеют один и тот же направляющий вектор, значит, они либо параллельны, либо совпадают (тут и определитель считать не надо).

Очевидно, что коэффициенты при переменных пропорциональны и .

Выясним, справедливо ли равенство :

Таким образом,

в) Найдем направляющие векторы прямых :

Вычислим определитель, составленный из координат данных векторов:
, следовательно, направляющие векторы коллинеарны и прямые либо параллельны, либо совпадают.

Коэффициент пропорциональности «лямбда» можно узнать прямо соотношения коллинеарных направляющих векторов . Впрочем, можно и через коэффициенты самих уравнений: .

Теперь выясним, справедливо ли равенство . Оба свободных члена нулевые, поэтому:

Полученное значение удовлетворяет данному уравнению (ему удовлетворяет вообще любое число).

Таким образом, прямые совпадают.

Ответ:

Очень скоро вы научитесь (или даже уже научились) решать рассмотренную задачу устно и буквально в считанные секунды – присмотрелись к уравнениям, и всё понятно.

2.5.2. Как найти прямую, параллельную данной?

2.4. Параметрические уравнениЯ прямой

| Оглавление |

Автор: Aлeксaндр Eмeлин

Источник

Пусть
даны две прямые l₁
и l₂
на плоскости:

Чтобы
определить их взаимное расположение,
достаточно решить систему уравнений:

(3.8)

Если
эта система имеет единственное решение
(х₀,
у₀),
то прямые l₁
и l₂,
пересекается в точке М₀(х₀,
у₀).
Если система (3.8) не имеет решений, то
прямые l₁
и l₂
не пересекаются, следовательно, l₁
|| l₂.
Если система (3.8) имеет бесконечное
множество решений, то l₁
и l₂
совпадают.

Однако
решить вопрос о взаимном расположении
l₁
и l₂
можно и не решая системы (3.3). Действительно,
из общего уравнения прямой l₁,
находим, что ее нормальный вектор
имеет координатыА₁
и В₁
, т.е.
= {А₁,
В₁},
а прямая l₂
имеет нормальный вектор
= {А₂,
В₂}.
Если векторы
,коллинеарны, то прямыеl₁
и l₂
либо параллельны, либо совпадают. Если
,неколлинеарны, то прямые пересекаются.
Зная, что коллинеарные векторы (и только
они) имеют пропорциональные координаты,
получаем: если,
то прямыеl₁
и l₂
пересекаются; если
то
прямыеl₁
и l₂параллельны;
если
то
прямыеl₁
и l₂совпадают.

Используя
нормальные векторы
,можно также найти угол между прямыми,
так как угол между нормальными векторами
равен одному из угловмежду прямымиl₁
и l₂(рис. 3.9).

Из
определения скалярного произведения
векторов получаем:,
поэтому.

Пусть
на плоскости заданы прямая
и точкаМ₀(х₀,
у₀).
Найдем расстояние d
от точки М₀(х₀,
у₀)
до прямой l
(рис. 3.10). Пусть М₁(х₁,
у₁)
– точка пересечения прямой l
и прямой, проходящей через точку М₀
перпендикулярно l.
Так как М₁
лежит на l,
то ее
координаты удовлетворяют уравнению
этой прямой, таким образом, имеем
тождество:

.
(3.9)

Рассмотрим
вектор
.
Этот вектор коллинеарен нормальному
вектору= {А₁,
В₁}
прямой l
и
,
поэтому косинус угла между векторамииравен либо 1, либо -1. Следовательно,,
откуда

Учитывая
тождество (3.9) получаем:

.
(3.10)

Пример
3.3. Найти
расстояние от точки пересечения прямых
l_l
и l₂
до прямой l₃.
Определить взаимное расположение пар
прямых l₁,
l₃
и l₂,
l₃,
если прямые заданы общими уравнениями:

Решение.Решим систему уравнений:

Получим:
х₀= 1, у₀= 2
– единственное
решение. Следовательно, прямые l₁
и l₂пересекается
в точке М₀(1,
2). Используя формулу (3.10), найдем расстояние
d
от М₀
до l₃:

Нормальные
векторы прямых l₁,
l₂
и l₃
соответственно будут
= {3, –2},= {1, 1},= {–6, 4}. Так как координатыипропорциональны 3/( – 6) = –2/3 и –2/41/(
–3), тоl₁
|| l₃.
Для
и
имеем:
1/(–6)1/4,
следовательно,l₂
и l₃
пересекаются.

3.3. Плоскость в пространстве

Пусть
в пространстве задана прямоугольная
система координат: 0 – начало координат,– единичные направляющие векторы осей
координат, соответственно 0х,
0у
и 0z.
Рассмотрим в пространстве произвольную
плоскость
.
Выведем уравнение этой плоскости, т.е.
уравнение, содержащее переменныех,
у,
z,
которому удовлетворяют координаты
любой точки, лежащей на плоскости
и не удовлетворяют координаты никакой
точки, не лежащей
на этой
плоскости.

Пусть
задана точка М₁(х₁,
у₁,
z₁)и вектор={А,
В,
C}
перпендикулярный плоскости
(нормальный вектор плоскости). ПустьM(x,
у,
z)
– произвольная точка, принадлежащая
плоскости
.
Тогда вектор

перпендикулярен
вектору
(рис. 3.11), а поэтому=
0 (условие перпендикулярности векторов
(см. разд. 2.4)) или

.
(3.11)

Итак,
координаты любой точки М,
лежащей в плоскости
,
удовлетворяют этому уравнению
и,
легко видеть, что координаты точки, не
лежащей в плоскости
,
не удовлетворяют уравнению (3.11).
Следовательно, уравнение (3.11) является
уравнением плоскости и называется
уравнением плоскостипо
точке и нормальному вектору.

Уравнение
(3.11) является уравнением первой степени
относительно текущих координат х,
у,
z.
Можно показать (аналогично тому, как
это было сделано в разд. 3.1), что всякое
уравнение первой степени относительно
x,
у,
z

(3.12)

является
уравнением некоторой плоскости (оно
называется общим
уравнением плоскости), причем вектор
={А,
В,
C},
является нормальным вектором плоскости.

Если
в уравнении (3.12) D
= 0, то этому
уравнению удовлетворяет тройка чисел
(0, 0, 0), т.е. соответствующая плоскость
проходит через начало координат. Нетрудно
видеть, что плоскость 0ху
имеет уравнение
,
плоскость 0xz
– уравнение
,
a плоскость 0yz
задается уравнением
.

Известно,
что плоскость однозначно определяется
тремя точками, не лежащими на одной
прямой. Пусть
иМ(х,
у,
z)
– произвольная точка плоскости
(рис. 3.12). Рассмотрим векторы