Как найти высшую точку подъема - Avtoru.top - решение различных проблем

Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.

Важные факты!График движения тела, брошенного под углом к горизонту:

α — угол, под которым было брошено тело

Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v_0x = v₀cosα. Ее проекция на ось ОУ равна v_0y = v₀sinα.
Проекция мгновенной скорости на ось ОХ равна: v_x = v₀cosα. Ее проекция на ось ОУ равна нулю: v_y = v₀sinα – gt.
Проекция ускорения свободного падения на ось ОХ равна нулю: g_x = 0. Ее проекция на ось ОУ равна –g: g_y = –g.

Кинематические характеристики

Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:

Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:

v_min = v₀cosα = v_h

Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:

v_max = v_o = v

Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: v_y = 0. Время подъема определяется следующей формулой:

Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:

Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:

l = s_x = v_0xt_полн = v₀cosα t_полн

Подставляя в выражение формулу полного времени полета, получаем:

Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:

Учитывая, что x₀ = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v₀cosα, данная формула принимает вид:

x = v₀cosα t

Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:

Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v₀sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:

Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:

Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?

Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:

v₀sinα = gt_под

Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:

Тело, брошенное под углом к горизонту с некоторой высоты

Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.

Важные факты!

График движения тела, брошенного под углом к горизонту с некоторой высоты:

Время падения тела больше времени его подъема: t_пад > t_под.

Полное время полета равно:

t_полн = t_пад + t_под

Уравнение координаты x:

x = v₀cosα t

Уравнение координаты y:

Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.

Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:

x = v₀cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.

Задание EF17562

С высоты Н над землёй начинает свободно падать стальной шарик, который через время t = 0,4 c сталкивается с плитой, наклонённой под углом 30° к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h = 1,4 м над землёй. Чему равна высота H? Сделайте схематический рисунок, поясняющий решение.

Алгоритм решения

1.Записать исходные данные.

2.Построить на чертеже начальное и конечное положения тела. Выбрать систему координат.

3.Выбрать нулевой уровень для определения потенциальной энергии.

4.Записать закон сохранения энергии.

5.Решить задачу в общем виде.

6.Подставить числовые значения и произвести вычисления.

Решение

Запишем исходные данные:

• Время падения стального шарика: t = 0,4 c.

• Верхняя точка траектории после абсолютно упругого удара о плиту: h = 1,4 м.

• Угол наклона плиты: α = 30^о.

Построим чертеж и укажем на нем все необходимое:

Нулевой уровень — точка D.

Закон сохранения энергии:

E_k0 + E_p0 = E_k + E_p

Потенциальная энергия шарика в точке А равна:

E_pA = mgH

Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.

В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:

EpB=mgl1

Перед ударом кинетическая энергия шарика равна:

EkB=mv22

Согласно закону сохранения энергии:

EpA=EpB+EkB

mgH=mgl1+mv22

Отсюда высота H равна:

H=mgl1mg+mv22mg=l1+v22g

Относительно точки В шарик поднимется на высоту h – l₁. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:

h−l1=v2sin2β2g=v2sin2(90−2α)o2g

Отсюда:

l1=h−v2sin2(90−2α)o2g

Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:

v=gt

Следовательно:

H=l1+v22g=h−(gt)2sin2(90−2α)o2g+(gt)22g

H=h−gt2sin2(90−2α)2+gt22=h−gt22(sin2(90−2α)o−1)

H=1,4−10·0,422(sin2(90−60)o−1)

H=1,4−5·0,16(sin230o−1)

H=1,4−0,8((12)2−1)=1,4−0,8(14−1)

H=1,4+0,6=2 (м)

Ответ: 20

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17980

В момент t=0 мячик бросают с начальной скоростью v₀ под углом α к горизонту с балкона высотой h (см. рисунок).

Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).

К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.

Алгоритм решения

Установить вид механического движения, исходя из условий задачи.
Записать формулы для физических величин, указанных в таблице, в соответствии с установленным видом механического движения.
Определить, как зависят эти величины от времени.
Установить соответствие между графиками и величинами.

Решение

Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.

Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.

Координата x меняется согласно уравнению координаты x:

Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:

Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:

В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.

Формула проекции скорости мячика на ось ОХ:

Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.

Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.

Остается последний вариант — координата y. Уравнение этой координаты имеет вид:

Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.

Теперь записываем установленные соответствия в порядке АБ: 42.

Ответ: 42

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18741

Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?

Для каждой величины определите соответствующий характер изменения:

увеличивается
уменьшается
не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Сделать чертеж, иллюстрирующий ситуацию.
Записать формулы, определяющие указанные в условии задачи величины.
Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.

Решение

Выполняем чертеж:

Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).

Горизонтальная составляющая скорости шарика определяется формулой:

v_x = v₀ cosα

Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).

Ответом будет следующая последовательность цифр — 33.

Ответ: 33

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 43.4k

Источник

Максимальная высота подъема тела, брошенного под углом к горизонту, формула

Максимальная высота подъема тела, брошенного под углом к горизонту определяется из формул времени максимального подъема и формулы координат тела

Максимальная высота подъема тела, брошенного под углом к горизонту

[
h_{max} = y(t_{hmax}) = u_0 t_{hmax} sin(α) — frac{gt_{hmax}^2}{2}
]

и после подстановки t_hmax в выражение (1) и его упрощения получим

[
h_{max} = frac{(u_0 sin(α))^2}{2g}
]

Здесь:
u₀ — начальная скорость тела (м/с),
α — угол, под которым брошено тело к горизонту (°),
g — ускорение свободного падения 9.81 (м/c²),
t_hmax — время подъема на максимальную высоту (c)

Вычислить, найти максимальную высоту подъема тела, брошенного под углом к горизонту по формуле (2).

Максимальная высота подъема тела, брошенного под углом к горизонту	стр. 420

Источник

Как найти максимальную высоту подъема

При броске тела вверх оно замедляется с ускорением g≈9,8 м/с², обусловленным гравитационным притяжением Земли. Именно поэтому в некоторый момент времени подброшенное тело останавливается и начинает движение в обратном направлении, вниз. Расстояние от точки смены направления движения тела до поверхности Земли и будет равно максимальной высоте подъема.

Вам понадобится

— секундомер;
— радар;
— калькулятор;
— угломер.

Инструкция

Найдите максимальную высоту подъема тела, брошено вверх при помощи секундомера. Не имеет значения, брошено ли тело вертикально вверх или под углом к горизонту. При помощи секундомера, засеките время, которое тело находилось в полете. Измеряйте значение времени в секундах. Поскольку половину времени, проведенного в полете тело поднимается, во вторую половину опускается, полученное значение поделите на 2.

Рассчитайте максимальную высоту подъема тела Н. Для этого возведите поделенное на 2 время полета t в квадрат. Полученное значение умножьте на ускорение свободного падения g≈9,8 м/с², а результат поделите на число 2, H=g∙t²/2. Высоту получите в метрах.

Пример. После броска с поверхности Земли тело снова упало на нее через 4 с, на какую максимальную высоту оно поднялось? Найдите время подъема тела на максимальную высоту. Оно равно половине всего времени движения 4/2=2 с. Подставьте значение в формулу H=g∙t²/2=9,8∙2²/2≈20 м. Если не требуется повышенная точность, значение ускорения свободного падения можно брать 10 м/с².

Определите максимальную высоту подъема тела, если известна его начальная скорость. Ее можно измерить специальным радаром. В некоторых устройствах, она изначально известна. В том случае, если тело запущено вертикально вверх с начальной скоростью v0, чтобы найти максимальную высоту подъема этого тела поделите квадрат этой начальной скорости на удвоенное значение ускорения свободного падения, H=v0²/2∙g. Скорость должна быть измерена в метрах в секунду.

Найдите максимальную высоту подъема тела, начальная скорость v0 которого направлена под углом к горизонту. При расчете учитывайте, что за подъем тела отвечает только вертикальная составляющая скорости, которая равна v0y= v0∙sin(α), где α – угол к горизонту, под которым тело начало свое движение, его измерьте угломером. Тогда для расчета максимальной высоты подъема тела можно использовать формулу, описанную в предыдущем пункте, а получившийся результат умножит на синус α, возведенный в квадрат H=(v0²/2∙g)∙sin²(α).

Источники:

максимальная высота

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Подскажите пожалуйста как найти наивысшую точку подъема??? Я нашел низкую точки траектории.
Вот само задание:
{На крыше самого высокого здания Петропавловска прикрепили канат.
Координата его точки подвески А (x0, y0, z0). Канат начинают раскачивать.
Координата одной из точки его наивысшего подъема B (x1, y1, z1).
Найдите координаты самой низкой точки траектории и другой наивысшей точки подъема.

Ввод
Вход начинается с ввода в столбик координат точек x0, y0, z0, x1, y1, z1 в диапазоне [0:100].

Вывод
В выходном файле вывести координаты самой низкой точки траектории и другой наивысшей точки подъема.

Пример
z.in
0
8
9
0
0
4

z.out
0.000 -1.434 9.000
0.000 0.000 14.000}

Pascal

Program zada4a;
uses crt;
var
  a, b, c, d: array [0 .. 2] of real;
  i: integer;
Begin
  WriteLn('Кординаты точки A:');
  for i := 0 to 2 do
    ReadLn(a[i]);
  WriteLn('Кординаты точки B:');
  for i := 0 to 2 do
    ReadLn(b[i]);
  c[0] := 2 * a[0] - b[0];
  c[1] := b[1];
  c[2] := 2 * b[2] - b[2];
  d[0] := a[0];
  d[1] := a[1] - sqrt((a[0] - b[0]) * (a[0] - b[0]) + (a[1] - b[1]) *
    (a[1] - b[1]) + (a[2] - b[2]) * (a[2] - b[2]));
  d[2] := a[2];
  WriteLn('Cx=', c[0]);
  WriteLn('Cy=', c[1]);
  WriteLn('Cz=', c[2]);
  WriteLn('Dx=', d[0]);
  WriteLn('Dy=', d[1]);
  WriteLn('Dz=', d[2]);
End.

Помогите пожалуйста, нужно срочно

Источник

Цели урока:

выделить этапы моделирования.
сформулировать основные задачи на каждом этапе
моделирования.
построить график функции.

Задачи урока:

Образовательные:

научить обобщать материал и выделять главное
научить применять полученные знания на
практике

Воспитательная:

формирование самостоятельности и
ответственности при изучении нового
материала

Развивающая:

развитие логического мышления

Методы обучения:

лекция
объяснительно — иллюстративный (презентация)
фронтальный опрос

План урока:

Организационный момент
Объяснение новой темы
Практическая работа
Подведение итогов
Домашнее задание.

1. Организационный момент.

2. Изучение новой темы.

Ход урока

Поскольку мы занимаемся изучением информатики
и компьютерных технологий, то и в моделировании
нас интересует ответ на вопрос: как создать
компьютерную модель? Представим этот вопрос
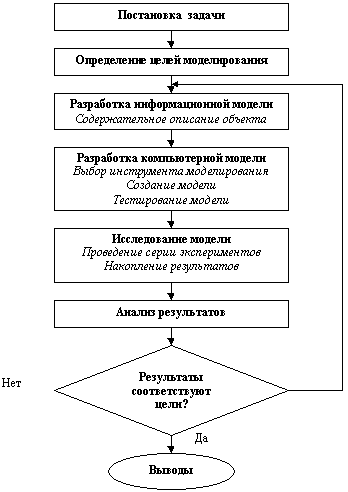
поэтапно в виде схемы.

Схема модели

Приложение 1

При решении конкретной задачи она может
уточняться и корректироваться в зависимости от
поставленной задачи и цели моделирования.

Рассмотрим процесс построения и исследования
модели на конкретном примере движения тела,
брошенного под углом к горизонту.

I этап — Постановка задачи. В процессе
тренировок теннисистов используются автоматы по
бросанию мяча в определенное место площадки.

Цель: задать необходимую скорость и угол
бросания мяча для попадания в площадку
определенного размера, находящимся на известном
расстоянии. Исследовать движение мяча,
брошенного с начальной скоростью ?₀ под
углом ? к горизонту, когда сопротивлением
воздуха можно пренебречь.

II этап — Разработка информационной модели.
Построим описательную модель процесса движения
тела с использованием физических объектов,
понятий и законов, то есть идеализированную
модель движения объекта.

Из условия задачи сформулируем основные
предположения:

мяч мал по сравнению с землей, поэтому его можно
считать материальной точкой;
изменение высоты мяча можно считать постоянной
величиной g = 9,8 м/с² и движение по оси Y можно
считать равноускоренным;
скорость бросания тела мала, поэтому
сопротивлением воздуха можно пренебречь и
движение по оси Х можно считать равномерным.

— Создание формализованной модели.
(Описание информационной модели записывается с
помощью какого-либо формального языка. В такой
модели с помощью формул, уравнений, неравенств и
так далее фиксируется формальные отношения
между начальными и конечными значениями свойств
объектов, а также накладываются ограничения на
допустимые значения этих свойств.)

Приложение 2

— Создание компьютерной модели. (Формальную
информационную модель преобразуем в
компьютерную, выразив ее на понятном для
компьютера языке. Для этого используем
программное обеспечение Microsoft Office ( электронные
таблицы EXCEL.)

Приложение 3

III этап — Компьютерный эксперимент.
(Компьютерная модель исследуется в приложении
электронные таблицы EXCEL, проводится сортировка
данных, строится график зависимости J ( t), Х(у).)

План эксперимента.

Тестирование

Провести тестовый расчет компьютерной модели
по данным, приведенным в таблице.

Приложение 4

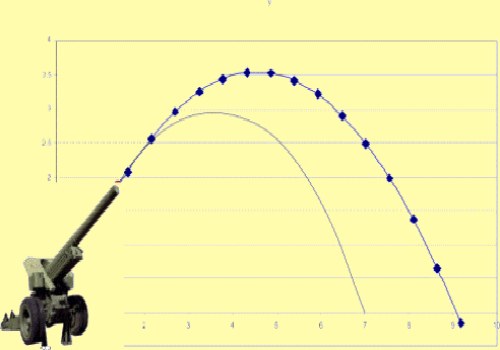
Эксперимент

Исследовать движение мяча.
Исследовать изменение движения тела при
изменении начальной скорости.
Исследовать изменение движения тела при
изменении угла бросания.
Изменяя начальную скорость и угол бросания,
исследовать характер движения тела и его
положение по отношению к площадке.

Приложение 5

IV этап — Анализ результатов моделирования.
(Результаты и выводы, полученные в экспериментах,
оформите в виде отчета в текстовом документе. В
отчете приведите ответы на следующие вопросы:

Как движется тело, брошенное под углом к
горизонту?
Как определить наивысшую точку подъема?
Как изменяется наибольшая высота подъема при
увеличении начальной скорости и неизменном угле
броска?
Как изменяется дальность полета при увеличении
начальной скорости и неизменном угле броска?

Подведение итогов: выставление оценок за
проведенную исследовательскую работу.

Домашнее задание. Разработать и исследовать
физическую модель для решения задач по теме:
«Гармонические колебания».

Пример: Дан пружинный маятник, совершающий
гармонические незатухающие колебания
(сопротивление среды не учитывать). Жесткость
пружины k (Н/м) и масса груза m (кг).

Исследовать зависимость периода колебания (Т),
от жесткости пружины (k), и построить график этой
зависимости. Предусмотреть возможность введения
любого значения массы груза (m). Жесткость k
меняется от 100 до 1000 Н/м, через каждые 100 Н/м.

Исследовать зависимость периода колебания (Т),
от массы груза (m), и построить график этой
зависимости. Предусмотреть возможность введения
любого значения жесткости пружины (k). Масса груза
m меняется от 1 до 10 кг, через каждые 1 кг.

Список литературы

Горстко А. Б. Информатика для школьников и
всех-всех-всех /
Горстко А. Б., Чердынцева М. И. — Ростов-на-Дону:
Изд-во «Феникс», 1996.
Ракитина Е. А. Решение типовых задач по
информационным технологиям / Ракитина Е. А.,
Бешенков С. А., Галыгина И. В., Галыгина Л. В.
//Информатика и образование . — 2004. — №4.
Информатика в школе. Решение типовых задач по
информатике. Часть 2. : Москва «Образование и
Информатика», Приложение к журналу
«Информатика и образование». — №1. — 2004.
Кутугина Е.С Моделирование. Учебное пособие. —
Томск, 2005. — 80с.

Источник

Кинематические характеристики

Тело, брошенное под углом к горизонту с некоторой высоты

Максимальная высота подъема тела, брошенного под углом к горизонту, формула

Вычислить, найти максимальную высоту подъема тела, брошенного под углом к горизонту по формуле (2).

Максимальная высота подъема тела, брошенного под углом к горизонту

Как найти максимальную высоту подъема

Не пропустите также: