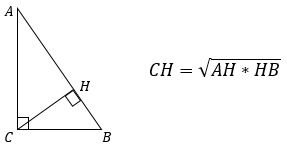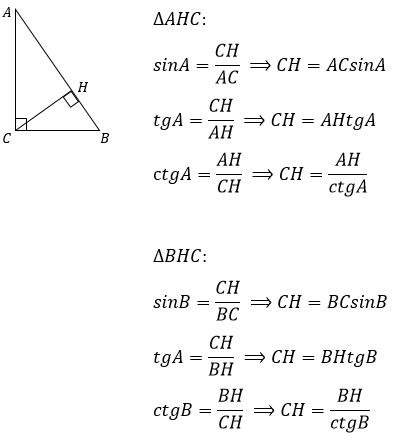Как найти высоты в прямоуг треуг

Высота в прямоугольном треугольнике

Вспомним определение. Высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.

В прямоугольном треугольнике катеты являются высотами друг к другу. Главный интерес представляет высота, проведённая к гипотенузе.

Один из типов экзаменационных задач в банке заданий ФИПИ — такие, где в прямоугольном треугольнике высота проведена из вершины прямого угла. Посмотрим, что получается:

sin A

cos A

Высота проведена к гипотенузе AB. Она делит треугольник на два прямоугольных треугольника — и . Смотрим внимательно на рисунок и находим на нем равные углы. Это и есть ключ к задачам по геометрии, в которых высота опущена на гипотенузу.

Мы помним, что сумма двух острых углов прямоугольного треугольника равна . Значит, , то есть угол равен углу . Аналогично, угол равен углу .

Иными словами, каждый из трех углов треугольника равен одному из углов треугольника (и треугольника ). Треугольники и называются подобными. Давайте нарисуем их рядом друг с другом.

Они отличаются только размерами. Стороны подобных треугольников пропорциональны. Что это значит?

Возьмем треугольники и . Стороны треугольника длиннее, чем стороны треугольника в раз:

Мы доказали свойство высоты прямоугольного треугольника. Его можно сформулировать как теорему.

Теорема 1. Высота прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, делит треугольника на три подобных друг другу треугольника:

При решении задач нам пригодится равенство углов треугольников и , а также пропорциональность их сторон. Обратите также внимание, что площадь треугольника можно записать двумя разными способами: как половину произведения катетов и как половину произведения гипотенузы на проведенную к ней высоту. В геометрии это называется «метод площадей» и часто применяется в решении задач.

Задача 1.

В треугольнике ABC угол C равен CH — высота, BC = 3, cos A = Найдите AH.

Решение:

Рассмотрим треугольник ABC. В нем известны косинус угла A и противолежащий катет BC. Зная синус угла A, мы могли бы найти гипотенузу AB. Так давайте найдем sin A:

sin + cos = 1.

Эта формула – основное тригонометрическое тождество. Конечно, вы его знаете:

sin

sin

sin A (поскольку значение синуса острого угла положительно).

Тогда:

Рассмотрим прямоугольный треугольник , . Поскольку

Отсюда

Ответ:

Задача 2.

В треугольнике ABC угол C равен 90 AB = 13, tg A . К гипотенузе проведена высота CH. Найдите AH.

Решение:

Это чуть более сложная задача. Ведь вам неизвестны катеты a и b.

Запишем теорему Пифагора: (1)

Нам известно также, что:

tg A (2)

Решая уравнения (1) и (2), найдем:

Запишем площадь треугольника AВС двумя способами:

и найдем длину .

Найти высоту, проведенную из вершины прямого угла, можно было и другим способом. Мы выбрали самый короткий путь — составили и решили систему уравнений, как в алгебре.

Теорема 2. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, равна произведению катетов, деленному на гипотенузу.

Доказательство:

Из прямоугольного треугольника ABC с прямым углом C и гипотенузой AB:

sin

Из прямоугольного треугольника AНС с прямым углом Н и гипотенузой AС:

sin

Мы разными способами вычислили синус одного и того же угла. Приравняем полученные выражения:

Найдем высоту:

Что и требовалось доказать.

Задача 3. Катеты прямоугольного треугольника равны 15 и 20.
Найдите высоту, проведенную к гипотенузе.

Решение:

Воспользуемся теоремой 2 о высоте прямоугольного треугольника:

Катеты BС и AС нам известны: BC = 15, AC = 20. Найдем гипотенузу AB с помощью теоремы Пифагора:

Найдем высоту, проведенную из вершины прямого угла:

Ответ: 12.

Теорема 3. В прямоугольном треугольнике квадрат высоты, проведенной из вершины прямого угла, равен произведению проекций катетов на гипотенузу.

Сейчас мы докажем эту полезную формулу.

Вспомним, что такое проекция точки на прямую. Например, из точки С опускаем СН — перпендикуляр к прямой AВ. Точка Н и будет проекцией точки С. Тогда AН – проекция катета AВ, а BН – проекция катета BС.

Обозначим:

Доказательство проведем двумя способами.

Первый способ доказательства:

Из прямоугольного треугольника BНС с прямым углом Н и гипотенузой BС:

tg

Из прямоугольного треугольника AНС с прямым углом Н и гипотенузой AС:

ctg

Заметим, что угол CBН – это угол CBA, а угол CAН – это угол BAC. Тогда:

tg

tg

Мы воспользовались тем, что тангенс и котангенс двух разных острых углов прямоугольного треугольника равны друг другу. Это следует из определения тангенса и котангенса.

Преобразуем получившееся выражение:

Что и требовалось доказать.

Второй способ доказательства:

Воспользуемся подобием треугольников, о которых говорится в теореме 1.

Рассмотрим пару прямоугольных треугольников AНC и BНC. Как было показано выше, эти треугольники подобны по двум углам, поэтому

Мы получили такое же соотношение, как и в первом способе доказательства.

Далее аналогично получим, что

Что и требовалось доказать.

Задача 4. На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH = 4, BH = 16. Найдите длину CH.

Решение:

Воспользуемся теоремой 3 о высоте прямоугольного треугольника:

Подставим данные задачи.

CH = 8.

Ответ: 8.

Разберем решения других задач ОГЭ и ЕГЭ по теме «Свойства высоты в прямоугольном треугольнике».

Задача 5. Катеты прямоугольного треугольника относятся как 3:4, а гипотенуза равна 50. Найти высоту, проведенную из вершины прямого угла и отрезки, на которые гипотенуза делится высотой.

Решение:

Рассмотрим прямоугольный треугольник ABС с гипотенузой AB. Проведем высоту CD=h.

Учитывая отношение катетов, обозначим их длины как: BC = 3x, AC = 4x.

Тогда по теореме Пифагора получим:

По условию гипотенуза AB = 50. Следовательно, х = 10, BC = 30, AC = 40.

Далее можно действовать разными способами. Например, так.

где по определению косинуса:

cos A cos B

Ответ:

Задача 6. В прямоугольном треугольнике ABC высота CD делит гипотенузу на отрезки AD = 3 см и BD = 2 см. Найти катеты треугольника.

Решение:

Найдем квадрат длины высоты с помощью теоремы 3:

Из прямоугольного треугольника ADC по теореме Пифагора найдем

см.

Из прямоугольного треугольника BDC по теореме Пифагора найдем

см.

Ответ: см и см.

Задача 7. Точка D является основанием высоты, проведенной из вершины прямого угла C треугольника ABC к гипотенузе AB. Найдите AC, если AD=8, AB=32.

Указание:

Найдите отрезок BD = AB — AD, после чего задача сводится к предыдущей.

Длину высоты прямоугольного треугольника можно также найти, если известны гипотенуза и один из острых углов треугольника.

h = c sincos = c sincos

Докажем эту формулу.

Рассмотрим прямоугольный треугольник ACD:

В то же время из треугольника AВC:

Таким образом, h = CD = AC cos⁡ = AB sincos = c sincos⁡

Аналогично, из треугольника BCD получим: h = CD = BC cos = AB sin⁡ cos = c sin cos⁡

Задача 8. В прямоугольном треугольнике гипотенуза равна 10, а один из острых углов 15 градусов. Найти высоту, проведенную из вершины прямого угла.

Решение:

Воспользуемся доказанной выше формулой:

h = c sincos = 10 sin cos = 5sin = 2,5.

Ответ: 2,5.

Задача 9. Высота прямоугольного треугольника делит его гипотенузу на отрезки 6 см и 4 см. Найдите площадь этого треугольника.

Решение:

Гипотенуза прямоугольного треугольника равна сумме данных отрезков:

см.

Найдем высоту, проведенную из вершины прямого угла к гипотенузе: см.

Площадь треугольника:

см

Ответ: см

Если вам понравился наш материал — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Высота прямоугольного треугольника, проведенная к гипотенузе

Как и в любом треугольнике прямоугольный треугольник имеет три высоты. Две из них совпадают с катетами, а вот третья высота, проведенная к гипотенузе, постоянно будоражит наши умы.

Поэтому представляю вашему вниманию основные формулы для ее нахождения.

Начну с самой важной.

1. Высота, проведенная к гипотенузе равна корню квадратному из произведения проекций катетов на эту гипотенузу.

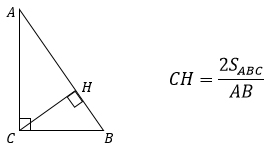
2. Высоту, проведенную к гипотенузе, можно найти, разделив удвоенную площадь прямоугольного треугольника на гипотенузу.

Такая формула получается из классический формулы нахождения площади треугольника: половина произведения основания на высоту, проведенную к этому основанию.

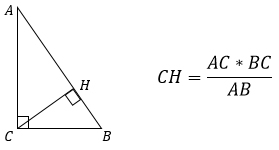
3. Высота, проведенная к гипотенузе, равна произведению катетов, деленному на гипотенузу.

Эта формула получится из второй если заменить площадь на половину произведения катетов.

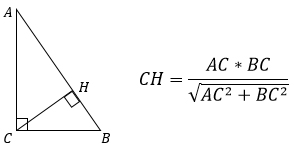
Т.к. АВ — гипотенуза, то ее можно выразить через катеты АС и ВС, используя теорему Пифагора. Тогда формула примет другой вид:

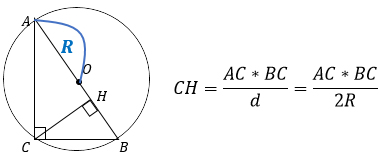
4. Высота, проведенная к гипотенузе, равна произведению катетов, деленному на диаметр описанной вокруг треугольника окружности (или на удвоенный радиус).

Так получается потому, что центр описанной окружности лежит в середине гипотенузы, значит, гипотенуза равна 2R или d.

5. Высоту, проведенную к гипотенузе, можно найти, используя геометрические определения синуса, тангенса и котангенса.

Надеюсь, что данная статья оказалась полезной!)

Готовься к экзамену вместе с нами! Заходи на нашу страницу в ВК.

Сумма квадратов катетов равна квадрату гипотенузы.

В буквах это так: 

• ( A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}})

или так: 

• ( {{c}^{2}}={{a}^{2}}+{{b}^{2}})

Помнишь шутку: «Пифагоровы штаны на все стороны равны!»?

Давай нарисуем эти самые пифагоровы штаны и посмотрим на них.

Правда, похоже на какие-то шорты? Ну и на какие стороны и где они равны? Почему и откуда возникла шутка? М-да… Кажется, у людей в античности с юмором явно проблемы.

Вовсе нет! А шутка эта связана как раз с теоремой Пифагора, точнее с тем, как сам Пифагор формулировал свою теорему. А формулировал он её так:

«Сумма площадей квадратов, построенных на катетах, равна площади квадрата, построенного на гипотенузе».

Правда, немножко по-другому звучит? И вот, когда Пифагор нарисовал утверждение своей теоремы, как раз и получилась такая картинка.

На этой картинке сумма площадей маленьких квадратов равна площади большого квадрата. А чтобы дети лучше запоминали, что сумма квадратов катетов равна квадрату гипотенузы, кто-то остроумный и выдумал эту шутку про Пифагоровы штаны.

Почему же мы сейчас формулируем теорему Пифагора так:

( {{c}^{2}}={{a}^{2}}+{{b}^{2}}),

а Пифагор мучился и рассуждал про площади?

Понимаешь, в древние времена не было… алгебры! Не было никаких обозначений ( displaystyle a,text{ }b,text{ }c,text{ }x) и так далее. Не было надписей ( displaystyle {{a}^{2}},text{ }{{b}^{2}},text{ }{{c}^{2}}).

Представляешь, как бедным древним ученикам было ужасно запоминать всё словами?! А мы можем радоваться, что у нас есть простая формулировка теоремы Пифагора

Давай её ещё раз повторим, чтобы лучше запомнить:

( A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}})

или

( {{c}^{2}}={{a}^{2}}+{{b}^{2}})

Теперь уже должно быть легко:

Квадрат гипотенузы равен сумме квадратов катетов.

Ну вот, самую главную теорему о прямоугольном треугольнике обсудили. Если тебе интересно, как она доказывается, то… сейчас мы ее докажем)

Нарисуем квадрат со стороной ( a+b).

Видишь, как хитро мы поделили его стороны на отрезки длин ( a) и ( b)!

А теперь соединим отмеченные точки:

Тут мы, правда, ещё кое что отметили, но ты сам посмотри на рисунок и подумай, почему так.

Чему же равна площадь большего квадрата?

Правильно, ( {{left( a+b right)}^{2}}).

А площадь меньшего?

Конечно, ( c^2).

Осталась суммарная площадь четырех уголков. Представь, что мы взяли их по два и прислонили друг к другу гипотенузами.

Что получилось? Два прямоугольника. Значит, площадь «обрезков» равна ( displaystyle 2ab).

Давай теперь соберем всё вместе.

( displaystyle underbrace{{{left( a+b right)}^{2}}}_{{{S}_{большого квадрата}}}=underbrace{2ab}_{{{S}_{«обрезков»}}}+underbrace{{{c}^{2}}}_{{{S}_{малого квадрата}} })

Преобразуем: ( {{a}^{2}}+2ab+{{b}^{2}}=2ab+{{c}^{2}})

то есть ( {{a}^{2}}+{{b}^{2}}={{c}^{2}})

Вот и побывали мы Пифагором – доказали его теорему древним способом

Можем обрадовать: для решения задач про прямоугольный треугольник можно просто заполнить следующие простые вещи:

• ( sin angle A=frac{a}{c});
• ( cos angle A=frac{b}{c});
• ( tg~angle A=frac{a}{b});
• ( ctg~angle A=frac{b}{a}).

А почему же всё только про угол ( A)? Где же угол ( B)?

Для того, чтобы в этом разобраться, нужно знать, как утверждения 1 — 4 записываются словами. 

Смотри, понимай и запоминай!

• ( displaystyle sin angle A=frac{a}{c})

Вообще-то звучит это так:

Синус острого угла в прямоугольном треугольнике равен отношению противоположного катета к гипотенузе.

А что же угол ( displaystyle B)?

Есть ли катет, который находится напротив угла ( displaystyle B), то есть противолежащий (для угла ( displaystyle B)) катет?

Конечно, есть! Это катет ( displaystyle b)!

• Значит, ( displaystyle sin angle B=frac{b}{c})

Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе. 

( displaystyle cos angle A=frac{b}{c})

Значит, ( displaystyle sin angle B=frac{b}{c})

А как же угол ( displaystyle B)?

Посмотри внимательно. Какой катет прилегает к углу ( displaystyle B)? Конечно же, катет ( displaystyle a).

Значит, для угла ( displaystyle B) катет ( displaystyle a) – прилежащий, и

• ( displaystyle cos angle B=frac{a}{c}).

А теперь, внимание! Посмотри, что у нас получилось:

Это очень удобно – если тебе дан в задаче синус одного угла прямоугольного треугольника, то ты знаешь и косинус другого!

Итак, запомни очень твёрдо:

В прямоугольном треугольнике синус одного острого угла равен косинусу другого и наоборот.

Теперь перейдём к тангенсу и котангенсу.

• ( displaystyle tg~angle A=frac{a}{b})

Как это теперь записать словами?

Катет ( displaystyle a) каким является по отношению к углу ( displaystyle A)? Противолежащим, конечно – он «лежит» напротив угла ( displaystyle A).

А катет ( displaystyle b)? Прилегает к углу ( displaystyle A).

Значит, что у нас получилось?

Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему.

• ( displaystyle ctg~angle A=frac{b}{a})

Видишь, числитель и знаменатель поменялись местами?

Котангенс острого угла в прямоугольном треугольнике равен отношению прилежащего катета к противолежащему.

Вспомним теперь про угол ( displaystyle angle B). Что будет для него? Правильно:

• ( displaystyle tg~angle B=frac{b}{a})( displaystyle ctg~angle B=frac{a}{b})

В прямоугольном треугольнике тангенс одного острого угла равен котангенсу другого.

Давай вкратце запишем всё, что мы узнали.

Признаки равенства прямоугольных треугольников:

I. По двум катетам

Прямоугольные треугольники равны, если два катета одного треугольника соответственно равны двум катетам другого треугольника.

II. По катету и гипотенузе

Прямоугольные треугольники равны, если катет и гипотенуза одного треугольника соответственно равны катету и гипотенузе другого.

III. По гипотенузе и острому углу

Прямоугольные треугольники равны, если гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого.

IV. По катету и острому углу

Прямоугольные треугольники равны, если катет и острый угол одного треугольника соответственно равны катету и острому углу другого треугольника.

Внимание! Здесь очень важно, чтобы катеты были «соответствующие». Например, если будет так:

То треугольники не равны, несмотря на то, что имеют по одному одинаковому острому углу.

Нужно, чтобы в обоих треугольниках катет был прилежащим, или в обоих – противолежащим.

Ты заметил, чем отличаются признаки равенства прямоугольных треугольников от обычных признаков равенства треугольников?

Загляни в тему «Треугольник» и обрати внимание на то, что для равенства «рядовых» треугольников нужно равенство трех их элементов: две стороны и угол между ними, два угла и сторона между ними или три стороны.

А вот для равенства прямоугольных треугольников достаточно всего двух соответственных элементов. Здорово, правда?

Примерно такая же ситуация и с признаками подобия прямоугольных треугольников.

Почему это так?

Рассмотрим вместо прямоугольного треугольника целый прямоугольник.

Что видим? 

Треугольник ( displaystyle ABC) – половина прямоугольника.

Проведём диагональ ( displaystyle CD) и рассмотрим точку ( displaystyle O) – точку пересечения диагоналей. Что известно про диагонали прямоугольника?

• Точкой пересечения диагонали делятся пополам
• Диагонали равны

И что из этого следует?

• Точкой пересечения диагонали делятся пополам

Запомни этот факт! Очень помогает!

А что ещё более удивительно, так это то, что верно и обратное утверждение.

Если медиана, проведенная к какой-нибудь стороне треугольника, оказалась равна половине этой стороны, то треугольник – прямоугольный.

Что же хорошего можно получить из того, что медиана, проведенная к гипотенузе, равна половине гипотенузы?

А давай посмотрим на картинку.

Здесь( displaystyle CO) – медиана и равна( frac{AB}{2}).

Что же это получилось за точка ( displaystyle O)?

Посмотри внимательно. У нас есть: ( OA=OB=OC), то есть расстояния от точки ( displaystyle O) до всех трёх вершин треугольника оказались равны. Но в треугольнике есть всего одна точка, расстояния от которой о всех трёх вершин треугольника равны, и это – ЦЕНТР ОПИСАННОЙ ОКРУЖНОСТИ. Значит, что получилось?

В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.

Посмотрим на ( Delta ABC) и ( Delta ACH).

У них общий ( angle A), и они оба – прямоугольные. Значит (вспоминаем только что прочитанные признаки подобия прямоугольных треугольников) – они подобны!

Еще раз. ( displaystyle begin{array}{l}Delta ABC, Delta ACH:\left{ begin{array}{l}angle CAB=angle CAH\angle C=90{}^circ ; angle H=90{}^circ end{array} right.Rightarrow \Rightarrow Delta ABCsim Delta ACHend{array})

Но у подобных треугольников все углы равны!

( angle HCA=angle CBA) (Посмотри на рисунок)

То же самое можно сказать и про ( Delta CBH) и ( Delta ABC)

А теперь нарисуем это вместе:

( displaystyle begin{array}{l}Delta ABC, Delta CBH:\left{ begin{array}{l}angle ABC=angle CBH\angle C=90{}^circ ; angle H=90{}^circ end{array} right.Rightarrow \Rightarrow Delta ABCsim Delta CBHRightarrow \Rightarrow angle BAC=angle BCHend{array})

Что видим?

У ( Delta BCH) и ( Delta CHA) одинаковые острые углы!( displaystyle Rightarrow Delta BCHsim Delta CHA)

Какую же пользу можно извлечь из этого «тройственного» подобия.

Ну, например – две формулы для высоты прямоугольного треугольника.

Чтобы писать меньше букв, обозначим:

( displaystyle AC=b); 
( displaystyle BC=a ); 
( displaystyle AB=c); 
( displaystyle CH=h) (посмотри на рисунке). 

Применяем подобие:( Delta ABCsim Delta ACH).

Запишем отношения соответствующих сторон:

Для нахождения высоты решаем пропорцию и получаем первую формулу «Высота в прямоугольном треугольнике»:

( displaystyle h=frac{ab}{c})

Как же получить вторую?

А теперь применим подобие треугольников ( BCH) и ( CAH).

Но сначала обозначим ( BH={{c}_{a}}) и ( CH={{c}_{b}}) ( смотри на рисунок)

Итак, применим подобие: ( displaystyle Delta BCHsim Delta CAH).

Значит,

Что теперь получится?

Опять решаем пропорцию и получаем вторую формулу «Высота в прямоугольном треугольнике»:

( displaystyle {{h}^{2}}={{c}_{a}}{{c}_{b}}) ,то есть ( displaystyle h=sqrt{{{c}_{a}}{{c}_{b}}})

Обе эти формулы нужно очень хорошо помнить и применять ту, которую удобнее.

Запишем их ещё раз:

( displaystyle h=frac{ab}{c})

( displaystyle h=sqrt{{{c}_{a}}{{c}_{b}}})

Ну вот, теперь, применяя и комбинируя эти знания с другими, ты решишь любую задачу с прямоугольным треугольником!

Так как катет, лежащий против угла  30°, равен половине гипотенузы, то

Так как катет, лежащий против угла  30°, равен половине гипотенузы, то

– медианы в прямоугольном треугольнике пересекаются в
одной точке, а точка пересечения делит их в соотношении два к одному считая от
вершины, из которой проведена медиана;

– медиана, проведённая из
вершины прямого угла к гипотенузе, равна половине гипотенузу;

– медиана, опущенная на гипотенузу прямоугольного треугольника, равна
радиусу окружности, описанной вокруг данного прямоугольного треугольника;

– сумма
квадратов медиан, опущенных на катеты прямоугольного треугольника равна пяти квадратам
медианы, опущенной на гипотенузу;

– сумма
квадратов медиан, опущенных на катеты прямоугольного треугольника равна пяти
четвёртых квадрата гипотенузы;

– медиана,
опущенная на гипотенузу, равна половине корня квадратного из суммы квадратов
катетов;

– медиана,
опущенная на гипотенузу, равна частному от деления длины катета на два синуса
противолежащего катету острого угла;

– медиана,
опущенная на гипотенузу, равна частному от деления длины катета на два косинуса
прилежащего катету острого угла;

– сумма квадратов сторон
прямоугольного треугольникаравна восьми квадратам медианы, опущенной на его
гипотенузу;

– медиана, проведённая к катету  а, равна
половине корня квадратного из суммы учетверённого квадрата катета  b  и квадрата катета  а;

– медиана, проведённая к катету  b, равна
половине корня квадратного из суммы учетверённого квадрата катета  а  и квадрата катета  b;

Обозначения в формулах.

a, b – катеты
прямоугольного треугольника;

с – гипотенуза
прямоугольного треугольника.

Если обозначить треугольник, как  АВС, то

ВС = а, АС = b, АВ = с

(то есть стороны  а,
b, с – являются
противолежащими соответствующим углам).

т_а –
медиана, проведённая к катету  а;

т_b – медиана,
проведённая к катету  b;

т_с –
медиана, проведённая к гипотенузе  с;

α (альфа) –
угол  САВ,
противолежащий стороне  а.

ЗАДАЧА:

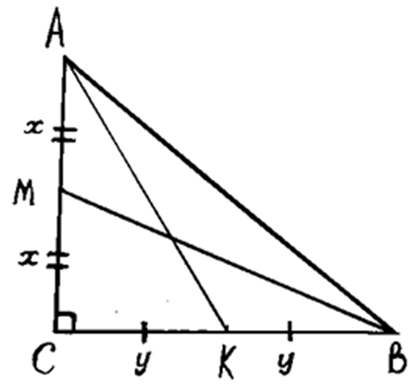
Две стороны треугольника равны  6 см  и  8 см. Медианы, проведённые к этим сторонам, пересекаются
под прямым углом. Найдите третью сторону треугольника.

РЕШЕНИЕ:

Начертим
чертёж.

Обозначим  

АN = х см. ВМ
= у см.

Тогда 

АО = ²/₃ х,
NО = ¹/₃ у,

ВО = ²/₃ х,
МО = ¹/₃ у.

АМ² = ОМ²
+ ОА²,

ВN² = ОВ² + ОN²,

5х² + 5у² = 225,

х² + у²
= 45.

АВ² = ВО²
+ ОА² =

= ⁴/₉ (х²
+ у²) = 20, то

АВ = √͞͞͞͞͞20 = 2√͞͞͞͞͞5 см.

ЗАДАЧА:

В треугольнике  АВС:

АВ = √͞͞͞͞͞41, ВС = 13, 

ВН – высота, опущенная на
сторону  АС, ВН = 5. 

Найдите
длину медианы АМ.

РЕШЕНИЕ:

Начертим чертёж.

В прямоугольном
треугольнике  ВНС  по
теореме Пифагора 

В прямоугольном
треугольнике  АВН  по
теореме Пифагора 

Опустим из точки  М  перпендикуляр  МD  на сторону АС, МD – средняя линия треугольника  ВНС, следовательно

МD = ¹/₂ ВН = ⁵/₂,

НD = DС = ¹/₂ НС = 6.

Тогда в прямоугольном треугольнике  АМD

∠ АDМ = 90°,

АD = АН + НD =

= 4 + 6 = 10,

МD = ⁵/₂.

По теореме Пифагора

ЗАДАЧА:

В прямоугольном треугольнике медианы, проведённые к
катетам равны  √͞͞͞͞͞52  и √͞͞͞͞͞73. Найдите длину
гипотенузы.

РЕШЕНИЕ:

Начертим чертёж.

Проведём медианы  АК
 и  ВМ. Пусть 

АК = √͞͞͞͞͞52,

ВМ = √͞͞͞͞͞73,

х – половина длины
стороны  АС,

у – половина длины
стороны  ВС. Тогда из
прямоугольных треугольников  АСК  и  ВСМ  имеем:

АК² = АС²
+ СК²,

ВМ² = МС²
+ ВС²

тогда  составим систему уравнений:

отсюда

5(х² + у²) = 125,

х² + у²
= 25,

АК² = 4(х²
+ у²).

АВ = 10.

ЗАДАЧА:

Медианы  СМ  и 
ВN  прямоугольного
треугольника  АВС (∠ С = 90°), перпендикулярны. Найдите катеты, если гипотенуза
равна  с.

РЕШЕНИЕ:

Начертим чертёж.

МА = МС = МВ = ^с/₂.

Пусть  NО = х,

Тогда 

ВО = ²/₃ х, МО = ^с/₆.

МВ² = МО² + ВО²,

Биссектриса прямоугольного треугольника.

Биссектрисою прямоугольного треугольника называют отрезок
биссектрисы угла треугольника, который соединяет его вершину с точкой на противоположной
стороне треугольника.

Биссектриса прямоугольного треугольника делит противоположную сторону на
отрезки, соответственно пропорциональные двум другим сторонам.

Связь угла  (α)  между
высотой и биссектрисой, проведёнными из прямого угла, определяется через острые
углы этого треугольника.

ЗАДАЧА:

Биссектриса прямого угла
прямоугольного треугольника образует с гипотенузой углы, один из которых
равен  70°. Найдите острые углы этого треугольника.

РЕШЕНИЕ:

Начертим чертёж.

∠ DBC = ∠ DBA = 45°,

∠ DCB = 180° – 70° – 45° = 65°,

∠ ADB = 180° – 70° = 110°,

∠ CAB = 180° – 110° – 45° = 25°.

ЗАДАЧА:

Биссектриса прямого угла
прямоугольного треугольника делит гипотенузу на отрезки длиной  15
см  и 
20
см. Найдите длины отрезков гипотенузы, на которые её делит высота треугольника.

РЕШЕНИЕ:

Биссектриса треугольника делит сторону на
отрезки, пропорциональные прилежащим сторонам.

Следовательно,

СВ
: АС = 15 : 20.

Пусть коэффициент этого
отношения будет  х. Тогда

АС = 20х, ВС
= 15х,

АВ = 20 + 15 = 35.

По теореме Пифагора:

АС² + ВС² = АВ^2,

400х²
+ 225х² = 1225.

х = √͞͞͞͞͞1,96 = 1,4,

АС = 20 ∙ 1,4 = 28,

ВС = 15 ∙ 1,4 = 21.

Катет прямоугольного треугольника есть среднее
пропорциональное между гипотенузой и отрезком гипотенузы, заключённым между
катетом и высотой.

ВС² = АВ ∙ ВН,

441 = 35 ∙ ВН,

ВН
=
12,6,

АН = 35 – 12,6 =
22,4.

ЗАДАЧА:

Угол между биссектрисой и
медианой прямоугольного треугольника, проведёнными из вершины прямого угла,
равен  14°.
Найдите меньший угол этого треугольника.

РЕШЕНИЕ:

Начертим чертёж.

Так как связь угла  (α)  между высотой и биссектрисой, проведёнными из
прямого угла, определяется через острые углы этого треугольника следующим
образом:

∠ ВАС
= 45° – α,

∠ ВСА
= 45° + α,

∠ α = ∠ МВD = 14°,

то меньший угол
треугольника  ВАС  будет равен:

∠ ВАС = 45° – 14° = 31°.

Задания к уроку 9