Как найти высоту в последнюю секунду падения

Решение: воспользуемся  уравнением пути для расчёта высоты h, с начальной скоростью равной нулю, за время падения t₁:

[ h=frac{gcdot t_{1}^{2}}{2}, ]

Тогда, за время падения без одной секунды, тело пройдёт путь, составляющий  3/4 всего пути (т.к. за последнюю секунду 1/4 всего пути по условию):

[ frac{3}{4}h=frac{gcdot {{left( {{t}_{1}}-1 right)}^{2}}}{2}, ]

[ frac{3}{4}frac{gcdot t_{1}^{2}}{2}=frac{gcdot {{left( {{t}_{1}}-1 right)}^{2}}}{2}, ]

[ frac{1}{4}t_{1}^{2}-2{{t}_{1}}+1=0, ]

Решая квадратное уравнение, получаем:
t₁ = 0,53 c – не подходит (должно быть больше одной секунды);
t₁ = 7,46 c  — это искомое время падения.
Тогда искомая высота:
h = 278 м

Скорость, время и высота свободного падения

Чтобы посчитать скорость свободного падения, а также время или расстояние (высоту) свободного падения, воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Скорость свободного падения

Расстояние и время свободного падения

Просто введите данные, и получите ответ.

Стоит обратить внимание, на то, что данный калькулятор не учитывает сопротивление воздуха (атмосферы) и других сил способных повлиять на скорость падения тела, кроме силы тяжести.

Теория

Ускорение свободного падения

Как найти скорость свободного падения

Время свободного падения

Высота свободного падения

См. также

Условие задачи:

В последнюю секунду свободного падения тело прошло путь вдвое больше, чем в предыдущую секунду. С какой высоты оно падало? (g=9,8 м/с²)

Задача №1.4.35 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(S_1=2S_2), (t_1=t_2=1) с, (g=9,8) м/с², (H-?)

Решение задачи:

Путь за последнюю секунду (S_1) – это разность пути за все время (t) и пути за (left( {t – {t_1}} right)) секунд. Аналогично, путь за предпоследнюю секунду (S_2) – это разность пути за (left( {t – {t_1}} right)) секунд и пути за (left( {t – {t_1}-{t_2}} right)) секунд. Аналитически это записывается так.

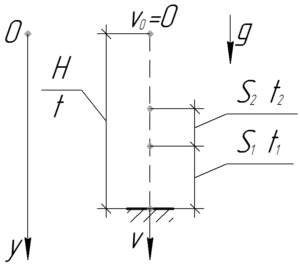
[{S_1} = frac{{g{t^2}}}{2} – frac{{g{{left( {t – {t_1}} right)}^2}}}{2}]

[{S_2} = frac{{g{{left( {t – {t_1}} right)}^2}}}{2} – frac{{g{{left( {t – {t_1} – {t_2}} right)}^2}}}{2}]

Так как по условию (S_1=2S_2), то справедливо:

[{t^2} – {left( {t – {t_1}} right)^2} = 2{left( {t – {t_1}} right)^2} – 2{left( {t – {t_1} – {t_2}} right)^2}]

Заменим (t_1) и (t_2) числами, тогда все сведется к следующему квадратному уравнению.

[{t^2} – 3{left( {t – 1} right)^2} + 2{left( {t – 2} right)^2} = 0]

Распишем два раза квадрат разности, в итоге получим:

[{t^2} – 3{t^2} + 6t – 3 + 2{t^2} – 8t + 8 = 0]

[ – 2t + 5 = 0]

[t = 2,5; с ]

Значит всего тело падало 2,5 с. Но это не ответ на вопрос задачи. Высоту, с которой бросили тело, можно найти по формуле:

[H = frac{{g{t^2}}}{2}]

[H = frac{{9,8 cdot {{2,5}^2}}}{2} = 30,6; м ]

Ответ: 30,6 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.4.34 С вертолета, находящегося на высоте 300 м, сброшен груз. Через какое время
1.4.36 Вертолет поднимается вертикально вверх со скоростью 10 м/с. На высоте 100 м
1.4.37 Вертолет двигался равномерно вниз. Из вертолета выпал груз. Когда

2016-11-18   

В последнюю секунду свободного падения с нулевой начальной скоростью тело прошло путь вдвое больший, чем в предыдущую секунду. С какой высоты упало тело?

Решение:

Обозначим через 0 ту точку, из которой тело начало движение. Начало системы координат помещаем в точку О. Так как тело движется вниз, ось у целесообразно направить также вниз (в этом случае значения координат тела по оси у будут положительными). Движение одномерное вдоль оси у, и оси х на рисунке нет (в любой момент времени координата тела по оси х равна нулю).

Отмечаем на рисунке положение тела в те моменты времени, о которых в задаче идет речь. Таких моментов времени четыре:

1) начальный момент времени $t = 0$ — ему соответствует точка 0;

2) начало предыдущей секунды $t_{1}$ ($t_{1}$ — время, которое показывает секундомер, включенный в момент $t = 0$, в тот момент, когда началась предыдущая секунда);

3) конец предыдущей — начало последней секунды $t_{2}$;

4) конец последней секунды (касание тела с поверхностью земли) $t_{3}$.

Запишем основное уравнение теории:

$y = y_{0} + v_{0y}t + frac{a_{y}t^{2}}{2}$,

применительно к условиям настоящей задачи. При этом учтем, что $y_{0} = 0$ в силу выбора начала системы отсчета; $v_{0y} = 0$ по условию задачи ($v_{0} = 0$); $a_{y} = g$, поскольку ось у направлена вниз. Таким образом, получаем:

$y = frac{gt^{2}}{2}$. (1)

Уравнение (1) записываем для всех тех моментов времени, о которых идет речь в условии задачи:

$y_{1} = frac{gt_{1}^{2}}{2}$, (2)

$y_{2} = frac{gt_{2}^{2}}{2}$, (3)

$y_{3} = frac{gt_{3}^{2}}{2}$, (4)

где через $y_{1}, y_{2}, y_{3}$ обозначены соответствующие данным моментам времени координаты.

Следующий шаг: информацию, содержащуюся в условии задачи в виде текста, следует записать с помощью математических соотношений.

В условии сказано, что пути, пройденные телом в последнюю и предыдущую секунды отличаются в два раза. Из рисунка видно, что путь за предыдущую секунду равен $y_{2} — y_{1}$, а за последнюю — $y_{3} — y_{2}$.

Следовательно:

$y_{3} — y_{2} = 2(y_{2}-y_{1})$ (5)

Кроме того, согласно тексту условия задачи:

$t_{2}-t_{1} = Delta t$ (6)

$t_{3} — t_{2} = Delta t$, (7)

где $Delta t = 1 с$.

На этом заканчивается «физический» этап решения. Переходим к «математическому» этапу. В задаче требуется найти высоту, с которой упало тело. Обращаясь к чертежу, видим, что эта высота есть уз — величина, которая непосредственно входит в систему уравнений.

Анализируем ситуацию: имеем систему из 6 уравнений (2—7) с 6-ю неизвестными $y_{1}, y_{2}, y_{3}, t_{1}, t_{2}, t_{3}$, из которой, следовательно, можно вычислить $y_{3}$.

Подставим $y_{1}, y_{2}$, и $y_{3}$ из (2, 3, 4) в (5) и воспользуемся разложением разности квадратов двух чисел:

$frac{g}{2}(t_{3}+t_{2})(t_{3}-t_{2}) = frac{g}{2} 2 (t_{2}+t_{1})(t_{2}-t_{1})$. (8)

С учетом (6) и (7), из (8) находим

$t_{3} + t_{2} = 2 (t_{1} + t_{2})$ или $t_{3} — t_{2} = 2t_{1}$.

С учетом (7), отсюда получаем:

$t_{1} = frac{ Delta t}{2}$,

$t_{2} = t_{1} + Delta t = frac{3}{2} Delta t$,

$t_{3} = t_{2} + Delta t = frac{5}{2} Delta t$.

Наконец, окончательно находим:

$y_{3} = frac{g left ( frac{5}{2} Delta t right )^{2}}{2} = frac{10 left ( frac{5}{2} right )^{2}}{2} = 31,25 м$.

Теория
и практика

электроники

Решение:

Выберем начало
отсчёта в той точке, откуда тело начало
падать,
а направление оси Х — вертикально вниз.
Тогда уравнение, описывающее движение
тела в выбранной системе координат,
будет иметь вид:

х=g*t²/2,
где g — ускорение свободного падения (в
нашем уравнении оно со знаком плюс, т.к.
направлено вертикально вниз и
направление оси Х мы также выбрали
вертикально вниз.

Пусть тело падало T
секунд. Найдём координаты тела через T-1
секунду и через T секунд после начала
падения. Разность этих координат x(T)-x(T-1)
и есть путь, который тело прошло за
последнюю секунду, т.е. x(T)-x(T-1)=75. У нас
получилось уравнение:

g*T²/2-g*(T-1)²/2=75

Единственное
неизвестное в этом уравнении — это T (время
падения тела). Найдём его:

10T²-10T²+20T-10=150

20T=160

T=8 секунд

Теперь, подставив
общее время падения (T), в уравнение
движения, легко найти — с какой высоты
упало тело (какой путь оно проделало за
время падения — с такой высоты и упало):

h=g*T²/2=10*64/2=320
метров