Как найти высоту треугольника на клетчатой бумаге - Avtoru.top

Вася Иванов

Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.

Источник

Тема 1.

Геометрия на плоскости (планиметрия)

Задачи на клетчатой бумаге

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

геометрия на плоскости (планиметрия)

Решаем задачи

На клетчатой бумаге с размером клетки 1× 1 изображен равносторонний треугольник. Найдите радиус описанной около него
окружности.

Показать ответ и решение

Отметим точки

ABCOE

причем BE = 9. Центр описанной окружности лежит на пересечении серединных перпендикуляров, в равностороннем
треугольнике серединные перпендикуляры — это и высоты, и медианы, и биссектрисы.

То есть центр описанной окружности лежит на высоте BE, которая также является и медианой. Пусть — центр этой
окружности (а значит, и точка пересечения медиан треугольника). Так как медианы треугольника точкой пересечения делятся в
отношении 2:1, считая от вершины, то откуда

OB = 2BE = 6
3

Заметим, что по определению радиус описанной около треугольника окружности — это отрезок, соединяющий центр окружности
с вершиной треугольника, то есть OB. Таким образом, радиус равен 6.

На клетчатой бумаге с размером клетки 1× 1 изображен равнобедренный прямоугольный треугольник. Найдите длину его
биссектрисы, выходящей из вершины прямого угла.

Показать ответ и решение

Так как треугольник равнобедренный, то биссектриса, проведенная к гипотенузе-основанию, является также медианой. По
свойству медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы. У
данного прямоугольного треугольника гипотенуза равна 5. Следовательно, медиана (она же биссектриса) равна
2,5.

На клетчатой бумаге с размером клетки 1 × 1 изображен треугольник ABC. Найдите длину средней линии, параллельной стороне
AB.

ABC

На клетчатой бумаге с клетками размером нарисована трапеция. Найдите её площадь. Ответ дайте в квадратных
миллиметрах.

Показать ответ и решение

Площадь трапеции равна произведению полусуммы оснований на высоту. Площадь нарисованной трапеции есть

2
0,5⋅(3 мм + 4 мм)⋅3 мм =10,5 мм

На клетчатой бумаге с размером клетки 1× 1 изображен угол. Найдите тангенс этого угла.

OAB

Показать ответ и решение

Проведем перпендикуляр к стороне OA. Получим прямоугольный треугольник OBH. Из него

OABH

На клетчатой бумаге с размером клетки 1× 1 изображен треугольник ABC. Найдите длину его биссектрисы, проведенной из
вершины

ACB

Показать ответ и решение

Из рисунка видно, что треугольник равнобедренный ( BA = BC ). Следовательно, биссектриса, опущенная из вершины будет
также являться медианой и высотой. Тогда биссектриса равна 3:

ACBH

На клетчатой бумаге с размером клетки 1× 1 изображен ромб. Найдите его площадь.

Показать ответ и решение

Проведем диагонали данного ромба:

Площадь ромба равна полупроизведению диагоналей, следовательно,

S = 1⋅4 ⋅6= 12
2

Показать ответ и решение

Проведем прямую и перпендикуляр AH :

CBAH

Из рисунка видно, что AH = 4.

Найдите угол ABC. Ответ дайте в градусах.

ACB

На клетчатой бумаге изображен треугольник ABC. Найдите его высоту, опущенную из вершины если длина стороны
равна 7.

Вершины треугольника лежат в узлах решетки.

BCA

На клетчатой бумаге с размером клетки 1 × 1 изображен треугольник ABC. Найдите площадь треугольника где —
средняя линия, параллельная стороне AB.

ACB

Показать ответ и решение

Пусть

По свойству средней линии с коэффициентом подобия, равным 2. Следовательно, их площади относятся как
коэффициент подобия в квадрате, то есть

SABC
SA′B′C-= 4

Высота треугольника ABC, опущенная из равна 2, AB = 7. Следовательно,

SABC = 1 ⋅2 ⋅7= 7
2

Тогда

7
SA′B′C = 4 = 1,75.

На клетчатой бумаге изображен треугольник. Найдите радиус вписанной в него окружности, если сторона одной клетки равна 3.

Показать ответ и решение

Будем искать радиус вписанной окружности по формуле где — площадь, — полупериметр.

Заметим, что треугольник равнобедренный:

ACBH

Так как длина стороны клетки равна 3, то BH = 9, следовательно,

∘----------
AB = AH2 +BH2 =15

Тогда

Заметим, что в задачах подобного типа можно вычислять все длины, как будто длина стороны клетки равна 1, а затем
умножать полученный ответ на 3. Если бы длина одной клетки была равна 1, то AH = 4, BH = 3, AB = 5 и r = 43.
Тогда после умножения на 3 также получили бы r =4. При решении задачи таким способом вычисления будут
легче.

На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь
закрашенного сектора.

Показать ответ и решение

Заметим, что закрашенная фигура состоит из двух непересекающихся частей,
равных и от круга:

Таким образом, ее площадь равна

1 1 (1 ) 3 3
4S + 2 ⋅ 4 S = 8S = 8 ⋅2,8= 1,05.

Найдите разность площади фигуры 1 и площади фигуры 2.

SS12

Показать ответ и решение

Площадь фигуры 1 можно посчитать следующим образом:

Площадь фигуры 2 — следующим образом:

Тогда

Размер клетки Найдите площадь фигуры с вырезанным кругом, выраженную в квадратных сантиметрах.

Показать ответ и решение

ABCDO

Искомая фигура состоит из квадрата ABCD без вырезанного круга с центром и двух половин круга такого же радиуса,
следовательно, площадь искомой фигуры равна площади квадрата ABCD :

На рисунке изображен треугольник. Найдите угол

На клетчатой бумаге с клетками размером 1 мм 1 мм нарисован невыпуклый
шестиугольник ABCDEF. Найдите его площадь. Ответ дайте в квадратных
миллиметрах.

AFEDCB

Показать ответ и решение

Дорисуем несколько отрезков как показано на рисунке ниже:

AFEDCBH

Площадь треугольника равна половине произведения основания на высоту к этому основанию. Площадь треугольника ABF
равна

Площадь треугольника CBH равна

Площадь трапеции FHDE равна

Тогда

2
SABCDEF = S△ABF + S△CBH + SFHDE = 7,5 мм

На клетчатой бумаге с клетками размером 1 мм 1 мм нарисован четырёхугольник. Найдите его площадь. Ответ дайте в
квадратных миллиметрах.

Показать ответ и решение

У данного четырёхугольника две стороны параллельны, а две другие не параллельны, следовательно, это трапеция. Площадь
трапеции равна произведению полусуммы оснований на высоту. Площадь нарисованной трапеции равна

2
0,5(2 мм + 3 мм )⋅4 мм = 10 мм

Найдите радиус окружности, вписанной в треугольник ABC, считая стороны квадратных клеток равными 1.

ACB

Показать ответ и решение

Так как радиус окружности, вписанной в прямоугольный треугольник, ищется по формуле где a, b — катеты,
— гипотенуза, то

√ -2---2
r = 3-+4-−-3-+-4-= 1
2

На клетчатой бумаге с размером клетки 1× 1 изображен угол. Найдите синус
этого угла.

Показать ответ и решение

Продлим одну из сторон тупого угла на отрезок так, чтобы

ABC

Заметим, что все вершины треугольника ABC находятся в узлах решетки,
причем AC = 3, BC = 4. Тогда

∘ -2---2
AB = 3 + 4 = 5

Так как синус острого угла (в прямоугольном треугольнике) — это отношение
противолежащего катета к гипотенузе, то

BC 4
sin ∠BAC = AB-= 5 = 0,8

Угол BAC с тупым углом — смежные, следовательно, их синусы равны,
значит, синус тупого угла равен также 0,8.

Источник

Рубрика Задание 3, Решаем ЕГЭ по математике Комментарии (0)

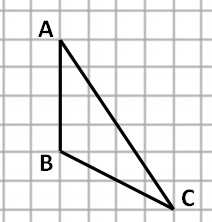
Задание. На клетчатой бумаге с размером клетки 1 × 1 изображен треугольник Δ АВС. Найдите длину его высоты, проведенной к прямой, содержащей сторону АВ.

Решение:

Продолжим сторону АВ, опустим из точки С перпендикуляр АН к продолжению стороны АВ.

АН – высота треугольника ΔАВС, проведенная к прямой содержащей сторону АВ.

По клеточкам легко найти, что АН = 4.

Ответ: 4

Понравилось? Нажмите

Источник

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: $frac{AD+BC}{2}=frac{4+2}{2}=3.$

Ответ: 3.

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла alpha равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна ${90}^{circ}.$ Тогда $angle alpha =frac{{90}^{circ}}{2}={45}^{circ}.$

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на $frac{sqrt{5}}{2}.$

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

${sin alpha }={sin angle AOB}=frac{4}{2sqrt{5}}=frac{2}{sqrt{5}}.$ Осталось умножить найденное значение синуса на $frac{sqrt{5}}{2}.$

$frac{2}{sqrt{5}}cdot frac{sqrt{5}}{2}=1$

Ответ: 1.

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где d_1 и d_2 — диагонали.

Получим:

Ответ: 12.

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Ответ: 18.

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: 12,5 .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: 10,5 .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна $frac{1}{2}cdot 3cdot 2=3.$

Площадь каждого из маленьких треугольников равна $frac{1}{2}cdot 1cdot 2=1.$

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как R=1 . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R=1 ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Ответ: .

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще $frac{1}{8}$ круга, то есть $frac{3}{8}$ круга.

Значит, нам надо умножить площадь круга на $frac{3}{8}$ . Получим:

$frac{3}{8}cdot 2,8 =1,05$

Ответ: 1,05.

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна pi R^2 , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в ${frac{4}{3}}^2 = frac{16}{9}$ раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Ответ: 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

Ответ: 20

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Ответ: 16.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Площадь треугольника, изображённого на клетчатой бумаге

Рассмотрим задачи,в которых требуется найти площадь треугольника изображённого на клетчатой бумаге.

Начнем с прямоугольных треугольников.

На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник.

Найти его площадь.

Площадь прямоугольного треугольника будем искать с помощью формулы

где a и b — катеты.

Длину катетов считаем по клеточкам.

1) a=2, b=5,

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найти его площадь.

Чаще всего площадь произвольного треугольника, изображённого на клетчатой бумаге, ищут по формуле

где a — сторона треугольника, h_a — высота, проведённая к этой стороне.

a и h_a вычисляем по клеточкам (одна из этих величин должна лежать на горизонтальной линии, другая — на вертикальной).

А как найти площадь, если ни одна из сторон треугольника не лежит на горизонтальной или вертикальной линии клеток?

Иногда площадь треугольника можно найти как разность площадей других фигур.

На клетчатой бумаге с размером клетки 1×1 изображён треугольник.

Найдите его площадь.

Обозначим вершины треугольника, площадь которого мы ищем, через A, B и C.

Площадь треугольника ABC можно найти как разность площадей прямоугольника AMNK и треугольников AKC, AMB и CBN:

Площади прямоугольных треугольников найдём по формуле

Как считать треугольник по клеткам

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Площадь треугольника равна разности площади большого квадрата, маленького квадрата и трех прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому

см 2 .

Приведём другое решение:

Воспользуемся формулой для нахождения площади треугольника

Одна из сторон данного треугольника является диагональю квадрата со стороной 6, а высота, проведённая к этой стороне, является диагональю квадрата со стороной 2. Тогда

Геометрия. Применение формул. Задача 5 Базового ЕГЭ по математике

Больше полезных формул — в нашем ЕГЭ-Справочнике.

В этой статье — основные типы заданий №5 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований:

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

Осталось умножить найденное значение синуса на

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где и — диагонали.

Получим:

Площадь трапеции равна произведению полусуммы оснований на высоту:

Нахождение площадей многоугольников сложной формы

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Площадь каждого из больших треугольников равна

Площадь каждого из маленьких треугольников равна

Тогда площадь четырехугольника

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Площадь круга, длина окружности, площадь части круга

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.

Значит, нам надо умножить площадь круга на . Получим:

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

14. Найдите площадь четырехугольника, вершины которого имеют координаты

источники:

http://ege.sdamgia.ru/search?search=%D0%BD%D0%B0%D0%B9%D0%B4%D0%B8%D1%82%D0%B5%20%D0%BF%D0%BB%D0%BE%D1%89%D0%B0%D0%B4%D1%8C%20%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B0%20%D0%BD%D0%B0%20%D0%BA%D0%BB%D0%B5%D1%82%D1%87%D0%B0%D1%82%D0%BE%D0%B9

http://ege-study.ru/ru/ege/materialy/matematika/zadanie-3-zadachi-na-kletchatoj-bumage-ili-koordinatnoj-ploskosti/

Источник

Площадь треугольника, изображённого на клетчатой бумаге

Как считать треугольник по клеткам

Геометрия. Применение формул. Задача 5 Базового ЕГЭ по математике

Не пропустите также: