Как найти высоту цилиндра вписанного в параллелепипед - Avtoru.top

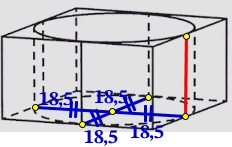
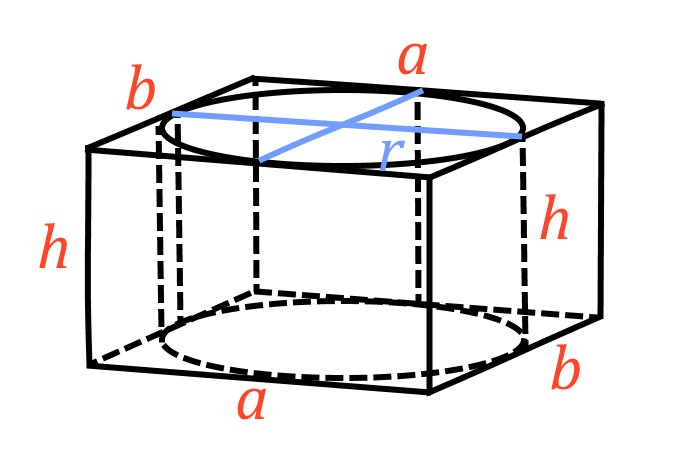
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 18,5. Объём параллелепипеда равен 5476. Найдите высоту цилиндра.

Источник: Ященко ЕГЭ 2023 (36 вар)

Решение:

Найдём длину и ширину параллелепипеда они равны двум радиусам:

а = r + r = 18,5 + 18,5 = 37
b = r + r = 18,5 + 18,5 = 37

Зная объём параллелепипеда из формулы объёма найдём его высоту:

V_{параллелепипеда} = a·b·h = 5476
37·37·h = 5476
1369·h = 5476
h = 5476/1369 = 4

Ответ: 4.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.6 / 5. Количество оценок: 28

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Прямоугольный параллелепипед описан около…

Задание:

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

Решение:

* Объем параллелепипеда V равен 16 — по условию. Радиус основания цилиндра r = 4.

* Выразим высоту из формулы объема параллелепипеда:
V = S_осн * h, где Sосн — площадь основания параллелепипеда, h — высота.
Высота цилиндра вписанного цилиндра равна высоте параллелепипеда.

* Так как r = 4, то сторона параллелепипеда a = 2r = 2 * 4 = 8

* В основании параллелепипеда квадрат, а значит площадь квадрата S_осн = 8 * 8 = 64 (ед)²

* V = S_осн * h
16 = 64 * h
h = 16/64
h = 1/4
h = 0.25

Ответ: 0.25

Источник

На чтение 1 мин. Просмотров 743

Интересная задача из типовых экзаменационных вариантов ЕГЭ по математике профильного уровня, на знание свойств сторон четырехугольника, в который можно вписать круг. А также вам потребуется знать формулу объема параллелепипеда.

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 18,5. Объем параллелепипеда равен 5476. Найдите высоту цилиндра.

Решение: Так как цилиндр вписан в параллелепипед, то и основание цилиндра (круг) вписано в основание параллелепипеда (прямоугольник).

Поскольку вписать в четырехугольник окружность можно тогда и только тогда, когда суммы противоположных сторон четырехугольника равны, то перед нами не прямоугольник, а квадрат.

Действительно, или , откуда мы получаем, что .

Объем параллелепипеда, в основании которого лежит квадрат, определяется по формуле:

, где — высота параллелепипеда и высота цилиндра (цилиндр вписан в параллелепипед), — сторона основания.

Поскольку круг вписан в квадрат, значит, радиус круга будет равен $r=frac{a}{2}$ , отсюда

Тогда формула объема параллелепипеда будет иметь вид:

откуда высота цилиндра $displaystyle h= frac{V}{(2r)^2}$

Подставляем данные:

$displaystyle h=frac{5476}{37^2}$ ,

$displaystyle h=frac{5476}{1369}=4$

Ответ:4

( 1 оценка, среднее 5 из 5 )

Источник

Прямоугольный параллелепипед описан около

Дорогие друзья! В этой публикации мы рассмотрим ещё несколько заданий с комбинацией двух тел – призмы и цилиндра, одно из них вписано в другое. Ставится вопрос о вычислении объёма одного из указанных тел. Конечно же, необходимо знать соответствующие формулы, понимать, что высоты таких тел равны (они общие).

Кроме этого, в одном из типов представленных задач используется свойство прямоугольного треугольника вписанного в окружность, его мы подробно (с доказательством) рассмотрели здесь. Рассмотрим задачи:

zadacha

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Радиус основания цилиндра равен 1. Это означает, что оба рёбра параллелепипеда в его основании равны 2. Высота общая. Таким образом, искомый объём:

Ответ: 4

zadacha

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 8. Объем параллелепипеда равен 128. Найдите высоту цилиндра.

Так как высота цилиндра и параллелепипеда общая, то вычислив высоту параллелепипеда мы естественно найдём высоту цилиндра.

Основанием параллелепипеда является квадрат, сторона которого равна диаметру цилиндра, то есть двум его радиусам. Поэтому сторона основания будет равна 16.

Объём параллелепипеда равен произведению трёх его рёбер, третье ребро это высота:

Ответ: 0,5

zadacha

В основании прямой призмы лежит прямоугольный треугольник с катетами 12 и 16. Боковые ребра равны 3/Пи. Найдите объем цилиндра, описанного около этой призмы.

Объём цилиндра равен:

Известно, что гипотенуза прямоугольного треугольника вписанного в окружность является диаметром этой окружности. По теореме Пифагора длина гипотенузы прямоугольного треугольника будет равна:

Значит радиус цилиндра будет равен 10, вычислим его объём:

Ответ: 300

zadacha

В основании прямой призмы лежит квадрат со стороной 6. Боковые ребра равны 4/Пи. Найдите объем цилиндра, описанного около этой призмы.

Для нахождения объёма цилиндра необходимо найти площадь его основания (или радиус основания):

Основание цилиндра это круг, диаметр которого совпадает с диагональю квадрата. Диагональ квадрата в основании призмы можем найти по теореме Пифагора:

Получили, что радиус круга (цилиндра) равен 6√2.

Таким образом, вычислим искомый объем:

Ответ: 288

27042. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

Посмотреть решение

27049.В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны 5/Пи. Найдите объем цилиндра, описанного около этой призмы.

Посмотреть решение

27050. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны 2/Пи. Найдите объем цилиндра, описанного около этой призмы.

Посмотреть решение

Нf этом всё. Успеха Вам!

C уважением, Александр.

*Делитесь информацией в социальных сетях.

Категория: Стереометрия ПРИЗМЫ | ЕГЭ-№2Объём

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

Источник

Задания

Версия для печати и копирования в MS Word

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 1. Объем параллелепипеда равен 5. Найдите высоту цилиндра.

Решение.

Это задание ещё не решено, приводим решение прототипа.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому сторона основания равна 8, а площадь основания равна 64. Тогда высота цилиндра равна

Ответ: 0,25.

Источник

Прямоугольный параллелепипед описан около…

Прямоугольный параллелепипед описан около

Не пропустите также: