Как найти вычислитель матрицы

Содержание:

  • Вычисления определителей второго порядка
  • Методы вычисления определителей третьего порядка
  • Приведение определителя к треугольному виду
  • Правило треугольника
  • Правило Саррюса
  • Разложение определителя по строке или столбцу
  • Разложение определителя по элементам строки или столбца
  • Теорема Лапласа

В общем случае правило вычисления определителей
$n$-го порядка
является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.

Вычисления определителей второго порядка

Чтобы вычислить определитель матрицы второго порядка, надо от произведения
элементов главной диагонали отнять произведение
элементов побочной диагонали:

$$left| begin{array}{ll}{a_{11}} & {a_{12}} \ {a_{21}} & {a_{22}}end{array}right|=a_{11} cdot a_{22}-a_{12} cdot a_{21}$$

Пример

Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$

Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$

Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$

Методы вычисления определителей третьего порядка

Для вычисления определителей третьего порядка существует такие правила.

Правило треугольника

Схематически это правило можно изобразить следующим образом:

Определитель матрицы по правилу треугольника

Произведение элементов в первом определителе, которые соединены прямыми,
берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.

$$left| begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$

$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.

Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$

$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$

Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$

Правило Саррюса

Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей
параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных,
со знаком «минус»:

$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$

Пример

Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ с помощью правила Саррюса.

Решение.

$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$

Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$

Разложение определителя по строке или столбцу

Определитель равен сумме произведений элементов строки определителя на их
алгебраические дополнения. Обычно выбирают
ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.

Пример

Задание. Разложив по первой строке, вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$

Решение. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right| leftarrow=a_{11} cdot A_{11}+a_{12} cdot A_{12}+a_{13} cdot A_{13}=$

$1 cdot(-1)^{1+1} cdot left| begin{array}{cc}{5} & {6} \ {8} & {9}end{array}right|+2 cdot(-1)^{1+2} cdot left| begin{array}{cc}{4} & {6} \ {7} & {9}end{array}right|+3 cdot(-1)^{1+3} cdot left| begin{array}{cc}{4} & {5} \ {7} & {8}end{array}right|=-3+12-9=0$

Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$

Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.

Пример

Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$

Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.

$$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$$

$$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$$

Определитель равен нулю, так как вторая и третья строки являются пропорциональными.

Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$

Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа.

Разложение определителя по элементам строки или столбца

Пример

Задание. Вычислить определитель
$left| begin{array}{llll}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|$ , разложив его по элементам какой-то строки или какого-то столбца.

Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй — пять третьих и от четвертой — три третьих строки, получаем:

$$left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=left| begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \ {5-5} & {4-0} & {3-5} & {2-10} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|$$

Полученный определитель разложим по элементам первого столбца:

$$left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=0+0+1 cdot(-1)^{3+1} cdot left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|+0$$

Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей — вторую:

$$left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|=left| begin{array}{rrr}{0} & {2} & {4} \ {4} & {-2} & {-8} \ {0} & {4} & {8}end{array}right|=4 cdot(-1)^{2+2} cdot left| begin{array}{ll}{2} & {4} \ {4} & {8}end{array}right|=$$

$$=4 cdot(2 cdot 8-4 cdot 4)=0$$

Ответ. $left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=0$

Замечание

Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.

Приведение определителя к треугольному виду

С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали.

Пример

Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.

Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:

$$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$$

Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:

$$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$$

Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):

$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$$

Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:

$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$$

Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:

$$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$$

$$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$$

Ответ. $Delta=-80$

Теорема Лапласа

Теорема

Пусть $Delta$ — определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю.

Пример

Задание. Используя теорему Лапласа, вычислить определитель
$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|$

Решение. Выберем в данном определителе пятого порядка две строки —
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):

$$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=left| begin{array}{cc}{1} & {-1} \ {4} & {-5}end{array}right| cdot(-1)^{2+4+2+4} cdot left| begin{array}{ccc}{2} & {0} & {5} \ {3} & {1} & {1} \ {1} & {2} & {1}end{array}right|+$$

$$+left| begin{array}{ll}{1} & {2} \ {4} & {0}end{array}right| cdot(-1)^{2+4+2+5} cdot left| begin{array}{rrr}{2} & {0} & {4} \ {3} & {1} & {0} \ {1} & {2} & {-2}end{array}right|+left| begin{array}{cc}{-1} & {2} \ {-5} & {0}end{array}right| cdot(-1)^{2+4+5} cdot left| begin{array}{ccc}{2} & {3} & {0} \ {3} & {2} & {1} \ {1} & {1} & {2}end{array}right|=$$

$$=-23+128+90=195$$

Ответ. $left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=195$

Читать дальше: обратная матрица.

Источник

Найти определитель матрицы

Этот калькулятор поможет Вам вычислить определитель, разложив его по строке или столбцу, либо предварительно получив нули в строке или столбце. Детерминант будет вычислен с выводом промежуточных результатов.

  • Оставляйте лишние ячейки пустыми для ввода неквадратных матриц.

  • Элементы матриц — десятичные (конечные и периодические) дроби: 1/3, 3,14, -1,3(56) или 1,2e-4; либо арифметические выражения: 2/3+3*(10-4), (1+x)/y^2, 2^0,5 (=2), 2^(1/3), 2^n, sin(phi), cos(3,142rad), a_1 или (root of x^5-x-1 near 1,2).

    • decimal (finite and periodic) fractions:

      1/3, 3,14, -1,3(56) или 1,2e-4

    • 2/3+3*(10-4), (1+x)/y^2, 2^0,5 (=2), 2^(1/3), 2^n, sin(phi), cos(3,142rad), a_1 или (root of x^5-x-1 near 1,2)

    • matrix literals:

      {{1,3},{4,5}}

    • operators:

      +, -, *, /, , !, ^, ^{*}, ,, ;, ≠, =, ⩾, ⩽, > и <

    • functions:

      sqrt, cbrt, exp, log, abs, conjugate, min, max, gcd, rank, adjugate, inverse, determinant, transpose, pseudoinverse, cos, sin, tan, cot, cosh, sinh, tanh, coth, arccos, arcsin, arctan, arccot, arcosh, arsinh, artanh и arcoth

    • units:

      rad, deg

    • special symbols:

      • pi, e, i — mathematical constants
      • k, n — integers
      • I or E — identity matrix
      • X, Y — matrix symbols
  • Используйте ↵ Ввод, Пробел, ←↑↓→, Backspace и Delete для перемещения по ячейкам, Ctrl⌘ Cmd+C/Ctrl⌘ Cmd+V — для копирования матриц.
  • Перетаскивайте матрицы из результата (drag-and-drop), или даже из текстового редактора.
  • За теорией о матрицах и операциях над ними обращайтесь к страничке на Википедии.

Источник

Определитель матрицы.

Навигация по странице:

  • Определение определителя матрицы
  • Свойства определителя матрицы
  • Методы вычисления определителя матрицы
    • Определитель матрицы 1×1
    • Определитель матрицы 2×2
    • Определитель матрицы 3×3
      • Правило треугольника для вычисления определителя матрицы 3-тего порядка
      • Правило Саррюса для вычисления определителя матрицы 3-тего порядка
    • Определитель матрицы произвольного размера
      • Разложение определителя по строке или столбцу
      • Приведение определителя к треугольному виду
      • Теорема Лапласа

Определитель матрицы или детерминант матрицы — это одна из основных численных характеристик квадратной матрицы, применяемая при решении многих задач.

Определение.

Определителем матрицы n×n будет число:

det(A) =  Σ (-1)N(α1,α2,…,αn)·aα11·aα22·…·aαnn
(α1,α2,…,αn)

где (α1,α2,…,αn) — перестановка чисел от 1 до n, N(α1,α2,…,αn) — число инверсий в перестановке, суммирование идёт по всем возможным перестановкам порядка n.

Обозначение

Определитель матрици A обычно обозначается det(A), |A|, или ∆(A).

Свойства определителя матрицы

  2. Определитель матрицы с двумя равными строками (столбцами) равен нулю.

  3. Определитель матрицы с двумя пропорциональными строками (столбцами) равен нулю.

  4. Определитель матрицы, содержащий нулевую строку (столбец), равен нулю.

  5. Определитель матрицы равен нулю если две (или несколько) строк (столбцев) матрицы линейно зависимы.

  6. При транспонировании значение определителя матрицы не меняется:

    det(A) = det(AT)

  7. Определитель обратной матрицы:

    det(A-1) = det(A)-1

  8. Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить другую строку (столбец), умноженную на некоторое число.

  9. Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить линейную комбинации других строк (столбцов).

  10. Если поменять местами две строки (столбца) матрицы, то определитель матрицы поменяет знак.

  11. Общий множитель в строке (столбце) можно выносить за знак определителя:

    a11a12…a1n
    a21a22…a2n
    ….
    k·ai1k·ai2…k·ain
    ….
    an1an2…ann

    =
    k·
    a11a12…a1n
    a21a22…a2n
    ….
    ai1ai2…ain
    ….
    an1an2…ann

  12. Если квадратная матрица n-того порядка умножается на некоторое ненулевое число, то определитель полученной матрицы равен произведению определителя исходной матрицы на это число в n-той степени:

    B = k·A   =>   det(B) = kn·det(A)

    где A матрица n×n, k — число.

  13. Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем:

    a11a12…a1n
    a21a22…a2n
    ….
    bi1 + ci1bi2 + ci2…bin + cin
    ….
    an1an2…ann

    =

    a11a12…a1n
    a21a22…a2n
    ….
    bi1bi2…bin
    ….
    an1an2…ann

    +

    a11a12…a1n
    a21a22…a2n
    ….
    ci1ci2…cin
    ….
    an1an2…ann

  14. Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.

  15. Определитель произведения матриц равен произведению определителей этих матриц:

    det(A·B) = det(A)·det(B)

Методы вычисления определителя матрицы

Вычисление определителя матрицы 1×1

Правило:

Для матрицы первого порядка значение определителя равно значению элемента этой матрицы:

∆ = |a11| = a11

Вычисление определителя матрицы 2×2

Правило:

Для матрицы 2×2 значение определителя равно разности произведений элементов главной и побочной диагоналей:

∆ = 
a11 a12
a21 a22
 = a11·a22 — a12·a21

Пример 1.

Найти определитель матрицы A

Решение:

det(A) = 
5 7
-4 1
 = 5·1 — 7·(-4) = 5 + 28 = 33

Вычисление определителя матрицы 3×3

Правило треугольника для вычисления определителя матрицы 3-тего порядка

Правило:

Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.

∆ = 
a11 a12 a13
a21 a22 a23
a31 a32 a33
 =

= 
a11·a22·a33 +
a12·a23·a31 +
a13·a21·a32 —
a13·a22·a31 —
a11·a23·a32 —
a12·a21·a33

Правило Саррюса для вычисления определителя матрицы 3-тего порядка

Правило:

Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:

∆ = 
a11 a12 a13 a11 a12
a21 a22 a23 a21 a22
a31 a32 a33 a31 a32
 =

= 
a11·a22·a33 +
a12·a23·a31 +
a13·a21·a32 —
a13·a22·a31 —
a11·a23·a32 —
a12·a21·a33

Пример 2.

Найти определитель матрицы A =

571
-410
203

Решение:

det(A) =

571
-410
203

=
5·1·3 + 7·0·2 + 1·(-4)·0 —
1·1·2 — 5·0·0 — 7·(-4)·3 = 15 + 0 + 0 — 2 — 0 + 84 = 97

Вычисление определителя матрицы произвольного размера

Разложение определителя по строке или столбцу

Правило:

Определитель матрицы равен сумме произведений элементов строки определителя на их алгебраические дополнения:

n
det(A) =  Σ aij·Aij — разложение по i-той строке
j = 1

Правило:

Определитель матрицы равен сумме произведений элементов столбца определителя на их алгебраические дополнения:

n
det(A) =  Σ aij·Aij — разложение по j-тому столбцу
i = 1

При разложение определителя матрицы обычно выбирают ту строку/столбец, в которой/ом максимальное количество нулевых элементов.

Пример 3.

Найти определитель матрицы A

Решение: Вычислим определитель матрицы разложив его по первому столбцу:

det(A) = 
2 4 1
0 2 1
2 1 1
 =

= 2·(-1)1+1·

21
11

+ 0·(-1)2+1·

41
11

+ 2·(-1)3+1·

41
21

=

= 2·(2·1 — 1·1) + 2·(4·1 — 2·1) = 2·(2 — 1) + 2·(4 — 2) = 2·1 + 2·2 = 2 + 4 = 6

Пример 4.

Найти определитель матрицы A

Решение: Вычислим определитель матрицы, разложив его по второй строке (в ней больше всего нулей):

det(A) =

2411
0200
2113
4023

=

— 0·

411
113
023

+ 2·

211
213
423

— 0·

241
213
403

+ 0·

241
211
402
=

= 2·(2·1·3 + 1·3·4 + 1·2·2 — 1·1·4 — 2·3·2 — 1·2·3) = 2·(6 +12 + 4 — 4 — 12 — 6) = 2·0 = 0

Приведение определителя к треугольному виду

Правило:

Используя свойства определителя для элементарных преобразований над строками и столбцами 8 — 11, определитель приводится к треугольному виду, и тогда его значение будет равно произведению элементов стоящих на главной диагонали.

Пример 5.

Найти определитель матрицы A приведением его к треугольному виду

Решение:

det(A) =

2411
0210
2113
4023

Сначала получим нули в первом столбце под главной диагональю. Для этого отнимем от 3-тей строки 1-ую строку, а от 4-той строки 1-ую строку, умноженную на 2:

det(A) =

2411
0210
2 — 21 — 41 — 13 — 1
4 — 2·20 — 4·22 — 1·23 — 1·2

=

2411
0210
0-302
0-801

Получим нули во втором столбце под главной диагональю. Для этого поменяем местами 2-ой и 3-тий столбцы (при этом детерминант сменит знак на противоположный):

det(A) = —

2141
0120
00-32
00-81

Получим нули в третьем столбце под главной диагональю. Для этого к 3-ему столбцу добавим 4-тий столбец, умноженный на 8:

det(A) = —

214 + 1·81
012 + 0·80
00-3 + 2·82
00-8 + 1·81

=
—
21121
0120
00132
0001
 = -2·1·13·1 = -26

Теорема Лапласа

Теорема:

Пусть ∆ — определитель n-ого порядка. Выберем в нем произвольные k строк (столбцов), причем k < n. Тогда сумма произведений всех миноров k-ого порядка, которые содержатся в выбранных строках (столбцах), на их алгебраические дополнения равна определителю.

Источник


Загрузить PDF


Загрузить PDF

Определители матриц часто используются в вычислениях, в линейной алгебре и аналитической геометрии. Вне академического мира определители матриц постоянно требуются инженерам и программистам, в особенности тем, кто работает с компьютерной графикой. Если вы уже знаете, как найти определитель матрицы размерностью 2×2, то из инструментов для нахождения определителя матрицы 3×3 вам будут необходимы только сложение, вычитание и умножение.

  1. Изображение с названием Find the Determinant of a 3X3 Matrix Step 1

    1

    Запишите матрицу размерностью 3 x 3. Запишем матрицу размерностью 3 x 3, которую обозначим M, и найдем ее определитель |M|. Далее приводится общая форма записи матрицы, которую мы будем использовать, и матрица для нашего примера:

    • M={begin{pmatrix}a_{{11}}&a_{{12}}&a_{{13}}\a_{{21}}&a_{{22}}&a_{{23}}\a_{{31}}&a_{{32}}&a_{{33}}end{pmatrix}}={begin{pmatrix}1&5&3\2&4&7\4&6&2end{pmatrix}}

  2. Изображение с названием Find the Determinant of a 3X3 Matrix Step 2

    2

    Выберите строку или столбец матрицы. Эта строка (или столбец) будет опорной. Результат будет одинаков, независимо от того, какую строку или какой столбец вы выберете. В данном примере давайте возьмем первую строку. Чуть позже вы найдете несколько советов касательно того, как выбирать строку или столбец, чтобы упростить вычисления.

    • Давайте выберем первую строку матрицы M в нашем примере. Обведите числа 1 5 3. В общей форме обведите a11 a12 a13.

  3. Изображение с названием Find the Determinant of a 3X3 Matrix Step 3

    3

    Зачеркните строку или столбец с первым элементом. Обратитесь к опорной строке (или к опорному столбцу) и выберите первый элемент. Проведите горизонтальную и вертикальную черту через этот элемент, вычеркнув таким образом столбец и строку с этим элементом. Должно остаться четыре числа. Будем считать эти элементы новой матрицей размерностью 2 x 2.

    • В нашем примере, опорной строкой будет 1 5 3. Первый элемент находится на пересечении первого столбца и первой строки. Вычеркните строку и столбец с этим элементом, то есть первую сроку и первый столбец. Запишите оставшиеся элементы в виде матрицы 2 x 2:
    •  1  5 3
    •  2  4 7
    •  4  6 2

  4. Изображение с названием Find the Determinant of a 3X3 Matrix Step 4

    4

    Найдите определитель матрицы 2 x 2. Запомните, что определитель матрицы {begin{pmatrix}a&b\c&dend{pmatrix}} вычисляется как ad — bc.[1]
     Опираясь на это, вы можете вычислить определитель полученной матрицы 2 x 2, которую, если хотите, можете обозначить как X. Умножьте два числа матрицы X, соединенных по диагонали слева направо (то есть так: ). Затем вычтите результат умножения двух других чисел по диагонали справа налево (то есть так: / ). Используйте эту формулу, чтобы вычислить определитель матрицы, которую вы только что получили.

    • В нашем примере определитель матрицы {begin{pmatrix}4&7\6&2end{pmatrix}} = 4*2 — 7*6 = -34.
    • Этот определитель называется минором элемента, который мы выбрали в нашей первоначальной матрице.[2]
       Другими словами, мы только что нашли минор a11.

  5. Изображение с названием Find the Determinant of a 3X3 Matrix Step 5

    5

    Умножьте полученный ответ на выбранный элемент матрицы M. Вспомните, какой элемент из опорной строки (или столбца) мы использовали, когда вычеркивали другие элементы строки и столбца, чтобы получить новую матрицу. Умножьте этот элемент на полученный минор (определитель матрицы 2×2, которую мы обозначили X).

    • В нашем примере мы выбирали элемент a11, который равнялся 1. Умножим его на -34 (определитель матрицы 2×2), и у нас получится 1*-34 = -34.

  6. Изображение с названием Find the Determinant of a 3X3 Matrix Step 6

    6

    Определите знак полученного результата. Далее вам понадобится умножить полученный результат на 1, либо на -1, чтобы получить алгебраическое дополнение (кофактор) выбранного элемента. Знак кофактора будет зависеть от того, в каком месте матрицы 3×3 стоит элемент. Запомните эту простую схему знаков, чтобы знать знак кофактора:

    • + — +
    • — + —
    • + — +
    • Поскольку мы работали с элементом a11, для которого стоит знак +, то мы будем умножать полученное значение на +1 (то есть оставим его как есть). Алгебраическое дополнение нашего элемента будет равно -34.
    • Вы также можете найти знак алгебраического дополнения по формуле (-1)i+j, где i и j — номер столбца и строки выбранного элемента соответственно.[3]

  7. Изображение с названием Find the Determinant of a 3X3 Matrix Step 7

    7

    Повторите все вышеописанные действия со вторым элементом опорной строки (или столбца). Вернитесь к исходной матрице размерностью 3×3 и строке, которую мы обвели в самом начале вычислений. Повторите все действия с этим элементом:

  8. Изображение с названием Find the Determinant of a 3X3 Matrix Step 8

    8

    Повторите с третьим элементом. Далее вам понадобится найти еще одно алгебраическое дополнение. Вычислите его для последнего элемента опорной строки или опорного столбца. Далее приводится краткое описание того, как вычисляется алгебраическое дополнение для a13 в нашем примере:

    • Зачеркните первую строку и третий столбец, чтобы получить матрицу {begin{pmatrix}2&4\4&6end{pmatrix}}
    • Ее определитель равен 2*6 — 4*4 = -4.
    • Умножьте результат на элемент a13: -4 * 3 = -12.
    • Элемент a13 имеет знак + в приведенной выше таблице, поэтому ответ будет -12.

  9. Изображение с названием Find the Determinant of a 3X3 Matrix Step 9

    9

    Сложите полученные результаты. Это последний шаг. Вам необходимо сложить полученные алгебраические дополнения элементов опорной строки (или опорного столбца). Сложите их вместе, и вы получите значение определителя матрицы 3×3.

    • В нашем примере определитель равен -34 + 120 + -12 = 74.

    Реклама

  1. Изображение с названием Find the Determinant of a 3X3 Matrix Step 10

    1

    Выбирайте в качестве опорной строки (или столбца) ту, что имеет больше нулей. Помните, что в качестве опорной вы можете выбрать любую строку или столбец. Выбор опорной строки или столбца не влияет на результат. Если вы выберете строку с наибольшим количеством нулей, вам придется выполнять меньше вычислений, поскольку вам будет необходимо вычислить алгебраические дополнения только для ненулевых элементов. Вот почему:

    • Допустим, вы выбрали 2 строку с элементами a21, a22, and a23. Чтобы найти определитель, вам будет необходимо найти определители трех различных матриц размерностью 2×2. Давайте назовем их A21, A22, and A23.
    • То есть определитель матрицы 3×3 равен a21|A21| — a22|A22| + a23|A23|.
    • Если оба элемента a22 и a23 равны 0, то наша формула становится намного короче a21|A21| — 0*|A22| + 0*|A23| = a21|A21| — 0 + 0 = a21|A21|. То есть необходимо вычислить только алгебраическое дополнение одного элемента.

  2. Изображение с названием Find the Determinant of a 3X3 Matrix Step 11

    2

    Используйте сложение строк, чтобы упростить матрицу. Если вы возьмете одну строку и прибавите к ней другую, то определитель матрицы не изменится. То же самое верно и для столбцов. Подобные действия можно выполнять несколько раз, кроме того, вы можете умножать значения строки на постоянную (перед сложением) для того, чтобы получить как можно больше нулей. Подобные действия могут сэкономить массу времени.

  3. Изображение с названием Find the Determinant of a 3X3 Matrix Step 12

    3

    Помните, что вычислять определитель треугольных матриц намного проще. Определитель треугольных матриц вычисляется как произведение элементов на главной диагонали, от a11 в верхнем левом углу до a33 в нижнем правом углу. Речь в данном случае идет о треугольных матрицах размерностью 3×3. Треугольные матрицы могут быть следующих видов, в зависимости от расположения ненулевых значений:[4]

    • Верхняя треугольная матрица: Все ненулевые элементы находятся на главной диагонали и выше нее. Все элементы ниже главной диагонали равны нулю.
    • Нижняя треугольная матрица: Все ненулевые элементы находятся ниже главной диагонали и на ней.
    • Диагональная матрица: Все ненулевые элементы находятся на главной диагонали. Является частным случаем вышеописанных матриц.

    Реклама

Советы

  • Описанный метод распространяется на квадратные матрицы любого ранга. Например, если вы используете его для матрицы 4×4, то после «вычеркивания» будут оставаться матрицы 3×3, для которых определитель будет вычисляться вышеупомянутым способом. Будьте готовы к тому, что вычислять определитель для матриц таких размерностей вручную — очень трудоемкая задача!
  • Если все элементы строки или столбца равны 0, то определитель матрицы тоже равен 0.

Реклама

Об этой статье

Эту страницу просматривали 119 322 раза.

Была ли эта статья полезной?

Источник

На чтение 6 мин. Просмотров 1.1k.

Матрица содержит в себе векторы-столбцы. Они по-разному ориентированы в пространстве. Характеристикой этого расположения и того матричного преобразования, которое может дать матрица, выступает определитель матрицы.

Определитель матрицы 2×2

Пусть дана квадратная матрица второго порядка:

A=begin{pmatrix} a_{11}& a_{12}\ a_{21}& a_{22} end{pmatrix}

Определителем (или детерминантом) второго порядка, соответствующим данной матрице, называется число a_{11}a_{22}-a_{12}a_{21}.

Определитель второго порядка записывается так:

detA=begin{vmatrix} a_{11}& a_{12}\ a_{21}& a_{22} end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}

Геометрический смысл определителя

Если нам дана квадратная матрица

A=begin{pmatrix} a_{11}& a_{12}\ a_{21}& a_{22} end{pmatrix}

То первый столбец дает нам координаты одного вектора, а второй столбец чисел — координаты второго вектора. Начало данных векторов — в точке начала координат.

Тогда определитель матрица дает нам площадь параллелограмма, построенного на данных векторах.

Рассмотрим на примере

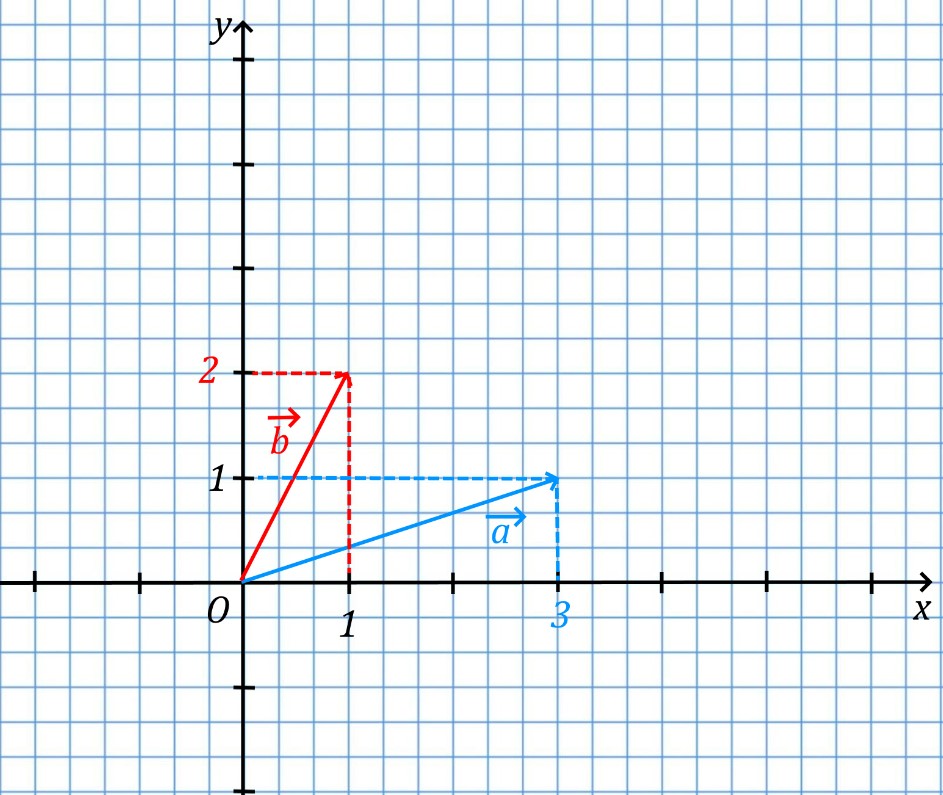
Пусть нам дана матрица с координатами:

A=begin{pmatrix} 3& 1\ 1& 2 end{pmatrix}

Нарисуем координатную плоскость и отметим на ней данные векторы.

Векторы a b

Векторы overline{a} и overline{b}

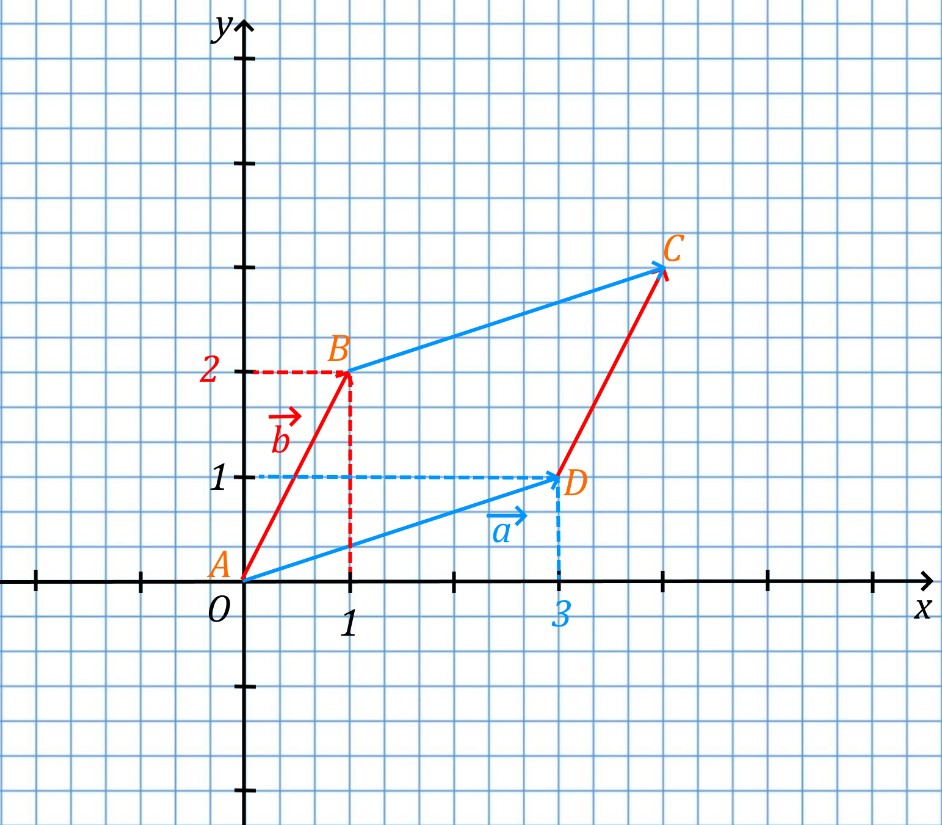
Где у вектора overline{a} координаты (3; 1), а у вектора overline{b} координаты (2; 1).

Теперь построим на этих векторах параллелограмм, считая, что векторы a и b его стороны. Получим:

Параллелограмм на векторах a и b

Параллелограмм на векторах overline{a} и overline{b}

Площадь данного параллелограмма и будет являться определителем матрицы. Площадь данного параллелограмма S_{ABCD}=5. И определитель матрицы:

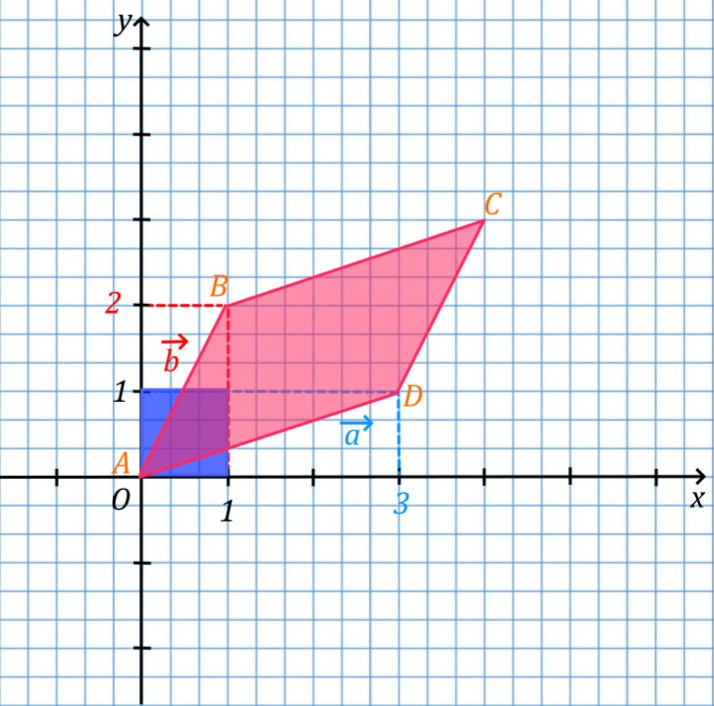
detA=begin{vmatrix} 3& 1\ 1& 2 end{vmatrix}=3 cdot 2-1 cdot 1=6-1=5

Однако, обычно в линейной алгебре говорят не о площади параллелограмма, а о матричном преобразовании. То есть о том, в какую фигуру матрица преобразует единичный квадрат, построенный на единичных векторах. Насколько она ее масштабирует в пространстве. То есть вот из такого квадрата (синий цвет) матричное преобразование делает параллелограмм с определенной площадью (отмечено красным цветом), равной по модулю определителю матрицы.

Матричное преобразование площади определитель матрицы

Матричное преобразование площади определитель матрицы

Однако иногда определитель матрицы может быть отрицательным числом. В этом случае площадь фигуры, построенной на векторах матрицы, будет равна модулю данного числа, а знак минус означает, что ориентация данной фигуры отрицательна.

Геометрический смысл определителя матрицы

Определитель показывает какой будет площадь единичного квадрата при матричном преобразовании. Она будет равна площади параллелограмма, который будет построен на векторах-столбцах матрицы. Первый столбец матрицы дает нам координаты первого вектора, а второй столбец  — координаты второго вектора.

Можно расширить геометрический смысл матрицы и на матрицы другого размера.

Таким образом, определитель матрицы 1×1 дает длину вектора, 2×2 — площадь параллелограмма, 3×3 — объем параллелепипеда, а nxn — объем n-мерного параллелепипеда.

Примеры на вычисление определителя второго порядка

Вычислить определители:

a) begin{vmatrix} 4& 7\ 2& 6 end{vmatrix}

Решение:

begin{vmatrix} 4& 7\ 2& 6 end{vmatrix}=4 cdot 6-7 cdot 2=24-14=10

Ответ: 10

б) begin{vmatrix} m^2& nm\ nm& n^2 end{vmatrix}

Решение:

begin{vmatrix} m^2& nm\ nm& n^2 end{vmatrix}=m^2 cdot n^2-nm cdot nm=m^2n^2-n^2m^2=0

Ответ: 0

Определитель третьего порядка

Пусть дана квадратная матрица третьего порядка:

A=begin{pmatrix} a_{11}& a_{12} & a_{13}\ a_{21}& a_{22} & a_{23} \ a_{31}& a_{32} & a_{33} end{pmatrix}

Определителем (или детерминантом) третьего порядка, соответствующим данной матрице, называется число:

a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{33}a_{21}-a_{11}a_{23}a_{32}

Определитель третьего порядка будет:

detA=begin{vmatrix} a_{11}& a_{12} & a_{13}\ a_{21}& a_{22} & a_{23} \ a_{31}& a_{32} & a_{33}end{vmatrix}= \ =a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{33}a_{21}-a_{11}a_{23}a_{32}

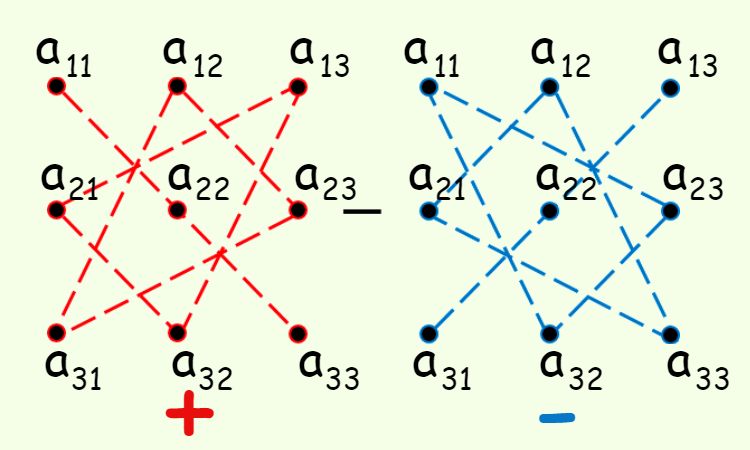
Правило треугольников

При вычислении определителей третьего порядка удобно пользоваться правилом треугольников (правилом Саррюса). Это правило проиллюстрируем на схеме:

Правило треугольников или правило Сарруса

Правило треугольников или правило Саррюса

Как пользоваться правилом треугольника:

На схеме есть две картинки — красная и синяя, красная картинка дает нам три положительных слагаемых в формуле определителя третьего порядка, а синяя — три отрицательных.

Умножаем так — сначала умножаем элементы матрицы по главной диагонали a_{11}a_{22}a_{33} потом в вершинах одного треугольника a_{12}a_{23}a_{31} и в вершинах другого треугольника: a_{21}a_{32}a_{13}. Все полученные множители складываем.

Теперь обратимся к синей картинке. Тут мы начинаем сначала перемножать элементы по побочной диагонали: a_{13}a_{22}a_{31}, а потом элементы в вершинах двух треугольников: a_{11}a_{32}a_{23} и a_{21}a_{12}a_{33}. Полученные множители записываем в формулу со знаком минус.

Примеры на вычисление определителя третьего порядка

a) Вычислить определитель матрицы:

A=begin{pmatrix} 2& 3 & 4\ 6& 5 & 7 \ 9& 0& 8 end{pmatrix}

Решение:

det A=begin{vmatrix} 2& 3 & 4\ 6& 5 & 7 \ 9& 0 & 8 end{vmatrix}=2 cdot 5 cdot 8+ 3 cdot 7 cdot 9+6cdot 0 cdot 4 — 4 cdot 5 cdot 9 — 3 cdot 6 cdot 8 — 7 cdot 0 cdot 2=80+189+0-180-144-0=-55

Ответ: det A=-55

б) Вычислить определитель матрицы 3×3:

A=begin{pmatrix} 2& 3 & 1\ 1& -5 & 6\ 2& -3& 4 end{pmatrix}

Решение:

Используем формулу определителя третьего порядка

det B=begin{vmatrix} 2& 3 & 1\ 1& -5 & 6\ 2& -3& 4 end{vmatrix}=2 cdot (-5) cdot 4+ 3 cdot 6 cdot 2+1cdot 1 cdot (-3) — 1 cdot (-5) cdot 2 — 2 cdot 6 cdot (-3) — 3 cdot 1 cdot 4=-40+36-3+10+36-12=27

Ответ: det B=27

в) Вычислите определитель единичной матрицы 3×3.

Решение:

Единичная матрица 3×3 имеет вид:

A=begin{pmatrix} 1& 1 & 1\ 1& 1 & 1\ 1& 1& 1 end{pmatrix}

Используем формулу определителя третьего порядка

det A=begin{vmatrix} 1& 1 & 1\ 1& 1 & 1\ 1& 1& 1 end{vmatrix}=1 cdot 1 cdot 1+ 1 cdot 1 cdot 1+1cdot 1 cdot 1 — 1 cdot 1 cdot 1 — 1 cdot 1 cdot 1 — 1 cdot 1 cdot 1=1+1+1-1-1-1=0

Действительно, в столбцах единичной матрицы три совпадающих вектора, на которых невозможно построить объемную фигуру, объем которой и определяет определитель матрицы третьего порядка. Поэтому мы и получили число 0.

Вообще говоря, любая матрица с одинаковыми строками и столбцами дает определитель, равный нулю. Можете проверить самостоятельно.

Ответ: 0

Разложение определителя по строке или столбцу, а также его свойства, миноры и дополнения элементов определителя рассмотрим далее.

Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Как найти свое место в спорте
  • Как найти проекцию стороны на гипотенузу
  • Как найти деда солдата
  • Террария как найти адамантитовую руду в террарии
  • Как найти дешевого дизайнера

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии