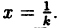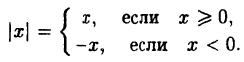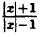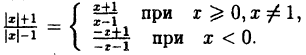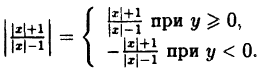Преобразование графиков функций
Анна Малкова
В этой статье мы расскажем об основных преобразованиях графиков функций. Что нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали. Как задать растяжение графика по горизонтали или вертикали. Как отразить график относительно оси Х или Y.
Очень жаль, что эта тема — полезная и очень интересная — выпадает из школьной программы. На нее постоянно не хватает времени. Из-за этого многим старшеклассникам не даются задачи с параметрами — которые на самом деле похожи на конструктор, где вы собираете решение из знакомых элементов. Хотя бы для того, чтобы решать задачи с параметрами, стоит научиться строить графики функций.
Но конечно, не только для того, чтобы сдать ЕГЭ. Первая лекция на первом курсе технического или экономического вуза посвящена функциям и графикам. Первые зачеты в курсе матанализа связаны с функциями и графиками.
Начнем со сдвигов графиков по Х и по Y.
1. Сдвиг по горизонтали.
Пусть функция задана формулой и
Тогда график функции
сдвинут относительно исходной на а вправо. График функции
сдвинут относительно исходной на а влево.
2. Сдвиг по вертикали.
Пусть функция задана формулой и С — некоторое положительное число. Тогда график функции
сдвинут относительно исходного на С вверх. График функции
сдвинут относительно исходного на С вниз.
Теперь растяжение графика. Или сжатие.
3. Растяжение (сжатие) по горизонтали.
Пусть функция задана формулой и
Тогда график функции
растянут относительно исходного в k раз по горизонтали, если
, и сжат относительно исходного в k раз по горизонтали, если
4. Растяжение (сжатие) по вертикали.
Пусть функция задана формулой и
Тогда график функции
растянут относительно исходного в М раз по вертикали, если
, и сжат относительно исходного в М раз по вертикали, если
И отражение по горизонтали.
5. Отражение по горизонтали.
График функции симметричен графику функции
относительно оси Y.
6. Отражение по вертикали.
График функции симметричен графику функции
относительно оси Х.
Друзья, не возникло ли у вас ощущения, что вы все это где-то видели? Да, наверняка видели, если когда-либо редактировали изображения в графическом редакторе на компьютере. Изображение можно сдвинуть (по горизонтали или вертикали). Растянуть (по горизонтали или вертикали). Отразить. И все это мы делаем с графиками функций.
И еще два интересных преобразования. Здесь в формулах присутствует знак модуля. Если не помните, что такое модуль, — срочно повторите эту тему.
7. Графики функций и
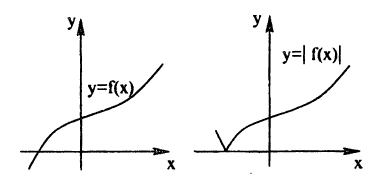
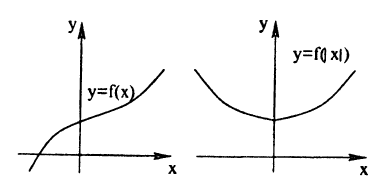
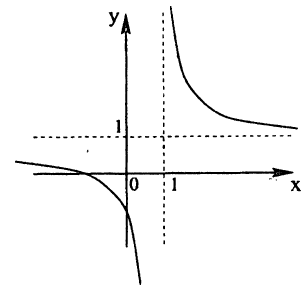
На рисунке изображен график функции Она специально взята такая — несимметричная относительно нуля.
Построим график функции
Конечно же, мы пользуемся определением модуля.
Это мы и видим на графике. Для неотрицательных значений х график остался таким же, как был. А вместо каждого отрицательного х мы взяли противоположное ему положительное число. И поэтому вся та часть графика функции, что лежала слева от оси Х, заменилась на зеркально отраженную правую часть графика.
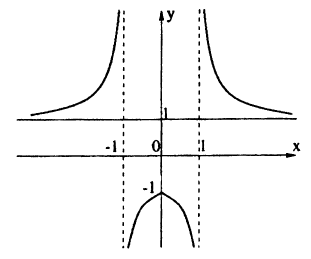
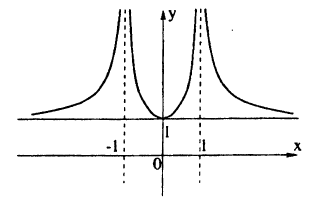
Теперь график функции Вы уже догадались, что будет. Вся часть графика, лежащая ниже оси Х, зеркально отражается в верхнюю полуплоскость. А верхняя часть графика, лежащая выше оси Х, остается на месте.
Как определить по формуле функции, будет график преобразован по горизонтали (по Х) или по вертикали (по Y)? Разница очевидна. Если сначала мы что-либо делаем с аргументом х (прибавляем к нему какое-либо число, умножаем на какое-либо число или берем модуль) — преобразование по Х. Если сначала мы нашли функцию, а затем уже к значению функции что-то прибавили, или на какое-нибудь число умножили, или взяли модуль, — преобразование по Y.
Вот самые простые задачи на преобразование графиков.
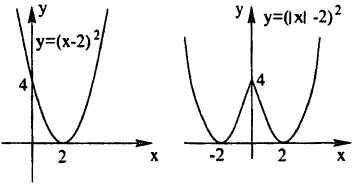
1. Построим график функции
Это квадратичная парабола, сдвинутая на 3 влево по x и на 1 вниз по y.
Вершина в точке
2. Построим график функции
Выделим полный квадрат в формуле.
График — квадратичная парабола, сдвинутая на 2 вправо по x и на 5 вниз по y.
Обратите внимание: график функции пересекает ось y в точке
На нашем графике это точка
Продолжение — в статье «Построение графиков функций».
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Преобразование графиков функций» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
07.05.2023

В этой статье я познакомлю вас с линейными преобразованиями графиков функций и покажу, как с помощью этих преобразований из графика функции 
Линейным преобразованием функции 

Наибольшие затруднения при построении графиков с помощью линейных преобразований вызывают следующие действия:
- Вычленение базовой функции, собственно, график которой мы и преобразовываем.
- Определения порядка преобразований.
Именно на этих моментах мы и остановимся подробнее.
Рассмотрим внимательно функцию
В ее основе лежит функция 
При построении графика функции 

Если бы мы совершали преобразования функции 
Рассмотрим какие виды линейных преобразований аргумента и функции существуют, и как их выполнять.
Преобразования аргумента.
1. f(x) 
1. Строим график фунции
2. Сдвигаем график фунции 
- влево, если b>0
- вправо, если b<0
Построим график функции
1. Строим график функции
2. Сдвигаем его на 2 единицы вправо:
2. f(x) 
1. Строим график фунции
2. Абсциссы точек графика 
Построим график функции 
1. Строим график функции
2. Все абсциссы точек графика 
3. f(x) 
1. Строим график фунции
2. Отображаем его симметрично относительно оси OY.
Построим график функции 
1. Строим график функции
2. Отображаем его симметрично относительно оси OY:
4. f(x) 
1. Строим график функции
2. Часть графика, расположенную левее оси ОY стираем, часть графика, расположенную правее оси ОY Достраиваем симметрично относительно оси OY:
График функции 
Построим график функции
1. Строим график функции 

2. Часть графика, расположенную левее оси OY (x<0) стираем:
3. Часть графика, расположенную правее оси OY (x>0) достраиваем симметрично относительно оси OY:
Важно! Два главных правила преобразования аргумента.
1. Все преобразования аргумента совершаются вдоль оси ОХ
2. Все преобразования аргумента совершаются «наоборот» и «в обратном порядке».
Например, в функции 
1. Берем модуль от х.
2. К модулю х прибавляем число 2.
Но построение графика мы совершали в обратном порядке:
Сначала выполнили преобразование 2. — сместили график на 2 единицы влево (то есть абсциссы точек уменьшили на 2, как бы «наоборот»)
Затем выполнили преобразование f(x) 
Коротко последовательность преобразований записывается так:
Теперь поговорим о преобразовании функции. Преобразования совершаются
1. Вдоль оси OY.
2. В той же последовательности, в какой выполняются действия.
Вот эти преобразования:
1. f(x)
1. Строим график функции y=f(x)
2. Смещаем его вдоль оси OY на |D| единиц
- вверх, если D>0
- вниз, если D<0
Построим график функции
1. Строим график функции
2. Смещаем его вдоль оси OY на 2 единицы вверх:
2. f(x)
1. Строим график функции y=f(x)
2. Ординаты всех точек графика умножаем на А, абсциссы оставляем без изменений.
Построим график функции
1. Построим график функции
2. Ординаты всех точек графика умножим на 2:
3. f(x)
1. Строим график функции y=f(x)
2. Отображаем его симметрично относительно оси ОХ.
Построим график функции 
1. Строим график функции 
2. Отображаем его симметрично относительно оси ОХ.
4. f(x)
1. Строим график функции y=f(x)
2. Часть графика, расположенную выше оси ОХ оставляем без изменений, часть графика, расположенную ниже оси OX, отображаем симметрично относительно этой оси.
Построим график функции
1. Строим график функции 

2. Теперь часть графика, расположенную ниже оси ОХ, отобразим симметрично относительно этой оси:
И последнее преобразование, которое, строго говоря, нельзя назвать преобразованием функции, поскольку результат этого преобразования функцией уже не является:
y=f(x) 
1. Строим график функции y=f(x)
2. Часть графика, расположенную ниже оси ОХ стираем, затем часть графика, расположенную выше оси ОХ достраиваем симметрично относительно этой оси.
Построим график уравнения
1. Строим график функции 
2. Часть графика, расположенную ниже оси ОХ стираем:
3. Часть графика, расположенную выше оси ОХ достраиваем симметрично относительно этой оси.
И, наконец, предлагаю вам посмотреть ВИДЕОУРОК в котором я показываю пошаговый алгоритм построения графика функции
График этой функции выглядит так:
И.В. Фельдман, репетитор по математике.
Преобразования графиков функций и уравнений
Часто возникают задачи, в которых требуется по графику функции y=f(x)y = f(x) построить график некоторой похожей функции. Такого типа задачи называют задачами на преобразование графиков функций. Наиболее известны два типа преобразований графиков – линейные преобразования графиков, а также преобразования графиков, связанные с модулями. Начнём со второго типа преобразований. Будем полагать, что нам задан график функции y=f(x)y = f(x).
Как построить график функции y=f(|x|)y = f(|x|)? По определению модуля:
y = f(|x|) y;=;f(vert xvert);=f(x), при x ≥0,f(-x), при x<0.=left{begin{array}{l}f(x),;mathrm{при};x;geq0,\f(-x),;mathrm{при};x<0.end{array}right.
Поэтому график функции y=f(|x|)y = f(|x|) состоит из двух частей:
y=f(x)y = f(x) – в правой полуплоскости, y=f(−x)y = f(−x) – в левой полуплоскости. Это означает, что можно сформулировать такое правило:
для построения графика y=f(|x|)y = f(|x|) нужно сохранить часть графика y=f(x)y = f(x) при x≥0x ≥ 0 (т. е. на оси ординат и справа от неё), а также симметрично отразить эту часть относительно оси `Оy`; часть графика y=f(x)y = f(x) при x<0x < 0 (т. е. слева от оси ординат) при этом нужно стереть.
Как построить график функции y=|f(x)|y =|f(x)|? По определению модуля:
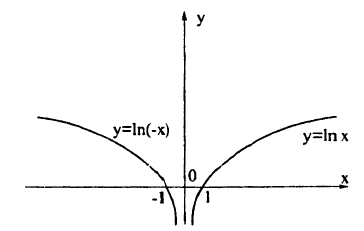
y = |f(x)| y;=;vert f(x)vert;=f(x), при f(x) ≥0,-f(x), при f(x)<0.=left{begin{array}{l}f(x),;mathrm{при};f(x);geq0,\-f(x),;mathrm{при};f(x)<0.end{array}right.
Поэтому можно сформулировать такое правило:
для построения графика функции y=|f(x)|y = |f(x)| нужно сохранить часть графика y=f(x)y = f(x), лежащую выше оси `Ox`, а часть графика, лежащую ниже оси `Ox`, симметрично отразить относительно этой оси.
Отметим, что для построения графика функции y=|f(|x|)|y = |f(|x|)| нужно последовательно провести преобразования ПР1 и ПР2 (в любом порядке).
Рассмотрим ещё один тип преобразований графиков с модулями.
Как построить множество точек `(x, y)` таких, что |y|=f(x)|y| = f(x)?
Сразу видно, что на новом графике не должно быть точек, для которых f(x)<0f(x) < 0. Поэтому нужно стереть часть графика функции y=f(x)y = f(x), лежащую ниже оси абсцисс. Если же f(x)≥0f(x) ≥ 0, то y=±f(x)y = ± f(x) и на новом графике каждому такому значению xx должно соответствовать две точки, симметричные относительно оси OxOx (если f(x)≥0f(x) ≥ 0, то точка одна).
Это означает, что часть графика функции y=f(x)y = f(x), лежащую выше оси абсцисс, нужно сохранить и симметрично отразить относительно оси OxOx.
Теперь перейдём к описанию так называемых линейных преобразований графиков. Выделяют, как правило, следующие три типа таких преобразований.
Переход от графика y=f(x)y = f (x) к графику y=af(x)y = af(x), где a≠1a ≠ 1.
Если aa – положительное число, то имеем два возможных случая:
а) a>1a > 1. В данном случае рассматриваемый переход является растяжением графика от оси абсцисс в `a` раз. Покажем на примере линейной функции y=xy = x (рис. 20). Положим a=2a = 2 и получим график функции y=2xy = 2x посредством растяжения имеющегося графика в два раза от оси абсцисс (рис. 21).
б) 0<a<10 < a < 1. В данном случае рассматриваемый переход является сжатием графика к оси ординат в 1/a1/a раз. Пусть имеется линейная функция y=xy = x. Если a=0,5a = 0,5, то получим график функции y=0,5xy = 0,5x посредством сжатия имеющегося графика в 1/a=21/a = 2 раза к оси абсцисс (рис. 22).
Заметим, что при a<0a < 0 нужно сначала построить график функции y=|a|f(x)y = |a|f(x), а потом симметрично его отобразить относительно оси абсцисс.
В частности, при a=–1a = –1 исходный график отражается относительно `Ox`.
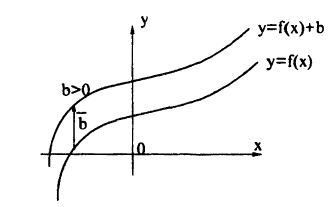
Переход от графика y=f(x)y = f(x) к графику y=f(x)+by = f(x) + b, где b≠0b ≠ 0 – некоторое число. Рассматриваемый переход является параллельным переносом графика вдоль оси ординат на bb единиц. Направление сдвига определяется знаком bb: если b>0b > 0, то график сдвигается вверх, а если b<0b < 0, то вниз.
Переход от графика y=f(x)y = f(x) к графику y=f(x+c)y = f(x + c), где с≠0с ≠ 0 – некоторое число. В этом случае исходный график сдвигается вдоль оси абсцисс на величину |c||c|. Но направление сдвига противоположно знаку числа `c:` если с>0с > 0, то график сдвигается влево, а если с<0с < 0, то вправо.
Рассмотрим несколько примеров построения графиков с использованием упомянутого выше набора преобразований.
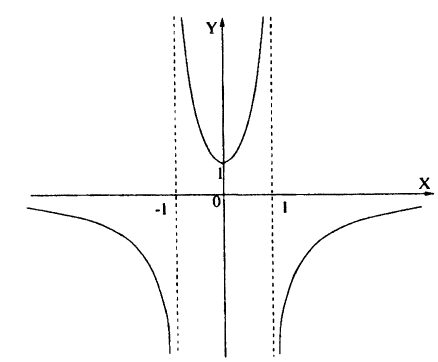
Построим ещё такой график y= ||x−1|−2|y = ||x − 1| − 2|.
Для этого нужно выполнить цепочку таких действий (рис 23).
а) Строим график функции y=x−1y = x − 1.
б) Выполняем ПР2: часть полученного графика, лежащая над осью OxOx сохраняется; а его часть, лежащая под осью OxOx отображается симметрично относительно оси OxOx.
с) Затем сдвигаем график вдоль оси OyOy на `2` единицы вниз (ПР5).
д) Выполняем ПР2 снова: часть полученного в предыдущем пункте графика, лежащая выше оси OxOx, сохраняется, а часть этого графика, которая лежит ниже оси OxOx, отображается симметрично относительно неё.
Построим график функции y=x2-9|x|-3y=dfrac{x^2-9}{vert xvert-3}.
ОДЗ: |x|−3≠0|x| − 3 ≠ 0, |x|≠3|x| ≠ 3, x≠3x ≠ 3, x≠−3x ≠ −3.
Воспользуемся известным тождеством
|x|2=x2|x|^2 = x^2. Имеем:
y=x2-9|x|-3=|x|2-9|x|-3=(|x|-3)(|x|+3)|x|-3=|x|+3y=dfrac{x^2-9}{vert xvert-3}=dfrac{vert xvert^2-9}{vert xvert-3}=dfrac{(vert xvert-3)(vert xvert+3)}{vert xvert-3}={vert xvert}+3.
Выполняем построения (рис. 24):
а) Строим график функции y=|x|y = |x|.
б) График y=|x|y = |x| сдвигаем вдоль оси OyOy на `3` единицы вверх (ПР5).
в) Исключаем из графика точки x=3x = 3, x=−3x = −3.
При решении задачи мы учли ОДЗ функции, исключив некоторые точки из графика. Такие точки изображаются, например, в виде выколотых точек (пустых не закрашенных кружков).
Параллельный перенос, сжатие и растяжение графиков. Построение графиков с модулями.
Графики многих функций можно получить из ранее рассмотренных с помощью элементарных геометрических преобразований: параллельного переноса, сжатия, растяжения, симметричного отображения. Рассмотрим некоторые из этих преобразований. Для каждого из элементарных преобразований предлагается два способа построения графика: с помощью преобразования графика и с помощью преобразования системы координат. Обучающийся должен выбрать тот, который кажется ему проще и овладеть им. В каждом случае считается известным график функции у = f(х).
Параллельный перенос графиков
График функции у = /(x) + Ь получается из графика функции у = f(х) с помощью его переноса на вектор b = (0; b). Действительно, в этом случае ко всем ординатам графика у = f(х) прибавляется величина b, что означает сдвиг графика вдоль оси Оу. Если b > 0, то график функции у = f(х) переносится вверх параллельно оси Oy на b, если b < 0, то график функции у = f(x) переносится вниз параллельно оси Oy на |b| (рис. 49). Заметим, что вместо переноса графика, можно перенести в противоположном направлении ось Ox (если b > 0 — вниз, если b < 0 — вверх), прибавив ко всем значениям по оси Oy величину b.
Пример:
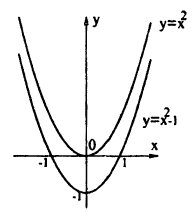
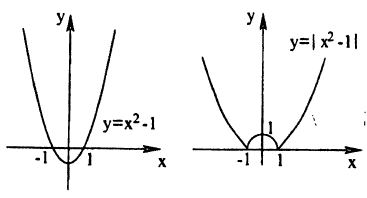
График функции у = x² — 1 (рис. 50) смещен на 1 вниз параллельно оси Oy относительно графика функции у = х².
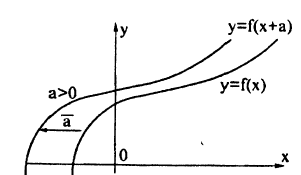
График функции у = f(x+a) получается с помощью переноса графика функции у = f(x) на вектор а = (—а;0). Действительно, перейдя к новым координатам X = х + α, Y = у параллельным переносом вдоль оси Ox на —а, заметим, что относительно новых координат получится исходный график функции Y = f(X). Если а > 0, то старые координаты получаются из новых сдвигом направо вдоль оси Ox на α, т.к. х = X — а. Если же сдвигать график, а не систему координат, то его нужно двигать в противоположном направлении — налево. Итак, если а > 0, то график функции у = f(x) переносится налево параллельно оси Ox на а, если а < 0, то график функции у = f(x) переносится направо вдоль оси Ox на ∣α∣ (рис. 51). Вместо переноса графика можно перенести в противоположном направлении ось Oy (если α > 0 — вправо, если α < 0 — влево), отняв от всех значений по оси Ox величину а.
Пример:
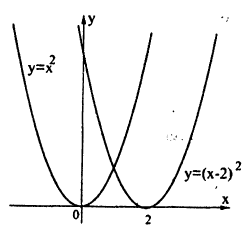
График функции у = (x- 2)² смещен на 2 ед. вправо параллельно оси Ox относительно графика функции у = х². (рис. 52).
Сжатие и растяжение графиков
График функции у = kf(x), где к ∈ R, получается с помощью ’’растяжения” графика функции у = f(x) в к раз в направлении от оси Ох. ’’Растяжение” здесь понимается как умножение на к ординат всех точек графика у = f(x)∙ При k > 1 это будет действительно растяжение в к раз от оси Ox вдоль оси Оу. При 0 < k < 1 это будет сжатие в 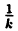
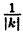
Вместо преобразования графика при k > 0 можно исправить значения по оси Оу, умножив их на k. При k < 0 в этом случае пришлось бы менять направление оси, что неудобно; лучше перевернуть график сверху вниз.
График функции у = f(kx), где k ∈ R, получается с помощью ’’сжатия” графика у = f(x) в к раз в направлении к оси Оу. ’’Сжатие” здесь понимается как деление на к абсцисс всех точек графика у = f(x). Действительно, если, например, f(1) =0, то, сделав замену X = kх, Y = у, получим, что функция у = f(kx) обращается в нуль при kх = 1, т.е. при
При k > 1 график функции у = f(x) сжимается в k раз к оси Oy вдоль оси Ох; при 0 < k < 1 график функции у = f(x) растягивается в 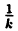
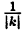
В частности, график функции у = f(-x) получается из графика функции у = f(-x) симметрией относительно оси Оу.
Вместо преобразования графика при k > 0 можно исправить значения по оси Ох, поделив их на k. При k < 0 в этом случае следует предварительно перевернуть график слева направо.
Пример:
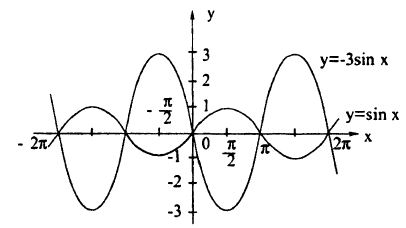
График функции у = cos 2х получается из графика у = cos х сжатием в 2 раза к оси Оу; график функции у = ln(—х) получается из графика у = ln х симметрией относительно оси Oy ( рис. 54).
Пользуясь изложенными методами, приведем последовательность преобразований при построении графика функции у = f(kx + b), если дан график функции у = f(x):
- нарисовать график функции у = f(x);
- получить график функции у = f(x + b), сдвинув исходный на вектор b = (-b; 0), как описано в п. 5.1;
- получить график функции у = f(kx + b), “сжав” предыдущий в к раз к оси Оу, как описано выше.
Пример:
Написать последовательность преобразований и построить график функции у = 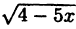
Решение:
Построение графика показано на рис. 55
Замечание:
Теперь понятно, что если функция у = f(x) периодическая с периодом Т, то функция у = К ∙ f(kx + b) + а тоже периодическая с периодом T₁ = 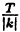
Построение графиков с модулями
График функции у = ∣f(x)∣ получается из графика функции у = f(x) следующим образом (рис. 56)
- все части графика функции у = f(x), лежащие ниже оси Ох, следует отобразить вверх симметрично относительно этой оси;
- оставшиеся внизу части исходного графика следует стереть.
Действительно, по определению модуля действительного числа имеем:
(5.1)
Таким образом, те участки исходного графика, которые лежат не ниже оси Ox (f(x) ≥ 0), менять не нужно, а для тех участков, которые лежат ниже оси Ох, нужно построить функцию у = —f(x). В соответствии с п. 5.2 это получается симметричным отображением исходного графика относительно оси Ох. Заметим, что полученный график лежит не ниже оси Ох, что естественно, т.к. |f(x)| ≥ 0 для ∀x ∈ D(f).
Пример:
Построение графика функции у = |х² — 1| показано на рис. 57.
График функции у = f (|x|) получается из графика функции у = f(х) следующим образом (рис. 58):
- все части графика функции у = f(x), лежащие слева от оси Оу, следует стереть;
- о оставшуюся часть графика следует отобразить налево симметрично относительно оси Оу.
Действительно, по определению модуля действительного числа имеем:
(5.2)
Таким образом, не нужно изменять те участки исходного графика, для которых х ≥ 0, а для х<0 (слева от оси Оу) следует построить график функции у = f(—х). В соответствии с п. 5.2 это получается симметричным отображением исходного графика относительно оси Оу. Заметим, что полученный график симметричен относительно оси Оу, что естественно, т.к. функция у = f(|x|) четная (докажите самостоятельно).
Пример:
Построение графика функции у = (|x| — 2)² показано на рис. 59
Элементарными методами можно строить эскизы графиков более сложных функций.
Пример:
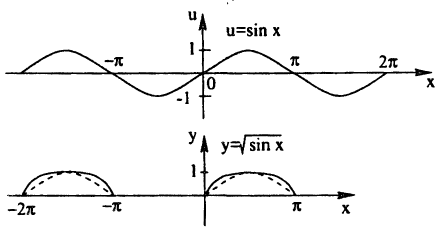
Построить эскиз графика у =
Решение:
Построение графика показано на рис. 60. Заметим, что график отсутствует там, где sin х < О, так как D(x) = {x| sin х ≥ 0}
Кроме того, так как √u > и при 0 < u < 1, то график у = 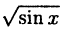
Построение графиков функций с примерами
Пример:
C помощью элементарных преобразований постройте график функции: у = x² — х — 2.
Решение:
Выделим полный квадрат из правой части уравнения функции: у = x² — х — 2 ⇔ y = x²-x+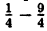
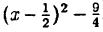
1) y =x²
2) у =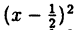
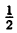
3) у = 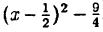
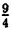
Пример:
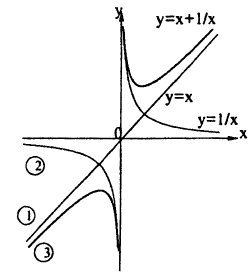
Используя сложение, деление функций, постройте график функции: у = х + 
Решение:
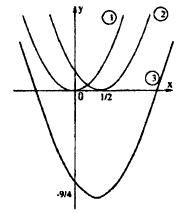
В одних осях координат нарисуем графики следующих функций (рис. 62):
1) у = х,
2) y=
3) y = x + 
Пример:
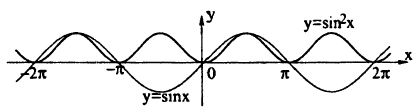
Постройте график сложной функции у = sin² х.
Решение:
В одних осях координат нарисуем графики функций:
1) y = sin x,
2) y = sin² х.
Учитывая, что квадрат числа меньшего единицы, меньше исходного числа, получим график (рис. 63)
Пример:
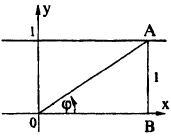
Постройте график функции в полярной системе координат: r = 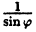
Решение:
Вычислим значения г для некоторых значений 
 |
0 | 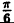 |
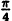 |
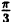 |
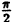 |
| r | ∞ | 2 | 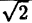 |
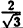 |
∞ |
Соединив плавной линией найденные точки, получим линию вдоль оси Ох, проходящую через точку (0;1). Докажем что эта линия — прямая (рис. 64). Действительно: из Δ ОAВ ⇒ cos
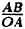
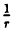
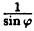
Пример:
Постройте линию, описываемую уравнением, у =
Решение:
Сначала построим график функции у =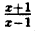
Наконец, строим линию описываемую уравнением у = 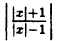
Пример:
Постройте линию, описываемую уравнением у =
Решение:
Для построения графика данного примера сначала постройте график функции у =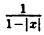
Ответ: рис. 68.
Пример:
Постройте линию, описываемую уравнением у = |х² — х -2|.
Решение:
Для построения графика данного примера сначала постройте график функции у = х² — х — 2. Затем отразите симметрично оси Ox ту часть графика, которая осталась снизу от оси Ох. Затем сотрите ту часть графика, которая расположена в нижней полуплоскости.
Ответ: рис. 69.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Найдите все преобразованные функции.

На этой странице сайта размещен вопрос Найдите все преобразованные функции? из категории
Алгебра с правильным ответом на него. Уровень сложности вопроса
соответствует знаниям учеников 10 — 11 классов. Здесь же находятся ответы по
заданному поиску, которые вы найдете с помощью автоматической системы.
Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по
заданной теме. На этой странице можно обсудить все варианты ответов с другими
пользователями сайта и получить от них наиболее полную подсказку.