|
|
Образующие циклической группы
|
|
09/10/14 |
Задание: Знаю, что по правилам нужно привести попытки решения, но у меня нет идей. Скорее всего, дело в том, что я ещё не совсем разобрался с понятием образующей( надеюсь разобраться на примере задачи ). Так-то нужная теория есть. — 24.10.2014, 22:37 — Имеются в виду вращения без переворотов, при которых Ответ есть( даже док-во, но оно мне непонятно ): повороты против часовой стрелки на 30, 150, 210 и 330 градусов.
|
|
|
|
|
ИСН |
Re: Образующие циклической группы
|
||
18/05/06 |
В любой непонятной ситуации начинай копать. © — менее минуты назад — Так, поступили обновления. У меня есть ответ на это тоже, но если я его напишу сейчас, Вы его не прочитаете. Выслушайте меня.
|
||
|
|
|||
|
RrX |
Re: Образующие циклической группы
|
|
09/10/14 |
Цитата: Выслушайте меня. Имеете в виду не отвечать пока на первый? Хорошо, слушаю.
|
|
|
|
|
ИСН |
Re: Образующие циклической группы
|
||
18/05/06 |
Так вот, значит, это. Сделайте что я говорю. Тупо проверьте все элементы, вот оно и будет. Мне не совсем понятно, почему тот же поворот на 60 градусов не будет образующим циклической группы Это что такое за обозначение и что за группа?
|
||
|
|
|||
|
RrX |
Re: Образующие циклической группы
|
|
09/10/14 |
Цитата: Это что такое за обозначение и что за группа? Множество вращений. Поворачиваем на Хотя я понимаю, к чему вы клоните. Подозреваю, что запутался в терминологии «группы вращений».
|
|
|
|
|
RrX |
Re: Образующие циклической группы
|
|
09/10/14 |
|
|
|
|
|
Otta |
Re: Образующие циклической группы
|
||
09/05/13 |
Ну как-то это совсем очевидно. Если его порядок менее двенадцати, то множество всех его степеней состоит из менее чем двенадцати значений.
|
||
|
|
|||
|
RrX |
Re: Образующие циклической группы
|
|
09/10/14 |
Otta , всё-таки я чего-то не понимаю в теории тут.
|
|
|
|
|
Otta |
Re: Образующие циклической группы
|
||
09/05/13 |
А Вы отвлекитесь от своих поворотов и вспомните определения 1) образующего элемента группы, 2) порядка элемента, 3) порядка группы.
|
||
|
|
|||
|
RrX |
Re: Образующие циклической группы
|
|
09/10/14 |
Otta , Естественно, для каждой циклической группы порядок будет разным. А группа вращений многоугольника так вообще бесконечна( или нет? )
|
|
|
|
|
Otta |
Re: Образующие циклической группы
|
||
09/05/13 |
Нет. Группа вращений многоугольника — эта группа таких вращений, которая многоугольник переводит в себя. Различая вершины. Тут у Вас много путаницы. Нарисуйте его и пронумеруйте вершины, что ли.
|
||
|
|
|||
|
ИСН |
Re: Образующие циклической группы
|
||
18/05/06 |
Множество вращений. Поворачиваем на Если повернуть второй раз на
|
||
|
|
|||
|
RrX |
Re: Образующие циклической группы
|
|
09/10/14 |
Цитата: Нет. Группа вращений многоугольника — эта группа таких вращений, которая многоугольник переводит в себя. Различая вершины. Тут у Вас много путаницы. Нарисуйте его и пронумеруйте вершины, что ли. Но для группы вращений обязательно, чтобы многоугольник «побывал» на всех своих вершинах? , хотел написал
|
|
|
|
|
VAL |
Re: Образующие циклической группы
|
||
27/06/08 |
Цитата: Но для группы вращений обязательно, чтобы многоугольник «побывал» на всех своих вершинах? Это что-то типа «Граф считает все счета на своем счету» Элементами группы являются не вершины, а повороты многоугольника вокруг центра, при которых многоугольник переходит сам в себя (хотя вершины при этом могут как-то переставляться). При этом два поворота считаются неразличимыми, если они одинаково действуют на все вершины. Групповой операцией является последовательное выполнение допустимых поворотов. Возьмите в качестве начального элемента поворот на
|
||
|
|
|||
|
RrX |
Re: Образующие циклической группы
|
|
09/10/14 |
Цитата: Элементами группы являются не вершины, а повороты многоугольника вокруг центра Это понятно. Цитата: При этом два поворота считаются неразличимыми, если они одинаково действуют на все вершины. А вот этого не знал. Цитата: Получите ли Вы при этом все элементы исходной группы? Нет. Получится циклическая группа, но элементами её будет лишь Ок, спасибо, необходимость порядка
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы
Рассмотрев
некоторые элементарные свойства групп,
перейдем к анализу взаимосвязей между
различными группами. Такой анализ мы
начнем с групп с совпадающими операциями.
Это приводит к понятию подгруппы группы.
Рассмотрим две группы
,
.
Определение. Группа
называется подгруппой группы
,
если
и групповые операции
и
совпадают на множестве
.
Утверждение. Для
того чтобы непустое подмножество
группы
было подгруппой, необходимо и достаточно
выполнения следующих условий:
-
если
(единичный
элемент группы принадлежит подгруппе);
-
(существует
обратный элемент).
Пример 1. Пусть
– аддитивная группа целых чисел. В ней
можно выделить ряд подгрупп:
1. – подгруппу чётных чисел. Легко проверить,
что множествос заданной операцией сложения образует
группу:
-
сумма
двух чётных чисел – чётное число; -
операция
сложения чётных чисел – ассоциативна; -
единичным
элементом является нуль – чётное число; -
число,
обратное чётному числу – чётное число.
2. – подгруппу чисел кратных
;
3. – подгруппу, содержащую только нуль;
4. – подгруппу целых чисел.
Пример 2. Рассмотрим
аддитивную группу рациональных чисел
.
В ней можно выделить следующие подгруппы:
-
подгруппу
целых чисел
;
-
все
подгруппы аддитивной группы целых
чисел;
Замечание. Мы
не можем утверждать, что дроби с нечётными
знаменателями образуют подгруппу,
поскольку любую такую дробь можно
представить в виде дроби с чётным
знаменателем: например, дробь
можно записать в виде
.
Следовательно, хотя в действительности
мы имеем в виду дроби с нечётными
знаменателями, следует применять лишь
приведённое выше точное название
подгруппы.
Пример 3. Рассмотрим
мультипликативную группу вещественных
чисел, отличных от нуля

В ней можно выделить следующие подгруппы:
-
мультипликативную
группу положительных вещественных
чисел
:
произведение двух положительных
вещественных чисел положительно (и
вещественно), единица – число
положительное, число, обратное
положительному, также положительно;
Замечание. 1.
В любой группе
можно выделить по крайней мере две
подгруппы:
-
–подгруппу,
содержащую только один единичный
элемент.
-
–подгруппу,
совпадающую с самой группой.
2.
В общем случае количество выделяемых
подгрупп в группе
зависит от мощности группы
.
Еслии множество
– конечно, то конечно и количество
выделяемых подгрупп. Если– бесконечно, то количество выделяемых
подгрупп может быть как конечно, так и
бесконечно.
Определение. Подгруппа
называется собственной подгруппой,
если:и
.
В
противном случае подгруппа
называется несобственной илитривиальной.
Итак,
– тривиальные подгруппы любой группы
.
Минимальная подгруппа. Пусть
произвольное подмножество множества
группы
,
попробуем выбрать подгруппугруппы
,
содержащуюи такую, что для всякой подгруппы
из того, что
будет вытекать включение
,
т.е.– минимальная подгруппа, содержащая
множество.
Лемма. Двух
минимальных подгрупп
и
,
содержащих,
не существует.
Доказательство. Действительно,
если
и
,
где,
– две минимальные подгруппы, то из того,
что,
а из того, что,
откуда следует, что.
Системы образующих. Пусть
– некоторая группа, и существует
семейство подгрупп {,
}
группы G, т.е..
Теорема. Пересечение
любого семейства подгрупп
группы G является подгруппой.
Доказательство. Пусть
e – единичный элемент группы G, тогда
свойства:
1. ,
2. ,
3. ,
характеризующие
всякую подгруппу, выполнены в
,
т.к. они выполнены в каждой из подгруппв отдельности. Это свойство групп
позволяет находить в любой группе
«наименьшую» или «минимальную»
подгруппу, содержащую заданное множествоэлементов группы G. Рассмотрим множество
элементов группы G. Наименьшая подгруппа,
которой принадлежат эти элементы,
содержится во всякой другой подгруппе,
включающей в себя помимо элементов
множества S, еще какие-то другие элементы
группы.
Выберем
теперь в качестве семейства
все те подгруппы, которые содержат
данное множество S, тогда их пересечение
(2.20)
и
будет минимальной «наименьшей»
подгруппой, содержащей множество S.
Определение. Подгруппа
,
определяемая в виде (2.20), называется
минимальной подгруппой, содержащей
множество S.
Замечание. На
первый взгляд минимальная подгруппа
задается неконструктивно, поскольку
необходимо перебирать все подгруппы,
содержащие заданное множество S, а затем
найти их пересечение. Необходимости в
этом, однако, нет. Покажем это.
Пусть
.
Поскольку подгруппасодержит элементы a, b, c, то три элемента
этой подгруппы уже известны. Кроме того,
мы знаем, что подгруппепринадлежит единичный элемент e. Из
обобщенной ассоциативности следует,
что вместе с каждым из элементов a, b, c
подгруппепринадлежат и все (целые) степени ее
элементов, а так же все произведения
степеней. Следовательно, подгруппасостоит из элементов вида:
, (2.21)
где
– целые числа.
Замечание. 1. Некоторые
из произведений вида (2.21) могут не
содержать какого либо из элементов {a,
b, c}, но их также можно представить в виде
(2.21), положив соответствующие показатели
степени равными нулю.
2. Единичный
элемент e также можно представить в виде
(2.21), положив все показатели степени
равными нулю.
Вывод. Подгруппа
,
порожденная элементами множества,
состоит из произведений степеней
образующих элементов вида (2.20).
Сформулируем
этот вывод в виде следующего утверждения.
Утверждение. Минимальная
подгруппа
группы G совпадает с множеством T,
состоящим из единичного элемента e и
всевозможных произведений:
,
(2.22)
где:
либо
,
либо.
Доказательство. Если
,
следовательно
и если
то множество T является подгруппой в G.
С другой стороны, каждая подгруппа H,
содержащая все
,
должна содержать все их обратныеи, стало быть, все их произведения вида
.
Поэтомуи T совпадает с пересечением всех этих
подгрупп.
Замечание. Далеко
не все произведения
будут различными элементами подгруппы
,
даже если условиться заменять все
встречающиеся пары,
взаимно обратных элементов единичным
элементом. В общем случае привопрос о равенстве произведений
достаточно сложен.
Определение. Если
подгруппа
,
порожденная элементами множества S,
совпадает со всей группой G, то элементы
множества S называютсясистемой
образующих
элементов группы
.
Определение. Если
множество S конечно, то группа
,
порожденная множеством S, называется
конечнопорожденной группой.
Утверждение. Каждая
группа G порождается какой-нибудь
системой образующих S.
Доказательство. Пусть
G – группа, порождённая конечным
множеством S своих элементов. Удаляя из
S «лишние» элементы, которые
записываются в виде произведения
оставшихся и их обратных, мы придем к
минимальной системе образующих
группы G, где
.
Это означает, что,
но,
если система образующихполучена из
удалением хотя бы одного элемента. Пусть
.
Тогда вместопишут также
.
Пример 1. Пусть
G – аддитивная группа целых чисел, т.е.
.
Необходимо найти минимальную подгруппугруппы G, порожденную множеством S, если:
1. ,
2. ,
3. ,
4. ,
5. .
Решение.
1. Если S={2}, то
;
-
Если
S={4, 6}, то
.
Ясно, что все элементы подгруппычетные т.к. общий элемент
этой подгруппы
можно представить в виде четного числа.
Естественно,
возникает вопрос, все ли четные числа
содержатся в данной подгруппе? Для
ответа на этот вопрос необходимо
проверить, принадлежит ли число два
этой подгруппе. Если число два принадлежит
подгруппе
,
то и все его степени (т.е. четные числа)
принадлежат этой подгруппе..
ПустьТогда имеем
,
следовательно,и подгруппа
будет содержать все элементы, порожденные
числом два, т.е. все четные числа. -
Если
S={0}, тогда
-
Если
S={1}, то
-
Если
S={–1}, то
Пример 2. Пусть
G – мультипликативная группа положительных
вещественных чисел, т.е.
.
Необходимо найти минимальную подгруппугруппы G, порожденную множеством S, если:
1.,
2..
Решение. 1. Если
,
то;
2. Если
S={1}, то
Пример 3. Пусть
– аддитивная группа рациональных чисел.
Необходимо найти минимальную подгруппугруппы G, порожденную множеством
.
Решение. В
минимальную подгруппу

рационального числа.
Кроме того, подгруппе
восьмых и т.д. Следовательно, эта подгруппа
содержит все дроби, в знаменатель которых
не входят никакие простые числа, кроме
2 (т.е. в знаменателе могут стоять лишь
степени числа 2). Но такие дроби образуют
подгруппу, содержащую все заданные
числа. Следовательно, минимальная
подгруппа
служит степень числа 2.
Соседние файлы в папке ЛЕКЦИИ АиГ
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Группоиды, полугруппы, группы
Рассмотрим алгебры, сигнатуры которых состоят из одной. бинарной операции. Эту операцию будем обозначать точкой и условно называть в этом случае умножением.
Группоидом называют любую алгебру , сигнатура которой состоит из одной бинарной операции. В группоиде на бинарную операцию нет никаких ограничений.
Группоид называют полугруппой, если его операция ассоциативна, т.е. для любых элементов
носителя
выполняется равенство
Пример 2.6. а. Множество свободных векторов вместе с операцией векторного умножения является группоидом, но не полугруппой, так как векторное умножение не ассоциативно.
б. Множество натуральных чисел вместе с операцией возведения в степень также будет только группоидом, так как .
в. Множество всех подмножеств множества
вместе с операцией
(разность множеств) тоже только группоид, поскольку указанная операция не ассоциативна.
г. Множество натуральных чисел вместе с операцией сложения будет полугруппой.
Группоид называют моноидом, если его операция ассоциативна и относительно операции существует нейтральный элемент. Его называют нейтральным элементом моноида
или единицей моноида и обозначают
.
Таким образом, моноид есть полугруппа, в которой для любого а имеют место равенства
, где
— нейтральный элемент (единица) моноида.
Поскольку нейтральный элемент относительно любой бинарной операции является единственным, мы можем рассматривать моноид как алгебру , сигнатура которой состоит из двух операций: бинарной операции
(умножение) и нульарной операции
(нейтрального элемента). Введение
в сигнатуру моноида удобно тем, что зачастую при рассмотрении конкретных примеров моноидов целесообразно явно указать нейтральный элемент относительно его операции. Например, алгебра
есть моноид всех бинарных отношений на множестве
с операцией композиции бинарных отношений, в котором нейтральным элементом является диагональ множества
.
Среди полугрупп выделяют полугруппы с коммутативной операцией — коммутативные полугруппы.
Пример 2.7. а. Множество всех бинарных отношений на произвольном множестве с операцией композиции отношений будет моноидом, нейтральным элементом которого служит диагональ множества
, поскольку для любых бинарных отношений
и
на множестве
имеют место равенства
и
.
б. Множество всех отображений некоторого множества в себя по операции композиции отображений есть моноид.
Напомним, что композиция отображений снова есть отображение и операция композиции имеет нейтральный элемент: тождественное отображение на себя. Поскольку любое отображение множества
в себя можно рассматривать как бинарное отношение на этом множестве, а композицию отображений — как частный случай композиции отношений, требуемые свойства операции композиции отображений выполняются (см. пример 2.7.а). При этом тождественному отображению соответствует диагональ
множества
. Этот моноид называют часто симметрическим моноидом или симметрической полугруппой множества
.
в. Алгебра , где носитель — множество
неотрицательных целых чисел, а сигнатура состоит из одной операции сложения, есть коммутативный моноид, в котором нейтральный элемент — это число 0. Действительно, сумма двух натуральных чисел есть натуральное число, операция сложения ассоциативна, коммутативна и для любого натурального числа
имеет место равенство
.
Обратим внимание на то, что свойства нейтральных элементов и нулей ассоциируются со свойствами чисел 1 и 0 относительно операций умножения и сложения чисел.
г. Алгебра , у которой носителем является множество целых чисел, а сигнатура состоит из одной операции умножения, есть коммутативный моноид. Нейтральным элементом этого моноида является число 1.
д. Пусть — конечное множество, а
— множество кортежей длины
. На множестве всех кортежей
определим операцию соединения (конкатенации) кортежей следующим образом:
Можно видеть, что введенная операция ассоциативна, но не имеет нейтрального элемента. Таким образом, построена полугруппа, но не моноид.
Чтобы превратить эту полугруппу в моноид, расширим носитель полугруппы, введя понятие нулевой декартовой степени произвольного множества
. Под
понимают одноэлементное множество
, единственный элемент которого называют пустым кортежем. Такое определение множества
объясняется следующим: мощность положительной декартовой степени
конечного множества равна
. При
должно быть
, откуда заключаем, что
— одноэлементное множество.
Обозначив , по определению для любого
полагаем
. В результате получим алгебру
, являющуюся моноидом, с нейтральным элементом
. Его называют свободным моноидом, порожденным множеством
.
Полурешетка в абстрактной алгебре
Полугруппу, операция которой коммутативна и идемпотентна, называют полурешеткой.
Пример 2.8. а. Алгебры (для произвольного фиксированного множества
) являются полурешетками, поскольку операции
и
ассоциативны, коммутативны и идемпотентны.
б. Алгебра , где
— операция вычисления наименьшего общего кратного двух чисел, является полурешеткой. Покажем, что указанная операция ассоциативна. Рассмотрим произвольные натуральные числа
и
. Каждое из этих чисел можно разложить на произведение простых чисел и представить в виде
где набор простых чисел выбран одинаковым для всех трех чисел, а некоторые из показателей
и
могут быть равными нулю. Тогда для чисел тип имеем
Таким образом, ассоциативность операции сводится к ассоциативности операции max вычисления наибольшего из двух натуральных чисел. Ассоциативность последней вытекает из очевидного тождества
, верного для любых чисел
и
.
Поскольку , операция
коммутативна, а так как для любого натурального числа справедливо равенство
, то операция идемпотентна.
в. Алгебра , где
— операция вычисления наибольшего общего делителя двух целых чисел, также является полурешеткой.
Способы задания группы как алгебры
Группоид называют группой, если операция ассоциативна, существует нейтральный элемент (единица)
относительно умножения и для каждого
существует такой элемент
, называемый обратным к
, что
.
Таким образом, группа — это алгебра , в которой для всех
выполняется равенство
, существует единственный элемент
, такой, что
для любого
, и для каждого
существует такой элемент
, что
. Короче говоря, группа — это моноид, в котором для каждого элемента существует обратный элемент.
Отметим, что задать группу как алгебру можно несколькими способами в зависимости от состава операций, включенных в сигнатуру.
Во-первых, в сигнатуру может быть включена единственная бинарная операция. В этом случае пишут , а все свойства операции описывают дополнительно.
Во-вторых, в сигнатуру может быть включена нульарная операция — нейтральный элемент группы. В этом случае пишут и дополнительно указывают существование обратного элемента относительно бинарной операции для всех элементов носителя.
Третий способ задания группы как алгебры вытекает из следующей теоремы.
Теорема 2.1. В любой группе для каждого
элемент, обратный к
, единственный.
Пусть в группе с единицей
для некоторого
существуют два элемента
и
, обратных к
. Тогда
в силу свойства единицы. Так как
, то
. Используя ассоциативность и учитывая, что
— элемент, обратный к а, получим
Единственность для каждого элемента обратного элемента
группы
позволяет обозначать его как
и операцию
вычисления (или взятия) обратного элемента ввести в сигнатуру группы. Таким образом, группу можно рассматривать и как алгебру
, сигнатура которой состоит из бинарной операции умножения, унарной операции взятия обратного элемента и нульарной операции — единицы группы (нейтрального элемента).
В дальнейшем в зависимости от контекста будем использовать все указанные варианты задания группы.
Среди групп также выделяют те, бинарная операция в которых коммутативна, — коммутативные (абелевы) группы. В коммутативных полугруппах и группах бинарную операцию часто обозначают знаком и называют сложением.
Уместно здесь рассмотреть вопрос о двух формах записи бинарной операции группы. В аддитивной записи операции ее обозначают знаком , нейтральный элемент — знаком
, а элемент, обратный к
относительно операции
, записывают в виде
, называя его при этом противоположным к
.
В мультипликативной записи операцию обозначают знаком , нейтральный элемент — знаком
, а элемент, обратный к
, записывают в виде
. В этом случае бинарную операцию группы часто называют умножением (также умножением группы или групповым умножением), а элемент
, как правило записываемый в виде
, — произведением элементов
и
.
В алгебраической литературе сложилась такая традиция, что аддитивная запись используется преимущественно для коммутативных групп. Поскольку одним из самых простых, распространенных и вместе с тем важных примеров коммутативной группы служит аддитивная группа целых чисел, то обозначения и термины для произвольной аддитивно записываемой коммутативной группы «скопированы» с терминов для группы . Аналогично мультипликативная запись произвольной группы » позаимствована» у мультипликативных групп рациональных и вещественных чисел.
Пример 2.9. а. Алгебра — коммутативная группа, поскольку на множестве целых чисел операция сложения ассоциативна и коммутативна, число 0 есть нейтральный элемент, и для каждого целого числа
существует обратный по сложению элемент, а именно число
, противоположное
. Рассматриваемую группу называют аддитивной группой целых чисел.
б. Множество всех биекций некоторого множества на себя с операцией композиции отображений есть группа.
Это следует из того, что композиция двух биекций есть биекция, операция композиции ассоциативна, ее нейтральный элемент — тождественное отображение — есть биекция, для всякой биекций
отображение
, обратное биекций
, определено, является биекцией и выполнены равенства
Эту группу называют симметрической группой множества , а в том случае, когда множество
конечно, — группой подстановок множества
. Если множество
состоит из
элементов, группу подстановок этого множества называют также симметрической группой степени
или группой подстановок n-й степени и обозначают
(см. пример 2.10).
в. Алгебры и
есть коммутативные группы. Их называют мультипликативной группой рациональных чисел и мультипликативной группой действительных чисел соответственно. В каждой из них число 1 есть нейтральный элемент (единица) группы, а обратный к числу
по операции умножения элемент
есть число
.
г. Для произвольно фиксированного множества рассмотрим алгебру
, где
— операция вычисления симметрической разности множеств. Операция
ассоциативна и коммутативна. Для любого
имеем
. Кроме того,
тогда и только тогда, когда
. Поэтому алгебра
является абелевой группой, в которой каждый элемент обратен сам себе, а нейтральный элемент — пустое множество.
д. Рассмотрим алгебру , в которой операция
(сложения по модулю
) определяется так: для любых двух
и
число
, называемое суммой чисел
и
по модулю
, равно остатку от деления арифметической суммы
на
. Можно проверить, что эта алгебра является коммутативной группой. Ее называют аддитивной группой вычетов по модулю
. Нейтральным элементом служит число 0, а обратным к числу
будет
, поскольку
.
е. Множество всех невырожденных (т.е. имеющих ненулевой определитель) числовых квадратных матриц порядка с операцией умножения матриц является группой. Действительно, произведение двух невырожденных матриц снова есть невырожденная матрица; единичная матрица порядка
невырожденная, и матрица, обратная к невырожденной, также является невырожденной. Эту группу будем обозначать
.
Из рассмотренных четырех видов алгебр — группоида, полугруппы, моноида и группы — последняя обладает наиболее интересными свойствами. Изучим более подробно операцию вычисления обратного элемента.
Теорема 2.2. Пусть — группа. Для любых элементов
верны тождества
В силу ассоциативности умножения группы имеем
Используя еще раз ассоциативность, определение элемента, обратного к данному, и свойства единицы, получим
Итак, . Точно так же доказывается, что
. Поэтому элемент
является обратным к элементу
. Согласно теореме 2.1, обратный элемент единственный, и поэтому
. Второе из доказываемых равенств следует непосредственно из определения элемента, обратного к данному. Действительно, определение элемента
, обратного к
, равенством
можно рассматривать как определение
— обратного элемента к
, которым является, согласно этим равенствам, элемент
. В силу теоремы 2.1 он единственный, то есть
.
Таким образом, мы установили, что элемент, обратный к произведению , равен
, а элемент, обратный к элементу, обратному к
, равен
.
Теорема 2.3. В любой группе справедливы левый и правый законы сокращения: если
, то
, и если
, то
.
Пусть . Умножая обе части этого равенства слева на элемент
, получаем
В силу ассоциативности групповой операции последнее равенство можно записать так:
Поскольку , то
, откуда
. Тем самым доказан левый закон сокращения. Аналогично доказывается и правый закон.
Пусть — группа,
и
— фиксированные элементы
. Рассмотрим задачу решения уравнений
(2.1)
(2.2)
в группе , т.е. поиска всех таких элементов
, для которых уравнение (2.1) (или (2.2)) превращается в тождество.
Теорема 2.4. В любой группе уравнения вида (2.1) и (2.2) имеют решения, и притом единственные.
Покажем, что есть решение (2.1). Действительно,
.
Докажем единственность решения. Пусть для фиксированных и
и некоторого
выполнено равенство
. В группе для любого
существует и однозначно определен элемент
, обратный к
. Умножив на него обе части равенства, получим
. В силу ассоциативности преобразуем последнее равенство к виду
. Поскольку
, то
, откуда
. Это решение единственное в силу единственности обратного элемента.
Аналогично из получаем
, и это решение также единственное.
Замечание. При использовании аддитивной записи операции для коммутативной группы оба написанных выше уравнения сводятся к одному:
а его решение есть . Правую часть этого равенства в коммутативной группе называют разностью элементов
и
и обозначают
. Саму же операцию, сопоставляющую упорядоченной паре
разность
, называют операцией вычитания. С учетом введенных обозначений решение уравнения в коммутативной группе можно записать так:
.
В случае коммутативной группы при употреблении для бинарной операции мультипликативной записи решения обоих уравнений имеют вид . Выражение
в коммутативной группе называют частным от деления
на
и обозначают
(или
), а саму операцию называют операцией деления. Решение уравнения в этом случае записывают в виде
(или
).
Пример 2.10. Рассмотрим группу подстановок n-й степени всех биекций n-элементного множества
. Произвольную биекцию
из
обычно записывают в виде
обозначая тем самым, что образ 1 (при отображении ) есть
, образ 2 есть
образ
есть
. Биекцию множества
на себя называют подстановкой этого множества. Подстановку, которая отображает
в
,
в
,
в
, а
в
, где
и все
попарно различны, а все элементы, отличные от
, отображаются сами в себя, называют циклом длины
и записывают ее в виде
. Например, подстановку из группы
можно записать в виде
.
Цикл длины 2 называют транспозицией. Транспозиция представляет такое отображение множества в себя, при котором два элемента меняются местами, а остальные остаются на своих местах. Так, полная запись транспозиции
в
будет иметь вид
Подстановка, обратная подстановке , есть подстановка, которая отображает
в 1,
в 2,
в
. Отметим, что при записи обратной подстановки элементы первой строки тем не менее записываются в обычном порядке:
.
В группе решим следующее уравнение:
Умножив обе части уравнения слева на
, получим
.
Далее, умножив полученное уравнение справа на
окончательно получим
.
Степень элемента в полугруппе
В полугруппе в общем случае законы сокращения и разрешимость уравнений типа (2.1) и (2.2) могут не иметь места. Например, в полугруппе квадратных матриц фиксированного порядка с операцией умножения матриц из матричного равенства , вообще говоря, не следует, что
. Это можно утверждать лишь при дополнительном предположении, что
. Можно доказать, что в свободном моноиде, порожденном некоторым конечным множеством, оба закона сокращения справедливы, но никаких обратных элементов не существует.
В полугруппе можно умножать любой элемент сам на себя, причем в силу ассоциативности операции полугруппы элемент
определен однозначно. Этот элемент называют n-й степенью элемента
и обозначают
. При этом
В моноиде вводят также нулевую степень элемента, полагая .
Если — группа, то можно ввести и отрицательные степени элемента согласно равенству
Без доказательства сформулируем утверждения о свойствах степеней.
Теорема 2.5. Для любой полугруппы .
Теорема 2.6. Для любой группы .
Определение 2.4. Полугруппу (в частности, группу) называют циклической, если существует такой элемент
, что любой элемент
полугруппы является некоторой (целой) степенью элемента
. Элемент
называют образующим элементом полугруппы (группы).
Пример 2.11. а. Полугруппа циклическая, с образующим элементом 1. При аддитивной записи бинарной операции возведение элемента
в положительную степень
есть сумма
этих элементов, и это записывают
(или
, без знака умножения).
б. Группа также циклическая. Для нее образующими элементами могут быть 1 и –1. Рассмотрим элемент 1. Тогда
Если в качестве образующего взять элемент –1, то , отрицательные целые числа получаются как положительные «степени» –1, а положительные — как отрицательные «степени» –1. Например,
.
в. Группа вычетов по модулю 3 циклическая, причем любой ее ненулевой элемент является образующим.
Действительно, для 1 имеем , а для 2 получим
Строение конечных циклических групп
Изучим подробнее строение конечных циклических групп, используя мультипликативную запись бинарной операции. Напомним, что конечная алгебра {конечная группа, в частности) — это алгебра, носитель которой — конечное множество.
Порядком конечной группы называют количество элементов в этой группе.
Так, например, аддитивная группа вычетов по модулю имеет порядок
. Симметрическая группа степени
, т.е. группа подстановок
, имеет порядок
!. Мультипликативная группа вычетов по модулю
, где
— простое число, имеет порядок
.
Порядок элемента а циклической группы — это наименьшее положительное , такое, что
.
Теорема 2.7. Порядок образующего элемента конечной циклической группы равен порядку самой группы.
Пусть — конечная циклическая группа с образующим элементом
и
— порядок этого элемента.
Тогда все степени попарно различны. Действительно, если
, то
.
Поскольку , получено противоречие с выбором
как порядка элемента
(ибо найдена степень, меньшая
, при возведении в которую элемента
получится единица).
Осталось доказать, что любая степень элемента принадлежит множеству
. Для любого целого
существуют также целые
, такие, что
, где
— целое и
. Тогда
Поскольку каждый элемент группы есть некоторая степень элемента
, то
и порядок группы равен
.
Из доказанной теоремы следует, что в бесконечной циклической группе не существует такого , что для образующего элемента
группы выполняется равенство
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

 -угольника.
-угольника. градусов.
градусов. группы
группы  — элемент, имеющий порядок
— элемент, имеющий порядок  в группе
в группе  .
. .
. градусов 1 раз, если повернуть второй раз, то возвращаемся в первый элемент цикла.
градусов 1 раз, если повернуть второй раз, то возвращаемся в первый элемент цикла. , где
, где  — единичный элемент группы.
— единичный элемент группы. .
. , то мы окажемся повёрнуты на
, то мы окажемся повёрнуты на  . Типа того:
. Типа того:  . Что означают Ваши слова о том, что мы якобы куда-то возвращаемся? Куда это, как это?
. Что означают Ваши слова о том, что мы якобы куда-то возвращаемся? Куда это, как это? .
.
 (или, что то же самое, на угол кратный
(или, что то же самое, на угол кратный  ).
).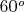 . Начните последовательно применять этот поворот. Получите ли Вы при этом все элементы исходной группы?
. Начните последовательно применять этот поворот. Получите ли Вы при этом все элементы исходной группы?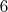 вращений многоугольника, а не все.
вращений многоугольника, а не все.