Как найти все корни методом хорд - Avtoru.top - решение различных проблем

Этот метод нахождения
простых корней широко применяется при
решении конечных уравнений. Другие
названия рассматриваемого метода: метод
ложного положения, метод линейной
аппроксимации, метод пропорциональных
частей, метод секущих.

Идея
метода хорд состоит в том, что на
достаточно малом промежутке
дуга кривойy=f(x)
заменяется стягивающей ее хордой. В
качестве приближенного значения корня
принимается точка пересечения хорды с
осью Ox,
т.е. это точка x=c.

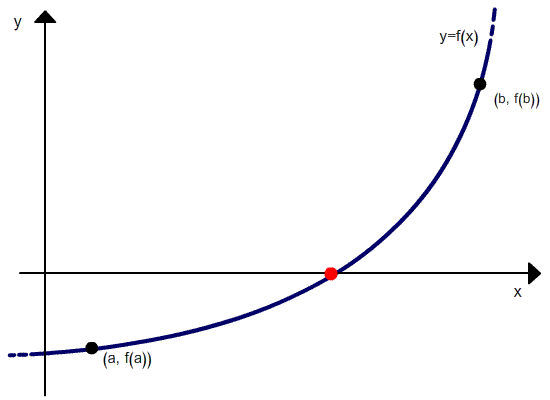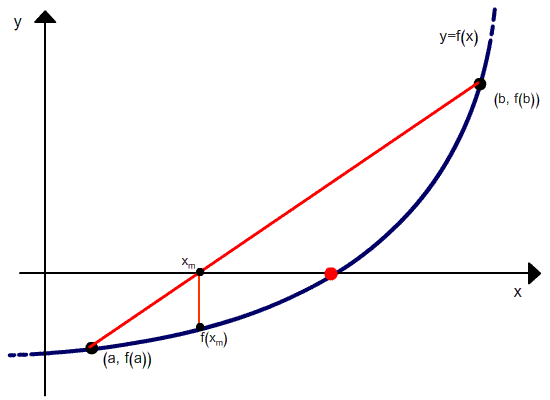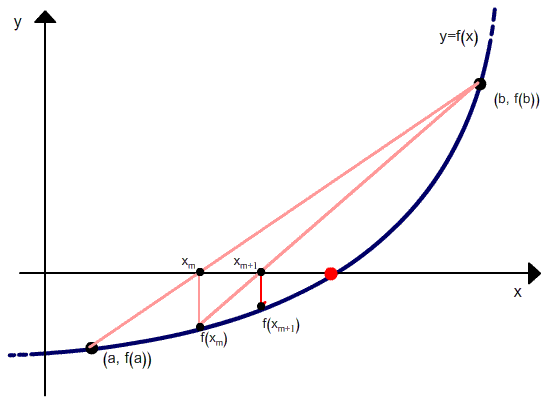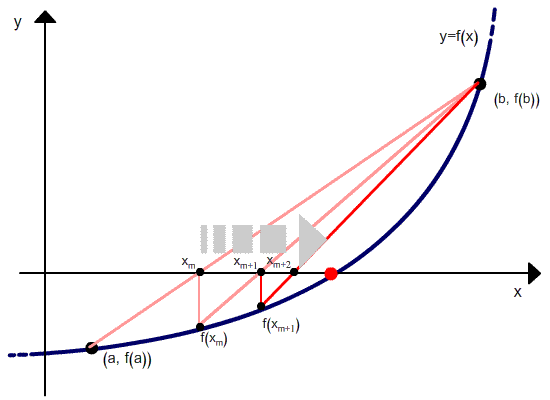
Пусть
дано уравнение
,
где-непрерывная
функция, имеющая в интервалепроизводные первого и второго порядков.
Корень считается отделенным и находится
на отрезке,
т.е..

Существуют
четыре случая расположения дуги кривой,
учитывая значения первой и второй
производных:

Рассмотрим
случай, когда первая и вторая производные
имеют одинаковые знаки, т.е.
.

Пусть,
например,
График функции проходит через точки.
Искомый корень уравненияесть абсцисса точки пересечения графика
функциис осьюOx.
Эта точка нам не известна, но вместо нее
возьмем точку с
пересечения хорды с осью Ox.
Эта точка x₁=c
является
приближенным значением корня.

Уравнение
хорды, проходящей через точки А₀
и В
имеет вид:

а
абсцисса ее точки пересечения x₁=c
с осью Ox
(т.е. когда
)
определяется
формулой:

Очевидно,
что точка x₁=c
обязательно
окажется внутри отрезка
,
при этом она будет тем ближе к искомому
корню, чем меньше кривизна графика
функции, а так как кривизна определяется
формулой:

Точка
x₁=c
будет тем ближе к некому корню
,
чем меньшеи чем большена отрезке.

Замечание
Хорда всегда расположена со стороны
вогнутости дуги графика и, как видно из
приведенных выше рисунков, точки x₁=c
всегда ближе точки x₀
к тому концу отрезка
,
в котором знак функциипротивоположен знаку ее второй производнойf’’(x).

Пример

Методом
хорд уточнить корень уравнения
отделенный на отрезке.

Решение

Имеем

=,f’(x)=3x²-1,
f’’(x)=6x.
Так как на отрезке
,
то точкаx₁=c
будет левым концом нового отрезка
;

Отметим,
что приближенное значение с
взято с недостатком, т.к. с<x₀
и при округлении с избытком есть опасность
«перешагнуть» через корень x₀.
В качестве отрезка
для дальнейшего уточнения следует
взять [1,1;2].

Если
значение приближенного корня x1
не устраивает, его можно уточнить,
применяя метод хорд к отрезку
.
Соединив точкуA₁(x₁,f(x₁))
с точкой
B(b,f(b))
находим
x₂
– точку
пересечения хорды с осью
Ox:

Продолжая этот
процесс, находим:

и
вообще

Процесс продолжается
до тех пор, пока не получим приближенный
корень с заданной степенью точности.

По
приведенным выше формулам вычисляются
корни и для случая, когда

Теперь
рассмотрим случай, когда первая и вторая
производные имеют разные знаки, т.е.
.

Пусть,
например,
В
этом случае соединив точки,
имеем уравнение хорды, проходящей черезA
и B_0:

Найдем
x₁
как точку пересечения хорды с осью
Ox,
полагая y=0:

Корень
теперь заключен внутри подотрезка
.

Применяя
метод хорд к отрезку
,
получим:

и
вообще

По
этим же формулам находится приближенное
значение корня и для случая, когда

С учетом сделанного
выше отметим, что выбор тех или иных
формул метода хорд обуславливается
правилом – неподвижным концом отрезка
является тот, для которого знак функции
совпадает со знаком ее второй производной.

Так,
если
,
то неподвижен конецb,
а все приближения к корню
x₀лежат со
стороны конца
a;
если же
,
то неподвижен конецa,
а все
приближения к корню
x₀лежат
со стороны конца b.

При
оценке погрешности приближения пользуются
формулой:,
где—
точное значение искомого корня, аи-приближения к нему, полученные на(n-1)
и
n-м
шагах.

Эта
формула применима, если выполнено
условие
где

Пример

Методом
хорд уточнить до
меньший корень уравнения,
отделенный на отрезке [-3,-2].

Решение

Проверим
выполнимость условия
,
учитывая что,.

Возьмем
середину отрезка [-3,-2], т.е. точку x=-2,5,
и выберем интервал [-3,-2,5]. Снова проверим
условие
:

Теперь
возьмем середину отрезка [-3,-2,5], т.е точку
x=-2,75.

На
суженном отрезке [-2,75;-2,5] сохраняется
условие монотонности функции (условие
).
Действительно,f(-2,75)=-2,75³+3*2,75²-3<0;
f(-2,5)=-2,5³+3*2,5²-3>0;

т.е.
6,189<2*3,75.

Таким
образом, для оценки погрешности корня,
лежащего на отрезке [-2,75;-2,5], можно
пользоваться формулой
,
т.е. процесс последовательного приближения
к корню следует продолжать до тех пор,
пока не будет выполнено условие.

Определим
знак второй производной f’’(x)
и установим, какой конец отрезка будет
неподвижным при использовании метода
хорд. Находим f’’(x)=6x+6
и
.
Значит, за неподвижный конец отрезка
нужно приниматьx=-2,75,
а вычисление вести по формулам:
и,
гдеa=-2,75;
f(a)=-1,1019.

Если
последнее выражение представить в виде:
,
то сразу же можно будет получать разность
между двумя последовательными
приближениями и производить проверку
на окончание вычислений, т.е. проверять
выполнение неравенства:

Все результаты
сведем в таблицу:

n	x_n			3	f(x_n)	x_n-a
0	-2,5	-15,625	6,250	18,75	0,125	0,25	-0,025
1	-2,525	-16,098	6,3756	19,1268	0,0288	0,225	-0,006
2	-2,531	-16,213	6,4060	19,2180	0,0050	0,219	-0,0009
3	-2,5319

Из
этой таблицы следует, что
,
поэтому, округляя
x³
до тысячных долей, получаем
.

Пример

Методом
хорд уточнить до
корень уравнения,
заключенный на отрезке.

Решение

Перепишем
уравнение в виде
и определимf’(x)=1-cos
x.
Для проверки выполнения условия
составим вспомогательную таблицу:

a	b	знаки	M	m	?		знак
f(a)	f(b)
0	1,57	—	+	1,00	0	10	0,785	—
0,785	1,57	—	+	1,00	0,29251	120,29251*	1,1775	+
0,785	1,1775	—	+	0,6172	0,2925	0,617220,292*	0,982	—
0,982	1,1775	—	+	0,6172	0,4446	0,6172<20,4446*

Из
последней строки этой таблицы видно,
что на отрезке [0,982;1,1775] условие
выполняется и, следовательно, при оценке
погрешности приближенного значения
корня по методу хорд можно воспользоваться
неравенством.
Корень уравнениянаходится на отрезке [0,982;1,1775].

Вторая
производная функции на этом интервале
положительна (т.к. f’’(x)=sinx>0
) и совпадает
со знаком функции в точке b=1,1775.

Следовательно,
этот конец отрезка является неподвижным,
а все приближения к корню x₀
лежат со стороны конца a=0,982.

Для вычисления
приближений по методу хорд в данной
задаче пользуемся формулами:

,
,
гдеb=1,1775,
f(b)=0,00416.

Составим следующую
таблицу:

n	x_n	—sin x_n		b-x_n
0	0,982	-0,83161	-0,09961	0,196	0,189
1	1,171	-0,92114	-0,00014	0,007	0,0002
2	1,1712

Итак,
с точностью до

Соседние файлы в папке Лекции Маркина

Источник

Численные методы решения нелинейных уравнений

Корни нелинейных уравнений

Пусть дано нелинейное уравнение

f(x)=0,qquad mathsf{(3.1)}

где f(x) — функция, определенная и непрерывная на некотором промежутке. В некоторых случаях на функцию f(x) могут быть наложены дополнительные ограничения, например, непрерывность первой и второй производных, что специально оговаривается. Функция f(x) может быть задана в виде алгебраического многочлена или трансцендентной функции (тогда ей соответствует алгебраическое или трансцендентное уравнение).

Требуется найти корни нелинейного уравнения (3.1), т.е. числа $x_{ast1},x_{ast2},ldots$ которые путем подстановки их в (3.1) превращают уравнение в верное числовое равенство. Числа $x_{ast1},x_{ast2},ldots$ называются также нулями функции f(x) .

На практике часто бывает выгодно уравнение (3.1) заменить равносильным ему уравнением (уравнения равносильны, если имеют одинаковые корни):

f_1(x)-f_2(x)=0,

(3.2)

где функции f_1(x),,f_2(x) — более простые, чем функция f(x) . Тогда при задании уравнения в виде (3.1) нулями функции f(x) являются точки пересечения f(x) с осью (рис. 3.1,д), а при задании в виде (3.2) — абсциссы точек пересечения функций f_1(x) и f_2(x) (рис. 3.1,б).

Точки пересечения функции с осью абсцисс

Замечания

1. Если $f(x)=a_nx^n+a_{n-1}x^{n-1}+ldots+a_0=P_n(x)$ — алгебраический многочлен, то уравнение (3.1) называется также алгебраическим n-й степени:

$P_n(x)equiv a_nx^n+a_{n-1}x^{n-1}+ldots+a_0=0,$

(3.3)

где a_n,ldots,a_0 — действительные числа, коэффициенты уравнения.

График сеточной функции

2. На практике встречаются задачи нахождения корней уравнения f(x_i)=0 , левая часть которого задана сеточной функцией y_i=f(x_i),~i=1,2,ldots,N (рис. 3.2).

Число $x_{ast}$ есть корень уравнения (3.1) кратности , если при $x=x_{ast}$ вместе с функцией f(x) обращаются в нуль ее производные до (k-1)-го порядка включительно, т.е. $f(x_{ast})= f'(x_{ast})= ldots= f^{(k-1)}(x_{ast})=0$ , а $f^{(k)}(x_{ast})ne0$ . Корень кратности к = 1 называется простым. На рис 3.1,с простыми корнями являются $x_{ast1},x_{ast2},x_{ast3}$ , a корни $x_{ast4},x_{ast5}$ — кратные.

В соответствии с классическим результатом Галуа алгебраическое уравнение (3.1) при ngeqslant5 не имеет решения в замкнутом (формульном) виде. Сеточные уравнения вообще не имеют формульных решений. Поэтому корни алгебраических (n>2) , трансцендентных и сеточных уравнений, как правило, определяются приближенно с заданной точностью.

Решение осуществляется в два этапа:

Первый этап. Находятся отрезки [a_i,b_i] , внутри каждого из которых содержится один простой или кратный корень $(x_{ast i}in[a_i,b_i])$ (см. рис. 3.1). Этот этап называется процедурой отделения корней. По сути на нем осуществляется грубое нахождение корней $x_{ast i}$ .

Второй этап. Грубое значение каждого корня $x_{ast i}$ уточняется до заданной точности одним из численных методов, в которых реализуются последовательные приближения. Порядок (скорость) сходимости метода определяется так же, как в методе простых итераций.

Отделение корней уравнения

Для отделения действительных корней полезно определять заранее число корней, а также верхнюю и нижнюю границы их расположения. Для этого используется ряд теорем.

Теорема 3.1 (о числе корней алгебраического уравнения (3.3)). Алгебраическое уравнение (3.3) n-й степени имеет ровно корней, действительных или комплексных, при условии, что каждый корень считается столько раз, какова его кратность.

Теорема 3.2 (о свойстве парной сопряженности комплексных корней уравнения (3.3)). Если $x_{ast i}=alpha+beta i$ — корень алгебраического уравнения (3.3) кратности , то число $overline{x_{ast i}}=alpha-beta i$ также является корнем той же кратности.

Следствие. Алгебраическое уравнение нечетной степени имеет по крайней мере один действительный корень.

Теорема 3.3 (об оценке модулей корней уравнения (3.3)). Пусть

$A=max bigl{|a_{n-1}|,ldots,|a_0|bigr},qquad B=max bigl{|a_n|,|a_{n-1}|,ldots, |a_1|bigr},$

где $a_k,~k=overline{0,n}$ — коэффициенты уравнения $a_nx^n+a_{n-1}x^{n-1}+ ldots+ a_{1}x+a_0=0$ . Тогда модули всех корней $x_{ast i}~(i=1,2,ldots,n)$ уравнения удовлетворяют неравенству

$frac{1}{1+dfrac{B}{|a_0|}}<|x_{ast i}| leqslant 1+frac{A}{|a_n|},quad i=1,2,ldots,n,$

(3.4)

т.е. корни уравнения расположены в кольце.

Следствие. Числа $r=frac{1}{1+dfrac{B}{|a_0|}}$ и $R=1+ frac{A}{|a_n|}$ являются соответственно нижней и верхней границами положительных корней алгебраического уравнения: $r<x_{ast i}^{+}<R$ . Аналогично числа и служат нижней и верхней границами отрицательных корней уравнения: $-R<x_{ast i}^{-}<-r$ .

Приведем полезные теоремы, используемые для более точного установления границ действительных корней алгебраических уравнений.

Теорема 3.4 (теорема Лагранжа о верхней границе положительных корней уравнения (3.3)). Пусть a_n>0 и a_i — первый отрицательный коэффициент в последовательности $a_n,a_{n-1},a_{n-2},ldots,a_1,a_0;~C$ — наибольшая из абсолютных величин отрицательных коэффициентов. Тогда за верхнюю границу положительных корней уравнения (3.3) может быть принято число

$R=1+sqrt[LARGE{n-i}]{frac{C}{a_n}},.$

(3.5)

Теорема 3.5 (о нижних и верхних границах положительных и отрицательных корней алгебраического уравнения). Пусть — верхняя граница положительных корней уравнения P_n(x)=0 ,

R_1 — верхняя граница положительных корней уравнения $P^1(x)= x^nP_n! left(frac{1}{x}right)=0$ ,
R_2 — верхняя граница положительных корней уравнения P^2(x)= P_n(-x)=0 ,
R_3 — верхняя граница положительных корней уравнения $P^3(x)= x^nP_n! left(-frac{1}{x}right)=0$ .

Тогда положительные корни $x_{ast i}^{+}$ и отрицательные корни $x_{ast i}^{-}$ уравнения (3.3) удовлетворяют неравенствам

$frac{1}{R_1}leqslant x_{ast i}^{+}leqslant R,qquad-R_2 leqslant x_{ast i}^{-}leqslant-frac{1}{R_3},.$

(3.6)

Теорема 3.6 (теорема Декарта о количестве действительных корней алгебраических уравнений). Число S_1 положительных корней (с учетом их кратностей) алгебраического уравнения P_n(x)=0 равно числу перемен знаков в последовательности коэффициентов $a_n,a_{n-1},ldots,a_0$ (коэффициенты, равные нулю, не учитываются) многочлена P_n(x) или меньше этого числа на четное число. Число S_2 отрицательных корней (с учетом их кратностей) алгебраического уравнения P_n(x)=0 равно числу перемен знаков в последовательности $a_n,a_{n-1},ldots,a_0$ многочлена P_n(-x) или меньше этого числа на четное число.

Теорема 3.7 (теорема Гюа о необходимом условии действительности всех корней алгебраического уравнения). Если алгебраическое уравнение (3.3) имеет все действительные корни, то квадрат каждого некрайнего коэффициента больше произведения двух его соседних коэффициентов.

Следствие. Если при каком-нибудь выполнено неравенство $a_k^2 leqslant a_{k-1}a_{k+1}$ , то уравнение (3.3) имеет по крайней мере одну пару комплексных корней.

Для отделения корней применяется следующая теорема.

Теорема 3.8. Если функция f(x) , определяющая уравнение f(x)=0 , на концах отрезка [a_i,b_i] принимает значения разных знаков, т.е. f(a_i)cdot f(b_i)<0 , то на этом отрезке содержится по крайней мере один корень уравнения. Если же f(x) непрерывна и дифференцируема и ее первая производная сохраняет знак внутри отрезка [a_i,b_i] $Bigl(mathop{operatorname{sign}}limits_{xin[a_i,b_i]} f'(x)=text{const}Bigr)$ , то на находится только один корень уравнения.

Способы отделения корней

В вычислительной практике обычно используются следующие способы отделения корней:

1) средствами машинной графики: функция f(x) представляется на дисплее и приближенно определяются отрезки, которым принадлежат точки $x_{ast i}$ ;

2) средствами математического анализа с помощью исследования функций и построения графиков (см. рис. 3.1,д);

3) формированием простых функций f_1(x) и f_2(x) таких, что получается равносильное уравнение в виде (3.2), и дальнейшим построением графиков этих функций (см. рис. 3.1,б).

▼ Примеры 3.1-3.3

Пример 3.1. Определить число положительных и отрицательных корней, а также их границы для уравнения

P_5(x)= x^5+2x^4-5x^3+8x^2-7x-3=0.

Решение

В данной задаче n=5,~ a_5=1,~ a_4=2,~ a_3=-5,~ a_2=8,~ a_1=-7,~ a_0=-3 . Согласно теореме 3.1 уравнение имеет пять корней. Поскольку n=5 , то по следствию из теоремы 3.2 уравнение имеет по крайней мере один действительный корень.

Оценим модули корней по теореме 3.3. Так как

A=max bigl{|2|,|-5|,|8|,|-7|,|-3|bigr}=8,qquad B=max bigl{|1|,|2|,|-5|, |8|,|-7|bigr}=8,

то $frac{1}{1+frac{8}{|-3|}}<|x_{ast i}|<1+frac{8}{|1|}$ или $frac{3}{11}<|x_{ast i}|<9$ , т.е. все корни лежат внутри данного кольца. По следствию из теоремы 3.3 это означает, что положительные корни удовлетворяют неравенству $frac{3}{11}<x_{ast i}^{+}<9$ , а отрицательные — неравенству $-9<x_{ast i}^{-}<-frac{3}{11}$ .

Применим теоремы 3.4 и 3.5 для уточнения приведенных результатов. Найдем верхнюю границу положительных корней. Так как a_3=-5 — первый отрицательный коэффициент в последовательности 1,2,-5,8,-7,-3 , то i=3 , а C=max bigl{|-5|,|-7|,|-3|bigr}=7 — наибольшая из абсолютных величин отрицательных коэффициентов. Следовательно, $R=1+sqrt[LARGE{(5-3)}]{frac{7}{1}}= 1+sqrt{7}cong3,!646$ .

Найдем нижнюю границу положительных корней. Составим уравнение:

$begin{aligned}P^{1}(x)&= x^nP_n! left(frac{1}{x}right)= x^5P_5!left(frac{1}{x} right)= x^5! left(frac{1}{x^5}+ frac{2}{x^4}-frac{5}{x^3}+frac{8}{x^2}-frac{7}{x}-3right)=\ &=-3x^5-7x^4+8x^3-5x^2+2x+1=0.end{aligned}$

или 3x^5+7x^4-8x^3+5x^2-2x-1=0 (старший коэффициент должен быть положительным). Для этого уравнения i=3,~ C=max bigl{|-8|,|-2|,|-1|bigr}=8 , поэтому $R_1=1+sqrt[LARGE{(5-3)}]{frac{8}{3}}=1+sqrt{frac{8}{3}}cong2,!632$ . Отсюда $frac{1}{R_1}=0,!38 leqslant x_{ast i}^{+}leqslant R=3,!646$ .

Уточним границы отрицательных корней. Составим уравнение:

P^2(x)=P_5(-x)= или x^5-2x^4-5x^3-8x^2-7x+3=0 .

Для этого уравнения i=4,~ C=maxbigl{|-2|,|-5|,|-8|,|-7|bigr}=8 , поэтому $R_2=1+ sqrt[LARGE{5-4}]{frac{8}{1}}=9$ . Составим уравнение

$begin{aligned}P^3(x)&= x^nP_n! left(-frac{1}{x}right)= x^5P_5! left(-frac{1}{x}right)= x^5! left(-frac{1}{x^5}+frac{2}{x^4}+frac{5}{x^3}+frac{8}{x^2}+frac{7}{x}-3right)=\ &=-3x^5+7x^4+8x^3+2x-1=0.end{aligned}$

или 3x^5-7x^4-8x^3-5x^2-2x+1=0 . Для этого уравнения i=4,~ C=max bigl{|-7|,|-8|,|-5|,|-2|bigr}=8 , поэтому $R_3=1+sqrt[LARGE{5-4}]{frac{8}{3}}=1+ frac{8}{3}cong3,!666$ . Отсюда находим: $-R_2=-9 leqslant x_{ast i}^{-}leqslant-frac{1}{R_3}=-0,!272$ . Заметим, что данный результат совпадает с полученным ранее.

Исследуем структуру корней уравнения. Так как квадрат каждого некрайнего коэффициента больше произведения двух его соседних коэффициентов, то по теореме 3.7 необходимое условие действительности всех корней уравнения выполняется.

На основе теоремы 3.6 определим число положительных и отрицательных корней. Выписываем коэффициенты многочлена P_n(x)=P_5(x)colon, 1,,2,-5,,8,-7,-3 . Так как число перемен знака S_1=3 , то число положительных корней равно трем или меньше на четное число, т.е. равно 1. Далее выписываем коэффициенты многочлена P_5(-x)colon, -1,,2,,5,,8,,7,-3 . Так как число перемен знаков S_2=2 , то число отрицательных корней равно двум или меньше на четное число, т.е. их вообще нет.

Пример 3.2. Отделить корни кубического уравнения x^3-x+1=0 .

Решение

Точка пересечения кубической параболы и прямой

Согласно теореме 3.1 уравнение имеет три корня, среди которых по крайней мере один действительный (следствие из теоремы 3.2, поскольку это уравнение нечетной степени).

Оценим модули корней уравнения по теореме 3.3. Так как

A=max bigl{|0|,|-1|,|1|bigr}=1,quad B=max bigl{|1|,|0|,|-1|bigr}=1 , то $frac{1}{1+dfrac{1}{|1|}}<|x_{ast i}|<1+frac{1}{|1|}$ или $frac{1}{2}<|x_{ast i}|<2$ .

Отсюда $frac{1}{2}<x_{ast i}^{+}<2$ и $-2<x_{ast i}^{+}<-frac{1}{2}$ .

Определим число положительных и отрицательных корней. Выписываем коэффициенты многочлена P_3(x)colon, 1,,0,-1,,1 . Так как число перемен знака S_1=2 (нулевой коэффициент не учитывается), то число положительных корней равно двум или меньше на четное число, т.е. они отсутствуют. Далее выписываем коэффициенты многочлена P_3(-x)=-x^3+x+1colon, -1,,0,,1,,1 . Так как число перемен знака S_2=1 (нулевой коэффициент не учитывается), то число отрицательных корней равно единице.

Отделим корни третьим способом. Для этого преобразуем уравнение к равносильному виду (3.2): x^3=x-1 и найдем точки пересечения фафиков y=x^3 и y=x-1 (рис. 3.3).

Очевидно, корень уравнения $x_{ast}in[-2;-1]$ .

Пример 3.3. Отделить корни уравнения третьего порядка x^3-x^2-9x+9=0 .

Решение

Процедура уточнения положения корня функции

Метод половинного деления

Пусть дано уравнение f(x)=0 и отделен простой корень $x_{ast}$ , т.е. найден такой отрезок [a_0,b_0] , что $x_{ast}in[a_0,b_0]$ и на концах отрезка функция имеет значения, противоположные по знаку (f(a_0)cdot f(b_0)<0) . Отрезок называется начальным интервалом неопределенности, потому что известно, что корень ему принадлежит, но его местоположение с требуемой точностью не определено.

Процедура уточнения положения корня заключается в построении последовательности вложенных друг в друга отрезков, каждый из которых содержит корень уравнения. Для этого находится середина текущего интервала неопределенности $c_k=frac{a_k+b_k}{2},~ k=0,1,2,ldots$ , и в качестве следующего интервала неопределенности из двух возможных выбирается тот, на концах которого функция f(x) имеет разные знаки (рис. 3.5).

Процесс завершается, когда длина текущего интервала неопределенности становится меньше заданной величины varepsilon , задающей точность нахождения корня. В качестве приближенного значения корня берется середина последнего интервала неопределенности.

Алгоритм метода половинного деления

1. Найти начальный интервал неопределенности L_0=[a_0,b_0] одним из методов отделения корней, задать малое положительное число varepsilon . Положить k=0 .

2. Найти середину текущего интервала неопределенности: $c_k=frac{a_k+b_k}{2}$ .

3. Если f(a_k)cdot f(c_k)<0 , то положить $a_{k+1}=a_k,~ b_{k+1}= c_k$ , а если f(c_k)cdot f(b_k)<0 , то принять $a_{k+1}=c_k,~ b_{k+1}= b_k$ . В результате находится текущий интервал неопределенности $L_{k+1}= [a_{k+1},b_{k+1}]$ .

4. Если $b_{k+1}-a_{k+1}leqslant varepsilon$ , то процесс завершить: $x_{ast}in L_{k+1}= [a_{k+1},b_{k+1}]$ . Приближенное значение корня можно найти по формуле $x_{ast}cong frac{a_{k+1}+b_{k+1}}{2}$ .

Если $b_{k+1}-a_{k+1}>varepsilon$ , положить k=k+1 и перейти к п.2.

Замечания

1. Метод имеет линейную, но безусловную сходимость, и его погрешность за каждую итерацию уменьшается в два раза:

$|b_1-a_1|=frac{|b_0-a_0|}{2};quad |b_2-a_2|= frac{|b_1-a_1|}{2}= frac{|b_0-a_0|}{2^2},quad ldots,quad |b_k-a_k|= |b_0-a_0|cdot2^{-k}.$

Из последнего соотношения можно оценить число итераций для достижения заданной точности varepsiloncolon

$|b_0-a_0|cdot2^{-k} leqslant varepsilon;qquad k geqslant log_{2}frac{|b_0-a_0|}{varepsilon},.$

Отсюда видно, что, например, для достижения точности $varepsilonapprox10^{-3}$ при (b_0-a_0)cong1 необходимо выполнить примерно десять итераций.

2. К достоинствам метода следует отнести то, что он позволяет найти простой корень уравнения $x_{ast}in[a_0,b_0]$ любых непрерывных функций f(x) при любых значениях a_0,,b_0 таких, что f(a_0)cdot f(b_0)<0 . Недостатки метода — он не обобщается на системы нелинейных уравнений и не может использоваться для нахождения корней четной кратности.

▼ Примеры 3.4-3.6

Пример 3.4. Найти корень уравнения x^3-x+1=0 методом половинного деления с точностью varepsilon_1=0,!01 и varepsilon_2=0,!0005 .

Решение

Пример 3.5. Найти корень уравнения x^3-x^2-9x+9=0 методом половинного деления с точностью varepsilon=0,!001 .

Решение

В примере 3.3 были отделены корни уравнения. Уточним корень, лежащий на отрезке [2,!5;4] . Результаты расчетов поместим в табл. 3.2.

$begin{aligned} mathit{Table~3.2}~&\ begin{array}{|c|c|c|c|c|c|c|c|} hline begin{matrix}{}\[-2pt]{}end{matrix} k& f(a_k)& a_k& b_k& f(b_k)& c_k=dfrac{a_k+b_k}{2}& f(c_k)& b_k-a_k\hline 0& -4,!125& 2,!5& 4& 21& 3,!25& 3,!5156& 1,!5\hline 1& -4,!125& 2,!5& 3,!25& 3,!5156& 2,!875& -1,!3769& 0,!75\hline 2& -1,!3769& 2,!875& 3,!25& 3,!5156& 3,!0625& 0,!78149& 0,!375\hline 3& -1,!3769& 2,!875& 3,!0625& 0,!7815& 2,!96875& -0,!3672& 0,!1875\hline 4& -0,!3672& 2,!9687& 3,!0625& 0,!7815& 3,!01562& 0,!18945& 0,!09375\hline 5& -0,!3672& 2,!9687& 3,!0156& 0,!1894& 2,!99218& -0,!0933& 0,!04687\hline 6& -0,!0933& 2,!9921& 3,!0156& 0,!1894& 3,!0039& 0,!0469& 0,!02344\hline 7& -0,!0933& 2,!9921& 3,!0039& 0,!0469& 2,!99804& -0,!02349& 0,!01172\hline 8& -0,!02349& 2,!99804& 3,!0039& 0,!0469& 3,!00097& 0,!011647& 0,!00586\hline end{array}& end{aligned}$

В результате найден интервал [2,!99804;3,!0039] и приближенное значение корня $x_{ast}cong3,!00097$ .

Пример 3.6. Отделить корни трансцендентного уравнения $x^2-e^{-x}=0$ и найти один из корней с точностью varepsilon=0,!01 .

Решение

1. Можно отделить корни уравнения, преобразовав его к равносильному виду $x^2=e^{-x}$ и определив абсциссу точек пересечения графиков функций y=f_1(x)=x^2 и $y=f_2(x)=e^{-x}colon, x_{ast}in[0,!5;1]$ . При этом f(0,!5)cdot f(1)<0 .

2. Уточним корень. Результаты расчетов приведем в табл. 3.3.

$begin{aligned} mathit{Table~3.3}~&\ begin{array}{|c|c|c|c|c|c|c|c|} hline begin{matrix}{}\[-2pt]{}end{matrix} k& f(a_k)& a_k& b_k& f(b_k)& c_k=dfrac{a_k+b_k}{2}& f(c_k)& b_k-a_k\hline 0& -0,!3565& 0,!5& 1& 0,!6321& 0,!75& 0,!09013& 0,!5\hline 1& -0,!3565& 0,!5& 0,!75& 0,!09013& 0,!625& -0,!1446& 0,!251\hline 2& -0,!1446& 0,!625& 0,!75& 0,!09013& 0,!6875& -0,!0301& 0,!125\hline 3& -0,!0301& 0,!6875& 0,!75& 0,!09013& 0,!7187& 0,!0292& 0,!0625\hline 4& -0,!0301& 0,!6875& 0,!7187& 0,!0292& 0,!7031& -0,!00069& 0,!0312\hline 5& -0,!00069& 0,!7031& 0,!7187& 0,!0292& 0,!7109& 0,!0142& 0,!0156\hline 6& -0,!00069& 0,!7031& 0,!7109& 0,!0142& 0,!707& 0,!0067& 0,!0078\hline end{array}& end{aligned}$

Вычисления показывают, что b_6-a_6=0,!7109-0,!7031=0,!0078< varepsilon= 0,!01 .

Поэтому $x_{ast}cong frac{0,!7109+0,!7031}{2}= c_6=0,!707$ .

Геометрическая интерпретация метода хорд

Метод хорд

Этот метод при тех же предположениях обеспечивает более быстрое нахождение корня, чем метод половинного деления. Для этого отрезок [a,b] делится не пополам, а в отношении |f(a)|,colon|f(b)| .

Геометрически метод хорд эквивалентен замене кривой y=f(x) хордой, проходящей через точки (a,f(a)) и (b,f(b)) (рис. 3.6).

Уравнение хорды имеет вид $frac{x-a}{b-a}= frac{y-f(a)}{f(b)-f(a)}$ . Полагая $x=x^{(1)}$ и y=0 , получаем

$x^{(1)}= a-frac{f(a)}{f(b)-f(a)}cdot(b-a).$

Предположим, что вторая производная f''(x) сохраняет постоянный знак, и рассмотрим два случая: f(a)>0,~ f''(a)>0 (рис. 3.7,д) и f(a)<0,~ f''(x)>0 (рис. 3.7,б). Случай f''(x)<0 сводится к рассматриваемому, если уравнение записать в форме: -f(x)=0 . Первому случаю (см. рис. 3.7,д) соответствует формула (3.7), а второму случаю (3.8) (см. рис. 3.7,б):

$begin{aligned}&x^{(0)}=b,\ &x^{(k+1)}=x^{(k)}-frac{f(x^{(k)})}{f(x^{(k)})-f(a)} bigl(x^{(k)}-abigr),quad k=0,1,2,ldotsend{aligned}$

(3.7)

$begin{aligned}&x^{(0)}=a,\ &x^{(k+1)}=x^{(k)}-frac{f(x^{(k)})}{f(b)-f(x^{(k)})}bigl(b-x^{(k)}bigr),quad k=0,1,2,ldots end{aligned}$

(3.8)

В первом случае остается неподвижным конец , а во втором случае конец .

Метод хорд

Замечание. Для выявления неподвижного конца используется условие f''(x)cdot f(t)>0 , где t=a или t=b . Если неподвижен конец , применяется формула (3.7), а если конец , — формула (3.8).

Пример 3.7. Найти корень уравнения x^3-x+1=0 методом хорд с точностью varepsilon=0,!001 .

Решение

Рассмотрим задачу нахождения корня на отрезке [-2;-1] (см. пример 3.2). Так как f(a)=f(-2)=-5, f(b)=f(-1)=-1 , a f''(x)=3x^2-1>0 на отрезке [-2;-1] , то f''(x)cdot f(b)>0 и, следовательно, имеем второй случай (см. рис. 3.7,б).

Положим $x^{(0)}=a=-2,~k=0$ . Тогда по формуле (3.8) получаем

$x^{(1)}= x^{(0)}-frac{f(x^{(0)})}{f(b)-f(x^{(0)})}bigl(b-x^{(0)}bigr)=-2-frac{-5}{1-(-5)}cdot(-1-(-2))=-1,!1666.$

Так как $Delta_1=|x^{(1)}-x^{(0)}|=0,!8334>varepsilon$ , то положим k=1 и продолжим процесс:

$x^{(2)}= x^{(1)}-frac{f(x^{(1)})}{f(b)-f(x^{(1)})}bigl(b-x^{(1)}bigr)=-1,!1666-frac{-0,!5786}{1-0,!5786}cdot bigl(-1-(-1,!1666)bigr)=-1,!3953.$

Так как $Delta_2=|x^{(2)}-x^{(1)}|=0,!2287>varepsilon$ , то положим k=2 и продолжим процесс:

$x^{(3)}= x^{(2)}-frac{f(x^{(2)})}{f(b)-f(x^{(2)})}bigl(b-x^{(2)}bigr)=-1,!3953-frac{-0,!3214}{1+0,!3214}cdot bigl(-1-(-1,!3953)bigr)=-1,!2991.$

Поскольку $Delta_3=|x^{(3)}-x^{(2)}|=0,!0962>varepsilon$ , положим k=3colon

$x^{(4)}= x^{(3)}-frac{f(x^{(3)})}{f(b)-f(x^{(3)})}bigl(b-x^{(3)}bigr)=-1,!2991-frac{-0,!1064}{1+0,!1064}cdot bigl(-1-(-1,!2991)bigr)=-1,!3347.$

Так как $Delta_4=|x^{(4)}-x^{(3)}|=0,!0356>varepsilon$ , положим k=4colon

$x^{(5)}= x^{(4)}-frac{f(x^{(4)})}{f(b)-f(x^{(4)})}bigl(b-x^{(4)}bigr)=-1,!3347-frac{-0,!043}{1+0,!043}cdot bigl(-1-(-1,!3347)bigr)=-1,!3209.$

Поскольку $Delta_5=|x^{(5)}-x^{(4)}|=0,!0138>varepsilon$ , положим k=5colon

$x^{(6)}= x^{(5)}-frac{f(x^{(5)})}{f(b)-f(x^{(5)})}bigl(b-x^{(5)}bigr)=-1,!3209-frac{-0,!0162}{1+0,!0162}cdot bigl(-1-(-1,!3209)bigr)=-1,!3261.$

Так как $Delta_6=|x^{(6)}-x^{(5)}|=0,!0052>varepsilon$ , положим k=6colon

$x^{(7)}= x^{(6)}-frac{f(x^{(6)})}{f(b)-f(x^{(6)})}bigl(b-x^{(6)}bigr)=-1,!3261-frac{-0,!0059}{1+0,!0059}cdot bigl(-1-(-1,!3261)bigr)=-1,!3241.$

Поскольку $Delta_7=|x^{(7)}-x^{(6)}|=0,!0020>varepsilon$ , положим k=7colon

$x^{(8)}= x^{(7)}-frac{f(x^{(7)})}{f(b)-f(x^{(7)})}bigl(b-x^{(7)}bigr)=-1,!3241-frac{-0,!00217}{1+0,!00217}cdot bigl(-1-(-1,!3241)bigr)=-1,!3248.$

Так как $Delta_8=|x^{(8)}-x^{(7)}|=0,!0007<varepsilon=0,!001$ , то корень уравнения $x_{ast}cong-1,!3248$ . Из анализа поведения Delta_k следует, что сходимость метода хорд линейная, однако более быстрая, чем сходимость метода половинного деления.

Абсцисса точки пересечения прямой и кривой

Метод простых итераций

Пусть известно, что корень $x_{ast}$ уравнения f(x)=0 лежит на отрезке G={aleqslant xleqslant b} .

Методика решения задачи

1. Уравнение f(x)=0 равносильным преобразованием привести к виду x=varphi(x) . Это преобразование может быть осуществлено различными путями, но для сходимости нужно обеспечить выполнение условия |varphi'(x)|leqslantchi<1 ( chi — некоторая константа). При этом задача сводится к нахождению абсциссы точки пересечения прямой y=x и кривой y=varphi(x) (рис. 3.8).

2. Задать начальное приближение $x^{(0)}in[a,b]$ и малое положительное число varepsilon . Положить k=0 .

3. Вычислить следующее приближение:

$x^{(k+1)}= varphi(x^{(k)}).$

(3.9)

4. Если $|x^{(k+1)}-x^{(k)}|leqslantvarepsilon$ , итерации завершаются и $x_{ast}cong x^{(k+1)}$ . Если $|x^{(k+1)}-x^{(k)}|>varepsilon$ , положить k=k+1 и перейти к п.3.

Замечание. В качестве условия завершения итераций при известном значении chi может быть использовано неравенство

$bigl|x^{(k+1)}-x^{(k)}bigr|leqslant frac{1-chi}{chi}cdot varepsilon.$

Проблемы сходимости и единственности численного решения, являющиеся главными при использовании этого метода, решаются и исследуются с помощью понятия о сжимающем отображении и теоремы о достаточном условии сходимости метода.

Отображение (функция) varphi(x) называется сжимающим в области с коэффициентом chi~(0leqslantchi<1) , если для любых двух x',,x'' из выполнено неравенство

bigl|varphi(x'')-varphi(x')bigr|leqslantchicdotbigl|x''-x'bigr|.

(3.10)

Теорема 3.9 (о сходимости метода простых итераций и единственности получаемого численного решения)

Пусть выполнены условия:

1. Нелинейное уравнение x=varphi(x) имеет решение $x_{ast}in G$ .

2. Отображение varphi(x) является сжимающим в области с некоторым коэффициентом chi~(0leqslantchi<1) .

Тогда:

а) решение $x_{ast}$ является единственным решением в области ;

б) последовательность $x^{(0)},x^{(1)},ldots,x^{(k+1)},ldots$ , определяемая по отображению на основе итерационного процесса, сходится к решению $x_{ast}$ со скоростью геометрической прогрессии, т.е. при выборе $x^{(0)}$ из условия $|x_{ast}-x^{(0)}|<R$ , где R>0 — некоторое малое число, справедливо неравенство

$bigl|x_{ast}-x^{(k)}bigr| leqslant chi^kcdot bigl|x_{ast}-x^{(0)}bigr|,quad k=0,1,2,ldots$

Теорема 3.9 утверждает, что при выполнении условий 1,2 существует окрестность $G(x_{ast},R)$ такая, что если взять $x^{(0)}$ в этой окрестности и вычислять $x^{(1)},x^{(2)},ldots$ по формуле (3.9), то в результате с любой наперед заданной точностью можно вычислить $x^{(k+1)}approx x_{ast}$ , соответствующее искомому (единственному) корню. Но так как эта окрестность неизвестна, то можно взять произвольное $x^{(0)}in G$ . Если при этом вычисляется последовательность $x^{(0)},x^{(1)},x^{(2)},ldots,x{(k)},ldots$ , сходящаяся к некоторому значению widehat{x} , то в силу теоремы $widehat{x}=x_{ast}$ . Если сходимость отсутствует, то надо взять другое $x^{(0)}in G$ и повторить расчет.

Теорема 3.10 (о достаточном условии сходимости метода простых итераций). Пусть выполнены условия:

1. Функция varphi(x) имеет производные для всех xin G .

2. Существует число chi,(0 leqslantchi<1,~chi=text{const}) , такое, что |varphi'(x)|leqslantchi для всех xin G .

Тогда отображение varphi(x) является сжимающим в с коэффициентом сжатия х и последовательность $x^{(0)},x^{(1)},ldots,x^{(k+1)},ldots$ , определяемая на основе итерационного процесса, сходится к решению $x_{ast}$ , то есть $x^{(k)}to x_{ast}$ при ktoinfty .

▼ Доказательство

В силу условия 1 справедлива теорема Лагранжа о конечных приращениях:

varphi(x'')-varphi(x')leqslant (x''-x')varphi'(delta) для forall x',x''in G ,

где delta — точка, лежащая между и x'' . Но тогда с учетом условия 2 и замены varphi'(delta) ее мажорантой chi получим

bigl|varphi(x'')-varphi(x')bigr|leqslant chicdot bigl|x''-x'bigr|,

т.е. отображение varphi(x) — сжимающее, и, таким образом, последовательность $x^{(0)},x^{(1)},ldots,x^{(k+1)},ldots$ сходится к некоторому widehat{x} . Но тогда в силу непрерывности в имеет место равенство $widehat{x}=x_{ast}$ .

Геометрическая интерпретация процесса сходимости и расходимости в зависимости от выполнения или невыполнения достаточного условия сходимости представлена на рис. 3.9.

Сходимость итерационных последовательностей

Из рис. 3.9 видно, что при 0<varphi'(x)<1 и при -1<varphi'(x)<0 (см.рис. 3.9,д,б) итерационные последовательности $x^{(0)},x^{(1)},x^{(2)},ldots$ сходятся к $x_{ast}$ . Причем в первом случае реализуется односторонняя (монотонная) сходимость, а во втором — двусторонняя (немонотонная). При |varphi'(x)|>1 (см.рис. 3.9,в,г) процесс расходится несмотря на то, что точка $x^{(0)}$ очень близка к $x_{ast}$ . Процессы на рис. 3.9,а,б соответствуют сжимающему отображению.

Преобразование уравнения f(x)=0 к равносильному виду x=varphi(x) может быть выполнено неоднозначно. Рассмотрим универсальные практические приемы равносильного преобразования f(x)=0 , дающие сжимающие отображения.

1. Можно заменить уравнение f(x)=0 на равносильное x=x+cf(x) , где c=text{const}ne0 . Тогда, принимая правую часть этого уравнения за varphi(x) и раскрывая |varphi'(x)|= |1+cf'(x)|<1 , получаем условие

-2<ccdot f'(x)<0.

(3.11)

Таким образом, можно найти константу на отрезке G=[a,b] так, чтобы удовлетворялись неравенства (3.11). При этом надо стремиться получить такую постоянную , которая бы больше отличалась от нуля, и тогда будет реализовы-ваться более быстрая сходимость.

Можно показать, что абсолютная погрешность метода оценивается по формуле (эта оценка выражается через два последовательных приближения)

$bigl|x^{(k+1)}-x_{ast}bigr|leqslant frac{chi}{1-chi}cdot bigl|x^{(k+1)}-x^{(k)}bigr|$

(3.12)

или по формуле (эта оценка выражается через два приближения $x^{(0)}$ и $x^{(1)}$ )

$bigl|x^{(k+1)}-x_{ast}bigr|leqslant frac{chi^{k+1}}{1-chi}cdot bigl|x^{(1)}-x^{(0)}bigr|.$

(3.13)

Из оценки следует условие выхода из итерационного процесса. Если значение chi неизвестно, то выход осуществляется по условию

$bigl|x^{(k+1)}-x^{(k)}bigr|leqslant varepsilon.$

2. Уравнение f(x)=0 заменяется равносильным (где знак в правой части выбирается из условия |varphi'(x)|<1 ):

$x=xmp frac{f(x)}{max|f'(x)|}equiv varphi(x)$ при xin G ,

3. Можно выразить из уравнения f(x)=0 так, чтобы для полученного уравнения x=varphi(x) выполнялось условие сходимости |varphi'(x)|<1 в окрестности искомого корня.

Замечание к доказательству. Выполнение условия $Delta_{k+1}= bigl|x^{(k+1)}-x^{(k)}bigr|leqslant varepsilon$ не гарантирует близости к точному решению (на рис. 3.10 достигается область, где условие окончания выполняется, но корень $x_{ast}$ расположен достаточно далеко от этой области).

Итерационный процесс и корень

▼ Примеры 3.8-3.10

Пример 3.8. Методом простых итераций с точностью varepsilon=0,!001 уточнить корень трансцендентного уравнения $x^2-e^{-x}=0$ , причем искомый корень $x_{ast}in[0,!5;1,!0]equiv G$ .

Решение

Пример 3.9. Найти решение уравнения x^3-x+1=0 методом простых итераций с точностью varepsilon_1=0,!01 и varepsilon_2=0,!001 .

Решение

Пример 3.10. Найти корни уравнения x^3-x^2-9x+9=0 методом простых итераций с точностью varepsilon=0,!001 .

Решение

1. Преобразуем уравнение к виду $x=varphi(x)colon, x=sqrt[LARGE{3}]{x^2+9x-9}$ .

В примере 3.3 была выполнена операция отделения корней и получены отрезки [-4;-2],,[0,5;2],,[2;4] .

Можно показать, что на отрезках [2;4],,[-4;-2] функция $varphi(x)= sqrt[LARGE{3}]{x^2+9x-9}$ удовлетворяет условию |varphi'(x)|<1 .

На отрезке [0,!5;2] используем другой вид уравнения: $x=frac{x^3}{9}-frac{x^2}{9}+1$ . Также легко проверить, что функция $varphi(x)=frac{x^3}{9}-frac{x^2}{9}+1$ удовлетворяет достаточному условию сходимости на отрезке [0,!5;2] .

2. В качестве начальных приближений выберем:
– точку $x^{(0)}=-2$ на отрезке [-4;-2] ;
– точку $x^{(0)}=0,!5$ на отрезке [0,!5;-2] ;
– точку $x^{(0)}=2$ на отрезке [2;4] ;.
В поставленной задаче varepsilon=0,!001 .

3,4. Выполним расчеты по формуле

$x^{(k+1)}= sqrt[LARGE{3}]{(x^{(k)})^2+9x^{(k)}-9},quad k=0,1,2,ldots$

с начальными значениями $x^{(0)}=-2$ и $x^{(0)}=2$ и по формуле

$x^{(k+1)}=frac{(x^{(k)})^3}{9}-frac{(x^{(k)})^2}{9}+1,quad k=0,1,2,ldots$

с начальным значением $x^{(0)}=0,!5$ .

Результаты расчетов занесены в табл. 3.6–3.8.

$begin{aligned}& begin{aligned} mathit{Table~3.6}~&\ begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}hline k&! scriptstyle{0}!&! scriptstyle{1}!&! scriptstyle{2}!&! scriptstyle{3}!&! scriptstyle{4}!&! scriptstyle{5}!&! scriptstyle{6}!&! scriptstyle{7}!&! scriptstyle{8}!&! scriptstyle{9}!&! scriptstyle{10}!&! scriptstyle{11}!&! scriptstyle{12}!\hline x^{(k)}&! scriptstyle{2,0000}!&! scriptstyle{2,3513}!&! scriptstyle{2,6056}!&! scriptstyle{2,7694}!&! scriptstyle{2,8682}!&! scriptstyle{2,9255}!&! scriptstyle{2,9582}!&! scriptstyle{2,9767}!&! scriptstyle{2,9870}!&! scriptstyle{2,9927}!&! scriptstyle{2,9959}!&! scriptstyle{2,9977}!&! scriptstyle{2,9987}!\hline bigl|x^{(k)}-x^{(k-1)}bigr|&! -!&! scriptstyle{0,3513}!&! scriptstyle{0,2543}!&! scriptstyle{0,1638}!&! scriptstyle{0,0988}!&! scriptstyle{0,0573}!&! scriptstyle{0,0327}!&! scriptstyle{0,0185}!&! scriptstyle{0,0102}!&! scriptstyle{0,0057}!&! scriptstyle{0,0032}!&! scriptstyle{0,0018}!&! scriptstyle{0,0010}!\hline end{array}& end{aligned}<br />\[6pt] & begin{aligned} mathit{Table~3.7}~&\ begin{array}{|c|c|c|}hline k& x^{(k)}& bigl|x^{(k)}-x^{(k-1)}bigr|\hline 0&-2,!0000&-\hline 1&-2,!8438& 0,!8438\hline 2&-2,!9816& 0,!1378\hline 3&-2,!9979& 0,!0163\hline 4&-2,!9997& 0,!0018\hline 5&-2,!99997& 0,!00027\hline end{array}&end{aligned} qquadqquadqquad begin{aligned} mathit{Table~3.8}~&\ begin{array}{|c|c|c|} hline k& x^{(k)}& bigl|x^{(k)}-x^{(k-1)}bigr|\hline 0& 0,!50000&-\hline 1& 0,!98611& 0,!4861\hline 2& 0,!99849& 0,!01238\hline 3& 0,!99983& 0,!00134\hline 4& 0,!99998& 0,!00015\hline end{array}& end{aligned}end{aligned}$

В результате получены приближенные значения корней:

$x_{1ast}cong-2,!99997,qquad x_{2ast}cong0,!99998,qquad x_{3ast}cong2,!9987.$

Обратим внимание на сильное различие в числе итераций, потребовавшихся для нахождения корней $x_{ast}=3$ (табл. 3.6) и $x_{ast}=-3$ (табл. 3.7), с помощью одной и той же формулы. Заметим, что в окрестности корня $x_{ast}=3$ значения модуля производной функции $varphi(x)=sqrt[LARGE{3}]{x^2+9x-9}$ равны:

С другой стороны, в окрестности корня $x_{ast}=-3$ имеем:

Анализ результатов показывает, что чем меньше значения модуля производной |varphi'(x)| , тем быстрее сходимость.

Метод Ньютона для решения нелинейных уравнений

Метод Ньютона (метод касательных, или метод линеаризации) является одним из наиболее популярных численных методов. Он быстро сходится (имеет квадратичную сходимость) и допускает различные модификации, приспособленные для решения векторных задач и сеточных уравнений. Однако этот метод эффективен при весьма жестких ограничениях на характер функции f(x)colon

Геометрическая интерпретация метода Ньютона

1) существование второй производной функции f(x) на множестве G={aleqslant xleqslant b} ;
2) удовлетворение первой производной условию f(x)ne0 для всех xin G ;
3) знакопостоянство f'(x),,f''(x) для всех xin G .

Поэтому его желательно использовать совместно с другими методами, например методом половинного деления, чтобы достигнуть диапазона widetilde{a}leqslant x leqslant widetilde{b} , где указанные условия начинают выполняться.

Геометрическая интерпретация метода Ньютона состоит в следующем. Задается начальное приближение $x^{(0)}$ . Далее проводится касательная к кривой y=f(x) в точке $x^{(0)}$ (рис. 3.11), т.е. кривая заменяется прямой линией. В качестве следующего приближения выбирается точка пересечения этой касательной с осью абсцисс. Процесс построения касательных и нахождения точек пересечения с осью абсцисс повторяется до тех пор, пока приращение не станет меньше заданной величины varepsilon .

Получим расчетную формулу метода Ньютона. Вместо участка кривой (точка соответствует $x_{ast}$ ) возьмем участок — касательную, проведенную в точке $(x^{(0)},f(x^{(0)}))$ ). Для этого отрезка справедливо конечное соотношение:

$frac{f(x^{(0)})-0}{x^{(0)}-x^{(1)}}= f'(x^{(0)})equiv operatorname{tg}alpha,$

где alpha — угол наклона касательной в точке $(x^{(0)},f(x^{(0)}))$ к оси абсцисс. Разрешая это соотношение относительно $x^{(1)}$ , получаем $x^{(1)}= x^{(0)}-frac{f(x^{(0)})}{f'(x^{(0)})}$ . Повторяя процесс, находим общую формулу:

$x^{(k+1)}= x^{(0)}-frac{f(x^{(k)})}{f'(x^{(k)})},quad k=0,1,2,ldots$

(3.14)

Подчеркнем, что если отбросить итерационный индекс, то (3.14) записывается в виде нелинейного уравнения

$x=x-frac{f(x)}{f'(x)}equiv varphi(x),$

(3.15)

которое, однако, на [a,b] не равносильно исходному, а является таковым только в одной точке при $x=x_{ast}$ . Поэтому данный метод не служит разновидностью метода простых итераций.

Применим теперь для вывода формулы (3.14) метод линеаризации. Положим, что итерационный процесс имеет вид

$x^{(k+1)}=x^{(k)}+delta^{(k)},quad k=0,1,2,ldots$

(3.16)

где $delta^{(0)}$ — поправка к k-му приближению, которую необходимо найти. Предполагая, что f(x) имеет непрерывную вторую производную, разложим $f(x^{(k)}+delta^{(k)})$ по формуле Тейлора относительно точки $x^{(k)}colon$

$f(x^{(k)}+delta^{(k)})= f(x^{(k)})+ delta^{(k)}f'(x^{(k)})+ frac{1}{2}(delta^{(k)})^2 f''(xi),$

где $xiin bigl(x^{(k)},x^{(k+1)}bigr)$ . Учитывая, что $fbigl(x^{(k)}+ delta^{(k)}bigr)=0$ (это соответствует нахождению точки пересечения с осью абсцисс), и оставляя только линейную (относительно $delta^{(k)}$ ) часть разложения (отсюда и название — метод линеаризации), записываем линейное относительно $delta^{(k)}$ уравнение

$f(x^{(k)})+ delta^{(k)} f'(x^{(k)})=0.$

Отсюда выражается поправка $delta^{(k)}=-frac{f(x^{(k)})}{f'(x^{(k)})}$ . Подставляя $delta^{(k)}$ в (3.16), получаем (3.14).

Теорема 3.11 (о достаточных условиях сходимости метода Ньютона). Пусть выполняются следующие условия:

1. Функция f(x) определена и дважды дифференцируема на [a,b] .

2. Отрезку [a,b] принадлежит только один простой корень $x_{ast}$ , так что f(a)cdot f(b)<0 .

3. Производные f'(x),,f''(x) на [a,b] сохраняют знак, и f'(x)ne0 .

4. Начальное приближение $x^{(0)}$ удовлетворяет неравенству $f(x^{(0)})cdot f''(x^{(0)})>0$ (знаки функций f(x) и f''(x) в точке $x^{(0)}$ совпадают).

Тогда с помощью метода Ньютона (3.14) можно вычислить корень уравнения f(x)=0 с любой точностью.

Замечания

1. Метод Ньютона характеризуется вторым порядком сходимости вблизи корня и первым порядком — вдали от него. Данную оценку проверяем для двух случаев, когда $x^{(k)}$ находится далеко от корня $x_{ast}$ (это возможно на первых итерациях) и когда $x^{(k)}$ располагается вблизи $x_{ast}$ .

Первый случай. Пусть отрезок $omega=[x^{(k)},x_{ast}]$ не мал. Тогда на основе теоремы Лагранжа получим (где $m_1=minlimits_{omega}|f'(x)|$ )

$bigl|f(x^{(k)})bigr|= bigl|f(x_{ast})-f(x^{(k)})bigr|= bigl|f'(xi)bigr|cdot bigl|x_{ast}-x^{(k)}bigr| geqslant m_1 bigl|x_{ast}-x^{(k)}bigr|.$

(3.17)

Преобразуем с использованием (3.17) итерационную формулу (3.14) (где $M_1= maxlimits_{xin[a,b]}|f'(x)|$ ):

$x^{(k+1)}=x^{(k)}-frac{f(x^{(k)})}{f'(x^{(k)})};qquad bigl|x^{(k+1)}-x^{(k)}bigr|= frac{|f(x^{(k)})|}{f'(x^{(k)})} geqslant frac{m_1}{M_1} bigl|x_{ast}-x^{(k)}bigr|.$

В силу монотонности последовательности $x^{(0)},x^{(1)},ldots$ имеем

$begin{gathered}x_{ast}-x^{(k+1)}= x_{ast}-x^{(k)}-bigl(x^{(k+1)}-x^{(k)}bigr),\ bigl|x_{ast}-x^{(k+1)}bigr|= bigl|x_{ast}-x^{(k)}bigr|-bigl|x^{(k+1)}-x^{(k)}bigr| geqslant bigl|x_{ast}-x^{(k)}bigr|- frac{m_1}{M_1} bigl|x_{ast}-x^{(k)}bigr|= left(1-frac{m_1}{M_1}right)! bigl|x_{ast}-x^{(k)}bigr|. end{gathered}$

Таким образом, вдали от корня получаем линейную сходимость

$bigl|x_{ast}-x^{(k+1)}bigr| leqslant ccdot bigl|x_{ast}-x^{(k)}bigr|$ , где $0 leqslant c=1-frac{m_1}{M_1}<1$ .

Второй случай. Пусть теперь отрезок $omega=[x^{(k)},x]$ мал, т.е. итерации выполняются вблизи корня. Тогда, полагая, что указанные выше предположения 1–4 теоремы 3.10 выполнены, разложим функцию f(x) в окрестности корня $x_{ast}$ относительно точки $x^{(k)}$ , учитывая члены до второго порядка. Получим

$Bigl.{f(x)}Bigr|_{x=x^{(k)}}= f(x^{(k)})+ bigl(x_{ast}-x^{(k)}bigr) f'(x^{(k)})+ bigl(x_{ast}-x^{(k)}bigr)^2 frac{1}{2}f''(xi)=0,$

где $xiin bigl(x^{(k)}-delta,,x^{(k)}+deltabigr)$ ( delta>0 — малая величина). Из данного соотношения выражаем $x_{ast}colon$

$x_{ast}=x^{(k)}-frac{f(x^{(k)})}{f'(x^{(k)})}-frac{(x_{ast}-x^{(k)})^2}{2f'(x^{(k)})},f''(xi).$

Но первые два слагаемых в правой части в соответствии с (3.14) равны $x^{(k+1)}$ . Тогда будем иметь

$x_{ast}-x^{(k)}=-frac{(x_{ast}-x^{(k)})^2}{2f'(x^{(k)})},f''(xi).$

Из последнего соотношения следует оценка погрешности (k+1)-го приближения через погрешность k-го приближения:

$bigl|x_{ast}-x^{(k+1)}bigr|leqslant frac{M_2}{2m_1} bigl|x_{ast}-x^{(k)}bigr|^2,$

(3.18)

где принято $M_2=maxlimits_{omega}|f''(x)|,~ m_1=minlimits_{omega}|f'(x)|$ . Оценка (3.18) свидетельствует о квадратичной сходимости метода касательных вблизи корня. С вычислительной точки зрения это означает, что на каждом приближении количество верных цифр результата удваивается.

2. Для нахождения комплексных корней уравнения f(z)=0 можно также использовать (3.14) в форме (где z=x+iy — комплексная переменная)

$z^{(k+1)}=z^{(k)}-frac{f(z^{(k)})}{f'(z^{(k)})},quad k=0,1,2,ldots$

Метод Ньютона может применяться не только для нахождения простых корней, но для определения кратных корней, т.е. когда на отрезке [a,b] содержащем корень, не выполняется условие f(a)cdot f(b)<0 (условие 2 теоремы 3.11). Наряду с теоремой 3.11 удобно также пользоваться следующей теоремой.

Достаточные условия сходимости метода Ньютона

Теорема 3.12 (достаточные условия сходимости метода Ньютона). Пусть:

а) дана функция f(x)colon Dto mathbb{R} , где — открытый интервал, и $f'(x)in operatorname{Lip}_{gamma}(D)$ ;

б) для некоторого rho>0 выполняется условие |f'(x)|leqslantrho при всех из .

Если уравнение f(x)=0 имеет решение $x_{ast}in D$ , то существует некоторое eta>0 , такое, что если $|x^{(0)}-x_{ast}|<eta$ , то последовательность $bigl{x^{(0)},x^{(1)},x^{(2)},ldotsbigr}$ , задаваемая формулой (3.14), существует и сходится к $x_{ast}$ . Более того, справедлива оценка

$bigl|x^{(k+1)}-x_{ast}bigr| leqslant frac{gamma}{2rho} bigl|x^{(k)}-x_{ast}bigr|^2,quad k=0,1,2,ldots$

Здесь обозначение $f'(x)in operatorname{Lip}_{gamma}(D)$ означает, что функция f'(x) непрерывна по Липшицу с константой gamma на множестве , то есть |f'(x)-f'(y)| leqslant gamma cdot|x-y| для любых x,,y из .

Замечания

1. Требование теоремы 3.12, чтобы производная f'(x) имела ненулевую нижнюю границу в , определяет, что значение $f'(x_{ast})$ должно быть ненулевым для квадратичной сходимости метода Ньютона. Если же $f'(x_{ast})=0$ , то $x_{ast}$ является кратным корнем, а метод Ньютона сходится лишь линейно.

2. Выполнение условий теоремы 3.12 гарантирует сходимость метода Ньютона только из «хорошего» начального приближения $x^{(0)}$ .

3. Метод Ньютона является локально сходящимся, так как он сходится с определенной скоростью к истинному решению при условии, что стартует в достаточной близости от этого решения.

Методика решения задачи

1. Задать начальное приближение $x^{(0)}$ так, чтобы выполнялось неравенство $f(x^{(0)})cdot f''(x^{(0)})>0$ , а также малое положительное число varepsilon . Положить k=0 .

2. Вычислить $x^{(k+1)}$ по формуле $x^{(k+1)}= x^{(k)}-frac{f(x^{(k)})}{f'(x^{(k)})}$ .

3. Если $|x^{(k+1)}-x^{(k)}|leqslant varepsilon$ , процесс завершить и положить $x_{ast}cong x^{(k+1)}$ .

Если $|x^{(k+1)}-x^{(k)}|>varepsilon$ , положить k=k+1 и перейти к п.2.

▼ Примеры 3.11-3.14

Пример 3.11. Методом Ньютона с точностью varepsilon=0,!001 уточнить корень трансцендентного уравнения $x^2-e^{-x}=0$ , причем искомый корень $x_{ast}in[0,!5;1,!0]equiv G$ .

Решение

Можно проверить, что на множестве удовлетворяются условия 1, 2, 3 теоремы 3.11, обеспечивающие сходимость метода касательных.

1. Зададим начальное приближение из условия 4. Так как для $f(x)=x^2-e^{-x}$ справедливо $f''(x)=2-e^{-x}>0$ на множестве G,~ f(a)=f(0,!5)<0, f(b)=f(1)>0 , то f(1)cdot f''(1)>0 , поэтому $x^{(0)}=1$ .

2,3. Результаты расчетов по формуле (3.14) $x^{(k+1)}= x^{(k)}-frac{(x^{(k)})^2-e^{-x^{(k)}}}{2x^{(k)}+e^{-x^{(k)}}},~k=0,1,2,ldots$ помещены в табл. 3.9.

$begin{aligned} mathit{Table~3.9}~&\ begin{array}{|c|c|c|c|c|} hline k& 0& 1& 2& 3\hline begin{matrix}{}\[-8pt]{}end{matrix} x^{(k)}& 1,!000& 0,!73304& 0,!70381& 0,!703467\hline begin{matrix}{}\[-8pt]{}end{matrix} bigl|x^{(k)}-x^{(k-1)}bigr|&-& 0,!27& 0,!029& 0,!00034\hline begin{matrix}{}\[-8pt]{}end{matrix} f(x^{(k)})& 0,!63212& 0,!05690& 0,!00065& 8,!25cdot10^{-7}\hline end{array}& end{aligned}$

Из табл. 3.9 можно сделать следующие выводы:

1. Для достижения заданной точности, проверяемой по модулю разности $bigl|x^{(k)}-x^{(k-1)}bigr|$ , потребовалось выполнить три приближения. Если же выход организовать по условию $bigl|f(x^{(k)})bigr|leqslant varepsilon$ , то достаточно двух приближений.

2. Вблизи корня $x_{ast}$ количество верных цифр в результатах $x^{(k)}$ удваивается, так что все цифры в $x^{(3)}$ являются верными, тогда как в $x^{(2)}$ верными являются первые три цифры после запятой.

3. Скорость сходимости метода Ньютона выше скорости сходимости метода простых итераций (та же точность была достигнута за пять итераций).

Пример 3.12. Методом Ньютона найти корень уравнения x^3-x+1=0 .

Решение

Пример 3.13. Найти корни уравнения x^3-x^2-9x+9=0 методом Ньютона с точностью varepsilon=0,!001 .

Решение

Процедура отделения корней была выполнена в примере 3.3. В качестве отрезков [a_i;b_i] , которым принадлежат корни уравнения, выберем [-4;-2], [2,!5;4], [0,!5;2] .

Так как f(-4)=-3,!5;~ f(-2)=15 , то есть f(-4)f(-2)<0 , производные f''(x)=6x-2<0, f'(x)=3x^2-2x-9>0 сохраняют знак при xin[-4;-2] , то условия сходимости выполняются.

Так как f(2,!5)=-4,!125;~ f(4)=21 , то есть f(2,!5)f(4)<0 , и производные f'(x)>0,~ f''(x)>0 сохраняют знак при xin[2,!5;4] , то условия сходимости на этом отрезке тоже выполняются.

Так как f(0,!5)=4,!375;~ f(2)=-5 , то есть f(0,!5)f(2)<0 , и производные f'(x)<0,~ f''(x)>0 сохраняют знак при xin[0,!5;2] , то условия сходимости выполняются.

1. Зададим начальные приближения: на отрезке [0,!5;2] выберем $x^{(0)}= 0,!5$ , так как f(0,!5)cdot f''(0,!5)>0 ; на отрезке [-4;-2] выберем $x^{(0)}=-4$ , так как f(4)cdot f''(4)>0 ; аналогично на отрезке [2,!5;4] выберем $x^{(0)}=4$ . В поставленной задаче varepsilon= 0,!001 .

2,3. Результаты расчетов по формуле (3.14) $x^{(k+1)}= x^{(k)}-frac{(x^{(k)})^3-(x^{(k)})^2-9x^{(k)}+9}{3(x^{(k)})^2-2x^{(k)}-9},~ k=0,1,2,ldots$ приведены в табл. 3.11–3.13.

$begin{aligned}& begin{aligned} mathit{Table~3.11}~&\ begin{array}{|c|c|c|c|c|c|} hline k& 0& 1& 2& 3& 4 \hline begin{matrix}{}\[-8pt]{}end{matrix} x^{(k)}&-4,!00000&-3,!255319&-3,!023383&-3,!000225&-3,!000000 \hline begin{matrix}{}\[-8pt]{}end{matrix} bigl|x^{(k)}-x^{(k-1)}bigr|&-& 0,!744681& 0,!231936& 0,!023158& 0,!000225 \hline end{array}& end{aligned}\[2pt] & begin{aligned} mathit{Table~3.12}~&\ begin{array}{|c|c|c|c|c|} hline k& 0& 1& 2& 3 \hline begin{matrix}{}\[-8pt]{}end{matrix} x^{(k)}&0,!5000& 0,!972973& 0,!9998246& 1,!0000000 \hline begin{matrix}{}\[-8pt]{}end{matrix} bigl|x^{(k)}-x^{(k-1)}bigr|&-& 0,!472973& 0,!0268516& 0,!0001754 \hline end{array}& end{aligned}\[2pt] & begin{aligned} mathit{Table~3.13}~&\ begin{array}{|c|c|c|c|c|c|c|} hline k& 0& 1& 2& 3& 4& 5 \hline begin{matrix}{}\[-8pt]{}end{matrix} x^{(k)}& 4,!0000& 3,!322581& 3,!051484& 3,!001674& 3,!000002& 3,!0000 \hline begin{matrix}{}\[-8pt]{}end{matrix} bigl|x^{(k)}-x^{(k-1)}bigr|&-& 0,!6774194& 0,!2710969& 0,!049809& 0,!001671& 2cdot10^{-6} \hline end{array}& end{aligned} end{aligned}$

В результате получены приближенные значения корней:

$x_{ast1}cong-3,!0000;qquad x_{ast2}cong1,!0000;qquad x_{ast3}cong 3,!0000.$

Пример 3.14. Найти корень уравнения x^2-2x+1=0 методом Ньютона с точностью varepsilon=0,!01 .

Решение

Очевидно, уравнение имеет один кратный корень $x_{ast}=1$ . Согласно замечанию к теореме 3.12 применение метода Ньютона для решения поставленной задачи сопровождается линейной сходимостью (табл. 3.14).

$begin{aligned} mathit{Table~3.14}~&\ begin{array}{|c|c|c|c|c|c|c|c|c|} hline k& 0& 1& 2& 3& 4& 5& 6& 7\hline begin{matrix}{}\[-8pt]{}end{matrix} x^{(k)}& 2& 1,!5& 1,!25& 1,!125& 1,!0625& 1,!03125& 1,!015625& 1,!007813 \hline begin{matrix}{}\[-8pt]{}end{matrix} bigl|x^{(k)}-x^{(k-1)}bigr|&-& 0,!5& 0,!25& 0,!125& 0,!0625& 0,!03125& 0,!015625& 0,!0078125 \hline end{array}& end{aligned}$

Полученное приближенное решение $x_{ast}cong1,!007813$ .

Нарушение знакопостоянства производных функции

Метод касательных

Метод касательных, являясь весьма эффективным средством численного анализа, к сожалению, имеет достаточно жесткие ограничения. Действительно, он не может применяться для сеточных уравнений (см. рис. 3.2); при нарушении знакопостоянства производных (рис. 3.12); при существовании неограниченных вторых производных и др. Так, если даже условие знакопостоянства нарушено вдали от корня, где выбрано $x^{(0)}$ , а вблизи корня выполняется, то все равно метод касательных неприменим (см. рис. 3.12), если не произвести сужения начального отрезка.

Кроме того, если функция f(x) очень сложная, то будет сложной и ее производная, и поэтому на каждой итерации приходится рассчитывать две функции, что снижает эффективность метода касательных.

Процесс последовательных приближений по методу Ньютона

В силу этого в ряде случаев могут оказаться более предпочтительными модификации метода касательных. Рассмотрим три из них.

Упрощенный метод Ньютона. Методика его применения совпадает с изложенной ранее, но вместо формулы (3.14) используется

$x^{(k+1)}=x^{(k)}-frac{f(x^{(k)})}{f'(x^{(0)})},quad k=0,1,2,ldotsqquad mathsf{(3.19)}$

Отличие от метода Ньютона заключается в том, что производная функции f(x) подсчитывается только в точке начального приближения, а на последующих итерациях не уточняется. Процесс последовательных приближений отражен на рис. 3.13. Первая итерация совпадает с первой итерацией метода Ньютона. На последующих итерациях соответствующие отрезки параллельны касательной, проведенной в начальной точке.

Для этой модификации снимаются некоторые ограничения метода касательных, например условие знакопостоянства производных. Сходимость упрощенного метода Ньютона линейная.

Пример 3.15. Найти корень уравнения x^3-x+1=0 упрощенным методом Ньютона.

Решение

Корень уравнения отделен в примере 3.2: $x_{ast}in[-2;-1]$ .

1. Выберем начальное приближение $x^{(0)}=-2$ и зададим varepsilon_1=0,!01 и varepsilon_2=0,!001 .

2,3. Выполним расчеты по формуле (3.19):

$x^{(k+1)}= x^{(k)}-frac{(x^{(k)})^3-x^{(k)}+1}{3(x^{(0)})^2-1}= x^{(k)}-frac{(x^{(k)})^3-x^{(k)}+1}{11},quad k=0,1,2,ldots$

Результаты расчетов приведены в табл. 3.15.

$begin{aligned} mathit{Table~3.15}~&\ begin{array}{|c|c|c||c|c|c|} hline begin{matrix} {}\[-6pt]{}end{matrix} k& x^{(k)}& bigl|x^{(k)}-x^{(k-1)}bigr|& k& x^{(k)}& bigl|x^{(k)}-x^{(k-1)}bigr|\hline 0&-2,!00001&-& 6&-1,!3388& 0,!0092\hline 1&-1,!5455& 0,!4545& 7&-1,!3333& 0,!0005\hline 2&-1,!4413& 0,!1042& 8&-1,!3299& 0,!00034\hline 3&-1,!3911& 0,!0502& 9&-1,!3279& 0,!002\hline 4&-1,!3637& 0,!0274& 10&-1,!3267& 0,!0012\hline 5&-1,!348& 0,!0157& 11&-1,!3259& 0,!0008\hline end{array}& end{aligned}$

При varepsilon=0,!01 получено решение $x_{ast}cong-1,!3388$ , а при varepsilon=0,!001 — решение $x_{ast}cong-1,!3259$ . Очевидно, по сравнению с методом Ньютона сходимость замедляется (см. пример 3.12).

Метод Ньютона-Бройдена

Этот метод позволяет увеличить скорость сходимости последовательных приближений благодаря использованию формулы

$x^{(k+1)}= x^{(k)}-c_kcdot frac{f(x^{(k)})}{f'(x^{(k)})},quad k=0,1,2,ldots$

(3.20)

где c_k — число, которое выбирается на каждой итерации так, чтобы уменьшить значение $bigl|f(x^{(k+1)})bigr|$ по сравнению с $bigl|f(x^{(k)})bigr|$ . При c_k=1 метод Ньютона-Бройдена совпадает с методом Ньютона.

Как правило, при плохой сходимости или ее отсутствии полагают 0<c_k<1 (рис. 3.14,д), а при хорошей сходимости для c_k=1 полагают c_k>1 (это ускоряет сходимость (рис. 3.14,б)).

Сходимость при методе Ньютона-Бройдена

На рис. 3.14 прямоугольниками отмечены точки $x^{(1)}$ , полученные при $c_0=1,~ delta^{(k)}= frac{f(x^{(k)})}{f'(x^{(k)})},~k=0,1,2,ldots$ , — поправка, соответствующая методу Ньютона, а точки $x^{(1)}=x^{(0)}-c_0delta^{(0)}$ получены по методу Ньютона-Бройдена.

Тангенс угла наклона секущей

Метод секущих

В этом методе производная функции f(x) подсчитывается с помощью конечно-разностных соотношений:

– в точке $x^{(0)}$ используется формула $f'(x^{(0)})approx frac{f(x^{(0)})-f(x^{(0)}-delta)}{delta}$ , где delta — малая положительная величина;

– в точках $x^{(k)},~k=1,2,ldots$ , используется формула $f'(x^{(k)})approx frac{f(x^{(k)})-f(x^{(k-1)})}{x^{(k)}-x^{(k-1)}}$ .

Вычисленное значение $f'(x^{(k)})$ определяет тангенс угла наклона секущей (рис. 3.15).

Методика применения метода секущих совпадает с описанной ранее, но вместо (3.14) используется формула

$x^{(k+1)}= x^{(k)}-frac{f(x^{(k)})}{f(x^{(k)})-f(x^{(k-1)})}cdot bigl(x^{(k)}-x^{(k-1)}bigr),quad k=1,2,ldots$

(3.21)

Аппроксимация сеточной функции

Замечания

1. Метод секущих является более экономичным по сравнению с методом Ньютона по количеству функций, подлежащих расчету: на каждой итерации в методе секущих необходимо рассчитать только значение $f(x^{(k)})$ , так как величина $f(x^{(k-1)})$ уже подсчитана на предыдущей итерации.

2. Метод секущих может применяться и для решения сеточных уравнений. Для сеточной функции производные в методе секущих определяются так же, но для определения $f(x^{(k)})$ в промежуточных точках осуществляется аппроксимация (как правило, интерполяция) функции f(x_i) (рис. 3.16). На этом рисунке штриховой линией показана аппроксимационная кривая.

3. Для всех описанных модификаций скорость сходимости по сравнению с методом касательных снижается: p<2 . Однако для некоторых из них (метод секущих) значение p>1 и может достигать p=1,!5 .

Пример 3.16. Методом секущих найти корень уравнения x^3-x+1=0 с точностью varepsilon=0,!001 .

Решение

1. Зададим начальное приближение $x^{(0)}=-2$ (см. пример 3.12).

2. Для вычисления $f'(x^{(0)})$ зададим delta=0,!1 . Тогда

$f'(x^{(0)})cong frac{f(-2)-f(-2,!1)}{0,!1}= frac{-5-(-6,!161)}{0,!1}= 11,!61.$

Отсюда $x^{(1)}= x^{(0)}-frac{f(x^{(0)})}{f'(x^{(0)})}=-2-frac{-5}{11,!61}=-1,!36934$ .

Дальнейшие расчеты выполняются по формуле (3.21):

$begin{aligned}x^{(2)}&=x^{(1)}-frac{f(x^{(1)})}{f(x^{(1)})-f(x^{(0)})}cdot bigl(x^{(1)}-x^{(0)}bigr)=-1,!56934-frac{-1,!29567}{3,!704325}cdot0,!43066=-1,!41871;\[2pt] x^{(3)}&=x^{(2)}-frac{f(x^{(2)})}{f(x^{(2)})-f(x^{(1)})}cdot bigl(x^{(2)}-x^{(1)}bigr)=-1,!41871-frac{-1,!43678}{0,!858893}cdot0,!15063=-1,!34211;\[2pt] x^{(4)}&=x^{(3)}-frac{f(x^{(3)})}{f(x^{(3)})-f(x^{(2)})}cdot bigl(x^{(3)}-x^{(2)}bigr)=-1,!34211-frac{-1,!07538}{0,!361404}cdot0,!0766=-1,!32613;\[2pt] x^{(5)}&=x^{(4)}-frac{f(x^{(4)})}{f(x^{(4)})-f(x^{(3)})}cdot bigl(x^{(4)}-x^{(3)}bigr)=-1,!32613-frac{-1,!00603}{0,!069348}cdot0,!01598=-1,!32474;\[2pt] x^{(6)}&=x^{(5)}-frac{f(x^{(5)})}{f(x^{(5)})-f(x^{(4)})}cdot bigl(x^{(5)}-x^{(4)}bigr)=-1,!32474-frac{-1,!000139}{0,!005936}cdot0,!00139=-1,!32472cong x_{ast}.\[2pt] end{aligned}$

Результаты расчетов приведены в табл. 3.16.

$begin{aligned} mathit{Table~3.16}~&\ begin{array}{|c|c|c|c|c|c|c|c|} hline k& 0& 1& 2& 3& 4& 5& 6\hline begin{matrix}{}\[-8pt]{}end{matrix} x^{(k)}&-2,!00000&-1,!56934&-1,!41871&-1,!34211&-1,!32613&-1,!32474&-1,!32472\hline begin{matrix}{}\[-8pt]{}end{matrix} bigl|x^{(k)}-x^{(k-1)}bigr|&-& 0,!43066& 0,!15063& 0,!07660& 0,!01598& 0,!00139& 0,!00002 \hline end{array}& end{aligned}$

Очевидно, метод сходится чуть хуже метода Ньютона (см. пример 3.12), однако скорость сходимости выше линейной.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Пусть имеется уравнение вида

f(x)= 0

где f(x) — заданная алгебраическая или трансцендентная функция.

Решить уравнение — значит найти все его корни, то есть те значения x, которые обращают уравнение в тождество.
Если уравнение достаточно сложно, то задача точного определения корней является в некоторых случаях нерешаемой. Поэтому ставится задача найти такое приближенное значение корня x_ПP, которое отличается от точного значения корня x* на величину, по модулю не превышающую указанной точности (малой положительной величины) ε, то есть

│x* – x_пр │< ε

Величину ε также называют допустимой ошибкой, которую можно задать по своему усмотрению.

Этапы приближенного решения нелинейных уравнений

Приближенное решение уравнения состоит из двух этапов:

Отделение корней, то есть нахождение интервалов из области определения функции f(x), в каждом из которых содержится только один корень уравнения f(x)=0.
Уточнение корней до заданной точности.

Отделение корней

Отделение корней можно проводить графически и аналитически.
Для того чтобы графически отделить корни уравнения, необходимо построить график функции f(x). Абсциссы точек его пересечения с осью Ox являются действительными корнями уравнения.

Для примера рассмотрим задачу решения уравнения

где угол x задан в градусах. Указанное уравнение можно переписать в виде
f(x)=0
Для графического отсечения корней достаточно построить график функции

Из рисунка видно, что корень уравнения лежит в промежутке x∈(6;8).

Аналитическое отделение корней

Аналитическое отделение корней основано на следующих теоремах.
Теорема 1. Если непрерывная функция f(x) принимает на концах отрезка [a; b] значения разных знаков, т.е.

то на этом отрезке содержится по крайней мере один корень уравнения.
Теорема 2. Если непрерывная на отрезке [a; b] функция f(x) принимает на концах отрезка значения разных знаков, а производная f'(x) сохраняет знак внутри указанного отрезка, то внутри отрезка существует единственный корень уравнения f(x) = 0.

Уточнение корней

Для уточнения корней может использоваться один из следующих методов:

Метод последовательных приближений (метод итераций)
Метод Ньютона (метод касательных)
Метод секущих (метод хорд)
Метод половинного деления (метод дихотомии)

Метод последовательных приближений (метод итераций)

Метод итерации — численный метод решения математических задач, используемый для приближённого решения алгебраических уравнений и систем. Суть метода заключается в нахождении по приближённому значению величины следующего приближения (являющегося более точным). Метод позволяет получить решение с заданной точностью в виде предела последовательности итераций. Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения решения.
Функциональное уравнение может быть записано в виде
x=f(x)
Функцию f(x) называют сжимающим отображением.

Последовательность чисел x₀, x₁ ,…, x_n называется итерационной, если для любого номера n>0 элемент x_n выражается через элемент x_n-1 по рекуррентной формуле

а в качестве x₀ взято любое число из области задания функции f(x).

Реализация на C++ для рассмотренного выше примера

Уравнение может быть записано в форме

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double find(double x, double eps)
{
  double rez; int iter = 0;
  cout << «x0= » << x << » «;
  do {
    rez = x;
    x = 1 / (sin(M_PI*x / 180));
    iter++;
  } while (fabs(rez — x) > eps && iter<20000);
  cout << iter << » iterations» << endl;
  return x;
}
int main()
{
  cout << find(7, 0.00001);
  cin.get();
  return 0;
}

Результат выполнения

Метод Ньютона (метод касательных)

Если известно начальное приближение x₀ корня уравнения f(x)=0, то последовательные приближения находят по формуле

Графическая интерпретация метода касательных имеет вид

Реализация на C++
Для заданного уравнения

производная будет иметь вид f'(x)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double find(double x, double eps)
{
  double f, df; int iter = 0;
  cout << «x0= » << x << » «;
  do {
    f = sin(M_PI*x / 180) — 1 / x;
    df = M_PI / 180 * cos(M_PI*x / 180) + 1 / (x*x);
    x = x — f / df;
    iter++;
  } while (fabs(f) > eps && iter<20000);
  cout << iter << » iterations» << endl;
  return x;
}
int main()
{
  cout << find(1, 0.00001);
  cin.get(); return 0;
}

Результат выполнения

Метод секущих (метод хорд)

Если x₀, x₁ — приближенные значения корня уравнения f(x) = 0 и выполняется условие

то последующие приближения находят по формуле

Методом хорд называют также метод, при котором один из концов отрезка закреплен, т.е. вычисление приближения корня уравнения f(x) = 0 производят по формулам:

Геометрическая интерпретация метода хорд:

Реализация на C++
В отличие от двух рассмотренных выше методов, метод хорд предполагает наличие двух начальных приближений, представляющих собой концы отрезка, внутри которого располагается искомый корень.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double find(double x0, double x1, double eps)
{
  double rez = x1, f0, f;
  int iter = 0;
  cout << «x0= » << x0 << » x1= » << x1 << » «;
  do {
    f = sin(M_PI*rez / 180) — 1 / rez;
    f0 = sin(M_PI*x0 / 180) — 1 / x0;
    rez = rez — f / (f — f0)*(rez — x0);
    iter++;
  } while (fabs(f) > eps && iter<20000);
  cout << iter << » iterations» << endl;
  return rez;
}
int main()
{
  cout << find(1.0, 10.0, 0.000001);
  cin.get(); return 0;
}

Результат выполнения

Метод половинного деления (метод дихотомии)

Если x₀, x₁ — приближенные значения корня уравнения f(x) = 0 и выполняется условие

то последующие приближения находятся по формуле

и вычисляется f(x_i). Если f(x_i)=0, то корень найден. В противном случае из отрезков выбирается тот, на концах которого f(x) принимает значения разных знаков, и проделывается аналогичная операция. Процесс продолжается до получения требуемой точности.

Геометрическая интерпретация метода дихотомии

Реализация на C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double func(double x)
{
  return (sin(M_PI*x / 180) — 1 / x);
}
double find(double x0, double x1, double eps)
{
  double left = x0, right = x1, x, fl, fr, f;
  int iter = 0;
  cout << «x0= » << x0 << » x1= » << x1 << » «;
  do {
    x = (left + right) / 2;
    f = func(x);
    if (f > 0) right = x;
    else left = x;
    iter++;
  } while (fabs(f) > eps && iter<20000);
  cout << iter << » iterations» << endl;
  return x;
}
int main()
{
  cout << find(1.0, 10.0, 0.000001);
  cin.get(); return 0;
}

Результат выполнения

Для численного поиска решения также можно использовать генетические алгоритмы.

Назад: Алгоритмизация

Источник

Немного теории о методе хорд под калькулятором.

Метод хорд

Критерий останова (погрешность)

Точность вычисления

Знаков после запятой: 4

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Метод хорд

Метод хорд можно рассматривать как комбинацию метода секущих (Метод секущих) и метода дихотомии — отличие от метода секущих состоит в том, что если в методе секущих в качестве точек следующей итерации выбираются последние рассчитанные точки, то в методе хорд выбираются те точки, в которых функция имеет разный знак, и соответственно, выбранный интервал содержит корень.

Вывод итерационной формулы аналогичен выводу формулы для метода секущих:

Положим, что у нас есть две точки, x0 и x1, в которых значения функции равны соответственно f(x0) и f(x1). Тогда уравнение прямой, проходящей через эти точки, будет

$frac{y - f(x_1)}{f(x_1)-f(x_0)}=frac{x - x_1}{x_1-x_0}$

Для точки пересечения с осью абсцисс (у=0) получим уравнение

$x = x_1 - frac{x_1 - x_0}{f(x_1)-f(x_0)}f(x_1)$

Но в отличие от метода секущих, после расчета следующего приближения в качестве второй точки выбирается не последняя, а та, в которой функция имеет разный знак со значением функции в вычисленной точке. Проиллюстрировано это ниже.

Источник

Метод хорд является двухшаговым, то есть новое приближение определяется двумя предыдущими итерациями. Поэтому необходимо задавать два начальных приближения корня.
Метод требует, чтобы начальные точки были выбраны по разные стороны от корня (то есть корень содержался в выбранном интервале), при этом величина интервала в процессе итераций не стремится к 0.

В качестве критерия останова берут один из следующих:

— значение функции на данной итерации стало меньше заданого ε.

$left|x_k-x_{k-1}right| < epsilon$ — изменение хk в результате итерации стало меньше заданого ε. При этом имеется в виду не интервальные значения, а два вычисленных значения, так как величина интервала не стремится к 0.

Подробнее: Метод хорд

Источник

Численные методы решения нелинейных уравнений. Метод хорд.

Метод хорд ( метод также известен как Метод секущих ) один из методов решения нелинейных уравнений и основан на последовательном сужении интервала, содержащего единственный корень уравнения . Итерационный процесс выполняется до того момента, пока не будет достигнута заданная точность .

В отличие от метода половинного деления, метод хорд предлагает, что деление рассматриваемого интервала будет выполняться не в его середине, а в точке пересечения хорды с осью абсцисс (ось — Х). Следует отметить, что под хордой понимается отрезок, который проведен через точки рассматриваемой функции по концам рассматриваемого интервала. Рассматриваемый метод обеспечивает более быстрое нахождение корня, чем метод половинного деления, при условии задания одинакового рассматриваемого интервала.

Геометрически метод хорд эквивалентен замене кривой хордой, проходящей через точки и (см. рис.1.).

Рис.1. Построение отрезка (хорды) к функции .

Уравнение прямой (хорды), которая проходит через точки А и В имеет следующий вид:

Данное уравнение является типовым уравнением для описания прямой вы декартовой системе координат. Наклон кривой задается по ординате и абсциссе с помощью значений в знаменателе и , соответственно.

Для точки пресечения прямой с осью абсцисс записанное выше уравнение перепишется в следующем виде:

В качестве нового интервала для прохождения итерационного процесса выбираем один из двух или , на концах которого функция принимает значения разных знаков. Противоположность знаков значений функции на концах отрезка можно определить множеством способов. Один из множества этих способов — умножение значений функции на концах отрезка и определение знака произведения путём сравнения результата умножения с нулём:

или .

Итерационный процесс уточнения корня заканчивается, когда условие близости двух последовательных приближений станет меньше заданной точности, т.е.

Рис.2. Пояснение к определению погрешности расчета.

Следует отметить, что сходимость метода хорд линейная, однако более быстрая, чем сходимость метода половинного деления.

Алгоритм нахождения корня нелинейного уравнения по методу хорд

1. Найти начальный интервал неопределенности одним из методов отделения корней. З адать погрешность расчета (малое положительное число ) и начальный шаг итерации ( ) .

2. Найти точку пересечения хорды с осью абсцисс:

3. Необходимо найти значение функции в точках , и . Далее необходимо проверить два условия:

— если выполняется условие , то искомый корень находится внутри левого отрезка положить , ;

— если выполняется условие , то искомый корень находится внутри правого отрезка принять , .

В результате находится новый интервал неопределенности, на котором находится искомых корень уравнения:

4. Проверяем приближенное значение корня уравнения на предмет заданной точности, в случае:

— если разность двух последовательных приближений станет меньше заданной точности , то итерационный процесс заканчивается. Приближенное значение корня определяется по формуле:

— если разность двух последовательных приближений не достигает необходимой точности , то необходимо продолжить итерационный процесс и перейти к п.2 рассматриваемого алгоритма.

Пример решения уравнений методом хорд

В качестве примера, рассмотрим решение нелинейного уравнения методом хорд. Корень необходимо найти в рассматриваемом диапазоне с точностью .

Вариант решения нелинейного уравнения в программном комплексе MathCAD .

Результаты расчетов, а именно динамика изменения приближенного значения корня, а также погрешности расчета от шага итерации представлены в графической форме (см. рис.1).

Рис.1. Результаты расчета по методу хорд

Для обеспечения заданной точности при поиске уравнения в диапазоне необходимо выполнить 6 итераций. На последнем шаге итерации приближенное значение корня нелинейного уравнения будет определяться значением: .

Примечание:

Модификацией данного метода является метод ложного положения ( False Position Method ), который отличается от метода секущих только тем, что всякий раз берутся не последние 2 точки, а те точки, которые находятся вокруг корня.

Следует отметить, что в случае если от нелинейной функции можно взять вторую производную алгоритм поиска может быть упрощен. Предположим, что вторая производная сохраняет постоянный знак, и рассмотрим два случая:

Случай №1: 0,

f»(a)>0″ width=»158″ height=»20″ border=»0″ />

Из первого условия получается, что неподвижной стороной отрезка является – сторона a .

Случай №2: 0″ width=»158″ height=»20″ border=»0″ />

Из второго условия получается, что неподвижной стороной отрезка является – сторона b .

В общем виде, для выявления неподвижного конца можно записать следующее условие: 0″ width=»122″ height=»20″ border=»0″ /> , где или .

Рис. 3. Примеры убывающей или возрастающей функции

Таким образом, в зависимости от вида функции получаются два выражения для упрощения поиска корня функции:

— если функция соответствует первому случаю (см. рис. 3), тогда формула будет иметь следующий вид:

, где k =0,1,2,…

— если функция соответствует второму случаю (см. рис. 3), тогда формула будет иметь следующий вид:

, где k =0,1,2,…

Случай сводится к рассматриваемому , если уравнение записать в форме: .

Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.

Метод хорд

Метод хорд — итерационный численный метод приближённого нахождения корня уравнения.

Немного теории о методе хорд под калькулятором.

Метод хорд

Вывод итерационной формулы аналогичен выводу формулы для метода секущих:

Для точки пересечения с осью абсцисс (у=0) получим уравнение

В качестве критерия останова берут один из следующих:

— значение функции на данной итерации стало меньше заданого ε.

— изменение хk в результате итерации стало меньше заданого ε. При этом имеется в виду не интервальные значения, а два вычисленных значения, так как величина интервала не стремится к 0.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ — Тема: Решение алгебраических и трансцендентных уравнений методами хорд и касательных.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Решение алгебраических и трансцендентных уравнений методами хорд и касательных.

— применить умения отделять корни алгебраических уравнений;

— применить умения решать алгебраические уравнений приближенными методами (метод хорд и касательных);

1. Рабочая тетрадь в клетку.

2. Раздаточный материал: инструкционные карты-20шт.

3. Калькулятор простой.

1. Методом хорд с точностью до 0,01 найдите приближенное значение наибольшего действительного корня следующего алгебраического уравнения.

2. Методом касательных с точностью до 0,01 найдите приближенное значение наибольшего действительного корня следующего алгебраического уравнения.

3. Комбинированным методом хорд и касательных решить уравнение с точностью до 0,01.

1. Внимательно прочитать тему и цель практической работы .

2. Изучить учебный материал по теме.

3. Ответить на вопросы.

4. Выполнить задания.

5. Подготовить отчет.

Пояснения к работе (учебный материал):

Предположим, что удалось найти достаточно малый промежуток , содержащий ровно один действительный корень уравнения (1).

Тогда, согласно теореме 5, непрерывная и дифференцируемая функция принимает на его концах значения разных знаков, т.е. .

Предположим, также, что промежуток столь мал, что во всех его точках сохраняют постоянный знак.

На рис. 1 – 4 изобразим схематические графики четырёх типов расположения дуги кривой.

Отдельно рассмотрим и опишем два случая.

Случай 1. на , т.е. либо и на , либо и на

Случай 2. на , т.е. либо и на , либо и на

Приведем алгоритм решения задачи в первом случае:

а) через точки и кривой проведем хорду AB . Ее уравнение имеет вид:

или ;

б) найдём абсциссу точки пересечения хорды АВ с осью Ох. Положив , получим ;

в) подставив значение в уравнение кривой , получим . Точка имеет координаты ;

г) через точки и кривой проведем хорду . Ее уравнение имеет вид:

или

д) найдем абсциссу точки пересечения хорды с осью . Положив , будем иметь:

;

е) в результате получим последовательность значений , , ,…, сходящуюся к .

После выполнения неравенства , где — выбранная нами точность приближения, процесс следует закончить.

Итак, в первом случае вычисления производятся по формулам:

;

(2)

Приведем алгоритм решения задачи во втором случае:

а) значения и находятся так же, как и в первом случае. Точка имеет координаты ;

б) через точки и кривой проведем хорду . Ее уравнение имеет вид: или ;

в) найдем абсциссу точки пересечения хорды с осью Ox . Положив , будем иметь: ;

г) дальнейшие действия такие же, как и в первом случае. Итак, во втором случае вычисления производятся по формулам:

Метод касательных (метод Ньютона).

При тех же предложениях, что и в методе хорд на рис. 5 и 8, изобразим схематически графики четырех типов расположения дуги кривой.

Отдельно рассмотрим и опишем два случая.

Случай 1. . на (см. рис. 5 и 8), т.е. либо и на , либо и на .

Случай 2. на (см. рис. 6 и 7), т.е. либо и на , либо и на .

Приведем алгоритм решения задачи в первом случае:

а) через точку проведем касательную к кривой . Ее уравнение имеет вид:

или ;

б) найдём абсциссу точки пересечения этой касательной с осью Ox . Положив , получим ;

в) подставив значение в уравнении кривой получим: . Точка имеет координаты ;

г) через точку проведем касательную к кривой . Ее уравнение имеет вид:

или ;

д) найдём абсциссу точки пересечения этой касательной с осью Ox . Положив , получим ;

е) в результате получим последовательность значений , , …, сходящуюся к .

После выполнения неравенства , где — выбранная нами точность приближения, процесс следует закончить.

Итак, в первом случае вычисления производятся по формулам:

Алгоритм решения задачи во втором случае будет таким же, как и в первом случае, только первая касательная будет проводиться через точку .

Итак, во втором случае вычисления проводятся по формулам:

Комбинированный метод хорд и касательных.

Пусть требуется найти действительный корень уравнения изолированный на отрезке . Предполагается, что и имеют разные знаки, а каждая из производных сохраняет определенный знак на отрезке изоляции. Возьмем на отрезке такую точку что и (при x, принадлежащем промежутку изоляции) имеют одинаковые знаки.

Воспользуемся формулами методов хорд и касательных:

Величины и принадлежат промежутку изоляции, причем и

Построим новую пару приближений к корню:

Точки и на числовой оси расположены между точками и , причем и имеют разные знаки.

Вычислим теперь значения

и т.д.

Каждая из последовательностей

…, …; …, …

стремится к искомому корню, причем одна из последовательностей монотонно возрастает, а другая – монотонно убывает. Пусть, например, тогда . Задав заранее достаточно малое мы можем, увеличивая добиться выполнения неравенства следовательно, при этом же значении будет выполняться неравенство Таким образом, является приближенным значением корня вычисленным с погрешностью, не превышающей

Так, например, для нахождения приближенного значения с точностью до 0,001 нужно определить таким образом, чтобы значения и вычисленные с точностью до 0,001, совпадали.

При выполнении практической работы рассмотрите следующие примеры:

Методом хорд найти положительный корень уравнения

С точностью

Прежде всего, отделяем корень. Так как

То искомый корень х лежит в интервале . Полученный интервал велик, поэтому разделим его пополам. Так как

то

Так как при и , то воспользуемся формулой (5) для решения поставленной задачи:

следовательно , продолжаем вычисления;

Таким образом, можно принять с точностью .

Заметим, что точный корень уравнения .

С помощью графического метода отделить корни трансцендентного уравнения и уточнить их методом Ньютона с точностью е=0,00001.

Решение. Запишем наше уравнение в виде . Строим графики данных функций.

Из рис. 3 видно, что данное уравнение имеет два корня: первый корень принадлежит отрезку [0,1; 1], а второй [1,1; 2].

Уточним корни методом касательных. Для этого вычислим производные.

Итерационная формула метода Ньютона в данном случае принимает вид.

Результаты вычислений представим в виде таблиц

источники:

http://planetcalc.ru/3712/

http://znanio.ru/media/metodicheskie-ukazaniya-po-vypolneniyu-prakticheskoj-raboty-po-chislennym-metodam-tema-reshenie-algebraicheskih-i-transtsendentnyh-uravnenij-metodami-hord-i-kasatelnyh-2568013

Источник

Численные методы решения нелинейных уравнений

Корни нелинейных уравнений

Отделение корней уравнения

Способы отделения корней

Метод половинного деления

Алгоритм метода половинного деления

Метод хорд

Метод простых итераций

Метод Ньютона для решения нелинейных уравнений

Достаточные условия сходимости метода Ньютона

Метод касательных

Метод Ньютона-Бройдена

Метод секущих

Этапы приближенного решения нелинейных уравнений

Отделение корней

Аналитическое отделение корней

Уточнение корней

Метод последовательных приближений (метод итераций)

Метод Ньютона (метод касательных)

Метод секущих (метод хорд)

Метод половинного деления (метод дихотомии)

Метод хорд

Метод хорд

Численные методы решения нелинейных уравнений. Метод хорд.

Численные методы решения нелинейных уравнений. Метод хорд.

Пример решения уравнений методом хорд

Метод хорд

Метод хорд

Метод хорд

Не пропустите также: