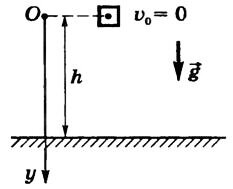
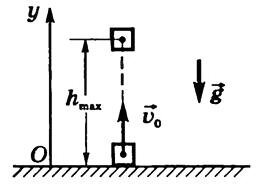
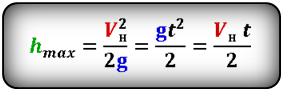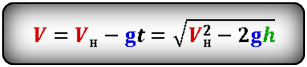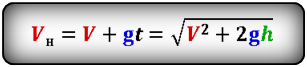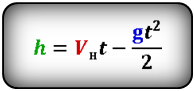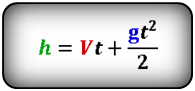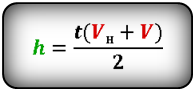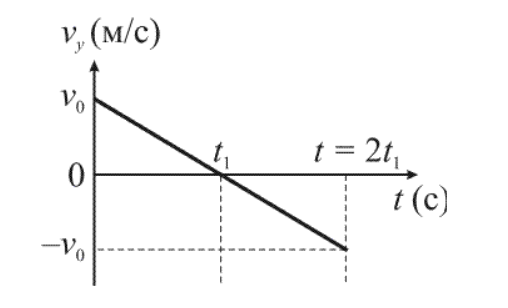Движение тела, брошенного вертикально вверх
Тело, брошенное вертикально вверх, движется равномерно замедленно с начальной скоростью u0 и ускорением
a = -g.
Перемещение тела за время t представляет собой высоту подъема h.
Для этого движения справедливы формулы:
Если:
u0 — начальная скорость движения тела ,
u — скорость падения тела спустя время t,
g — ускорение свободного падения, 9.81 (м/с²),
h — высота на которую поднимется тело за время t,
t — время,
То, движение тела, брошенного вертикально вверх описывается следующими формулами:
Высота подъема тела за некоторое время, зная конечную скорость
[ h = frac{u_0 + u}{2} t ]
Высота подъема тела за некоторое время, зная ускорение свободного падения
[ h = u_0 t — frac{g t^2}{2} ]
Скорость тела через некоторое время, зная ускорение свободного падения
[ u = u_0 — gt ]
Скорость тела на некоторой высоте, зная ускорение свободного падения
[ u = sqrt{ u_0^2 — 2gh} ]
Максимальная высота подъема тела, зная первоначальную скорость и ускорение свободного падения
Тело, брошенное вертикально вверх, достигает максимальной высоты в тот момент, когда его скорость обращается в ноль. Поднявшись на максимальную высоту тело начинает свободное падение вниз.
[ h_{max} = frac{u_0^2}{2g} ]
Время подъема на максимальную высоту подъема тела, зная первоначальную скорость и ускорение свободного падения
[ t_{hmax} = frac{u_0}{g} ]
Примечание к статье: Движение тела, брошенного вертикально вверх
- Сопротивление воздуха в данных формулах не учитывается.
- Ускорение свободного падения имеет приведенное значение (9.81 (м/с²)) вблизи земной поверхности. Значение g на других расстояниях от поверхности Земли изменяется!
Движение тела, брошенного вертикально вверх |
стр. 409 |
|---|
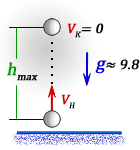
1. Формулы максимальной высоты и времени за которое тело поднялось на максимальную высоту
h max
— максимальная высота достигнутая телом за время t
Vк — конечная скорость тела на пике, равная нулю
Vн — начальная скорость тела
t — время подъема тела на максимальную высоту h
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула максимальной высоты (h max):
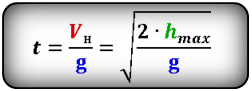
Формула времени за которое тело достигло максимальную высоту (t):
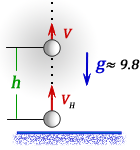
2. Формулы скорости, высоты и времени тела брошенного вертикально вверх под воздействием силы тяжести
h — расстояние пройденное телом за время t
Vн — начальная скорость тела
V — скорость тела в момент времени t
t — время подъема за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 — ускорение свободного падения
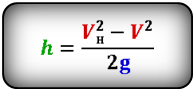
Формула скорости тела в момент времени t (V):
Формула начальной скорости тела (Vн):
Формулы высоты тела в момент времени t (h):
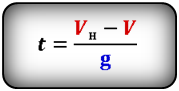
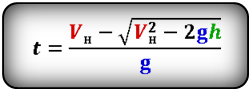
Формулы времени, за которое тело достигло высоту h (t):
- Подробности
-
Опубликовано: 04 августа 2015
-
Обновлено: 13 августа 2021
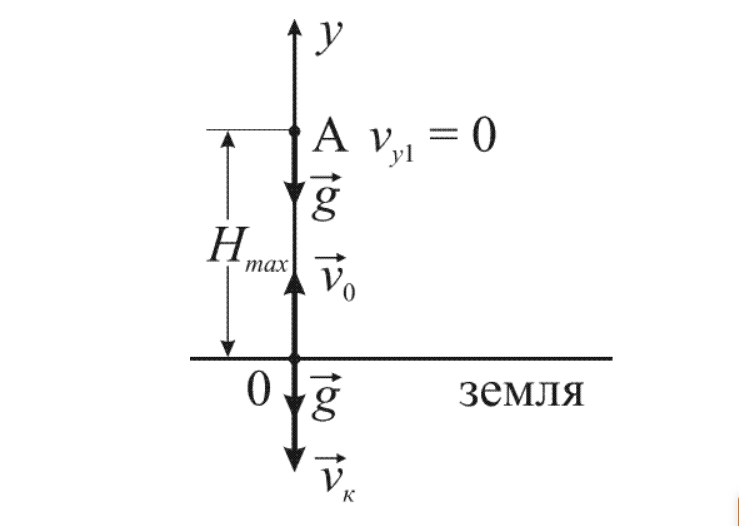
Если тело бросить вертикально вверх при наличии начальной скорости υ0, оно будет двигаться равнозамедленно с ускорением, равным a=-g=-9,81υc2.
Рисунок 1
Формулы вычисления показателей движения брошенного тела
Высота подбрасывания h за время t и скорость υ через промежуток t можно определить формулами:
tmax — это время, за которое тело достигает максимальной высоты hmax=h, при υ=0, а сама высота hmax может быть определена при помощи формул:
Когда тело достигает высоты, равной hmax, то оно обладает скоростью υ=0 и ускорением g. Отсюда следует, что тело не сможет оставаться на этой высоте, поэтому перейдет в состояние свободного падения. То есть, брошенное вверх тело – это равнозамедленное движение, при котором после достижения hmax изменяются знаки перемещения на противоположные. Важно знать, какая была начальная высота движения h0. Общее время тела примет обозначение t, время свободного падения — tп, конечная скорость υк, отсюда получаем:
Если тело брошено вертикально вверх от уровня земли, то h0=0.
Время, необходимое для падения тела с высоты, куда предварительно было брошено тело, равняется времени его подъема на максимальную высоту.
Так как в высшей точке скорость равняется нулю видно:
Конечная скорость υк тела, брошенного от уровня земли вертикально вверх, равна начальной скорости υ0 по величине и противоположна по направлению, как показано на ниже приведенном графике.
Рисунок 2
Примеры решения задач
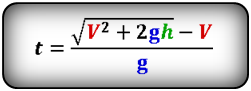
Тело было брошено вертикально вверх с высоты 25 метров со скоростью 15 м/с. Через какой промежуток времени оно достигнет земли?
Дано: υ0=15 м/с, h0=25 м, g=9,8 м/с2.
Найти: t.
Решение
t=υ0+υ02+gh0g=15+152+9,8·259,8=3,74 с
Ответ: t=3,74 с.
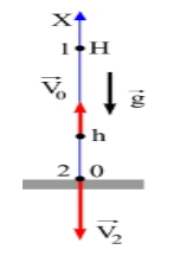
Был брошен камень с высоты h=4 вертикально вверх. Его начальная скорость равняется υ0=10 м/с. Найти высоту, на которую сможет максимально подняться камень, его время полета и скорость, с которой достигнет поверхности земли, пройденный телом путь.
Дано: υ0=10 м/с, h=4 м, g=9,8 м/с2.
Найти: H, t, v2, s.
Решение
Рисунок 3
H=h0υ022g=4+1029,8=14,2 м.
t=υ0+υ02+gh0g=10+102+9,8·49,8=1,61 с.
υ2=υk=2gH=2·9,8·14,2=16,68 м/с.
s=H-h0+H=2H-h0=2·14,2=24,4 м.
Ответ: H=14,2 м; t=1,61 с; v2=16,68 м/с; s=24,4 м.
Движение тела, брошенного вертикально
Свободно падающее тело может двигаться прямолинейно или по криволинейной траектории. Это зависит от начальных условий. Рассмотрим это подробнее.
Свободное падение без начальной скорости (υ0 = 0) (рис. 1).
Рис. 1
При выбранной системе координат движение тела описывается уравнениями:
(~upsilon_y = gt, y = frac{gt^2}{2} .)
Из последней формулы можно найти время падения тела с высоты h[~t = sqrt{frac{2h}{g}}]. Подставляя найденное время в формулу для скорости, получим модуль скорости тела в момент падения[~upsilon = sqrt{2gh}].
Движение тела, брошенного вертикально вверх с начальной скоростью (~vec upsilon_0) (рис. 2).
Рис. 2
Движение тела описывается уравнениями:
(~upsilon_y = upsilon_0 — gt, y = upsilon_0 t — frac{gt^2}{2} .)
Из уравнения скорости видно, что тело движется равнозамедленно вверх, достигает максимальной высоты, а затем движется равноускоренно вниз. Учитывая, что при y = hmax скорость υy = 0 и в момент достижения телом первоначального положения y = 0, можно найти[~t_1 = frac{upsilon_0}{g}] — время подъема тела на максимальную высоту;
(~h_{max} = frac{upsilon^2_0}{2g}) — максимальная высота подъема тела;
(~t_2 = 2t_1 = frac{2 upsilon_0}{g}) — время полета тела;
(~upsilon_{2y} = -upsilon_0) — проекция скорости в момент достижения телом первоначального положения.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 14-15.
Если некоторое тело будет свободно падать на Землю, то при этом оно будет совершать равноускоренное движение, причем скорость будет возрастать постоянно, так как вектор скорости и вектор ускорения свободного падения будут сонаправлены между собой.
Если же подбросить некоторое тело вертикально вверх и при этом считать, что сопротивление воздуха отсутствует, то можно считать, что оно тоже совершает равноускоренное движение с ускорением свободного падения, которое вызвано силой тяжести. Только в этом случае скорость, которую мы придали телу при броске, будет направлена вверх, а ускорение свободного падения направлено вниз, то есть они будут противоположно направлены друг к другу. Поэтому скорость будет постепенно уменьшаться.
Через некоторое время наступит момент, когда скорость станет равняться нулю. В этот момент тело достигнет своей максимальной высоты и на какой-то момент остановится. Очевидно, что, чем большую начальную скорость мы придадим телу, тем на большую высоту оно поднимется к моменту остановки.
Далее, тело начнет равноускоренно падать вниз под действием силы тяжести.
Формулы для равноускоренного движения применимы для движения тела, брошенного вверх. V0 всегда > 0
Движение тела, брошенного вертикально вверх, является прямолинейным движением с постоянным ускорением. Если направить координатную ось OY вертикально вверх, совместив начало координат с поверхностью Земли, то для анализа свободного падения без начальной скорости можно использовать формулу (y = y_0+v_0yt+frac{a_yt^2}{2}),
положив (υ_0 >0, y_0 = 0, y=H, a = –g.) Или (H=y_0+v_{0y}t-frac{gt^2}2).
Вблизи поверхности Земли, при условии отсутствия заметного влияния атмосферы скорость тела, брошенного вертикально вверх, изменяется во времени по линейному закону: (v=v_0-gt), если тело поднялось на максимальную высоту, то (v=0), а (v=v_0-gt).
Скорость тела на некоторой высоте h можно найти по формуле: (v=sqrt{{v_0}^2-2gh}).
Максимальная высота подъема тела пропорциональна квадрату начальной скорости: (H=frac{{v_0}^2}{2g}).
Формула высота подъема тела за некоторое время при известной конечной скорости: (h=frac{v+v_0}2t.)
Свободно падающее тело может двигаться прямолинейно или по криволинейной траектории. Это зависит от начальных условий. Рассмотрим это подробнее.
Свободное падение без начальной скорости: ((υ_0 = 0)). При выбранной системе координат движение тела описывается уравнениями: (υ_y=gt, y =frac{gt^2}2.) Из последней формулы можно найти время падения тела с высоты h: (t = sqrt{frac{2h}g} .) Подставляя найденное время в формулу для скорости, получим модуль скорости тела в момент падения: (υ= sqrt{2gh}.)
Если тело подбросить, то оно сначала движется равнозамедленно вверх, достигает максимальной высоты, а затем движется равноускоренно вниз. Учитывая, что при (y = h_{max}) скорость (υ_y = 0) и в момент достижения телом первоначального положения (y = 0), можно найти
(t_1=υ_0cdot g ) – время подъема тела на максимальную высоту;
(h_{max}) – максимальная высота подъема тела;
(t_2=2t_1=frac{2υ_0}g ) – время полета тела;
(v_{2y}=-v_0) – проекция скорости в момент достижения телом первоначального положения.