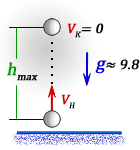
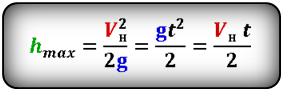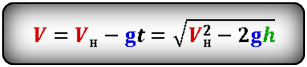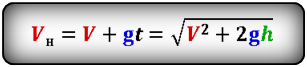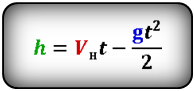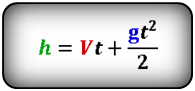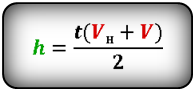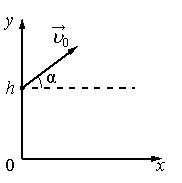1. Формулы максимальной высоты и времени за которое тело поднялось на максимальную высоту
h max
— максимальная высота достигнутая телом за время t
Vк — конечная скорость тела на пике, равная нулю
Vн — начальная скорость тела
t — время подъема тела на максимальную высоту h
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула максимальной высоты (h max):
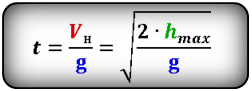
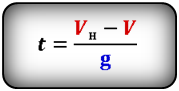
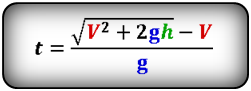
Формула времени за которое тело достигло максимальную высоту (t):
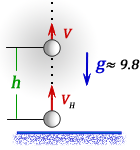
2. Формулы скорости, высоты и времени тела брошенного вертикально вверх под воздействием силы тяжести
h — расстояние пройденное телом за время t
Vн — начальная скорость тела
V — скорость тела в момент времени t
t — время подъема за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула скорости тела в момент времени t (V):
Формула начальной скорости тела (Vн):
Формулы высоты тела в момент времени t (h):
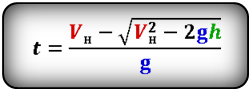
Формулы времени, за которое тело достигло высоту h (t):
- Подробности
-
Опубликовано: 04 августа 2015
-
Обновлено: 13 августа 2021
Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.
Важные факты!График движения тела, брошенного под углом к горизонту:
α — угол, под которым было брошено тело
- Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
- Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v0x = v0cosα. Ее проекция на ось ОУ равна v0y = v0sinα.
- Проекция мгновенной скорости на ось ОХ равна: vx = v0 cosα. Ее проекция на ось ОУ равна нулю: vy = v0 sinα – gt.
- Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0. Ее проекция на ось ОУ равна –g: gy = –g.
Кинематические характеристики
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:
vmin = v0 cosα = vh
Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:
vmax = vo = v
Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: vy = 0. Время подъема определяется следующей формулой:
Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
l = sx = v0x tполн = v0 cosα tполн
Подставляя в выражение формулу полного времени полета, получаем:
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v0 cosα, данная формула принимает вид:
x = v0 cosα t
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v0 sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:
Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:
Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?
Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:
v0 sinα = gtпод
Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:
Тело, брошенное под углом к горизонту с некоторой высоты
Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.
Важные факты!
График движения тела, брошенного под углом к горизонту с некоторой высоты:
Время падения тела больше времени его подъема: tпад > tпод.
Полное время полета равно:
tполн = tпад + tпод
Уравнение координаты x:
x = v0 cosα t
Уравнение координаты y:
Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.
Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:
x = v0 cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.
Задание EF17562
С высоты Н над землёй начинает свободно падать стальной шарик, который через время t = 0,4 c сталкивается с плитой, наклонённой под углом 30° к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h = 1,4 м над землёй. Чему равна высота H? Сделайте схематический рисунок, поясняющий решение.
Алгоритм решения
1.Записать исходные данные.
2.Построить на чертеже начальное и конечное положения тела. Выбрать систему координат.
3.Выбрать нулевой уровень для определения потенциальной энергии.
4.Записать закон сохранения энергии.
5.Решить задачу в общем виде.
6.Подставить числовые значения и произвести вычисления.
Решение
Запишем исходные данные:
• Время падения стального шарика: t = 0,4 c.
• Верхняя точка траектории после абсолютно упругого удара о плиту: h = 1,4 м.
• Угол наклона плиты: α = 30о.
Построим чертеж и укажем на нем все необходимое:
Нулевой уровень — точка D.
Закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep
Потенциальная энергия шарика в точке А равна:
EpA = mgH
Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.
В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:
EpB=mgl1
Перед ударом кинетическая энергия шарика равна:
EkB=mv22
Согласно закону сохранения энергии:
EpA=EpB+EkB
mgH=mgl1+mv22
Отсюда высота H равна:
H=mgl1mg+mv22mg=l1+v22g
Относительно точки В шарик поднимется на высоту h – l1. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:
h−l1=v2sin2β2g=v2sin2(90−2α)o2g
Отсюда:
l1=h−v2sin2(90−2α)o2g
Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:
v=gt
Следовательно:
H=l1+v22g=h−(gt)2sin2(90−2α)o2g+(gt)22g
H=h−gt2sin2(90−2α)2+gt22=h−gt22(sin2(90−2α)o−1)
H=1,4−10·0,422(sin2(90−60)o−1)
H=1,4−5·0,16(sin230o−1)
H=1,4−0,8((12)2−1)=1,4−0,8(14−1)
H=1,4+0,6=2 (м)
Ответ: 20
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17980
В момент t=0 мячик бросают с начальной скоростью v0 под углом α к горизонту с балкона высотой h (см. рисунок).
Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).
К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.
Алгоритм решения
- Установить вид механического движения, исходя из условий задачи.
- Записать формулы для физических величин, указанных в таблице, в соответствии с установленным видом механического движения.
- Определить, как зависят эти величины от времени.
- Установить соответствие между графиками и величинами.
Решение
Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.
Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.
Координата x меняется согласно уравнению координаты x:
Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:
Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:
В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.
Формула проекции скорости мячика на ось ОХ:
Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.
Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.
Остается последний вариант — координата y. Уравнение этой координаты имеет вид:
Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.
Теперь записываем установленные соответствия в порядке АБ: 42.
Ответ: 42
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18741
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
- увеличивается
- уменьшается
- не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулы, определяющие указанные в условии задачи величины.
- Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.
Решение
Выполняем чертеж:
Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
vx = v0 cosα
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
Ответ: 33
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 43.3k
Движение тела, брошенного под углом к горизонту!
Опубликовано 22 Апр 2014
Рубрика: О жизни | 9 комментариев

…за несколько минут до окончания матча. Но, растеряв в концовке все преимущество, уже уступала одно очко 49:50. Дальше произошло невероятное! Иван Едешко бросает мяч из-за лицевой линии через всю площадку под кольцо американцев, где наш центровой Александр Белов принимает мяч в окружении двух соперников и вкладывает его в корзину. 51:50 – мы олимпийские чемпионы!!!
Я, будучи тогда ребенком, испытал сильнейшие эмоции – сначала разочарование и обиду, затем сумасшедший восторг! Эмоциональная память об этом эпизоде врезалась в мое сознание на всю жизнь! Посмотрите видео в Интернете по запросу «золотой бросок Александра Белова», не пожалеете.
Американцы тогда не признали поражения и отказались от получения серебряных медалей. Возможно ли за три секунды сделать то, что совершили наши игроки? Вспомним физику!
В этой статье мы рассмотрим движение тела, брошенного под углом к горизонту, составим в Excel программу решения этой задачи при различных сочетаниях исходных данных и попытаемся ответить на поставленный выше вопрос.
Это достаточно широко известная задача в физике. В нашем случае тело, брошенное под углом к горизонту – это баскетбольный мяч. Мы рассчитаем начальную скорость, время и траекторию полета мяча, брошенного через всю площадку Иваном Едешко и попавшего в руки Александра Белова.
Математика и физика полета баскетбольного мяча.
Представленные ниже формулы и расчет в excel являются универсальными для широкого круга задач о телах, брошенных под углом к горизонту и летящих по параболической траектории без учета влияния трения о воздух.
Расчетная схема представлена на рисунке, расположенном ниже. Запускаем программу MS Excel или OOo Calc.
Исходные данные:
1. Так как мы находимся на планете Земля и рассматриваем баллистическую задачу – движение тел в поле тяжести Земли, то первым делом запишем основную характеристику гравитационного поля – ускорение свободного падения g в м/с2
в ячейку D3: 9,81
2. Размеры баскетбольной площадки – 28 метров длина и 15 метров ширина. Расстояние полета мяча почти через всю площадку до кольца от противоположной лицевой линии по горизонтали x в метрах впишем
в ячейку D4: 27,000
3. Если принять, что бросок Едешко совершил с высоты около двух метров, а Белов поймал мяч как раз где-то на уровне кольца, то при высоте баскетбольного кольца 3,05 метра расстояние между точками вылета и прилета мяча составит по вертикали 1 метр. Запишем вертикальное перемещение y в метрах
в ячейку D5: 1,000
4. По моим замерам на видеозаписи угол вылета мяча α0 из рук Едешко не превышал 20°. Введем это значение
в ячейку D6: 20,000
Результаты расчетов:
Основные уравнения, описывающие движение тела, брошенного под углом к горизонту без учета сопротивления воздуха:
x=v0*cosα0*t
y=v0*sinα0*t—g*t2/2
5. Выразим время t из первого уравнения, подставим во второе и вычислим начальную скорость полета мяча v0 в м/с
в ячейке D8: =(D3*D4^2/2/COS (РАДИАНЫ(D6))^2/(D4*TAN (РАДИАНЫ (D6)) -D5))^0,5 =21,418
v0=(g*x2/(2*(cosα0)2*(x*tgα0—y))0,5
6. Время полета мяча от рук Едешко до рук Белова t в секундах рассчитаем, зная теперь v0, из первого уравнения
в ячейке D9: =D4/D8/COS (РАДИАНЫ(D6)) =1,342
t=x/(v0*cosα0)
7. Найдем угол направления скорости полета мяча αi в интересующей нас точке траектории. Для этого исходную пару уравнений запишем в следующем виде:
y=x*tgα0—g*x2/(2*v02*(cosα0)2)
Это уравнение параболы – траектории полета.
Нам необходимо найти угол наклона касательной к параболе в интересующей нас точке – это и будет угол αi. Для этого возьмем производную, которая представляет собой тангенс угла наклона касательной:
y’=tgα0—g*x/(v02*(cosα0)2)
Рассчитаем угол прилета мяча в руки Белова αi в градусах
в ячейке D10: =ATAN (TAN (РАДИАНЫ(D6)) -D3*D4/D8^2/COS (РАДИАНЫ (D6))^2)/ПИ()*180 =-16,167
αi= arctg y’=arctg(tgα0— g*x/(v02*(cosα0)2))
Расчет в excel, в принципе, закончен.
Иные варианты расчетов:
Используя написанную программу, можно быстро и просто при других сочетаниях исходных данных произвести вычисления.
Пусть, даны горизонтальная x=27 метров, вертикальная y=1 метр дальности полета и начальная скорость v0=25 м/с.
Требуется найти время полета t и углы вылета α0 и прилета αi
Воспользуемся сервисом MS Excel «Подбор параметра». Я неоднократно в нескольких статьях блога подробно рассказывал, как им пользоваться. Детальнее об использовании этого сервиса можно почитать здесь.
Устанавливаем в ячейке D8 значение 25,000 за счет изменения подбором значения в ячейке D6. Результат на рисунке внизу.
Исходные данные в этом варианте расчета в excel (как, впрочем, и в предыдущем) выделены синими рамками, а результаты обведены красными прямоугольными рамками!
Устанавливая в таблице Excel некоторое интересующее значение в одной из ячеек со светло-желтой заливкой за счет подбора измененного значения в одной из ячеек со светло-бирюзовой заливкой, можно получить в общем случае десять различных вариантов решения задачи о движении тела, брошенного под углом к горизонту при десяти разных наборах исходных данных!!!
Ответ на вопрос:
Ответим на вопрос, поставленный в начале статьи. Мяч, посланный Иваном Едешко, долетел до Белова по нашим расчетам за 1,342с. Александр Белов поймал мяч, приземлился, подпрыгнул и бросил. На все это у него было «море» времени – 1,658с! Это действительно достаточное с запасом количество времени! Детальный просмотр по кадрам видеозаписи подтверждает вышесказанное. Нашим игрокам хватило трех секунд, чтобы доставить мяч от своей лицевой линии до щита соперников и забросить его в кольцо, вписав золотом свои имена в историю баскетбола!
Ссылка на скачивание файла: dvizheniye-tela-broshennogo-pod-uglom-k-gorizontu (xls 18,0KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
Движение тела, брошенного вертикально вверх
Тело, брошенное вертикально вверх, движется равномерно замедленно с начальной скоростью u0 и ускорением
a = -g.
Перемещение тела за время t представляет собой высоту подъема h.
Для этого движения справедливы формулы:
Если:
u0 — начальная скорость движения тела ,
u — скорость падения тела спустя время t,
g — ускорение свободного падения, 9.81 (м/с²),
h — высота на которую поднимется тело за время t,
t — время,
То, движение тела, брошенного вертикально вверх описывается следующими формулами:
Высота подъема тела за некоторое время, зная конечную скорость
[ h = frac{u_0 + u}{2} t ]
Высота подъема тела за некоторое время, зная ускорение свободного падения
[ h = u_0 t — frac{g t^2}{2} ]
Скорость тела через некоторое время, зная ускорение свободного падения
[ u = u_0 — gt ]
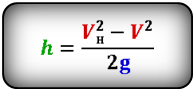
Скорость тела на некоторой высоте, зная ускорение свободного падения
[ u = sqrt{ u_0^2 — 2gh} ]
Максимальная высота подъема тела, зная первоначальную скорость и ускорение свободного падения
Тело, брошенное вертикально вверх, достигает максимальной высоты в тот момент, когда его скорость обращается в ноль. Поднявшись на максимальную высоту тело начинает свободное падение вниз.
[ h_{max} = frac{u_0^2}{2g} ]
Время подъема на максимальную высоту подъема тела, зная первоначальную скорость и ускорение свободного падения
[ t_{hmax} = frac{u_0}{g} ]
Примечание к статье: Движение тела, брошенного вертикально вверх
- Сопротивление воздуха в данных формулах не учитывается.
- Ускорение свободного падения имеет приведенное значение (9.81 (м/с²)) вблизи земной поверхности. Значение g на других расстояниях от поверхности Земли изменяется!
Движение тела, брошенного вертикально вверх |
стр. 409 |
|---|
В статье подробно, начиная с основ и базовых определений, рассказано о движении тела брошенного под углом к горизонту. Здесь вы найдете формулы параметров движения: общее время, дальность полета, максимальная высота. Также в конце приложены примеры задач с решениями.
Определение. Баллистическое движение — это движение некоторого тела в поле тяжести Земли при условии, что тело имеет вертикальную и горизонтальную проекции скорости.
Вначале вспомним основные формулы для равноускоренного движения.
Изменение скорости с течением времени задаётся соотношением
vₓ = v₀ₓ + aₓt,
где vₓ — конечная проекция скорости, v₀ₓ — начальная проекция скорости, aₓ — проекция ускорения тела.
Изменение координаты x во времени можно найти, используя следующее соотношение:
x = x₀ + v₀ₓt + aₓt² / 2,
где x — конечная координата тела, x₀ — начальная координата, v₀ₓ — начальная проекция скорости тела вдоль оси OX, aₓ — проекция ускорения тела.

Замечание 1. Перемещением тела за время t называется величина Sₓ = x – x₀.
Замечание 2. Так как эти выражения справедливы для проекций, то их можно записать и в векторном виде.
Баллистическое движение — это случай равноускоренного движения (с постоянным ускорением свободного падения g). Любое тело, брошенное под углом α к горизонту, имеет некоторую вертикальную и горизонтальную проекции скорости (рис. 1).
Далее движение необходимо разбить на два участка:
- Горизонтальное
- Вертикальное
По горизонтали тело движется с одинаковой скоростью (обычно пренебрегаем силами различного трения):
v₁ = v₀cos(α)
А по вертикали это обычное движение тела, брошенного вертикально вверх с начальной скоростью:
v₂ = v₀sin(α)
Общее время движения
Разобьём траекторию на два участка. Первый — участок, на котором тело продолжает подниматься, а второй — участок, где тело спускается. Обозначим t₁ время подъёма тела (от нуля до максимальной высоты подъема), t₂ — время спуска тела.
Из уравнения движения:
v₀sin(α) – gt₁ = 0
(так как конечная проекция скорости в верхней точке траектории равна нулю),
t₁ = v₀sin(α) / g.
Найдём время спуска:
–gt₂ = –v₀sin(α),
(т. к. конечная скорость тела будет такая же, как и начальная),
t₂ = v₀sin(α) / g.
Общее время движения:
t = t₁ + t₂ = 2v₀sin(α) / g.
Замечание.Время спуска и время подъёма тела одинаковые. Это связано с тем, что движение симметрично.
Дальность полета
Так как по горизонтали (вдоль оси ОХ) движение тела равномерное, то, зная общее время движения, найдём дальность полета L:
L = tv₁ = (2v₀sin(α) / g) · v₀cos(α) = 2v₀²sin(α)cos(α) / g.
Замечание. Используя формулу из тригонометрии
2sin(α)cos(α) = sin(2α),
получим:
L = 2v₀²sin(2α) / g.
Следовательно, максимальная дальность полета тела будет при броске под углом 45° к горизонту (так как sin(90°) = 1).
Максимальная высота подъёма тела
Рассмотрим движение тела в проекции на ось OY:
H = v₀sin(α)t₁ – gt₁² / 2.
После подставления времени подъёма получим
H = v₀²sin²(α) / (2g).
Давайте теперь решим некоторые задачи.
Задачи
Задача 1. Пуля, летящая горизонтально со скоростью v = 500 м/с, пробивает первый листок бумаги. Найти, на каком расстоянии S находится второй листок бумаги, если известно, что его пуля пробила на h = 20 см ниже, чем первый.
Решение. Найдём, за какое время пуля прошла расстояние между листами. Нам известно, что за это же время она опустилась на высоту h = 20 см. Тогда:
h = gt² / 2,
t = √(2h/g).
Теперь, зная время движения пули между листами, найдём расстояние, которое прошла пуля за это время:
S = tv = v · √(2h/g) = 100 м.
Ответ: S = 100 м.
Задача 2. Школьник может бросить мяч в спортивном зале с максимальной скоростью v = 25 м/с. Пренебрегая силами сопротивления воздуха, найти максимальную дальность полета мяча в спортивном зале, если высота зала равна h = 4 м. Считать, что мяч не ударяется о потолок.
Решение. Пусть мальчик бросил мяч под некоторым углом α к горизонту. Тогда дальность полета мяча равна:
L = 2v₀²sin(α)cos(α) / g.
Как обсуждалось выше, тело имеет максимальную дальность полета, если его бросить под углом α = 45° к горизонту. Но в данной задаче возможно, что при таком угле мяч ударится о потолок. Проверим, какова максимальная высота подъёма мяча при условии, что угол равен α = 45°.
H = v₀²sin²(α) / (2g) = 16 м.
Следовательно, угол, под которым мальчик бросит мяч, будет значительно меньше. Найдём максимальный угол, при котором мяч не столкнется с потолком. Этот угол будет соответствовать предельному случаю, когда мяч побывает на высоте h = 4 м.
h = v₀²sin²(α) / (2g) => sin²(α) = 2gh / v₀².
Из основного тригонометрического тождества
sin²(α) + cos²(α) = 1
найдём cos²(α):
cos²(α) = 1 – 2gh / v₀².
Подставив все выражения в дальность полета L, получим:
L = 2√(2gh(v₀² – 2gh)) / g = 42 м.
Ответ: L = 42 м.
Замечание. Если в задаче не приведены числовые значения (задача в общем виде), то необходимо записать 2 ответа. Первый ответ при условии высокого потолка, при h > H —
L = 2v₀²sin(α)cos(α) / g, α = 45°.
И при h < H получаем ответ
L = 2√(2gh(v₀² – 2gh)) / g.
Список литературы
- Черноуцан А. Учебно-справочное пособие для старшеклассников и абитуриентов. М., 2000.
- Белолипецкий С. Н., Еркович О. С., Казаковцева В. А., Цвецинская Т. С. Задачник по физике. М., 2005.
Автор: Роман Федоренко