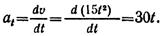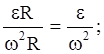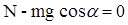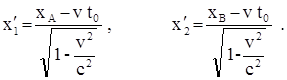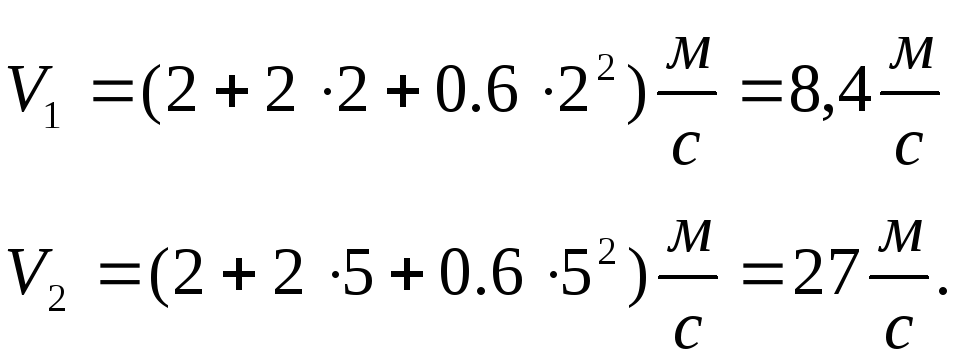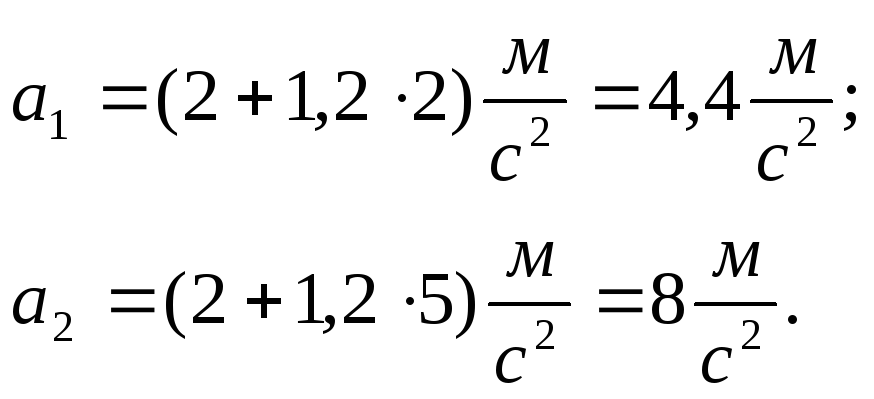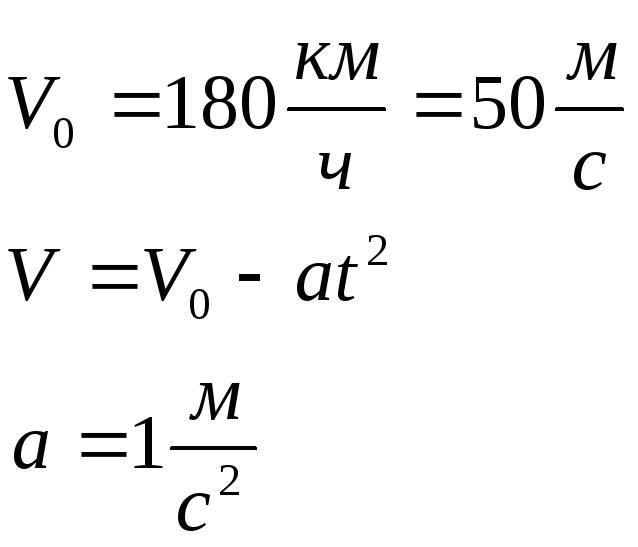Время, скорость, расстояние
О чем эта статья:
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
- Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.
Расстояние обозначается латинской буквой s.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути
Чтобы найти расстояние, нужно умножить скорость на время движения:
s = v × t
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
- Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.
Время движения обозначается латинской буквой t.
Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.
Формула времени
Чтобы найти время, нужно разделить расстояние на скорость:
t = s : v
Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров в минуту на 15 минут, мы определим расстояние от дома до магазина:
s = v × t = 50 × 15 = 750 (м)
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).
100 м : 25 с = 4 м/с
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
Значит, скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.
Ответ: первый школьник добежал быстрее.
Если известны скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:
t = s : v = 500 : 100 = 5 (мин)
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.
Перемещение и путь при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.
При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:
Пример №1. По графику определить перемещение тела в момент времени t=3 с.
Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:
Извлекаем из графика необходимые данные:
- Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
- Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).
Подставляем известные данные в формулу:
Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.
Варианты записи формулы перемещения
Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:
В итоге получается формула:
Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».
Если начальная скорость равна 0 (v0 = 0), эта формула принимает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:
Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.
Перемещение при разгоне и торможении тела
Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают ( а ↑↑ v ). Если векторы имеют противоположное направление ( а ↑↓ v ), движение следует описывать в два этапа:
Этап торможения
Время торможения равно разности полного времени движения и времени второго этапа:
Когда тело тормозит, через некоторое время t1оно останавливается. Поэтому скорость в момент времени t1 равна 0:
При торможении перемещение s1 равно:
Этап разгона
Время разгона равно разности полного времени движения и времени первого этапа:
Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t2 равна:
При разгоне перемещение s2 равно:
При этом модуль перемещения в течение всего времени движения равен:
Полный путь (обозначим его l), пройденный телом за оба этапа, равен:
Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с 2 . Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.
В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:
Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:
Подставляем выраженные величины в формулу:
Перемещение в n-ную секунду прямолинейного равноускоренного движения
Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:
За первую секунду тело переместится на расстояние, равное:
За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:
За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:
Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:
Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:
Формула перемещения за n-ную секунду
Пример №4. Автомобиль разгоняется с ускорением 3 м/с 2. Найти его перемещение за 6 секунду.
Подставляем известные данные в формулу и получаем:
Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:
где t — время одного промежутка, а n — порядковый номер этого промежутка.
Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с 2 . Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.
Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.
Подставляем известные данные в формулу:
Проекция и график перемещения
Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ ( v ↑↑OX), а вектора скорости и ускорения сонаправлены ( v ↑↑ a ), принимает следующий вид:
График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно ( v ↓↑ a ), принимает следующий вид:
Определение направления знака проекции ускорения по графику его перемещения:
- Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
- Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.
Пример №6. Определить ускорение тела по графику его перемещения.
Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:
Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:
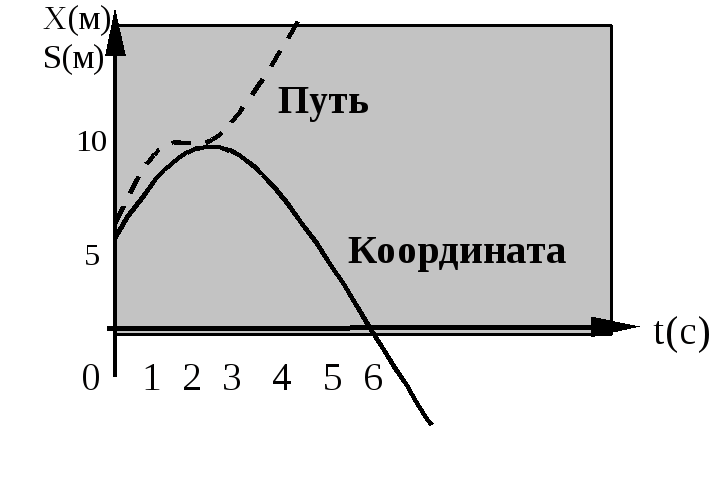
График пути
График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.
В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:
- 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
- 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.
Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.
Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.
При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:
Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
Решение
Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.
Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:
x ( t ) = x 0 + v 0 t + a t 2 2 . .
Теперь мы можем выделить кинематические характеристики движения тела:
Перемещение тела определяется формулой:
s = v 0 t + a t 2 2 . .
Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:
x ( t ) = v 0 t + a t 2 2 . . = 5 t − 3 t 2
Кинетическая энергия тела определяется формулой:
Скорость при прямолинейном равноускоренном движении равна:
v = v 0 + a t = 5 − 6 t
Поэтому кинетическая энергия тела равна:
E k = m ( 5 − 6 t ) 2 2 . . = 0 , 2 2 . . ( 5 − 6 t ) 2 = 0 , 1 ( 5 − 6 t ) 2
Следовательно, правильная последовательность цифр в ответе будет: 34.
pазбирался: Алиса Никитина | обсудить разбор | оценить
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
pазбирался: Алиса Никитина | обсудить разбор | оценить
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:
Теперь рассчитаем пути s1и s2, а затем сложим их:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Примеры решения задач
Пример 1. По заданному закону движения S =10 + 20t — 5t 2 ([S] = м; [t] = с) определить вид движения, начальную скорость и касательное ускорение точки, время до остановки.
(Рекомендуется обойтись без расчетов, использовать метод сравнения заданного уравнения с уравнениями различных видов движений в общем виде.)

1. Вид движения: равнопеременное
2. При сравнении уравнений очевидно, что
- начальный путь, пройденный до начала отсчета – 10 м;
- начальная скорость 20 м/с;
- постоянное касательное ускорение at/2 = 5 м/с ; at= — 10 м/с .
- ускорение отрицательное, следовательно, движение замедленное (равнозамедленное), ускорение направлено в сторону, противоположную направлению скорости движения.
3. Можно определить время, при котором скорость точки будет равна нулю:
v = S’ = 20 — 2 • 5t; v = 20 – 10t = 0; t = 20/10 = 2 c.
Примечание. Если при равнопеременном движении скорость растет, значит, ускорение — положительная величина, график пути — вогнутая парабола. При торможении скорость падает, ускорение (замедление) — отрицательная величина, график пути — выпуклая парабола (рис. 10.4).
Пример 2. Точка движется по желобу из точки А в точку D (рис. 10.5).

Скорость движения считать постоянной. Радиус участка АВ = 10 м, радиус участка ВС= 5 м.
Решение
1. Рассмотрим участок АВ. Касательное ускорение равно нулю (v = const).
Нормальное ускорение (ап = v 2 /r) при переходе через точку В увеличивается в 2 раза, оно меняет направление, т. к. центр дуги АВ не совпадает с центром дуги ВС.
2. На участке ВС:
— касательное ускорение равно нулю: at = 0;
— нормальное ускорение при переходе через точку С меняется: до точки С движение вращательное, после точки С движение становится прямолинейным, нормальное напряжение на прямолинейном участке равно нулю.
3. На участке CD полное ускорение равно нулю.
Пример 3. По заданному графику скорости найти путь, пройденный за время движения (рис. 10.6).
Решение
1. По графику следует рассмотреть три участка движения. Первый участок — разгон из состояния покоя (равноускоренное движение).
Второй участок — равномерное движение: v = 8 м/с; a2 = 0.
Третий участок — торможение до остановки (равнозамедленное движение).
2. Путь, пройденный за время движения, будет равен:
Пример 4. Тело, имевшее начальную скорость 36 км/ч, прошло 50 м до остановки. Считая движение равнозамедленным, определить время торможения.
Решение
1. Записываем уравнение скорости для равнозамедленного движения:
Определяем начальную скорость в м/с: vо = 36*1000/3600 = 10 м/с.
Выразим ускорение (замедление) из уравнения скорости: a = — v0/t
2. Записываем уравнение пути: S = vot/2 + at 2 /2. После подстановки получим: S = vot/2
3. Определяем время до полной остановки (время торможения):
Пример 5. Точка движется прямолинейно согласно уравнению s = 20t – 5t 2 (s — м, t — с). Построить графики расстояний, скорости и ускорения для первых 4 с движения. Определить путь, пройденный точкой за 4 с, и описать движение точки.
Решение
1. Точка движется прямолинейно по уравнению s = 20t – 5t 2 следовательно, скорость точки u = ds/d/t = 20 — 10t и ускорение a = at = dv/dt = —10 м/с 2 . Значит, движение точки равнопеременное (a = at = —10 м/c 2 = const) с начальной скоростью v0 = 20 м/с.
2. Составим зависимость числовых значений s и v для первых 4 с движения
3. По приведенным числовым значениям построим графики расстояний (рис. а), скорости (рис. б) и ускорения (рис. в), выбрав масштабы для изображения по осям ординат расстояний s, скорости v и ускорения а, а также одинаковый для всех графиков масштаб времени по оси абсцисс. Например, если расстояние s = 5 м изображать на графике длиной отрезка ls = 10 мм, то 5м = μs*10мм, где коэффициент пропорциональности μs и есть масштаб по оси Os : μs = 5/10 = 0,5 м/мм (0,5 м в 1 мм); если модуль скорости v = 10 м/с изображать на графике длиной lv =10 мм, то 10 м/c = μv * 10 мм и масштаб по оси Ov μv = 1 м/(с-мм) (1 м/с в 1 мм); если модуль ускорения а = 10 м/с 2 изображать отрезком la = 10 мм, то, аналогично предыдущему, масштаб по оси Оа μa = 1 м/(с 2 -мм) (1 м/с 2 в 1 мм); и наконец, изображая промежуток времени Δt = 1 с отрезком μt = 10 мм, получим на всех графиках масштаб по осям Ot μt = 0,1 с/мм (0,1 с в 1 мм).
4. Из рассмотрения графиков следует, что в течение времени от 0 до 2 с точка движется равнозамедленно (скорость v и ускорение в течение этого промежутка времени имеют разные знаки, значит, их векторы направлены в противоположные стороны); в период времени от 2 до 4 с точка движется равноускоренно (скорость v и ускорение имеют одинаковые знаки, т. е. их векторы направлены в одну сторону).
За 4 с точка прошла путь so_4 = 40 м. Начав движение со скоростью v0 = 20 м/с, точка по прямой прошла 20 м, а затем вернулась в исходное положение, имея ту же скорость, но направленную в противоположную сторону.
Если условно принять ускорение свободного падения g = 10 мс 2 и пренебречь сопротивлением воздуха, то можно сказать, что графики описывают движение точки, брошенной вертикально вверх со скоростью а0 = 20 м/с.
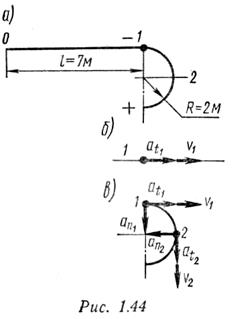
Решение
Время, необходимое для перемещения точки из положения 0 (начала отсчета) в положение 1, определим из уравнения движения, подставив частные значения расстояния и времени:
Уравнение изменения скорости
Скорость точки в положении 1
Уравнение изменения касательного ускорения
Касательное ускорение точки в положении 1
Нормальное ускорение точки на прямолинейном участке траектории равно нулю. Скорость и ускорение точки в конце этого участка траектории показаны на рис.1.44, б.
Определим скорость и ускорение точки в начале криволинейного участка траектории. Очевидно, что v1 = 11,5 м/с, аt1 = 14,2 м/с 2 .
Нормальное ускорение точки в начале криволинейного участка
Скорость и ускорение в начале криволинейного участка показаны на рис. 1.44, в (векторы at1 и aa1 изображены без соблюдения масштаба).
Положение 2 движущейся точки определяется пройденным путем, состоящим из прямолинейного участка 0 — 1 и дуги окружности 1 — 2, соответствующей центральному углу 90°:
Время, необходимое для перемещения точки из положения 0 в положение2,
Скорость точки в положении 2
Касательное ускорение точки в положении 2
Нормальное ускорение точки в положении 2
Ускорение точки в положении 2
Скорость и ускорения точки в положении 2 показаны на рис. 1.44, в (векторы at„ и аПг изображены без соблюдения масштаба).

Решение
Уравнение изменения скорости
Время t1 определим из уравнения изменения скорости, подставив частные значения скорости и времени:
Определим положение точки на траектории в момент 3 с:
Дуга окружности длиной 135 м соответствует центральному углу
Уравнение изменения касательного ускорения
Касательное ускорение точки в момент tt
Нормальное ускорение точки в момент tt
Ускорение точки в момент tx
Скорость и ускорение точки в момент времени t1 показаны на рис. 1.45, б.
Как видно из рис. 1.45, б
Пример 8. В шахту глубиной H = 3000 м с поверхности земли без начальной скорости брошен предмет. Определить, через сколько секунд звук, возникающий в момент удара предмета о дно шахты, достигнет поверхности земли. Скорость звука 333 м/с.
Решение
Уравнение движения свободно падающего тела
Время, необходимое для перемещения предмета от поверхности земли до дна шахты, определим из уравнения движения:
Звук распространялся с постоянной скоростью 333 м/с. Уравнение распространения звука
Время достижения звуком поверхности земли
Тогда время с момента начала движения предмета до момента достижения звуком поверхности земли
Пример 9. По заданным уравнениям движения точки x = 2t 2 , y = 2t (x и у — в метрах, t — в секундах) найти уравнение траектории, а также скорость и ускорение точки в момент времени t = 2 с.
Решение
Для определения траектории точки нужно из уравнений движения исключить параметр t — время.
Выразим t через х из первого уравнения:
и подставим это значение во второе уравнение:
Траекторией точки является парабола, симметричная относительно оси х.
Чтобы найти скорость точки, нужно определить ее составляющие по координатным осям
Находим скорость точки
При t = 2 с получаем
Находим составляющие ускорения точки
Контрольные вопросы и задания
1. Запишите формулу ускорения при прямолинейном движении.
2. Запишите формулу ускорения (полного) при криволинейном движении.
3. 
4. Параметры движения не меняются.
4. По заданному уравнению движения точки S = 25 + 1,5t + 6t 2 определите вид движения и без расчетов, используя законы движения точки, ответьте, чему равны начальная скорость и ускорение.
5. По заданному уравнению движения точки S = 22t — 4t 2 постройте графики скорости и касательного ускорения.
6. По графику скоростей точки определите путь, пройденный за время движения (рис. 10.8).
7. Точка движется по дуге. Охарактеризуй движение точки (рис. 10.9).
источники:
http://spadilo.ru/peremeshhenie-i-put-pri-ravnouskorennom-pryamolinejnom-dvizhenii/
http://mydocx.ru/12-105317.html
Примеры решения задач по теме №1
«Механика и элементы специальной теории относительности»
Задача 1 Уравнение движения точки по прямой имеет вид: x = A+Bt+Ct 3 , где А = 4 м, В = 2 м/c, С = 0,2 м/с 3 . Найти: 1) положение точки в моменты времени t = 2 c и t = 5 с; 2) среднюю скорость за время, протекшее между этими моментами; 3) мгновенные скорости в указанные моменты времени; 4) среднее ускорение за указанный промежуток времени; 5) мгновенные ускорения в указанные моменты времени.
| x = A + Bt + Ct 3 A = 4 м B = 2 м/c C = 0,2 м/c 3 t1 = 2 c; t2 = 5 c | Решение 1. Чтобы найти координаты точки, надо в уравнение движения подставить значения t1 и t2: x1 = (4+2×2+0,2×2 3 ) м = 9,6 м, x2 = (4+2×5+0,2×5 3 ) м = 39 м. |
| x1, x2, — ? u1, u2 — ? , a1, a2 — ? | 2. Средняя скорость  , , |

3. Мгновенные скорости найдем, продифференцировав по времени уравнение движения:
u1 = (2+3×0,2×2 2 ) м/с = 4,4 м/c;
u2 = (2+3×0,2×5 2 ) м/с = 17 м/с.
4. Среднее ускорение 
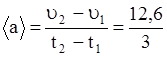
5. Мгновенное ускорение получим, если продифференцируем по времени выражение для скорости: a = 2×3×Ct = 6Ct.
a1 = 6×0,2×2 м/c 2 = 2,4 м/с 2 ;
a2 = 6×0,2×5 м/с 2 = 6 м/с 2 .
Ответ: x1 = 9,6 м; x2 = 39 м; áuñ = 9,8 м/с; u1 = 4,4 м/c; u2 = 17 м/с; áаñ = 4,2 м/с 2 ; a1 = 2,4 м/с 2 ; a2 = 6 м/с 2 .
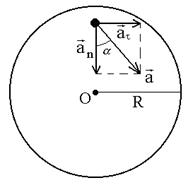
Задача 2 Маховик вращается равноускоренно. Найти угол a, который составляет вектор полного ускорения 
Поскольку в условии дано лишь число оборотов, перейдем к угловым величинам. Применив формулы: at = eR, an = w 2 R, где R – радиус маховика, получим
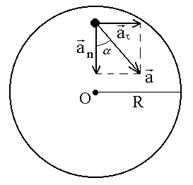
так как маховик вращается равноускоренно, найдем связь между величинами e и w;
Поскольку w0 = 0; j = 2pN, то w 2 = 2e×2pN = 4pNe.
Подставим это значение в формулу, получим:

Задача 3 Две гири с массами m1 = 2 кг и m2 = 1 кг соединены нитью, перекинутой через невесомый блок. Найти ускорение a, с которым движутся гири, и силу натяжения нити 
На тело 1 и тело 2 действуют только две силы – сила тяжести и сила
натяжения нити. Для первого тела имеем

для второго тела

Так как сила трения в блоке отсутствует,

Ускорения тел а1 и а2 направлены в противоположные стороны и равны по модулю:

Получаем из выражений (1) и (2) систему уравнений
Выберем ось Х, как показано на рисунке и запишем полученную систему уравнений
в проекции на ось Х
Решая эту систему относительно а и FН, получаем:


Ответ: a= 3,3 м/c 2 ; FH = 13 Н.
Задача 4 К ободу однородного диска радиусом R=0,2 м приложена касательная сила F=98,1 Н. При вращении на диск действует момент сил трения
МТР=4,9 Н×м. Найти массу m диска, если известно, что диск вращается с угловым ускорением e=100 рад/с 2 .
относительно выбранной оси ( MF — момент силы F, Mтр – момент сил трения);

Учитывая, что MF=F×R, получаем 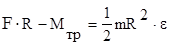
Отсюда 
Задача 5 На гладкой горизонтальной поверхности находятся две одинаковые соприкасающиеся шайбы. Третья такая же шайба налетает на них со скоростью v0 = 6 м/с, направленной по общей касательной к неподвижным шайбам. После столкновения налетевшая шайба движется вдоль первоначального направления со скоростью v1 = 2 м/с. Найти величину энергии, перешедшей во внутреннюю энергию тел при столкновении. Масса каждой шайбы m = 100 г.



Поскольку размеры всех шайб одинаковы, то скорости v2 и v3, направленные вдоль прямых,
соединяющих центры шайб в момент удара, составляют одинаковые углы a = 30 о с осью X, а так как массы всех шайб по условию равны, то очевидно, что скорости v2 и v3 равны по модулю, то есть v2 = v3 = v.
Теперь запишем закон сохранения импульса для проекций импульсов взаимодействующих тел на ось X:
Тогда mv0 = mv1 + 2 mv сosa.
Отсюда 
Энергию, перешедшую во внутреннюю энергию тел при частично неупругом ударе, можно найти как разность кинетической энергии налетающей шайбы до удара и суммарной кинетической энергии всех тел после удара:

Ответ: DU = 1,07 Дж.
Задача 6 Небольшое тело массой m равномерно втащили на горку, действуя силой, которая в каждой точке направлена по касательной к траектории. Найти работу этой силы, если высота горки h, длина ее основания l, и коэффициент трения m.

Работу, совершаемую силой 

Для этого необходимо предварительно найти силу 




Выберем координатные оси х и у таким образом, чтобы ось х была направлена по касательной к траектории (вдоль перемещения 
Запишем векторное равенство в проекциях на эти координатные оси:
oсь x:
oсь y:
Тогда 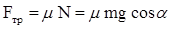

Теперь можно найти выражение для элементарной работы, совершаемой силой F при перемещении тела на расстояние dr. При этом учтем, что угол между векторами 

Тогда 
Из рис. видно, что 

Тогда 
и полная работа, совершаемая силой F при втаскивании тела на горку:


Ответ: 
Задача 7 Круглая платформа радиусом R=1,0 м, момент инерции которой J=130 кг×м 2 , вращается по инерции вокруг вертикальной оси, делая n1=1,0 об/с. На краю платформы стоит человек, масса которого m=70 кг. Сколько оборотов в секунду n2 будет совершать платформа, если человек перейдет в её центр? Момент инерции человека рассчитывать как для материальной точки.
| R = 1м J = 130 кг × м 2 n1 = 1c -1 m = 70 кг | Решение Согласно условию задачи, платформа с человеком вращается по инерции. Это означает, что результирующий момент всех внешних сил, приложенных к вращающейся системе, равен нулю. Следовательно, для системы “платформа + человек” выполняется закон сохранения момента импульса, который запишем в скалярной форме относительно оси, совпадающей с осью вращения и направленной по угловой скорости: |
| n2 — ? |
где L1 — импульс системы «платформа + человек на краю платформы», L2 — импульс системы «платформа + человек в центре платформы».
где mR 2 — момент инерции человека, J1 = J+mR 2 — момент инерции системы «платформа + человек на краю платформы», J2 — момент инерции системы «платформа + человек в центре платформы», w1 и w2 — соответствующие угловые скорости системы. Решая систему уравнений (1) — (3), получаем
Задача 8 В условно неподвижной системе отсчета К в точках с координатами xA и xB = xA + l, где l = 1 км, одновременно происходят два события A и B. На каком расстоянии l¢АВ друг от друга зафиксирует эти события наблюдатель в системе К¢, движущейся со скоростью v = 0,4×с вдоль оси X? Какой промежуток времени Dt¢ между этими событиями зафиксирует наблюдатель в системе К¢?

Обозначим через t0 момент времени, когда в системе К происходят события А и В. Тогда событие А в этой системе обладает пространственно – временными координатами xA и t0, а событие В – координатами xB и t0. В системе К¢ событие А обладает пространственно–временными координатами x1¢ и t1¢, а событие В – координатами x2¢ и t2¢. Связь координат каждого из событий можно записать с помощью преобразований Лоренца.
Найдя разность этих выражений, получим расстояние между точками, в которых происходят события А и В в системе К¢.
Видно, что расстояние l¢АВ, разделяющее события А и В в любой системе, движущейся относительно К, больше, чем это же расстояние, измеренное в системе К, в которой оба события одновременны. Рассчитаем расстояние l¢АВ.
Моменты времени, в которые в системе К¢ наблюдатель зафиксирует события А и В, также могут быть найдены из преобразований Лоренца:
Видно, что события А и В в системе отсчета К¢ не являются одновременными. Если xB > xA и система К¢ движется в положительном направлении оси X, как и задано в условии, то t2¢ — t1¢ .
Примеры решения задач. Задача 1 Уравнение движения точки по прямой имеет вид: x = A+Bt+Ct3, где А = 4 м, В = 2 м/c, С = 0,2 м/с3
Задача 1 Уравнение движения точки по прямой имеет вид: x = A+Bt+Ct 3 , где А = 4 м, В = 2 м/c, С = 0,2 м/с 3 . Найти: 1) положение точки в моменты времени t = 2 c и t = 5 с; 2) среднюю скорость за время, протекшее между этими моментами; 3) мгновенные скорости в указанные моменты времени; 4) среднее ускорение за указанный промежуток времени; 5) мгновенные ускорения в указанные моменты времени.
- I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
- I. Решение логических задач средствами алгебры логики
- I. Розв’язати задачі
- I. Ситуационные задачи и тестовые задания.
- II Съезд Советов, его основные решения. Первые шаги новой государственной власти в России (октябрь 1917 — первая половина 1918 гг.)
- II. Основные задачи и функции
- II. Решение логических задач табличным способом
- II. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ ВОИ
- II. Цель и задачи государственной политики в области развития инновационной системы
- III. Решение логических задач с помощью рассуждений
- III. Цели и задачи социально-экономического развития Республики Карелия на среднесрочную перспективу (2012-2017 годы)
- IV. Определите, какую задачу взаимодействия с практическим психологом поставил перед собой клиент.
| x = A + Bt + Ct 3 A = 4 м B = 2 м/c C = 0,2 м/c 3 t1 = 2 c; t2 = 5 c | Решение 1. Чтобы найти координаты точки, надо в уравнение движения подставить значения t1 и t2: x1 = (4+2×2+0,2×2 3 ) м = 9,6 м, x2 = (4+2×5+0,2×5 3 ) м = 39 м. |
| x1, x2, — ? u1, u2 — ? , a1, a2 — ? | 2. Средняя скорость  , , |

3. Мгновенные скорости найдем, продифференцировав по времени уравнение движения:
u1 = (2+3×0,2×2 2 ) м/с = 4,4 м/c;
u2 = (2+3×0,2×5 2 ) м/с = 17 м/с.
4. Среднее ускорение 
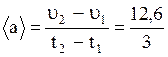
5. Мгновенное ускорение получим, если продифференцируем по времени выражение для скорости: a = 2×3×Ct = 6Ct.
a1 = 6×0,2×2 м/c 2 = 2,4 м/с 2 ;
a2 = 6×0,2×5 м/с 2 = 6 м/с 2 .
Ответ: x1 = 9,6 м; x2 = 39 м; áuñ = 9,8 м/с; u1 = 4,4 м/c; u2 = 17 м/с; áаñ = 4,2 м/с 2 ; a1 = 2,4 м/с 2 ; a2 = 6 м/с 2 .
Задача 2 Маховик вращается равноускоренно. Найти угол a, который составляет вектор полного ускорения 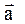
Поскольку в условии дано лишь число оборотов, перейдем к угловым величинам. Применив формулы: at = eR, an = w 2 R, где R – радиус маховика, получим
так как маховик вращается равноускоренно, найдем связь между величинами e и w;
Поскольку w0 = 0; j = 2pN, то w 2 = 2e×2pN = 4pNe.
Подставим это значение в формулу, получим:
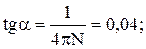
Задача 3 Две гири с массами m1 = 2 кг и m2 = 1 кг соединены нитью, перекинутой через невесомый блок. Найти ускорение a, с которым движутся гири, и силу натяжения нити 
На тело 1 и тело 2 действуют только две силы – сила тяжести и сила
натяжения нити. Для первого тела имеем

для второго тела

Так как сила трения в блоке отсутствует,

Ускорения тел а1 и а2 направлены в противоположные стороны и равны по модулю:

Получаем из выражений (1) и (2) систему уравнений
Выберем ось Х, как показано на рисунке и запишем полученную систему уравнений
в проекции на ось Х
Решая эту систему относительно а и FН, получаем:


Ответ: a= 3,3 м/c 2 ; FH = 13 Н.
Задача 4 К ободу однородного диска радиусом R=0,2 м приложена касательная сила F=98,1 Н. При вращении на диск действует момент сил трения
МТР=4,9 Н×м. Найти массу m диска, если известно, что диск вращается с угловым ускорением e=100 рад/с 2 .
относительно выбранной оси ( MF — момент силы F, Mтр – момент сил трения);

Учитывая, что MF=F×R, получаем 
Отсюда 
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.007 сек.)
Уравнение движения материальной точки по прямой имеет вид х=А+Вt+Сt2 , где А=4 м, В=2 м/с, С=-0,5 м/с2.
| 🎓 Заказ №: 21947 |
| ⟾ Тип работы: Задача |
| 📕 Предмет: Физика |
| ✅ Статус: Выполнен (Проверен преподавателем) |
| 🔥 Цена: 149 руб. |
👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
⚡ Условие + 37% решения:
Уравнение движения материальной точки по прямой имеет вид х=А+Вt+Сt2 , где А=4 м, В=2 м/с, С=-0,5 м/с2 . Для момента времени t1=2 секунды определить координату точки и мгновенное ускорение. Найти путь, пройденный точкой, и среднюю скорость за промежуток времени от t1=2с до t2=6с.
Решение 1. Координату точки, для которой известно кинематическое уравнение движения, найдем, подставив в уравнение движения заданное значение времени 1 t : x1=А+Вt+Сt2 Подставив в это выражение значения постоянных А, В, С, и 1 t , произведем вычисления: x1(t1)=4+42-0,52 2=8 м (1) x1 8 м. 2. Уравнение, описывающее зависимость скорости от времени, найдем, продифференцировав координату x по времени: B Ct dt dx v 3 (2)
Научись сам решать задачи изучив физику на этой странице:
|
Услуги:
|
Готовые задачи по физике которые сегодня купили:





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Уравнение движения точки по прямой имеет вид: х=-1-4t+t2 (м). Найти: Готовое решение: Заказ №7326






Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
Уравнение движения точки по прямой имеет вид: х=-1-4t+t2 (м). Найти:
1) путь и перемещение точки за промежуток времени от t1=1 c до t2=3 с;
2) среднюю скорость и среднее ускорение точки за этот промежуток;
3) скорость и ускорение точки в момент времени t=3 c.
Дано:
Определить: s, ∆x , , ,
Решение:
1) Определим координаты точки в моменты времени t 1 =1 c и t 2 =3 с:
Следовательно, точка к моменту времени t 2 =3 с вернулась в положение, в котором была в момент времени t 1 =1 c . Перемещение точки .
Я и моя команда оказывает помощь в учёбе по любым предметам и заданиям любой сложности.
Решение задач является неотъемлемой частью обучения в любом учебном заведении, и я смогу помочь в решение задач по любым предметам.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
http://studall.org/all-63351.html
http://lfirmal.com/%D0%A3%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5-%D0%B4%D0%B2%D0%B8%D0%B6%D0%B5%D0%BD%D0%B8%D1%8F-%D0%BC%D0%B0%D1%82%D0%B5%D1%80%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B9-%D1%82%D0%BE%D1%87-6/
http://natalibrilenova.ru/uravnenie-dvizheniya-tochki-po-pryamoj-imeet-vid-h-1-4tt2-m-najti-gotovoe-reshenie-zakaz-7326/
Примеры решения задач
Задача 1.Уравнение
движения материальной точки по прямой
имеет вид x
= 4 +
2 t
+
+ 0,2
. Найти:
1) положение точки
в момент времени
= 2 с,
= 5 с;
-
среднюю скорость
за время, протекшее между этими моментами; -
мгновенные скорости
в указанные моменты времени; -
среднее ускорение
за указанный промежуток времени; -
мгновенные
ускорения в указанные моменты времени.

x
= 4
+ 2 t
+
+ 0,2
м
=
2 с
= 5
с
-?
-?
V
-?
V2
—?
V
-?
a
—?
-?
-?
Решение
1) Положение точки
определяется значением координаты x
в указанные моменты времени. Подставим
заданные момент времени t1
и t2
в уравнение движения:
= (4 + 2.2
+ 4 + 0,2 .
8)м = 13,6 м; x2
= (4 + 2.5
+ 52
+ 0,2 .
53)м
= 64 м.
2) Значение средней
скорости
,
гдеx
— изменение расстояния за промежуток
времени t.
-
Общее выражение
мгновенной скорости имеет вид
.
Подставив
в это выражение заданные значения
времени, получим
-
Среднее ускорение
,
где V
— изменение скорости за промежуток
времени t.
-
Общее выражение
мгновенного ускорения имеет вид
Подставив численное
значение
и
,
получим
Ответ:
Задача 2.
Начертить график зависимости координаты
и пути от времени движения, заданного
уравнением x
= 5
+ 4
t
.
Решение Для построения графика найдем характерные значения координаты: начальную координату, максимальную координату и равную нулю, моменты времени, соответствующие им.
1) Начальная
координата соответствует t
= 0,
=
x=
5.
2) Максимального
значения координата достигает в тот
момент, когда скорость меняет знак
(точки начинают двигаться в обратном
направлении). Этот момент времени найдем,
взяв первую производную от координаты
по времени и приравняв ее нулю:
,
откуда t
= 2 c.
Максимальная
координата равна
.
3) Найдем момент
времени, когда координата равна нулю:
.
Решая это квадратное
уравнение, получим два корня:
= 5 c,
= 1
c.
Второй корень
физического смысла не имеет. Для
построения графика зависимости координаты
от времени имеем:
t
= 0;
= 5 м;
V0
= 4
м/с;
t
= 2 c;
xmax
= 9 м;
V0
= 0;
t
= 5 c;
x
= 0.
График
зависимости пути от времени строим,
исходя из того, что:
1) путь и координата
совпадают, пока скорость не изменит
знак;
2) начиная с момента
изменения знака скорости, координата
убывает, а путь возрастает по тому же
закону, по которому убывает координата
(рис.1.2).
Рис.1.2
Задача 3.
Поезд движется с начальной скоростью
V0
=180 км/ч.
Внезапно на пути возникает препятствие,
и машинист включает тормозной механизм.
С этого момента скорость изменяется по
закону V
= V0
– α
t2.
Каков тормозной путь поезда? Через какое
время после начала торможения он
остановится?
Дано:
S
— ?, t
— ?
Решение
Поезд в условиях
задачи можно принять за материальную
точку. Движение поезда исследуется
формально, без выяснения причин,
обуславливающих изменение движения.
Известен закон изменения одного из
параметров движения – скорости. Нужно
определить другие величины, характеризующие
движение поезда.
Стоящая задача
формулируется следующим образом:
скорость материальной точки изменяется
по закону V
= V0
– α
.
Определить время движения и путь, который
она пройдет до остановки, если при t
= 0,
x
= 0,
V
= V0.
Для нахождения
закона движения данной материальной
точки имеем одно уравнение
Интегрируем
уравнение с учетом начальных условий:
Время движения
поезда определяется из условия, что
скорость его равна 0 (остановка)
отсюда
Подставив числовые
значения, получаем
Тормозной путь
Ответ: t
= 7 c,
S
= 230 м.
Задача 4.
Камень брошен вертикально вверх над
колодцем глубиной h
= 10 м с
начальной скоростью V0
= 14 м/с. Через
сколько времени камень достигнет дна
колодца?
Д
h
= 10 м
V0
= 14 м/с
tк
— ?
Соседние файлы в папке Часть 1
- #
- #
- #
- #
- #
- #
Evklid61
5 лет назад
Светило науки — 699 ответов — 1478 раз оказано помощи
Производная пути по времени определяет скорость движения точки.
Поэтому v=S'(t)=(3t-4)/t^3. Момент, когда точка остановится, это v=0.
решаем уравнение (3t-4)/t^3=0=>3t-4=0, 3t=4, t=4/3.
То есть, через 4/3 (наверное секунд, в задаче не указано размерность) точка остановится.
(0 оценок)
To use your Google Account on a browser (like Chrome or Safari), turn on cookies if you haven’t already.
Important: If you get a message that cookies are turned off, you need to turn them on to use your account.
In Chrome
- On your computer, open Chrome.
- At the top right, click More
Settings.
- Under «Privacy and security,» click Site settings.
- Click Cookies and site data.
- From here, you can:
- Turn on cookies: Next to «Blocked,» turn on the switch.
- Turn off cookies: Turn off Allow all cookies.
Learn how to change more cookie settings in Chrome.
In other browsers
For instructions, check the support website for your browser.
Why cookies are helpful
Cookies are files created by sites you visit. They make your online experience easier by saving browsing information. With cookies, sites can:
- Keep you signed in
- Remember your site preferences
- Give you locally relevant content
We use cookies to improve our services. To learn more, read our Privacy Policy.
Fix problems
If you can’t use your Google Account and get a message that cookies are turned off:
- Follow the steps above to turn on cookies.
- Try signing in again.
If you still get the error message, here are some possible solutions. Try each one, then try signing in.
- Open a new browser window.
- Clear your browser’s cache and cookies. Learn how to clear cache and cookies.
- Browse in private. Learn how to browse privately in Chrome.
- Change your browser’s privacy settings. Learn how to change privacy settings.
Was this helpful?
How can we improve it?