Не могу найти формулы, как найти ширину и высоту вписанного в эллипс прямоугольника, зная вертикальный и горизонтальный радиусы эллипса и соотношения сторон прямоугольника.
Пример:
горизонтальный радиус = 10
вертикальный радиус = 5
ширина = 2 высоты
нужно найти значения высоты и ширины, если прямоугольника вписан в эллипс
Если есть готовая npm-библиотека с этими формулами или пример на JS, прошу подсказать.
Математиков прошу подсказать сами формулы, гугление предлагает мне только окружности с одним радиусом.
Всем спасибо!
We’re lucky that the ellipse is centered at the origin. 
In this case, the inscribed rectangle is also centered at the origin. If $P = (x, y)$ is the vertex of the inscribed rectangle at the first quadrant, then the smaller rectangle spanned by the origin and point $(x, y)$ is similar to the inscribed rectangle.
Each side of the inscribed rectangle is $2$ times that of the smaller rectangle. Hence, the area of the inscribed rectangle is $2^2 = 4$ times that of the smaller rectangle. The sides of the smaller rectangle are $x$ and $y$ respectively so we have $x colon y = 3 colon 2$. This means we have $2x = 3y$.
Plugging it into the equation of the ellipse, we have
begin{align}
4x^2 + 9y^2 &= 144 \
(2x)^2 + (3y)^2 &= 144 \
(2x)^2 + (2x)^2 &= 144 \
8x^2 &= 144 \
x^2 &= 18 Rightarrow x = pm3sqrt{2}
end{align}
Since $(x, y)$ is in the first quadrant, we have $x = 3sqrt{2}$ and hence $y = 2sqrt{2}$. The area of the smaller rectangle is $xy = 12$, so the area of the inscribed rectangle is $4xy = 4 cdot 12 = 48$.
Update
I have incorporated @zwim’s comment into the answer. Yeah, it’s more natural this way, thanks @zwim! 
Прямоугольник вписан в эллипс с осями [math]2a[/math] и [math]2b[/math]. Каковы должны быть стороны прямоугольника, чтобы его площадь была наибольшей?
Верно ли мое решение?
Обозначим через x и y половины сторон прямоугольника, тогда площадь прясоугольника вписанного в эллипс равен [math]2xcdot2y[/math], где [math]x[/math] и [math]y[/math] находим из уравнения эллипса
[math]frac{x^2}{a^2}+frac{y^2}{b^2}=1[/math], [math]x[/math]-одна стороны прямоугольника; [math]y=bsqrt{1-frac{x^2}{a^2}}[/math] — вторая сторона прямоугольника
тогда площадь прямоугольника [math]=f(x)=2xcdot2y=2xcdotfrac{2b}{a}cdotsqrt{a^2-x^2}[/math]
[math]f'(x)=frac{4b(a^2-2x^2)}{asqrt{a^2-x^2}}[/math]
[math]f'(x)=0[/math]
[math]x_1=asqrt{2}[/math], [math]x_2=-asqrt{2}[/math] (не удовл.)
[math]x=frac{a}{sqrt2}[/math]
[math]y=bsqrt{1-frac{a^2}{2a^2}}=frac{b}{sqrt2}[/math]
т.к. оси эллипса [math]2b[/math] и [math]2a[/math], значит [math]x=asqrt{2}[/math], [math]y=asqrt{2}[/math]
Заранее спасибо огромное!
Задача состоит в следующем:
Найти прямоугольник наибольшей площади, вписанный в эллипс.
Условия и ограничения:
- Оптимальное решение не нужно (а оно есть?
), скорость важнее
- Очевидно, оси эллипса параллельны осям координат
- Вписанный прямоугольник также ориентирован по осям координат
- (Самое главное)Мой размякший мозг, который чем-то подобным занимался несколько лет назад
Объясняю, для чего это нужно:
есть некоторая рабочая область, на которой находятся объекты различной формы. У каждого объекта есть свойство Текст. Оный и требуется отобразить. Для простоты для каждой формы вычисляется прямоугольник, в который текст будет выводиться.
Т.е. особая точность не нужна, т.к. скорость пересчета влияет на скорость отрисовки.
В крайнем случае, «пошлите» меня к какому-нить сборищу алгоритмов по геометрии, что-то с кандачка не получается нарыть более-менее приличных.
NB Я знаю, что в эллипс можно вписать бесконечное число прямоугольников
Здравствуйте, Spaider, Вы писали:
S>Задача состоит в следующем:
S>Найти прямоугольник наибольшей площади, вписанный в эллипс.
S>Условия и ограничения:
S>
-
S>
- Оптимальное решение не нужно (а оно есть?
), скорость важнее
S> - Очевидно, оси эллипса параллельны осям координат
S> - Вписанный прямоугольник также ориентирован по осям координат
S> - (Самое главное)Мой размякший мозг, который чем-то подобным занимался несколько лет назад
S>
S>Объясняю, для чего это нужно:
S>есть некоторая рабочая область, на которой находятся объекты различной формы. У каждого объекта есть свойство Текст. Оный и требуется отобразить. Для простоты для каждой формы вычисляется прямоугольник, в который текст будет выводиться.
S>Т.е. особая точность не нужна, т.к. скорость пересчета влияет на скорость отрисовки.
S>В крайнем случае, «пошлите» меня к какому-нить сборищу алгоритмов по геометрии, что-то с кандачка не получается нарыть более-менее приличных.
S>NB Я знаю, что в эллипс можно вписать бесконечное число прямоугольников
Условия: Пересечение диагоналей прямоугольника и осей эллипса совпадают. И для простоты, считаем эту точку пересечения началом координта. Тогда уравнение эллипса :
x^2/a^2 + y^2/b^2 = 1
Решение:
Координаты верхнего левого угла прямоугольника:
x = a*(b^2/(1 + b^2))^0.5
y = (b^2/(1 + b^2))^0.5
Алексей.
… << RSDN@Home 1.1.3 stable >>
Здравствуйте, Spaider, Вы писали:
S>Найти прямоугольник наибольшей площади, вписанный в эллипс.
Параметрическое уравнение эллипса: {x,y}(t) = {X·cos(t),Y·sin(t)} где X,Y — полуоси.
Вершины прямоугольника (-x,-y), (-x,+y), (+x,+y), (+x,-y).
Стороны прямоугольника равны 2x и 2y.
Площадь прямоугольника, очевидно, равна 4xy.
S(t) = 4XY·cos(t)·sin(t) = 4XY·sin(2t)/2 = 2XY·sin(2t)
Максимум достигается при t=45°, sin(2t)=1, sin(t)=cos(t)=sqrt(2)/2.
x = X·sqrt(2)/2
y = Y·sqrt(2)/2
Здравствуйте, Кодт, Вы писали:
К>Здравствуйте, Spaider, Вы писали:
S>>Найти прямоугольник наибольшей площади, вписанный в эллипс.
К>Максимум достигается при t=45°, sin(2t)=1, sin(t)=cos(t)=sqrt(2)/2.
К>x = X·sqrt(2)/2
К>y = Y·sqrt(2)/2
Ага-ага, большое спасибо.
3. Аналитическая геометрия на плоскости
3.5 Эллипс
Выпишем еще раз каноническое уравнение эллипса,
begin{equation}
frac{x^2}{a^2}+frac{y^2}{b^2}=1,
label{ell1}
end{equation}
см. соответствующий рисунок 5.
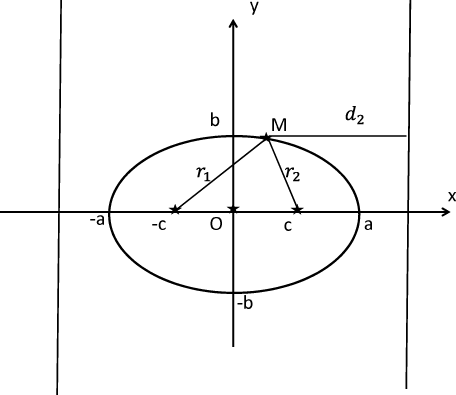
При каноническом описании полагают, что $a>b>0$. Заметим, что если $a=b$, то эллипс превращается в окружность. Точки $(a,0), , (-a,0), , (0, b),, (0, -b)$ называют вершинами эллипса, параметр $a$ — большая полуось, параметр $b$ — малая полуось. Далее, вводят параметр $c=sqrt{a^2-b^2}$, точки $(c,0), , (-c,0)$ называют фокусами эллипса. Величину $varepsilon = c/a$ называют эксцентриситетом эллипса. Она характеризует вытянутость эллипса. Из определений следует, что для эллипса $0 leq varepsilon leq 1$.
Рис 5: Эллипс и его директрисы.
Опишем сначала элементарные свойства эллипса, следующие непосредственно из канонического уравнения (19).
1. Из этого уравнения следует, что если точка $(x,y)$ принадлежит эллипсу, то выполняются неравенства $|x| leq a $, $|y| leq b$. Таким образом, все точки эллипса лежат в этом прямоугольнике (конечном!).
2. Так как переменные $x,y$ входят в уравнение эллипса только в квадратах, то из того, что $(x,y)$ лежат на эллипсе следует, что точки $(pm x, , pm y)$ также лежат на эллипсе при любом выборе знаков. Это означает, что эллипс симметричен при отражении относительной осей координат и имеет центр симметрии, точку $O$.
Эллипс можно описать как геометрическое место точек. Для этого соединим точку $M$, лежащую на эллипсе, с фокусами. Соответствующие отрезки называются фокальными радиусами точки (см. рис. 5, отрезки $r_1, , r_2$).
Теорема. Для того, чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее фокальных радиусов равнялась $2a$,
begin{equation}
r_1+r_2=2a.
label{ell2}
end{equation}
Доказательство.
Теорема. Для того, чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение расстояния от этой точки до фокуса к расстоянию до соответствующей директрисы было равно эксцентриситету эллипса,
begin{equation}
r_2/d_2=varepsilon. (21)
label{ell3}
end{equation}
Доказательство.
Пример.
Решение типовых задач.
Задачи.