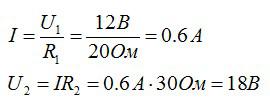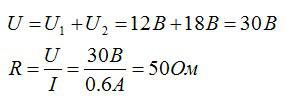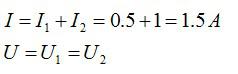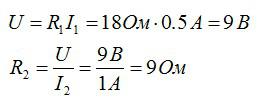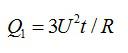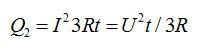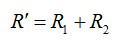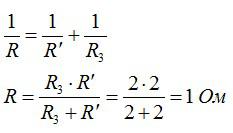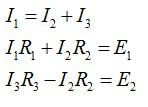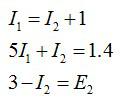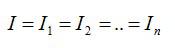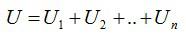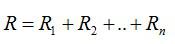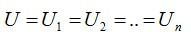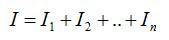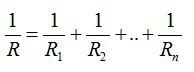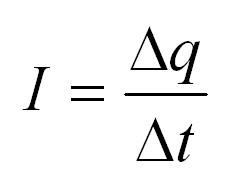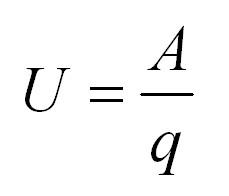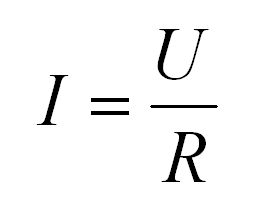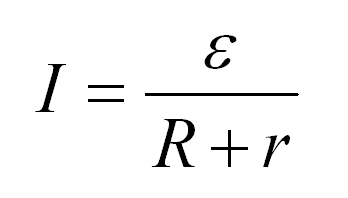Последовательное и параллельное соединение
Последовательное и параллельное соединение очень широко используется в электронике и электротехнике и порой даже необходимо для правильной работы того или иного узла электроники. И начнем, пожалуй, с самых простых компонентов радиоэлектронных цепей — проводников.
Для начала давайте вспомним, что такое проводник? Проводник — это вещество или какой-либо материал, который отлично проводит электрический ток. Если какой-либо проводник отлично проводит электрический ток, то он в любом случае обладает каким-либо сопротивлением. Сопротивление проводника мы находим по формуле:
ρ – это удельное сопротивление, Ом × м
R – сопротивление проводника, Ом
S – площадь поперечного сечения, м 2
Более подробно об этом я писал здесь.
Следовательно, любой проводник представляет из себя резистор с каким-либо сопротивлением. Значит, любой проводник можно нарисовать так.
Последовательное соединение проводников
Сопротивление при последовательном соединении проводников
Последовательное соединение проводников — это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.
последовательное соединение резисторов
Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.
Получается, можно записать, что
формула при последовательном соединении резисторов
У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.
То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор RAB .
показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:
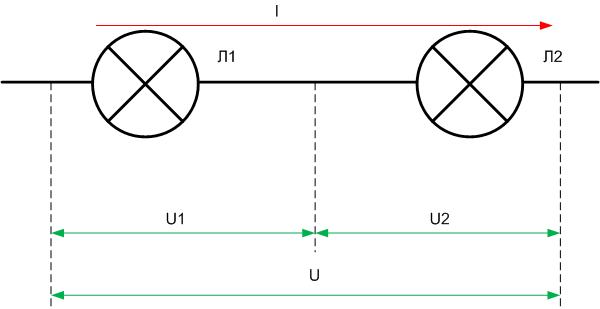
Сила тока через последовательное соединение проводников
Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.
Получается, если через резистор RAB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R1 , R2 , R3 , то получится, что через них течет та же самая сила тока, которая текла через резистор RAB .
сила тока через последовательное соединение проводников
Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R1 течет такая же сила тока, как и через резистор R2 и такая же сила тока течет через резистор R3 .
Напряжение при последовательном соединении проводников
Давайте еще раз рассмотрим цепь с тремя резисторами
Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?
Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.
Пусть у нас будет цепь с такими параметрами.
Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.
Получается, что в данном случае RAB =R1 + R2 + R3 = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.
Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения UR1 , UR2 , UR3 . Но как это сделать?
Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.
Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.
Мы получили самый простой делитель напряжения.
Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.
Параллельное соединение проводников
Параллельное соединение проводников выглядит вот так.
параллельное соединение резисторов
Ну что, думаю, начнем с сопротивления.
Сопротивление при параллельном соединении проводников
Давайте пометим клеммы как А и В
В этом случае общее сопротивление RAB будет находиться по формуле
Если же мы имеем только два параллельно соединенных проводника
То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.
Напряжение при параллельном соединении проводников
Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.
Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn
Сила тока при параллельном соединении проводников
Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.
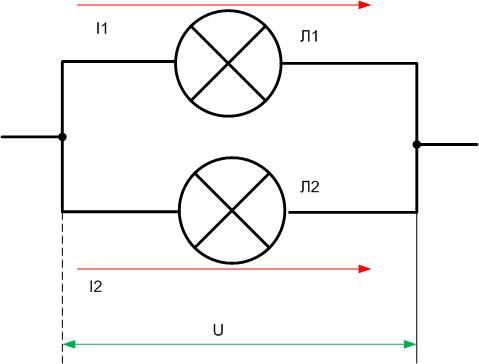
Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.
Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что
Если бы у нас еще были резисторы, соединенные параллельно, то для них
В этом случае, сила тока в цепи будет равна:
Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.
Воспользуемся формулами, которые приводили выше.
Если бы у нас еще были резисторы, соединенные параллельно, то для них
Далее, воспользуемся формулой
чтобы найти силу тока, которая течет в цепи
2-ой способ найти I
Чтобы найти Rобщее мы должны воспользоваться формулой
Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них — «калькулятор резисторов«. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть Rобщее = 1,25 Ом.
Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.
Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.
Источник
Задачи на параллельное и последовательное соединение проводников с подробными решениями
Что бы ни происходило в мире, учиться надо всегда. Кстати, для тех, кто не знает, как организовать учебу на удаленке, мы подготовили отдельную статью. А сегодня займемся решением задач на последовательное и параллельное соеднинение проводников. Решение задач – отличный способ, чтобы успокоить нервы и не поддаваться панике.
Присоединяйтесь к нам в телеграме: там вас ждут актуальные новости и приятные скидки.
Последовательное и параллельное соединение проводников: решение задач
Как решать задачи с параллельным и последовательным соединением проводников? Для начала повторите теорию, вспомните общую памятку по решению физических задач и на всякий случай держите под рукой формулы.
Задача №1 на последовательное соединение проводников
Проводники сопротивлением 20 Ом и 30 Ом соединены последовательно. Напряжение на концах первого проводника равно 12 В. Определите напряжение, сопротивление и силу тока в цепи на втором проводнике, а также полное напряжение.
Для последовательного соединения проводников:
Ответ: 50 Ом; 18 В; 0,6 А; 30 В.
Задача №2 на параллельное соединение проводников
Два проводника соединены параллельно. Сила тока в первом проводнике равна 0,5 А, во втором — 1 А. Сопротивление первого проводника составляет 18 Ом. Определите сопротивление второго проводника и силу тока на всем участке цепи.
Для параллельного соединения:
При решении задач не забывайте проверять размерности величин и при необходимости переводить их в систему СИ.
Ответ: 1,5 А; 9 Ом.
Задача №3 на последовательное и параллельное соединение проводников
Электрогрелка состоит из трех одинаковых секций. Во сколько раз быстрее грелка будет нагревать некоторое количество воды от 10 до 100 градусов Цельсия при параллельном включении всех секций, нежели при последовательном их включении?
Пусть сопротивление каждой секции равно R. Тогда при параллельном включении их в сеть напряжение на каждой секции равно напряжению в сети (U), и на трех секциях будет выделяться тепло:
При последовательном соединении суммарное сопротивление цепи равно 3R, а выделяющееся количество теплоты:
Как видим, выделяющееся тепло для первой схемы в 9 раз больше, так что и скорость нагрева воды будет в 9 раз выше.
Ответ: в 9 раз.
Задача №4 на смешанное соединение проводников
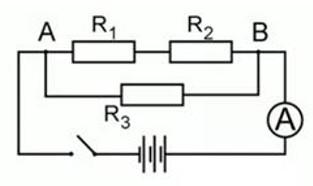
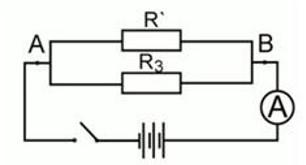
Участок цепи состоит из двух последовательно соединенных сопротивлений, каждое из которых равно 1 Ом. К этим двум резисторам параллельно подключают еще одно сопротивление, значение которого составляет 2 Ом. Всю эту цепь подключают к источнику тока, который создает на концах данного соединения напряжение 2,4 В. Определите силу тока во всей электрической цепи.
Согласно схеме, искомая сила тока – это сила тока, протекающая через амперметр.
Резисторы R1 и R2 соединены последовательно, резистор R3 – параллельно к ним.
Резисторы 1 и 2 можно заменить эквивалентным сопротивлением R со штрихом и перерисовать схему в упрощенном виде:
Сопротивления R3 и R со штрихом соединены параллельно, можно найти общее сопротивление электрической цепи по формуле для параллельного соединения:
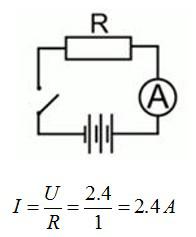
Теперь цепь можно перерисовать в еще более упрощенном виде и рассчитать силу тока по закону Ома:
Ответ: 2.4 А.
Задача №5 на закон Кирхгофа
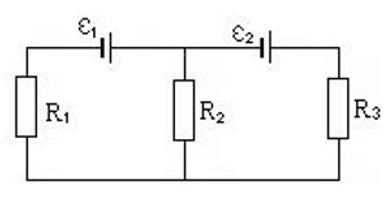
Три сопротивления R1 = 5 Ом, R2 = 1 Ом, R3 = 3 Ом и два источника тока соединены так, как показано на рисунке. Внутренними сопротивлениями источников тока можно пренебречь. ЭДС первого источника тока равна 1,4 В, и сила тока, текущего через сопротивление R3, равна I3= 1 А. Определите ЭДС второго источника тока.
Выберем направление обхода контуров по часовой стрелке и запишем закон Кирхгофа для точки A (расположим ее между двумя источниками и сопротивлением R2) и двух контуров:
Решая систему уравнений, получаем ответ: Е2=3.6 В.
Ответ: 3.6 В.
Вопросы на параллельное и последовательное соединение проводников
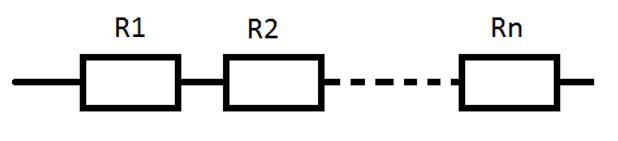
Вопрос 1. Схематически изобразите последовательное соединение проводников
Ответ. На рисунке ниже изображен участок цепи с последовательно соединенными проводниками:
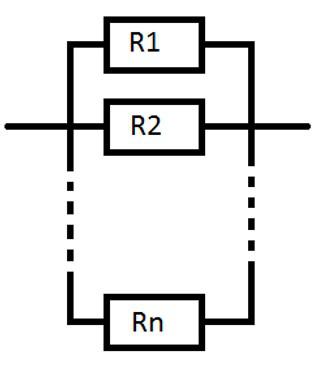
Вопрос 2. Схематически изобразите параллельное соединение проводников
Ответ. На рисунке ниже изображено параллельное соединение проводников:
Вопрос 3. Приведите основные формулы и соотношения для последовательного соединения проводников.
Ответ. При последовательном соединении:
- Сила тока во всех проводниках одинакова.
Общее напряжение равно сумме напряжений на каждом проводнике.
Полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Вопрос 4. Приведите основные формулы и соотношения для параллельного соединения проводников.
Ответ. Для параллельного соединения проводников:
- Напряжение на всех проводниках одинаково.
Сила тока в неразветвленной цепи равна сумме токов в параллельно соединенных проводниках.
Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Вопрос 5. Какие электрические цепи нельзя рассчитать с помощью формул для последовательного и параллельного соединения проводников?
Ответ. С помощью приведенных выше формул можно рассчитать лишь относительно простые электрические цепи. Для расчета сложных цепей, включающих в себя несколько источников тока и состоящих из многих резисторов, применяются правила Кирхгофа.
Нужна помощь в решении задач или любых других учебных заданий? Обращайтесь в профессиональный сервис для учащихся: мы найдем верное решение.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Источник
Содержание
- Виды соединений электрических проводников
- Последовательное
- Параллельное
- Смешанное
- Как вычисляются напряжение, сила тока и электрическая мощность в зависимости от подключения
- При параллельном соединении
- При последовательном соединении
- Примеры расчетов
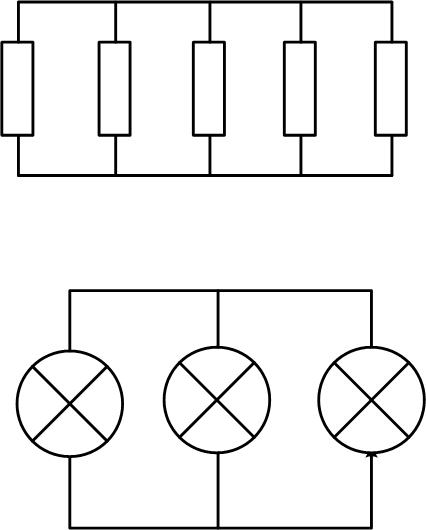
- Для резисторов
- Для лампочек
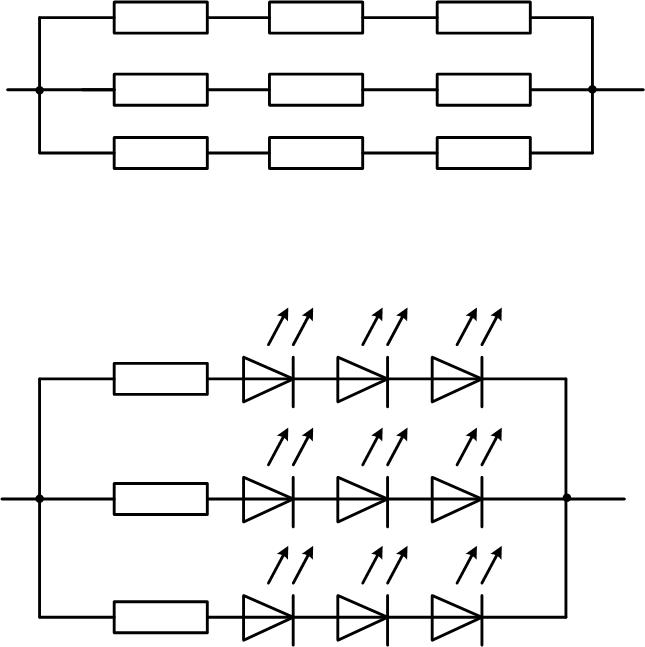
- Для светодиодов
При разработке электрических цепей применяется последовательное и параллельное соединение проводников. Умение анализировать (как количественно, так и качественно) и рассчитывать такие схемы является базовым принципом знаний электротехники.
Виды соединений электрических проводников
Основными схемами подключения являются параллельное и последовательное соединение. Также существуют комбинации из этих двух включений.
Последовательное
При последовательном (в зарубежной терминологии serial) соединении выводы элементов соединяются так, чтобы получилась цепочка. Один вывод устройства подключается к одному соседнему звену, а второй – к другому, с противоположной стороны.
Параллельное
При параллельном (parallel) включении одноименные выводы элементов цепи соединяются между собой. Практический пример – лампы в многорожковой люстре или повторители светового сигнала поворота в автомобиле.
Смешанное
В одной цепи схема подключения может быть комбинированной – serial+parallel. Часть элементов подключена в параллель, образуя звенья. Эти звенья могут быть включены в последовательную цепочку. Или наоборот – последовательные цепи включаются параллельно.
Как вычисляются напряжение, сила тока и электрическая мощность в зависимости от подключения
Параметры электрической цепи рассчитываются по-разному в зависимости от типа подключения. Чтобы разобраться, какова будет сила тока, проходящего через каждое сопротивление, можно воспользоваться первым законом Кирхгофа. Одна из его формулировок гласит, что алгебраическая сумма токов, втекающих в узел, равна сумме токов, вытекающих из узла. Остальные зависимости будут вытекать из данного рассуждения.
При параллельном соединении
Если рассмотреть параллельное соединение, например, трех резисторов, то можно отметить, что втекающий ток I в узле 1 распадается на три ветви I1, I2, I3, причем Кирхгоф утверждает, что их сумма I1+ I2+ I3 = I. В узле 2 все токи стекаются в один ток, и снова I= I1+ I2+ I3.
Очевидно, что напряжение на каждом резисторе одинаково и равно U, следовательно, по закону Ома:
- I1=U/R1;
- I2=U/R2;
- I3=U/R3;
- I=U/Rобщ.
Отсюда U/Rобщ= U/R1+ U/R2+ U/R3, после сокращения обеих частей на U получается формула для нахождения общего сопротивления при параллельном соединении резисторов:
1/Rобщ= 1/R1+ 1/R2+ 1/R3.
Отсюда следует, что при параллельном соединении общее сопротивление будет меньше наименьшего сопротивления в наборе. При соединении двух резисторов формула принимает вид Rобщ=R1* R2/(R1+ R2).
Также из равенства I=U/R1+U/R2+U/R3 следует, что токи через параллельно включенные резисторы распределяются обратно пропорционально значениям их сопротивлений – чем выше сопротивление, тем ниже ток, и наоборот. Если все резисторы имеют одинаковый номинал, то ток, текущий через каждый из них, находится делением общего тока на количество сопротивлений. Если элементов в сборке три, то через каждый течет треть общего тока, а если параллельно включены n одинаковых резисторов, то через каждый протекает I/n.
Так как электрическая мощность равна P=U*I, а напряжение на каждом резисторе равно, то мощность, выделяемая на каждом элементе, распределяется пропорционально току и обратно пропорционально сопротивлению резистора. Если все элементы одинаковы, то и мощность на них будет рассеиваться одинаковая.
Для наглядности видео.
При последовательном соединении
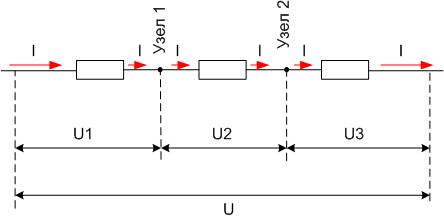
Если рассматривать последовательную цепь из трех элементов, можно заметить, что ток, втекающий в узел 1 будет равен вытекающему. В узле 2 выполняется то же самое соотношение и так до бесконечности.
Отсюда сила тока в последовательном соединении будет одинакова для любого элемента и равна I. Напряжение, приложенное к цепи и равное I*R, распределится между резисторами:
U=U1+U2+U3=I*R1+I*R2+I*R3 = I* Rобщ
После сокращения на I можно найти общее сопротивление цепи. Оно равно сумме составляющих, и общее значение сопротивления будет выше сопротивления любого элемента:
Rобщ=R1+R2+R3
Очевидно, что падение напряжения в последовательной цепи прямо пропорционально сопротивлению каждого элемента – чем выше сопротивление, тем выше на нем напряжение. Точно так же, эти соотношения выполняются для цепи из n элементов.
Примеры расчетов
В качестве практических примеров можно рассмотреть несколько вариантов расчетов параметров цепи в разных схемах соединения.
Для резисторов
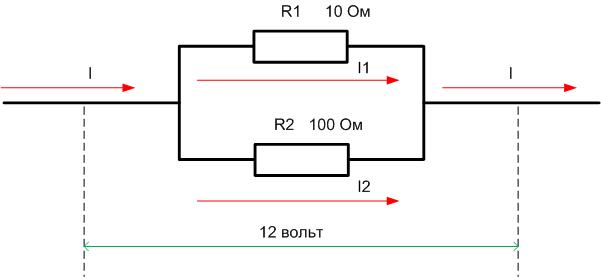
Самым простым примером расчета будет цепь из двух сопротивлений – 10 Ом и 100 Ом, соединенных в цепочку. К цепи приложено 12 вольт.
Сначала надо найти Rобщ, оно равно сумме R1 и R2. Rобщ=100+10=110 Ом. Отсюда ток в цепи I=U/R=12/110=0,109 ампер. Падение на каждом элементе можно вычислить исходя из равенств U1=I*R1 и U2=I*R2. Отсюда U1=1,1 В, а U2=10,9 В. Очевидно, что U1/U2=R1/R2. На первом элементе будет рассеиваться мощность P1=U1*I=1,1*0,109=0,12 ватт (для практики подойдет стандартный компонент на 0,125 ватт), а на втором – P2=U2*I=10,9*0,109=1,19 ватт (для практической реализации понадобится двухваттник).
Если соединить эти же два резистора параллельно и подать то же самое напряжение, то параметры распределятся по-другому.
Сначала надо определить Rобщ=R1*R2/(R1+R2)=110*10/(110+10)=1100/120=9,17 Ом (меньше наименьшего значения в 10 Ом). Общий ток составит I=U/Rобщ=12/9,17=1,31 ампер. Через первый элемент потечет I1=U/R1=12/10=1,2 ампер, через второй I2=U/R2=12/100=0,12. Очевидно, что I1+I2=I (с учетом погрешностей округления). Мощности потребуются такие:
- P1=I1*U=1,2*12=14,2 ватт;
- P2=I2*U=0,12*12=1,42 ватт.
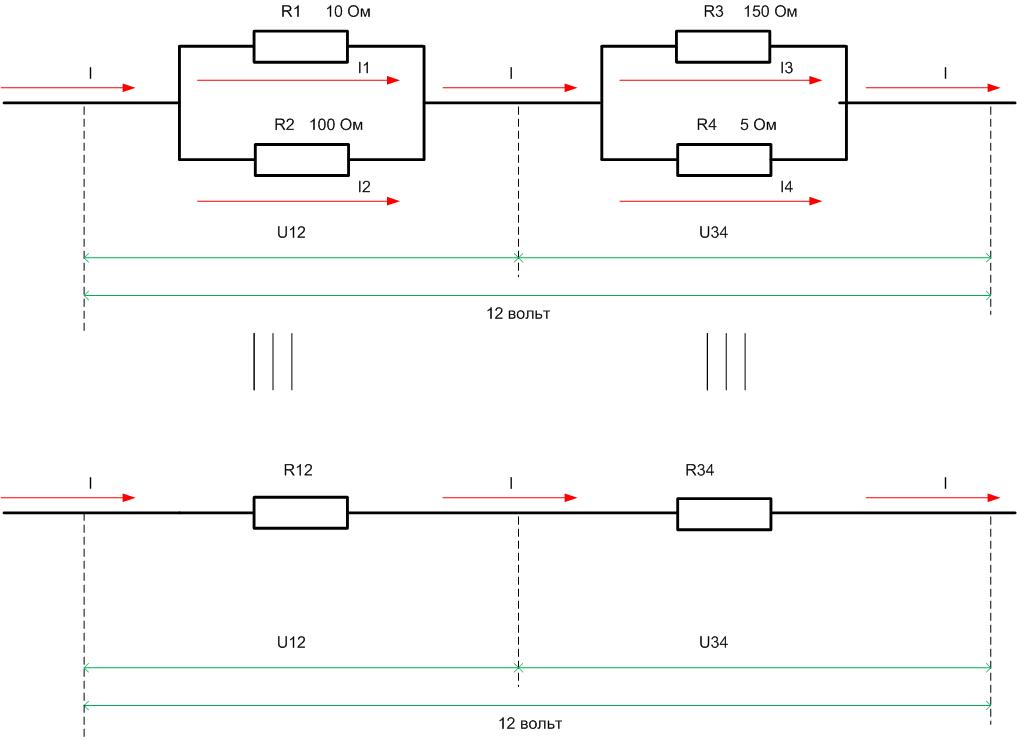
Если имеется смешанное соединение элементов, надо сначала преобразовать схему к однотипному виду – параллельному или последовательному. Пусть имеется схема следующего вида.
В данном случае удобно заменить параллельную сборку R1 и R2 на резистор с эквивалентным сопротивлением R12, а R3 и R4 – на R34. Сначала находится R12=R1*R2/(R1+R2)=9,17 Ом. Тем же способом рассчитывается R34=150*5/(150+5)=4,8 Ом. Тогда общее сопротивление эквивалентной цепи будет равно R12+R34=9,17+4,8=13,97 Ом.
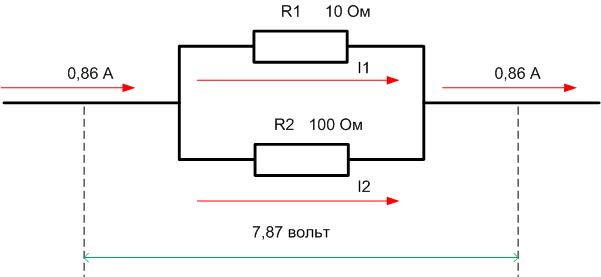
Отсюда I=U/R=12/13,97=0,86 ампер. На “гирлянде» R1R2 падает U12=I*R12=0,86*9,17=7,87 вольт, а на R3R4 падение составит U34= I*R34=0,86*4,8=4,13 вольт. Дальше надо вернуться к исходной схеме и рассмотреть отдельно участок схемы R1R2 с найденными параметрами.
Отсюда I1=U/R1=7,87/10=0,787 ампер, I2=U/R2=7,87/100=0,0787 ампер. По мощностям – P1=U*I1=7,87*0,787=6,2 ватт, P2= U*I2=7,87*0,0787=0,62 ватт.
Аналогично рассчитывается и участок, содержащий элементы R3R4.
Читайте также
Последовательное и параллельное подключение аккумуляторных батарей
Для лампочек
Точно такими же способами можно рассчитать параметры цепи, состоящей из двух или более лампочек накаливания – на практике с такой ситуацией можно столкнуться чаще. Но есть две проблемы. Первая из них – на лампочках и в технических данных на них не указывается сопротивление нити. Его придется пересчитывать исходя из номинального напряжения и мощности. Так как P=U*I, а I=U*R, то P=U2/R, а R=U2/P. Так, для 10-ваттной лампочки на 12 вольт сопротивление нити будет равно 122/10=144/10=14,4 Ом. Можно рассчитать характеристики цепи для двух последовательно и параллельно соединенных лампочек.
В первом случае ток, текущий через каждую лампу будет общим, и равным I=U/Rобщ=12/(14,4+14,4)=12/28,8=0,42 А. На каждой лампе упадет U/2=6 вольт. А электрическая мощность каждого элемента составит 0,42*6=2,5 Вт, что составляет ¼ от номинала лампочки. Такое уменьшение произошло из-за двукратного снижения тока и двукратного снижения напряжения. Естественно, лампочки будут светиться далеко не в полный накал. Чтобы довести яркость свечения до нормальной, придется вдвое увеличивать напряжение, что одновременно вдвое увеличит ток.
Если лампочки соединить в параллель, то на каждой из них упадет номинальный уровень в 12 вольт. Через каждый элемент потечет I=U/R= 12/14,4=0,83 А, а мощность на каждой лампочке будет равна P=U*I=12*0,83=10 ватт, то есть, номинал. И каждая нить будет светить в полный накал. Но вся цепь будет потреблять 20 ватт и через нее потечет 0,83*2=1,66 А, что вдвое больше значения для одной лампы.
Есть и вторая проблема. В общем случае сопротивление зависит от тока и приложенного напряжения, но у ламп накаливания эта зависимость выражена ярко. Нить в холодном состоянии имеет низкое сопротивление, а номинального значения достигает при прогреве в номинальном режиме. Поэтому данные выше расчеты верны лишь для штатного напряжения 12 вольт. В других условиях характеристики лампы будут другими, и, по большому счету, расчет для параллельного случая неточен – сопротивление нити будет меньше 14,4 Ом. Зато это свойство позволяет применять лампу в качестве стабилизатора тока – при увеличении его значения нить нагреется, сопротивление вырастет, ток упадет примерно до прежнего уровня. При его уменьшении произойдет обратный процесс со снижением уровня накала нити лампочки.
Рекомендуем посмотреть видео урок «Просто физика»
Для светодиодов
Еще сложнее ситуация со светодиодами. В отличие от лампочек они стабилизируют напряжение, причем не всегда, а только после открывания. Иными словами, сначала при росте напряжения на последовательной цепочке (LED+резистор), она ведет себя согласно закону Ома. После того, как светодиод открылся (и начал светиться), увеличение падения на нем прекратилось, и рост напряжения на цепочке ведет к росту тока и увеличению U на резисторе. На полупроводниковом приборе напряжение остается стабильным (в зависимости от технологии изготовления – от 1,2 до 3 вольт или выше), хотя ток через него также растет.
По мере освоения приемов расчета можно научиться анализировать все более сложные схемы, содержащие как параллельное, так и последовательное подключение элементов. Потом можно переходить к следующему этапу – анализ и расчет устройств, содержащих реактивные (а впоследствии – и нелинейные) компоненты.
Загрузить PDF
Загрузить PDF
В параллельной цепи резисторы соединены таким образом, что электрический ток в цепи делится между резисторами и проходит через них одновременно (сравните это с автодорогой, которая разделяется на две параллельные дороги и делит поток машин на два потока, движущихся параллельно друг другу). В этой статье мы расскажет вам, как вычислить напряжение, силу тока и сопротивление в параллельной цепи.
Шпаргалка
- Формула для вычисления общего сопротивления RT в параллельной цепи: 1/RT = 1/R1 + 1/R2 + 1/R3 + …
- Напряжение в параллельной цепи одинаковое на каждом ее элементе: VT = V1 = V2 = V3 = …
- Формула для вычисления общей силы тока в параллельной цепи: IT = I1 + I2 + I3 + …
- Закон Ома: V = IR
-
1
Определение. Параллельная цепь — это цепь, в которой ток течет из точки А в точку В одновременно по нескольким элементам цепи (то есть поток электронов разбивается на несколько потоков, которые на конечном участке цепи вновь объединяются в единый поток). В большинстве задач, в которых присутствует параллельная цепь, нужно вычислить напряжение, сопротивление и силу тока.
- Элементы, подключенные параллельно, находятся на отдельных ветвях цепи.
-
2
Сила тока и сопротивление в параллельных цепях. Представьте себе автостраду с несколькими полосами, на каждой из которых установлен пункт пропуска, замедляющий движение автомобилей. Построив новую полосу, вы увеличите скорость движения (даже если и на этой полосе вы поставите пункт пропуска). Аналогично с параллельной цепью — добавив новую ветвь, вы уменьшите общее сопротивление цепи и увеличите силу тока.
-
3
Общая сила тока в параллельной цепи равна сумме силы тока на каждом элементе этой цепи. То есть, если известна сила тока на каждом резисторе, сложите эти силы тока, чтобы найти общую силу тока в параллельной цепи: IT = I1 + I2 + I3 + …
-
4
Общее сопротивление в параллельной цепи. Оно вычисляется по формуле: 1/RT = 1/R1 + 1/R2 + 1/R3 + …, где R1, R2 и так далее — это сопротивление соответствующих элементов (резисторов) этой цепи.
- Например, параллельная цепь включает два резистора и сопротивление каждого равно 4 Ом. 1/RT = 1/4 + 1/4 → 1/RT = 1/2 → RT = 2 Ом. То есть общее сопротивление параллельной цепи с двумя элементами, сопротивления которых равны, в два раза меньше сопротивления каждого резистора.
- Если какая-либо ветвь параллельной цепи не имеет сопротивления (0 Ом), то весь ток пройдет именно через эту ветвь.[1]
-
5
Напряжение. Напряжение — это разность электрических потенциалов между двумя точками электрической цепи. Так как здесь рассматриваются две точки без учета пути движения тока по цепи, напряжение в параллельной цепи одинаково на каждом элементе этой цепи, то есть: VT = V1 = V2 = V3 = …
-
6
Вычислите значения неизвестных величин по закону Ома. Закон Ома описывает взаимосвязь между напряжением V, силой током I и сопротивлением R: V = IR. Если вам известны значения двух величин из этой формулы, вы можете найти значение третьей величины.
- Вы можете применить закон Ома для всей цепи (V = ITRT) или для одной ветви этой цепи (V = I1R1).
Реклама
-
1
Нарисуйте таблицу, чтобы облегчить решение задачи, особенно если неизвестны значения сразу нескольких величин в данной параллельной цепи.[2]
Рассмотрим пример электрической цепи с тремя параллельными ветвями. Обратите внимание, что здесь под ветвями подразумеваются резисторы с сопротивлениями R1, R2, R3.R1 R2 R3 Общее Единицы измерения V В I А R Ом -
2
Внесите в таблицу данные вам значения. Например, к электрической цепи подключена батарея, напряжение которой равно 12 В. Цепь включает три параллельные ветви с сопротивлениями 2 Ом, 4 Ом, 9 Ом.
R1 R2 R3 Общее Единицы измерения V 12 В I А R 2 4 9 Ом -
3
Заполните значения напряжения для каждого элемента цепи. Помните, что общее напряжение в параллельной цепи и напряжение на каждом резисторе этой цепи равны.
R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I А R 2 4 9 Ом -
4
Вычислите силу тока на каждом резисторе по закону Ома. Так как теперь в каждом столбце вашей таблицы есть значения двух величин, вы с легкостью вычислите значение третей величины при помощи закона Ома: V = IR. В нашем примере нужно найти силу тока, поэтому перепишите формулу закона Ома следующим образом: I = V/R
R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I 12/2 = 6 12/4 = 3 12/9 = ~1,33 А R 2 4 9 Ом -
5
Вычислите общую силу тока. Помните, что общая сила тока в параллельной цепи равна сумме сил тока на каждом элементе этой цепи.
R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I 6 3 1,33 6 + 3 + 1,33 = 10,33 А R 2 4 9 Ом -
6
Вычислите общее сопротивление. Сделайте это одним из двух способов. Либо используйте формулу
1/RT = 1/R1 + 1/R2 + 1/R3, либо формулу закона Ома: R = V/I.R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I 6 3 1.33 10,33 А R 2 4 9 12 / 10,33 = ~1,17 Ом Реклама
-
1
Вычислите мощность тока по формуле: P = IV. Если вам дана мощность тока на каждом участке цепи, то общая мощность вычисляется по формуле: PT = P1 + P2 + P3 + ….
-
2
Вычислите общее сопротивление в параллельной цепи, состоящей из двух ветвей (двух резисторов).
- RT = R1R2 / (R1 + R2)
-
3
Найдите общее сопротивление в параллельной цепи, если сопротивление всех резисторов одинаково: RT = R1 / N, где N — количество резисторов в цепи.[3]
- Например, если в параллельной цепи два резистора с одинаковым сопротивлением, то общее сопротивление цепи будет вдвое меньше сопротивления одного резистора. Если в цепи восемь одинаковых резисторов, то общее сопротивление будет в восемь раз меньше сопротивления одного резистора.
-
4
Вычислите силу тока на каждом резисторе, если напряжение неизвестно. Это можно сделать, воспользовавшись правилом Кирхгофа.[4]
Вам необходимо вычислить сопротивление каждого резистора и общую силу тока в цепи.- Два резистора в параллельной цепи: I1 = ITR2 / (R1 + R2)
- Несколько (более двух) резисторов в параллельной цепи. В этом случае для вычисления I1 найдите общее сопротивление всех резисторов за исключением R1. Для этого воспользуйтесь формулой для вычисления общего сопротивления в параллельной цепи. Затем используйте правило Кирхгофа, заменив R2 полученным значением.
Реклама
Советы
- В параллельной цепи напряжение одинаково на всех резисторах.
- Возможно, в вашем учебнике закон Ома представлен следующей формулой: E = IR или V = AR. Здесь присутствуют другие обозначения величин, но суть закона Ома не меняется.
- Общее сопротивление часто именуется эквивалентным сопротивлением.
- Если у вас нет калькулятора, найти общее сопротивление, используя значения R1, R2 и так далее, довольно проблематично. Поэтому воспользуйтесь законом Ома.
- Если в задаче дана параллельно-последовательная цепь, сделайте вычисления для ее параллельного участка, а затем для полученной последовательной цепи.
Реклама
Об этой статье
Эту страницу просматривали 172 982 раза.
Была ли эта статья полезной?
Что такое напряжение в сети электричества.
Напряжение – это физическая величина, которая характеризует электрическое поле. Иными словами, оно показывает, какую работу оно совершает при перемещении одного положительного заряда на определённое расстояние.
За единицу напряжения в международной системе принимается такой показатель на концах проводника, при котором заряд в 1 Кл совершает работу в 1 Дж для перемещения его по этому проводнику. Общепринятой единицей измерения напряжения считается 1 В – Вольт.
Важно! Работа измеряется в Джоулях, заряды в Кулонах, а напряжение в Вольтах, следовательно, 1 Вольт равняется 1 Джоулю, деленному на 1 Кулон.
Чему равно напряжение.
Напряжение напрямую связано с работой тока, зарядом и сопротивлением. Чтобы измерить напряжение непосредственно в электрической цепи, к ней нужно подключить вольтметр. Он присоединяется к цепи параллельно, в отличие от амперметра, который подключается последовательно. Зажимы измерительного прибора крепятся к тем точкам, между которыми нужно вычислить напряжение. Чтобы он правильно показал значение, нужно включить цепь. На схемах вольтметр обозначается буквой V, обведенной в кружок.
Напряжение обозначается латинской [U], а измеряется в [В]. Оно равно работе, которое совершает поле при перемещении единичного заряда. Формула напряжения тока – это U = A/q, где A – работа тока, q – заряд, а U – само напряжение.
Вам это будет интересно Учимся читать электросхемы
Обратите внимание! В отличие от магнитного поля, где заряды неподвижны, в электрическом поле они находятся в постоянном движении.
Формула закона Ома
Свои опыты Ом направлял на изучение такой физической величины, как сопротивление, в результате чего в 1826 году он стал автором закона, который не потерял совей актуальность вплоть до сегодняшнего дня. Из своих опытов Ом вывел, что в различных цепях сила тока может возрастать с различной скоростью, и происходит это по мере увеличения напряжения.
Также, Ом сделал вывод, что каждый проводник обладает индивидуальными свойствами проводимости.
Сопротивление обозначается заглавной латинской [R] и измеряется в Омах. Сопротивление – физическая величина, характеризующая свойства проводника оказывать влияние на идущий по нему ток. Оно прямо пропорционально напряжению в сети и обратно пропорционально силе тока. В виде формулы данный закон можно записать как R = U/I, где U – напряжение, а I – сила тока. 1 Ом равняется 1 Вольту, деленному на 1 Ампер.
Запомните! Реостат – прибор, обеспечивающий возможность изменять сопротивление. Прежде всего, он влияет на показатель R в цепи, а, следовательно, на 2 другие величины, описанные в законе Ома. Силу тока может помочь определить амперметр.
Из формулы закона Ома можно вывести практически любую зависимость, связанную с электричеством. Также, существует понятие удельного сопротивления проводника – физической величины, которая демонстрирует, каким сопротивлением будет обладать проводник из определенного вещества. Обозначается эта величина буквой ρ и через неё можно также найти сопротивление в цепи как произведению удельного сопротивления и длины проводника, деленного на площадь его поперечного сечения.
Важно! В виде формулы нахождение сопротивления через удельное сопротивление выглядит так: R = ρ*(l/S), где l – длина проводника, а S – площадь поперечного сечения.
Вам это будет интересно Особенности измерения света
Физический смысл удельного сопротивления показывает, какое влияние будет оказывать проводник длиной в 1 м с площадью поперечного сечения в 1 квадратный мм, изготовленный из определенного вещества. Измеряется в Омах, умноженных на метр: [ρ] = [Ом*м].
Метод контурных токов
Рассмотренный выше метод расчета электрических цепей при анализе больших и разветвленных цепей приводит к неоправданно трудоемким расчетам, поэтому редко применяется. Более широко используется метод контурных токов, позволяющий значительно сократить количество уравнений. При этом вместо токов в ветвях электрической цепи определяются так называемые контурные токи при помощи второго закона Кирхгофа. Таким образом, количество требуемых уравнений будет равняться числу независимых контуров. В качестве примера рассчитаем цепь изображённую на рисунке ниже
Если бы мы вели расчёт цепи по методу законов Ома и Кирхгофа, то необходимо было бы решить систему из пяти уравнений. Для расчёта по методу контурных токов необходимо всего три уравнения.
Советуем изучить Зарядное устройство для автомобильного аккумулятора своими руками
В начале расчёта выделяют независимые контуры, в нашем случае это: E1R1R2E2, E2R2R4E3R3 и E3R4R5. Затем контурам присваивают произвольно направленный контурный ток, который имеет одинаковое направление для всех участков выбранного контура, в нашем случае для первого контура контурный ток будет Ia, для второго – Ib, для третьего – Ic. Как видно из рисунка некоторые контурные токи соответствуют токам в ветвях
Остальные же токи можно найти как разность двух контурных токов
В результате выбора контурных токов можно составить систему уравнений по второму закону Кирхгофа
Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений
В результате решения системы получим Ia = I1 = 4,286 А, Ib = I3 = 3,571 А, Ic = I5 = -0,714 А, I2 = -0,715 А, I4 = 4,285 А. Так же как и в предыдущем случае если токи получаются отрицательными, значит действительное направление противоположно принятому. Таким образом, токи I2 и I5 имеют направление противоположное изображённым на рисунке.
Как найти сопротивление нагрузки
Сопротивление нагрузки обозначается латинскими буквами Rn или Rн. По сути, это является тем же сопротивлением участка цепи и вычисляется также по формулам закона Ома. Нагрузка обозначается символами, которые на электрической схеме изображаются в виде крестиков в кружке – лампочкой; то есть двигатель, лампа, конкретный прибор и т. д.
Каждая нагрузка имеет своё собственное сопротивление. Например, если к сети подключена одна лампочка, то сопротивление нагрузки – показатель этого единственного прибора в цепи. Если к цепи подключено несколько нагрузок, то сопротивление считается суммарно для каждой из них.
Сопротивление нагрузки вычисляется в соответствии с законом Ома, то есть Rn = U/I. Если к сети подключено несколько нагрузок, то оно будет рассчитываться следующим образом: сначала находится сопротивление каждой отдельной «лампочки». Далее Rn вычисляется в зависимости от того, какой тип подключения в цепи: последовательное или параллельное. При параллельном 1/R = 1/R1 + 1/R2 + 1/Rn, где n –количество подключенных приборов. Если же соединение последовательное, общее R равно сумме всех R цепи.
Дополнительные методы расчета цепей
Подключение светодиода через резистор и его расчет
В зависимости от сложности устройства (электрической схемы), выбирают оптимальную технологию вычислений.
Метод узлового напряжения
Основные принципы этого способа базируются на законе Ома и постулатах Кирхгофа. На первом этапе определяют потенциалы в каждом узле. Далее вычисляют токи в отдельных ветвях с учетом соответствующих электрических сопротивлений (отдельных компонентов или эквивалентных значений). Проверку делают по рассмотренным правилам.
Метод эквивалентного генератора
Эта технология подходит для быстрого расчета тока в одной или нескольких контрольных ветвях.
В данной методике общую цепь представляют в виде источника тока с определенным напряжением и внутренним сопротивлением. Далее выполняют вычисления по контрольной ветви с применением стандартного алгоритма.
Как найти с помощью формулы напряжение
Людей, интересующихся электричеством и физикой, всегда волнует вопрос, как найти напряжения, если известны другие характеристики. Его можно найти через многие формулы: в соответствии с законом Ома, через работу тока, путём сложения всех напряжений в электрической цепи и практическим способом – с помощью вольтметра. Как вычислить показатель с помощью последнего способа было описано выше.
Важно! В цепях с последовательным соединением общее напряжение – сумма значений каждой нагрузки. При параллельном соединении общее напряжение равно значению каждой лампочки, у которых оно также эквивалентно.
Вам это будет интересно Особенности поперечного сечения
По каким формулам вычисляется напряжение через работу и сама сила тока, рассказывают на уроках физики, так как эти величины считаются базовыми. Работа тока равна произведению напряжения и заряда: A = U*q. Также, из этой формулы выводится A = U*I*t, так как заряд – произведение силы тока и времени. Из них следует, что U = A/q или U = A/(I*t). Кроме того, одной из основных является формула напряжения, выведенная из закона Ома: U = R/I.
Важно! Определить напряжение можно и через мощность электрического тока. Мощность [P] равна A/t, и, так как A = U*I*t, конечная формула выглядит, как P = (U*I*t)/t. Здесь t сократится, и останется P = U*I, из которой следует, что U = P/I.
Как найти силу тока через сопротивление и напряжение
Сила тока обозначается латинскими [I] или [Y], и она зависит от количества заряда, перенесенного от одного полюса к другому за определенный промежуток времени, т.е. I = q/t. Измеряется сила тока в амперах, а узнать её значение в цепи можно при помощи амперметра.
Существуют формулы определения силы тока через напряжение и сопротивление. В первом случае произведение силы тока на время равняется работе, деленной на напряжение: I*t = A/U, во втором – по закону Ома, I = U/R. Через мощность сила будет равняться P/U.
При последовательном соединении, сила тока одинакова на всех участках цепи, следовательно, равна общему значению в цепи. В противоположном случае сила электрического тока равняется сумме силы тока всех нагрузок.
Таким образом, существует огромное множество формул для нахождения силы тока, напряжения и сопротивления. Они всегда могут пригодиться для теории, а на практике всегда помогут специальные приборы – амперметр и вольтметр.
Для переменного тока
В цепи переменного тока закон Ома может иметь некоторые особенности, описанные ниже.
Импеданс, Z
В цепи переменного тока, сопротивление кроме активной (R), может иметь как емкостную (C), так и индуктивную (L) составляющие. В этом случае вводится понятие электрического импеданса, Z (полного или комплексного сопротивления для синусоидального сигнала). Упрощенные схемы комплексного сопротивления приведены на рисунках ниже, слева для последовательного, справа для параллельного соединения индуктивной и емкостной составляющих.
Последовательное включение R, L, C
Параллельное включение R, L, C
Также, полное сопротивление, Z зависит не только от емкостной (C), индуктивной (L) и активной (R) составляющих, но и от частоты переменного тока.
| Импеданс, Полное сопротивление, Z | |
| При последовательном включении R, L, C | При параллельном включении R, L, C |
| Z=√(R2+(ωL-1/ωC)2) | Z=1/ √(1/R2+(1/ωL-ωC)2) |
| где, | |
| ω = 2πγ — циклическая, угловая частота; γ — частота переменного тока. |
Коэффициент мощности, Cos(φ)
Коэффициент мощности, в самом простом понимании, это отношение активной мощности (P) потребителя электрической энергии к полной (S) потребляемой мощности, т. е.
Cos(φ) = P / S
Он также показывает насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.Изменяется от 0 до 1. Если нагрузка не содержит реактивных составляющих (емкостной и индуктивной), то коэффициент мощности равен единице.Чем ближе Cos(φ) к единице, тем меньше потерь энергии в электрической цепи.
Исходя из вышеперечисленных понятий импеданса Z и коэффициента мощности Cos(φ), характерных для переменного тока, выведем формулу закона Ома, коэффициента мощности и их производные для цепей переменного тока:
| I = U / Z | где | I — сила переменного тока, измеряемая в Амперах, (A) |
| U — напряжение переменного тока, измеряемое в Вольтах, (V) | ||
| Z — полное сопротивление (импеданс), измеряется в Омах, (Ω) |
Производные формулы:
| Сила тока, | I= | U/Z | P/(U×Cos(φ)) | √(P/Z) |
| Напряжение, | U= | I×Z | P/(I×Cos(φ)) | √(P×Z) |
| Полное сопротивление, импеданс | Z= | U/I | P/I² | U²/P |
| Мощность, | P= | I²×Z | I×U×Cos(φ) | U²/Z |
Программа «КИП и А» имеет в своем составе блок расчета закона Ома как для постоянного и переменного тока, так и для расчета импеданса и коэффициента мощности Cos(φ). Скриншоты представлены на рисунках внизу:
Закон Ома для постоянного тока
Закон Ома для переменного тока
Расчет полного сопротивления
Расчет коэффициента мощности Cos(φ)
Как высчитать вольты
Причиной написания данной статьи явилась не сложность этих формул, а то, что в ходе проектирования и разработки каких-либо схем часто приходится перебирать ряд значений чтобы выйти на требуемые параметры или сбалансировать схему. Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.
В радиоэлектронике и электротехнике закон Ома и формула расчёта мощности используются чаше чем какие-либо из всех остальных формул. Они определяют жесткую взаимосвязь между четырьмя самыми ходовыми электрическими величинами: током, напряжением, сопротивлением и мощностью.
Закон Ома. Эту взаимосвязь выявил и доказал Георг Симон Ом в 1826 году. Для участка цепи она звучит так: сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению
Так записывается основная формула:
Путем преобразования основной формулы можно найти и другие две величины:
Мощность. Её определение звучит так: мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
Формула мгновенной электрической мощности:
Ниже приведён онлайн калькулятор для расчёта закона Ома и Мощности. Данный калькулятор позволяет определить взаимосвязь между четырьмя электрическими величинами: током, напряжением, сопротивлением и мощностью. Для этого достаточно ввести любые две величины. Стрелками «вверх-вниз» можно с шагом в единицу менять введённое значение. Размерность величин тоже можно выбрать. Также для удобства подбора параметров, калькулятор позволяет фиксировать до десяти ранее выполненных расчётов с теми размерностями с которыми выполнялись сами расчёты.
Когда мы учились в радиотехническом техникуме, то приходилось запоминать очень много всякой всячины. И чтобы проще было запомнить, для закона Ома есть три шпаргалки. Вот какими методиками мы пользовались.
Первая — мнемоническое правило. Если из формулы закона Ома выразить сопротивление, то R = рюмка.
Вторая — метод треугольника. Его ещё называют магический треугольник закона Ома.
Если оторвать величину, которую требуется найти, то в оставшейся части мы получим формулу для её нахождения.
Третья. Она больше является шпаргалкой, в которой объединены все основные формулы для четырёх электрических величин.
Пользоваться ею также просто, как и треугольником. Выбираем тот параметр, который хотим рассчитать, он находиться в малом кругу в центре и получаем по три формулы для его расчёта. Далее выбираем нужную.
Калькулятор закона Ома
Введите 2 значения, чтобы получить другие значения, и нажмите кнопку Рассчитать :
Калькулятор закона Ома переменного тока
Введите 2 значения амплитуды + фазовый угол, чтобы получить другие значения, и нажмите кнопку Calculate :
Формула закона Ома
Напряжение V в вольтах (В) равно току I в амперах (А), умноженному на сопротивление R в омах (Ом):
Мощность P в ваттах (Вт) равна напряжению V в вольтах (В), умноженному на ток I в амперах (A):
Формула закона Ома переменного тока
Напряжение V в вольтах (V) равно силе тока I в амперах (A), умноженному на импеданс Z в омах (Ω):
Комплексная мощность S в вольтах (ВА) равна напряжению V в вольтах (В), умноженному на ток I в амперах (A):
Закон Ома для «чайников»: понятие, формула, объяснение
Говорят: «не знаешь закон Ома – сиди дома». Так давайте же узнаем (вспомним), что это за закон, и смело пойдем гулять.
Основные понятия закона Ома
Как понять закон Ома? Нужно просто разобраться в том, что есть что в его определении. И начать следует с определения силы тока, напряжения и сопротивления.
Сила тока I
Пусть в каком-то проводнике течет ток. То есть, происходит направленное движение заряженных частиц – допустим, это электроны. Каждый электрон обладает элементарным электрическим зарядом (e= -1,60217662 × 10 -19 Кулона). В таком случае через некоторую поверхность за определенный промежуток времени пройдет конкретный электрический заряд, равный сумме всех зарядов протекших электронов.
Отношение заряда к времени и называется силой тока. Чем больший заряд проходит через проводник за определенное время, тем больше сила тока. Сила тока измеряется в Амперах.
Напряжение U, или разность потенциалов
Это как раз та штука, которая заставляет электроны двигаться. Электрический потенциал характеризует способность поля совершать работу по переносу заряда из одной точки в другую. Так, между двумя точками проводника существует разность потенциалов, и электрическое поле совершает работу по переносу заряда.
Физическая величина, равная работе эффективного электрического поля при переносе электрического заряда, и называется напряжением. Измеряется в Вольтах. Один Вольт – это напряжение, которое при перемещении заряда в 1 Кл совершает работу, равную 1 Джоуль.
Сопротивление R
Ток, как известно, течет в проводнике. Пусть это будет какой-нибудь провод. Двигаясь по проводу под действием поля, электроны сталкиваются с атомами провода, проводник греется, атомы в кристаллической решетке начинают колебаться, создавая электронам еще больше проблем для передвижения. Именно это явление и называется сопротивлением. Оно зависит от температуры, материала, сечения проводника и измеряется в Омах.
Памятник Георгу Симону Ому
Формулировка и объяснение закона Ома
Закон немецкого учителя Георга Ома очень прост. Он гласит:
Сила тока на участке цепи прямо пропорционально напряжению и обратно пропорциональна сопротивлению.
Георг Ом вывел этот закон экспериментально (эмпирически) в 1826 году. Естественно, чем больше сопротивление участка цепи, тем меньше будет сила тока. Соответственно, чем больше напряжение, тем и ток будет больше.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Данная формулировка закона Ома – самая простая и подходит для участка цепи. Говоря «участок цепи» мы подразумеваем, что это однородный участок, на котором нет источников тока с ЭДС. Говоря проще, этот участок содержит какое-то сопротивление, но на нем нет батарейки, обеспечивающей сам ток.
Если рассматривать закон Ома для полной цепи, формулировка его будет немного иной.
Пусть у нас есть цепь, в ней есть источник тока, создающий напряжение, и какое-то сопротивление.
Закон запишется в следующем виде:
Объяснение закона Ома для полой цепи принципиально не отличается от объяснения для участка цепи. Как видим, сопротивление складывается из собственно сопротивления и внутреннего сопротивления источника тока, а вместо напряжения в формуле фигурирует электродвижущая сила источника.
Кстати, о том, что такое что такое ЭДС, читайте в нашей отдельной статье.
Как понять закон Ома?
Чтобы интуитивно понять закон Ома, обратимся к аналогии представления тока в виде жидкости. Именно так думал Георг Ом, когда проводил опыты, благодаря которым был открыт закон, названный его именем.
Представим, что ток – это не движение частиц-носителей заряда в проводнике, а движение потока воды в трубе. Сначала воду насосом поднимают на водокачку, а оттуда, под действием потенциальной энергии, она стремиться вниз и течет по трубе. Причем, чем выше насос закачает воду, тем быстрее она потечет в трубе.
Отсюда следует вывод, что скорость потока воды (сила тока в проводе) будет тем больше, чем больше потенциальная энергия воды (разность потенциалов)
Сила тока прямо пропорциональна напряжению.
Теперь обратимся к сопротивлению. Гидравлическое сопротивление – это сопротивление трубы, обусловленное ее диаметром и шероховатостью стенок. Логично предположить, что чем больше диаметр, тем меньше сопротивление трубы, и тем большее количество воды (больший ток) протечет через ее сечение.
Сила тока обратно пропорциональна сопротивлению.
Такую аналогию можно проводить лишь для принципиального понимания закона Ома, так как его первозданный вид – на самом деле довольно грубое приближение, которое, тем не менее, находит отличное применение на практике.
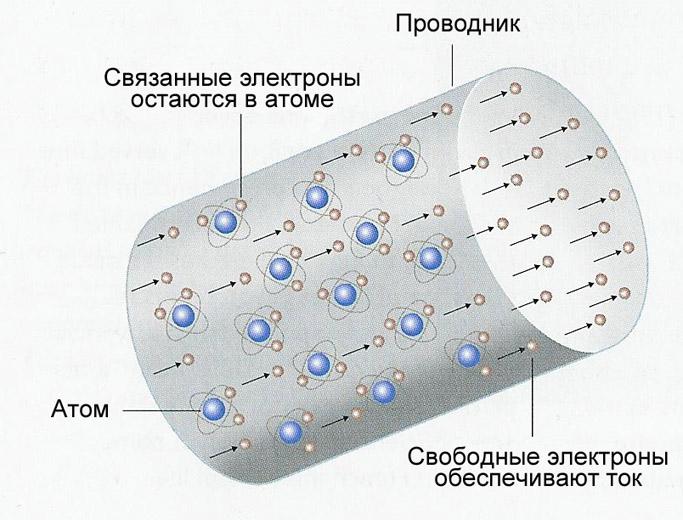
В действительности, сопротивление вещества обусловлено колебанием атомов кристаллической решетки, а ток – движением свободных носителей заряда. В металлах свободными носителями являются электроны, сорвавшиеся с атомных орбит.
Ток в проводнике
В данной статье мы постарались дать простое объяснение закона Ома. Знание этих на первый взгляд простых вещей может сослужить Вам неплохую службу на экзамене. Конечно, мы привели его простейшую формулировку закона Ома и не будем сейчас лезть в дебри высшей физики, разбираясь с активным и реактивным сопротивлениями и прочими тонкостями.
Если у Вас возникнет такая необходимость, Вам с удовольствием помогут сотрудники нашего студенческого сервиса. А напоследок предлагаем Вам посмотреть интересное видео про закон Ома. Это действительно познавательно!
- Контрольная работа от 1 дня / от 120 р. Узнать стоимость
- Дипломная работа от 7 дней / от 9540 р. Узнать стоимость
- Курсовая работа 5 дней / от 2160 р. Узнать стоимость
- Реферат от 1 дня / от 840 р. Узнать стоимость
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.