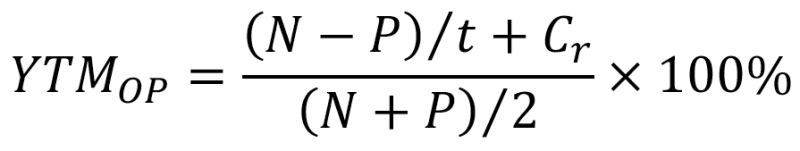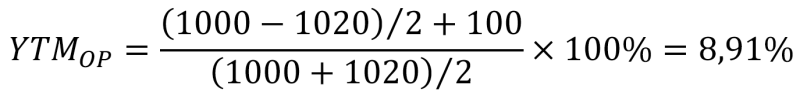Как найти внутреннюю доходность облигации

1.8.
Внутренняя доходность облигации.

Временная
структура процентных ставок.

Анализ финансовых
инвестиций в условиях определенности
будем изучать на примере ценных бумаг
с фиксированным доходом. Наиболее
распространенным видом таких ценных
бумаг являются облигации.

Облигация
– это обязательство выплатить в
определенные моменты времени в будущем
заранее установленные денежные суммы.
Основные параметры облигации –
номинальная цена (номинал), дата погашения,
размеры и сроки платежей по облигации.
С момента эмиссии и до погашения облигации
продаются и покупаются на фондовом
рынке. Рыночная цена облигации
устанавливается на основе спроса и
предложения и может быть равна ее
номиналу, выше или ниже номинала.

Будем рассматривать
облигации в условиях определенности:
эмитент не может отозвать облигацию до
установленной даты погашения, платежи
по облигации задаются фиксированными
значениями в определенные моменты
времени. При этом поступление будущих
доходов точно в указанные сроки и в
полном объеме считается гарантированным.
Про такие облигации говорят, что они не
имеют кредитного риска. Основным фактором
риска остается процентный риск – риск
изменения рыночных процентных ставок.

Рассмотрим
облигацию, по которой через t₁
, t₂,…,
t_n
лет от текущего момента времени t
= 0, где
0
< t₁
< t₂
<…< t_n,
обещают выплатить денежные суммы С₁,
С₂,…,
С_n
соответственно. Очевидно, что C_i
> 0, i
= 1, 2,…, n.
Пусть P
– рыночная стоимость облигации в момент
t =
0. Тогда естественно считать, что P
< С₁
+ С₂
+…+ С_n.
Момент
времени t =
0 – это момент, в который предполагается
произвести инвестицию в облигацию или
момент покупки облигации. Момент времени
t = t_n,
когда выполняется последний платеж по
облигации, называют моментом погашения
облигации, а срок
T = t_n
(в годах) – сроком до погашения. Два
показателя в основном интересуют
инвестора – доходность и цена облигации.
Внутренняя
доходность
– самый важный и наиболее широко
используемый показатель оценки облигации.
Известен также как доходность
к погашению.

Определение.
Годовая
внутренняя доходность облигации r
– это годовая ставка сложных процентов,
по которой современная
стоимость потока платежей по облигации
равна рыночной стоимости облигации в
момент t
= 0:

.
(8.1)

Здесь внутренняя
доходность облигации определяется как
годовая доходность денежного потока
С₁,
С₂,…,С_n,
стоимость которого P
(см. параграф 1.4).

В зарубежной
практике существует рыночное соглашение,
согласно которому если платежи по
облигации выплачиваются через равные
промежутки времени m
раз в году, то для дисконтирования членов
денежного потока применяется годовая
номинальная ставка внутренней доходности
j
:

.

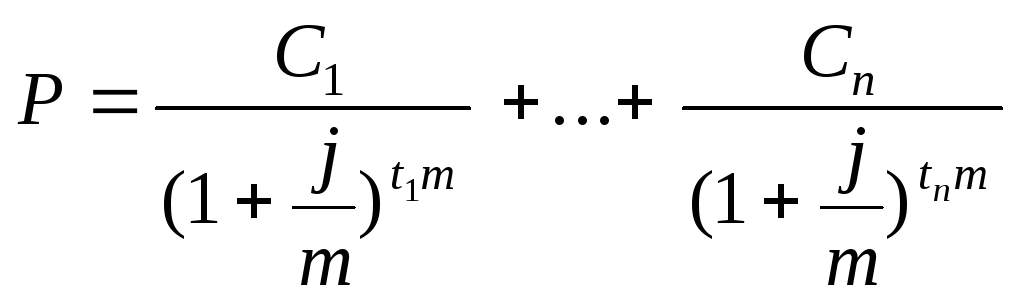
Свойства внутренней
доходности облигации.

1.
Ставка внутренней доходности облигации
равна преобладающей рыночной процентной
ставке для инвестиций в альтернативные
финансовые инструменты с такой же
степенью риска. Или короче – ставка
внутренней доходности облигации равна
доходности сравнимых с ней инструментов.

2.
Годовая внутренняя доходность облигации
– это ставка доходности, получаемая
инвестором, если выполняются два условия:

1) инвестор владеет
облигацией до момента ее погашения t
= t_n;

2) все платежи по
облигации реинвестируются по ставке,
равной внутренней доходности облигации
r
в момент ее покупки.

Покажем, что при
выполнении этих условий среднегодовая
доходность инвестиции в облигацию равна
ее внутренней доходности. Покупку
облигации, затем владение ею до момента
погашения с реинвестированием поступающих
доходов будем рассматривать как
финансовую операцию (см. параграф 1.2).
Срок операции T
= t_n
лет. Денежная оценка начала операции
P(0) – это
рыночная цена покупки облигации P
в
момент t
= 0.
Согласно (8.1), P
=
.
Денежная оценка момента погашения
облигации t
= t_n
для инвестора при выполнении условий
1), 2) – это сумма P(t_n)
=
.
Согласно определению доходности
финансовой операции (2.2):

P(t_n)
= P,

где

— среднегодовая доходность инвестиции
в облигацию на срок T
= t_n
лет. Подставим в это равенство выражения
для P
и P(t_n):

=
.

Откуда получаем
r
=
.

Таким образом,
среднегодовая доходность инвестиции
в облигацию, равная r,
реализуется в день погашения облигации
при выполнении условий 1), 2). Отсюда
другое название внутренней доходности
– доходность к погашению. Если пункты
1) или 2) не выполняются, то реальная
доходность, получаемая инвестором,
может быть выше или ниже внутренней
доходности облигации. Риск, с которым
сталкивается инвестор при покупке
облигации, –
это риск того, что будущие ставки
реинвестирования будут ниже ставки
внутренней доходности. Этот риск
называется реинвестиционным риском,
или риском ставки реинвестирования.

Внутренняя
доходность облигации используется для
оценки привлекательности альтернативных
инструментов инвестирования. При прочих
равных условиях, чем выше доходность к
погашению облигаций данного выпуска,
тем более привлекательным он является.

Рассмотрим
задачу определения внутренней доходности
облигации. Внутренняя доходность
облигации – это решение уравнения
(8.1). Согласно теореме 4.1, это уравнение
при выполнении условия P
< С₁
+ С₂
+…+ С_n
имеет единственное положительное
решение. Это решение находят, используя
приближенные методы. Один из них – метод
линейной интерполяции (изложен
в параграфе 1.4, примеры 4.2, 4.4).

Пример 8.1.
Определить
годовую внутреннюю доходность r
облигации, поток платежей по которой
указан в таблице:

Приближенное
значение внутренней доходности облигации
найдем методом линейной интерполяции.
Согласно определению годовой внутренней
доходности облигации

.

Необходимо
найти решение уравнения F(r)
= 0, где

F(r)
=
.

Так как 948 <
50 + 1050, то
согласно теореме 4.1 существует единственное
положительное решение этого уравнения.
Так как F(0,07)
= –
15,8396,
F(0,08)
= 1,4979,
то
искомая внутренняя доходность r
(0,07;
0,08). По формуле (4.8) находим первое
приближение

r_л1
= 0,07 +
.

При этом значение
функции F(r_л1)
= 0,02567
> 0. Значит,
решение r
(0,07;
0,07914). Следующий шаг метода дает

r_л2
= 0,07 +
.

Поэтому можно
считать, что r

0,07913
или 7,913 % с точностью до третьего знака
после запятой.

Определение.
Облигация
называется чисто дисконтной, если по
этой облигации производится только
одна выплата.

Определение.
Внутренняя доходность чисто дисконтной
облигации без кредитного риска, срок
до погашения которой t
лет, называется годовой безрисковой
процентной ставкой для инвестиций на
t
лет. Другое название – годовая спот-ставка.

Пусть А
– погашаемая сумма по чисто дисконтной
облигации, t
лет — срок
до погашения, Р
– рыночная цена облигации в момент t
= 0, r(t)
– внутренняя
доходность облигации. Тогда согласно
определению внутренней доходности
облигации,

.

Отсюда

(8.2)

– годовая
безрисковая процентная ставка для
инвестиций на t

лет.

В качестве примера
чисто дисконтных облигаций, не имеющих
кредитного риска, можно привести
бескупонные облигации Казначейства
США. Доходности казначейских бумаг
служат эталоном при оценке всех видов
облигаций.

Рассмотрим, как
можно оценить любую облигацию, если на
рынке имеются чисто дисконтные облигации.
Пусть на рынке имеется облигация В
без кредитного
риска, по которой через t₁
, t₂,…,
t_n
лет обещают выплатить денежные суммы
С₁,
С₂,…,
С_n
соответственно. Облигацию В
можно оценить, если рассматривать ее
как портфель из чисто дисконтных
облигаций В₁,
В₂,…,
В_n
со сроками погашения через t₁
, t₂,…,
t_n
лет соответственно. Предположим,
выполняются следующие условия:

1) известны годовые
безрисковые процентные ставки r(t₁),
r(t₂),
…, r(t_n)
для
инвестиций на t₁
, t₂,…,
t_n
лет, отсчитанных от момента t
= 0;

2) чисто дисконтные
облигации В₁,
В₂,…,
В_n
можно приобрести на рынке в любом
количестве без трансакционных расходов.
Тогда для этих облигаций имеем

,

i
= 1, 2, …, n,
где P_i
– текущая
рыночная цена одной облигации i
– го вида, A_i
– погашаемая
сумма по этой облигации,
r(t_i)
— ее
внутренняя доходность. Платеж С₁
от портфеля погашается облигациями В₁,
платеж С₂
– облигациями В₂,
и т.д., платеж С_n
– облигациями В_n.
Тогда в портфеле
,
i
= 1, 2, …, n,
облигаций
каждого вида. Следовательно, стоимость
портфеля в момент t
= 0 равна

.

Тогда рыночная
стоимость облигации В
в момент t
= 0 составляет

.
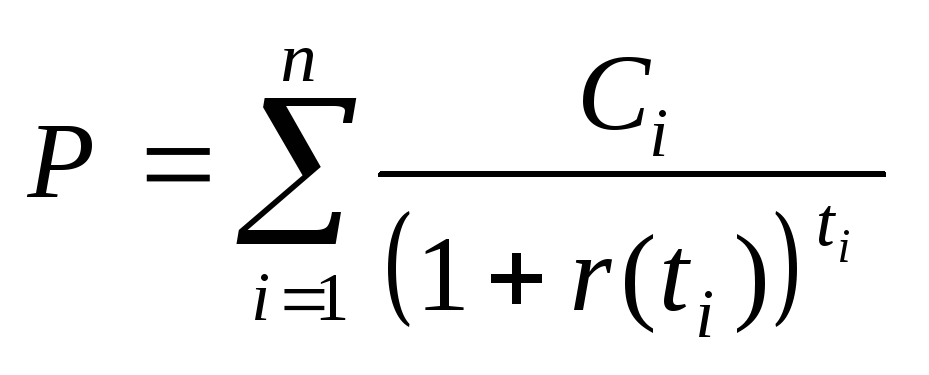
(8.3)

Каждый платеж по
облигации В
индивидуально дисконтируется по
соответствующей безрисковой процентной
ставке.

Определение.
Набор годовых безрисковых процентных
ставок r(t₁),
r(t₂),
…, r(t_n)
для инвестиций на t₁
, t₂,…,
t_n
лет, отсчитанных от момента t
= 0, где
,
называется временной структурой
процентных ставок.

Таким образом,
если известна временная структура
процентных ставок, то стоимость облигации,
не имеющей кредитного риска, может быть
рассчитана по формуле (8.3).

Определение.
График функции
r
= r(t),
где r(t)
— годовая безрисковая процентная ставка
для инвестиций на t
лет, называется кривой доходностей (или
кривой спот-ставок).

В условиях реального
рынка всегда существует лишь конечный
набор чисто дисконтных облигаций
(например, не существует бескупонных
долговых обязательств Казначейства
США со сроком погашения больше одного
года). Поэтому кривую доходностей
невозможно построить только по наблюдениям
на рынке. В связи с этим строят теоретическую
кривую доходностей. Для этого, используя
доходности реально существующих чисто
дисконтных облигаций, рассчитывают
теоретические значения доходностей
для различных сроков инвестирования.
Существует несколько методов получения
теоретических значений доходностей.
Один из них называется «процедурой
бутстреппа».
Рассмотрим этот метод на примере.

Пример 8.2.
На рынке имеются государственные
облигации А, В, С, D,
Е, потоки платежей по которым и цены в
момент t
= 0 указаны в таблице:

А и В – чисто
дисконтные облигации. Их внутренние
доходности r(0,5)
= 5,25 % и r(1)
= 6,3 %, определенные по формуле (8.2), являются
безрисковыми процентными ставками для
инвестиций на 0,5 года и 1 год. Зная эти
две ставки, можно вычислить теоретическую
безрисковую процентную ставку для
инвестиций на 1,5 года, используя облигацию
С. Цена облигации С по формуле (8.3) равна

118,71 =
,

где r(0,5)
= 0,0525, r(1)
= 0,063. Тогда

118,71 =
.

Откуда получаем
теоретическую годовую безрисковую
процентную ставку для инвестиций на
1,5 года: r(1,5)
= 6,9 %. Данная ставка – это та ставка,
которую предлагал бы рынок по 1,5 — годовым
чисто дисконтным облигациям, если бы
такие ценные бумаги существовали на
самом деле.

Зная теоретическую
1,5 – годовую безрисковую процентную
ставку, можно вычислить теоретическую
двухлетнюю безрисковую процентную
ставку, используя облигацию
D:

135,64 =
.

Откуда r(2)
= 7,1 % — теоретическая двухлетняя безрисковая
процентная ставка. Применяя еще раз
описанную процедуру для облигации E,
определяем теоретическую 2,5 — летнюю
безрисковую процентную ставку: r(2,5)
= 7,9 %.

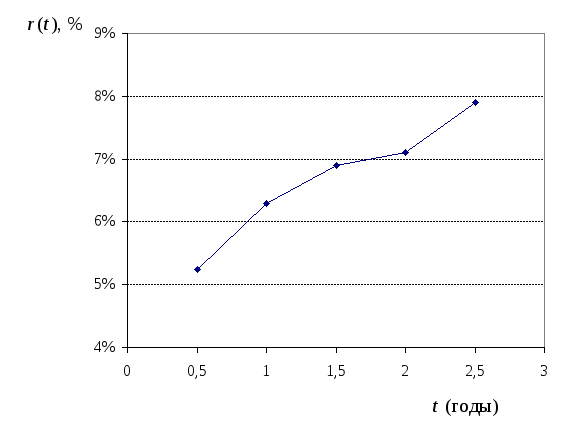
Безрисковые
процентные ставки r(0,5),
r(1),
r(1,5),
r(2),
r(2,5),
построенные с помощью такого процесса,
задают временную структуру процентных
ставок по 2,5 — летнему диапазону
относительно момента времени, к которому
относятся цены облигаций.

Зная временную
структуру процентных ставок r(t₁),
r(t₂),
…, r(t_n),
можно построить кривую доходностей.
Один из методов построения кривой –
линейное интерполирование. Полагают

,

,
i
= 1, 2, …, n
– 1. (8.4)

К
ривая
доходностей для временной структуры,
полученной в примере 8.2, при использовании
линейного интерполирования имеет вид:

Рис.
1.8.1

Пользуясь
кривой доходностей, можно определить
приближенное значение безрисковой
процентной ставки для инвестиций на
любой срок от t₁
до
t_n
лет. Например, так как 1,25
[1;1,5],
то

r(1,25)

r(1)

= 0,066.

Другой способ
построения кривой доходностей –
интерполирование (n
– 1) – го
порядка:

r(t)

+

(8.5)

…………………..

+
,

где t
[t₁,
t_n].
Тогда r(t)
– многочлен
степени (n
– 1) относительно переменной t.
При t
= t₁,
t₂,
…, t_n
значения многочлена совпадают с r(t₁),
r(t₂),
…, r(t_n)
соответственно. Уравнение кривой
доходностей для временной структуры,
полученной в примере 8.2, имеет вид:

r(t)

0,00633
t⁴
— 0,031 t³
+ 0,04442 t²
— 0,00325 t
+ 0,0465, где
t
[0,5; 2,5].

Пользуясь полученной
кривой, вычислим стоимость облигации
без кредитного риска, платежи по которой
относительно момента t
= 0 указаны
в таблице:

Рыночная стоимость
данной облигации
в момент t
= 0 составляет,
согласно (8.3):

P
=
.

Приближенные
значения годовых безрисковых процентных
ставок для инвестиций на 0,7 года и 1,7
года равны соответственно:

r(0,7)

0,00633(0,7)⁴
— 0,031(0,7)³
+ 0,04442(0,7)²
— 0,003250,7
+ 0,0465 = 0,0569,

r(1,7)

0,00633(1,7)⁴
— 0,031(1,7)³
+ 0,04442(1,7)²
— 0,003251,7
+ 0,0465 = 0,0699.

Тогда рыночная
стоимость данной облигации

P
=
=
112,14.

Рассмотренная
«процедура бутстреппа» получения
теоретических значений безрисковых
процентных ставок может быть использована,
если на рынке имеются подходящие для
этой процедуры облигации. Рассмотрим
еще один метод получения теоретических
значений процентных ставок.

Предположим,
известна временная структура процентных
ставок r(t₁),
r(t₂),
…, r(t_k)
для
инвестиций на t₁
, t₂,…,
t_k
лет, а на
рынке имеется облигация без кредитного
риска стоимостью P,
по которой через
t₁
, t₂,…,
t_k,
t<sub>k
+ 1</sub>,
…, t_n
лет обещаны выплаты С₁,
С₂,…,
С_k,
С_k+1,…,
С_n
соответственно. Приближенные значения
безрисковых процентных ставок r(t_k+1),
r(t_k+2),
…, r(t_n)
можно найти, используя линейную
интерполяцию на отрезке [t_k,
t_n].
Для этого полагают r(t_n)
= r.

Безрисковая
процентная ставка r(t_k)
известна. Тогда

,

,

………………..
(8.6)

,

r(t_n)
= r,

где t<sub>k
+ 1</sub>,
t<sub>k
+ 2</sub>,
…, t_n
–
1[t_k,
t_n].

Так как стоимость
облигации P
в момент t
= 0 известна,
то

.
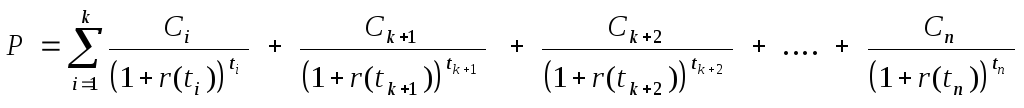
(8.7)

Подставляя в это
выражение вместо r(t<sub>k
+ 1</sub>),
r(t<sub>k
+ 2</sub>),
…, r(t_n)
равенства (8.6), получим уравнение с одним
неизвестным r.
Решение этого уравнения находим методом
линейной интерполяции. Зная r,
по формулам (8.6) находим безрисковые
процентные ставки r(t_k+1),
r(t_k+
2),
…, r(t_n).
Таким
образом, имеем временную структуру
процентных ставок r(t₁),
r(t₂),
…,
r(t_k),
r(t_k+1),…,
r(t_n)
по t_n
– летнему диапазону относительно
момента t
= 0.

Пример
8.3. Используя
линейное интерполирование, построить
кривую доходностей, если известны
годовые безрисковые процентные ставки:

r(0,5)
= 0,06; r(1)
= 0,07; r(1,5)
= 0,08

и дана облигация
(без кредитного риска) со следующим
потоком платежей:

Уравнение
(8.7) для данной облигации имеет вид:

.

Используем линейное
интерполирование на отрезке [1,5;
2,5]. Так как
r(1,5)
= 0,08, r(2,5)
= r,
то r(2)0,08
+ r=
0,04 + 0,5
r.
Тогда достаточно решить уравнение

86,01581 =
.

Решая это уравнение
методом линейной интерполяции, найдем
r

0,10489.

Следовательно,
r(2)

0,04 + 0,5
r
= 0,09245, r(2,5)0,10489.
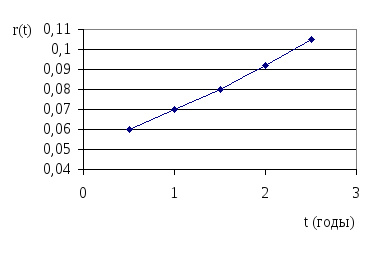
Таким образом, по заданным r(0,5)
= 0,06; r(1)
= 0,07; r(1,5)
= 0,08 и вычисленным

r
(2)

0,092;
r(2,5)0,105
значениям безрисковых процентных ставок
можно построить кривую доходностей:

Рис. 1.8.2

Кривая доходностей,
полученная для облигаций, не имеющих
кредитного риска, используется также
для оценки рискованных инструментов
на рынке. Теоретические значения
безрисковых процентных ставок с
добавлением премии за риск используются
для оценки всех видов облигаций. Кроме
того, форма кривой доходностей
рассматривается как отображение
вероятного направления будущих изменений
процентных ставок денежного рынка. На
рис. 1.8.3 показаны четыре основные формы
кривой доходностей: 1 – нормальная
(возрастающая) кривая; 2 – обратная
(убывающая) кривая; 3 – «горбатая» кривая;
4 – плоская (горизонтальная) кривая.

Рис. 1.8.3

Есть две основные
теории, объясняющие форму кривых
доходностей, –
теория ожиданий и теория сегментации
рынка [13,
14].
Возрастающая кривая чаще всего означает
предполагаемый рост темпа инфляции.
Убывающая кривая чаще всего свидетельствует
об ожидаемом снижении темпа инфляции.
Горизонтальная кривая доходностей
означает, что годовые безрисковые
процентные ставки для инвестиций на
все сроки одинаковы. Горизонтальная
кривая используется при изучении ряда
важнейших понятий теории финансовых
инвестиций с
фиксированным доходом. Например
таких, как дюрация и показатель выпуклости
облигации, стоимость инвестиции в
облигацию, иммунизация портфеля
облигаций.

154

Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+

АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).

ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.

Облигации считаются самым простым финансовым инструментом на бирже. Однако при этом у данных ценных бумаг есть свои нюансы, о которых должен знать каждый инвестор прежде, чем их купить. В этой статье расскажем о том, что такое доходность облигации, от чего она зависит и как её посчитать.

Что такое доходность облигации простыми словами

Облигация — долговое обязательство эмитента бумаги (того, кто её выпустил) перед держателем (тем, кто ей владеет). Эта бумага подтверждает, что тот, кто выпустил облигацию (компания или государство), одолжил капитал у инвестора с обещанием вернуть деньги с процентами в определённый срок.

Чтобы понимать, насколько прибыльна долговая бумага, инвестор должен уметь рассчитать её доходность. Если говорить простыми словами, доходом по облигации называется величина прибыли, полученная инвестором от вложений в ценную бумагу.

От чего зависит доход

Факторов, влияющих на доход облигации, много. Рассмотрим основные.

Рост котировок. Заработать инвестор может путём продажи бумаги по цене выше её покупки, так как облигациям, как и другим ценным бумагам на рынке, характерна волатильность.

Волатильность — показатель изменчивости цены актива за определённый промежуток времени.

Размер купона. Процент по облигации называется купоном. Эмитент облигации платит инвестору определённую сумму раз в месяц / квартал / год за то, что он одолжил у инвестора деньги.

По способу получения купонного дохода долговые бумаги бывают трёх видов:

• Купонная облигация. Инвестору в равные промежутки времени начисляется купонный платёж, а в конце срока обращения выплачивается обратно номинал бумаги.
• Облигация с плавающим купоном. Доходность по бумаге не фиксирована и изменяется вместе с внешними показателями: инфляцией, ключевой ставкой ЦБ и т. д.
• Дисконтная облигация. По ним не выплачиваются проценты за владение. Доходность бескупонной облигации фиксирована и формируется за счёт разницы между ценой покупки ниже номинала и первоначальной стоимостью облигации.

Погашение облигации. Это дата, в которую долговая бумага перестаёт торговаться на рынке. Как правило, в этот день эмитент выплачивает последний купон и возвращает инвестору номинал в полном размере.

Если инвестор приобрёл облигацию изначально ниже цены номинала, то при погашении, помимо купонов, он получит доход в виде курсовой разницы бумаги. Если же облигация покупалась по цене выше её первоначальной стоимости, то после выплаты номинала инвестор зафиксирует убыток.

Какие бывают виды

Чтобы выбрать облигацию, нужно сперва оценить её доходность. С одной стороны, инвестору не обязательно самостоятельно рассчитывать все показатели. Доходность бумаг можно узнать на сайтах Московской и Санкт-Петербургской бирж, а также в онлайн-приложении своего брокера.

С другой стороны, долговые бумаги не всегда продаются по номинальной стоимости. Соответственно, облигация может принести как больше прибыли, так и меньше ранее заявленным значениям. И чтобы правильно определить эту величину, необходимо различать виды доходности по облигациям.

Купонный доход

Данный показатель необходим, чтобы понимать, какой процент от номинала облигации (купон) начисляется каждый месяц / квартал / полгода / год.

Несмотря на то, что купонный доход выплачивается в определённые сроки, сумма купона начисляется инвестору ежедневно. Поэтому, если решите продать облигацию раньше следующего платежа, то уже начисленные неполные купоны вы не потеряете — следующий держатель облигации выплатит вам накопленный купонный доход (НКД) автоматически.

В этом примере есть и обратный эффект. Если вы только покупаете облигацию, то при выплате очередного купонного дохода часть полученной прибыли с вас спишут в пользу предыдущего владельца. Сумма списаний зависит от того, сколько дней прошло с момента выплаты прошлого купона.

Текущая доходность облигации

Если купонная доходность облигации определяется на основе номинала бумаги, то текущая учитывает только реальную цену приобретения бумаги на рынке.

Доходность к погашению облигации (простая)

Доходность к погашению облигации — экономический показатель, который отражает прибыльность бумаги на протяжении всего срока её обращения.

Простая доходность к погашению учитывает не только реальную цену покупки, но и ожидаемую стоимость погашения.

Если инвестор намерен владеть облигацией до конца её срока, то планируемая цена погашения бумаги будет равна её номиналу.

Эффективная к погашению

Эффективная доходность облигации — полный доход инвестора от вложений в долговую бумагу с учётом реинвестирования купонов по аналогичной купонной ставке.

Как рассчитать доходность облигации

Определить доходность долговой ценной бумаги можно 4 способами. Перед тем как считать доходность облигации, важно узнать некоторые данные:

• номинал облигации;
• размер купона / купонную ставку;
• срок погашения бумаги;
• рыночную стоимость облигации;
• частоту купонных выплат.

1 способ. Если покупать облигацию по номиналу и определять только купонный доход, потребуется следующая формула:

Купонный доход, за год = (Размер годовых купонов / Номинал) × 100%

Пример расчёта доходности облигации.

Эмитент выпустил облигацию номиналом 1000 руб. с ежеквартальной выплатой 25 руб. Определим купонный доход.

Купонный доход, за год = (25 руб. х 4 / 1000 руб.) х 100% = 10%

Таким образом, годовой купонный доход составляет 10%. Для простоты восприятия в данном случае учитывается тот факт, что инвестор приобрёл корпоративную облигацию по номиналу и держал её в своём инвестиционном портфеле весь срок обращения.

2 способ. При приобретении бумаги по цене, отличной от номинала, необходимо будет рассчитать текущую доходность облигации:

Доходность, годовых = (Купонный доход за год / Цена покупки облигации) × 100%

Пример расчёта справедливой доходности облигации.

Номинал долговой бумаги компании А равен 1000 р. Доходность по облигации составляет 8%. Купонный доход за год — 80 р. Инвестор покупает эту бумагу на вторичном рынке по цене 970 р. Определим её текущую доходность.

Доходность, годовых = (80 р. / 970 р.) х 100% = 8,24%

В данном случае показатель выше первоначальной купонной ставки, так как текущая стоимость облигации ниже номинала. По доходности бумага выглядит привлекательной, её необходимо покупать.

3 способ. Если же инвестор купил облигацию не по номиналу и знает, по какой цене он готов будет её продать, то его расчёт должен сводиться к формуле простой доходности облигации:

((Номинал − Полная цена покупки + Все купоны за период владения) / Полная цена покупки) × (365 / Количество дней до погашения) × 100%

Определим простую доходность к погашению долговой бумаги на основе следующего примера.

Номинал облигации — 1000 руб. Купон в размере 20 руб. выплачивается 4 раза в год (каждый квартал). Срок обращения — 2 года. Облигация начала торговаться на рынке 1 марта. При этом инвестор приобретает бумагу по цене 950 руб. 1 июня, сразу же после первой выплаты купона. Соответственно, предыдущему владельцу инвестор не перечисляет ничего из накопленного купонного дохода (НКД).

Купонов для выплат осталось 7 (4 раза х 2 года − 1 купон). Общая сумма оставшихся купонов — 140 руб. (7 х 20 р). Количество дней до погашения — 638 (365 х 2 года − 92 дня).

Примечание. Суммарно весенних дней в календаре — 92.

Считаем:

((1000 руб. − 950 руб. + 140 руб.) / 950 руб.) × (365 / 638) × 100% = 11,44%

Получается, что годовая доходность облигации составит 11,44% с учетом неполученного купона, но с ценовым дисконтом при покупке.

4 способ. Наиболее объективным и полным вариантом определения доходности облигации с учётом возможности реинвестирования купонных платежей можно считать формулу расчёта эффективной доходности:

• YTM_OP — доходность к погашению;
• C_r — сумма купонных выплат за год;
• P — текущая рыночная цена облигации;
• N — номинал облигации;
• t — лет до погашения.

Простой пример для расчёта эффективной доходности.

Номинал облигации — 1000 руб. Инвестор приобрел бумагу за 1020 руб. Ставка купона — 10%. Соответственно, сумма купонных выплат составит 100 руб. Срок обращения — 2 года.

Рассчитаем:

Итоговая доходность по бумаге составляет для инвестора не 10% годовых, а лишь 8,91%.

Налог на доход и комиссия брокера

По состоянию на 2022 год ставка НДФЛ по операциям с ценными бумагами равна 13%. Налоговым агентом на фондовом рынке является сам брокер. Это значит, что при продаже ценной бумаги из полученного инвестором дохода брокерская фирма автоматически вычтет сумму налога.

Если совокупный доход за год более 5 млн руб., то сумма превышения данного порога облагается НДФЛ по ставке 15%.

Помимо налогов, с инвестора также взимаются различные комиссии — сборы со стороны брокера. Их размер зависит от выбранного вами тарифа.

За что брокер может взимать комиссию:

• За ведение счёта. Как правило, российские брокеры взимают подобную комиссию, если клиент совершал хоть одну торговую операцию за месяц.
• За сделки. Это основной вид брокерской комиссии. Плата в пользу брокера взимается за каждую покупку и продажу ценной бумаги. У всех посредников величина сбора разная и может варьироваться в диапазоне от 0,05 до 0,1% от суммы сделки.
• За вывод средств. Согласно тарифу, брокер имеет право взимать с клиента фиксированный процент от величины вывода средств. Однако данная форма комиссии всё реже практикуется на рынке.
• За доступ к торговым платформам. Зачастую брокер не берёт комиссию за установку торгового терминала, разработанного брокерской компанией. Однако посредник может взять с инвестора фиксированную комиссию, если сумма депозита меньше заявленной для бесплатной установки ПО.
• Депозитарная комиссия. Когда инвестор откроет у посредника брокерский счёт, ему автоматически открывается и депозитарный счёт для учёта ценных бумаг. Сейчас почти все российские брокеры отказались от данной комиссии. Однако нередко этот вид комиссии может быть прописан в общих условиях тарифа.

Важно! Прежде чем выбрать брокера, тщательно ознакомьтесь с тарифными планами каждого. Зачастую в правилах пользования тарифом могут прописываться дополнительные комиссии за те или иные действия, совершаемые инвестором.

Сегодня вручную это делается редко, однако для правильного использования калькуляторов все равно надо знать, как рассчитать доходность облигаций. Предлагаем разобраться в этом на простых примерах.

Основная формула, как рассчитать доходность облигаций

Главной формулой для того, чтобы рассчитать доходность облигаций, как и любого другого вида инвестирования, принято считать такую:

Доходность = (Общая полученная сумма — Сумма вложения) / Сумма вложения * 100%.

Допустим, мы вложили во что-то 100 рублей и получили доход в 10 рублей. То есть в конце срока наш приход составил 110 рублей. Считаем:

Берем 110, отнимаем 100 равно 10, десять делим на вложенные 100 и умножаем на 100% равно 10% годовых.

Это универсальная формула простого процента. Далее рассмотрим детали и особенности ее применения в разных ситуациях.

Расчет доходности бескупонной облигации

Начнем с самого простого вариант — облигация без купона, продается с дисконтом и гасится по номиналу. По такому принципу работают, например, казначейские облигации США и масса других ценных бумаг. В России до дефолта 1998 года так выпускались ГКО, государственные краткосрочные облигации.

Допустим, мы покупаем бескупонную облигацию номиналом 1000 рублей за 950 рублей. Считаем по формуле:

От 1000 рублей отнимаем 950 рублей равно 50 рублей — это наш доход в рублях. Переводим его в проценты. Результат 50 рублей делим на вложенные 950 рублей и умножаем на 100% равно 5.2% годовых.

Расчет доходности купонной облигации

Усложним наш пример. Предположим, к ценной бумаге прилагается купон в размере 5%. То есть выплаты составят уже не 1000 рублей, а с купоном в размере 50 рублей.

Считаем общую сумму того, что будет выплачено через год. Берем 1000 рублей номинала и прибавляем 50 рублей итого равно 1050 рублей.

Вставляем результат в нашу базовую формулу и получаем:

Полученная сумма 1050 рублей минус то, что вложили 950 рублей равно 100 рублей, делим на то, что вложили, то есть на 950 рублей и умножаем на 100% равно 10.52%.

Учет налогов при расчете доходности облигаций

По состоянию на 2021 год инвестор, покупающий облигации, уплачивает два вида налогов. Первый — на полученный доход физическим лицом в размере 13%. При этом на купон НДФЛ платится сразу. То есть при получении дохода брокер, являющийся налоговым агентом, сразу его вычтет.

Вторая часть того же самого налога снимается тогда, когда инвестор получает прибыль при продаже или при погашении ценной бумаги, если она куплена с дисконтом.

Самый простой вариант точного расчета — предварительно скорректировать поступающие деньги на обязательные выплаты. В нашем примере и с 50 рублей купона, и с дисконта придется заплатить по 13%. Корректируем:

Считаем налог: 50 рублей умножить на 0.13 равно 6.5 рублей. То есть на руки по купону клиент получит 50 минус 6.50 рублей равно 43.5.

Еще 6.5 будет удержано налога на доход, полученный на прирост денег в результате покупки облигации с дисконтом.

Корректируем наш результат в базовой формуле.

Первым делом рассчитываем, что получим через год на руки после того, как брокер вычтет налог.

Номинал облигации в 1000 рублей плюс купон с удержанным налогом 43.50 минус налог на прирост стоимости от цены с дисконтом 6.50 рублей итого 1037 рублей.

Опять подставляем результат в базовую формулу. От 1037 рублей отнимаем 950 рублей итого доход в деньгах составит 87 рублей. Далее считаем доходность: 87 разделить на инвестиции в размере 950 рублей и умножить на 100% равно 9.16%. Результат, как это принято при расчете процентов, сокращен до второго знака после запятой.

Повышенная налоговая ставка

В нашем примере доход по купону равен 5%. Однако он может быть любым. Если слишком большим, то облигация будет продаваться не с дисконтом, а с премией, то есть дороже номинала. Доходность рассчитывается также, просто по купонам будет прибыль, а по премии — убыток, который скорректирует поступление денег до обычных рыночных условий. С точки зрения финансовой математики размер дисконта, или премии, или размер купона не имеют значения, результат считается одинаково.

Но есть разница с точки зрения налогообложения. По российскому закону, если ставка купона больше ставки рефинансирования ЦБ плюс 5%, то налог на доходы на сумму превышения составит не 13, а 35%. Это надо учитывать.

Пока ставка ЦБ оставалась высокой, это не имело практического значения. Но когда она достигнет в результате снижения, скажем, 3%, то разница окажется заметной. Рассмотрим это на примере.

Допустим, купон по облигации 10%. И она, разумеется, торгуется с премией. При этом ставка ЦБ стала как в Европе, для примера, 2%. Тогда 2+5 равно 7%, и все, что выше, идет под 35% налога.

Если номинал облигации равен 1000 рублей, то до налогов купон составит 100 рублей. Из них 70 рублей облагаются налогом 13%, а еще 30 рублей — 35%. По первой части брокер удержит 9.1 рублей, а по второй, по части превышения — еще 10.50 рублей, итого в сумме 19.60 рублей.

Далее как обычно, подставляем в базовую формулу, что получаем на руки: номинал 1000 рублей плюс купон 100 рублей минус налоги 19.60 рублей итого 1080.40 рублей. А вложили мы,1000 рублей. Тогда получается, что доходность равна 1080.40 минус 1000 рублей разделить на 1000 рублей и умножить на 100% равно 8.04%.

Как рассчитать доходность за несколько лет, доходность к погашению

В нашем примере мы исходили из того, что погашение происходит ровно через год после покупки. А если нет? Тогда в формулу нужно добавить ту часть, которая сделает поправку на сроки. То есть полученный результат умножим на количество дней в году, предположим, 365, хотя по некоторым инструментам сроки традиционно отличаются, разделить на число дней до погашения.

Смысл этой операции заключается в том, чтобы привести доход за любой срок к годовому проценту. Таким образом, мы получим возможность сравнивать все инструменты по одному критерию — годовой доходности.

Возьмем еще раз самый первый пример и предположим, что купленная на тех же условиях бумага будет погашена через два года, а не через год. Пересчитываем с поправкой на это, подставив те же цифры в формулу:

Доходность = (Полученная сумма — Сумма вложения) / Сумма вложения *365/Число дней до погашения *100%.

Итак, 1100 рублей, которые мы получим при погашении минус 1000 рублей вложенных равно 100 рублей. Умножаем на 365 деленные на 730, то есть и умножаем результат на 100% итого получится 5 процентов годовых.

Не сложно посчитать, что если бы удалось получить те же деньги за полгода, а не за год, то доходность такой облигации была бы в два раза выше, а не ниже.

Сложные проценты

В заключение приведем еще одну формулу, как рассчитать сложные проценты, если удастся полностью реинвестировать получаемые деньги в течение нескольких лет.

Для того, чтобы правильно посчитать полную доходность такого вложения, надо узнать, сколько денег будет получено с учетом сложного процента. Сделать это можно по формуле:

S = P*(1+ i)^n (в степени n),

где S – получаемая сумма, P – цена облигации при покупке, i – процент в сотых долях, а n – число выплат.

Например, облигация номиналом 1000 рублей, срок обращения не один, а два года, купон 5%, то, есть ι = 0,05. Подставляем в формулу и получаем:

Вложенная 1000 * (1+0.05)^2 или 1000 умножить на 1.05 в квадрате итого равно 1000*1.1025 равно 1102.5 рубля. Именно столько получит инвестор за два года в случае, если он полностью реинвестирует купон.

Далее проводим обычный расчет, как мы и делали ранее.

Как рассчитать на практике

В действительности никто вручную в наше время проценты не считает. Соответствующие функции есть в программе Excel, а также на многих сайтах в Интернете. В том числе популярностью пользуется онлайн калькулятор, расположенный на сайте Московской биржи. Его преимущество в том, что он использует котировки в реальном времени, то есть их не надо вводить вручную.

Еще стоит отметить, что обычно в торговых системах на странице облигаций автоматически напротив каждой из них подсчитывается в отдельной колонке доходность по бумаге к погашению.

Однако при этом у всех готовых решений есть, чаще всего, один общий недостаток: они не учитывают налоги.

Оказывается, чем больше бумаг купить, тем больше будет доходность. В статье вы найдете формулы — они помогут рассчитать, сколько вы сможете заработать на облигациях

Облигация — это способ одолжить деньги государству или компании. За это они вам будут платить несколько раз в год проценты — купоны. Облигации — защитная часть инвестиционного портфеля. Их потенциальная доходность ниже акций, но выше депозита в банке. Они считаются надежным инструментом потому, что цена облигаций меньше всех других активов подвержена колебаниям, и потому, что вы получаете стабильные выплаты по ним.

Облигации бывают государственные, муниципальные, корпоративные, еврооблигации. Компания или государство может не выплатить вам деньги только в том случае, если обанкротится. Поэтому самые надежные облигации — государственные. Вероятность банкротства целой страны менее вероятна, чем отдельно взятой компании.

Цена облигаций на бирже рассчитывается в процентах от номинальной стоимости. Номинальная стоимость российских облигации обычно ₽1000 за штуку. И если вы увидите цену на бирже в 105%, это значит, что за облигацию вы заплатите ₽1050. А если цена облигации 95%, то заплатить нужно будет ₽950. Практически у всех облигаций есть дата погашения — день, когда государство или компания вернут вам номинальную стоимость облигации, то есть 100%.

Вы можете увидеть на бирже годовую доходность облигации 4%, 6%, 8%, 10% или даже 15% при условии, что вы гасите ее за 100% от номинала. Это столько, сколько принесет вам ежегодно ваше вложение, если вы дождетесь погашения облигации государством или компанией. Кажется, что это — беспроигрышный вариант с хорошей доходностью и минимальными рисками. Однако у облигаций есть много деталей, которые могут уменьшить эти красивые цифры доходности. О них поговорим по порядку и посчитаем доходность двух облигаций на примере.

Считаем доходность облигаций

Когда мы говорим про комиссии по облигациям, имеем в виду в первую очередь комиссии, которые берет с инвестора брокер. Чтобы узнать, какие комиссии вы заплатите при торговле на бирже, нужно внимательно выбирать тариф. Обратить внимание в первую очередь нужно на следующие пункты:

— плата за ведение счета и при каких условиях нужно будет платить. Многие брокеры снимают деньги только в том месяце, когда вы совершали сделки. Если в определенный месяц вы не торговали, платить не придется;

— плата за депозитарий. Депозитарий — это место, где хранятся ваши
ценные бумаги 
. На сегодняшний день большинство брокеров отменило эту комиссию. Но все равно лучше перепроверить;

— комиссия от суммы каждой сделки. Это плата, которую с вас снимут при любой покупке или продаже какого-либо инструмента на бирже.

Эти пункты важны при расчете доходности облигации, которую вы планируете купить.

Перед тем как покупать облигацию, нужно обратить внимание на НКД — накопленный купонный доход. Это часть купона, которая накопилась по конкретной облигации после выплаты предыдущего купона. Она тоже прибавится к стоимости облигации. Также есть комиссия Мосбиржи при любой сделке, но она небольшая — 0,01%

Давайте попробуем рассчитать потенциальную доходность реальной облигации. Для примера возьмем ОФЗ SU25083RMFS5 и представим, что вы продержите бумагу до даты погашения. Когда будете считать доходность, советуем выписать все исходные данные нужной вам облигации. Их можно посмотреть на сайте Мосбиржи в строке поиска. Подставляйте свои значения в формулы и считайте доходность.

Цена на 5 июня 2020 года — 103,58%, или ₽1035,8 (обычно в приложениях брокеров на карточках облигаций показывают цену так:
рыночная стоимость 
+ НКД)

• Годовая доходность — 4,52%
• Накопленный купонный доход — ₽33,17
• Комиссия за сделку — 0,3% (не от номинала облигации, а от текущей цены вместе с НКД)
• Комиссия за ведение счета или фиксированные ежемесячный платеж — ₽99
• Срок погашения — 15 декабря 2021 года, то есть через полтора года и 10 дней.
• Размер купона — ₽34,9

Всю доходность съела плата за обслуживание счета. Поэтому будьте внимательны при выборе тарифа у брокера. Чем больше облигаций за раз вы покупаете, тем меньше вашей будущей доходности съедают комиссии. При покупке, например, десяти облигаций не забудьте умножить цену одной облигации на десять, комиссию за сделку на десять и НКД на десять. Подсчитаем доходность той же самой облигации, но при условии, что вы купили десять штук.

Чем больше облигаций вы купите, тем больше заработаете. Но не забывайте про цену облигаций. Обычно она колеблется не сильно. Поэтому облигация за 112% вряд ли вам принесет много денег при погашении, ее можно считать дорогой.

Также должна настораживать и облигация за 70%. Покупать бумагу по такой цене рискованно. Чрезмерно низкая стоимость может говорить о том, что
эмитента 
ждет банкротство или он не выполняет свои обязательства по выплатам. Не забудьте и про НКД. Пакет облигаций лучше покупать сразу после того, как по ним был выплачен купон. Так размер НКД, который обычно прибавляется к стоимости облигации, будет минимальным.

На момент написания статьи большинство государственных облигаций торгуется выше номинала. Сейчас в России низкая ставка — 5,5% годовых. Многие облигации выпускались давно при более высоких ставках. Из-за того что ставка ЦБ снизилась, ставки на депозиты также стали ниже. За ними снизились и ставки по облигациям, а вот их цена выросла.

Все материалы нашего проекта доступны в Яндекс.Дзене. Подписывайтесь, чтобы быть в курсе

Стоимость компании на рынке, рассчитанная из количества акций компании, умноженного на их текущую цену. Капитализация фондового рынка – суммарная стоимость ценных бумаг, обращающихся на этом рынке.

Лицо, выпускающее ценные бумаги. Эмитентом может быть как физическое лицо, так и юридическое (компании, органы исполнительной власти или местного самоуправления).

Финансовый инстурмент, используемый для привлечения капитала. Основные типы ценных бумаг: акции (предоставляет владельцу право собственности), облигации (долговая ценная бумага) и их производные.
Подробнее

Долговая ценная бумага, владелец которой имеет право получить от выпустившего облигацию лица, ее номинальную стоимость в оговоренный срок. Помимо этого облигация предполагает право владельца получать процент от ее номинальной стоимости либо иные имущественные права.

Облигации являются эквивалентом займа и по своему принципу схожи с процессом кредитования. Выпускать облигации могут как государства, так и частные компании.