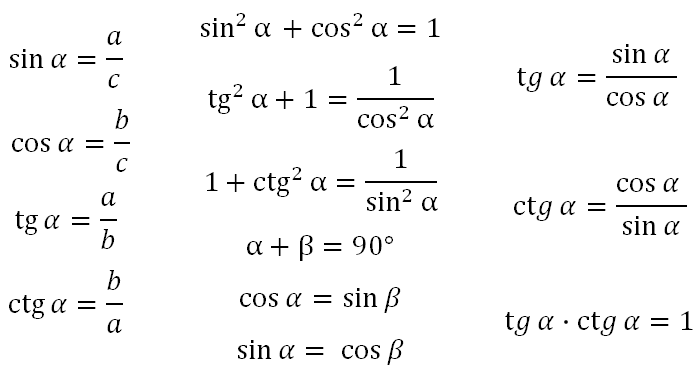Как найти внешний угол треугольника при синусе - Avtoru.top

Внешний угол треугольника. Синус и косинус внешнего угла

В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?

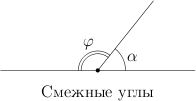
Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна $180^{circ}$ .

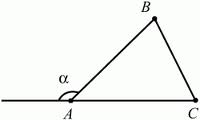
Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине — это угол, смежный с углом alpha . Если угол alpha острый, то смежный с ним угол — тупой, и наоборот.

Обратите внимание, что:

$sin left( 180^{circ} - alpha right) = sin alpha;$
$cos left( 180^{circ} - alpha right) = - cos alpha;$
$tg , left( 180^{circ} - alpha right) = - , tg , alpha.$

Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.

Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

1. В треугольнике ABC угол равен $90^{circ}$ , $cos A = genfrac{}{}{}{0}{displaystyle 4}{displaystyle sqrt{17}}$ . Найдите тангенс внешнего угла при вершине .

Пусть varphi — внешний угол при вершине .

$cos varphi = - cos A = - genfrac{}{}{}{0}{displaystyle 4}{displaystyle sqrt{17}}.$

Зная , найдем по формуле:

$genfrac{}{}{}{0}{displaystyle 1}{displaystyle cos^2 varphi}= 1 + tg^2 , varphi.$

Получим: $tg , varphi= - genfrac{}{}{}{0}{displaystyle 1}{displaystyle 4} = - 0,25.$

2. В треугольнике ABC угол равен $90^{circ}$ , . Найдите синус внешнего угла при вершине .

Задача решается за четыре секунды. Поскольку сумма углов и равна $90^{circ}$ , . Тогда и синус внешнего угла при вершине также равен 0,1 .

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Внешний угол треугольника. Синус и косинус внешнего угла» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
07.05.2023

Источник

Внешний угол треугольника

Углы треугольника бывают внутренние и внешние. Что такое внешний угол треугольника? Как его найти?

Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине.

Как построить внешний угол треугольника? Нужно продлить сторону треугольника.

∠3 — внешний угол при вершине А,

∠2 — внешний угол при вершине С,

∠1 — внешний угол при вершине В.

Сколько внешних углов у треугольника?

При каждой вершине треугольника есть два внешних угла. Чтобы построить внешний угол при вершине треугольника, можно продлить любую из двух сторон, на которых лежит данная вершина. Таким образом получаем 6 внешних углов.

Внешние углы каждой пары при данной вершины равны между собой (как вертикальные):

Поэтому, когда говорят о внешнем угле треугольника, не важно, какую из сторон треугольника продлили.

Чему равен внешний угол?

Теорема (о внешнем угле треугольника)

Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Дано : ∆АВС, ∠1 — внешний угол при вершине С.

∠1 и ∠С (∠АСВ) — смежные, поэтому их сумма равна 180º, значит, ∠1=180º-∠С=180º-(180º-(∠А+∠В))=180º-180º+(∠А+∠В)=∠А+∠В.

Теорема о внешнем угле треугольника: формулировка и задачи

В данной публикации мы рассмотрим одну из основных теорем в геометрии 7 класса – о внешнем угле треугольника. Также разберем примеры решения задач, чтобы закрепить представленный материал.

Определение внешнего угла

Для начала вспомним, что такое внешний угол. Допустим у нас есть треугольник:

Смежный с внутренним углом ( λ ) треугольника угол при той же вершине является внешним. На нашем рисунке он обозначен буквой γ .

γ + λ = 180°

Формулировка теоремы

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

Из данной теоремы следует, что внешний угол треугольника больше любого из несмежных с ним внутренних углов.

Примеры задач

Задание 1
Дан треугольник, в котором известны значения двух углов – 45° и 58°. Найдите внешний угол, смежный с неизвестным углом треугольника.

Решение
Воспользовавшись формулой теоремы получаем: 45° + 58° = 103°.

Задание 1
Внешний угол треугольника равен 115°, а один из несмежных с ним внутренних углов – 28°. Вычислите значения оставшихся углов треугольника.

Решение
Для удобства будем использовать обозначения, указанные на рисунках выше. Известный внутренний угол примем за α .

Исходя из теоремы: β = γ – α = 115° – 28° = 87° .

Угол λ является смежным с внешним, а значит вычисляется по следующей формуле (следует из свойства внешнего угла): λ = 180° – γ = 180° – 115° = 65° .

Внешний угол треугольника. Синус и косинус внешнего угла

Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна .

Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине — это угол, смежный с углом . Если угол острый, то смежный с ним угол — тупой, и наоборот.

Обратите внимание, что:

Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Ты нашел то, что искал? Поделись с друзьями!

1. В треугольнике угол равен , . Найдите тангенс внешнего угла при вершине .

Пусть — внешний угол при вершине .

Зная , найдем по формуле

2. В треугольнике угол равен , . Найдите синус внешнего угла при вершине .

Задача решается за четыре секунды. Поскольку сумма углов и равна , . Тогда и синус внешнего угла при вершине также равен .

источники:

Теорема о внешнем угле треугольника: формулировка и задачи

http://ege-study.ru/ru/ege/materialy/matematika/vneshnij-ugol-treugolnika/

Источник

Внешний угол треугольника. Синус и косинус внешнего угла

В некоторых
задачах ЕГЭ требуется найти синус,
косинус или тангенс внешнего
угла
треугольника. А что такое внешний
угол треугольника?

Давайте
вспомним сначала, что такое смежные
углы.
Вот они, на рисунке. У смежных углов
одна сторона общая, а две другие лежат
на одной прямой. Сумма смежных углов
равна

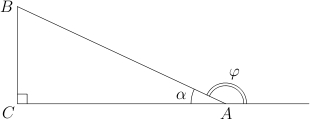
Возьмем
треугольник и продолжим одну из его
сторон. Внешний угол

при
вершине

—
это угол, смежный с углом

. Если
угол

острый, то смежный с ним угол —
тупой, и наоборот.

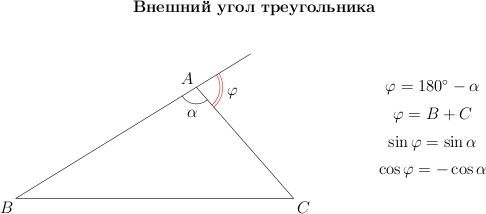
Обратите
внимание, что:

Запомните
эти важные соотношения. Сейчас мы берем
их без доказательств. В разделе
«Тригонометрия», в теме «Тригонометрический
круг»,
мы вернемся к ним.

Легко
доказать, что внешний
угол треугольника равен сумме двух
внутренних углов, не смежных с ним.

1.
В треугольнике

угол

равен

,

.
Найдите тангенс внешнего угла при
вершине

Пусть

—
внешний угол при вершине

.
Имеем:

Зная

,
найдем

по формуле

Получим:

2.
В треугольнике

угол

равен

,

.
Найдите синус внешнего угла при вершине

.

Задача
решается за четыре секунды. Поскольку
сумма углов

равна
,

.
Тогда и синус внешнего угла при
вершине

также равен

.

Высота в прямоугольном треугольнике

Вспомним,
что высота
треугольника —
это перпендикуляр, опущенный из его
вершины на противоположную сторону.

В
прямоугольном треугольнике катеты
являются высотами друг к другу. Главный
интерес представляет высота, проведённая
к гипотенузе.

Один
из типов экзаменационных задач В6 в
банке заданий ФИПИ — такие, где
в прямоугольном треугольнике высота
проведена из вершины прямого угла.
Посмотрим, что получается:

Высота
проведена к гипотенузе

.
Она делит треугольник

на два
прямоугольных треугольника —

и
.
Смотрим внимательно на рисунок
и находим на нем равные
углы.
Это и есть ключ к задачам по геометрии,
в которых высота опущена на гипотенузу.

Мы помним,
что сумма двух острых углов прямоугольного
треугольника равна

.
Значит,

,
то есть угол

равен
углу

.
Аналогично, угол

.

Иными
словами, каждый из трех углов
треугольника

равен
одному из углов треугольника

и треугольника

.
Треугольники

называются подобными.
Давайте нарисуем их рядом друг
с другом.

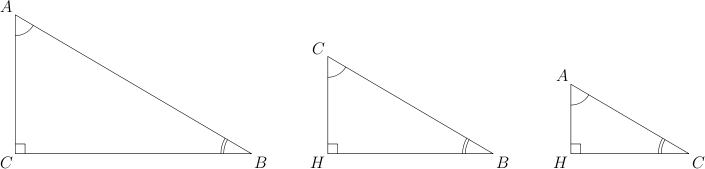
Они
отличаются только размерами. Стороны
подобных треугольников пропорциональны.
Что это значит?

Возьмем
треугольники

и
.
Стороны треугольника

длиннее,
чем стороны треугольника

,
в некоторое число

раз:

При
решении задач нам пригодится равенство
углов треугольников

и
,
а также пропорциональность их сторон.
Обратите также внимание, что площадь
треугольника

можно
записать двумя разными способами: как
половину произведения катетов и как
половину произведения гипотенузы
на проведенную к ней высоту.

1.
В треугольнике

угол

равен

,

—
высота,

,

.
Найдите

.

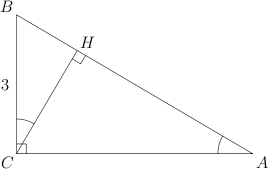
Рассмотрим
треугольник

.
В нем известны косинус угла

и противолежащий катет

.
Зная синус угла
,
мы могли бы найти гипотенузу

.
Так давайте найдем

:

(поскольку
значение синуса острого угла положительно).
Тогда:

Рассмотрим
прямоугольный треугольник

,

.
Имеем:

Отсюда,
поскольку

:

и
тогда

Ответ:

.

2.
В треугольнике

угол

равен

,

,

.
Найдите высоту

Сделайте
чертеж и рассмотрите прямоугольный
треугольник

Ответ:

.

3.
В треугольнике

угол

равен

,

,

.
К гипотенузе проведена высота

.
Найдите

Это
чуть более сложная задача. Ведь вам
неизвестны катеты

и
.

Зато
можно записать теорему Пифагора:

Нам
известно также, что

Решая
эту систему из двух уравнений, найдем:

Запишем
площадь треугольника

двумя
способами:

и найдем

.

Найти
высоту, проведенную из вершины прямого
угла, можно было и другим способом.
Мы выбрали самый короткий путь —
составили и решили систему уравнений.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
30.03.201540.15 Mб22спицын мартыненко.djvu
#
#
#
#
#
#
#
#

Источник

24
Мар 2012

03 Задание (2022)

Если в геометрической задаче присутствуют слова «внешний угол треугольника«, нам надо вспомнить несколько фактов:

1. Внешним углом треугольника называется угол, смежный с каким-либо углом треугольника:

2. Сумма смежных углов равна 180°

3. Внешний угол треугольника равен сумме двух углов, не смежных с ним:

Чтобы найти синус, косинус или тангенс внешнего угла треугольника, нужно найти эту функцию соответствующего внутреннего угла, а затем воспользоваться следующим формулами приведения:

$cos(180^{circ}-{alpha})=-cos{alpha}$ (1)

$sin(180^{circ}-{alpha})=sin{alpha}$ (2)

$tg(180^{circ}-{alpha})=-tg{alpha}$ (3)

Необходимо также вспомнить, как тригонометрические функции острого угла выражаются одна через другую:

$sin{alpha}=sqrt{1-cos^2{alpha}}$

$cos{alpha}=sqrt{1-sin^2{alpha}}$

$cos{alpha}=sqrt{1/{1+tg^2{alpha}}}$

Прежде чем приступать к разбору решений задач, рекомендую вам прочитать статью о соотношении сторон и углов в прямоугольном треугольнике.

Рассмотрим решение задач из Открытого банка заданий для подготовки к ЕГЭ по математике: .

1. Задание B7 (№ 27382)

В треугольнике ABC угол C равен 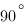$90^{circ}$ , , . Найдите тангенс внешнего угла при вершине A.

Найдем тангенс угла А, а затем воспользуемся формулой приведения.

АС=4, ВС найдем по теореме Пифагора:

$BC=sqrt{{AB}^2-{AC}^2}=sqrt{17-16}=1$

Отсюда . Соответственно, по формуле приведения (3), тангенс внешнего угла при вершине А равен -0,25.

Ответ: -0,25

2. Задание B7 (№ 27386)

В треугольнике ABC угол C равен 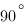$90^{circ}$ , синус внешнего угла при вершине A равен 0,1. Найдите .

Воспользуемся формулой приведения (2): sinA=0,1

Ответ: 0,1.

3. Задание B7 (№ 27387)

В треугольнике ABC угол C равен 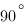$90^{circ}$ , синус внешнего угла при вершине A равен . Найдите .

Найдем сначала sin A. Он равен синусу внешнего угла треугольника при вершине А. То есть .

Найдем cosA c помощью основного тригонометрического тождества:

$cosA=sqrt{1-({7/25})^2}=sqrt{{576}/{625}}={24}/{25}=0,96$

Ответ: 0,96

4. Задание B7 (№ 27389)

В треугольнике ABC угол C равен 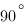$90^{circ}$ , синус внешнего угла при вершине A равен . Найдите .

Найдем сначала sin A. Он равен синусу внешнего угла треугольника при вершине А. То есть .

Сумма острых углов прямоугольного треугольника равна 90°, поэтому $sinB=sin(90^{circ}-A)=cosA=0,96$

Ответ: 0,96

5. Задание B7 (№ 27392)

В треугольнике ABC угол C равен 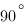$90^{circ}$ , косинус внешнего угла при вершине A равен . Найдите .

Если косинус внешнего угла при вершине A равен , то cos A=. Отсюда sinA=0,96

Ответ: 0,96

И.В. Фельдман, репетитор по математике.

Купить видеокурс «ВСЯ ГЕОМЕТРИЯ. Часть В»

Для вас другие записи этой рубрики:

Вычисление элементов прямоугольных треугольников. ОГЭ (ГИА) Задание 9, ЕГЭ Задание 6 (часть 2)

Видеолекция 15. Решение Задания В6. Часть 2: четырехугольники

Видеокурс «Вся ГЕОМЕТРИЯ. Часть В»

Вписанный четырехугольник. Задание 6

Окружность. Касательная. Вписанные углы. ОГЭ (ГИА) задание 10, ЕГЭ Задание 6

Задание В7 (2015): вписанный и центральный угол

Источник

Внешний угол треугольника. Продолжаем рассматривать задачи на решение прямоугольного треугольника. Такие типы заданий имеются в прототипах открытого банка заданий по математике. Некоторые примеры мы уже рассмотрели в статьях «Прямоугольный треугольник. Часть 1» и «Прямоугольный треугольник. Часть 2». В этой статье разберём задачи, в которых необходимо определить значения тригонометрических функций внешнего угла треугольника (или внутреннего, когда дано значение внешнего).

Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине

Угол DAB является внешним.

Стоит повторить определения синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике, также основные тригонометрические формулы для решения прямоугольного треугольника. Вспомним основные из них:

А также формулы приведения (не все). Отмечу одну типичную ошибку, которую допускают (из-за невнимательности). При решении подобных задач часто используется формула основного тригонометрического тождества:

Из неё мы получаем:

*Запись с ошибкой (её часто допускают — теряют квадрат):

Будьте внимательны!

Рассмотрим задачи:

В треугольнике ABC угол C равен 90⁰, sin A = 0,27. Найдите синус внешнего угла при вершине А.

Углы ВАС и BAD смежные, значит:

По свойству синуса:

А лучше раз и навсегда запомнить сам факт того, что синусы смежных углов равны, и вам даже не будет необходимости что-то записывать при решении такой задачи, ответ вы озвучите сразу.

Ответ: 0,27

Решите самостоятельно:

Посмотреть решение

В треугольнике ABC угол C равен 90⁰, . Найдите тангенс внешнего угла при вершине A.

Углы ВАС и BAD смежные, значит:

Значит по свойству тангенса (используем формулу приведения):

То есть необходимо найти тангенс угла ВАС. Известно, что:

Синус угла ВАС нам известен. Найдём его косинус.

Из основного тригонометрического тождества:

Вычисляем тангенс:

Таким образом tg BAD = – tg BAC = – 0,3

Ответ: – 0,3

Решите самостоятельно:

Посмотреть решение

В треугольнике ABC угол C равен 90⁰, АВ = 6, . Найдите косинус внешнего угла при вершине A.

Углы ВАС и BAD смежные, значит:

По свойству косинуса:

Найдём cos BAC Для этого необходимо найти сторону АС. По теореме Пифагора:

Значит АС = 3.

По определению косинуса:

Таким образом, cos DAB = – cos BAC = – 0,5.

Ответ: – 0,5

Решите самостоятельно:

Посмотреть решение

В треугольнике ABC угол C равен 90⁰, косинус внешнего угла при вершине A равен . Найдите sin A.

Углы ВАС и BAD смежные, значит:

В данной задаче можем найти косинус угла ВАС, а затем используя основное тригонометрическое тождество синус этого угла.

По свойству косинуса (используем формулу приведения):

Значит

Найдём sin BAC. Из основного тригонометрического тождества получим:

Ответ: 0,9

В треугольнике ABC угол C равен 90⁰, тангенс внешнего угла при вершине A равен –2/9. Найдите tg = B.

Из свойств прямоугольного треугольника мы знаем, что tg ABC = ctg BAC.

Найдём ctg BAC. Известно, что tg BAC ∙ ctg BAC = 1, значит

Тангенс угла ВАС найти не сложно. Углы BAC и BAD смежные. Это значит, что

По свойству тангенса:

Значит

Таким образом:

Ответ: 4,5

В треугольнике ABC угол C равен 90⁰, косинус внешнего угла при вершине A равен – 0,7; АВ = 20. Найдите AC.

Найти АС мы сможем, если нам будет известен косинус угла ВАС. Так как по определению косинуса в прямоугольном треугольнике:

Найдём косинус. По его свойству:

*Использовали формулу приведения.

Значит

Таким образом:

Ответ: 14

Решите самостоятельно:

Посмотреть решение

В треугольнике ABC АС = ВС, АВ = 12, тангенс внешнего угла при вершине A равен . Найдите AC.

Построим высоту CH.

Найдём тангенс внутреннего угла. По свойству тангенса:

Сторона АС является гипотенузой в прямоугольном треугольнике АСН. В этом треугольнике зная тангенс острого угла и один катет мы без труда можем найти второй катет.

Высота проведённая к основанию равнобедренного треугольника является медианой, то есть АН = ВН, a АВ = 2АН: