Как найти вершины прямоугольника 5 класс

Прямоугольник

• Свойства диагоналей

Прямоугольник — это выпуклый многоугольник. Прямоугольник образуется замкнутой ломаной линией, состоящей из четырёх звеньев, и той частью плоскости, которая находится внутри ломаной.

В тексте прямоугольники обозначаются четырьмя прописными латинскими буквами, стоящими при вершинах —  ABCD.

У прямоугольников противоположные стороны параллельны и равны:

В прямоугольнике  ABCD  точки  A,  B,  C  и  D  — это вершины прямоугольника, отрезки  AB,  BC,  CD  и  DA  — стороны. Углы, образованные сторонами, называются внутренними углами или просто углами прямоугольника.

Главное отличие прямоугольников от остальных четырёхугольников — четыре прямых внутренних угла:

Свойства диагоналей

Отрезки, соединяющие противолежащие вершины прямоугольника, называются диагоналями.

Отрезки  AC  и  BD  — диагонали,  O  — точка пересечения диагоналей.

В любом прямоугольнике можно провести всего две диагонали. Они обладают следующими свойствами:

• диагонали прямоугольника равны

  AC = BD;

• точка пересечения делит каждую диагональ на два равных отрезка

  AO = OC    и    BO = OD;

• так как диагонали равны, то и отрезки, на которые они разделяются в точке пересечения, тоже равны между собой:

  AO = OC = BO = OD;

• каждая диагональ делит прямоугольник на два равных треугольника:

  ΔABC = ΔCDA    и    ΔDAB = ΔBCD.

Квадрат — прямоугольник, у которого все стороны равны. Диагонали квадрата обладают всеми свойствами диагоналей прямоугольника. Также диагонали квадрата имеют и дополнительных свойства:

• диагонали квадрата пересекаются под прямым углом, то есть они взаимно перпендикулярны:

  AC ⊥ BD;

• диагонали квадрата делят его на четыре равных треугольника:

  ΔABO = ΔBCO = ΔCDO = ΔDAO;

• диагонали квадрата делят внутренние углы на две равные части, то есть они являются биссектрисами.

Как найти координаты вершин прямоугольника: практическое руководство

Прямоугольник — это чаще всего четырехугольник, у которого все углы прямые, и противоположные стороны равны. Найти координаты вершин прямоугольника может быть необходимо, например, чтобы создать графическое изображение, вычислить его площадь или периметр.

Метод 1: использование формул

1. Определите координаты центра прямоугольника — это среднее значение координат вершин.

2. Вычислите половину длины и ширины прямоугольника, используя формулы:

   l/2 = (x1 + x2) / 2
   w/2 = (y1 + y2) / 2
   

   Где l — длина прямоугольника, w — ширина, (x1, y1) и (x2, y2) — координаты двух противоположных вершин.

3. Найдите координаты остальных вершин, добавив или вычитая половину длины и/или ширины из центра прямоугольника:

   x3 = x_center + l/2
   y3 = y_center + w/2
   
   x4 = x_center - l/2
   y4 = y_center - w/2
   

Метод 2: использование векторной алгебры

1. Определите направляющие векторы сторон прямоугольника, вычислив разность координат смежных вершин:

   u = (x2 - x1, y2 - y1)
   v = (x3 - x2, y3 - y2)
   

2. Поместите начало координат в одну из вершин и запишите координаты векторов:

   x1 = (0, 0)
   x2 = (u1, u2)
   x3 = (u1 + v1, u2 + v2)
   x4 = (v1, v2)
   

3. Добавьте координаты начальной вершины к каждому вектору, чтобы получить итоговые координаты вершин:

   (x1 + x2), (x1 + x3), (x1 + x4), x2, x3, x4
   

   Где + — операция сложения векторов.

Метод 3: использование тригонометрии

1. Определите длину и ширину прямоугольника, используя формулу гипотенузы:

   l = sqrt((x2 - x1)^2 + (y2 - y1)^2)
   w = sqrt((x3 - x2)^2 + (y3 - y2)^2)
   

2. Вычислите углы между сторонами прямоугольника функцией atan2:

   alpha1 = atan2(y2 - y1, x2 - x1)
   alpha2 = atan2(y3 - y2, x3 - x2)
   

3. Найдите координаты остальных вершин, используя углы и длины, вычисленные на первых двух шагах:

   x4 = x1 + l * cos(alpha1 + pi/2)
   y4 = y1 + l * sin(alpha1 + pi/2)
   
   x3 = x2 + w * cos(alpha2 + pi/2)
   y3 = y2 + w * sin(alpha2 + pi/2)
   
   x4 = x3 + l * cos(alpha2 + pi/2)
   y4 = y3 + l * sin(alpha2 + pi/2)
   

   Где pi — число Пи.

Вывод

Независимо от того, какой метод вы выберете, чтобы найти координаты вершин прямоугольника, важно понимать, что необходимы координаты хотя бы двух противоположных вершин. От этого зависит точность результата. Также важно учитывать формат координат (декартовы, полярные и т.д.), чтобы правильно использовать формулы.

Учебник: Математика. Г.В.Дорофеев, И.Ф.Шарыгин и др. – М.: «Просвещение», 2017.

Цель: развивать представление о  прямоугольнике как о геометрической фигуре, научить строить с помощью  чертежных инструментов прямоугольник, закрепить умения вычислять периметр прямоугольника.

Задачи:

• Образовательная: применять умения нахождения периметра прямоугольника в решении практических задач;
• Развивающая: развивать познавательную активность, пространственное воображение, навыки самостоятельной работы; логическое мышление; навыки самооценки, рефлексивные способности;
• Воспитательная: воспитание интереса к предмету, умение работать в коллективе, культуре общения.

Оборудование: презентация к уроку (приложение 1),  мультимедийное оборудование, раздаточный материал, индивидуальные карточки для самостоятельной работы,  листы нелинованной бумаги, ножницы.

Ход урока

1. Организационный момент

Здравствуйте, ребята! Садитесь.

С каким настроением вы пришли сегодня на урок?

Итак, начинаем наш урок.

2. Устный опрос. (слайд)

Ну-ка, в сторону карандаши!
Ни бумажек, ни ручек, ни мела!
Устный счет! Мы творим это дело
Только силой ума и души!

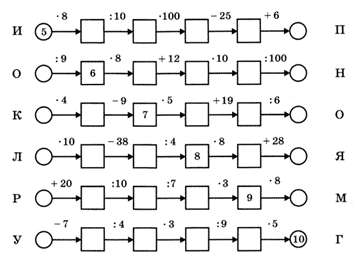
Игра «Кто быстрее» (слайд)

(класс разбивается на 2 команды)

Расположите ответы в порядке убывания и узнаете тему урока…

ОТВЕТ

3. Объяснение нового материала

Итак, тема нашего сегодняшнего урока…… , (слайд) записываем в тетрадь. Вы уже знакомы с этой фигурой. Но все ли вы помните, мы сейчас проверим.

Работа с математическим текстом (приложение 2)

Задание: прочитать внимательно данный материал, отметить карандашом по тексту то, что уже известно, и то, что не известно.

Прямоугольник — это четырехугольник, у которого все углы прямые.

Прямоугольник имеет четыре вершины, которые обозначаются большими латинскими буквами. По этим вершинам обозначается и сам прямоугольник, с какой вершины начать обозначение — не имеет значения, поэтому один прямоугольник можно назвать четырьмя разными способами:

ABCD,   BCDA,    CDAB,   DABC.

У прямоугольника четыре стороны. Важным свойством прямоугольника является равенство противоположных сторон.

Длины сторон помогают найти периметр прямоугольника.

Чтобы найти периметр прямоугольника, надо сложить длины двух соседних сторон и сумму увеличить в два раза.

Р = 2∙(а + b).

В любом прямоугольнике имеется две диагонали. Диагональ — отрезок, соединяющий две несоседние вершины. Диагональ делит прямоугольник на два равных треугольника.

— Что вам известно?

— Что новое вы узнали о прямоугольнике?

Вывод: (слайд) Прямоугольник – это такой четырехугольник, у которого все углы прямые.

(слайд) Посмотрите вокруг и назовите предметы, которые имеют форму прямоугольника.

Работа с учебником: рис. 7.8 стр. 140 – Есть ли среди этих геометрических фигур прямоугольник?  Как проверить, что противоположные стороны прямоугольника равны между собой?

(слайд) Отгадайте загадку:

Он давно знакомый мой.
Каждый угол в нём прямой.
Все четыре стороны
Одинаковой длины.
Вам его представить рад.
Как зовут его? (Квадрат)

— Квадрат – это прямоугольник или нет?

— Чем квадрат отличается от прямоугольника?

— Можно ли назвать любой прямоугольник квадратом, а квадрат – прямоугольником?

Работа в парах: заполнить таблицу – дети должны найти четыре сходства квадрата и прямоугольника и обдумать, какое общее название имеют эти фигуры.

(слайды)

Рассмотрим алгоритм построения прямоугольника

1. Начертим прямой угол и обозначим его вершину буквой А;
2. От точки А отложим на одной стороне угла отрезок, равный 2 см, а на другой 3 см. Обозначим концы отрезков буквами B и D;
3. Построим прямой угол с вершиной в точке В, и отложим на стороне угла отрезок ВС, равный 3 см;
4. Соединим точки С и D отрезком.

4. Закрепление

1. Постройте на листе нелинованной бумаги:

а) прямоугольник со сторонами 4 см и 5 см;

б) квадрат со стороной 4 см 3 мм.

(слайд)

2. Найдите периметр квадрата со стороной:

а) 5 см; б) 7 см 5 мм; в) 10 см 3 мм.

(Ответы: 20 см, 30 см, 41 см 2 мм)

3. Найдите периметр прямоугольника со сторонами 3 м 45 см и 1 м 70 см.

(Ответ: (345 + 170) * 2 = 1030 см = 10 м 30 см)

5. Литературная минутка. (слайд)

Учитель читает стихотворение, а командам надо сделать решение на бумаге

Жили-были два брата:
Треугольник с квадратом.
Старший — квадратный
Добродушный, приятный.
Младший — треугольный,
Вечно недовольный.
Стал расспрашивать квадрат:
— Почему ты злишься, брат?
Тот кричит ему: — Смотри,
Ты полней меня и шире,
У меня углов лишь три,
У тебя же их четыре!
Но квадрат ответил: — Брат!
Я же старше, я — квадрат:
Я сказал еще нежней:
— Неизвестно, кто нужней!
Но настала ночь, и к брату,
Натыкаясь на столы,
Младший лезет воровато
Срезать старшему углы.
Уходя сказал:
— Приятных я тебе Желаю снов!
Знать, ложился — был квадратным,
А проснешься без углов!
Но наутро младший брат
Страшной мести был не рад.
Поглядел он — нет квадрата,
Онемел, стоял без слов…
Вот так месть! Теперь у брата
Восемь новеньких углов.

6. Физпауза

Один ученик – 1 метр.

Построить прямоугольник с периметром 12 м.

(4 + 2) * 2 = 12

Построить квадрат с таким же периметром.

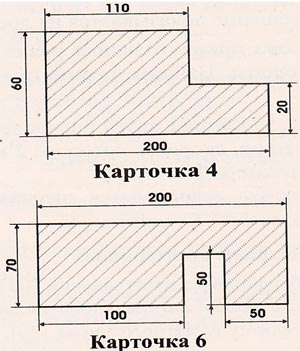
7. Практическая работа. Работа в группах. (приложение 3)

На партах фигуры. Найти периметр, сделав необходимые измерения.

8. Проверка знаний

Учитель: Проверим, как вы поняли новый материал.

Графический диктант (+ – да, – нет)

1. Прямоугольник – это четырёхугольник, в котором все углы прямые
2. Смежные стороны прямоугольника – это длина и ширина.
3. Периметр – это произведение сторон прямоугольника.
4. Диагональ – это отрезок, соединяющий две противоположные вершины прямоугольника.
5. Квадрат это прямоугольник с равными сторонами.

(Ответ:  ++-++)

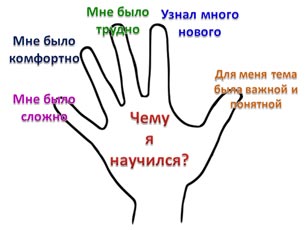
9. Рефлексия «Все в твоих руках» (слайд)

Ребятам предлагается обвести свою руку и выбрать нужный пальчик с надписью. На ладошке написать ответ на вопрос «Чему я научился на уроке?»

10. Оценивание. Выставление оценок

Кто работал лучше всех?

Учитель:

Окончен урок, и выполнен план.
Спасибо, ребята, огромное вам.
За то, что упорно и дружно трудились,
И знания точно уж вам пригодились.

11. Дом. задание

п. 7.2 №541

Дополнительное задание.

Сложите из спичек фигуру, изображенную на рисунке.

• Сколько здесь квадратов?  (5)
• Как убрать 2 спички, чтобы осталось 3 квадрата?
• Чтобы осталось 2 квадрата?

Прямоугольник –
это четырехугольник, у которого все углы являются прямыми.

Прямоугольник имеет четыре вершины, которые
обозначаются большими латинскими буквами. По этим вершинам обозначается и сам
прямоугольник, с какой вершины начать обозначение – не имеет значения, поэтому
один прямоугольник можно назвать четырьмя разными способами:

ABCD, BCDA, CDAB, DABC

У прямоугольника четыре стороны. Важным
свойством прямоугольника является равенство противоположных сторон.

Длины сторон помогаю найти периметр прямоугольника.
Чтобы найти периметр прямоугольника, надо сложить длины двух соседних сторон и
сумму увеличить в два раза.

P=2(a+b).

Площадь прямоугольника находится по формуле:

S=ab, где a и b— стороны
прямоугольника.

В любом прямоугольнике имеется две диагонали. Диагональ
– отрезок, соединяющий две несоседние вершины. Диагональ делит прямоугольник на
два равных треугольника.

Прямоугольник –
это четырехугольник, у которого все углы являются прямыми.

Прямоугольник имеет четыре вершины, которые
обозначаются большими латинскими буквами. По этим вершинам обозначается и сам
прямоугольник, с какой вершины начать обозначение – не имеет значения, поэтому
один прямоугольник можно назвать четырьмя разными способами:

ABCD, BCDA, CDAB, DABC

У прямоугольника четыре стороны. Важным
свойством прямоугольника является равенство противоположных сторон.

Длины сторон помогаю найти периметр
прямоугольника. Чтобы найти периметр прямоугольника, надо сложить длины двух
соседних сторон и сумму увеличить в два раза.

P=2(a+b).

Площадь прямоугольника находится по формуле:

S=ab, где a и b— стороны
прямоугольника.

В любом прямоугольнике имеется две диагонали. Диагональ
– отрезок, соединяющий две несоседние вершины. Диагональ делит прямоугольник на
два равных треугольника.

Прямоугольник –
это четырехугольник, у которого все углы являются прямыми.

Прямоугольник имеет четыре вершины, которые
обозначаются большими латинскими буквами. По этим вершинам обозначается и сам
прямоугольник, с какой вершины начать обозначение – не имеет значения, поэтому
один прямоугольник можно назвать четырьмя разными способами:

ABCD, BCDA, CDAB, DABC

У прямоугольника четыре стороны. Важным
свойством прямоугольника является равенство противоположных сторон.

Длины сторон помогаю найти периметр
прямоугольника. Чтобы найти периметр прямоугольника, надо сложить длины двух
соседних сторон и сумму увеличить в два раза.

P=2(a+b).

Площадь прямоугольника находится по формуле:

S=ab, где a и b— стороны
прямоугольника.

В любом прямоугольнике имеется две диагонали. Диагональ
– отрезок, соединяющий две несоседние вершины. Диагональ делит прямоугольник на
два равных треугольника.