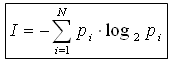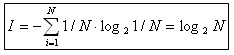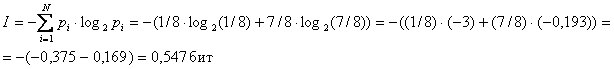Материал разработан на 2 спаренных урока.
Цели уроков: Сформировать у учащихся понимание вероятности, равновероятных событий и событий с различными вероятностями. Научить находить количество информации, используя вероятностный подход. Создать в Excel информационную модель для автоматизации процесса вычислений в задачах на нахождение количества информации, используя формулу Шеннона.
Требования к знаниям и умениям:
Учащиеся должны знать:
- какие события являются равновероятными, какие неравновероятными;
- как найти вероятность события;
- как найти количество информации в сообщении, что произошло одно из неравновероятных событий;
- как найти количество информации в сообщении, когда возможные события имеют различные вероятности реализации.
Учащиеся должны уметь:
- различать равновероятные и неравновероятные события;
- находить количество информации в сообщении, что произошло одно из равновероятных событий или одно из не равновероятных событий;
- создать информационную модель для автоматизации процесса решения задач на нахождение количества информации с помощью прикладных программ.
Оборудование: доска, компьютер, мультимедийный проектор, карточки с заданиями, карточки-памятки, справочный материал.
Урок 1. Вероятностный подход к определению количества информации. Формула Шеннона
Ход урока
I. Организационный момент.
II. Проверка домашнего задания.
III. Постановка цели урока.
Задача: Какое сообщение содержит большее количество информации?
- В библиотеке 8 шкафов. Книга нашлась в 3-м шкафу; (Отв.: 3 бит.)
- Вася получил за экзамен оценку 4 (по 5-бальной системе единицы не ставят). (Отв.: 2 бит.)
- Бабушка испекла 12 пирожков с капустой, 12 пирожков с повидлом. Маша съела один пирожок. (Отв.: 1 бит.)
- Бабушка испекла 8 пирожков с капустой, 16 пирожков с повидлом. Маша съела один пирожок.
Первые три варианта учащиеся решают без затруднения. События равновероятны, поэтому можно применить для решения формулу Хартли. Но третье задание вызывает затруднение. Делаются различные предположения. Роль учителя: подвести учащихся к осмыслению, что в четвертом варианте мы сталкиваемся с ситуацией, когда события неравновероятны. Не все ситуации имеют одинаковые вероятности реализации. Существует много таких ситуаций, у которых вероятности реализации различаются. Например, если бросают несимметричную монету или «правило бутерброда».
Сегодня на уроке мы должны ответить на вопрос: как вычислить количество информации в сообщении о неравновероятном событии.
IV. Объяснение нового материала.
Для вычисления количества информации в сообщении о неравновероятном событии используют следующую формулу: I=log2(1/p)
где I – это количество информации, р – вероятность события.
Вероятность события выражается в долях единицы и вычисляется по формуле: р=K/N,
где К – величина, показывающая сколько раз произошло интересующее нас событие, N – общее число возможных исходов какого-то процесса.
Вернемся к нашей задаче.
Пусть К1 – это количество пирожков с повидлом, К1=24
К2 – количество пирожков с капустой, К2=8
N – общее количество пирожков, N = К1 +К2=24+8=32
Вычислим вероятность выбора пирожка с разной начинкой и количество информации, которое при этом было получено.
Вероятность выбора пирожка с повидлом: р1=24/32=3/4=0,75.
Вероятность выбора пирожка с капустой: р2=8/32=1/4=0,25.
Обращаем внимание учащихся на то, что в сумме все вероятности дают 1.
Вычислим количество информации, содержащееся в сообщении, что Маша выбрала пирожок с повидлом: I1=log2(1/p1)= log2(1/0,75)= log21,3=1,15470 бит.
Вычислим количество информации, содержащееся в сообщении, если был выбран пирожок с капустой: I2=log2(1/p2)= log2(1/0,25)= log24=2 бит.
Пояснение: если учащиеся не умеют вычислять значение логарифмической функции, то можно использовать при решении задач этого урока следующие приемы:
- Ответы давать примерные, задавая ученикам следующий вопрос: «В какую степень необходимо возвести число 2, чтобы получилось число, стоящее под знаком логарифма?».
- Применить таблицу из задачника-практикума под редакцией Семакина И.Г. и др.
Приложение 1. «Количество информации в сообщении об одном из N равновероятных событий: I= log2N». (Приложение вы можете получить у автора статьи.)
При сравнении результатов вычислений получается следующая ситуация: вероятность выбора пирожка с повидлом больше, чем с капустой, а информации при этом получилось меньше. Это не случайность, а закономерность.
Качественную связь между вероятностью события и количеством информации в сообщении об этом событии можно выразить так: чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии.
Вернемся к нашей задаче с пирожками. Мы еще не ответили на вопрос: сколько получим информации при выборе пирожка любого вида?
Ответить на этот вопрос нам поможет формула вычисления количества информации для событий с различными вероятностями, которую предложил в 1948 г. американский инженер и математик К.Шеннон.
Если I-количество информации, N-количество возможных событий, рi — вероятности отдельных событий, где i принимает значения от 1 до N, то количество информации для событий с различными вероятностями можно определить по формуле:
можно расписать формулу в таком виде:
Рассмотрим формулу на нашем примере:
I = — (р1∙log2p1 + р2∙log2p2)= — (0,25∙ log20,25+0,75∙ log20,75)≈-(0,25∙(-2)+0,75∙(-0,42))=0,815 бит
Теперь мы с вами можем ответить на вопрос задачи, которая была поставлена в начале урока. Какое сообщение содержит большее количество информации?
- В библиотеке 8 шкафов. Книга нашлась в 3-м шкафу; (Отв.: 3 бит.)
- Вася получил за экзамен 3 балла (по 5-бальной системе единицы не ставят). (Отв.: 2 бит.)
- Бабушка испекла 12 пирожков с капустой, 12 пирожков с повидлом. Маша съела один пирожок. (Отв.: 1 бит.)
- Бабушка испекла 8 пирожков с капустой, 16 пирожков с повидлом. Маша съела один пирожок. (Отв.: 0,815 бит.)
Ответ: в 1 сообщении.
Обратите внимание на 3 и 4 задачу. Сравните количество информации.
Мы видим, что количество информации достигает максимального значения, если события равновероятны.
Интересно, что рассматриваемые нами формулы классической теории информации первоначально были разработаны для технических систем связи, призванных служить обмену информацией между людьми. Работа этих систем определяется законами физики т.е. законами материального мира. Задача оптимизации работы таких систем требовала, прежде всего, решить вопрос о количестве информации, передаваемой по каналам связи. Поэтому вполне естественно, что первые шаги в этом направлении сделали сотрудники Bell Telephon Companie – X. Найквист, Р. Хартли и К. Шеннон. Приведенные формулы послужили К. Шеннону основанием для исчисления пропускной способности каналов связи и энтропии источников сообщений, для улучшения методов кодирования и декодирования сообщений, для выбора помехоустойчивых кодов, а также для решения ряда других задач, связанных с оптимизацией работы технических систем связи. Совокупность этих представлений, названная К. Шенноном “математической теорией связи”, и явилась основой классической теории информации. (Дополнительный материал можно найти на сайте http://polbu.ru/korogodin_information или прочитав книгу В.И. Корогодин, В.Л. Корогодина. Информация как основа жизни. Формула Шеннона.)
Можно ли применить формулу К. Шеннона для равновероятных событий?
Если p1=p2=..=pn=1/N, тогда формула принимает вид:
Мы видим, что формула Хартли является частным случаем формулы Шеннона.
V. Закрепление изучаемого материала.
Задача: В корзине лежат 32 клубка красной и черной шерсти. Среди них 4 клубка красной шерсти.
Сколько информации несет сообщение, что достали клубок красной шерсти? Сколько информации несет сообщение, что достали клубок шерсти любой окраски?
Дано: Кк=4;N=32
Найти: Iк, I
Решение:
- Найдем количество клубков черной шерсти: Кч=N- Кк; Кч=32-4=28
- Найдем вероятность доставания клубка каждого вида: pк= Кк/N=4/32=1/8; pч= Кч/N=28/32=7/8;
- Найдем количество информации, которое несет сообщение, что достали клубок красной шерсти: Iк= log2(1/(1/ pк))= log2(1/1/8)= log28=3 бит
- Найдем количество информации, которое несет сообщение, что достали клубок шерсти любой окраски:
Ответ: Iк=3 бит; I=0,547 бит
VI. Подведение итогов урока.
Вопросы:
- Объясните на конкретных примерах отличие равновероятного события от неравновероятного?
- С помощью какой формулы вычисляется вероятность события.
- Объясните качественную связь между вероятностью события и количеством информации в сообщении об этом событии.
- В каких случаях применяется формула Шеннона для измерения количества информации.
- В каком случае количество информации о событии достигает максимального значения.
Урок 2. Применение ЭТ Excel для решения задач на нахождение количества информации
Пояснение: При решении задач на нахождение количества информации учащиеся не вычисляли значение логарифма, т.к. не знакомы с логарифмической функцией. Урок строился таким образом: сначала решались однотипные задачи с составлением формул, затем разрабатывалась табличная модель в Excel, где учащиеся делали вычисления. В конце урока озвучивались ответы к задачам.
Ход урока
I. Постановка целей урока
На этом уроке мы будем решать задачи на нахождение количества информации в сообщении о неравновероятных событиях и автоматизируем процесс вычисления задач данного типа.
Для решения задач на нахождение вероятности и количества информации используем формулы, которые вывели на прошлом уроке:
рi=Ki/N; Ii=log2(1/pi);
II. Решение задач.
Ученикам дается список задач, которые они должны решить.
Задачи решаются только с выводами формул, без вычислений.
Задача №1
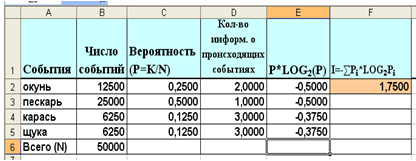
В озере обитает 12500 окуней, 25000 пескарей, а карасей и щук по 6250. Какое количество информации несет сообщение о ловле рыбы каждого вида. Сколько информации мы получим, когда поймаем какую-нибудь рыбу?
Дано: Ко=12500; Кп=25000; Кк= Кщ=6250
Найти: Iо, Iп, Iк, Iщ, I
Решение:
- Найдем общее количество рыбы: N= Ко+Кп+Кк+Кщ.
- Найдем вероятность ловли каждого вида рыбы: pо= Ко/N; pп= Кп/N; pк= pщ= Кк/N.
- Найдем количество информации о ловле рыбы каждого вида: Iо= log2( 1/pо); Iп=log2 (1/pп ); Iк= Iщ= log2 (1/pк )
- Найдем количество информации о ловле рыбы любого вида: I= pо∙log2pо+ pп∙log2pп +pк∙log2pк +pщ∙log2pщ
III. Объяснение нового материала.
Задается вопрос ученикам:
1. Какие трудности возникают при решении задач данного типа? (Отв.: Вычисление логарифмов).
2. Нельзя ли автоматизировать процесс решения данных задач? (Отв.: можно, т.к. алгоритм вычислений в этих задачах один и тот же).
3. Какие программы используются для автоматизации вычислительного процесса? (Отв.: ЭТ Excel).
Давайте попробуем сделать табличную модель для вычисления задач данного типа.
Нам необходимо решить вопрос, что мы будем вычислять в таблице. Если вы внимательно присмотритесь к задачам, то увидите, что в одних задачах надо вычислить только вероятность событий, в других количество информации о происходящих событиях или вообще количество информации о событии.
Мы сделаем универсальную таблицу, где достаточно занести данные задачи, а вычисление результатов будет происходить автоматически.
Структура таблицы обсуждается с учениками. Роль учителя обобщить ответы учащихся.
При составлении таблицы мы должны учитывать:
- Ввод данных (что дано в условии).
- Подсчет общего количества числа возможных исходов (формула N=K1+K2+…+Ki).
- Подсчет вероятности каждого события (формула pi= Кi/N).
- Подсчет количества информации о каждом происходящем событии (формула Ii= log2(1/pi)).
- Подсчет количества информации для событий с различными вероятностями (формула Шеннона).
Прежде чем демонстрировать заполнение таблицы, учитель повторяет правила ввода формул, функций, операцию копирования (домашнее задание к этому уроку).
При заполнении таблицы показывает как вводить логарифмическую функцию. Для экономии времени учитель демонстрирует уже готовую таблицу, а ученикам раздает карточки-памятки по заполнению таблицы.
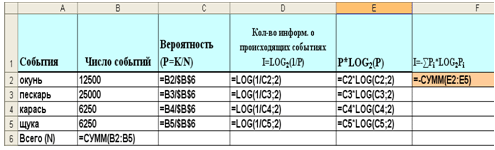
Рассмотрим заполнение таблицы на примере задачи №1.
Рис. 1. Режим отображения формул
Рис. 2. Отображение результатов вычислений
Результаты вычислений занести в тетрадь.
Если в решаемых задачах количество событий больше или меньше, то можно добавить или удалить строчки в таблице.
VI. Практическая работа.
1. Сделать табличную модель для вычисления количества информации.
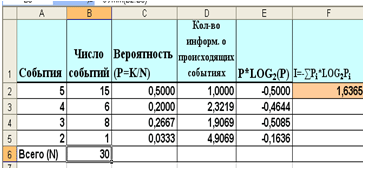
2. Используя табличную модель, сделать вычисления к задаче №2 (рис.3), результат вычисления занести в тетрадь.
Рис. 3
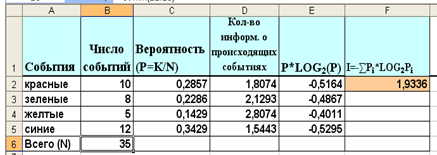
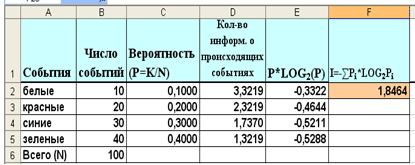
3. Используя таблицу-шаблон, решить задачи №3,4 (рис.4, рис.5), решение оформить в тетради.
Рис. 4
Рис. 5
4. Сохранить таблицы в своих папках под именем «инф_вероятность».
Задача №2
В классе 30 человек. За контрольную работу по информатике получено 15 пятерок, 6 четверок, 8 троек и 1 двойка. Какое количество информации несет сообщение о том, что Андреев получил пятерку?
Задача№3
В коробке лежат кубики: 10 красных, 8 зеленых, 5 желтых, 12 синих. Вычислите вероятность доставания кубика каждого цвета и количество информации, которое при этом будет получено.
Задача№4
В непрозрачном мешочке хранятся 10 белых, 20 красных, 30 синих и 40 зеленых шариков. Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика?
VII. Подведение итогов урока.
Учитель оценивает работу каждого ученика. Оценивается не только практическая работа на компьютере, но и оформление решения задачи в тетради.
VIII. Домашняя работа.
1. Параграф учебника «Формула Шеннона», компьютерный практикум после параграфа.
2. Доказать, что формула Хартли – частный случай формулы Шеннона.
Литература:
- Соколова О.Л. «Универсальные поурочные разработки по информатике. 10-й класс.» – М.: ВАКО, 2007.
- Угринович Н.Д. «Информатика и ИКТ. Профильный уровень. 10 класс» — Бином, Лаборатория знаний, 2007 г.
- Семакин И.Г., Хеннер Е.К. «Информатика. Задачник – практикум.» 1 том, — Бином, Лаборатория знаний, 2008 г.
пусть вероятность выпадения осадков в виде дождя равна (0,5), ветра — (0,25), грозы и молнии — (0,125). Определим, какое количество информации получим при реализации одного из них.
Решение.
Согласно формуле Шеннона получим:
I=−0,5⋅log20,5+0,25⋅log20,25+0,125⋅log20,125+0,125⋅log20,125==−−0,5−0,5−0,375−0,375=1,75.
Ответ: (1,75) бит.
Вероятностный подход к измерению информации
Существует три подхода к измерению информации: алфавитный, содержательный и вероятностный. Для того, чтобы изучить последний, необходимо ознакомиться с такой наукой, как теория вероятностей.
Теория вероятности – это раздел математики, изучающий случайные события.
Основным понятием в этой науке является вероятность события. Когда мы говорим о вероятности события, в обычной жизни мы подразумеваем некоторую меру возможности его возникновения. В теории вероятности есть четкое определение вероятности, которого нужно придерживаться. Допустим, у вас есть несколько исходов какого-то события, например, вы подбрасываете монету. Может выпасть орел, а может – решка, при этом монета идеальна и симметрична, и вероятность выпадения орла и решки одинакова (в теории вероятности говорят, что эти события «равновероятны»). В описанном нами случае вероятность каждого исхода равна 1/2. Интуитивно мы это понимаем, а с точки зрения теории вероятности это число получилось из определения вероятности события. По определению
Вероятность события равна количеству «нужных» исходов, деленному на количество всех возможных:
(Вероятность = frac{Количество подходящих вариантов}{Количество всех возможных вариантов})
Вероятность изменяется в пределах от 0 до 1.
Пример. Кидают игральный кубик. Какова вероятность, что выпадет четное число?
Решение:
Всего исходов 6 (6 сторон кубика), а нужных нам – 3 (2, 4, 6).
Вероятность = 3/6 = 1/2.
Пример. В вагоне поезда 20 мест. Вам выдают билет случайным образом. На кассе сказали, что вероятность того, что вы получите место у окна, равна 2/5. Сколько мест у окна в вагоне?
Решение:
Количество мест у окна – x. Вероятность равна x/20 = 2/5. Отсюда получаем x = 8.
Вероятность нескольких событий
Пускай есть не одна монета, а три. И мы подбрасываем их одновременно. Мы уже знаем, что для каждой монеты вероятность выпадения орла или решки равна 1/2. Найдем, чему равна вероятность того, что на всех трех монетах сразу выпадет орел.
Можем просто посчитать по известной нам формуле. При подбрасывании трех монет возможно всего 8 исходов: ооо, оор, оро, орр, роо, рор, рро, ррр.
Выпадение на всех трех монетах орла — это 1 исход. Получается, вероятность равна 1/8.
А сейчас посчитаем, чему равна вероятность выпадения орла хотя бы на одной монете?
Выпадение хотя бы на одной орла — это 7 исходов (все ситуации, кроме ррр). Как видите, такой способ считать вероятность составных событий не очень удачный. В теории вероятности есть правила, которые позволяют избежать таких сложностей.
События происходят одновременно
Если необходимо найти вероятность И первого, И второго, И третьего … событий (т.е. вероятность одновременного выполнения исходов), то вероятности перемножаются.
Вернемся к примеру с подбрасыванием трех монет.
Вероятность выпадения орла на каждой монете отдельно равна 1/2, значит, вероятность одновременного выполнения этих трех событий равна 1/2 × 1/2 × 1/2 = 1/8.
Должно произойти хотя бы одно из нескольких событий
Если необходимо найти вероятность ИЛИ первого, ИЛИ второго, ИЛИ третьего … событий (т.е. вероятность выполнения хотя бы исходов), то вероятности складываются.
Это правило хорошо иллюстрируется тем, как мы считали вероятность того, что орел выпадет хотя бы на одной монете. Вероятность каждого из исходов (ооо, оор, оро, орр, роо, рор, рро, ррр) была равна 1/8, а всего их 7. Складываем 1/8 7 раз и получаем 7/8.
Вероятность того, что произойдёт хотя бы одно из независимых событий, можно вычислить путём вычитания из 1 произведения вероятностей противоположных событий, то есть для примера нахождения вероятности выпадения орла хотя бы на одной монете достаточно решить выражение: 1 – 1/8 = 7/8. От единицы мы отняли вероятность неподходящего исхода (ррр), и получили тот же ответ.
Пример. Бросают два игральных кубика. Какова вероятность, что на обоих кубиках выпадет четное число?
Решение:
Вероятность того, что на каждом кубике в отдельности выпадет четное число, равна 1/2 (см. пример выше). По условию надо, чтобы события произошли одновременно, поэтому перемножаем вероятности и получаем 1/4.
Пример. Какова вероятность, что хотя бы на одном из двух кубиков выпадет четное число?
Решение:
Теперь нам подходят варианты, когда четное число: на первом ИЛИ на втором ИЛИ на обоих кубиках сразу. Вероятность каждого из этих событий в отдельности равна 1/4. Чтобы найти итоговую вероятность в этом случае, необходимо сложить вероятности трех перечисленных случаев: 1/4 + 1/4 + 1/4 = 3/4.
Сущность вероятностного подхода к измерению информации
Теория вероятности и теория информации тесно связаны. Когда мы узнаем о выполнении какого-то события, мы получаем определенную информацию, которую можно измерить.
Чем менее вероятно событие, тем более «ценно» оно с точки зрения информации.
Редкое событие несет больше информации, и наоборот, частое, вероятное событие – меньше. Это выражает следующая формула, которая связывает вероятность события с количеством информации, которое оно несет:
(2^{i} = frac{1}{p},)
где p — вероятность события, а i — количество информации (в бит).
Пример. В корзине есть 4 шара, из них 1 синий, остальные — красные. Наугад достают два шара. Какое количество информации несет в себе сообщение о том, что один из шаров — красный, а второй — синий?
Решение:
Сначала посчитаем вероятность. Вероятность достать красный шар: 3/4. Вероятность достать после этого синий шар: 1/3 (потому что шаров стало на 1 меньше).
Надо, чтобы эти события произошли вместе поэтому перемножаем вероятности и получаем: 3/4 × 1/3 = 1/4.
Теперь посчитаем количество информации:
2i = 1/(1/4).
Значит, 2i = 4, откуда i = 2 бита.


Данный урок хочу посвятить теме «Измерение информации».
Выделяют следующие подходы к определению количества информации:
- Вероятностный подход
- Равновероятностный
- Неравновероятностный
- Алфавитный подход
Данные подходы изучаются в школьном курсе информатики.
Вероятностный подход
Вероятностный подход связан с таким понятием как ВЕРОЯТНОСТЬ.
ВЕРОЯТНОСТЬ — это отношение количества тех наблюдений, при которых рассматриваемое событие наступило, к общему количеству наблюдений. Такая трактовка допустима в случае достаточно большого количества наблюдений или опытов.
Вероятность обозначают буквой p.

Единицы измерения информации: бит, байт, кбайт и т.д.
За 1 бит информации принимают такое количество информации, которое находится в сообщении о том, что произошло одно событие из двух равновероятных.
1 бит — это количество информации, уменьшающее неопределенность знаний в два раза.
При РАВНОВЕРОЯТНОСТНОМ ПОДХОДЕ вероятности наступления того или иного события равны.
Для измерения количества информации, полученной нами при равновероятном событии, используем формулу
(где N — количество возможных исходов события (2 стороны в примере с монеткой),
i — количество информации, которое мы получим, при том или ином исходе события)
Пример: Мы подбрасываем монетку. В большинстве своих случаев (не учитывает ребро) она может упасть либо на ОРЕЛ, либо на РЕШКУ. Вероятность наступления данных событий равны (5050) — т.е. это равновероятностный подход. 2 равновероятных события. Таким образом: 2=2i. i=1 биту. Это то количество информации, которое мы получим, когда монетка упадет, и мы узнаем, на какую сторона выпала (орел или решка).
Другие задачи с разбором и для самостоятельного решения на тему «Вероятностный подход к измерению информации» смотрите в следующих выпусках.
При НЕРАВНОВЕРОЯТНОСТНОМ ПОДХОДЕ вероятности исходов событий не равны.
Пример: В коробке 16 карандашей. Из них 8 синих, 4 красных, 4 зеленых. Вероятность достать из коробки синий карандаш больше, чем вероятность достать зеленый или красный.
Для измерения количества информации при неравновероятностном подходе используют следующие формулы:
(где К — количество интересующих нас событий (достать синий карандаш K=8), N — общее количество события)
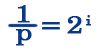
Вторая формула называется формулой Шеннона (правда в другом виде). В оригинале формула Шеннона выглядит так
Использование или неиспользовании этой формулы зависит от того, знают ли ученики про логарифм или нет.
Задача: В коробке 16 карандашей. Из них 8 синих, 4 красных, 4 зеленых. Сколько бит информации мы получим, вытащив из коробки синий карандаш?
Решение.
- Определим вероятность получения синего карандаша. Итак, количество интересующих нас событий (достать синий карандаш) равна 8. Общее количество событий равно 4+4+8=16.
- Вероятность p=8/16.
- Поставив получившееся значение в формулу 1/p=2i , получим: 2=2i.
- Получаем, что i=1 Биту.
Ответ: 1 бит информации мы получим, вытащив синий карандаш из коробки.
Продолжение рассмотрения этой темы смотрите в следующих постах.
Часть 2
Спасибо за внимание!
Вы можете оставить комментарий, или ссылку на Ваш сайт.
Оставить комментарий
Слайд 1
Вероятность в и н ф о р м а т и к е м а т е м а т и к е и ф и з и к е. Учебное пособие и приложение Курилов И.А. и Потапов Артем
Слайд 2
Что такое вероятность ? Относительная частота событий и ее свойства Вероятность события и его свойства Теорема о сложении вероятностей Условная вероятность Зависимые и независимые события . Теорема умножения вероятностей Формула полной вероятности и формула Байеса Вероятностный подход к измерению количества информации . Теория вероятностей на ЕГЭ по математике Вероятность в физике . Содержание
Слайд 3
Вероятность — численная мера возможности наступления некоторого события. Вероятность С практической точки зрения, вероятность события — это отношение количества тех наблюдений, при которых рассматриваемое событие наступило, к общему количеству наблюдений. Такая трактовка допустима в случае достаточно большого количества наблюдений и опытов . Например , если среди встреченных на улице людей примерно половина — женщины , то можно говорить , что вероятность того , что встреченный на улице человек окажется женщиной , равна 1 /2 . Другими словами, оценкой вероятности события может служить частота его наступления в длительной серии независимых повторений случайного эксперимента.
Слайд 4
Пусть проводится N испытаний , в каждом из которых может появиться или не появиться событие A . По завершении испытаний оказалось, что событие A наступило M раз. Свойства Относительная частота событий и ее свойства Определение. Относительной частотой (частостью) события называют число P*(A )= M/N где M- число появлений события A,N-общее число проведенных испытаний . Пример 1.Стрелок сделал 100 выстрелов по мишени и попал 90 раз. Пусть событие A = {попадание в мишень при одном выстреле}. Тогда P(A )=90/100=0.9 Пример 2.Посажено 70 плодовых деревьев, на другой год оказалось, что прижилось 5 0 . Событие A — {посаженное дерево приживается}. Получаем P(A )=50/70=0.71
Слайд 5
1 . Частость события — величина безразмерная и изменяется на множестве 2. Частость достоверного события равна 1 . 3. Частость невозможного события равна 0. 4. Частость случайного события изменяется на множестве (0, 1 ). Свойства 1 — 4 легко доказываются с помощью определения частоты и классификации событий. Так, например, пусть событие A достоверно . Это означает, что в серии из N испытаний оно наступило N раз Свойства частости события . [0,1]={P*(A):0 P*(A) 1}. P*(A)= =1
Слайд 6
Вероятностью события A называется отношение числа m равновозможных элементарных событий, благоприятных для A, к числу n всех возможных элементарных событий. Вероятность события A обозначают P(A ). Таким образом , Пример . Брошена игральная кость. Найти вероятность события A = {выпало четное число очков }. Решение . Элементарными событиями, благоприятными для A , являются события: А 1 = {выпадение 2 очков}, А 2 = {выпадение 4 очков}, А 3 = {выпадение 6 очков}. Всего таких событий 3.Имеется шесть элементарных событий, n = 6, следовательно, C войства вероятности события 1 ) . Так как , каково бы ни было по своей природе событие A . 2 ) . Если A — событие невозможное, то P(A ) = 0. 3 ) . Если B — событие достоверное, то P(B ) = 1 Пример по сложнее Вероятность события и его свойства P(A)= P(A)= = . 0≤m≤n, то 0≤P(A)≤1
Слайд 7
Пример. Найти вероятность события A= {выигрыш наибольшей суммы при игре в лото по 1 билету}, если для этого необходимо угадать 5 из 36 чисел . Решение. При наличии одного билета имеется одно благоприятное для A элементарное событие = {все 5 чисел угаданы правильно}, то есть m=1 Число n всех элементарных событий равно числу всевозможных групп из 5 чисел, отличающихся хотя бы одним числом, т. е. n P(A)= Число сочетаний из n по k равно биномиальному коэффициенту ( читается “ биномиальный коэффициент из n по k ”) (
Слайд 8
Суммой или объединением двух событий A и B называется событие C, состоящее в появлении хотя бы одного из них. Обозначают C=A+B или C=(A или B ). Вероятность наступления одного из двух несовместных событий равна сумме их вероятностей, т. е. P(A+B )=P(A)+P(B) Доказательство Теорема сложения для большего числа попарно несовместных событий формулируется и доказывается аналогично : P (A или, B или C) = P(A+B+C)=P(A)+P(B)+P(C). Следствие Теорема о сложении вероятностей Пример
Слайд 9
Пусть n- число всех возможных элементарных событий, при которых может наступить событие A или событие B . Пусть m A — число равновозможных элементарных событий, благоприятных для A, m B — такое же число для события B . Имеем Очевидно , m А +m В — число элементарных событий, благоприятных для появления события или A , или B , так что Теорема сложения для большего числа попарно несовместных событий формулируется и доказывается аналогично P(A или , B или C)=P(A+B+C) = P(A)+P(B)+P(C). Очевидно , m А +m В — число элементарных событий, благоприятных для появления события или A , или B , так что P(A)= ,P(B)= P(A или B)=P(A+B)=
Слайд 10
Следствие 1. Если события A, B, C образуют полную группу, то сумма их вероятностей равна 1. Действительно, в результате испытания обязательно произойдет из этих событий (или B, или A, или C). Поэтому A+B +C- событие достоверное и P(A+B+C)=1 Следствие 2 . Сумма вероятностей двух противоположных событий A и не A равна1. Противоположные события являются частным случаем событий, образующих полную группу, поэтому В частности, если вероятность попадания в мишень при одном выстреле равна 0,8, то вероятность промаха равна 1–0,8 = 0,2 . P(A)+P( A) =1 P( A)= 1- P(A).
Слайд 11
Очевидно , что по крайней мере одна из взятых деталей окажется стандартной, если произойдет любое из трех несовместных событий: B – одна деталь стандартная, две нестандартные; C – две детали стандартные, одна нестандартная и D – три детали стандартные . Таким образом, событие A можно представить в виде суммы этих трех событий: A=B+C+D . По теореме сложения имеем P(A)=P(B)+P(C)+P(D). Находим вероятность каждого из этих событий Сложив найденные величины, получим P(B)= P(C)= P(D)= P(A)= Пример.В ящике в случайном порядке разложены 20 деталей, причем пять из них стандартные. Рабочий берет наудачу три детали. Найти вероятность того, что по крайней мере она из взятых деталей окажется стандартной .
Слайд 12
Условная вероятность — вероятность наступления одного события при условии, что другое событие уже произошло . Условной вероятностью ( два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е. В частности, отсюда получаем формулы для условной вероятности: Пример Условная вероятность P(AB)=P(B)⋅P(A|B)=P(A)⋅P(B|A). P(A|B)= , P(B|A )= . (B)=P(B|A)
Слайд 13
Решение . Пусть А — событие, состоящее в том, что на линию вышел трамвай маршрута №1, В — маршрута №2. Рассмотрим все события, которые могут при этом быть (в условиях нашей задачи ): AA,AB,BA,BB . Из них нас будут интересовать только первое и третье, когда вторым выйдет трамвай маршрута №1. Так как все эти события совместны, то: отсюда искомая вероятность P(AA)=P(A) P(A | A)= ; P(BA )=P(B) P(A | B)= ; P=P(AA)+P(BA)= В трамвайном парке имеются 15 трамваев маршрута №1 и 10 трамваев маршрута №2. Какова вероятность того, что вторым по счету на линию выйдет трамвай маршрута №1 ?
Слайд 14
Вероятность произведения двух независимых событий А,В равна произведению их вероятностей : События А, В называются зависимыми , если вероятность каждого из них зависит от того, произошло или нет другое событие. Вероятность события В, вычисленная в предположении, что другое событие А уже осуществилось, называется условной вероятностью . Вероятность произведения двух зависимых событий А, В равна произведению вероятности одного из них на условную вероятность другого : Вероятность события В при условии появления события А : Зависимые и независимые события Р(В) = Р(В | А), Р(А) = Р(А | В) или Р(В | А) – Р(В) = 0 Р(АВ) = Р(А) P (В) P(A В) = Р(В) Р(А | В) или Р(АВ) = Р(А) Р(В | А) Р( B | A ) = События А,В называются независимыми , если вероятности каждого из них не зависит от того, произошло или нет другое событие.Вероятности независимых событий называются безусловными. Если два события А и В – независимые, то справедливы равенства:
Слайд 15
Теорема умножения вероятностей Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило : Пример 1 .В корзине 7 яблок, 3 груши и 4 апельсина. Наудачу взяли 3 раза по фрукту. Найти вероятность того, что фрукты были взяты в последовательности: яблоко, груша, апельсин . Пример 2.Имеем 2 урны с шарами: в первой 20 шаров, из них 1 1 окрашенных , во второй 30 шаров, из них 21 окрашенных . Взяли по одному шару из каждой урны. А – оба шара окрашены. Найти P(A). Решение. P(A)= , (B)= , (C)= P(A)=P( ) P( )=
Слайд 16
Вероятность хотя бы одного появления события А в n испытаниях . Если имеется n испытаний, вероятность появления события A в каждом из которых одинакова и равна P(A) , то вероятность появления хотя бы одного из этих событий вычисляется по формуле : где q – вероятность противоположного к A события . Пример . Стрелок 4 раза стреляет по мишени ( n=4 ); вероятность попадания при каждом выстреле p=0.8 . Найти вероятность хотя бы одного попадания . Решение . P(A)=1-
Слайд 17
Формула полной вероятности и формула Байеса Если событие А может произойти только при выполнении одного из событий , которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле Эта формула называется формулой полной вероятности . Событие А может произойти только вместе с каким-либо из событий , которые будем называть гипотезами. Тогда по формуле полной вероятности Если событие А произошло, то это может изменить вероятности гипотез . По теореме умножения вероятностей откуда Аналогично, для остальных гипотез Полученная формула называется формулой Байеса Пример P(A)=P( P P( +…+P( P( ). , ,…, P( P( ) P =P(A) P , P( A)= , i=1,…,n. P( A)=
Слайд 18
В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% — продукция первого предприятия, 30% — продукция второго предприятия, 50% — продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии — 5% и на третьем — 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта. Решение . Обозначим через В событие, заключающееся в том, что будет куплена продукция высшего сорта, через обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям. Можно применить формулу полной вероятности : Подставляя эти значения в формулу полной вероятности, получим искомую вероятность : P( )=0.2 P =0.1 P( P P( )=0.5 P =0.2 P(B)=0.2 0.1+0.3 0.05+0.5 0.2=0.135 , ,
Слайд 19
Сообщение является информативным, если оно пополняет нас знаниями или уменьшает неопределенность наших знаний. Пример 1 . Мы бросаем монету и пытаемся угадать. Какой стороной она упадет. Возможен один результат из двух, перед броском существует неопределенность знаний. После броска наступает полная неопределенность знаний. Так как из двух равновероятных событий произошло одно, то неопределенность наших знаний уменьшилось в 2 раза. Пример 2 . вытягивание билета на экзамене. Количество информации, которое находится в сообщении о том, что произошло одно событие из двух равновероятных, принято за единицу измерения информации и равно 1 биту . 1 бит – это количество информации, уменьшающее неопределенность наших знаний в 2 раза. Существует формула, которая связывает между собой количество возможных событий и количество информации. , где N — количество возможных вариантов , I – количество информации . Если из этой формулы можно выразить количество информации, то получится Вероятностный подход к измерению количества информации в информатике Задачи N=2 I I=log 2 N
Слайд 20
1.Какое количество информации несет сообщение о результате жребия при бросании монеты (например, выпал орел )? Решение. Можно выбрать один вариант из двух возможных (орел или решка) Ответ 1 бит (так как = 2 ) 2 . В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержит сообщение о первом выпавшем номере (например, выпал номер 15) Решение. выбрали один вариант из 32 =32 Ответ 5 3. В школьной библиотеке 16 стеллажей с книгами. На каждом стеллаже 8 полок. Библиотекарь сообщил Пете, что нужная ему книга находится на пятом стеллаже на третьей сверху полке. Какое количество информации библиотекарь передал Пете? Решение : существует 16*8 = 128 вариантов местонахождения книги. Из этого количеств вариантов необходимо выбрать один. Следовательно, N = 128, а I = 7, т.к. 128 = Ответ: 7 бит. 2 1 2 5 2 7
Слайд 21
Случай, при котором события неравновероятны Неравновероятные события — это события, вероятность появления которых зависит от условий проведения эксперимента Для вычисления количества информации в сообщении о неравновероятном событии используют следующую формулу: ( формула Шеннона) где I – это количество информации, р – вероятность события. Задача . Бабушка испекла 8 пирожков с капустой, 16 пирожков с повидлом. Маша съела один пирожок. Какое количество информации несет сообщение о том что Маша съела пирожок с капустой . Мы сталкиваемся с ситуацией, когда события неравновероятны. Вероятность выбора пирожка с капустой: Вычислим количество информации, содержащееся в сообщении, если был выбран пирожок с капустой: При сравнении результатов вычислений получается следующая ситуация: вероятность выбора пирожка с повидлом больше, чем с капустой, а информации при этом получилось меньше. Это не случайность, а закономерность. Качественную связь между вероятностью события и количеством информации в сообщении об этом событии можно выразить так: чем меньше вероятность некоторого события,тем больше информации содержит сообщение об этом событии . I=log 2 (1/p) р= = =0,25. =log 2 ( )= log 2 (1/0,25)= log 2 4=2 бит.
Слайд 22
Задачи по теории вероятностей, входящие в сборники для подготовки к ЕГЭ по математике. 1.Ученика попросили назвать число от 1 до 100 . Какова вероятность того, что он назовет число кратное пяти? 1 ,2,3,4,5,6…100 Каждое пятое число из данного множества делится на 5 . Значит, вероятность равна . 2.Брошена игральная кость. Найдите вероятность того, что выпадет нечетное число очков. 1,3,5 — нечетные числа; 2,4,6 — четные. Вероятность нечетного числа очков равна . Ответ : .
Слайд 23
3.Монета брошена три раза. Какова вероятность выпадение двух орлов и одной решки ? Задачу можно сформулировать по-другому: бросили три монеты одновременно. На решение это не повлияет. Бросаем монету. У этого действия два возможных исхода: орел и решка Две монеты — уже четыре исхода: ОО РО ОР РР Три монеты -8 исходов так как = 8 ООО ОРО ОРР РРО ООР РОО РОР РРР Два орла и одна решка выпадают в трех случаях из восьми. Ответ : = 0.375 2 3
Слайд 24
4.В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах. Мы знаем, что вероятность события равна отношению числа благоприятных исходов к общему числу исходов. Но как посчитать все эти исходы ? Кодируем монеты числами: 1 , 2 (это пятирублёвые), 3,4,5,6 (это десятирублёвые). Запишем, что у нас в первом кармане. Для этого составим все возможные комбинации из набора 123456 . Набор из трёх цифр будет трёхзначным числом. Очевидно, что в наших условиях 123 и 231 — это один и тот же набор цифр. Чтобы ничего не пропустить и не повториться, располагаем соответствующие трехзначные числа по возрастанию:
Слайд 25
123 ,124,125,126,134,135,136,145,146,156 Мы перебрали все возможные комбинации, начинающиеся на 1 . 234,235,236,245,246,256,345,346,356,456 . Всего 20 возможных исходов. У нас есть условие —цифры с номерами 1 и 2 не должны оказаться вместе. Это значит, например, что комбинация 356 нам не подходит — она означает, что цифры 1 и 2 обе оказались в не в первом, а во втором кармане . Благоприятные для нас исходы — такие, где есть либо только 1, либо только 2. Вот они: 134, 135, 136, 145, 146, 156, 234, 235, 236, 245, 246, 256 – всего 12 благоприятных исходов. Тогда искомая вероятность равна Ответ: . .
Слайд 26
5.Чтобы поступить в институт на специальность “ Лингвистика ” , абитуриент З. должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность “ Коммерция ” , нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание. Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0. 6, по русскому языку — 0 . 8, по иностранному языку — 0 . 7 и по обществознанию — 0 . 5 . Найдите вероятность того, что абитуриент З , сможет поступить хотя бы на одну из двух упомянутых специальностей . В задаче не спрашивается, будет ли абитуриент З , учиться и на лингвистике, и на коммерции сразу и получать два диплома. Здесь надо найти вероятность того, что абитуриент З , сможет поступить хотя бы на одну из двух данных специальностей – то есть наберет необходимое количество баллов.
Слайд 27
Для того чтобы поступить хотя бы на одну из двух специальностей, абитуриент З. должен набрать не менее 70 баллов по математике. И по русскому. И еще – обществознания или иностранный язык. Вероятность набрать 70 баллов по математике для него равна 0 . 6. Вероятность набрать баллы по математике и русскому равна 0 . 6• 0 . 8. Для иностранного языка и обществознания н ам подходят варианты, когда абитуриент набрал баллы по обществознанию, по иностранному языку или по обоим. Не подходит вариант, когда ни по иностранному языку, ни по обществознанию он не набрал баллов. Значит, вероятность сдать обществознание или иностранный язык не ниже чем на 70 баллов равна 1 – 0 . 5 • 0 . 3. В результате вероятность сдать математику, русский и обществознание или иностранный равна 0 . 6 • 0 . 8 • (1 — 0 . 5 • 0 . 3) = 0 . 408 Ответ : 0.408
Слайд 28
Понятие вероятности появилось в физике в связи с развитием кинетической теории газов. Когда было установлено, что газ состоит из большого числа движущихся частиц, то возник вопрос о том, с какими скоростями движутся частицы газа — его молекулы . Вероятность в физике. Английский физик Дж. Максвелл построил первую теорию идеального газа, в которой состояние газа задавалось не положением и скоростью каждой частицы, а функцией распределения — вероятностью найти молекулу с заданной скоростью в заданном месте сосуда.
Слайд 29
Из теории Максвелла следовало, что большая часть молекул газа имеет скорость где k — постоянная Больцмана, Т — абсолютная температура, m — масса молекул Это значение называют наиболее вероятной скоростью. Понятие вероятности оказалось очень плодотворным. С ее помощью можно рассчитывать различные процессы, в которых участвуют много частиц и в которых роль отдельных частиц становится незаметной. Это такие процессы, как теплопроводность, перемешивание — диффузия, химические реакции и многие другие. Их изучает статистическая физика . *Оказалось , однако, что даже для одной определенной частицы нельзя точно измерить координату и импульс одновременно и что результат опыта можно предсказать только в вероятностной форме . v= ( Из графика видно, что наибольшее число молекул обладает среднестатистической скоростью!
Слайд 30
Пример: Так как нет возможности точно измерить траекторию частицы, значит, нельзя и дать точный ответ на вопрос о том, на какой угол отклонится летящий протон в поле атомного ядра. Можно лишь указать вероятность его отклонения на тот или иной угол. Нельзя сказать также, когда распадается определенный радиоактивный атом, можно лишь указать вероятность того, что он распадается через t секунд. В таблицах пишут, например, что скорость света равна величина в скобках называется стандартным отклонением. В данном случае из теории вероятности следует, что истинная скорость света не может отличаться от написанной более чем на 1,2 единицы в последнем знаке с вероятностью 68,3%. Дело в том, что в любом опыте существует большое количество неучтенных факторов. В случае скорости света такими факторами могут быть непостоянство температуры, неточность в измерении длины волны и т. д., но они могут сказываться лишь в восьмом знаке после запятой. Степень достоверности этого утверждения и оценивается вероятностью . Теория вероятности очень важна при вычислении достоверных значений основных физических величин. 2,997924580(1,2)•10 8 м/с;