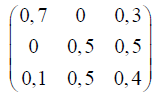МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное
государственное автономное образовательное
учреждение
высшего
профессионального образования
«САНКТ-ПЕТЕРБУРГСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
АЭРОКОСМИЧЕСКОГО
ПРИБОРОСТРОЕНИЯ
КАФЕДРА
«Прикладной математики»
Лабораторная
работа
защищена
с оценкой
Руководитель
|
Ст. |
Соколовская |
|||
ОТЧЕТ
О ЛАБОРАТОРНОЙ РАБОТЕ
«Определение
количества информации, содержащегося
в
сообщении»
ВАРИАНТ
№8
по
дисциплине: ИНФОРМАТИКА
Работу
выполнил(а)
|
студент(ка) |
М453кс |
21.11.14 |
Григорьев |
||
Санкт-Петербург
2014
-
Цель
работы
Получение
практических навыков численного
определения количества
информации,
содержащейся в сообщении.
-
Таблица
№1
|
№ п/п |
Символ |
Код |
Число |
Вероятность |
Ii |
Pi*Ii |
|
1 |
0 |
48 |
0 |
0 |
0 |
0 |
|
2 |
1 |
49 |
659 |
0,0564792595 |
4,1461350159 |
0,2341706355 |
|
3 |
2 |
50 |
657 |
0,0563078505 |
4,1505201106 |
0,233706866 |
|
4 |
3 |
51 |
379 |
0,0324820021 |
4,9442156327 |
0,1605980224 |
|
5 |
4 |
52 |
279 |
0,023911553 |
5,3861483591 |
0,1287911718 |
|
6 |
5 |
53 |
159 |
0,0136270141 |
6,1973867156 |
0,0844518759 |
|
7 |
6 |
54 |
158 |
0,0135413096 |
6,2064889227 |
0,0840439878 |
|
8 |
7 |
55 |
105 |
0,0089989715 |
6,7960241532 |
0,061157228 |
|
9 |
8 |
56 |
305 |
0,0261398697 |
5,2576042384 |
0,1374330899 |
|
10 |
9 |
57 |
371 |
0,0317963661 |
4,9749942943 |
0,1581867401 |
|
11 |
А |
192 |
5127 |
0,4394069249 |
1,1863704885 |
0,5212994082 |
|
12 |
Б |
193 |
714 |
0,0611930065 |
4,0304894069 |
0,2466377645 |
|
13 |
В |
194 |
3073 |
0,2633699006 |
1,9248376193 |
0,5069442924 |
|
14 |
Г |
195 |
853 |
0,0731059308 |
3,7738677396 |
0,2758921136 |
|
15 |
Д |
196 |
2156 |
0,1847788824 |
2,4361282081 |
0,4501450477 |
|
16 |
Е |
197 |
6469 |
0,5544223517 |
0,8509426735 |
0,4717816382 |
|
17 |
Ё |
168 |
0 |
0 |
0 |
0 |
|
18 |
Ж |
198 |
252 |
0,0215975317 |
5,5329897474 |
0,1194989215 |
|
19 |
З |
199 |
1040 |
0,0891326706 |
3,4879018579 |
0,3108860072 |
|
20 |
И |
200 |
6005 |
0,5146554679 |
0,9583211403 |
0,4932052149 |
|
21 |
Й |
201 |
763 |
0,0653925266 |
3,9347304241 |
0,2573019638 |
|
22 |
К |
202 |
1756 |
0,150497086 |
2,7321925414 |
0,411187016 |
|
23 |
Л |
203 |
2477 |
0,212290024 |
2,2358915177 |
0,4746574639 |
|
24 |
М |
204 |
2142 |
0,1835790195 |
2,4455269061 |
0,4489474317 |
|
25 |
Н |
205 |
4952 |
0,424408639 |
1,2364740717 |
0,5247702779 |
|
26 |
О |
206 |
5731 |
0,4911724374 |
1,02569849 |
0,5037948274 |
|
27 |
П |
207 |
1862 |
0,1595817621 |
2,6476323133 |
0,4225138299 |
|
28 |
Р |
208 |
3963 |
0,3396468975 |
1,5578924189 |
0,5291333267 |
|
29 |
С |
209 |
3389 |
0,2904525197 |
1,7836257494 |
0,5180585931 |
|
30 |
Т |
210 |
3929 |
0,3367329448 |
1,5703232184 |
0,5287795616 |
|
31 |
У |
211 |
1282 |
0,1098731574 |
3,1860891243 |
0,3500656717 |
|
32 |
Ф |
212 |
408 |
0,0349674323 |
4,8378443289 |
0,169166994 |
|
33 |
Х |
213 |
873 |
0,0748200206 |
3,7404318273 |
0,2798591863 |
|
34 |
Ц |
214 |
439 |
0,0376242715 |
4,7321925414 |
0,178045297 |
|
35 |
Ч |
215 |
1232 |
0,1055879328 |
3,2434831302 |
0,3424726788 |
|
36 |
Ш |
216 |
205 |
0,0175694206 |
5,8307895714 |
0,1024435946 |
|
37 |
Щ |
217 |
156 |
0,0133699006 |
6,224867452 |
0,083225859 |
|
38 |
Ъ |
218 |
71 |
0,0060850189 |
7,3605225514 |
0,0447889185 |
|
39 |
Ы |
219 |
1298 |
0,1112444292 |
3,1681950029 |
0,3524440447 |
|
40 |
Ь |
220 |
904 |
0,0774768598 |
3,6900907085 |
0,2858966404 |
|
41 |
Э |
221 |
299 |
0,0256256428 |
5,2862679967 |
0,1354640153 |
|
42 |
Ю |
222 |
313 |
0,0268255057 |
5,220250824 |
0,140035868 |
|
43 |
Я |
223 |
1546 |
0,132499143 |
2,915945067 |
0,3863602223 |
|
44 |
. |
46 |
2531 |
0,2169180665 |
2,2047778788 |
0,4782561545 |
|
45 |
, |
44 |
1019 |
0,0873328762 |
3,5173313347 |
0,3071786622 |
|
46 |
: |
58 |
371 |
0,0317963661 |
4,9749942943 |
0,1581867401 |
|
47 |
; |
59 |
80 |
0,0068563593 |
7,188341576 |
0,0492858524 |
|
48 |
— |
45 |
100 |
0,0085704491 |
6,8664134811 |
0,0588482472 |
|
49 |
32 |
11668 |
1 |
0 |
0 |
|
|
50 |
( |
40 |
277 |
0,023740144 |
5,3965275048 |
0,12811434 |
|
Всего |
84797 |
7,2674837161 |
||||
|
Полная |
||||||
|
Энтропия |
13,3281133049 |
-
Таблица
2
-
Рабочие
формулы:
Ii=-log2pi
Ii
— количество информации; p-вероятность
вхождения символа;
D=(Hmax-H)/Hmax
Hmax—
максимальное значение энтропии; D
—относительная избыточность;
Dabc=Hmax-H
Dabc—
абсолютная избыточность;
Pi
= ki/K
Pi
–
вероятность вхождения символа в текст,
ki
— число вхождений символов в текст, K
— всего символов в текст;
Iср=
Iср
=∑ pi
(-log2
pi)
= H
—
энтропия источника;
H1
= loga
N
– Исходная неопределенность по методы
Хартли
N—
число возможных значений принятого
слова после получения сообщения;
Разрядность
–
округление неопределенности (ROUNDUP)
-
Вывод:
По
итогам лабораторной работы я получил
практические навыки численного
определения количества информации,
содержащегося в сообщении. Также можно
сделать вывод, что в разных алфавитах,
на примере рассмотренных стандартной
кодовой таблицы ASCII
и меры Хартли их неопределенность,
разрядность кода, абсолютная избыточность
и относительная избыточность отличаются.
Если нам не известен алфавит, то нужно
использовать стандартную кодовую
таблицу ASCII, а если не известен, то нужно
использовать меру Хартли.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Помогаю со студенческими работами здесь
Подсчитать число вхождений каждого символа в файл
Дан символьный файл f Подсчитать число вхождений в файл каждой из букв a, b, c, d, e, f и вывести…
Подсчитать количество вхождений каждого символа в строку
например у Вас есть строка:
asddsg
В выходной файле, куда Вы запишите результаты работы программы…
Подсчитать количество появлений каждого символа в файле
Написать программу, которая считывает текстовый файл и подсчитывает число появлений в нем каждого…

Для каждого символа заданного текста указать сколько раз он встречается в тексте на С++
Искать еще темы с ответами
Или воспользуйтесь поиском по форуму:
2
Информационные веса символов алфавита и вероятность
Кудрявцева Е.В.,
учитель информатики
гимназии №4 г. Перми
Символы в тексте встречаются с одинаковой частотой?
Как рассчитать частоту появления определенного символа в естественном языке?
Кол-во вхождений данного символа
Частота =
Кол-во всех символов текста
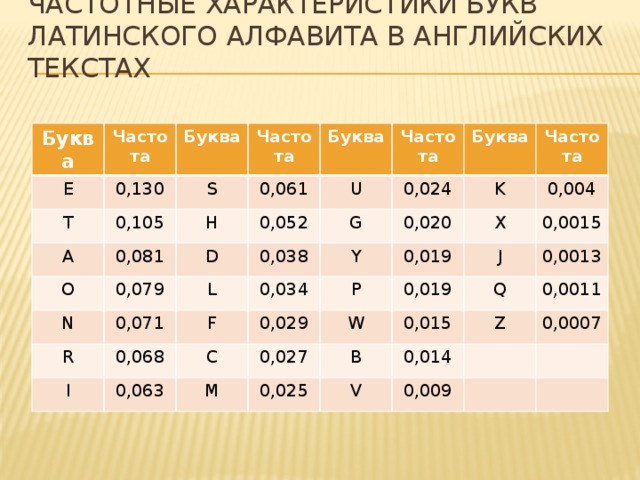
Частотные характеристики букв латинского алфавита в английских текстах
Буква
Частота
E
0,130
T
Буква
Частота
A
S
0,105
0,081
0,061
O
H
Буква
D
0,079
U
N
0,052
Частота
0,038
0,071
0,024
Буква
R
G
L
0,068
Частота
I
Y
0,020
0,034
F
K
0,063
0,029
0,019
0,004
P
C
X
0,0015
0,019
W
J
0,027
M
0,0013
0,015
0,025
Q
B
V
0,0011
0,014
Z
0,0007
0,009
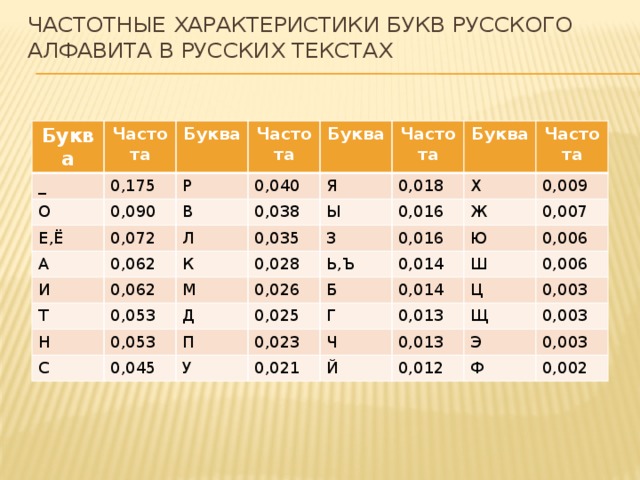
Частотные характеристики букв русского алфавита в русских текстах
Буква
_
Частота
0,175
Буква
О
Частота
Р
Е,Ё
0,090
0,072
0,040
Буква
В
А
Л
И
0,038
0,062
Я
Частота
0,062
0,018
0,035
Ы
Буква
К
Т
0,053
М
Н
0,028
0,016
Х
З
Частота
0,053
0,009
0,026
0,016
Ж
С
Ь,Ъ
Д
0,045
0,007
0,014
Б
0,025
Ю
П
0,014
0,023
0,006
У
Г
Ш
0,013
Ч
Ц
0,006
0,021
0,003
0,013
Щ
Й
0,003
Э
0,012
0,003
Ф
0,002
Информационный вес символа с учетом вероятности его появления в тексте
i = log 2 (1/P)
Р – вероятность появление данного символа
Для буквы «О»: i = log 2 (1/0,09) = 3,47 бита
Для буквы «Ф»: i = log 2 (1/0,002) = 8,97 бита
! Чем реже встречается символ, тем больше информации
несет его появление.
Пример
Вычислите информационный объем слова «десятиклассник» с учетом частотных характеристик символов. Произведите вычисления с помощью электронных таблиц.
Клод элвуд шеннон (1916-2001)
- Решил проблему неизмеряемости информации.
- Основал теорию информации.
- Предложил слово «бит» для наименьшей единицы измерения информации.
Формула Шеннона
H = P 1 log 2 (1/P 1 ) + P 2 log 2 (1/P 2 ) +…+ P N log 2 (1/P N )
H – средняя информативность символа в алфавите
P k – вероятность (частота) встречаемости k-ого символа
N – мощность алфавита
Для русского языка средняя информативность символа равна 4,36 бита.
? Для английского языка вычислите самостоятельно с помощью MS Excel
Домашнее задание
Читать §1.2.1 и 1.2.3,
Упражнения 8, 9 после §1.2.3
Насколько возможен снегопад? Какова вероятность выиграть в лотерею? Возможность, шанс, вероятность – эти слова мы произносим ежедневно. Они же являются терминами математической теории вероятности.
Математическая теория вероятности вышла на первый план в XVII веке – в дискуссиях об игре в кости.
Вероятность — очень лёгкая тема, если концентрироваться на смысле задач, а не на формулах. Во-первых, что такое вероятность? Это шанс, что какое-то событие произойдёт. Если мы говорим, что вероятность некоторого события 50%, что это значит? Что оно либо произойдет, либо не произойдет — одно из двух. Т.е. подсчитать значение вероятности очень просто — нужно взять количество подходящих нам вариантов и разделить на количество всех возможных вариантов.
Возьмем самый простой пример – подбросим монету. Какова вероятность, что выпадет «орел»? Ответ очевиден – ½. Когда мы говорим, что подбрасываем монету, мы предполагаем, что это симметричная монета, что вероятность выпадения «орла» равна вероятности выпадения «решки». Мы выяснили, что шанс получить «решку» при подбрасывании монеты это ½. Как мы получаем ½? Всего у нас два возможных варианта (орёл и решка), из них нам подходит один (решка), так мы и получаем вероятность ½.
Зафиксируем формулу для нахождения вероятности:
$ Вероятность= frac {количество; подходящих; вариантов}{количество; возможных; вариантов}$
Вероятность может выражаться в процентах:
$ Вероятность ; 100 (%)= frac {количество; подходящих; вариантов}{количество; возможных; вариантов} cdot 100% $
Важно: на экзамене вам нужно будет записать ответ в числах, не в процентах.
Пример: в урне 10 шаров: 6 белых и 4 черных. Какова вероятность вынуть из урны черный шар?
Решение. Что необходимо для нахождения вероятности? Посчитать количество подходящих вариантов и количество возможных вариантов. Всего шаров – 10, подходящих (т.е. черных) – 4, значит:
$ Вероятность ;=frac {4}{10}=0,4 $
Принято, что вероятность изменяется от 0 (никогда не произойдет – невозможное событие) до 1 (абсолютно точно произойдет – достоверное событие).
Пример: в урне 12 шаров: 6 белых и 6 черных. Какова вероятность вынуть из урны красный шар?
Решение. Интуитивно понятно, что поскольку в урне нет красных шаров, то и вероятность равна нулю. Давайте посчитаем количество подходящих вариантов и количество возможных вариантов. Всего шаров – 10, подходящих (т.е. красных) – 0, значит:
$ Вероятность ;=frac {0}{10}=0 $
В рассмотренном примере событие, заключающееся в вынимании красного шара, невозможное.
Зафиксируем еще одну формулу:
Вероятность подходящих событий + вероятность неподходящих событий = 1
Пример: найдите вероятность того, что при однократном подбрасывании игрального кубика выпадет число, не кратное трем.
Решение. Давайте найдем вероятность противоположного события, что выпадет число, кратное трем. Сколько подходящих событий? Количество подходящих событий (выпадет три, выпадет шесть) – 2, всего событий – 6 (граней на игральном кубике).
$ Вероятность ;(кратно;3)=frac {2}{6}=frac {1}{3} $
Значит, мы можем найти искомую вероятность:
$ Вероятность ;(не кратно;3)=1-frac {1}{3}=frac {2}{3} $
Теперь мы точно понимаем, как считать вероятность отдельного события, но понятно, что на этом всё не заканчивается. Чтобы жизнь была веселее, в задачах на вероятность обычно происходят как минимум два события, и надо посчитать вероятность с учетом каждого из них.
Вероятность нескольких событий:
Подсчитываем вероятность каждого события в отдельности, затем между дробями ставим знаки:
1. Если нужно первое И второе событие, то умножаем.
2. Если нужно первое ИЛИ второе событие, то складываем (если события не могут совпасть).
Пример. Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны P1=0,7, P2=0,6. Какова вероятность попадания обоими орудиями одновременно при одном залпе?
Решение. Вероятности каждого из событий в отдельности уже даны, нужно только понять, какой знак поставить. Нам нужно, чтобы произошло первое и второе событие одновременно, значит, умножаем.
P= P1· P2 = 0,7· 0,6 = 0,42.
Пример. Вероятность того, что в магазине будет продана пара мужской обуви 44-го размера, равна 0,12, 45-го – 0,04, 46-го и большего – 0,01. Какова вероятность того, что будет продана пара мужской обуви не меньше 44-го размера?
Решение. Снова вероятности каждого из событий нам даны. Что будем делать с ними? Нам подходят события: продана обувь 44-го размера ИЛИ продана обувь 45-го размера ИЛИ продана обувь 46-го и выше размеров. Значит, складываем вероятности каждого из событий:
P = 0,12 + 0,04 + 0,01 = 0,17.
Для понимания практического применения теории вероятности давайте рассмотрим еще вот такой шуточный пример. В местном зоопарке живет мартышка (можно дать ей имя). Допустим, что у нее есть старенькая пишущая машинка с 26 клавишами для букв латинского алфавита, одна – с точкой, одна – с запятой, одна – с вопросительным знаком и один пробел, итого – 30 клавиш. Сидит себе наша мартышка в углу и нажимает клавиши наугад. Любая последовательность букв имеет ненулевую вероятность оказаться напечатанной, а это значит, что есть шанс, что мартышка дословно напечатает пьесы Шекспира. Шансы у нее минимальные, но они точно отличны от нуля. Давайте разберемся, какова вероятность того, что наша мартышка напечатает последовательность из 8 символов “To be or” («быть или не»). Что мы должны для этого сделать? Сначала мы должны посчитать вероятность появления каждого символа. Представим 8 ячеек, в которых окажутся 8 символов, включая пробелы:
| t | o | b | e | o | r |
Что нужно, чтобы посчитать вероятность появления одного символа? Правильно, нужно
узнать, сколько всего возможно символов и сколько подходящих. Сколько возможных вариантов для одной ячейки? Помним, что всего у воображаемой нами печатающей машинки 30 клавиш, а значит, 30 возможных вариантов. Для первой ячейки – 30, для второй ячейки – 30, и т.д. Какова вероятность символа «t» в первой ячейке? Подходящий символ -1, количество возможных символов – 30, значит, вероятность равна 1/30. Какова вероятность символа «o» во второй ячейке? Тоже 1/30. Составим таблицу:
| Символ | t | o | b | e | o | r | ||
|---|---|---|---|---|---|---|---|---|
| Вероятность появления символа | 1/30 | 1/30 | 1/30 | 1/30 | 1/30 | 1/30 | 1/30 | 1/30 |
Как посчитать вероятность того, что будут напечатаны именно указанные 8 символов? Какая ситуация нам нужна? Нам необходимо, чтобы произошло И первое, И второе, И третье …. И восьмое события, то есть мы должны перемножить вероятности каждого из событий. Получим:
$ P=big(frac{1}{30}big)^{8}=frac{1}{6561}cdot 10^{-8} $
Получили очень малую вероятность. Чтобы понять, насколько она мала, давайте посчитаем, сколько времени придется ждать, чтобы мартышка напечатала указанные символы. Допустим, мартышка бьет по клавише раз в секунду (не прерываясь на сон и другие дела), тогда ожидаемое время составляет чуть более 20 800 лет. Поэтому если вдруг вы затаили дыхание в ожидании Шекспира – выдыхайте, у нее довольно долго будет получаться всякая нечитаемая последовательность типа «xo?h,yt?»
Простые вычисления и кодирования сообщений
МИНОБРНАУКИ
РОССИИ
Федеральное
государственное бюджетное образовательное учреждение
Высшего
профессионального образования
«Пензенский
государственный технологический университет»
(ПензГТУ)
Факультет
«Информационных и образовательных технологий»
Кафедра «Информационные
технологии и системы»
Дисциплина
«Основы теории информации»
КОНТРОЛЬНАЯ РАБОТА
Дисциплина «Основы теории информации»
Выполнил:
студент группы 13ИС2Б
Чинков М.Ю
Проверил: ст.
преподаватель каф. ИТС
Пенза 2015
ВВЕДЕНИЕ
Цель данной контрольной работы — актуализация знаний в предмете «Основы
теории информации».
В рамках контрольной работы было выполнено 5 заданий в соответствии с
моим вариантом (вариант №23):
. Определить среднее количество информации, содержащееся в сообщении,
используемом три независимых символа S1, S2, S3. Известны вероятности появления
символов p(S1)=p1, p(S2)=p2, p(S3)=p3. Оценить избыточность сообщения.
. В условии предыдущей задачи учесть зависимость между символами,
которая задана матрицей условных вероятностей P(Si / Sj).
. Провести кодирование по одной и блоками по две буквы, используя
метод Шеннона — Фано. Сравнить эффективности кодов (величина энтропии). Данные
взять из задачи 1.
. Алфавит передаваемых сообщений состоит из независимых букв Si.
Вероятности появления каждой буквы в сообщении заданы. Определить и сравнить
эффективность кодирования сообщений методом Хаффмана при побуквенном
кодировании и при кодировании блоками по две буквы.
. Определить пропускную способность канала связи, по которому
передаются сигналы Si. Помехи в канале определяются матрицей условных
вероятностей P(Si / Sj). За секунду может быть передано N = 10 сигналов.
Простые вычисления и кодирования сообщений в заданиях были сделаны
вручную, более сложные были сделаны с помощью среды разработки MATLAB R2014a.
Формулы и решения задач были введены с помощью программы MathType.
.
1. ОПРЕДЕЛЕНИЕ
СРЕДНЕГО КОЛИЧЕСТВА ИНФОРМАЦИИ
Энтропия источника — среднее количество информации в одном сообщении. Не
следует путать энтропию с количеством информации в одном конкретном сообщении.
Если в источнике есть множество сообщений, точно знать о каждом из них
необязательно. В этом заключается преимущество среднего значения количества
информации. Усреднение позволило Шеннону оценить как редкие, так и частые
сообщения. Энтропия характеризует источник сообщения. Аналогично можно получить
и “энтропийную характеристику сигнала”.
Задание: определить среднее количество информации, содержащееся в
сообщении, используемом три независимых символа S1, S2, S3. Известны
вероятности появления символов p(S1)=p1, p(S2)=p2, p(S3)=p3. Оценить
избыточность сообщения. Вариант №23: p1=0.12; p2=0.13; p3=0.75.
Решение. Максимальное среднее количество информации на символ сообщения
имеет место при равновероятном распределении и равно, согласно формуле
Рассчитаем
среднее количество информации на символ сообщения при заданных вероятностях по
формуле, где n — число символов в алфавите, p — вероятность появления события.
Оценим
избыточность сообщения по формуле.
Максимальная энтропия.
Реальная
энтропия.
Избыточность
сообщения.
2. ЗАВИСИМОСТЬ
МЕЖДУ СИМВОЛАМИ МАТРИЦЫ УСЛОВНЫХ ВЕРОЯТНОСТЕЙ
В большинстве реальных случаев появление элемента хi в сообщении зависит
от того, какой элемент хj был предшествующим. Взаимосвязь элементов в сообщении
характеризуется матрицей условных вероятностей.
Задание: в условии предыдущей задачи учесть зависимость между символами,
которая задана матрицей условных вероятностей P(Si / Sj).
Вариант №23.
Решение. Рассчитаем энтропию источника по формуле.
Подставим
числовые данные, используя задание 1.
Вычисление
энтропии в программе MATLAB.
=p1*((0.7*log2(0.7)+0.3*log2(0.3)))+p2*((0.5*log2(0.5)+0.5*log2(0.5))++p3*(-(0.1*log2(0.1)+0.5*log2(0.5)+0.4*log2(0.4)));
3. КОДИРОВАНИЕ
МЕТОДОМ ШЕННОНА-ФАНО
Кодирование Шеннона — Фано (англ. Shannon-Fano coding) — алгоритм
префиксного неоднородного кодирования. Относится к вероятностным методам сжатия
(точнее, методам контекстного моделирования нулевого порядка). Алгоритм Шеннона
— Фано использует избыточность сообщения, заключённую в неоднородном
распределении частот символов его (первичного) алфавита, то есть заменяет коды
более частых символов короткими двоичными последовательностями, а коды более
редких символов — более длинными двоичными последовательностями. Алгоритм был
независимо друг от друга разработан Шенноном (публикация «Математическая теория
связи», 1948 год) и, позже, Фано (опубликовано как технический отчёт).
Задание: провести кодирование по одной и блоками по две буквы, используя
метод Шеннона — Фано. Сравнить эффективности кодов (величина энтропии). Данные
взять из задачи 1.
Решение. Проведем кодирование методом Шеннона — Фэно и рассчитаем
характеристики кода. Пусть исходный алфавит состоит из трех (по одной букве) и
девяти (по две буквы) букв и заданы их вероятности. Проведем разбиения по
алгоритму Шеннона — Фэно и составим кодовые комбинации.
|
xi |
P(xi) |
1 |
2 |
3 |
4 |
|
P3 |
0.75 |
0 |
0 |
1 |
|
|
P2 |
0.13 |
0 |
0 |
0 |
1 |
|
P1 |
0.12 |
0 |
0 |
0 |
Кодовые комбинации по одной букве.
|
xi |
P(xi) |
1 |
2 |
3 |
4 |
5 |
|
p3p3 |
0.5625 |
1 |
1 |
|||
|
p3p2 |
0.0975 |
1 |
0 |
|||
|
p2p3 |
0.0975 |
0 |
1 |
1 |
||
|
p3p1 |
0.09 |
0 |
1 |
0 |
||
|
p1p3 |
0.09 |
0 |
0 |
1 |
1 |
|
|
p2p2 |
0.0169 |
0 |
0 |
1 |
0 |
|
|
p2p1 |
0.0156 |
0 |
0 |
0 |
1 |
|
|
p1p2 |
0.0156 |
0 |
0 |
0 |
0 |
1 |
|
p1p1 |
0.0144 |
0 |
0 |
0 |
0 |
0 |
Кодовые комбинации по две буквы.
Рассчитаем энтропию по формуле.
Рассчитаем
среднюю длину кодовой комбинации по формуле.
Рассчитаем
эффективность кода, согласно формуле.
Энтропия
источника. По одной букве:
Средняя
длина кодовой комбинации источника. По одной букве:
По
две буквы:
Эффективность
кода. По одной букве:
По
две буквы:
4. КОДИРОВАНИЕ
АЛГОРИТМОМ ХАФФМАНА
Один из первых алгоритмов эффективного кодирования информации был
предложен Д.А. Хаффманом в 1952 году.
Идея алгоритма состоит в следующем: зная вероятности символов в
сообщении, можно описать процедуру построения кодов переменной длины, состоящих
из целого количества битов.
Символам с большей вероятностью ставятся в соответствие более короткие
коды.
Коды Хаффмана обладают свойством префиксности (то есть ни одно кодовое
слово не является префиксом другого), что позволяет однозначно их декодировать.
Классический алгоритм Хаффмана на входе получает таблицу частот встречаемости
символов в сообщении.
Далее на основании этой таблицы строится дерево кодирования Хаффмана
(Н-дерево).
Задание: алфавит передаваемых сообщений состоит из независимых букв Si.
Вероятности появления каждой буквы в сообщении заданы. Определить и сравнить
эффективность кодирования сообщений методом Хаффмена при побуквенном
кодировании и при кодировании блоками по две буквы. Вариант №23:
(0,8;0,0;0,08;0,12).
Решение. Проведем кодирование методом Шеннона-Фэно.
|
xi |
P(xi) |
1 |
2 |
3 |
|
p1 |
0.8 |
1 |
||
|
p4 |
0.12 |
0 |
1 |
|
|
p3 |
0.08 |
0 |
0 |
1 |
|
p2 |
0 |
0 |
0 |
0 |
По одной букве.
|
xi |
P(xi) |
|
P1p1 |
0.64 |
|
P4p1 |
0.096 |
|
P1p4 |
0.096 |
|
P3p1 |
0.064 |
|
P1p3 |
0.064 |
|
P4p4 |
0.0144 |
|
P4p3 |
0.0096 |
|
P3p4 |
0.0096 |
|
P3p3 |
0.0064 |
|
P4p2 |
0 |
|
P2p4 |
0 |
|
P3p2 |
0 |
|
P2p3 |
0 |
|
P2p1 |
0 |
|
P1p2 |
|
|
P2p2 |
0 |
По две буквы.
Проведем кодирование по методу Хаффмена. Исходный алфавит состоит из
нескольких букв с заданными вероятностями. Составим таблицу.
|
xi |
P(xi) |
Вспомогательный столбец |
|
p1 |
0.8 |
0.8 |
|
p4 |
0.12 |
0.2 |
|
p3 |
0.08 |
|
|
p2 |
0 |
По одной букве
|
xi |
P(xi) |
Вспомогательные столбцы |
||||
|
P1p1 |
0.64 |
0.64 |
||||
|
P4p1 |
0.096 |
0.096 |
0.192 |
0.36 |
||
|
P1p4 |
0.096 |
0.096 |
0.168 |
|||
|
P3p1 |
0.064 |
0.064 |
0.128 |
|||
|
P1p3 |
0.064 |
0.064 |
0.040 |
|||
|
P4p4 |
0.0144 |
0.0144 |
||||
|
P4p3 |
0.0096 |
0.0096 |
0.0256 |
|||
|
P3p4 |
0.0096 |
0.0160 |
||||
|
P3p3 |
0.0064 |
|||||
|
P4p2 |
0 |
|||||
|
P2p4 |
0 |
|||||
|
P3p2 |
0 |
|||||
|
P2p3 |
0 |
|||||
|
P2p1 |
0 |
|||||
|
P1p2 |
0 |
|||||
|
P2p2 |
0 |
По две буквы.
Характеристики кода рассчитываются по тем же формулам, что и для кода
Шеннона-Фано.
Рассчитаем энтропию по формуле.
Рассчитаем
минимальную среднюю длину кодовой комбинации по формуле.
Рассчитаем
эффективность кода, согласно формуле.
Энтропия
источника. По одной букве:
По
две буквы:
Средняя
длина кодовой комбинации источника. По одной букве:
По
две буквы:
Эффективность
кода. По одной букве:
По
две буквы:
5. ПРОПУСКНАЯ
СПОСОБНОСТЬ КАНАЛА СВЯЗИ
хаффман
код шеннон символ
Пропускная способность — метрическая характеристика, показывающая
соотношение предельного количества проходящих единиц (информации, предметов,
объёма) в единицу времени через канал, систему, узел. В информатике определение
пропускной способности обычно применяется к каналу связи и определяется
максимальным количеством переданной или полученной информации за единицу
времени.
Задание: Определить пропускную способность канала связи, по которому
передаются сигналы Si. Помехи в канале определяются матрицей условных
вероятностей P(Si / Sj). За секунду может быть передано N = 10 сигналов.
Вариант №23.
Решение. Рассчитаем условную энтропию по формуле.
Рассчитаем
пропускную способность канала связи по формуле.
Условная
энтропия.
Пропускная
способность канала связи.
заключение
В рамках контрольной работы были изучены различные алгоритмы решения
задач на определение среднего количества информации, содержащейся в сообщении,
определение пропускной способности канала связи и алгоритмы кодирования
сообщений (метод Шеннона-Фано, алгоритм Хаффмана).
Было выполнено 5 заданий:
. Определить среднее количество информации, содержащееся в
сообщении, используемом три независимых символа S1, S2, S3. Известны
вероятности появления символов p(S1)=p1, p(S2)=p2, p(S3)=p3. Оценить
избыточность сообщения.
. В условии предыдущей задачи учесть зависимость между символами,
которая задана матрицей условных вероятностей P(Si / Sj).
. Провести кодирование по одной и блоками по две буквы, используя
метод Шеннона — Фано. Сравнить эффективности кодов (величина энтропии). Данные
взять из задачи 1.
. Алфавит передаваемых сообщений состоит из независимых букв Si.
Вероятности появления каждой буквы в сообщении заданы. Определить и сравнить
эффективность кодирования сообщений методом Хаффмана при побуквенном
кодировании и при кодировании блоками по две буквы.
. Определить пропускную способность канала связи, по которому
передаются сигналы Si. Помехи в канале определяются матрицей условных
вероятностей P(Si / Sj). За секунду может быть передано N = 10 сигналов.
Простые вычисления и кодирования сообщений в заданиях были сделаны
вручную, более сложные были сделаны с помощью среды разработки MATLAB R2014a.
Формулы и решения задач были введены с помощью программы MathType.
список литературы
1. Зверева
Е.Н. Сборник примеров и задач по основам теории информации и кодирования
сообщений/ Е.Н. Зверева, Е.Г.Лебедько. — СПб: НИУ ИТМО, 2014. — 76 с.
. Калинцев
С.В. Методические указания к контрольной работе по курсу «Теория кодирования»/
С.В.Калинцев. -2012. — 20 с.