Значащие цифры десятичного числа – это все его цифры, начиная с первой ненулевой слева.
Пример 1
x = 0.002036, цифры 2036 являются значащими;
x = 2.27×106, значащими цифрами являются цифры 2, 2, 7;
x = 2270000, все цифры этого числа являются значащими.
Значащая цифра в записи числа верна, если абсолютная погрешность числа меньше или равна пяти единицам разряда, следующего за этой цифрой.
Пример 2
Определить, сколько верных значащих цифр содержит число:
x = 0.002306 ± 0.00001.
Для определения числа верных значащих цифр запишем x и Dx таким образом, чтобы легко было сравнить разряды этих чисел:
x = 0.002306, абсолютная погрешность Dx = 0.00001.
x = 0.002306,
Dx = 0.00001.
Третья значащая цифра (0) не может быть верной, так как она одного порядка с погрешностью. Верными могут быть цифры, которые стоят перед ней (2, 3). Цифра 3 будет верной, если Dx £ 0.00005. В нашем случае это условие выполнено, следовательно, 2, 3 – верные значащие цифры.
Цифры в записи числа, следующие за верными, называются сомнительными.
Пример 3
x = 1.121 ± 0.003;
x = 1.121;
Dx = 0.003.
В числе x = 1.121 три верные значащие цифры (1, 1, 2) и одна сомнительная (1).
Пример 4
x = 0.002306 ± 0.00007;
x = 0.002306;
Dx = 0.00007.
В числе x = 0.002306 одна верная значащая цифра (2), три сомнительные (3, 0, 6).
Пример 5
x = 12.3 ± 0.5;
x = 12.3;
Dx = 0.5.
В числе x = 12.3 три значащие цифры, две верные значащие цифры (1, 2), одна сомнительная (3).
Пример 6
x = 12.3 ± 0.8;
x = 12.3;
Dx = 0.8.
В числе x = 12.3 одна верная значащая цифра (1), две сомнительные (2, 3).
При записи абсолютной и относительной погрешностей используют, как правило, одну-две значащие цифры. Приближенные числа принято записывать следующим образом: сначала записывают все верные значащие цифры, затем одну-две сомнительные. То есть в записи приближенного числа, как правило, число значащих цифр на одну-две больше, чем число верных значащих цифр.
Практическое правило. Одна верная значащая цифра в записи числа соответствует приблизительно относительной погрешности 10 %. И наоборот, относительная погрешность 10 % соответствует приблизительно одной верной значащей цифре. Две верные значащие цифры соответствуют относительной погрешности 1 %, три верные значащие цифры – относительной погрешности 0.1 %.
Задача довольно простая для внимательного человека:
1) в числе 912 правильных цифр нет, т. е. ни одной из этих цифр нет в искомом числе вообще;
2) в числе 341 две цифры правильные, но не на тех местах, а так как цифры 1 в числе нет, то две цифры искомого числа — 3 и 4;
3) в числе 462 правильная цифра только одна, и это 4, причем она не может быть ни первой, ни второй, значит, она на третьей позиции, причем цифр 6 и 2 в искомом числе тоже нет;
4) в числе 503 правильная цифра только одна, и это 3, причем она не может быть ни первой, ни последней, значит, она на втором месте, а цифр 5 и 0 в искомом числе нет;
5) цифры на второй и третьей позиции известны, значит, из числа 785 берем первую цифру, которая верная и на своем месте;
6) искомое число — 734.
Ответ: 734.
Создатель теории приближенных вычислений А. Н. Крылов говорил: «При производстве всяких численных вычислений надо руководствоваться правилом: точность вычислений должна соответствовать точности данных и той практической потребности, для которой вычисления производятся». Ему же принадлежат слова: «Помните, что каждая неверная цифра — это ошибка, всякая лишняя цифра — это пол-ошибки».
Приближенные числа записываются, как правило, при помощи десятичных дробей. Между записью приближенных и точных чисел есть различия. Если перед нами точное число, то вес его цифры являются верными, точными. Что же касается приближенного числа, то некоторые его цифры верны, а другие являются сомнительными.
Цифра десятичного разряда приближенного числа 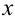
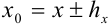
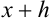
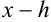
Проверку на верные и сомнительные цифры нужно начинать слева направо с наивысшего разряда. Все цифры, стоящие правее первой найденной сомнительной цифры, автоматически считаются сомнительными.
Пример №45.4.
Найдите верные и сомнительные цифры в записи числа 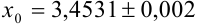
Решение:
Поскольку 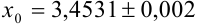

Начинаем проверку на верные и сомнительные цифры с наивысшего разряда — единиц. Видим, что цифры 3,45 одинаковы в левой и правой части двойного неравенства (т.е. в записи 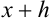
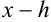
Цифры в разряде тысячных в правой и левой части двойного неравенства отличаются (1 и 5), следовательно, в записи приближенного числа 3,4531 цифра 3, стоящая в разряде тысячных, и цифра 1, стоящая за ней, являются сомнительными.
Итак, точное число 
Ответ:
Для записи приближенных чисел существуют следующие правила:
- Оставлять в записи числа только верные цифры.
- Если в десятичной дроби последние верные цифры нули, то их надо выписывать.
- Если число содержит на конце целой части сомнительные цифры, то они должны быть заменены на
, где
— число цифр, которые нужно заменить.
- Граница абсолютной погрешности числа, содержащего только верные цифры, равна единице последнего разряда.
Проиллюстрируем применение данных правил на конкретных примерах.
1. Поскольку в записи числа следует оставлять только верные цифры, то в примере 45.4 точное значение 
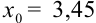
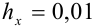
2. Если задано число 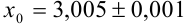

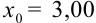
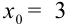
3. Пусть задано число 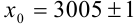

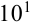
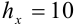
В науке принято записывать числа в стандартном виде, т.е. в виде 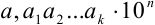
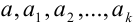
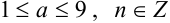
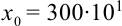
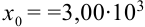
Значащими цифрами числа называют все его верные цифры, за исключением нулей, стоящих левее первой отличной от нуля цифры.
Например, число 0,712 содержит три значащие цифры: 7, 1, 2. Число 0,00012 — две значащие цифры: 1 и 2. Число 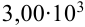
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Предмет высшая математика
Другие лекции по высшей математике, возможно вам пригодятся:
Данная статья будет наиболее актуальна для школьников и студентов, но думаю, что стоит прочитать и просто для общего развития. Частенько бывает, что вы не знаете ответ на вопрос в тесте и начинаете гадать, что же выбрать? В такие моменты многие полагаются на удачу, но существует более хороший способ правильно ответить на тест, о котором я и хочу рассказать.
Маленькая предыстория. Придумали этот способ с другом, обучаясь в школе, когда проходили теорию вероятности по алгебре, поэтому для некоторых это не будет новым, поскольку все до банальностей просто
Приступим. Я буду показывать на примере, т.к по-другому будет слишком сухо и не понятно. Такое прокатит только с тестами, где в ответе содержится несколько вариантов ответа. Я взял задание по русскому языку с ЕГЭ 2014. Итак, начнем:
Вот есть у нас задание, где нужно выбрать правильный ответ. Ответ содержит несколько цифр.
1) Подчеркиваем / обводим цифры, которые повторяются. Я подчеркнул одинаковыми цветами одинаковые буквы.
2) Теперь смотрим частоту повторения.
– Цифра (1) у меня встречается 3 раза
– Цифра (2) у меня встречается 2 раза
– Цифра (3) у меня встречается 4 раза
– Цифра (4) у меня встречается 3 раза
3) Теперь смотрим наиболее часто встречающиеся цифры, у меня это 3 ( но ее можно не учитывать, поскольку каждый ответ содержит ее ), 4 и 1.
4) Смотрим на ответы, которые не содержат наиболее часто встречаются цифры.
– Первый вариант у меня не содержит цифру один, значит навряд ли он верный.
– Второй вариант у меня не содержит цифру четыре, что тоже означает, что он навряд ли является верным.
– Остается два варианта ответа, но вариант под номером три содержит все три наиболее часто встречающихся комбинации ответа, что означает, что он точно может быть верным. Но и вариант четыре содержит эти три варианта, а так же еще и вариант два, но он встречается реже. С чего можно сделать вывод, что вариант три точно содержит все правильные ответы, однако есть и вариант, что вариант четыре верный, однако из-за того, что цифра два встречается только два раза из четырех, я бы не стал рисковать и выбрал именно вариант три.
Можно проверить, какой же на самом деле правильный ответ ( брал задание из пробникв яндексе, где можно посмотреть на правильный ответ) :
Вот так можно решать такие тесты, но все же кроме такое теории лучше и своими знаниями проверять. А так мне это не раз помогало
682 614 206 738 780 взломайте замок
Загадки на логику
Предлагаем вам решить интересную логическую задачу со взломом кода цифрового замка.
Итак имеются данные по цифрам кода замка. На основе этих исходных данных необходимо логически размышляя подобрать правильный код, который откроет замок.
Код замка состоит из трех цифр. Ниже приводятся данные о цифрах, на основе которых вы сможете подобрать правильный код.
6 8 2 — среди этих цифр одна подходящая и расположена на правильном месте.
6 1 4 — одна из этих цифр верная, но расположена не на своем месте.
2 0 6 — две из этих цифр подходят, но расположены не на своем месте.
7 3 8 — здесь все не верно, эти цифры не подходят.
7 8 0 — одна из этих цифр подходит к коду, но расположена не верно.
Внимание!
Ниже приведен правильный ответ!
Правильный ответ и решение:
Итак код замка 0 4 2.
Как получились эти цифры:
Из исходных данных мы знаем, что из цифр 7 3 8 не подходит ни одна, сразу от них избавляемся и не рассматриваем их в коде.
Далее берем цифры 7 8 0 — из них подходит только 0, так как выше мы выяснили что 7 и 8 не подходят, однако 0 стоит не на своем месте, то есть он должен стоять на первом или втором месте.
Далее берем данные про 6 8 2 и 6 1 4, здесь исключаем цифру 6, так как она не может удовлетворять сразу двум условиям( верная и расположена на правильном месте и верная, но расположена не на своем месте) и учитывая что 8 мы уже откинули выше, остается 2, которая стоит на треьем месте.
Из условия 206, где две цифры подходящие, но расположены не на своем месте, для цифры 0 получается только первое место.
Из условия для 614, где одна цифра верная но расположена не на своем месте, получается, что это не может быть 1, так как другого места ей нету, остается только 4, расположенная на втором месте.
Похожие новости

Все загадки
Все загадки

Все загадки
Все загадки
Все загадки
Все загадки


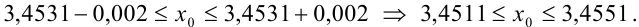
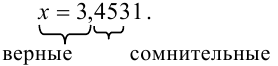
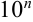 , где
, где  — число цифр, которые нужно заменить.
— число цифр, которые нужно заменить.




.png)