Решение: : Рассмотрим уравнение координаты:
x = Xm∙соs(ω∙t + φ0),
где: х – координата тела, Хm – амплитуда, ω – угловая скорость, φ0 – начальная координата.
Для нахождения скорости возьмем первую производную по времени от х:
υ = — ω∙Хm∙sin(ω∙t+ φ0), υ = — 0,4∙π∙sin(4πt+π/4).
Для нахождения ускорения возьмем вторую производную по времени от х:
а = — ω2∙Хm∙соs(ω∙t+ φ0), а = -0,16∙π∙соs(4πt+π/4).
аmax = 0,5 м/с2, Fmax = m∙a, Fmax = 0,5 м/с2∙10∙10-3 кг, = 5∙10-3 Н.
[ {{E}_{Kmax }}=frac{mcdot upsilon _{max }^{2}}{2}, ]
υmax = 1,256 м/с, ЕКmax = 7,9∙10-3 Дж. Ответ: 5∙10-3 Н, 7,9∙10-3 Дж.
Сила и потенциальная энергия при колебании
Сила и потенциальная энергия при колебании
При всяком колебании около положения равновесия на тело действует сила, «желающая» возвратить тело в положение равновесия. Когда точка удаляется от положения равновесия, сила замедляет движение, когда точка приближается к этому положению, сила ускоряет движение.
Проследим за этой силой на примере маятника. Грузик маятника находится под действием силы тяжести и силы натяжения нити. Разложим силу тяжести на две составляющие – одну, направленную вдоль нити, и другую, идущую перпендикулярно к ней по касательной к траектории. Для движения существенна лишь касательная составляющая силы тяжести. Она-то и есть в этом случае возвращающая сила. Что касается силы, направленной вдоль нити, то она уравновешивается противодействием со стороны гвоздика, на котором висит маятник, и принимать ее в расчет надо лишь тогда, когда нас интересует вопрос, выдержит ли нить тяжесть колеблющегося тела.
Обозначим через x величину смещения грузика. Перемещение происходит по дуге, но мы ведь условились изучать колебания вблизи положения равновесия. Поэтому мы не делаем различия между величиной смещения по дуге и отклонением груза от вертикали. Рассмотрим два подобных треугольника (рис. 45). Отношение соответствующих катетов равно отношению гипотенуз, т.е.


Величина mg/l во время колебания не меняется. Эту постоянную величину мы обозначим буквой k, тогда возвращающая сила равна F = kx. Мы приходим к следующему важному выводу: величина возвращающей силы прямо пропорциональна величине смещения колеблющейся точки от положения равновесия. Возвращающая сила максимальна в крайних положениях колеблющегося тела. Когда тело проходит среднюю точку, сила обращается в нуль и меняет свой знак или, иными словами, свое направление. Пока тело смещено вправо, сила направлена влево, и наоборот. Маятник служит простейшим примером колеблющегося тела. Однако мы заинтересованы в том, чтобы формулы и законы, которые мы находим, можно было бы распространить на любые колебания.
Период колебания маятника был выражен через его длину. Такая формула годится лишь для маятника. Но мы можем выразить период свободных колебаний через постоянную возвращающей силы k. Так как k = mg/l, то l/g = m/k, и, следовательно,

Эта формула распространяется на все случаи колебания, так как любое свободное колебание происходит под действием возвращающей силы.
Выразим теперь потенциальную энергию маятника через смещение из положения равновесия x. Потенциальная энергия грузика, когда он проходит низшую точку, может быть принята за нуль, и отсчет высоты подъема следует вести от этой точки. Обозначив буквой h разность высот точки подвеса и положения отклонившегося груза, запишем выражение потенциальной энергии: U = mg(l ? k) или, пользуясь формулой разности квадратов,

Но, как видно из рисунка, l2 ? h2 = x2, l и h различаются весьма мало, и поэтому вместо l + h можно подставить 2l. Тогда U = (mg/2l)x2, или

Потенциальная энергия колеблющегося тела пропорциональна квадрату смещения тела из положения равновесия.
Проверим правильность выведенной формулы. Потеря потенциальной энергии должна равняться работе возвращающей силы. Рассмотрим два положения тела – x2 и x1. Разность потенциальных энергий

Но разность квадратов можно записать как произведение суммы на разность. Значит,

Но x2 ? x1 есть путь, пройденный телом, kx1 и kx2 – значения возвращающей силы в начале и в конце движения, а (kx1 + kx2)/2 равно средней силе.
Наша формула привела нас к правильному результату: потеря потенциальной энергии равна произведенной работе.
Читайте также
Глава 14 РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ (II)
Глава 14
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ (II)
§1. Работа§2. Движение при наложенных связях§3. Консервативные силы§4. Неконсервативные силы§5. Потенциалы и поля§ 1. РаботаВ предыдущей главе мы ввели много новых понятий и идей, играющих важную роль в физике. Идеи эти столь важны,
ЭНЕРГИЯ ИЗ СРЕДЫ — ВЕТРЯК И СОЛНЕЧНЫЙ ДВИГАТЕЛЬ — ДВИЖУЩАЯ ЭНЕРГИЯ ИЗ ЗЕМНОГО ТЕПЛА — ЭЛЕКТРИЧЕСТВО ИЗ ЕСТЕСТВЕННЫХ ИСТОЧНИКОВ
ЭНЕРГИЯ ИЗ СРЕДЫ — ВЕТРЯК И СОЛНЕЧНЫЙ ДВИГАТЕЛЬ — ДВИЖУЩАЯ ЭНЕРГИЯ ИЗ ЗЕМНОГО ТЕПЛА — ЭЛЕКТРИЧЕСТВО ИЗ ЕСТЕСТВЕННЫХ ИСТОЧНИКОВ
Есть множество веществ помимо топлива, которые возможно смогли бы давать энергию. Огромное количество энергии заключено, например, в
2. Центробежная сила
2. Центробежная сила
Раскройте зонтик, уприте его концом в пол, закружите и бросьте внутрь мячик, скомканную бумагу, носовой платок – вообще какой-нибудь легкий и неломкий предмет. Вы убедитесь, что зонтик словно не желает принять подарка: мяч или бумажный ком сами
Сила = геометрия
Сила = геометрия
Несмотря на постоянные болезни, Риман в конечном счете изменил бытующие представления о значении силы. Еще со времен Ньютона ученые считали силу мгновенным взаимодействием удаленных друг от друга тел. Физики называли ее «дальнодействием», это означало,
Самая загадочная сила природы
Самая загадочная сила природы
Не говорю уже о том, как мало у нас надежды найти когда-нибудь вещество, непроницаемое для тяготения. Причина тяготения нам неизвестна: со времен Ньютона, открывшего эту силу, мы ни на шаг не приблизились к познанию ее внутренней сущности. Без
Глава 3 Гравитация — первая фундаментальная сила
Глава 3
Гравитация — первая фундаментальная сила
С небес на землю и обратно
В современной физике говорят о четырех фундаментальных силах. Первой открыли силу гравитации. Известный школьникам закон всемирного тяготения определяет силу притяжения F между любыми массами
73 Сила в сантиметрах, или Наглядно закон Гука
73
Сила в сантиметрах, или Наглядно закон Гука
Для опыта нам потребуются: воздушный шарик, фломастер.
В школе проходят закон Гука. Жил такой знаменитый ученый, который изучал сжимаемость предметов и веществ и вывел свой закон. Закон этот очень простой: чем сильнее мы
Сила – вектор
Сила – вектор
Сила, так же как и скорость, есть векторная величина. Ведь она всегда действует в определенном направлении. Значит, и силы должны складываться по тем правилам, которые мы только что обсуждали.Мы часто наблюдаем в жизни примеры, иллюстрирующие векторное
Ускорение и сила
Ускорение и сила
Если на тело силы не действуют, то оно может двигаться только без ускорения. Напротив, действие на тело силы приводит к ускорению, и при этом ускорение тела будет тем большим, чем больше сила. Чем скорее мы хотим привести в движение тележку с грузом, тем
Сила Кориолиса
Сила Кориолиса
Своеобразие мира вращающихся систем не исчерпывается существованием радиальных сил тяжести. Познакомимся с еще одним интересным эффектом, теория которого была дана в 1835 году французом Кориолисом.Поставим перед собой такой вопрос: как выглядит
Великая сила «пустяков»
Великая сила «пустяков»
У Леночки Казаковой может оторваться пуговица от платья, но она от этого не перестанет быть Леночкой Казаковой. Законы науки, особенно законы физики, не допускают ни малейшего неряшества. Воспользовавшись аналогией, можно сказать, что законы
Лошадиная сила и работа лошади
Лошадиная сила и работа лошади
Мы часто слышим выражение «лошадиная сила» и привыкли к нему. Поэтому мало кто отдает себе отчет в том, что это старинное наименование совершенно неправильно. «Лошадиная сила» – не сила, а мощность и притом даже не лошадиная. Мощность – это
Сила звука
Сила звука
Как ослабевает звук с расстоянием? Физик ответит вам, что звук ослабевает «обратно пропорционально квадрату расстояния». Это означает следующее: чтобы звук колокольчика на тройном расстоянии был слышен так же громко, как на одинарном, нужно одновременно
В данной теме разговор пойдёт
о математическом и пружинном маятниках и их важных характеристиках.
Рассмотрим для начала
математический маятник. Математическим маятником называется находящаяся
в гравитационном поле материальная точка, подвешенная на невесомой и
нерастяжимой нити, прикрепленной к подвесу. Математический маятник
— это модель малых реальных колебаний тела под действием силы тяготения
при условии, что можно пренебречь:
1) размерами подвешенного
тела, по сравнению с длиной нити;
2) сопротивлением движению
тела;
3) массой нити и ее
деформацией.
Рассмотрим подробно колебания
математического маятника в инерциальной системе отсчета, относительно которой точка его подвеса движется
прямолинейно и равномерно или же покоится. И так, пусть в начальный момент
времени маятник покоится в положении равновесия. Тогда, действующие на маятник
сила упругости нити и сила тяжести материальной точки взаимно компенсируются.
Теперь отклоним маятник на
некоторое расстояние от точки равновесия и отпустим его. В этом случае, сила
тяжести и сила упругости нити уже не будут компенсировать друг друга. Разложим
вектор силы тяжести на две составляющих — тангенциальную и нормальную.
Как видим, тангенциальная
составляющая силы тяжести направлена к положению равновесия, то есть она
является возвращающей силой. При этом она сообщает материальной точке
тангенциальное ускорение и маятник начнет двигаться к положению равновесия с
возрастающей по модулю скоростью. А нормальная составляющая силы тяжести, как
видно из рисунка, направлена вдоль нити против силы упругости. Их
равнодействующая сообщает маятнику нормальное ускорение, которое изменяет
направление вектора скорости. В результате маятник начинает двигаться по дуге.
Чем ближе маятник будет
подходить к положению равновесия, тем меньше становиться значение возвращающей
силы и тем больше становиться скорость движения маятника. Дойдя до положения
равновесия, возвращающая сила становится равной нулю.
При этом скорость движения
маятника достигает своего максимума и, не останавливаясь, маятник продолжает
свое движение дальше уже по инерции, поднимаясь по дуге вверх. При этом вновь
возникает возвращающая сила, которая становится тем больше, чем выше
поднимается маятник. Но так как возвращающая сила теперь направлена против
движения маятника, то его скорость убывает и в точке D
скорость маятника становится равной нулю.
Маятник на мгновение
останавливается, а затем начинает двигаться в обратном направлении к положению
равновесия. Опять пройдя его по инерции, маятник, замедляя свое движение,
дойдет до точки А, тем самым совершив одно полное колебание. А так как
силы сопротивления отсутствуют, то после этого движение маятника будет
повторяться в уже описанной последовательности.
Получим уравнение, описывающее
свободные колебания математического маятника. Пусть маятник в данный момент
времени находится в точке B.
Его смещение от положения
равновесия в этот момент равно длине дуги CB.
Пусть длина нити подвеса
маятника равна l, а его масса m. Из
рисунка видно, что значение возвращающей силы (то есть тангенциальной
составляющей силы тяжести), можно найти как произведение модуля силы тяжести на
синус угла отклонения маятника от вертикали.
Из геометрии известно, что по
определению синус острого угла есть отношение противолежащего катета к
гипотенузе. Также из геометрии известно, что при малых углах (то есть когда
острый угол меньше десяти градусов) синус угла можно заменить его градусной мерой.
Перепишем уравнение для
тангенциальной составляющей силы тяжести с учетом последнего равенства.
Обратите внимание на знак «минус»
в этой формуле. Его здесь ставят потому, что тангенциальная составляющая силы
тяжести направлена к положению равновесия, а смещение отсчитывают от положения
равновесия. Теперь применим второй закон Ньютона для нашего маятника, в
проекциях на направление касательной к траектории движения математического
маятника.
Таким образом, имеются два
уравнения, в которых равны их левые части. А раз равны левые, то и правые части
этих равенств также должны быть равными. Сократив полученное равенство на массу
маятника, приходим к тому, что тангенциальное ускорение математического
маятника прямо пропорционально его смещению и направлено к положению равновесия.
Эту формулу называют динамическим
уравнением движения математического маятника.
Теперь перепишем это уравнение
следующим образом
А теперь сравним его с уравнением гармонических
колебаний.
Из такой записи видно, что колебания
математического маятника являются гармоническими. А так как рассмотренные
колебания происходили только под действием внутренних сил, то это
были свободные колебания. Таким образом, можно сделать важный
вывод о том, что при малых углах отклонения свободные колебания
математического маятника являются гармоническими.
Также из анализа формул
следует, что циклическая частота колебаний маятника равна квадратному корню из
отношения ускорения свободного падения к длине маятника.
Помня о том, что период
колебаний и циклическая частота связаны друг с другом обратной
пропорциональностью, получим формулу, по которой можно рассчитать период свободных
колебаний математического маятника.
Полученная формула называется формулой
Гюйгенса, так впервые была получена нидерландским физиком Христианом Гюйгенсом.
Следует обратить внимание на
то, что эту формулу можно использовать для расчета периода при
выполнении одновременно двух условий:
1) колебания маятника
должны быть малыми, так как эта формула дает результаты приемлемой
точности (ошибка менее одного процента) при углах, не превышающих 4º;
2) точка подвеса
маятника должна покоиться или двигаться прямолинейно и равномерно относительно
инерциальной системы отсчета, в которой находится маятник.
Дело в том, что если точка
подвеса математического маятника движется с некоторым ускорением, то изменяется
сила натяжения нити. Это приводит к изменению возвращающей силы, а,
следовательно, частоты и периода колебаний. В этом случае в формуле периода
математического маятника ускорение свободного падения следует заменить на
так называемое «эффективное» ускорение маятника в неинерциальной системе
отсчета.
«Эффективное» ускорение
можно найти, как векторную сумму ускорения свободного падения и вектора,
противоположного вектору ускорения, с которым движется маятник.
Теперь рассмотрим колебания
пружинного маятника. Пружинным маятником называется система,
состоящая из пружины жесткостью k и материальной точки массой m.
В простейшей модели
пружинного маятника рассматривают только упругую деформацию пружины и пренебрегают:
1) любыми силами сопротивления;
2) размерами тела, то есть
тело принимают за материальную точку;
3) массой пружины.
Различают два вида
пружинных маятников — горизонтальный и вертикальный.
В горизонтальном
пружинном маятнике, колебания тела происходят вдоль горизонтальной прямой.
У вертикального
пружинного маятника колебания происходят вдоль вертикальной прямой.
Рассмотрим более подробно
колебания идеального горизонтального пружинного маятника. Пусть в начальный
момент времени пружина не деформирована, и тело находится в положении
равновесия.
Теперь выведем тело из
положения равновесия, например, сжав пружину на некоторую величину, и отпустим
его. И так, со стороны деформированной пружины на тело начнет действовать сила
упругости, которая всегда будет направленна к положению равновесия, и под
действием этой силы тело начнет ускоренно двигаться. При этом в самом крайнем
положении на тело действует максимальная сила упругости, так как здесь
абсолютное удлинение пружины наибольшее. Значит и ускорение тела в этом
положении максимальное.
При движении тела к положению
равновесия абсолютное удлинение пружины начинает уменьшаться, а, следовательно,
уменьшается и ускорение, сообщаемое силой упругости. Но так как ускорение
сонаправлено со скоростью, то скорость маятника увеличивается и в положении
равновесия, как и в случае с математическим маятником, она будет максимальна.
Достигнув положения
равновесия, тело не остановится (хотя в этом положении пружина не
деформирована), а будет по инерции двигаться дальше, растягивая пружину.
Возникающая при этом сила упругости направлена теперь против движения тела и
тормозит его. В точке D тело
на мгновение остановится, так как его скорость окажется равной нулю. Но
ускорение в этой точке максимально, так как максимальна действующая сила
упругости и под действием этой силы тело начнет двигаться в обратную сторону, к
положению равновесия.
Вновь пройдя его по инерции,
тело, сжимая пружину и замедляя движение, дойдет до точки A,
то есть совершит одно полное колебание. После этого движение маятника будет
повторяться в описанной последовательности.
Таким образом, причинами
свободных колебаний пружинного маятника являются действие силы упругости,
возникающей при деформации пружины, и инертность тела.
Получим уравнение, описывающее
движение пружинного маятника. И так, согласно второму закону Ньютона,
единственный результат действия силы упругости — это сообщение телу ускорения.
По закону Гука, сила упругости
прямо пропорциональна смещению тела и противоположно ему направлена.
Перепишем второй закон Ньютона
с учетом определения силы упругости пружины.
Как видно из уравнения, ускорение
маятника прямо пропорционально смещению и противоположно ему по направлению.
Перепишем уравнение следующим
образом
Полученное равенство является динамическим
уравнением движения пружинного маятника.
Сравнивая его с уравнением
гармонических колебаний, видим, что пружинный маятник совершает
гармонические колебания с циклической частотой равной
Учитывая, что период колебаний
и циклическая частота связаны друг с другом обратной пропорциональностью,
получим формулу, по которой можно рассчитать период свободных колебаний
пружинного маятника.
По этой же формуле можно
рассчитывать и период колебаний вертикального пружинного маятника.
Основные выводы:
Рассмотрели математический и
пружинный маятники. Рассмотрели условия возникновения свободных гармонических
колебаний в таких системах. А также вспомнили формулы, по которым можно
рассчитать период свободных колебаний математического и пружинного маятников.
.Маятники
представляют собой протяженные тела
различной формы и размеров, совершающие
колебания около точки подвеса или
опоры. Такие системы называются
физическими маятниками. В состоянии
равновесия, когда центр тяжести находится
на вертикали под точкой подвеса (или
опоры), сила тяжести уравновешивается
(через упругие силы деформированного
маятника) реакцией опоры. При отклонении
из положения равновесия сила тяжести
и упругие силы определяют в каждый
момент времени угловое ускорение
маятника, т. е. определяют характер его
движения (колебания). Мы рассмотрим
теперь динамику колебаний подробнее
на простейшем примере так называемого
математического маятника, который
представляет собой грузик малого
размера, подвешенный на длинной тонкой
нити.
В математическом маятнике
мы можем пренебречь массой нити и
деформацией грузика, т. е. можем считать,
что масса маятника сосредоточена в
грузике, а упругие силы сосредоточены
в нити, которую считают нерастяжимой.
Посмотрим теперь, под действием каких
сил происходит колебание нашего маятника
после того, как он каким-либо способом
(толчком, отклонением) выведен из
положения равновесия.
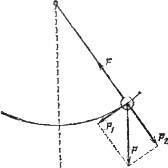
Рис.
15. Возвращающая сила Р1 при отклонении
маятника от положения равновесия
Когда
маятник покоится в положении равновесия,
то сила тяжести, действующая на его
грузик и направленная вертикально
вниз, уравновешивается силой натяжения
нити. В отклоненном положении (рис. 15)
сила тяжести Р действует под углом к
силе натяжения F, направленной вдоль
нити. Разложим силу тяжести на две
составляющие: по направлению нити (Р2)
и перпендикулярно к нему (P1). При
колебаниях маятника сила натяжения
нити F несколько превышает составляющую
P2 — на величину центростремительной
силы, которая заставляет груз двигаться
по дуге. Составляющая же Р1 всегда
направлена в сторону положения
равновесия; она как бы стремится
восстановить это положение. Поэтому
ее часто называют возвращающей силой.
По модулю Р1 тем больше, чем больше
отклонен маятник.
Итак, как только
маятник при своих колебаниях начинает
отклоняться от положения равновесия,
скажем, вправо, появляется сила Р1
замедляющая его движение тем сильнее,
чем дальше он отклонен. В конечном счете
эта сила его остановит и повлечет
обратно к положению равновесия. Однако
по мере приближения к этому положению
сила P1 будет становиться все меньше и
в самом положении равновесия обратится
в нуль. Таким образом, через положение
равновесия маятник проходит по инерции.
Как только он начнет отклоняться влево,
опять появится растущая с увеличением
отклонения сила Р1, но теперь уже
направленная вправо. Движение влево
опять будет замедляться, затем маятник
на мгновение остановится, после чего
начнется ускоренное движение вправо
и т. д.
Колебания
– движения
или процессы, характеризующиеся опре-
деленной
повторяемостью во времени.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Формулы пружинного маятника в физике
Формулы пружинного маятника
Определение и формулы пружинного маятника
Определение
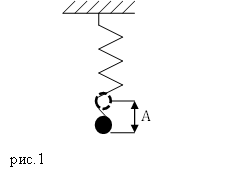
Пружинным маятником называют систему, которая состоит из упругой пружины, к которой прикреплен груз.
Допустим, что масса груза равна $m$, коэффициент упругости пружины $k$. Масса пружины в таком маятнике обычно не учитывается. Если рассматривать вертикальные движения груза (рис.1), то он движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе.
Уравнения колебаний пружинного маятника
Пружинный маятник, совершающий свободные колебания является примером гармонического осциллятора. Допустим, что маятник совершает колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза имеет вид:
[ddot{x}+{omega }^2_0x=0left(1right),]
где ${щu}^2_0=frac{k}{m}$ — циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:
[x=A{cos left({omega }_0t+varphi right)=A{sin left({omega }_0t+{varphi }_1right) } }left(2right),]
где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; ${(omega }_0t+varphi )$ — фаза колебаний; $varphi $ и ${varphi }_1$ — начальные фазы колебаний.
В экспоненциальном виде колебания пружинного маятника можно записать как:
[Re tilde{x}=Releft(Acdot exp left(ileft({omega }_0t+varphi right)right)right)left(3right).]
Формулы периода и частоты колебаний пружинного маятника
Если в упругих колебаниях выполняется закон Гука, то период колебаний пружинного маятника вычисляют при помощи формулы:
[T=2pi sqrt{frac{m}{k}}left(4right).]
Так как частота колебаний ($nu $) — величина обратная к периоду, то:
[nu =frac{1}{T}=frac{1}{2pi }sqrt{frac{k}{m}}left(5right).]
Формулы амплитуды и начальной фазы пружинного маятника
Зная уравнение колебаний пружинного маятника (1 или 2) и начальные условия можно полностью описать гармонические колебания пружинного маятника. Начальные условия определяют амплитуда ($A$) и начальная фаза колебаний ($varphi $).
Амплитуду можно найти как:
[A=sqrt{x^2_0+frac{v^2_0}{{omega }^2_0}}left(6right),]
начальная фаза при этом:
[tg varphi =-frac{v_0}{x_0{omega }_0}left(7right),]
где $v_0$ — скорость груза при $t=0 c$, когда координата груза равна $x_0$.
Энергия колебаний пружинного маятника
При одномерном движении пружинного маятника между двумя точками его движения существует только один путь, следовательно, выполняется условие потенциальности силы (любую силу можно считать потенциальной, если она зависит только от координат). Так как силы, действующие на пружинный маятник потенциальны, то можно говорить о потенциальной энергии.
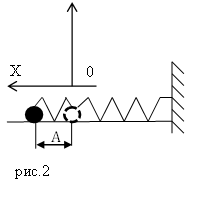
Пусть пружинный маятник совершает колебания в горизонтальной плоскости (рис.2). За ноль потенциальной энергии маятника примем положение его равновесия, где поместим начало координат. Силы трения не учитываем. Используя формулу, связывающую потенциальную силу и потенциальную энергию для одномерного случая:
[E_p=-frac{dF}{dx}(8)]
учитывая, что для пружинного маятника $F=-kx$,
тогда потенциальная энергия ($E_p$) пружинного маятника равна:
[E_p=frac{kx^2}{2}=frac{m{{omega }_0}^2x^2}{2}left(9right).]
Закон сохранения энергии для пружинного маятника запишем как:
[frac{m{dot{x}}^2}{2}+frac{m{{omega }_0}^2x^2}{2}=const left(10right),]
где $dot{x}=v$ — скорость движения груза; $E_k=frac{m{dot{x}}^2}{2}$ — кинетическая энергия маятника.
Из формулы (10) можно сделать следующие выводы:
- Максимальная кинетическая энергия маятника равна его максимальной потенциальной энергии.
- Средняя кинетическая энергия по времени осциллятора равна его средней по времени потенциальной энергии.
Примеры задач с решением
Пример 1
Задание. Маленький шарик, массой $m=0,36$ кг прикреплен к горизонтальной пружине, коэффициент упругости которой равен $k=1600 frac{Н}{м}$. Каково было начальное смещение шарика от положения равновесия ($x_0$), если он при колебаниях проходит его со скоростью $v=1 frac{м}{с}$?
Решение. Сделаем рисунок.
По закону сохранения механической энергии (так как считаем, что сил трения нет), запишем:
[E_{pmax}=E_{kmax }left(1.1right),]
где $E_{pmax}$ — потенциальная энергия шарика при его максимальном смещении от положения равновесия; $E_{kmax }$ — кинетическая энергия шарика, в момент прохождения положения равновесия.
[E_{kmax }=frac{mv^2}{2}left(1.2right).]
Потенциальная энергия равна:
[E_{pmax}=frac{k{x_0}^2}{2}left(1.3right).]
В соответствии с (1.1) приравняем правые части (1.2) и (1.3), имеем:
[frac{mv^2}{2}=frac{k{x_0}^2}{2}left(1.4right).]
Из (1.4) выразим искомую величину:
[x_0=vsqrt{frac{m}{k}}.]
Вычислим начальное (максимальное) смещение груза от положения равновесия:
[x_0=1cdot sqrt{frac{0,36}{1600}}=1,5 cdot {10}^{-3}(м).]
Ответ. $x_0=1,5$ мм
Пример 2
Задание. Пружинный маятник совершает колебания по закону: $x=A{cos left(omega tright), } $где $A$ и $omega $ — постоянные величины. Когда возвращающая сила в первый раз достигает величины $F_0,$ потенциальная энергия груза равна $E_{p0}$.
В какой момент времени это произойдет?
Решение. Возвращающей силой для пружинного маятника является сила упругости, равная:
[F=-kx=-kA{cos left(omega tright)left(2.1right). }]
Потенциальную энергию колебаний груза найдем как:
[E_p=frac{kx^2}{2}=frac{kA^2{{cos }^2 left(omega tright) }}{2}left(2.2right).]
В момент времени, который следует найти $F=F_0$; $E_p=E_{p0}$, значит:
[frac{E_{p0}}{F_0}=-frac{A}{2}{cos left(omega tright) }to t=frac{1}{omega } arc{cos left(-frac{2E_{p0}}{AF_0}right) }.]
Ответ. $t=frac{1}{omega } arc{cos left(-frac{2E_{p0}}{AF_0}right) }$
Читать дальше: формулы равноускоренного прямолинейного движения.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!