Алгоритм Форда-Фалкерсона
Время на прочтение
3 мин
Количество просмотров 41K
Привет, Хабр!
В свободное от учебы время пишу статьи, которых мне не хватало несколько лет назад.
При решении задачи о максимальном потоке я столкнулся с тем, что во всех мне известных источниках было дано формальное описание самих алгоритмов, что очень сильно затрудняло понимание изложенного материала. И в этой статье я попробую на базовом уровне разобрать Алгоритм Форда-Фалкерсона на конкретном примере, чтобы после прочтения данной статьи, вы хотя бы понимали основную суть самого алгоритма.
Постановка задачи
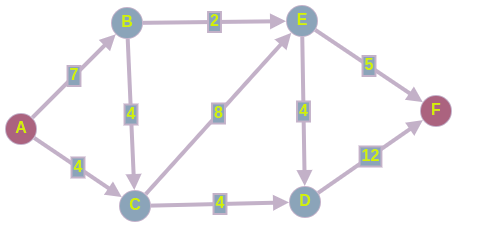
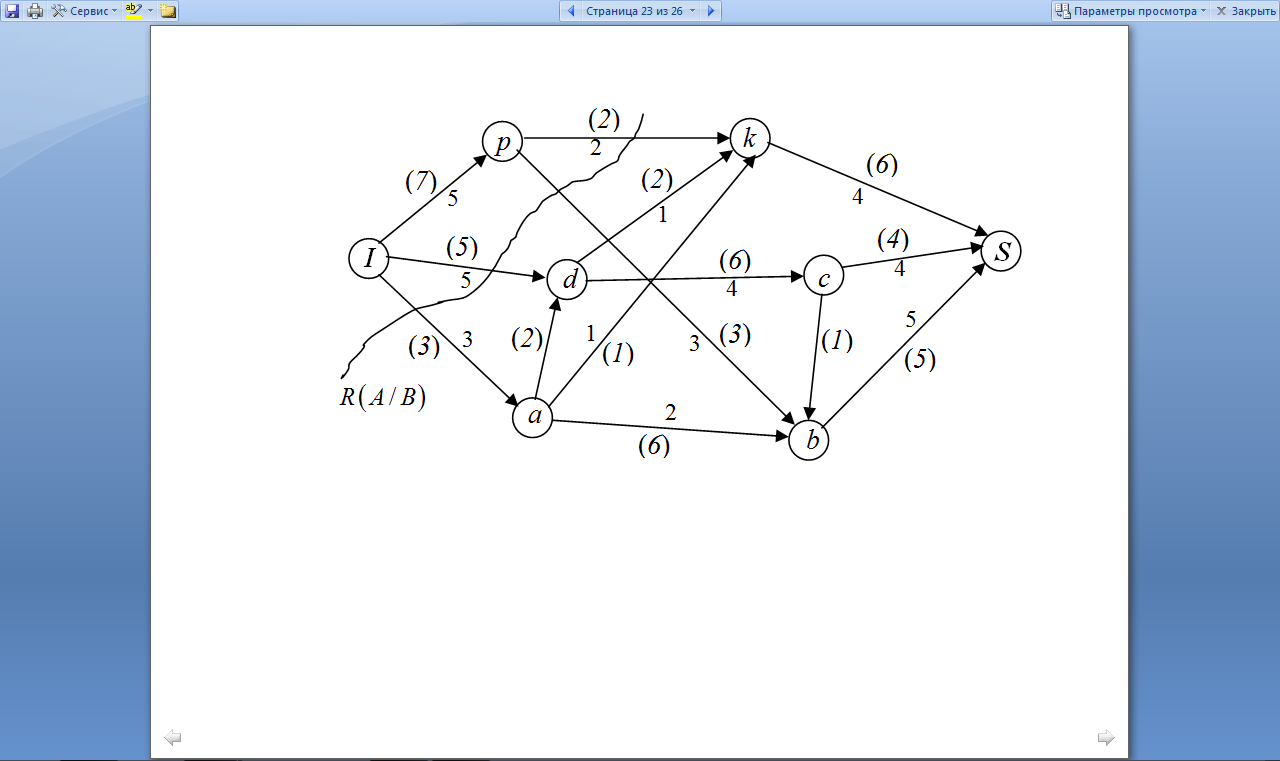
Имеется следующий ориентированный граф, в котором вес ребра обозначает пропускную способность между вершинами. Нужно найти максимальный поток, который можно пропустить из истокав сток
.
Как работает сам алгоритм?
Следует понимать остаточную сеть как тот же граф, который имеется на входе, но в этом случае мы будем производить над ним некоторые операции:
-
Отправлять определенное количество потока из текущей вершины в соседние.
-
Возвращать определенное количество потока из соседних вершин в текущую.
-
В начальный момент времени поток, который мы хотим провести через нашу сеть, должен быть равен нулю. Остаточная сеть совпадает с исходной сетью.
-
Находим любой путь из истока в сток в остаточной сети. Если путь не находим, утверждается, что поток является максимальным.
-
Пускаем через найденный путь поток равный минимальному весу ребра, которое входит в множество рёбер найденного пути.
-
Из веса рёбер на этом пути высчитываем размер потока, который мы пустили.
-
А к весу обратных рёбер (будем считать, что они существуют в остаточной сети и равны 0) прибавляем размер потока. Другими словами, на предыдущем шаге мы отправили некоторое количество потока из текущей вершины в следующую, а теперь при желании можем вернуть это же количество потока обратно в текущую.
-
Возвращаемся обратно к нахождению пути в остаточной сети после модификации.
Разбор конкретного примера
Разобьем одну итерацию проведения потока по выбранному пути на маленькие шаги, чтобы визуально стало понятно, как меняется остаточная сеть после проталкивания очередного потока.
-
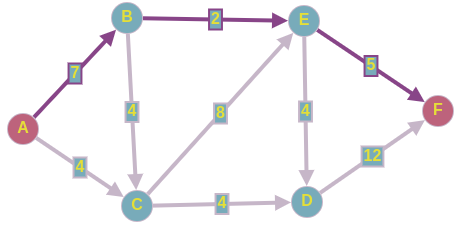
Допустим наш алгоритм нашел следующий путь из вершины
в
нашей остаточной сети, которая на момент начала, совпадает с исходным графом.
-
Сколько потока можем провести по этому пути???
— Больше2 ед.мы никак не сможем пустить, пропускаем наш поток по этим рёбрам из истока в сток.
Получаем следующее:
Рёбра с нулевым весом можно удалять. Таким образом, на первой итерации мы смогли увеличить максимальный поток на 2 ед.
Теперь дело за малым, остается всего лишь итерироваться до тех пор, пока существует путь из в
.
-
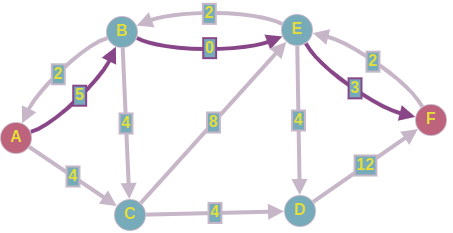
Допустим, на 2-ой итерации мы нашли такой путь в нашей остаточной сети:
Пропускаем 3 ед. потока по этому пути, и перестраиваем остаточную сеть.
Получаем следующее:
-
На 3-ей итерации нашли такой путь в нашей модифицированной остаточной сети:
Пускаем 1 ед. потока по этому пути и перестраиваем нашу остаточную сеть.
Получим следующую картину:
-
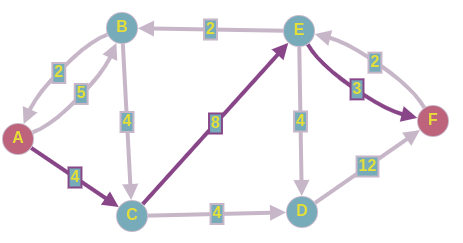
На 4-ой итерации находим следующий путь в остаточной сети:
Пускаем 4 ед. потока по этому пути и перестраиваем нашу остаточную сеть.
Получим следующую картину:
На этом этапе наш алгоритм прекратит выполнение из-за того, что пути из истока в сток не существует. И ответом к поставленной задаче будет служить сумма потоков всех найденных увеличивающихся путей.
Ответ: 10 ед.
Спасибо большое за внимание, надеюсь, был полезен!
Буду рад любым отзывам или поправкам для повышения доступности изложения материала!
Источники
-
Паша и Алгосы
-
Инструмент для работы с графами
Если на сети сформирован некоторый
поток, то для ответа на вопрос: будет ли
он максимальным, используют теорему
Форда-Фалкерсона.
Теорема 12.1. (Теорема Форда-Фалкерсона)
Максимальный поток в сети равен
минимальной пропускной способности по
всем разрезам:
.
Алгоритм нахождения максимального потока на сети.
Этап 1. Насыщение потока.
Шаг 1. Сформировать произвольный
начальный поток.
Шаг 2. Найти оставшиеся возможные
пути из истока
в сток
,
имеющие только ненасыщенные дуги. Если
такой путь найден, то переходим к шагу
3. Если путь не найден, то переходим к
шагу 4.
Шаг 3. Увеличить поток по
найденному пути таким образом, чтобы
одна из дуг стала насыщенной.
Шаг 4. Получившийся поток насыщен.
Этап 2. Пометка вершин сети.
(Перераспределение потока.)
Шаг 5. Вершину
пометить «».
Шаг 6. Пусть
– любая из уже помеченных вершин;
– некоторая непомеченная вершина,
смежная с вершиной
.
Вершину
помечаем
,
если данные вершины соединены ненасыщенной
дугой
,
и помечаем
,
если соединены непустой дугой
.
После пометки вершин возможны два
случая: вершина
оказалась либо помеченной (шаг 7), либо
непомеченной (шаг 8).
Шаг 7. Вершина
оказалась помеченной. Значит, существует
последовательность помеченных вершин
от
к
.
В этой последовательности каждая
последующая вершина помечена буквой
предыдущей вершины. На дугах
последовательности определяем новый
поток. Увеличиваем на
единиц поток на дугах, имеющих направление
от
к
и уменьшаем на
единиц поток на дугах, имеющих обратное
направление. Число
равно наименьшей разнице между пропускной
способностью и потоком дуг, входящих в
последовательность. Поток можно
увеличивать (уменьшать) на прямых
(обратных) дугах настолько, пока одна
из дуг не станет насыщенной (пустой).
Перераспределение увеличивает поток
на
единиц в вершину
.
Далее вновь переходим к пометке вершин
(шаг 5).
Этап 3. Определение максимального
потока.
Шаг 8. Вершина
осталась непомеченной. Пусть
– множество всех помеченных вершин,
– множество всех непомеченных вершин.
Тогда дуги, связывающие два подмножества
вершин
и
,
определяют разрез
.
Таким образом, найден поток
и разрез
,
для которого выполняется условие
.
Пример 2.
На сети из примера 1. сформировать
максимальный по величине поток,
направленный из истока
в сток
.
Выписать ребра, образующие на сети
разрез минимальной пропускной способности.
Решение. Этап 1.
Шаг 1. Воспользуемся тем, что в
примере 12.1. был уже сформирован некоторый
поток на сети.
Шаг 2. Путь
содержит насыщенную дугу
.
Больше нельзя добавить потока по этому
пути. Пути
,
и
содержат насыщенные дуги.
Но путь
имеет две дуги, которые еще ненасыщенные.
Шаг 3. Увеличиваем поток по
найденному пути:
.
Значит, на этом пути поток увеличиваем
на 1 единицу, и тем самым дуга
стала насыщенной.
Шаг 4. Таким образом, получаем
насыщенный поток, поскольку каждый
рассмотренный путь содержит хотя бы
одну насыщенную дугу.
Этап 2.
Выясним, является ли построенный поток
максимальным по величине. Строим сеть,
на которой отметим все вершины и
ненасыщенные дуги. На этой сети разность
пропускных способностей дуги и проходящего
по ней потока обозначим числом в
квадратных скобках.
Шаг 5, 6. Вершину
пометить
.
На шаге 6 предусматривается пометка
вершин, смежных с вершиной I,
соединенных ненасыщенными дугами. Но
на построенной сети таких вершин нет.
В результате вершина S
оказалась непомеченной.
Этап 3. Шаг 8. Так как
вершина S непомеченная,
то поток, сформированный на сети,
получился максимальным.
Строим разрез на сети. Разбиваем множество
вершин на два подмножества: A
и B. Так как только
одна вершина оказалась помеченной, то
множество A состоит
из одной вершины I, а
остальные образуют множество B:
.
Проводим разрез
,
который состоит из дуг
и
:
.
Определяем величину максимального
потока
:
(ед.)
Пример 3.
На заданной сети в скобках указаны
пропускные способности дуг. Требуется
сформировать на сети максимальный
поток, направленный из истока
в сток
,
и выписать ребра, образующие на сети
разрез минимальной пропускной способности.
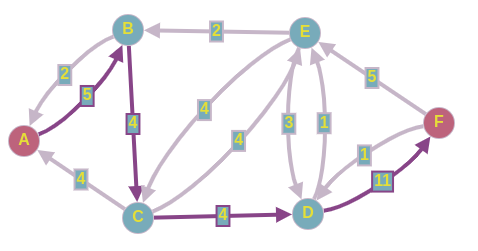
Решение. Этап 1.
Сформируем на сети какой-либо начальный
поток. Рассмотрим путь
.
Поскольку
,
по этому пути пропускаем поток в 2
единицы. На сети значение потока обозначим
числами без скобок. По пути
пропускаем поток в 4 единицы, так как
.
По пути
пропускаем поток в 3 единицы, так как
.
Таким образом, начальный поток имеет
вид:
,
,
.
Объём перевозки 2+4+3=9 ед.
Каждый из рассмотренных путей содержит
насыщенную дугу, поэтому эти пути
насыщенные. На сети есть еще пути, которые
содержат ненасыщенные дуги, а именно:
,
и
.
Для первого пути дополнительно увеличим
поток на 2 единицы, так как
.
Второй и третий пути содержат одну и ту
же дугу
с минимальной для них оставшейся
разностью
.
Поэтому для увеличения потока на 1
единицу выберем, например, путь
.
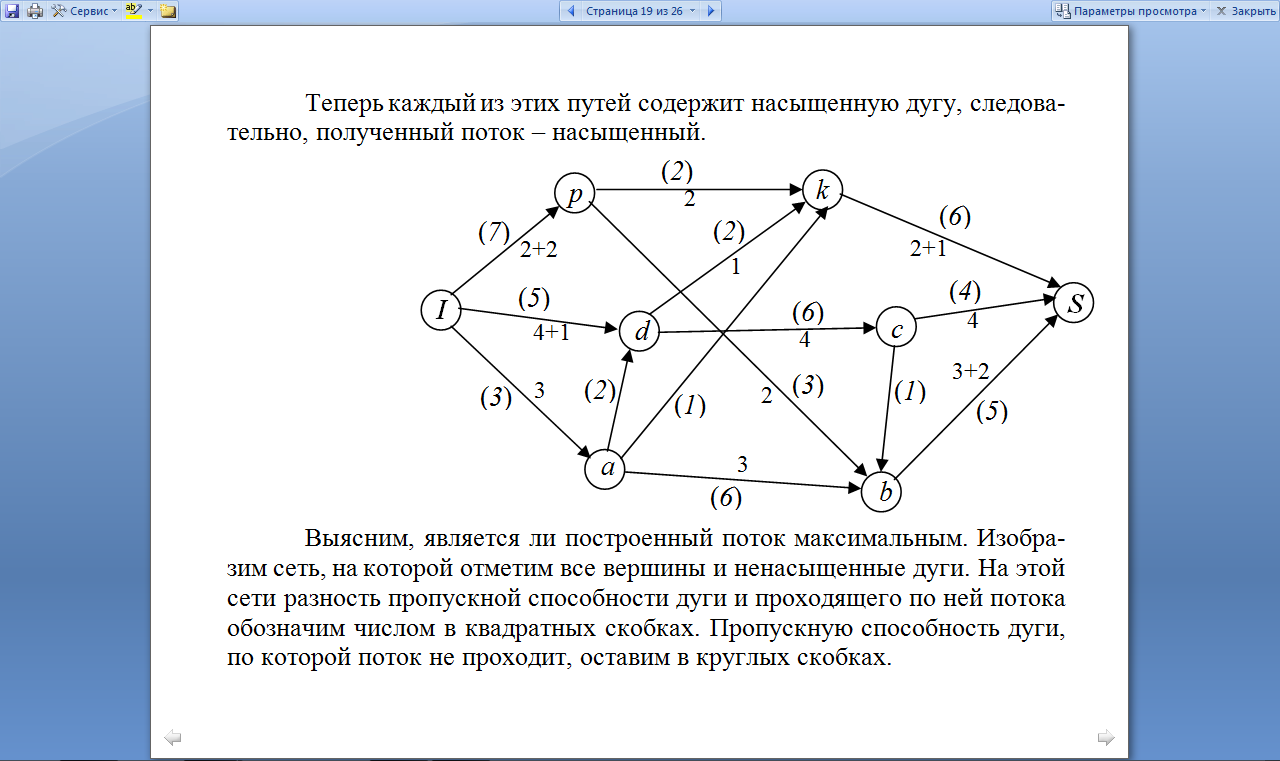
Теперь каждый из этих путей содержит
насыщенную дугу, следовательно, полученный
поток – насыщенный (объём 12 ед.).
Выясним, является ли построенный поток
максимальным. Изобразим сеть, на которой
отметим все вершины и ненасыщенные
дуги. На этой сети разность пропускной
способности дуги и проходящего по ней
потока обозначим числом в квадратных
скобках. Пропускную способность дуги,
по которой поток не проходит, оставим
в круглых скобках.
Видим, что на сети исток I
и сток S связаны дугами.
Значит, можно добавить какое-то количество
потока по ненасыщенным дугам, при этом
придется перераспределить поток.
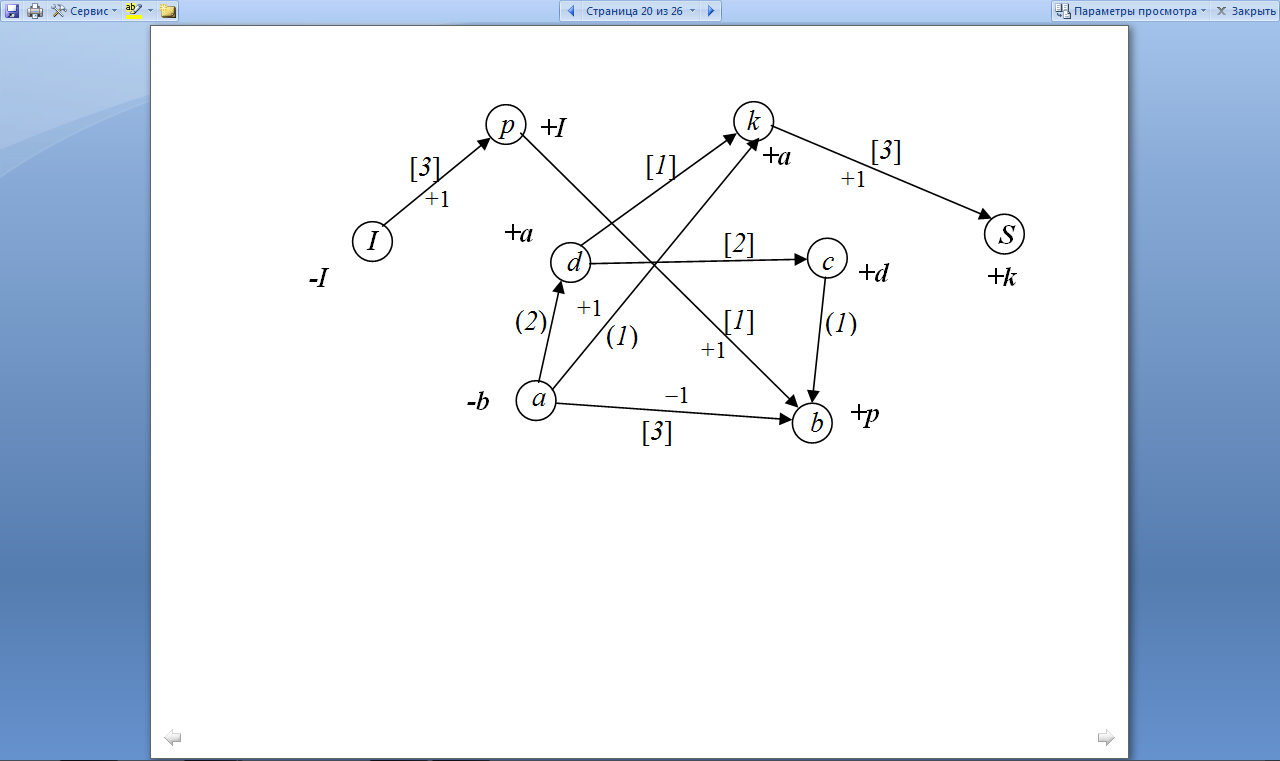
Этап 2.
На построенной
сети помечаем вершины. Вершину
пометим
.
Смежную ей вершину
помечаем
,
так как эти вершины соединяет ненасыщенная
дуга
.
Вершину
помечаем
,
так как вершины
и
соединяет ненасыщенная дуга
.
Вершину
помечаем
,
так как вершины
и
соединяет непустая дуга
.
Вершины
и
помечаем
,
так как они соединены с вершиной
ненасыщенными дугами
и
.
Вершина
смежная вершине
,
и эти вершины соединены ненасыщенной
дугой
,
поэтому вершину
помечаем
.
Вершина
смежная вершине
,
и эти вершины соединены ненасыщенной
дугой
,
поэтому вершину
помечаем
.
Вершина
оказалась помеченной. Значит, существует
последовательность помеченных вершин
от
к
:
.
В этой последовательности каждая
последующая вершина помечена буквой
предыдущей вершины. Перераспределим
поток на этом пути.
Определим число
:
=
min{[3=7-4], [1=3-2], 3, 1, [3=6-3]}=
.
Увеличиваем на 1 единицу поток на дугах,
имеющих направление от
к
:
,
,
,
.
Уменьшаем на 1 единицу поток на дугах,
имеющих обратное направление:
.
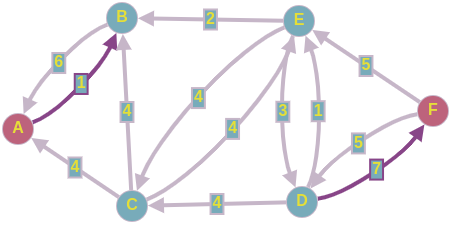
Получаем следующую сеть с новым
сформированным потоком, который изображен
на рисунке.
Проверим, будет ли построенный поток
максимальным. Изобразим сеть, на которой
отметим все вершины и ненасыщенные
дуги, как сделали выше.
Вновь помечаем вершины. Вершину
пометим
.
Смежную ей вершину
помечаем
,
так как эти вершины соединяет ненасыщенная
дуга
.
Все остальные вершины, в том числе и
вершина
,
остаются непомеченными. Значит, поток
на сети максимальный.
Этап 3.
Как видно на
последней сети исток
и сток
не связны дугами. Значит, поток,
изображенный на предпоследней сети,
является максимальным.
Строим разрез на
сети. Разбиваем множество вершин на два
подмножества: A
и B.
Помеченные вершины образуют множество
,
непомеченные – множество
.
Проводим
разрез
,
который состоит из дуг
,
,
,
:
.
Определяем величину
максимального потока
:
(ед.)
Соседние файлы в папке Лекции_2
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
The Ford-Fulkerson algorithm is a widely used algorithm to solve the maximum flow problem in a flow network. The maximum flow problem involves determining the maximum amount of flow that can be sent from a source vertex to a sink vertex in a directed weighted graph, subject to capacity constraints on the edges.
The algorithm works by iteratively finding an augmenting path, which is a path from the source to the sink in the residual graph, i.e., the graph obtained by subtracting the current flow from the capacity of each edge. The algorithm then increases the flow along this path by the maximum possible amount, which is the minimum capacity of the edges along the path.
Problem:
Given a graph which represents a flow network where every edge has a capacity. Also, given two vertices source ‘s’ and sink ‘t’ in the graph, find the maximum possible flow from s to t with the following constraints:
- Flow on an edge doesn’t exceed the given capacity of the edge.
- Incoming flow is equal to outgoing flow for every vertex except s and t.
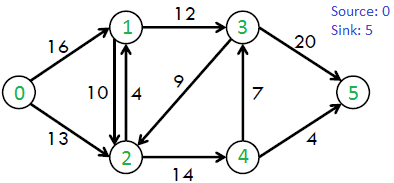
For example, consider the following graph from the CLRS book.
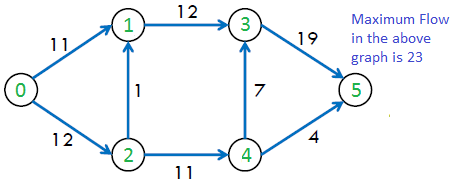
The maximum possible flow in the above graph is 23.
Prerequisite : Max Flow Problem Introduction
Ford-Fulkerson Algorithm
The following is simple idea of Ford-Fulkerson algorithm:
- Start with initial flow as 0.
- While there exists an augmenting path from the source to the sink:
- Find an augmenting path using any path-finding algorithm, such as breadth-first search or depth-first search.
- Determine the amount of flow that can be sent along the augmenting path, which is the minimum residual capacity along the edges of the path.
- Increase the flow along the augmenting path by the determined amount.
- Return the maximum flow.
Time Complexity: Time complexity of the above algorithm is O(max_flow * E). We run a loop while there is an augmenting path. In worst case, we may add 1 unit flow in every iteration. Therefore the time complexity becomes O(max_flow * E).
How to implement the above simple algorithm?
Let us first define the concept of Residual Graph which is needed for understanding the implementation.
Residual Graph of a flow network is a graph which indicates additional possible flow. If there is a path from source to sink in residual graph, then it is possible to add flow. Every edge of a residual graph has a value called residual capacity which is equal to original capacity of the edge minus current flow. Residual capacity is basically the current capacity of the edge.
Let us now talk about implementation details. Residual capacity is 0 if there is no edge between two vertices of residual graph. We can initialize the residual graph as original graph as there is no initial flow and initially residual capacity is equal to original capacity. To find an augmenting path, we can either do a BFS or DFS of the residual graph. We have used BFS in below implementation. Using BFS, we can find out if there is a path from source to sink. BFS also builds parent[] array. Using the parent[] array, we traverse through the found path and find possible flow through this path by finding minimum residual capacity along the path. We later add the found path flow to overall flow.
The important thing is, we need to update residual capacities in the residual graph. We subtract path flow from all edges along the path and we add path flow along the reverse edges We need to add path flow along reverse edges because may later need to send flow in reverse direction (See following link for example).
https://www.geeksforgeeks.org/max-flow-problem-introduction/
Below is the implementation of Ford-Fulkerson algorithm. To keep things simple, graph is represented as a 2D matrix.
C++
#include <iostream>
#include <limits.h>
#include <queue>
#include <string.h>
using namespace std;
#define V 6
bool bfs(int rGraph[V][V], int s, int t, int parent[])
{
bool visited[V];
memset(visited, 0, sizeof(visited));
queue<int> q;
q.push(s);
visited[s] = true;
parent[s] = -1;
while (!q.empty()) {
int u = q.front();
q.pop();
for (int v = 0; v < V; v++) {
if (visited[v] == false && rGraph[u][v] > 0) {
if (v == t) {
parent[v] = u;
return true;
}
q.push(v);
parent[v] = u;
visited[v] = true;
}
}
}
return false;
}
int fordFulkerson(int graph[V][V], int s, int t)
{
int u, v;
int rGraph[V]
[V];
for (u = 0; u < V; u++)
for (v = 0; v < V; v++)
rGraph[u][v] = graph[u][v];
int parent[V];
int max_flow = 0;
while (bfs(rGraph, s, t, parent)) {
int path_flow = INT_MAX;
for (v = t; v != s; v = parent[v]) {
u = parent[v];
path_flow = min(path_flow, rGraph[u][v]);
}
for (v = t; v != s; v = parent[v]) {
u = parent[v];
rGraph[u][v] -= path_flow;
rGraph[v][u] += path_flow;
}
max_flow += path_flow;
}
return max_flow;
}
int main()
{
int graph[V][V]
= { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 },
{ 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 },
{ 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 } };
cout << "The maximum possible flow is "
<< fordFulkerson(graph, 0, 5);
return 0;
}
Java
import java.io.*;
import java.lang.*;
import java.util.*;
import java.util.LinkedList;
class MaxFlow {
static final int V = 6;
boolean bfs(int rGraph[][], int s, int t, int parent[])
{
boolean visited[] = new boolean[V];
for (int i = 0; i < V; ++i)
visited[i] = false;
LinkedList<Integer> queue
= new LinkedList<Integer>();
queue.add(s);
visited[s] = true;
parent[s] = -1;
while (queue.size() != 0) {
int u = queue.poll();
for (int v = 0; v < V; v++) {
if (visited[v] == false
&& rGraph[u][v] > 0) {
if (v == t) {
parent[v] = u;
return true;
}
queue.add(v);
parent[v] = u;
visited[v] = true;
}
}
}
return false;
}
int fordFulkerson(int graph[][], int s, int t)
{
int u, v;
int rGraph[][] = new int[V][V];
for (u = 0; u < V; u++)
for (v = 0; v < V; v++)
rGraph[u][v] = graph[u][v];
int parent[] = new int[V];
int max_flow = 0;
while (bfs(rGraph, s, t, parent)) {
int path_flow = Integer.MAX_VALUE;
for (v = t; v != s; v = parent[v]) {
u = parent[v];
path_flow
= Math.min(path_flow, rGraph[u][v]);
}
for (v = t; v != s; v = parent[v]) {
u = parent[v];
rGraph[u][v] -= path_flow;
rGraph[v][u] += path_flow;
}
max_flow += path_flow;
}
return max_flow;
}
public static void main(String[] args)
throws java.lang.Exception
{
int graph[][] = new int[][] {
{ 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 },
{ 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 },
{ 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 }
};
MaxFlow m = new MaxFlow();
System.out.println("The maximum possible flow is "
+ m.fordFulkerson(graph, 0, 5));
}
}
Python
from collections import defaultdict
class Graph:
def __init__(self, graph):
self.graph = graph
self. ROW = len(graph)
def BFS(self, s, t, parent):
visited = [False]*(self.ROW)
queue = []
queue.append(s)
visited[s] = True
while queue:
u = queue.pop(0)
for ind, val in enumerate(self.graph[u]):
if visited[ind] == False and val > 0:
queue.append(ind)
visited[ind] = True
parent[ind] = u
if ind == t:
return True
return False
def FordFulkerson(self, source, sink):
parent = [-1]*(self.ROW)
max_flow = 0
while self.BFS(source, sink, parent) :
path_flow = float("Inf")
s = sink
while(s != source):
path_flow = min (path_flow, self.graph[parent[s]][s])
s = parent[s]
max_flow += path_flow
v = sink
while(v != source):
u = parent[v]
self.graph[u][v] -= path_flow
self.graph[v][u] += path_flow
v = parent[v]
return max_flow
graph = [[0, 16, 13, 0, 0, 0],
[0, 0, 10, 12, 0, 0],
[0, 4, 0, 0, 14, 0],
[0, 0, 9, 0, 0, 20],
[0, 0, 0, 7, 0, 4],
[0, 0, 0, 0, 0, 0]]
g = Graph(graph)
source = 0; sink = 5
print ("The maximum possible flow is %d " % g.FordFulkerson(source, sink))
C#
using System;
using System.Collections.Generic;
public class MaxFlow {
static readonly int V = 6;
bool bfs(int[, ] rGraph, int s, int t, int[] parent)
{
bool[] visited = new bool[V];
for (int i = 0; i < V; ++i)
visited[i] = false;
List<int> queue = new List<int>();
queue.Add(s);
visited[s] = true;
parent[s] = -1;
while (queue.Count != 0) {
int u = queue[0];
queue.RemoveAt(0);
for (int v = 0; v < V; v++) {
if (visited[v] == false
&& rGraph[u, v] > 0) {
if (v == t) {
parent[v] = u;
return true;
}
queue.Add(v);
parent[v] = u;
visited[v] = true;
}
}
}
return false;
}
int fordFulkerson(int[, ] graph, int s, int t)
{
int u, v;
int[, ] rGraph = new int[V, V];
for (u = 0; u < V; u++)
for (v = 0; v < V; v++)
rGraph[u, v] = graph[u, v];
int[] parent = new int[V];
int max_flow = 0;
while (bfs(rGraph, s, t, parent)) {
int path_flow = int.MaxValue;
for (v = t; v != s; v = parent[v]) {
u = parent[v];
path_flow
= Math.Min(path_flow, rGraph[u, v]);
}
for (v = t; v != s; v = parent[v]) {
u = parent[v];
rGraph[u, v] -= path_flow;
rGraph[v, u] += path_flow;
}
max_flow += path_flow;
}
return max_flow;
}
public static void Main()
{
int[, ] graph = new int[, ] {
{ 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 },
{ 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 },
{ 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 }
};
MaxFlow m = new MaxFlow();
Console.WriteLine("The maximum possible flow is "
+ m.fordFulkerson(graph, 0, 5));
}
}
Javascript
<script>
let V = 6;
function bfs(rGraph, s, t, parent)
{
let visited = new Array(V);
for(let i = 0; i < V; ++i)
visited[i] = false;
let queue = [];
queue.push(s);
visited[s] = true;
parent[s] = -1;
while (queue.length != 0)
{
let u = queue.shift();
for(let v = 0; v < V; v++)
{
if (visited[v] == false &&
rGraph[u][v] > 0)
{
if (v == t)
{
parent[v] = u;
return true;
}
queue.push(v);
parent[v] = u;
visited[v] = true;
}
}
}
return false;
}
function fordFulkerson(graph, s, t)
{
let u, v;
let rGraph = new Array(V);
for(u = 0; u < V; u++)
{
rGraph[u] = new Array(V);
for(v = 0; v < V; v++)
rGraph[u][v] = graph[u][v];
}
let parent = new Array(V);
let max_flow = 0;
while (bfs(rGraph, s, t, parent))
{
let path_flow = Number.MAX_VALUE;
for(v = t; v != s; v = parent[v])
{
u = parent[v];
path_flow = Math.min(path_flow,
rGraph[u][v]);
}
for(v = t; v != s; v = parent[v])
{
u = parent[v];
rGraph[u][v] -= path_flow;
rGraph[v][u] += path_flow;
}
max_flow += path_flow;
}
return max_flow;
}
let graph = [ [ 0, 16, 13, 0, 0, 0 ],
[ 0, 0, 10, 12, 0, 0 ],
[ 0, 4, 0, 0, 14, 0 ],
[ 0, 0, 9, 0, 0, 20 ],
[ 0, 0, 0, 7, 0, 4 ],
[ 0, 0, 0, 0, 0, 0 ] ];
document.write("The maximum possible flow is " +
fordFulkerson(graph, 0, 5));
</script>
Output
The maximum possible flow is 23
Time Complexity : O(|V| * E^2) ,where E is the number of edges and V is the number of vertices.
Space Complexity :O(V) , as we created queue.
The above implementation of Ford Fulkerson Algorithm is called Edmonds-Karp Algorithm. The idea of Edmonds-Karp is to use BFS in Ford Fulkerson implementation as BFS always picks a path with minimum number of edges. When BFS is used, the worst case time complexity can be reduced to O(VE2). The above implementation uses adjacency matrix representation though where BFS takes O(V2) time, the time complexity of the above implementation is O(EV3) (Refer CLRS book for proof of time complexity)
This is an important problem as it arises in many practical situations. Examples include, maximizing the transportation with given traffic limits, maximizing packet flow in computer networks.
Dinc’s Algorithm for Max-Flow.
Exercise:
Modify the above implementation so that it that runs in O(VE2) time.
Last Updated :
09 Apr, 2023
Like Article
Save Article
Сеть состоит из ориентированного графа G=(V={1,…,n}, A={(i,j)},i,j∈V)G = (V = {1, dots, n},~A = {(i,j)}, i,j in V) с двумя выделенными вершинами ss — источник и tt — сток. Каждая дуга обладает пропускной способностью uiju_{ij}. (i,j)∈A:uij>0(i,j) in A :u_{ij} gt 0
Поток: fij,(i,j)∈Af_{ij}, (i,j) in A и его свойства:
- fij≥0f_{ij} ge 0
- fij≤uij ∀(i,j)∈Af_{ij} le u_{ij} ~ forall (i,j) in A
- ∑j:(j,i0)∈Afji0−∑j:(i0,j)∈Afi0j=0, ∀i0∈V,i0≠s,tsumlimits_{j:(j,i_0) in A}f_{ji_0} — sumlimits_{j:(i_0,j) in A}f_{i_0j} = 0, ~forall i_0 in V, i_0neq s,t — сохранение потока
∑(s,j)∈Afsj−∑(j,s)∈Afjs=M(f)sumlimits_{(s,j) in A}f_{sj} — sumlimits_{(j,s) in A}f_{js} = M(f) — величина потока (Суммарный поток выходящий из истока минус суммарный поток входящий в исток)
Задача о максимальном потоке
Необходимо найти поток fi,j′f_{i,j}’, такой что M(f′)=maxfijM(f) M(f’) = maxlimits_{f_{ij}}M(f), то есть величина потока максимальна.
Пример сети с построенным максимальным потоком
Алгоритм Форда-Фалкерсона
Пусть πpi — это путь
по прямой дуге: δij=uij−fij>0delta_{ij} = u_{ij} — f_{ij} gt 0 fij=fij+δ(π)f_{ij} = f_{ij} + delta(pi)
По обратной дуге: δkj=fkj>0delta_{kj} = f_{kj} gt 0 fkj=fkj−δ(π)f_{kj} = f_{kj} — delta(pi)
δ(π)=min(i,j)∈πδi,jdelta(pi) = minlimits_{(i,j) in pi}delta_{i,j}
Увеличивающий путь — это путь πpi (последовательность дуг из истока в сток), для которого величина δ(π)>0delta(pi) gt 0, которая определяется следующим образом: для каждой дуги (i,j)(i,j) входящей в путь πpi вычисляется величина δij={uij−fij>0,прямая дугаfji>0,обратная дугаdelta_{ij} = left{ begin{matrix} u_{ij} — f_{ij} > 0 & ,прямая ~ дуга\ f_{ji} > 0 & ,обратная ~ дуга end{matrix} right. и δ(π)=min(i,j)∈πδijdelta(pi) = minlimits_{(i,j) in pi} delta_{ij}.
неформально это путь из истока в сток, вдоль которого можно увеличить поток на некоторую величину.
Про обратную дугу — можно забирать поток назад
Алгоритм
- fijf_{ij} — начальный поток (fij=0f_{ij}=0)
- Увеличить путь πpi на δ(π)delta(pi) [итеративно]
- Если нет увеличивающего пути — остановка. [нашли максимальный поток]
Пусть uij∈Nu_{ij} in N — закончится, так как как минимум на 1 каждый раз увеличивается, поэтому алгоритм не зациклится.
Алгоритм Карзанова
G(f)=(V,A(f))G(f) = (V, A(f)) — остаточная сеть
A(f)A(f):
- (i,j)∈A,fij<uij(i,j) in A, f_{ij} lt u_{ij} (i,j)→A(f)(i,j) to A(f) vij=uij−fijv_{ij} = u_{ij} — f_{ij}
- (i,j)∈A,fij>0(i,j) in A, f_{ij} gt 0 (j,i)→A(f)(j,i) to A(f) vji=fijv_{ji} = f_{ij}
Слоистая сеть G∗(f)=(V∗,A∗(f))G^*(f)= (V^*, A^*(f)) включает в себя множество всех кратчайших путей (по числу дуг) из источника в сток по слоям:
Нулевой слой V0={s}V_0 = {s}
Первый слой V1={i:(s,i)∈A(f)}V_1 = { i : (s,i) in A(f)}
Второй слой V2={j:(j,i)∈A(f),i∈V1,j∉V1∪V0V_2 = {j: (j,i) in A(f), i in V_1, j notin V_1 cup V_0 и так далее, на последнем слое может быть не только сток, в промежуточных может быть тупиковые, поэтому надо убирать висячие узлы как только дошли до стока и инцидентные им дуги.
Тупиковый поток — поток, относительно которого нет прямого увеличивающего пути (содержит только прямые дуги) из источника в сток.
Алгоритм
- Начальный нулевой поток в G
- Построить G(f) — остаточную сеть
- Если нет прямого пути из s в t, то стоп ff — максимальный поток
- Построить G∗(f)G^*(f) — слоистую сеть
- Построить тупиковый поток в G∗(f)G^*(f) — gijg_{ij}
- Изменить потоки: (i,j)∈A∗(f)(i,j) in A^*(f) — прямая fij=fij+gijf_{ij} = f_{ij} + g_{ij} , для обратных дуг (i,j)∈A∗(f)(i,j) in A^*(f) fij=fij−gijf_{ij} = f_{ij} — g_{ij}
- Перейти на 2 шаг
Разрез: , V=Vc∪V‾cV = V_c cup overline{V}_c, Vc∩V‾c=∅V_c cap overline{V}_c = empty, s∈Vcs in V_c, t∈V‾ct in overline{V}_c
u(Vc,V‾c)=∑i∈Vc,j∈V‾cuiju(V_c, overline{V}_c) = sumlimits_{i in V_c, j in overline{V}_c} u_{ij} — пропускная способность разреза
Разрез с минимальной пропускной способностью называется минимальным разрезом.
Теорема о максимальном потоке и минимальном разрезе. Величина максимального потока в сети равна величине минимального разреза в сети.
Задача составления допустимого расписания с прерываниями для многопроцессорной системы:
Пусть имеется mm — процессоров. Задано N={1,…,n}N = {1,…,n } — число работ и для каждой работы заданы tit_i — длительность , (bi,fi](b_i, f_i] — директивный интервал ii-ой работы (bi<fib_i lt f_i и ti≤fi−bit_i le f_i — b_i). Во время выполнения работ допускаются прерывания и переключения. Требуется ответить на вопрос существует ли допустимое расписание и как его построить.
Сведение задачи к задачи поиска максимального потока в сети:
Обозначим y0<y1<y2<…ypy_0 lt y_1 lt y_2 lt … y_p — все упорядоченные значения bi,fib_i, f_i
Составим отрезки Ij=(yj−1,yj],j=1,p‾I_j=(y_{j-1}, y_j], j=overline{1,p}
Сеть будет состоять из узлов ss, tt , IjI_j, wiw_i
Δj=yj−yj−1Delta_j = y_j — y_{j-1} — длительность интервала IjI_j
Добавляем дуги (s,Ij)(s, I_j) с пропускной способностью mΔjmDelta_j
Добавляем дуги (Ij,wi)(I_j,w_i), если Ij⊂(bi,fi]I_j sub (b_i, f_i] пропускной способностью ΔjDelta_j
Добавляем дуги (wi,s)(w_i, s) пропускной способностью tit_i
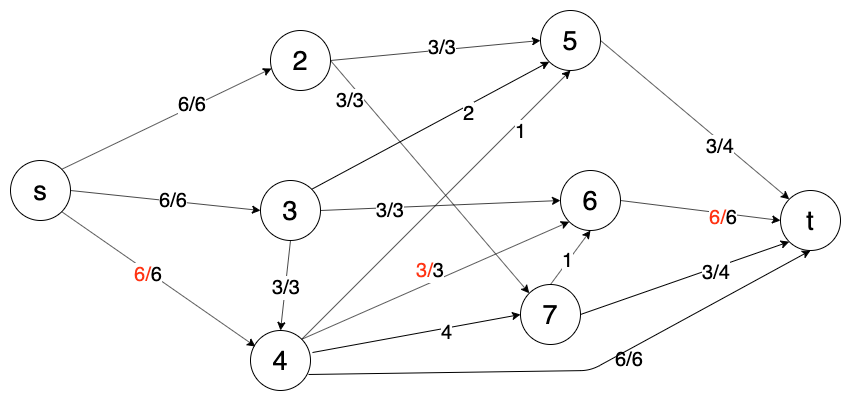
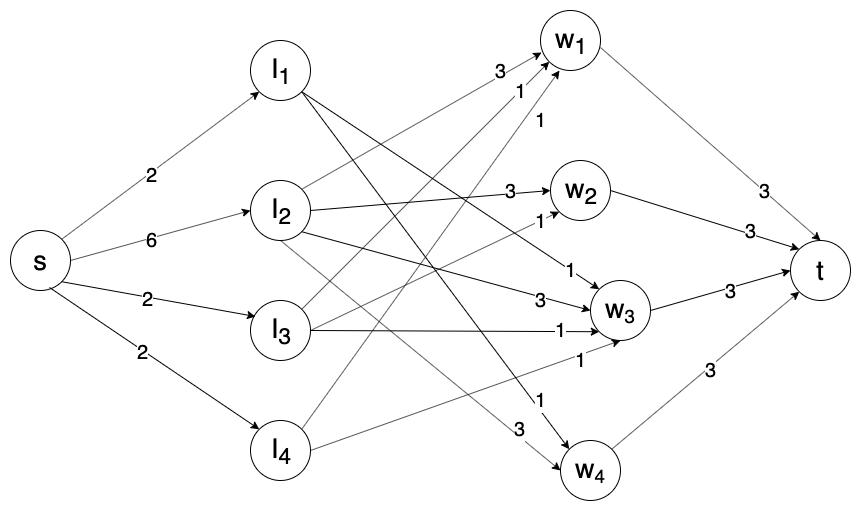
Пример сети для задачи при m=2m=2
Раб.bifiti1163215330634043begin{matrix}Раб. & b_i & f_i & t_i \
1 & 1 & 6 &3 \
2 & 1 & 5 &3 \
3 & 0 & 6 & 3\
4 & 0 & 4 & 3\
end{matrix}
I1=[0,1],I2=[1,4],I3=[4,5],I4=[5,6]I_1 = [0,1], I_2 = [1,4], I_3 = [4,5], I_4=[5,6]
Теорема. Допустимое расписание существует, тогда и только тогда, когда Максимальный поток в G насыщает все выходные дуги.
Как можно искать увеличивающий путь
Есть состояния у каждого узла : Н,ПН,ПП{Н,ПН,ПП} — непомеченный, помеченный непросмотренный, помеченный просмотренный
Метим следующие для рассмотрения вершины по которым теоретически можно получить увеличивающий путь
- S [-], S — ПНПН
- Если нет ПНПН, то останавливаемся (нет увеличивающих путей)
- i−ПНi — ПН, ∀j−Н,(i,j)∈A,fij<uijforall j — Н, (i,j) in A, f_{ij} lt u_{ij} — метим [i][i], j−ПНj — ПН
i−ПНi — ПН, ∀j−Н,(i,j)∈A,fij>0forall j — Н, (i,j) in A, f_{ij} gt 0 — метим [i][i], j−ПНj — ПН
далее i−ППi — ПП
- Если t−Нt — Н, то переходим на шаг 2
Если t−Пt — П — построить увеличивающий путь от истока к стоку
Как строить тупиковый поток
i∈V∗(f),i≠s,ti in V^*(f), ineq s,t
a(i)=min{∑(j,i)∈A∗(f)vji,∑(j,i)∈A∗(f)vij}a(i)= min{ sumlimits_{(j,i) in A^*(f)}v_{ji}, sumlimits_{(j,i) in A^*(f)}v_{ij}} — пропускная способность узла
a(s)=∑(s,j)∈A∗(f)vsja(s) = sumlimits_{(s,j) in A^*(f)}v_{sj}
a(s)=∑(j,s)∈A∗(f)vjta(s) = sumlimits_{(j,s) in A^*(f)}v_{jt}
i0i_0 — самый слабый узел a(i0)=mini∈V∗(f)a(i)a(i_0) = minlimits_{i in V^*(f)}a(i)
Выбираем его
ai0a_{i_0} — будем проталкивать поток от i0i_0 до стока и до истока (можно по разным дугам, но разрешена только одна недонасыщенная)
После этого вершина i0i_0 исключается из сети и все полностью насыщенные дуги (если дуги были не полностью насыщены и остались в сети то им изменяем пропускную способность)
и так сначала, пока не останется тупиковый поток